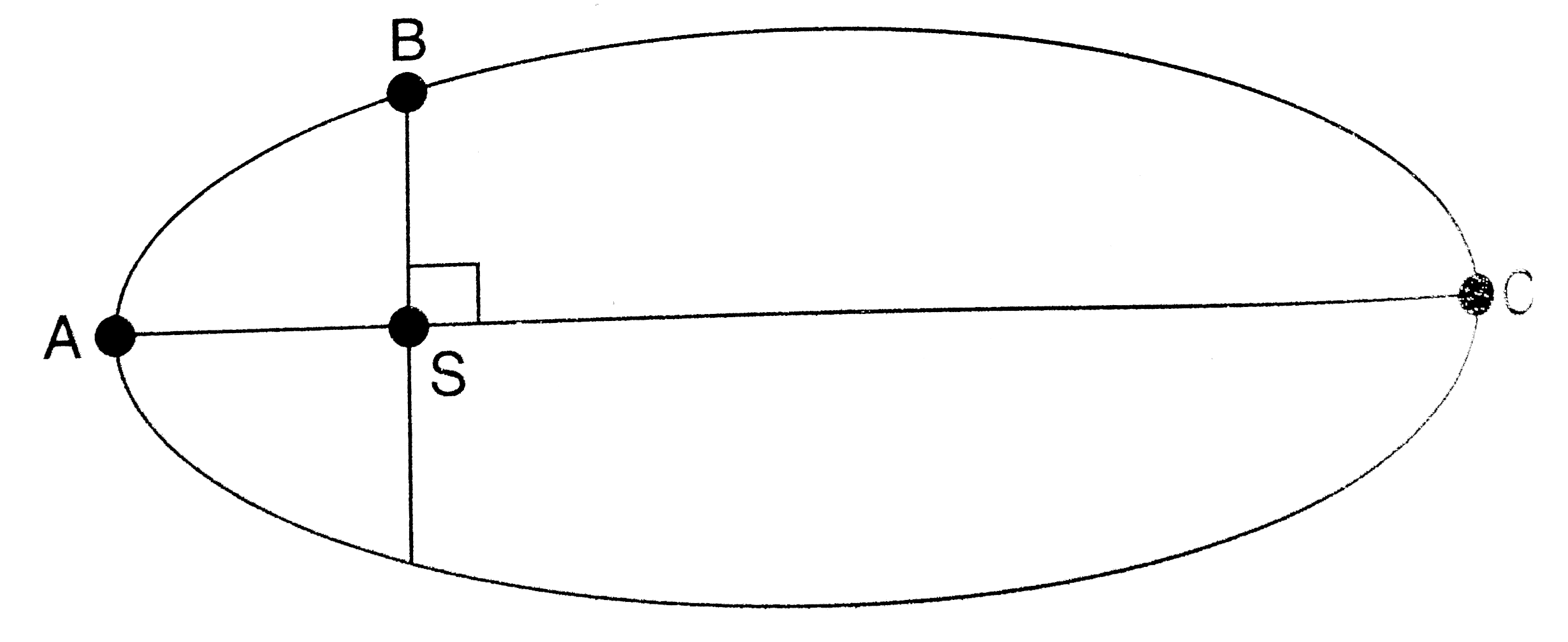
Kepler'S Laws Of Planetary Motion And Newton'S Law Of Gravitation from A2Z PHYSICS (HINGLISH) GRAVITATION for Class 11
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| A2Z PHYSICS (HINGLISH) | Kepler'S Laws Of Planetary Motion And Newton'S Law Of Gravitation |
| Medium | English |
| Academic Year | 2023-2024 |
Question 27
Imagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force of attraction between the planet and the star is proportional to R−5/2, then
(a) T2 is proportional to R2
(b) T2 is proportional to R7/2
(c) T2 is proportional to R3/3
(d) T2 is proportional to R3.75.View SolutionQuestion 114
In the following four periods
(i) Time of revolution of a satellite just above the earth's surface (Tst)
(ii) Period of oscillation of mass inside the tunnel bored along the diameter of the earth (Tma)
(iii) Period of simple pendulam having a length equal to the earth's raduis in a unifrom field of 9.8N/kg(Tsp)
(iv) Period of an infinite length simple pendulam in the earth's real gravitational field (Tis)View SolutionQuestion 116
The little prince ( the main charcter of the novel written by Antione de saint-Exupery) lives on the spherical planet named B−612, the density of which is 5200kg/m3. The little prince noticed that if he quickens his pace, he feels himself ligheter. when he reached the speed of 2m/s he became weightless, and began to orbit about the planet as a satellite. what is escape speed on the surface of planet?View SolutionQuestion 117
A satellite moves estwards very near the surface of the Earth in equitorial plane with speed (v0). Another satellite moves at the same height with the same speed in the equatorial plane but westwards. If R =radius of the Earth and ω be its angular speed of the Earth about its own axis. Then find the approximate difference in the two time period as observed on the earth.View SolutionQuestion 118
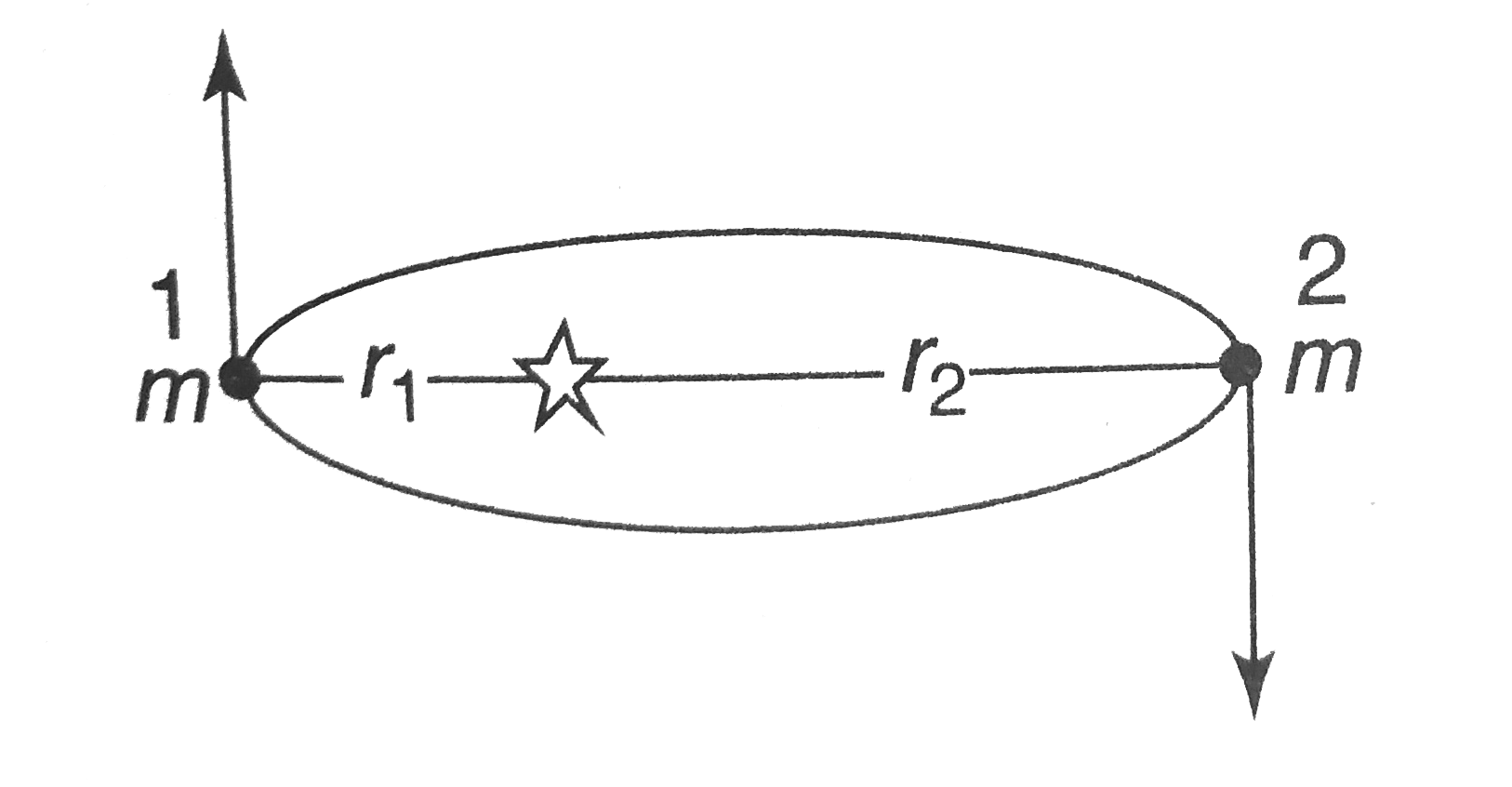
Two satellites S1andS2 revole round a planet in coplanar circular orbits in the same sanse. Their periods of revolution are 1 hour and 8 hour respectively. The radius of the orbit of S1is104km, When S2isclosest→S1 find
(i) the speed of S2relative→S_1<br>(ii)theanga––rspeedofS_2asactuallyobservedbyan∗ronautisS_1.View SolutionQuestion 141
If a particles of mass m is projected with minimum velocity form the surface of a star with kinetic energy K1GMma and potential energy at surface of the star K2GMma towards the star of same mass m and radius a (K1 and K2 are constant) to reach the other star. Find the distance between the centre of the two stars: View SolutionQuestion 145
A projectile rises upto a maximum height of R/(1−K2) where K is a constant and R is the radius of earth. If the velocity of projectile with which it should be fired upwards form the surface of the earth to reach this height is equal to the product of a coeffiecient and escape velocity then this coeffiecient is equal to:View SolutionQuestion 148
Binary stars of comparable masses rotates under the influence of each other's gravity at a distance [2Gω2]1/3 where ω is the angular velocity of each of the system. If difference between the masses of two stars is 6 units. Find the ratio of the masses of smaller to bigger star.
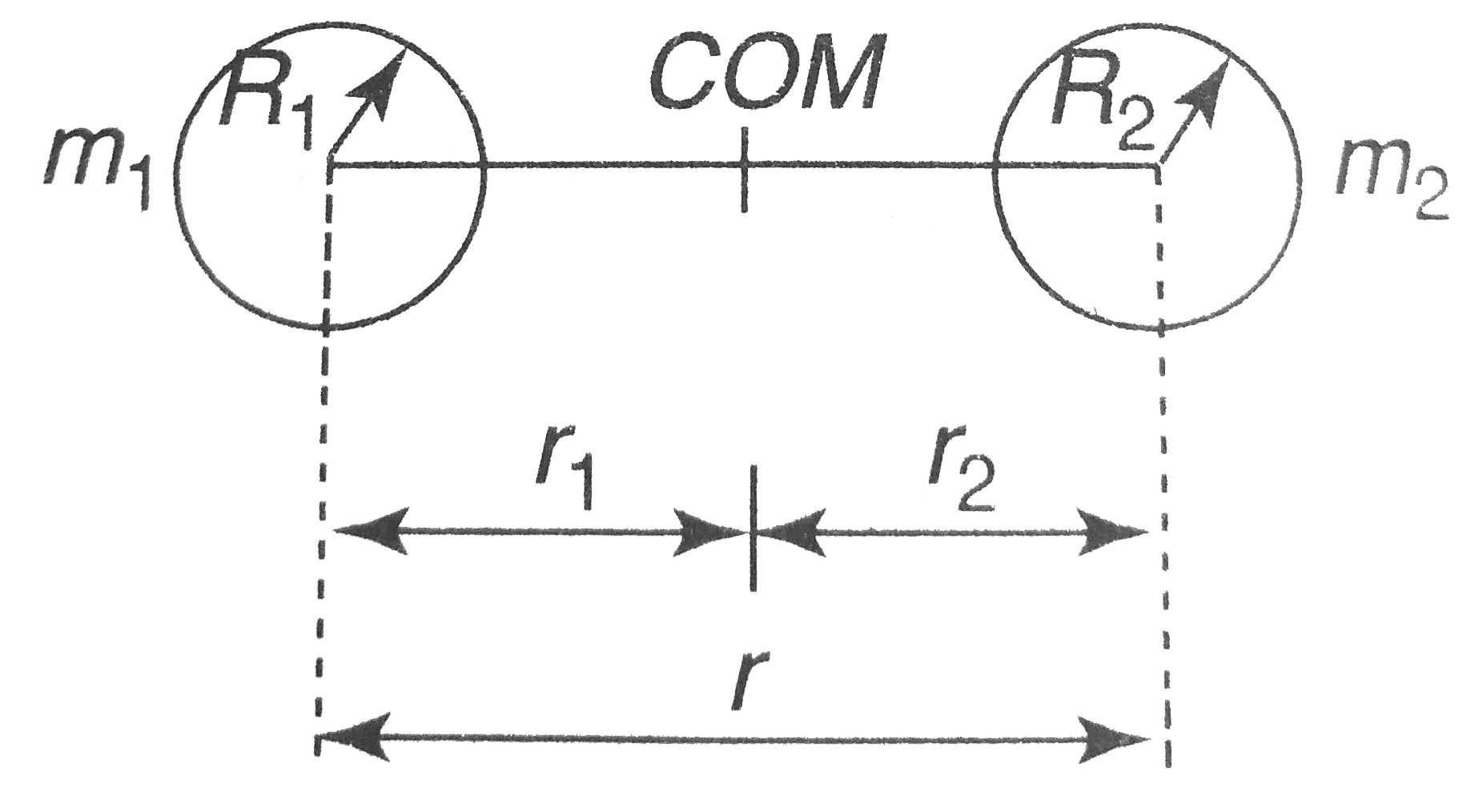 View Solution
View SolutionQuestion 150
Two planets revolve with same angular velocity about a star. The radius of orbit of outer planet is twice the radius of orbit of the inner planet. If T is time period of the revolution of outer planet, find the time in which inner planet will fall into the star. If it was suddenly stopped. View SolutionQuestion 156
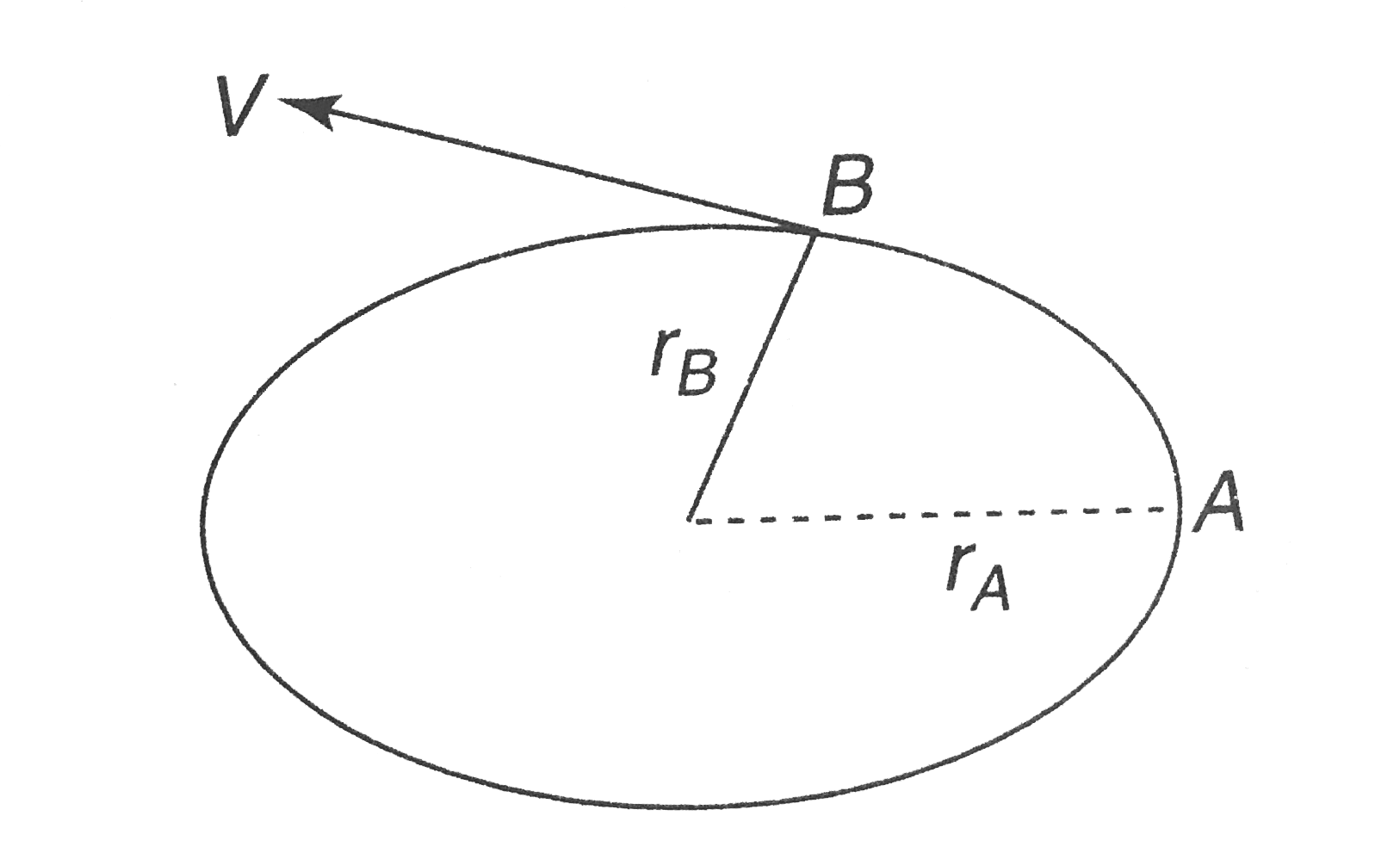
A particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between thesetwo. (Use GMR=6.4×107m2/s2). The speed V1 if particle pasess grazing the surface of the earth is
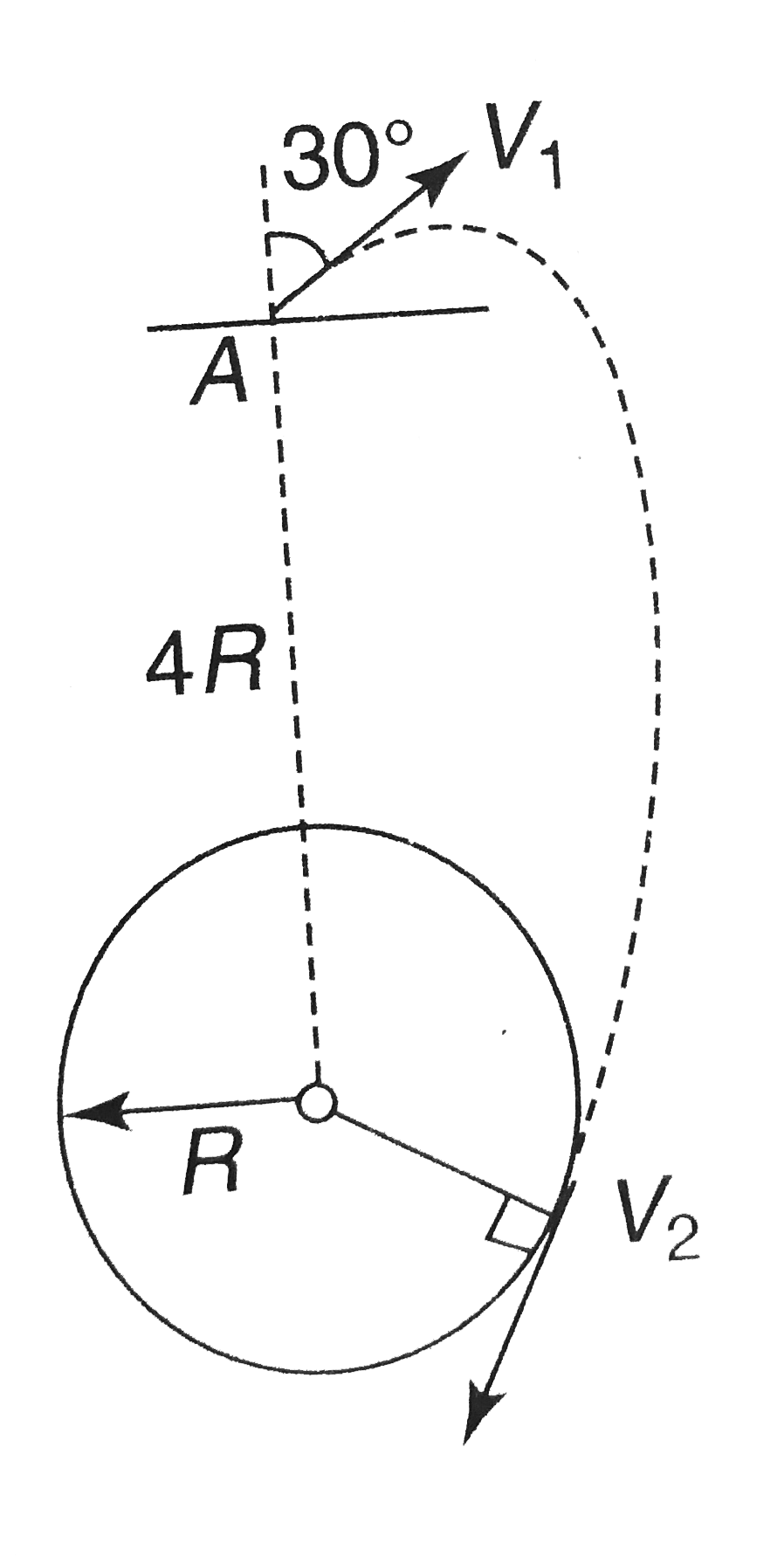 View Solution
View SolutionQuestion 157
Three identical stars, each of mass M, from an equilateral triangle (stars are positioned at the corners) that rotates around the centre of the triangle. The system is isolated and edge length of the triangle is L. The amount of work done, that is required ot dismantle the system, is:View SolutionQuestion 161
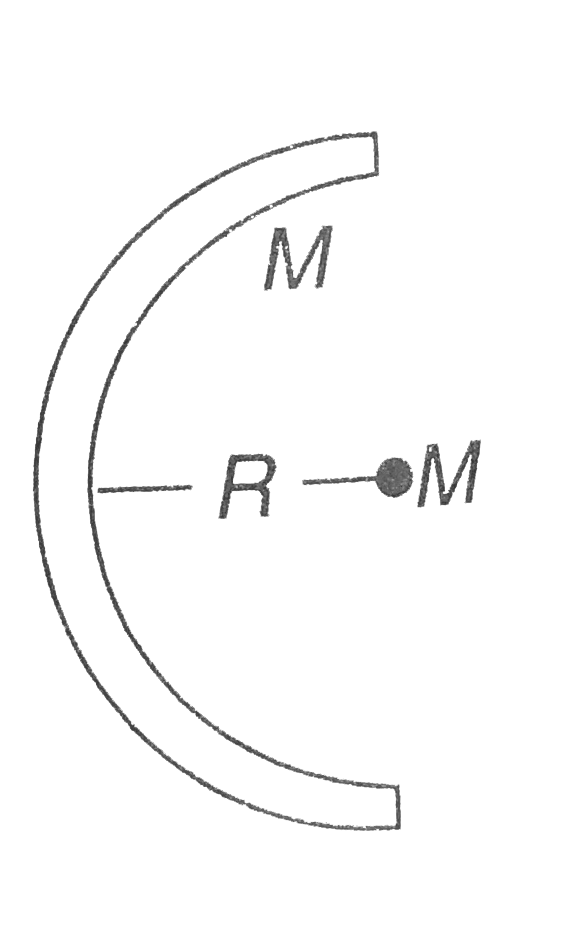
A cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]View SolutionQuestion 171
Assertion: When distance between bodies is doubled and also mass of each body is also doubled, gravitational force between them remains the same.
Reason: According to Neweton's law gravitational, force is directely proportional to mass of bodies and inversely proportional to square of distance between them.View SolutionQuestion 197
A particle of mass m is thrown upwards from the surface of the earth, with a velocity u. The mass and the radius of the earth are, respectively, M and R. G is gravitational constant g is acceleration due to gravity on the surface of earth. The minimum value of u so that the particle does not return back to earth is View SolutionQuestion 206
a projectile is fired from the surface of the earth with a velocity of 5ms−1 and angle θ with the horizontal. Another projectile fired from another planet with a velocity of 3ms−1 at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth.The value of the acceleration due to gravity on the planet is in ms−2 is given (g=9.8ms−2)View SolutionQuestion 209
Kepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described as View SolutionQuestion 210
Two spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is View SolutionQuestion 243
Different points in the earth are at slightly different distance from the sun and hence experience different force due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the CM (centre of mass) causing translation and a net torque at the CM causing rotation around an axis through the CM. for the earth-sun system (approximating the earth as a uniform density sphere). View SolutionQuestion 250
Suppose that the acceleration of a free fall at the surface of a distant planet was found to be equal to that at the surface of the earth. If the diameter of the planet were twice the diameter of the earth, then the ratio of mean density of the planet to that of the earth would be View SolutionQuestion 255
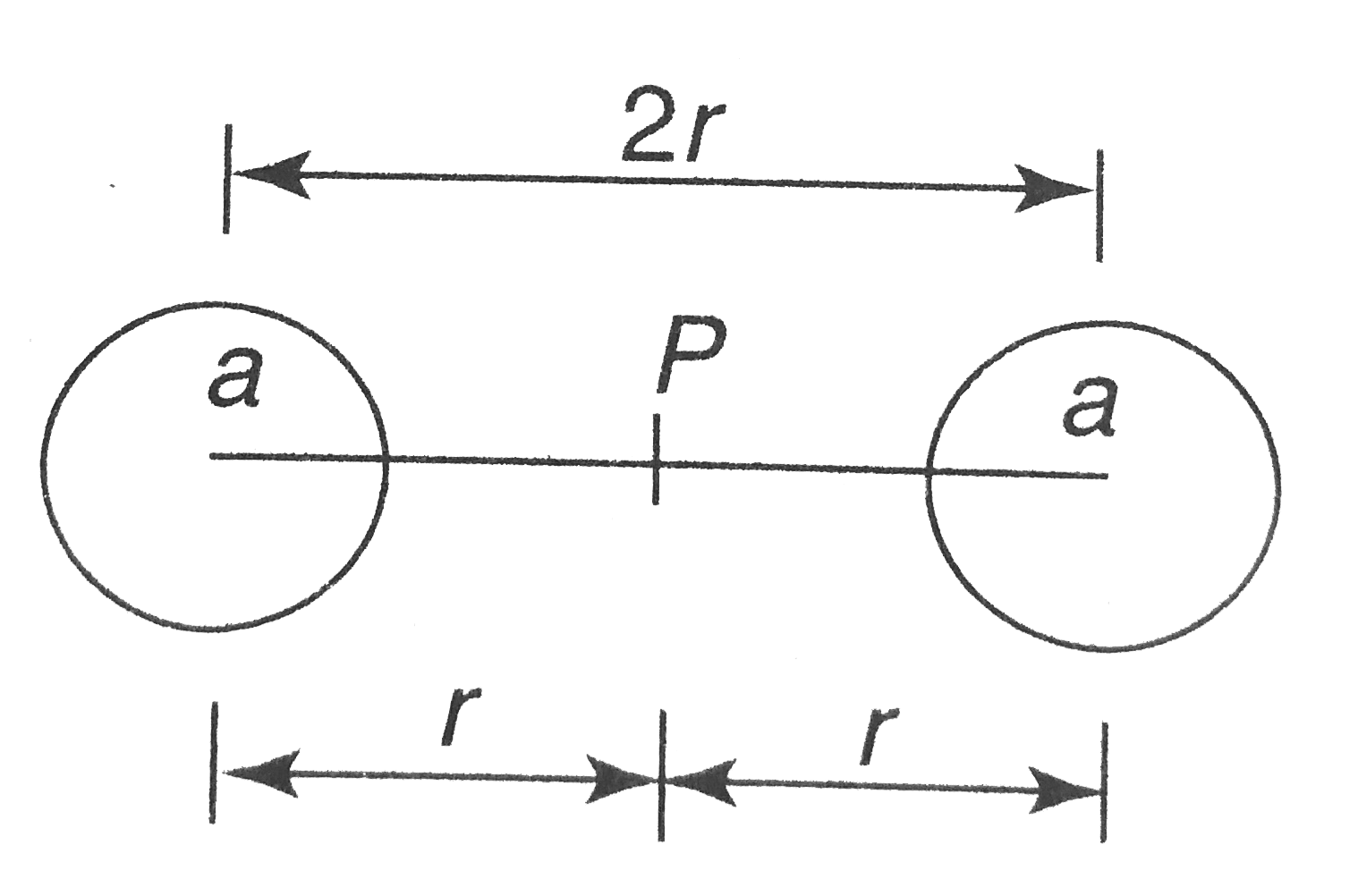
Consider two solid uniform spherical objects of the same density ρ. One has radius R and the other has radius 2R. They are in outer space where the gravitational fields from other objects are negligible. If they are arranged with their surface touching, what is the contact force between the objects due to their traditional attraction? View SolutionQuestion 269
Assertion: When distance between bodies is doubled and also mass of each body is also doubled, gravitational force between them remains the same.
Reason: According to Neweton's law gravitational, force is directely proportional to mass of bodies and inversely proportional to square of distance between them.View Solution