Exercise from ARIHANT PHYSICS (HINGLISH) GRAVITATION for Class 11
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| ARIHANT PHYSICS (HINGLISH) | Exercise |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Two lead balls of mass m and 2 m are placed at a separation d. A third ball of mass m is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is 6Gm2d2 . What is the location of the third ball?View SolutionQuestion 2
Four identical point masses m each are kept at the vertices A, B, and C of a cube having side length ‘a’ (see figure). Another identical mass is placed at the center point D of the cube. (a) Where will you place a fifth identical mass so that the net gravitational force acting on mass at D becomes zero? (b) Calculate the net gravitational force acting on the mass at D.
 View Solution
View SolutionQuestion 3
Two point masses m and M are held at rest at a large distance from each other. When released, they begin moving under their mutual gravitational pull.Find their relative acceleration (a) when separation between them becomes x.Integrate the expression of a obtained above to calculate the relative velocity of the two masses when their paration is x. Write the velocity of centre of mass of the system when separation between them is x.View SolutionQuestion 5
An astronaut landed on a planet and found that his weight at the pole of the planet was one third of his weight at the pole of the earth. He also found himself to be weightless at the equator of the planet. The planet is a homogeneous sphere of radius half that of the earth. Find the duration of a day on the planet. Given density of the earth =d0.View SolutionQuestion 7
The earth is a homogeneous sphere of mass M and radius R. There is another spherical planet of mass M and radius R whose density changes with distance r from the centre as p=p0r. (a) Find the ratio of acceleration due to gravity on the surface of the earth and that on the surface of the planet. (b) Find p0.View SolutionQuestion 8
A planet having mass equal to that of the earth (M=6×1024kg) has radius R such that a particle projected from its surface at the speed of light (c=3×108ms−1) just fails to escape. Assuming Newton’s Law of gravitation to be valid calculate the radius and mass density of such a planet. Are the numbers realistic? Note: The radius that you calculated is known as Schwarzschild radius. Actually we need to use theory of general relativity for solving this problem.View SolutionQuestion 9
Angular speed of rotation of the earth is ω0. A train is running along the equator at a speed v from west to east. A very sensitive balance inside the train shows the weight of n object as W1. During the return journey when the train is running atsame speed from east to west the balance shows the weight of the object to be W2. Weight of the object when the train is at rest was shown to be W0 by the balance. Calculate W2–W1.View SolutionQuestion 11
The angular speed of rotation of the earth is ω=7.27×10−5rads−1and its radius is R=6.37×106m. Calculate the acceleration of a man standing at a place at 40∘ latitude. [cos40∘=10.77] If the earth suddenly stops rotating, the acceleration due to gravity on its surface will becomeg0=9.82ms−2. Find the effective value of acceleration due to gravity (g) at 40∘ latitude taking into account the rotation of the earth.View SolutionQuestion 12
A planet has radius (136) th of the radius of the earth. The escape velocity on the surface of the planet was found to be 1√6 times the escape velocity from the surface of e earth. The planet is surrounded by a thin layer of atmosphere having thickness h (ltlt radius of the planet). The average density of the atmosphere on the planet is d and cceleration due to gravity on the surface of the earth is ge. Find the value of atmospheric pressure on the surface of the planet.View SolutionQuestion 14
A man can jump up to a height of h0=1m on the surface of the earth. What should be the radius of a spherical planet so that the man makes a jump on its surface and escapes out of its gravity? Assume that the man jumps with same speed as on earth and the density of planet is same as that of earth. Take escape speed on the surface of the earth to be 11.2 km/s and radius of earth to be 6400 km.View SolutionQuestion 15
It is known that if the length of the day were T0 hour, a man standing on the equator of the earth would have felt weightlessness. Assume that a person is located inside a deep hole at the equator at a distance of R2rom the centre of the earth. What should be the time period of rotation of the earth for such a person to feel weightlessness? [R = radius of the earth] View SolutionQuestion 17
Suppose that the gravitational attraction between a star of mass M and a planet of mass m is given by the expression F=KMmr2 where K and n are constants. If the orbital peed of the planets were found to be independent of their distance (r) from the star, calculate the time period (T0) of a planet going around the star in a circular orbit of radius r0.View SolutionQuestion 19
Imagine an astronaut inside a satellite going around the earth in a circular orbit at a speed of √gR2 where R is radius of the earth and g is acceleration due to gravity on the surface of the earth. What is weight experienced by the astronaut inside the satellite? Assume that an alien demon stops the satellite and holds it at rest. What is eight experienced by the astronaut now? The demon now releases the satellite (from rest). What is weight experienced by the astronaut now?View SolutionQuestion 21
(a) Estimate the average orbital speed of the earth going around the sun. The average Earth-sun distance is 1.5×1011m. (b) An asteroid going around the sun has an average orbital speed of 15 km/s. Is the asteroid farther from the sun or closer to the sun as compared to the Earth? Explain your answer.View SolutionQuestion 22
Assume that the earth is not rotating about its axis and that Scientists have developed an engine which can propel vehicles to very high speed on the surface of the earth. What is the maximum possible speed for any such vehicle running on surface of the earth. Earth is a sphere of radius R = 6400 km and acceleration due to gravity on the surface is g=10m/s2View SolutionQuestion 25
A planet goes around the sun in an elliptical orbit. The minimum distance of the planet from the Sun is 2×1012m and the maximum speed of the planet in its path is 40kms−1. Find the rate at which its position vector relative to the sun sweeps area, when the planet is at a distance 2.2×1012 from the sun.View SolutionQuestion 26
To launch a satellite at a height h above the surface of the earth (radius R) a two stage rocket is used . The first stage is used to lift the satellite to the desired height and the econd stage is used to impart it a tangential velocity so as to put it in a circular orbital. Assume (incorrectly) that the mass of rocket is negligible and that there is no tmospheric resistance. If E1 and E2 are the energies delivered by the first and the second stage of the rocket. Calculate the ratio E2E2 Calculate the time period of the satellite if it is given that E2E2=1. Take mass of the earth to be M.View SolutionQuestion 27
A satellite of mass m is going around the earth in a circular orbital at a height R2 from the surface of the earth. The satellite has lived its life and a rocket, on board, is fired to ake it leave the gravity of the earth. The rocket remains active for a very small interval of time and imparts an impulse in the direction of motion of the satellite. Neglect any hange in mass due to firing of the rocket. Find the minimum impulse imparted by the rocket to the satellite. Find the minimum work done by the rocket engine. Mass of the earth = M, Radius of the earth = RView SolutionQuestion 29
Three identical particles, each of mass m, are located in space at the vertices of an equilateral triangle of side length a. They are revolving in a circular orbital under mutual ravitational attraction. Find the speed of each particle. Find the acceleration of the centre of mass of a system comprising of any two particles. Assume that one of the particles suddenly loses its ability to exert gravitational force. Find the velocity of the centre of mass of the system of other two particles after this.View SolutionQuestion 31
A large non rotating star of mass M and radius R begins to collapse under its own gravity and ultimately becomes very small (nearly a point mass). Assume that the density remains uniform inside the sphere in any stage. Plot the variation of gravitational field intensity (well, you can call it cceleration due to gravity) at a distance R2from the centre vs the radius (r) of the star.View SolutionQuestion 32
At a depth h1=R2 from the surface of the earth acceleration due to gravity is g1. It’s value changes by Δg1 when one moves down further by 1 km. At a height h2 above the urface of the earth acceleration due to gravity is g9. It’s value changes by Δg2when one moves up further by 1 km. If Δg1=Δg2 find h2. Assume the earth to be a uniform phere of radius R.View SolutionQuestion 34
A tunnel is dug along a chord of non rotating earth at a distance d=R2 [R = radius of the earth] from its centre. A small block is released in the tunnel from the surface of the arth. The block comes to rest at the centre (C) of the tunnel. Assume that the friction coefficient between the block and the tunnel wall remains constant at μ.
 Calculate work done by the friction on the block. Calculate μ.View Solution
Calculate work done by the friction on the block. Calculate μ.View SolutionQuestion 35
Diameter of a planet is 10d∘, its mean density is ρ∘4 and mass of its atmosphere is 10m∘ where d∘, ρ∘ and m∘ are diameter, mean density and mass of atmosphere respectively for the earth. Assume that mean density of atmosphere is same on the planet and the earth and height of atmosphere on both the planets is very small compared to their radius. Find the ratio of atmospheric pressure on the surface of the planet to that on the earth. If a mercury barometer reads 76 cm on the surface of the earth, find its reading on the surface of the planet.View SolutionQuestion 36
A particle of mass m is projected upwards from the surface of the earth with a velocity equal to half the escape velocity. (R is radius of earth and M is mass of earth)Calculate the potential energy of the particle at its maximum. Write the kinetic energy of the particle when it was at half the maximum height.View SolutionQuestion 37
A uniform spherical planet is rotating about its axis. The speed of a point on its equator is v and the effective acceleration due to gravity on the equator is one third its value at the poles. Calculate the escape velocity for a particle at the pole of the planet. Give your answer in multiple of v.View SolutionQuestion 38
A planet is a homogeneous ball of radius R having mass M. It is surrounded by a dense atmosphere having density ρ=σ∘r where simga∘ is a constant and r is distance from the centre of the planet. It is found that acceleration due to gravity is constant throughout the atmosphere of the planet. Find simga∘in terms of M and R.View SolutionQuestion 39
A projectile is to be launched from the surface of the earth so as to escape the solar system. Consider the gravitational force on the projectile due to the earth and the sun nly. The projectile is projected perpendicular to the radius vector of the earth relative to the centre of the sun in the direction of motion of the earth. Find the minimum speed of projection relative to the earth so that the projectile escapes out of the solar system. Neglect rotation of the earth. mass if the sum Ms2×1030kg, Mass of the earth Me=6.4×1024kg Radius if the earthRe=6.4×106m, Earth- Sun distence r=1.5×1011mView SolutionQuestion 40
Assume that there is a tunnel in the shape of a circular arc through the earth. Wall of the tunnel is smooth. A ball of mass m is projected into the tunnel at A with speed v. The all comes out of the tunnel at B and escapes out of the gravity of the earth. Mass and radius of the earth are M and R respectively and radius of the circle shaped tunnel is also . Find minimum possible value of v (call it v0) If the ball is projected into the tunnel with speed v0, calculate the normal force applied by the tunnel wall on the ball when it is closest to the centre of the earth. It is given that the closest distance between the ball and the centre of the earth is R2
 View Solution
View SolutionQuestion 41
A celestial body, not bound to sun, will only pass by the sun once. Calculate the minimum speed of such a body when it is at a distance of 1.5×1011m from the sun (this is verage distancebetween the sun & the earth and is known as astronomical unit- A.U.) The mass of the sun is M˜–2×1030kg. G=6.67×10−11N−m2kg2 Show that this speed is√2 times greater than speed of earth around the sun, assuming circular trajectoryView SolutionQuestion 42
A body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.View SolutionQuestion 43
An astronaut on the surface of the moon throws a piece of lunar rock (mass m) directly towards the earth at a great speed such that the rock reaches the earth. Mass of the earth = M, Mass of the moon =M81 Radius of the earth = R, Distance between the centre of the earth and the moon = 60R In the course of its journey calculate the maximum gravitational potential energy of the rock Find the minimum possible speed of the rock when it enters the atmosphere of the earth.View SolutionQuestion 44
The radius of the circular path of a geostationary satellite was inadvertently madeδr=1km larger than the correct radius r = 42000 km Calculate the difference in angular peed of the satellite and the earth. If the satellite was exactly above a house on the equator on a particular day, what will be angular separation between the house and the satellite a year later?View SolutionQuestion 45
A spy satellite S1, travelling above the equator is taking pictures at quick intervals. The satellite is travelling from west to east and is ready with picture around the whole equator in 8 hours. Another similar satellite S2, travelling in the same plane is travelling from east to west and is able to take pictures around the whole equator in 6 hours. Find the ratio of radii of the circular paths of the satellite S1 and S2.View SolutionQuestion 47
The astronomical phenomenon when the planet Venus passes directly between the Sun and the earth is known as Venus transit. For two separate persons standing on the arth at points M and N the Venus appears as black dots at points M’ and N’ on the Sun. The orbital period of Venus is close to 220 days. Assuming that both earth and Venus revolve on circular paths and taking distance MN = 1000 km, calculate the distance M’N’ on the surface of the Sun.[Take(2.75)1/3=1.4]
 View Solution
View SolutionQuestion 48
Satellite A is following a circular path of radius a around the earth another satellite B follows an elliptical path around the earth. The two satellites have same mechanical energy and their orbits intersect. Find the speed of satellite B at the point where its path intersects with the circular orbit of A. Take mass of earth to be M.
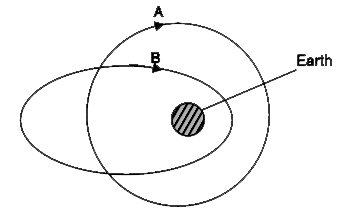 View Solution
View SolutionQuestion 50
Energy of a satellite going around the earth in an elliptical orbit is given by −GMm2a where M and m are masses of the earth and the satellite respectively and 2a is the major axis of the elliptical path. A satellite is launched tangentially with a speed √3GM5R from a height h = R above the surface of the earth. Calculate its maximum distance from the centre of the earthView SolutionQuestion 52
An asteroid was fast approaching the earth. Scientists fired a rocket which hit the asteroid at a distance of 5 R from the centre of the earth (R = radius of the earth). mmediately after the hit the asteroid’s velocity (V0) was making an angle of θ=30∘ with the line joining the centre of the earth to the asteroid. The asteroid just grazed past the surface of the earth. Find V0 [Mass of the earth = M]
 View Solution
View SolutionQuestion 53
A satellite is orbiting around the earth in a circular orbit. Its orbital speed is V0. A rocket on thrust to the satellite directed radially away from the centre of the earth. The uration of the engine burn is negligible so that it can be considered instantaneous. Due to this thrust a velocity variation ΔV is imparted to the satellite. Find the minimum value of the ratio ΔVV0 for which the satellite will escape out of the gravitational field of the earth.View SolutionQuestion 55
A satellite is at a distance r1 from the centre of the earth at its apogee. The distance is r)(2) when it is at perigee. Mass of the earth is M. Calculate the maximum speed of the satellite in its orbit around the earth. Estimate the maximum speed of the moon going around the earth. For moon r1˜−400,000km and r2˜−360,00kmView SolutionQuestion 56
A satellite is going around the earth in an elliptical orbit and has maximum and minimum distance from the centre of earth equal to 10r and r respectively. It was planned to fire on board rocket so as to increase the energy of the satellite by maximum amount. Assume that the rocket is fired for a small time (almost instantaneous) and gives an impulse J to the satellite in forward direction. Take J to be small compared to overall momentum of the satellite.View SolutionQuestion 57
A satellite is going around the earth in an elliptical orbit and has maximum and minimum distance from the centre of earth equal to 10r and r respectively. It was planned to fire on board rocket so as to increase the energy of the satellite by maximum amount. Assume that the rocket is fired for a small time (almost instantaneous) and gives an impulse J to the satellite in forward direction. Take J to be small compared to overall momentum of the satellite.View SolutionQuestion 58
Imagine a smooth tunnel along a chord of nonrotating earth at a distance R2 from the centre. R is the radius of the earth. A projectile is fired along the tunnel from the centre of the tunnel at a speed V∘=√gR [g is acceleration due to gravity at the surface of the earth]. (a) Is the angular momentum [about the centre of the earth] of the projectile onserved as it moves along the tunnel? (b) Calculate the maximum distance of the projectile from the centre of the earth during its course of motion.View SolutionQuestion 60
There is an infinite thin flat sheet with mass density η per unit area. Find the gravitational force, due to sheet, on a point mass m located at a distance x from the sheet.Consider a large flat horizontal sheet of material density r and thickness t, placed on the surface of the earth. The density ϕof the earth is ϕ0 If it is found that ravitational field intensity just between the sheet is larger than field just above it, prove that rho_(@)lt(3)/(2)rho. View SolutionQuestion 61
A spaceship is orbiting the earth in a circular orbit at a height equal to radius of the earth (Rc=6400km) from the surface of the earth. An astronaut is on a space walk outside the spaceship. He is at a distance of l = 200 m from the ship and is connected to it with a simple cable which can sustain a maximum tension of10 N. Assume that the centre of the earth, the spaceship and the astronaut are in a line. Mass of astronaut along with all his accessories is 100 kg. Do you think that a weak cable that can only take a load of 10 N, can prevent him from drifting in space ? Make a guess. Estimate the tension in the cable. [Acceleration due to gravity on the surface of[Earth=9.8m/s2]View SolutionQuestion 62
Earth is rotating about its axis with angular speed Ω0and average density of earth is ρ. It is proposed to make a space elevator by placing a long rod with uniform mass density extending from just above the surface for the earth out to a radius nR (R is radius of the earth). Prove that the rod can remain above the same point on the equator all time if, n2+n=8πGp3ω2 density of the earthView SolutionQuestion 63
A body is projected up from the surface of the earth with a velocity half the escape velocity at an angle of 30∘ with the horizontal. Neglecting air resistance and earth’s otation, find (a) the maximum height above the earth’s surface to which the body will rise. (b) will the body move around the earth as a satellite?View SolutionQuestion 64
A near surface earth satellite has cylindrical shape with cross sectional area ofs=0.5M2 and mass of M = 10 kg. It encounters dust which has density of D=1.6XX10−11KG/ms. Assume that the dust particles are at rest and they stick to the satellite’s front face on collision. Take mean density of earth to beρ=5500kg/m3Find the drag force experienced by the satelliten
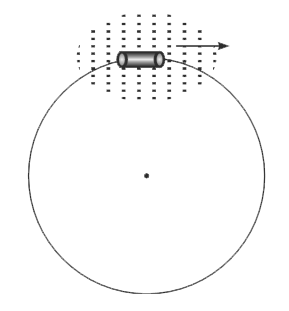 If the dust extends throughout the orbit, find the change in velocity and radius of
the circular path of the satellite in one revolution.View Solution
If the dust extends throughout the orbit, find the change in velocity and radius of
the circular path of the satellite in one revolution.View Solution


