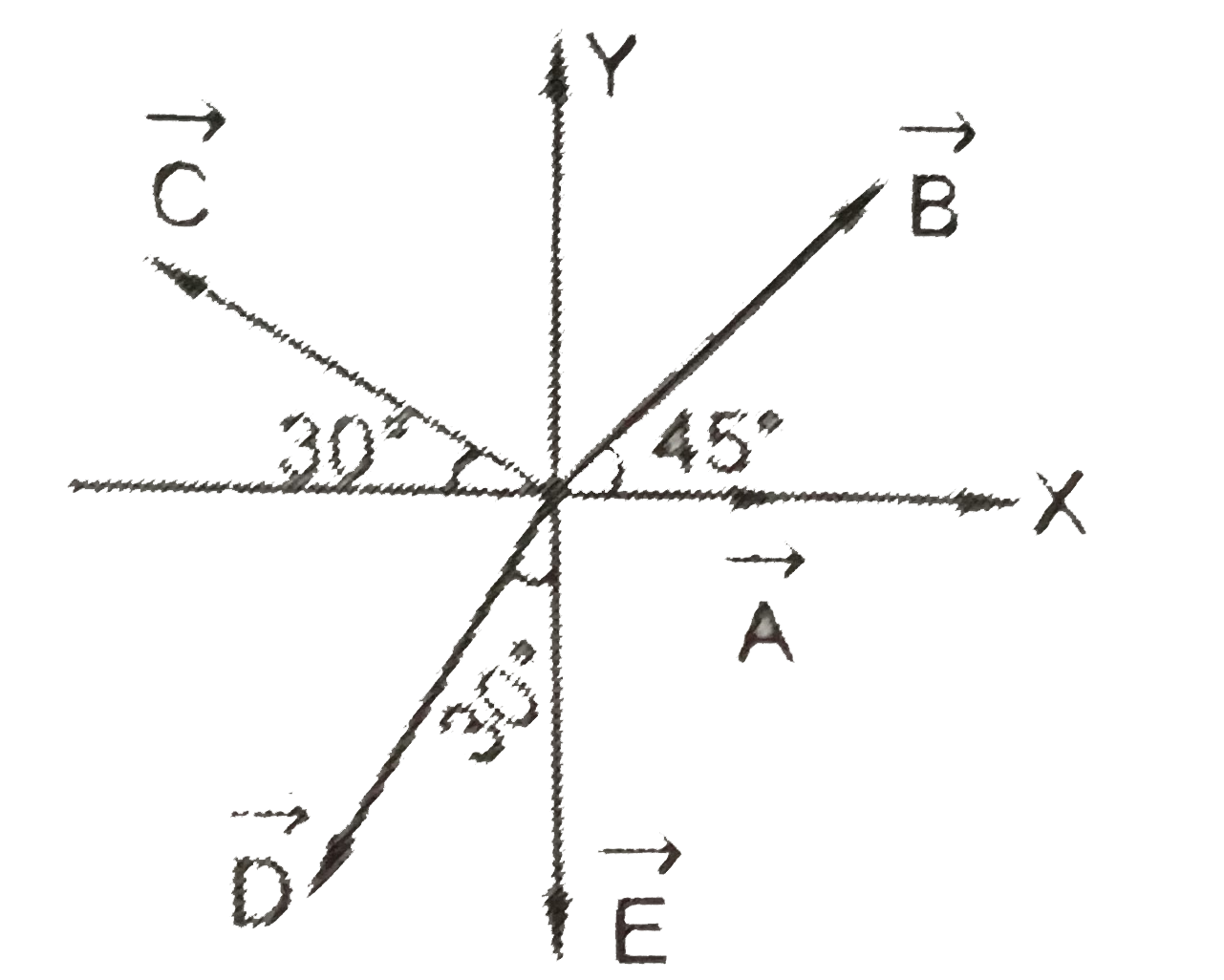
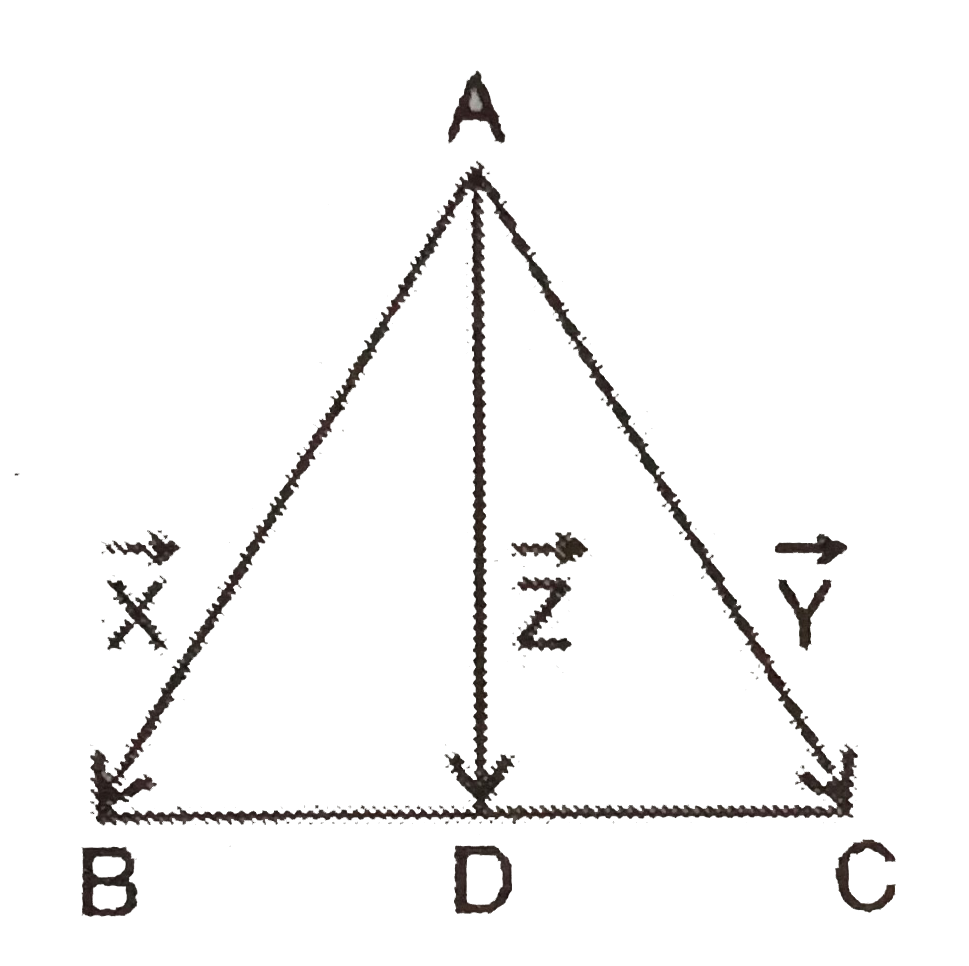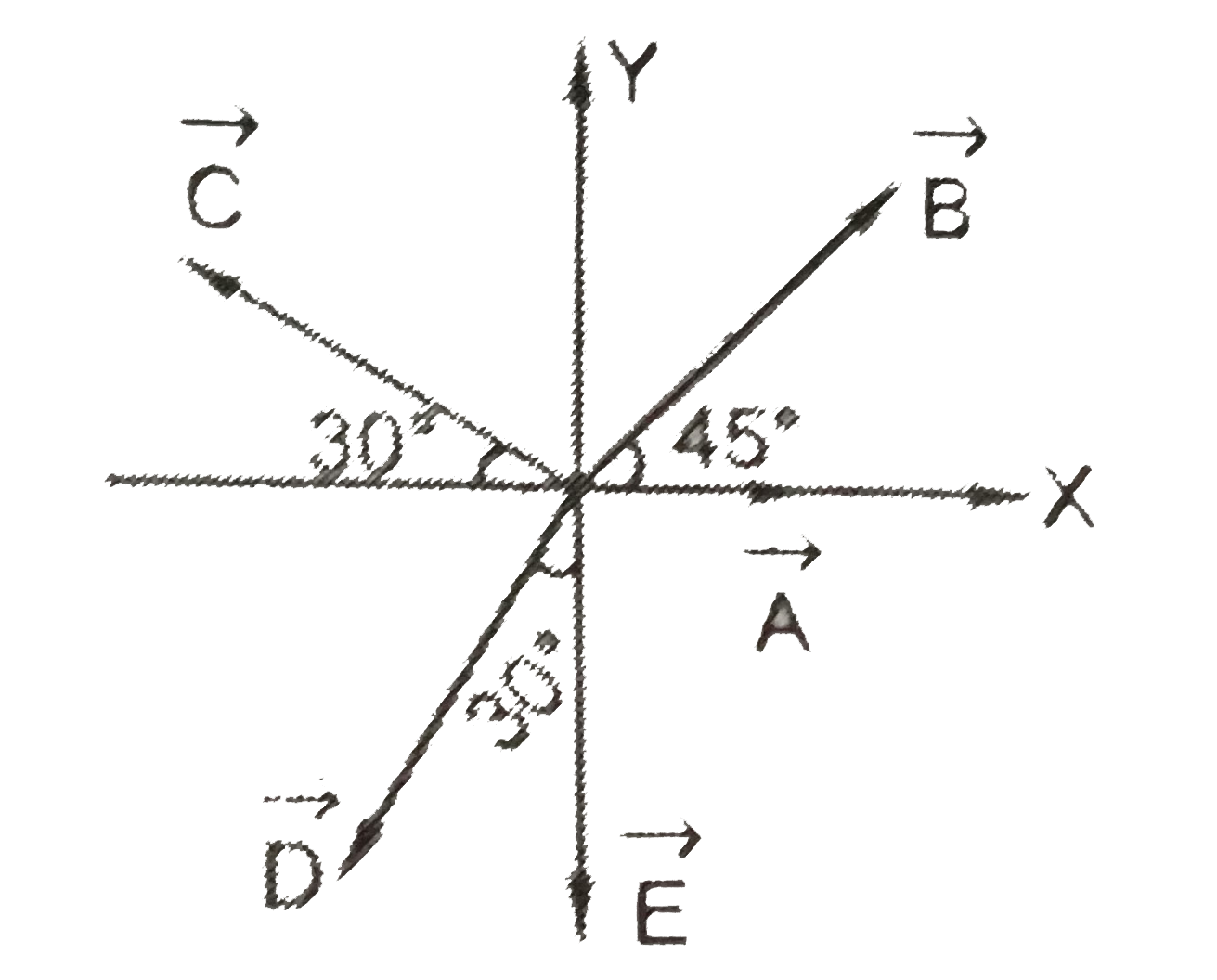PROBLEMS FOR PARCTICE from GR BATHLA & SONS PHYSICS (HINGLISH) VECTORS for Class 11
| Class 11 | PHYSICS |
| Chapter | VECTORS |
| GR BATHLA & SONS PHYSICS (HINGLISH) | PROBLEMS FOR PARCTICE |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
State whether the folowing statements are trune or false giving reason in brief :
(a) As adiidtion of vector is commutive so subtraction must also be
(b) Component of a vector is equal to their difference to itself is zero
(c) Angle between two vectors can be greater than m180∘
(d) A vector cannot be divided by a vector.View SolutionQuestion 6
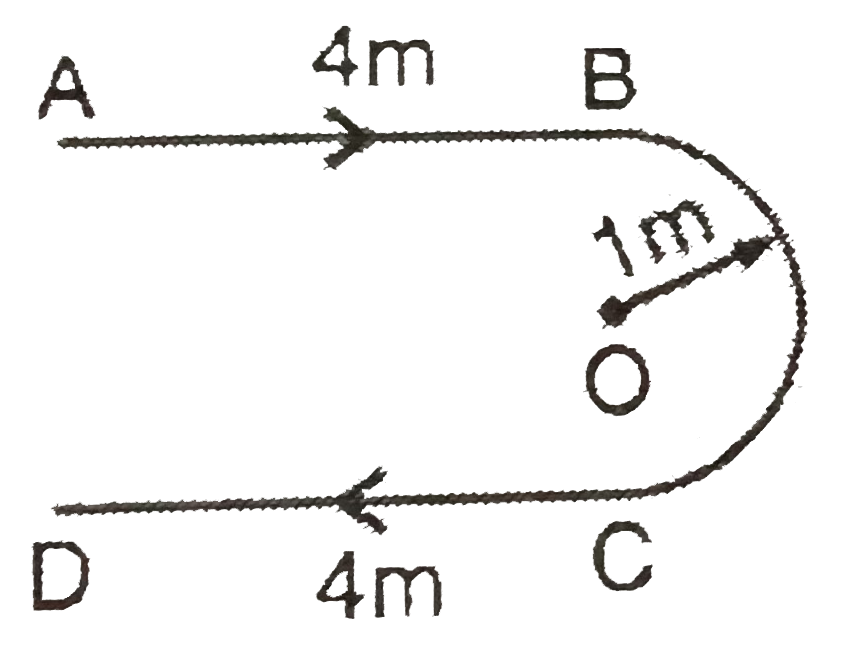
A room has dimensions 3m×4m×5m. A fly starting at one corner ends up at the diametrocally opposite corner .
(a). What is the magnetic of its displacement ?
(b) Could the length of its path be less than this distance ?
(c) Choosing a situtable cooridinate system find the position vector .
(d) If the fly does not fly but walks , what is the lenght of the shortest path it can take ?View SolutionQuestion 16
The particle of mass m is projected at t=0 from a point O on the ground with speed v0 at an angle 45∘ to the horizontal as shown in Figure 3.44. Compute the magnitude and direction of the angular mometum of the particle about the point O at position :

When the velocity of the paticle is , →V=(0,7v0)ˆi−(0.3v0)ˆjView SolutionQuestion 17
A river flows at 3 m/s and is 300 m wide . A man swing across the rivers with a velocity of 2 m/s directed always perpendicular to the flow of current . (a) How long does it take the man to cross the river ? (b) In what direction does he actually moves to cross the relative to the shore ? (c) How far down the fiver(from the starting point ) does he reach the opposite bank?View SolutionQuestion 19
The width of a rivers is 25m and in it water is flowing with a velocity of 4m/min . A boatman is standing on the bank of the river . He want to sail the boat to a point at the other bank which is directly opposite to him . In what time will he cross the river , if he can sail the boat at 8m/min. relative to the water ?View SolutionQuestion 108
A lion is at some instant a position A(2m,6m,−1m) and a goat is at position B(1m,2m,8m). The lion is free to move but the goat is unable to move due to some injury . The lion runs towards the goat and reches it in time 2 sec. A verage velocity of the lion can be expreseed as:View SolutionQuestion 173
Sppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are

Answer the following questions.
At Q torque acting on the mass can be expressed as :View SolutionQuestion 174
Sppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are
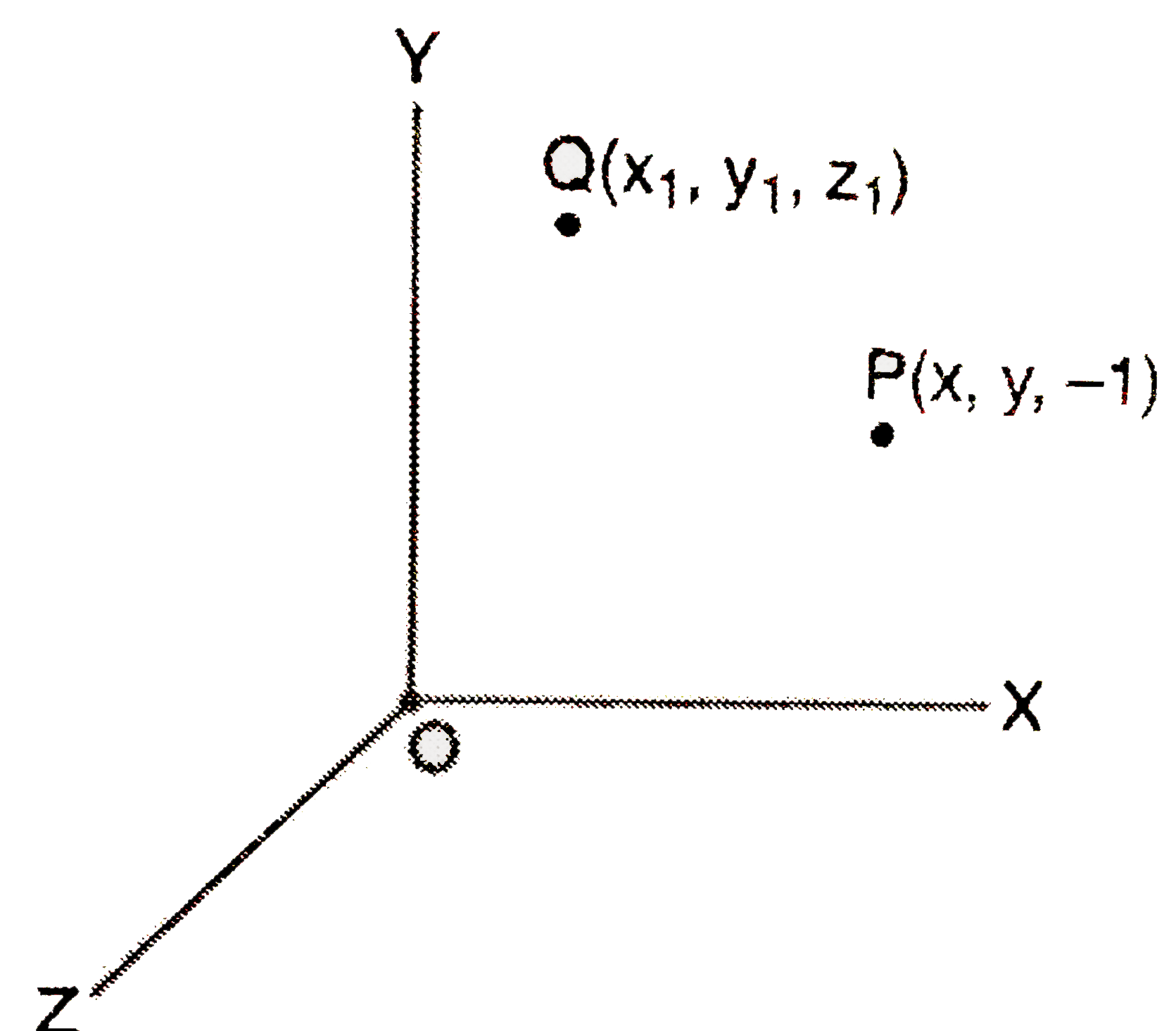
Answer the following questions.
Coordinates of P are :View SolutionQuestion 175
Sppose that a point mass 'm' is moving under a constant force →F=2ˆi−ˆj+ˆk netweon . At some instant , t=0, point P(xm, ym, -1m) [m- metre ] is the instantaneous position of the mass. We know that torque can be expressed as the cross- product of position vector and forces vector, i.e.,
τ=→r×→F . At P, torque can be expessed as τ=(−4ˆj−4ˆk)Nm At some other instant, t=3 sec, the point mass has another instantaneous position Q(x1,y1,z1) such that the displacement vectors between points P and Q and the given force are mutually perpendicular. Also, x-component of torqure at Q is zero and y z-components are equal in magnitude and direction along the negative direction of the respective axes. Using a definite scale, if we construct a parallelogram with the position vectors of Q and the gives force →F as its adjacent sides , area of this parallelogram is 2√2m2 . Area of the given parallelogram , in fact , represents a physical quantity whose magnitude in SI system can be expressed as 5 times the gives are
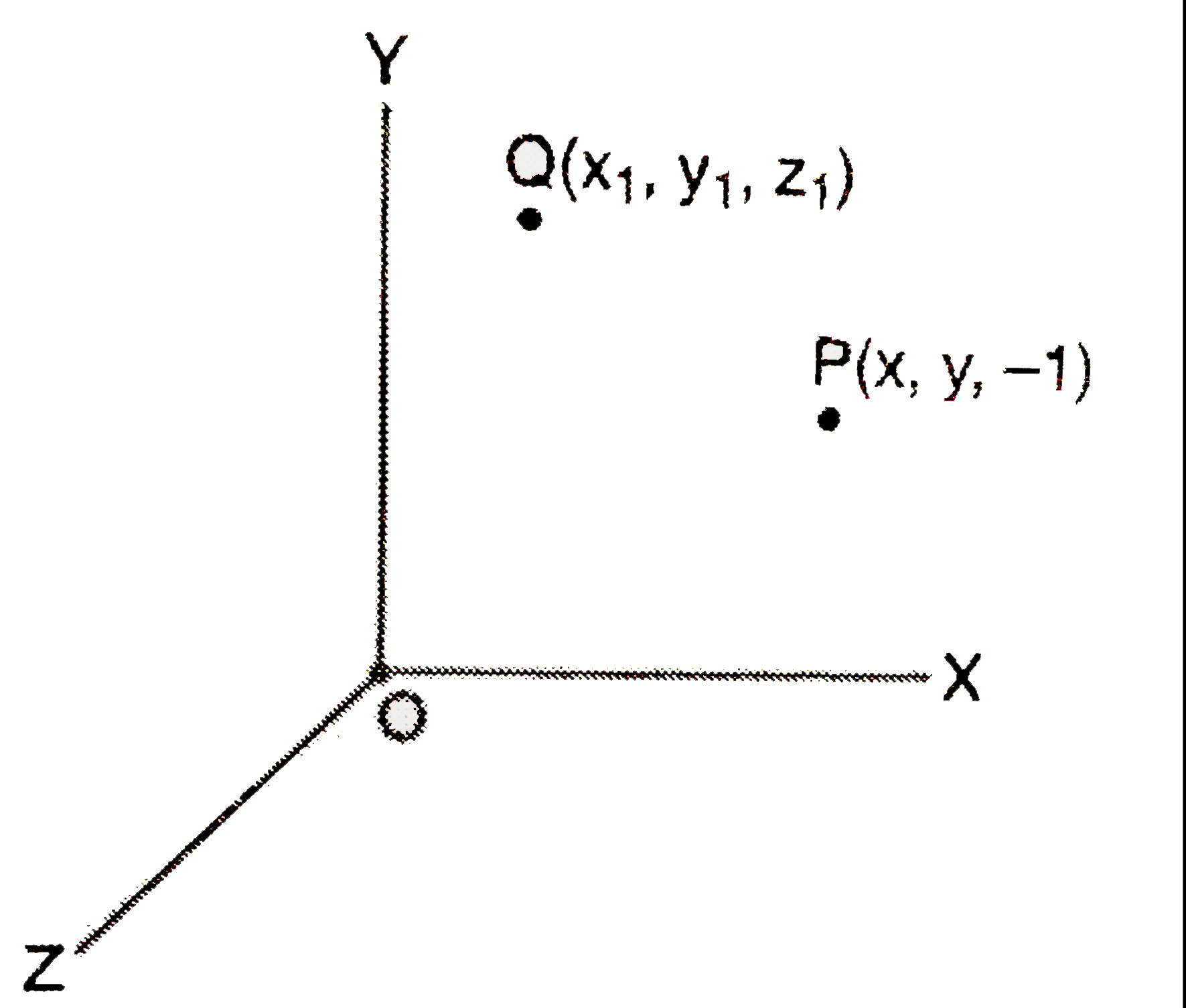
Answer the following questions.
Work done the for the motion of the points mass from P to Q is :View SolutionQuestion 176
Consider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
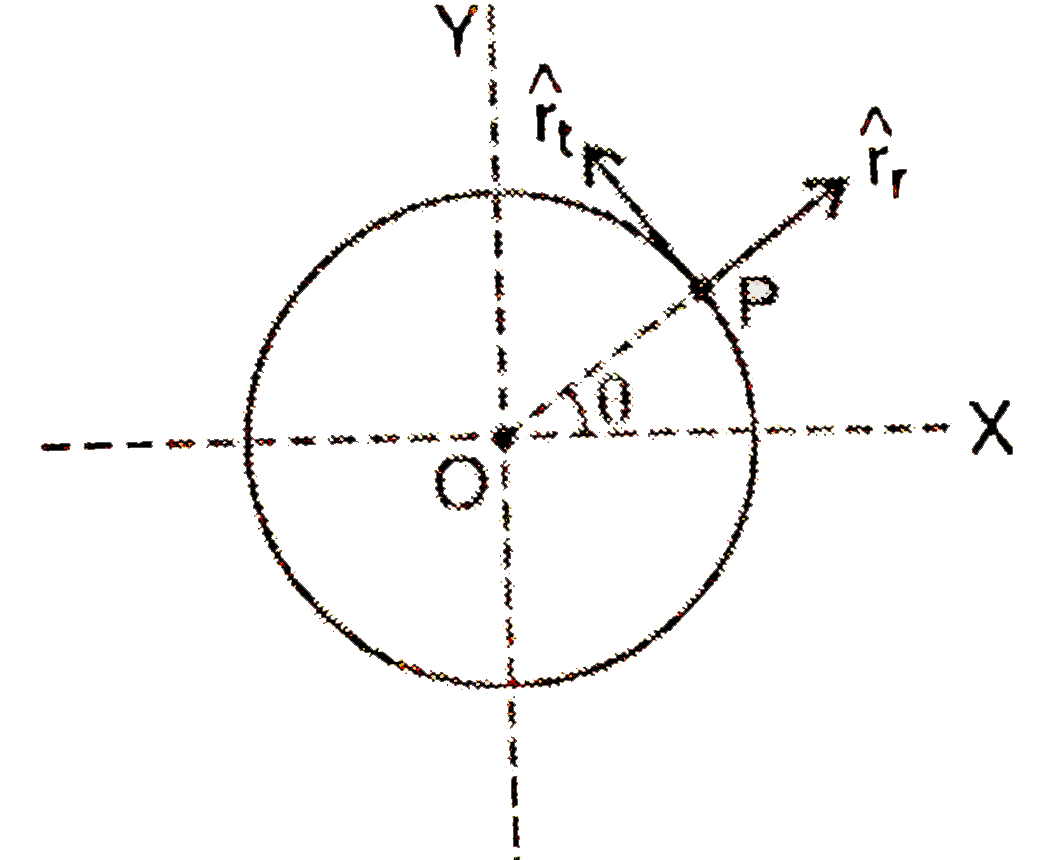
Answer the following questions :
For any instantantaneous position of the objected P, the radial unit vector ˆrr can be expressed as :View SolutionQuestion 177
Consider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
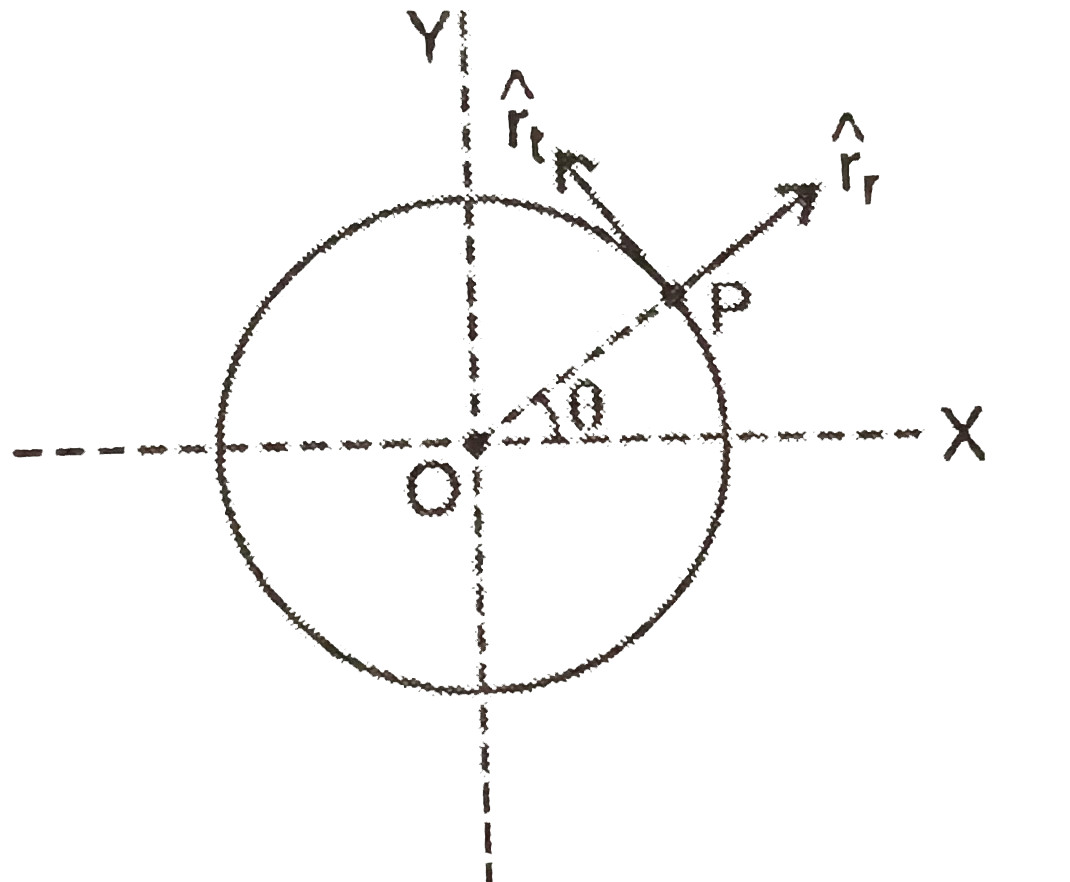
Answer the following questions :
For any position of the objected P, the tangential unit vector can be expressed as :View SolutionQuestion 178
Consider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.

Answer the following questions :
In trems of ˆrr,ˆrt and θ,ˆi can be expressed as :View Solution


 .
.