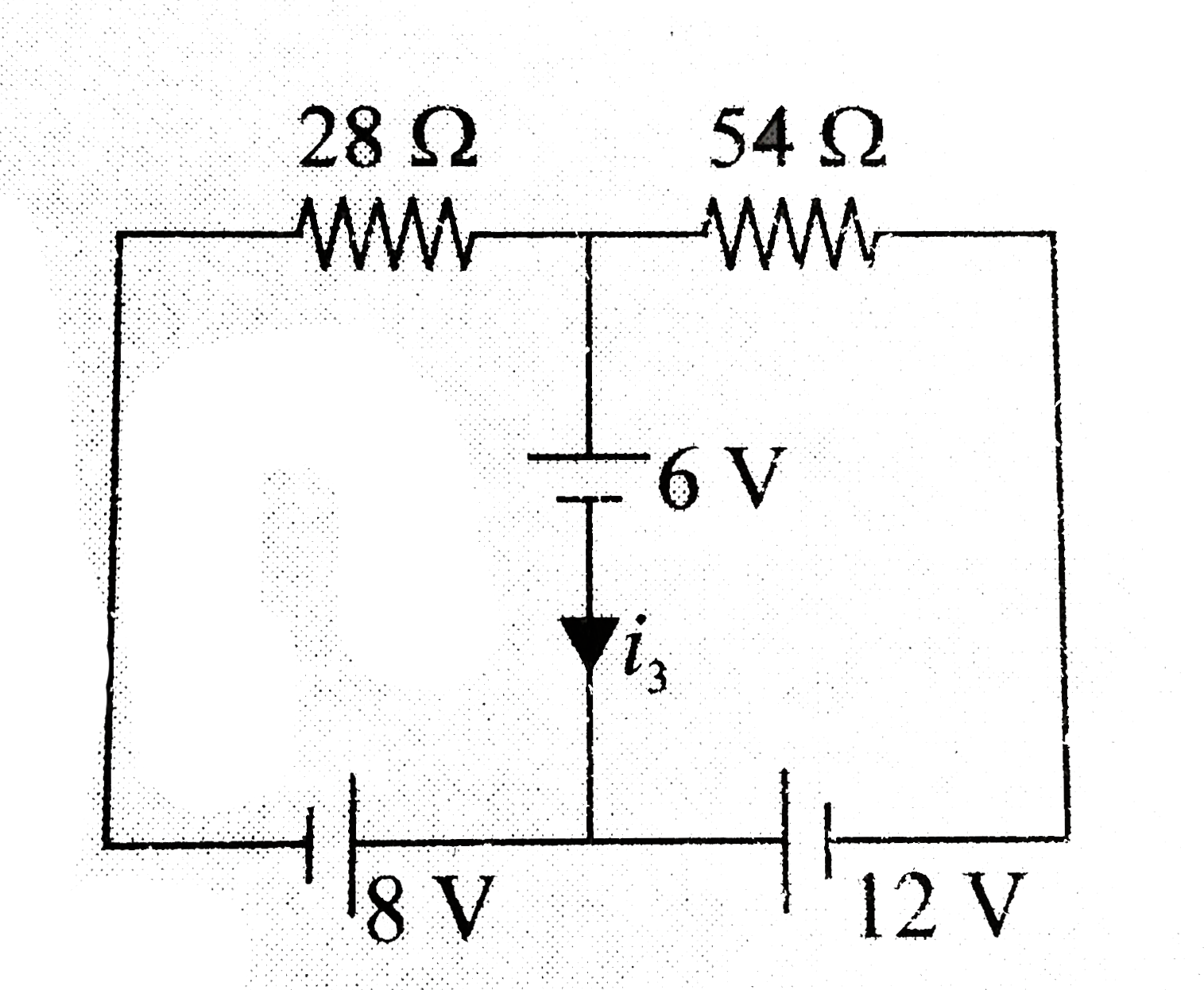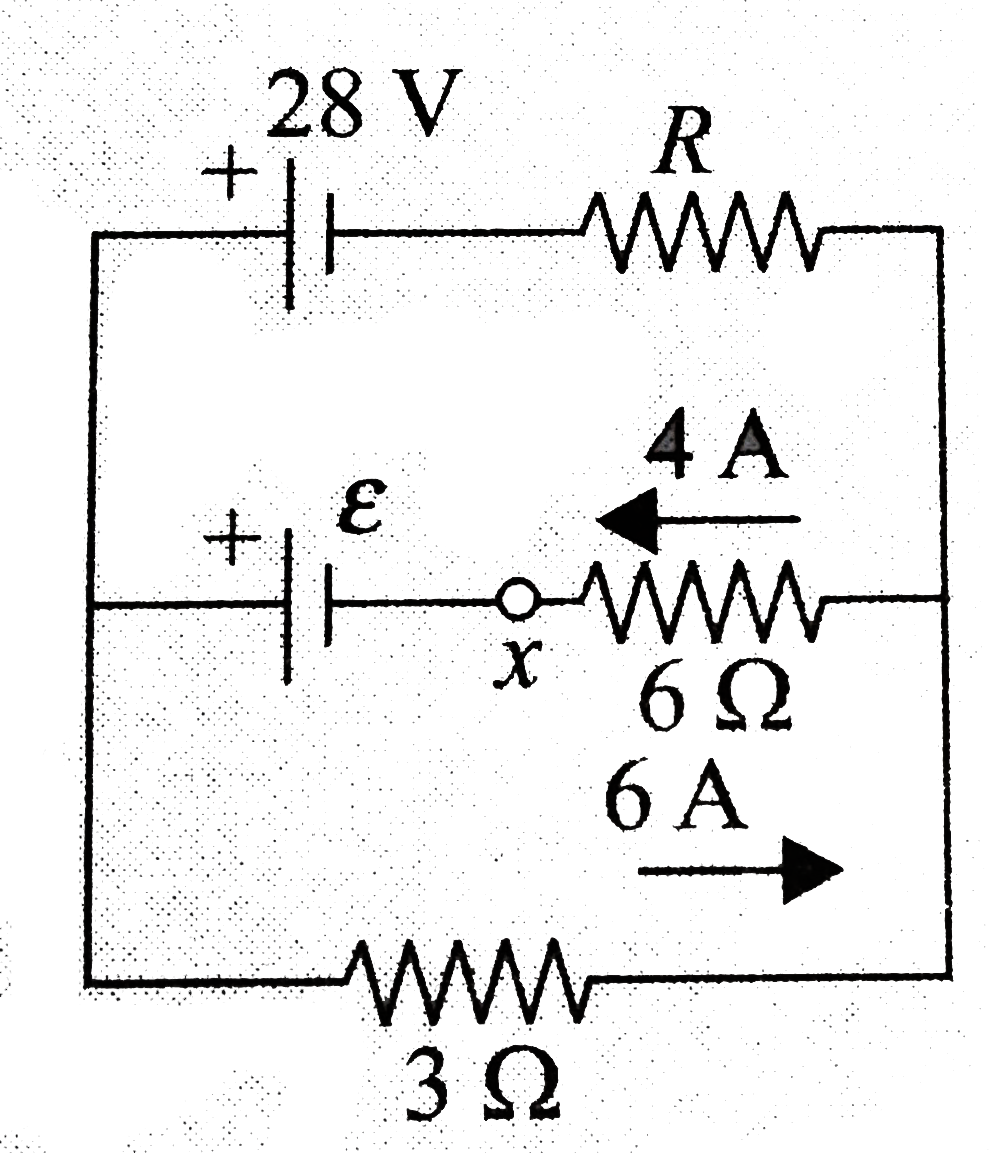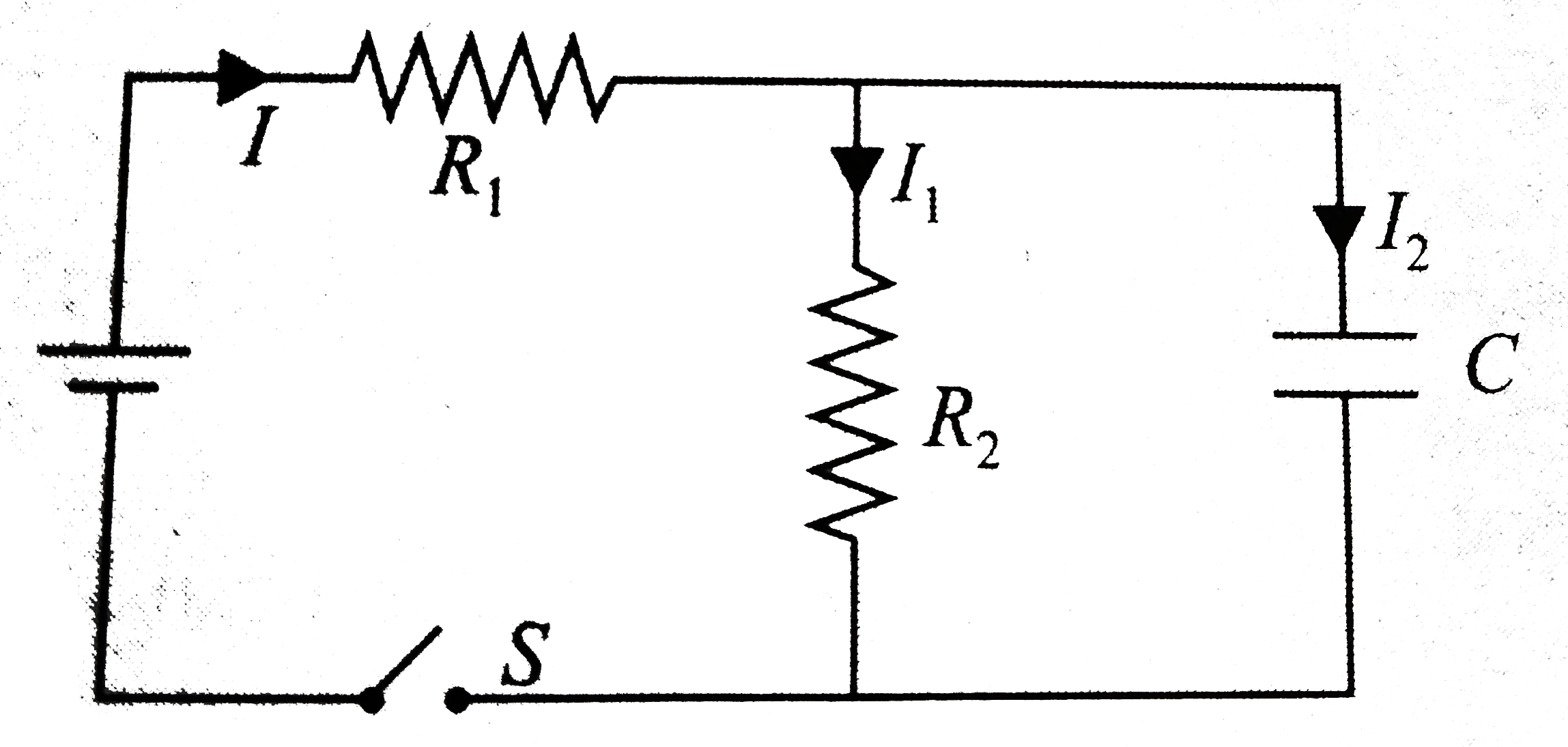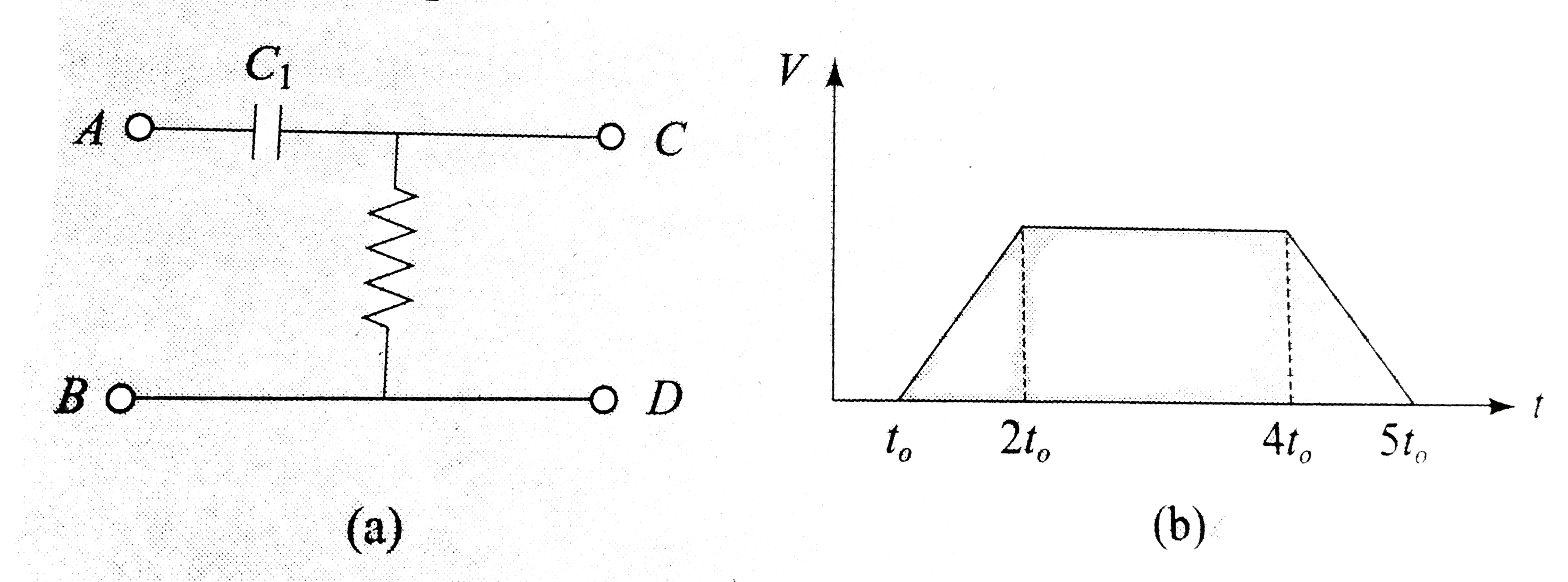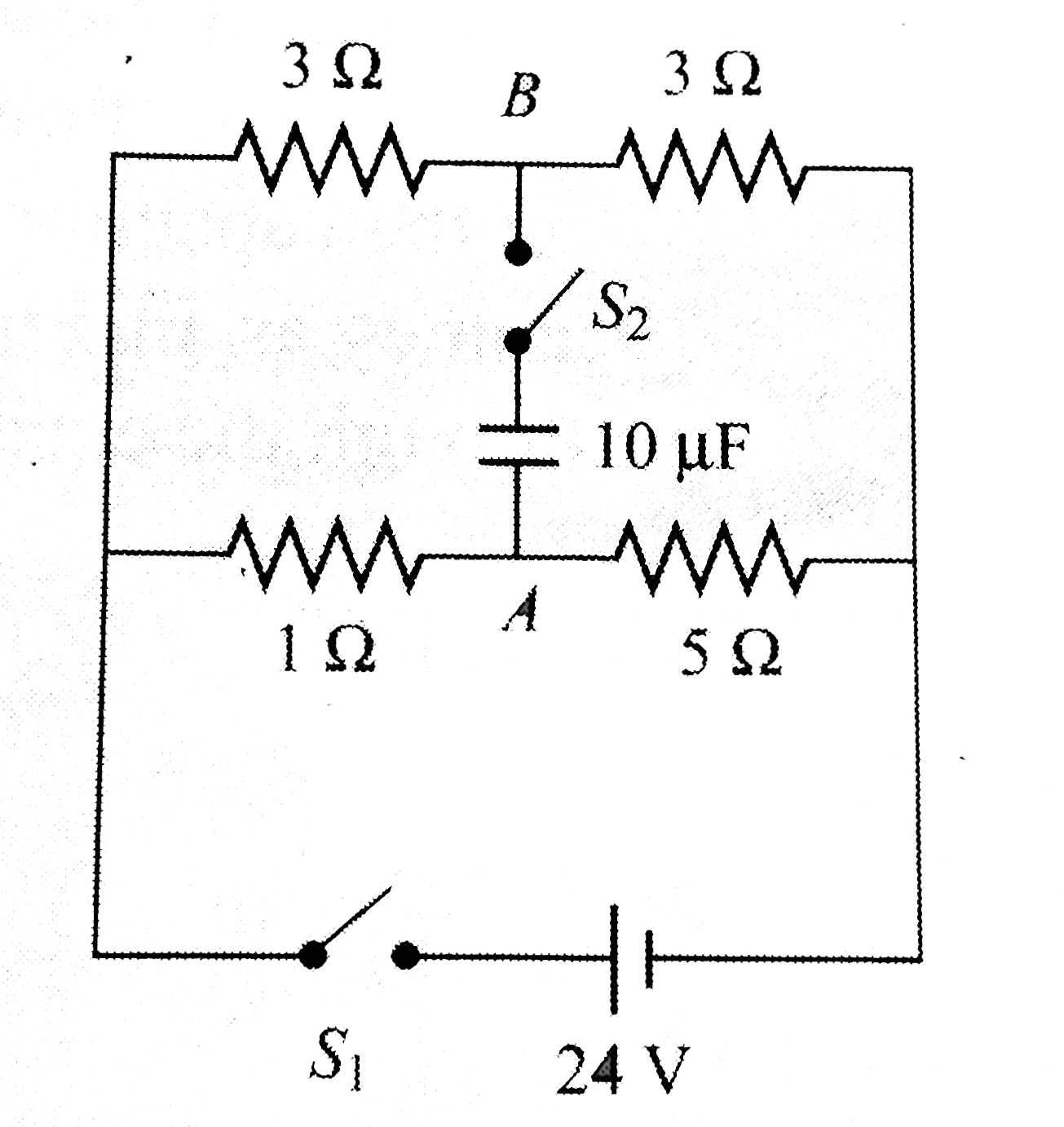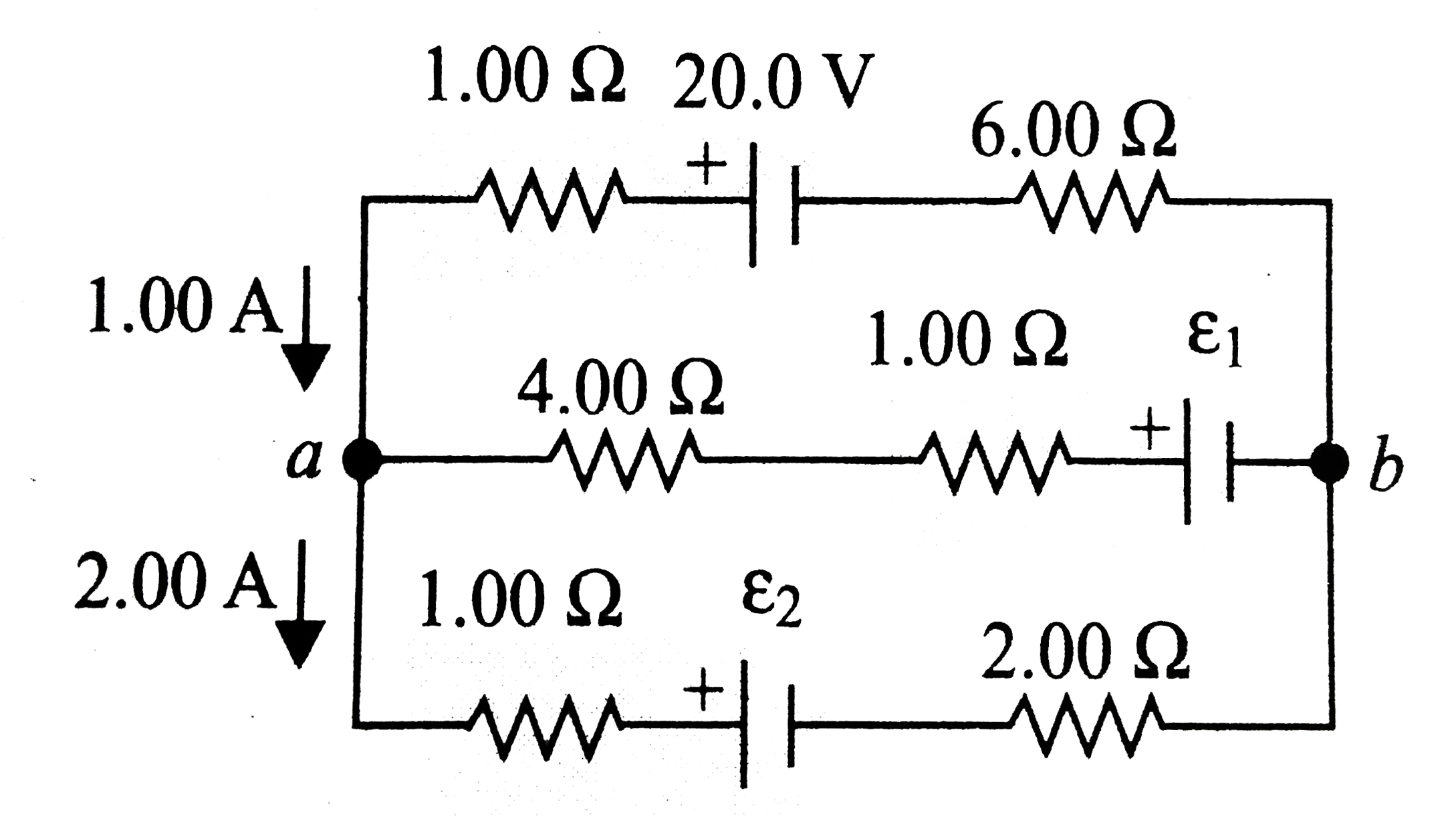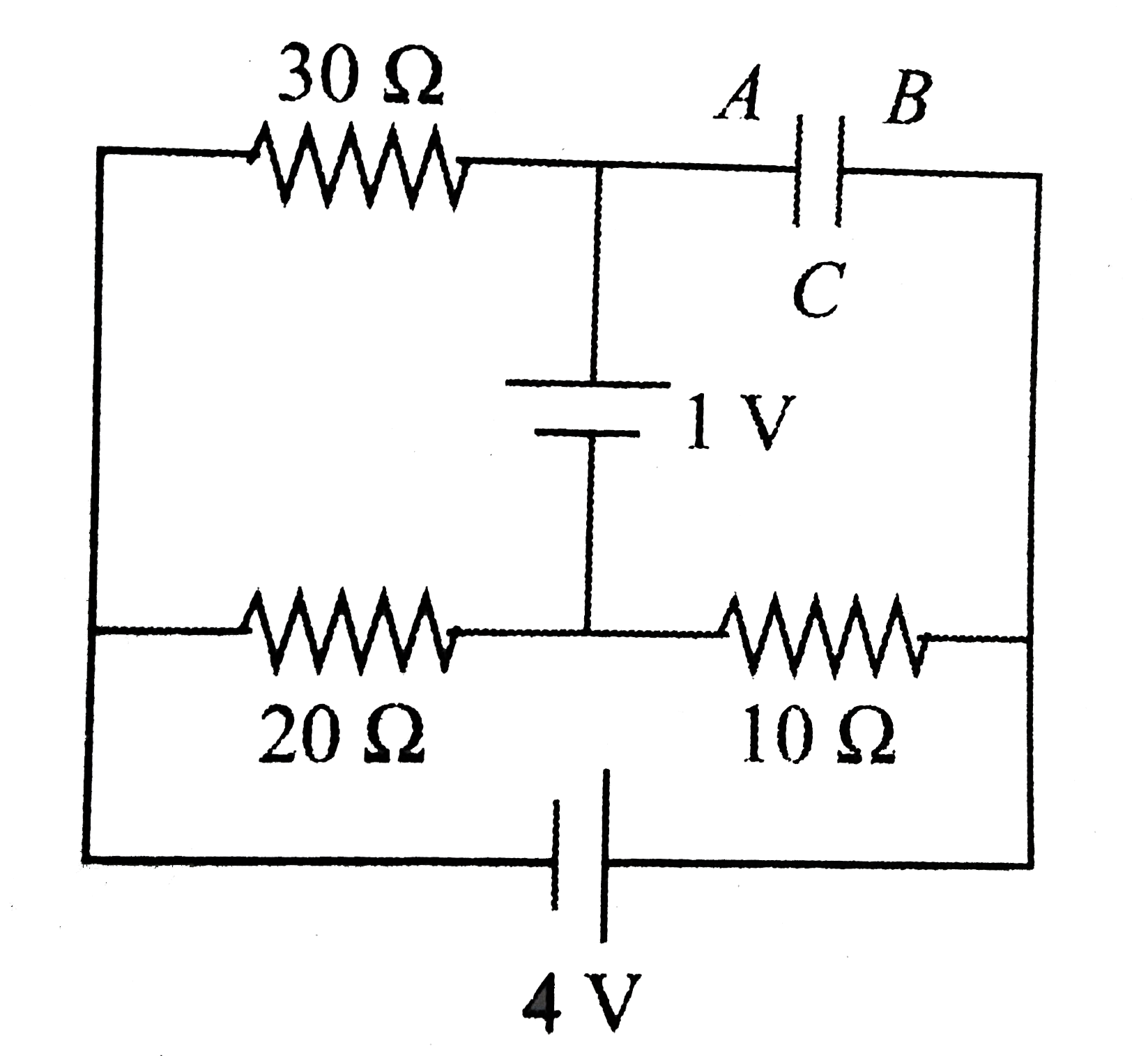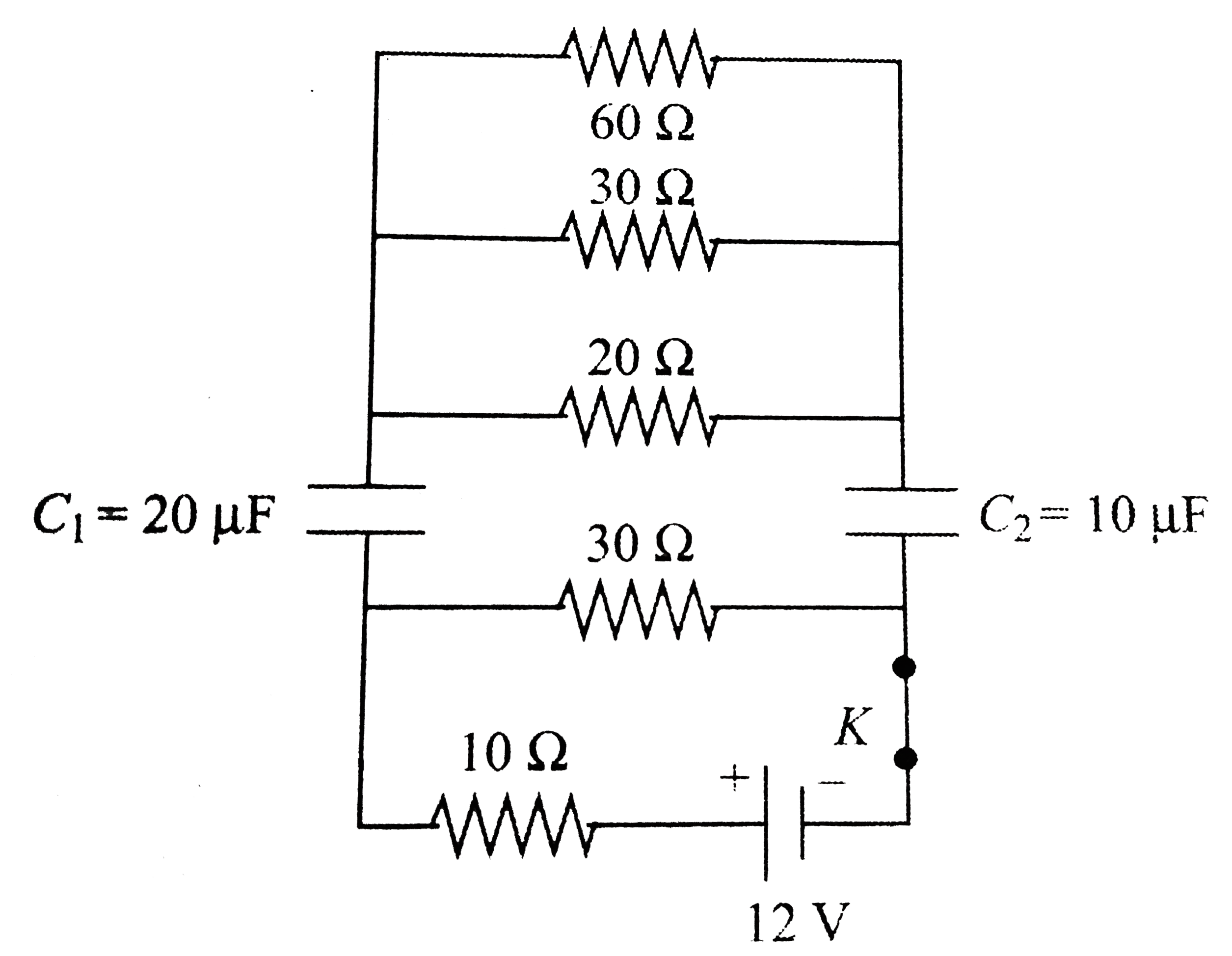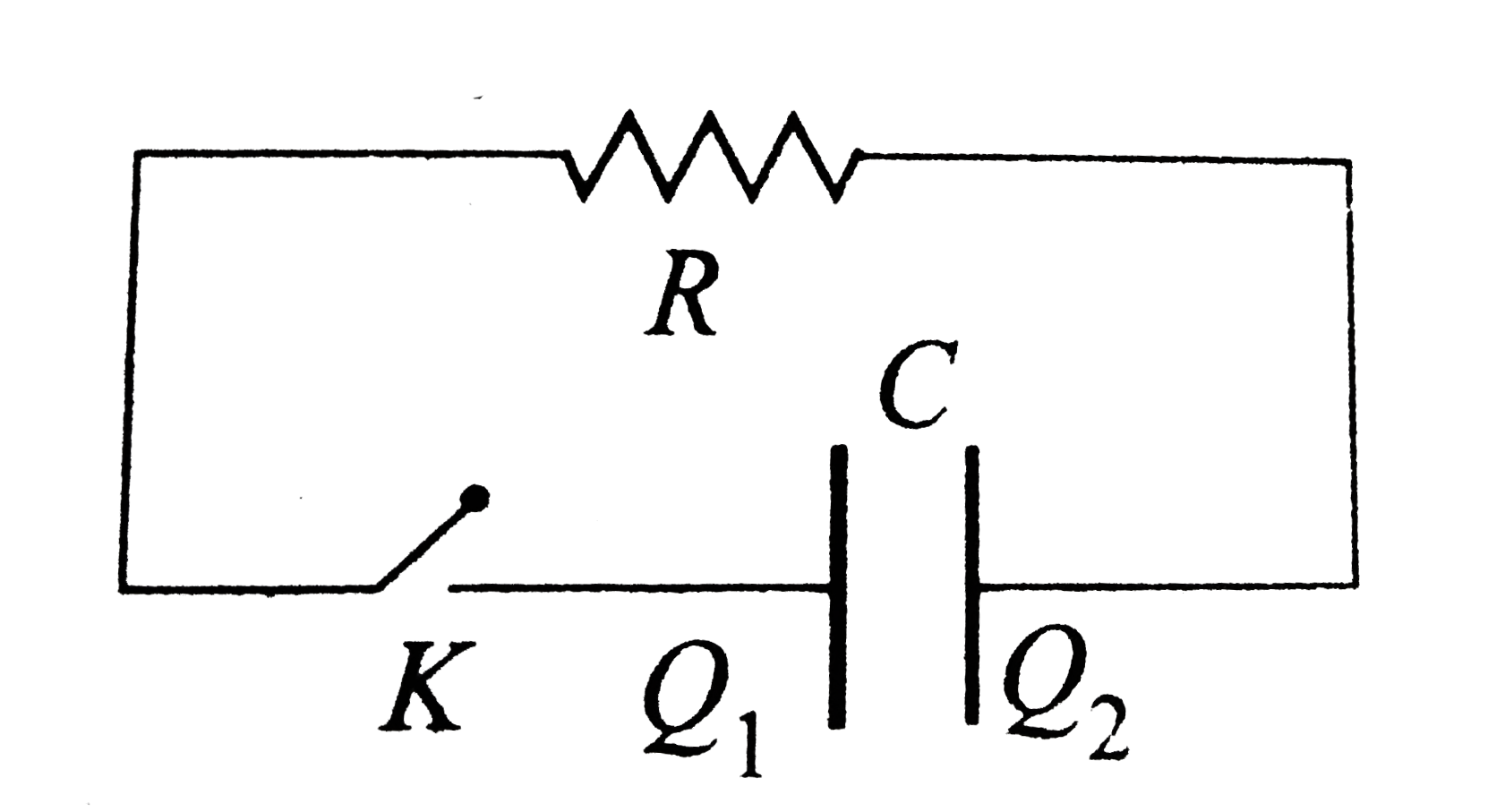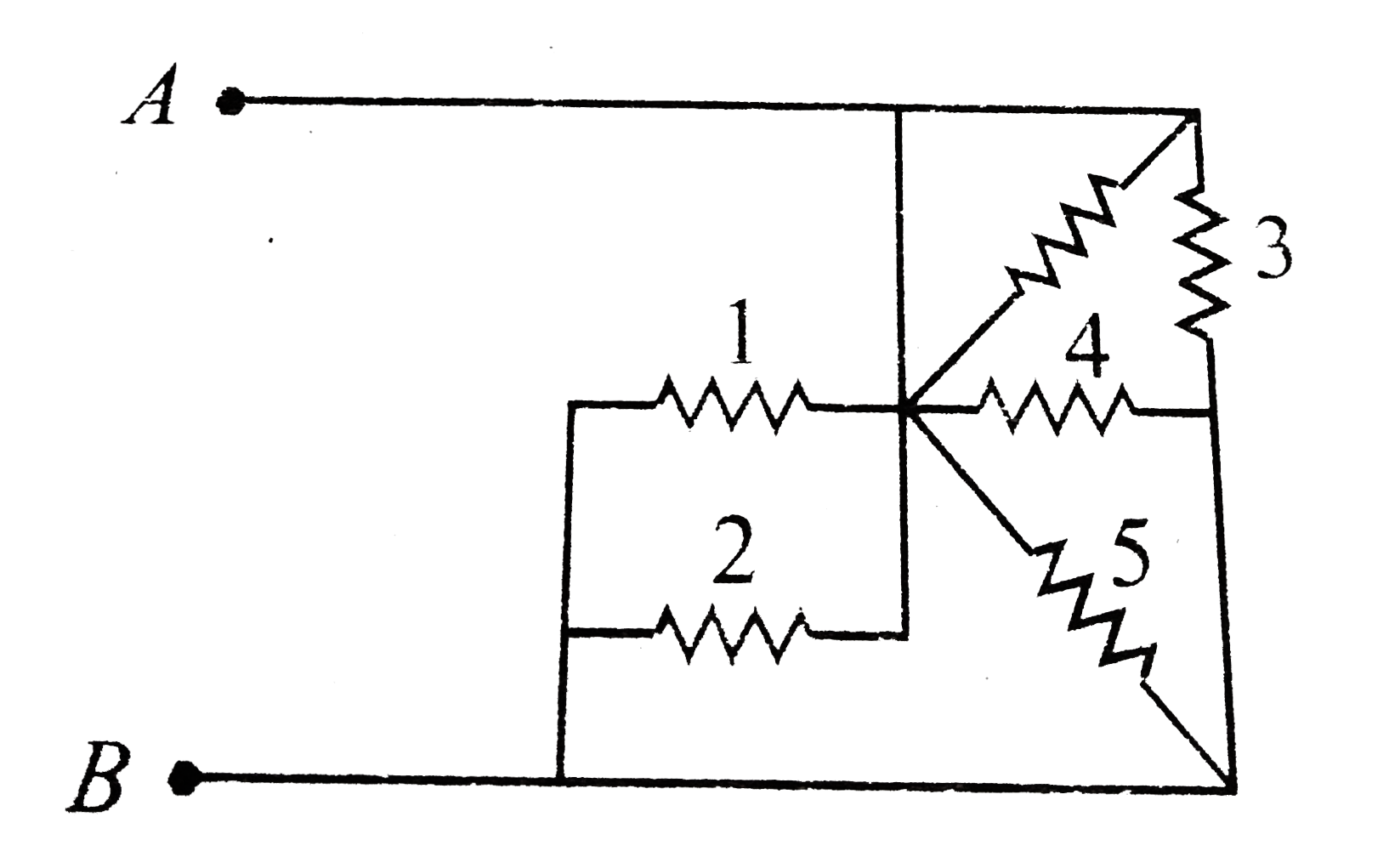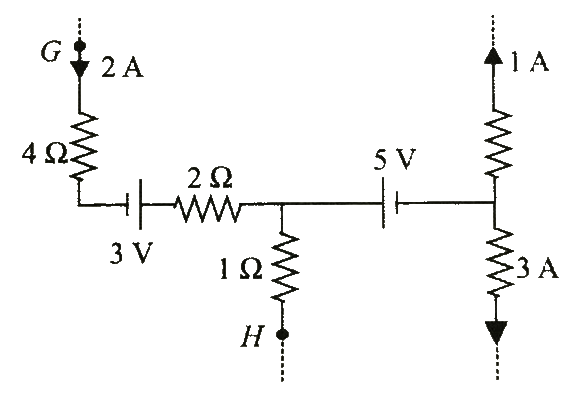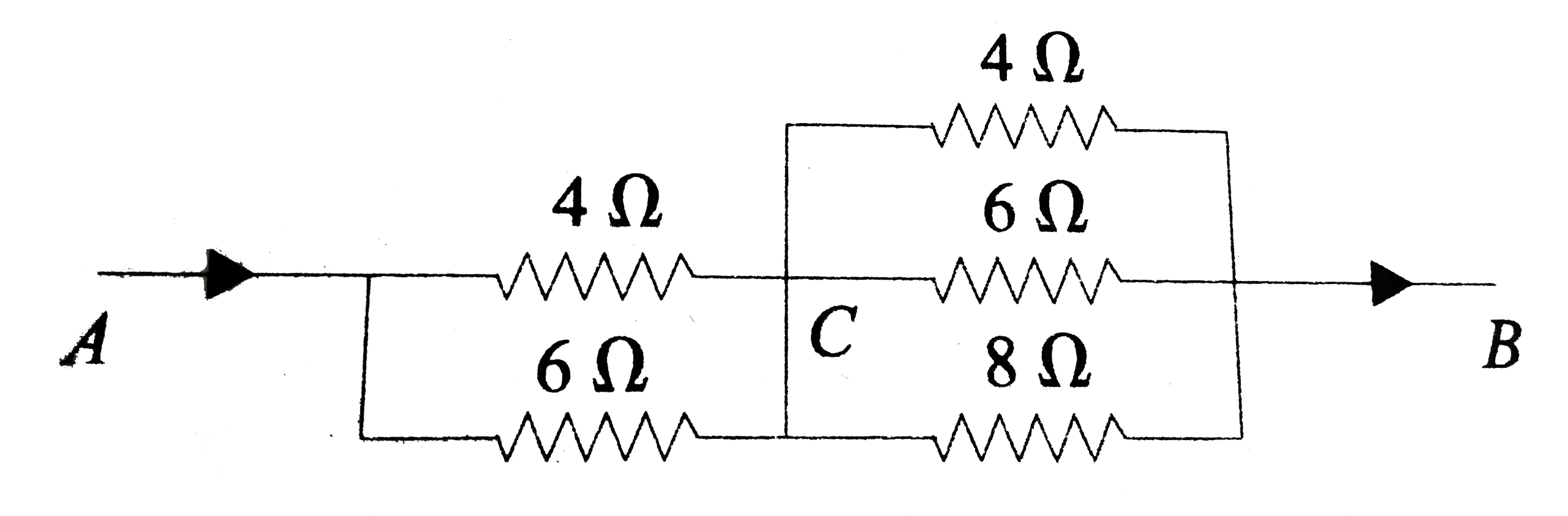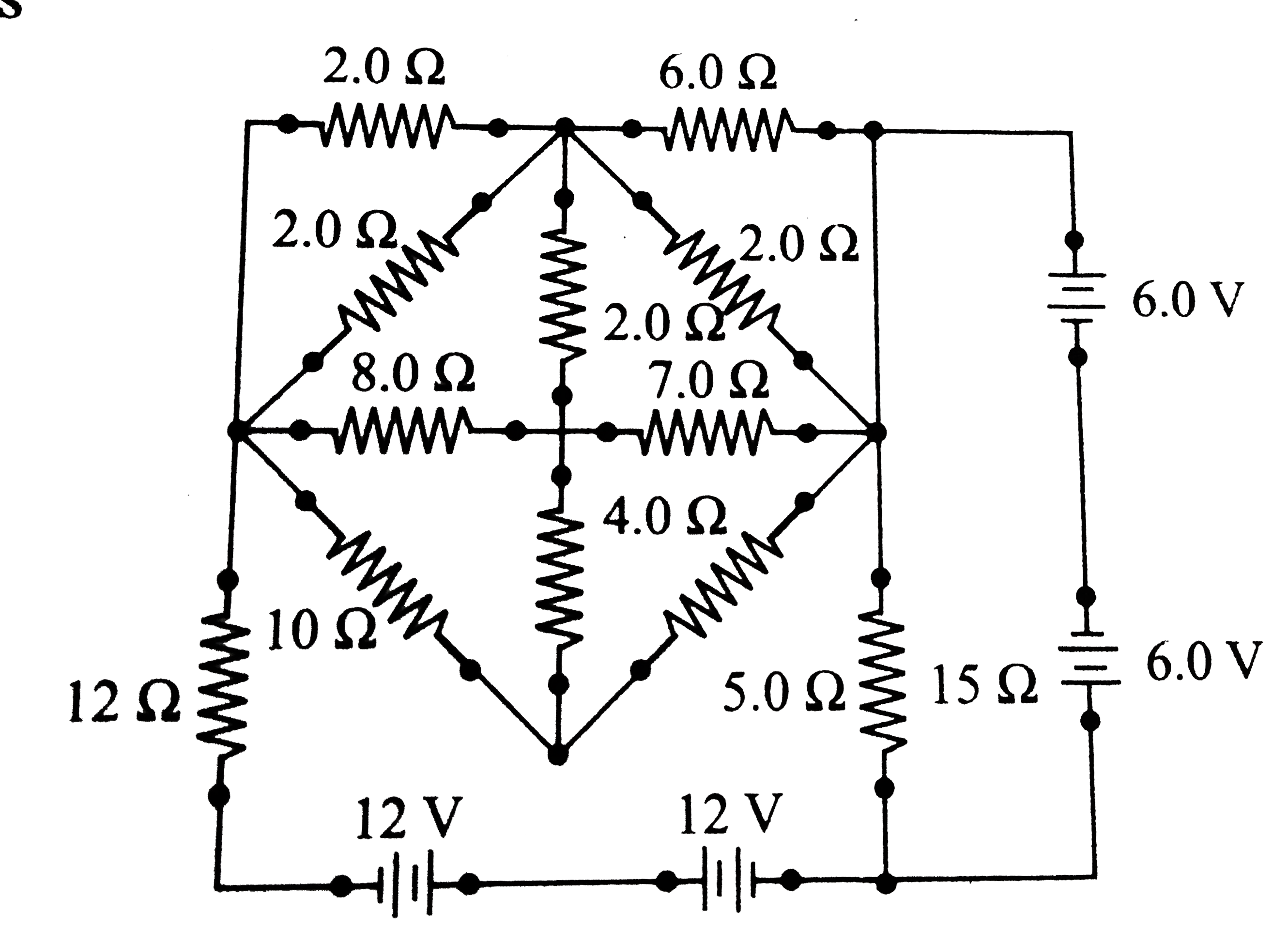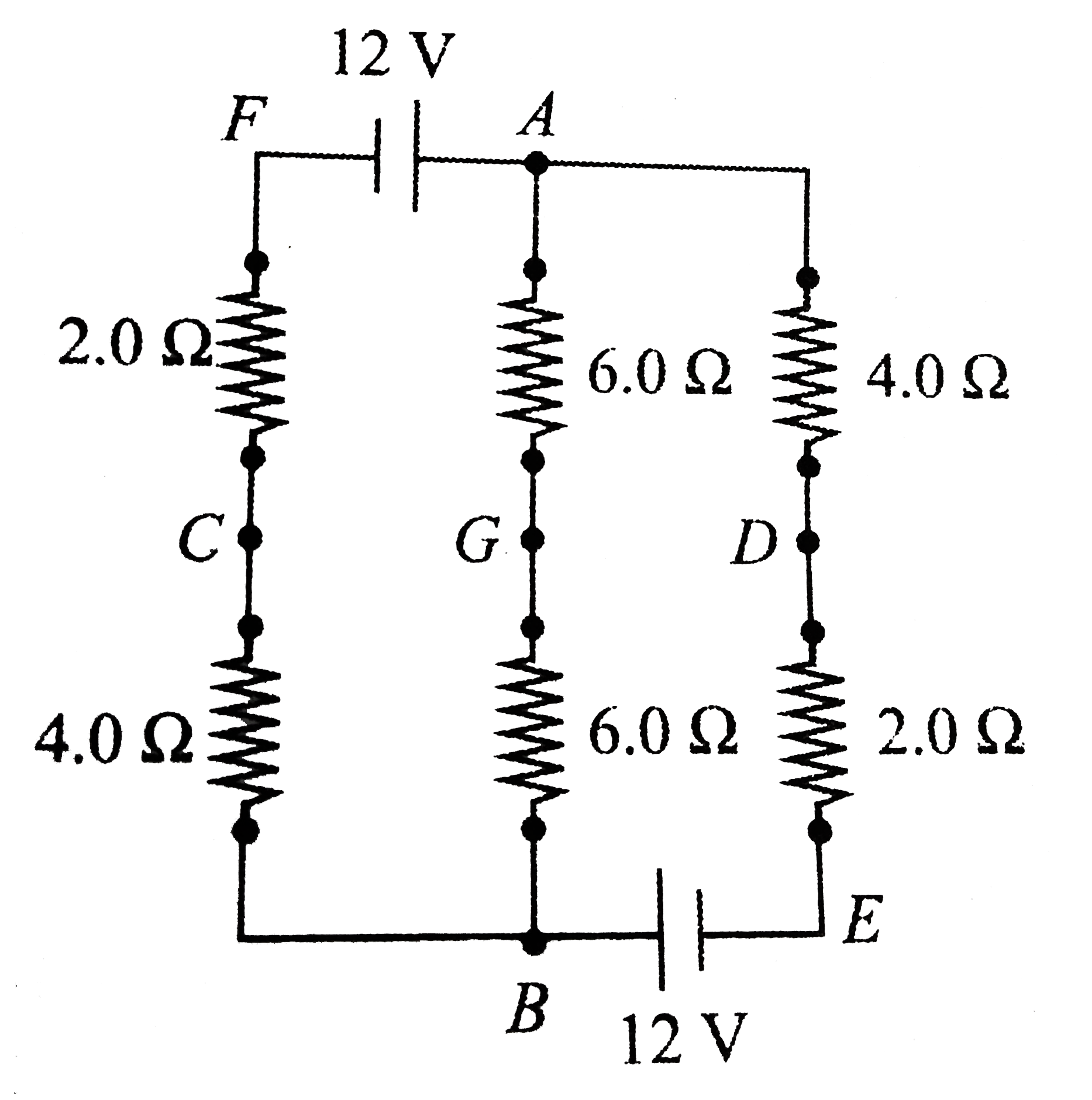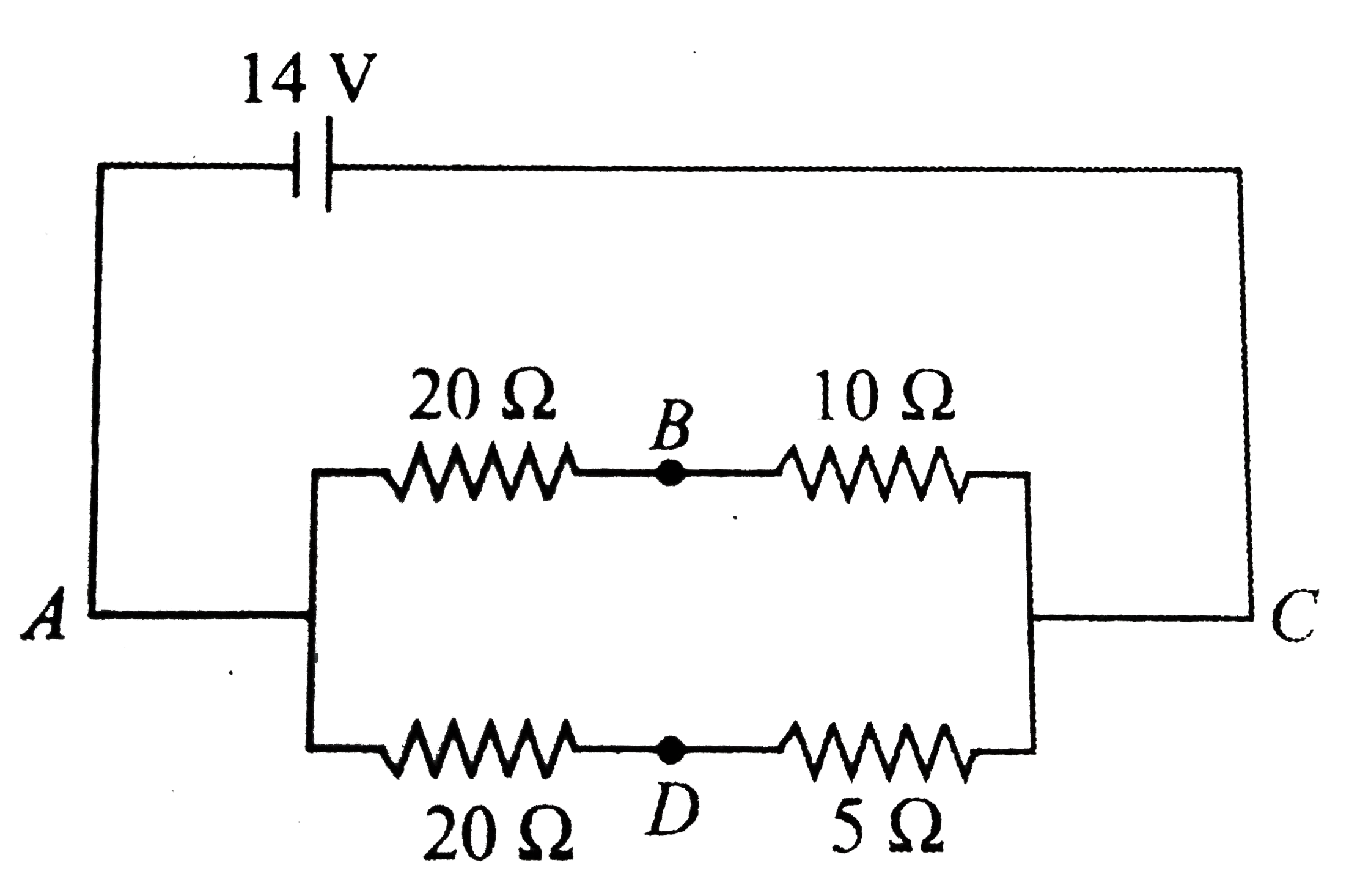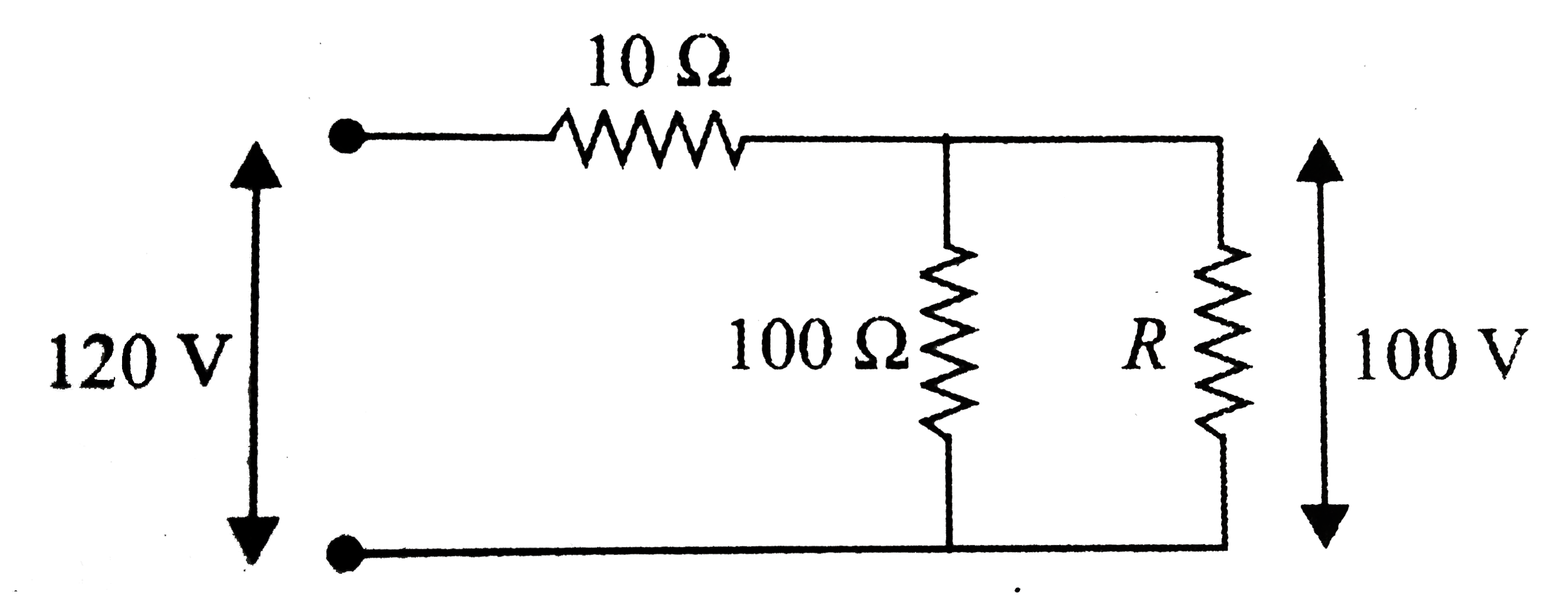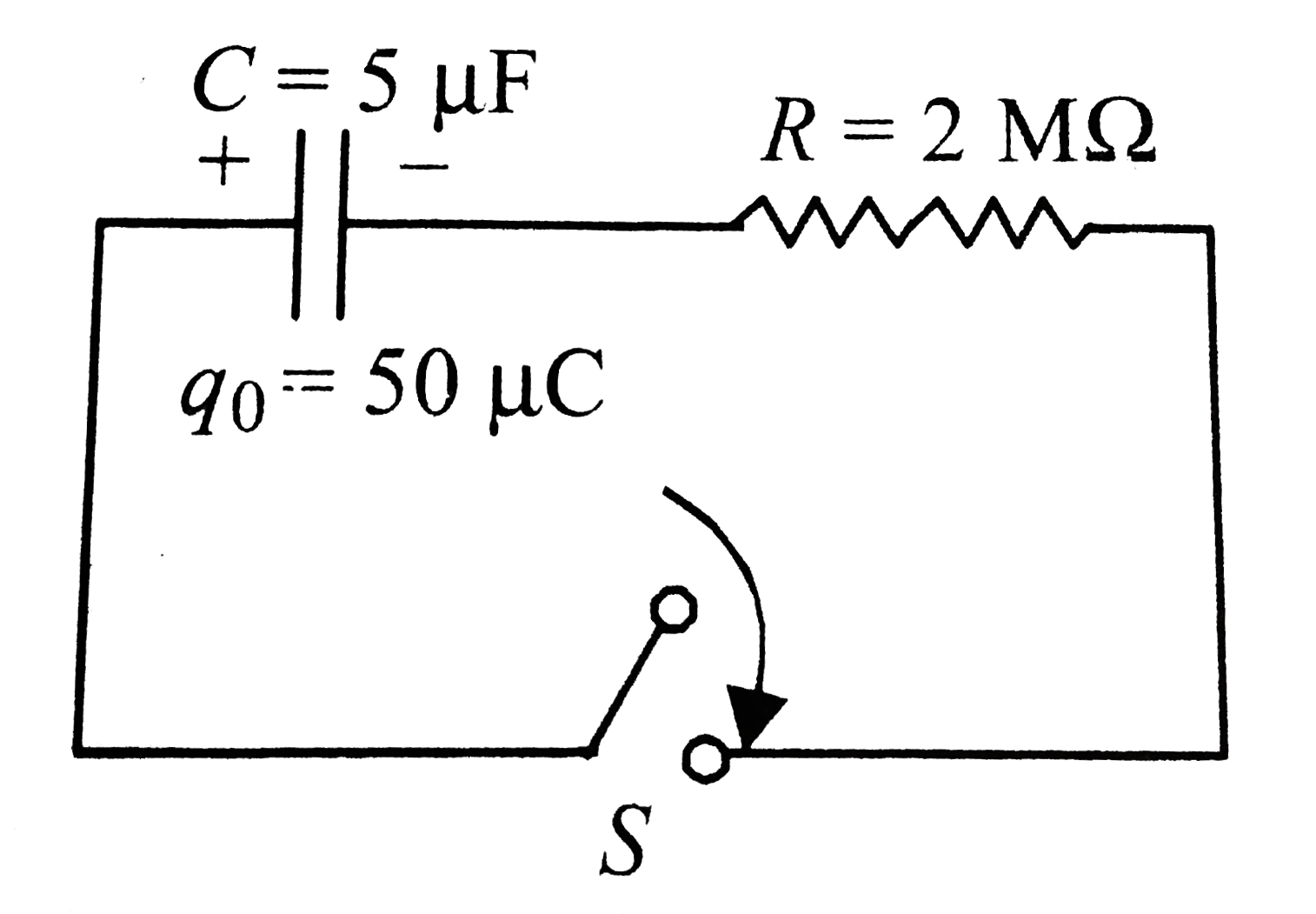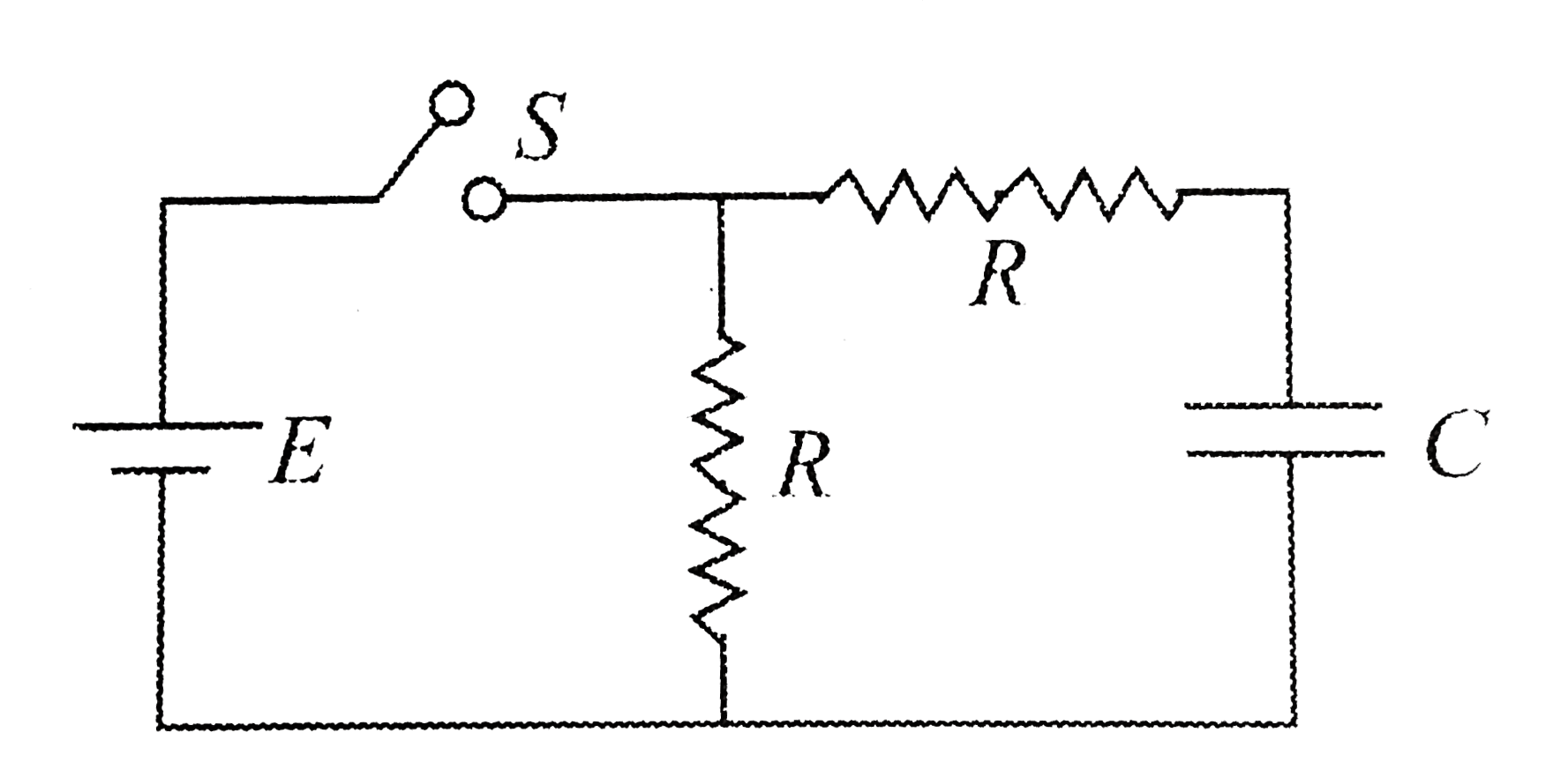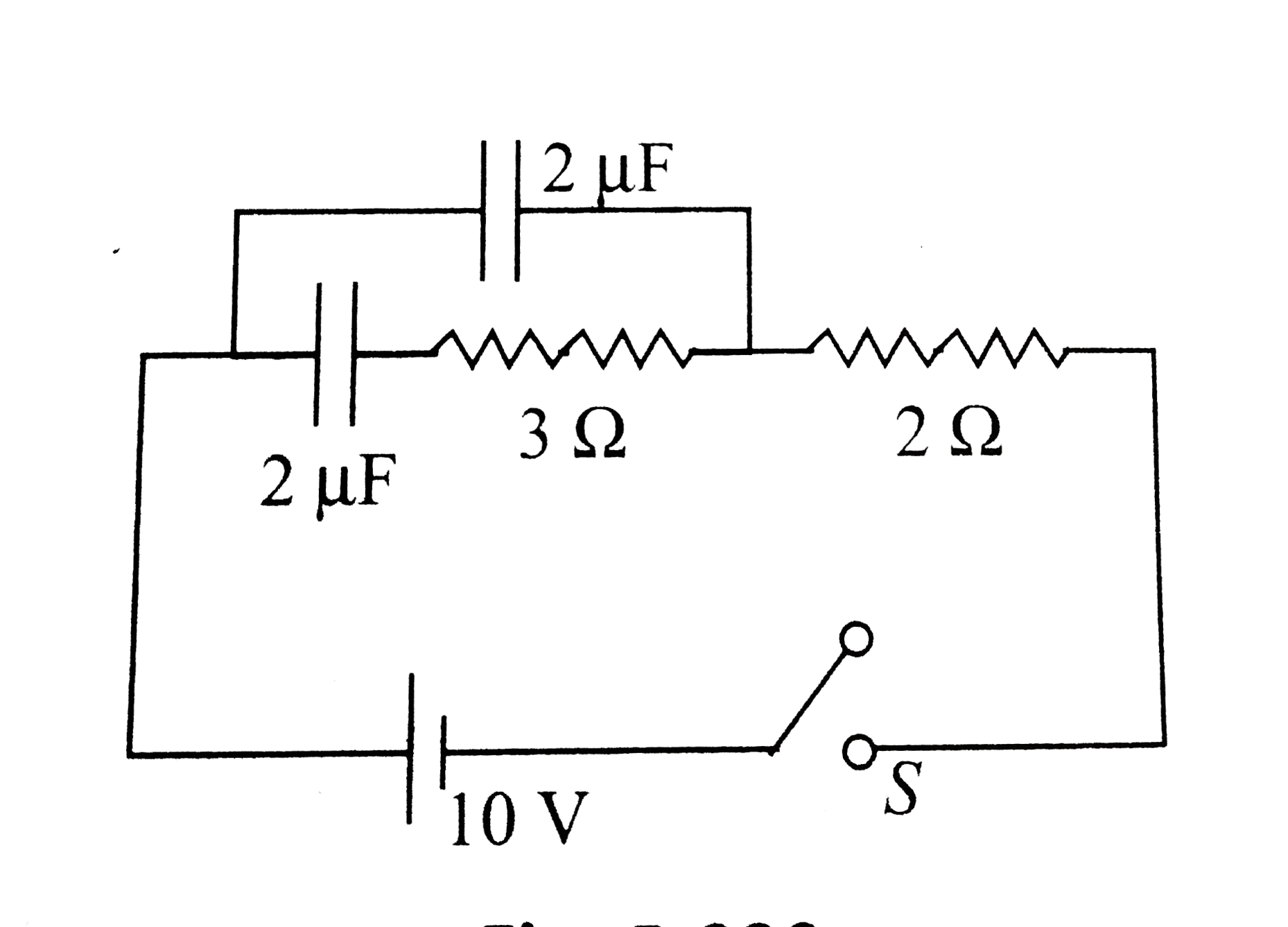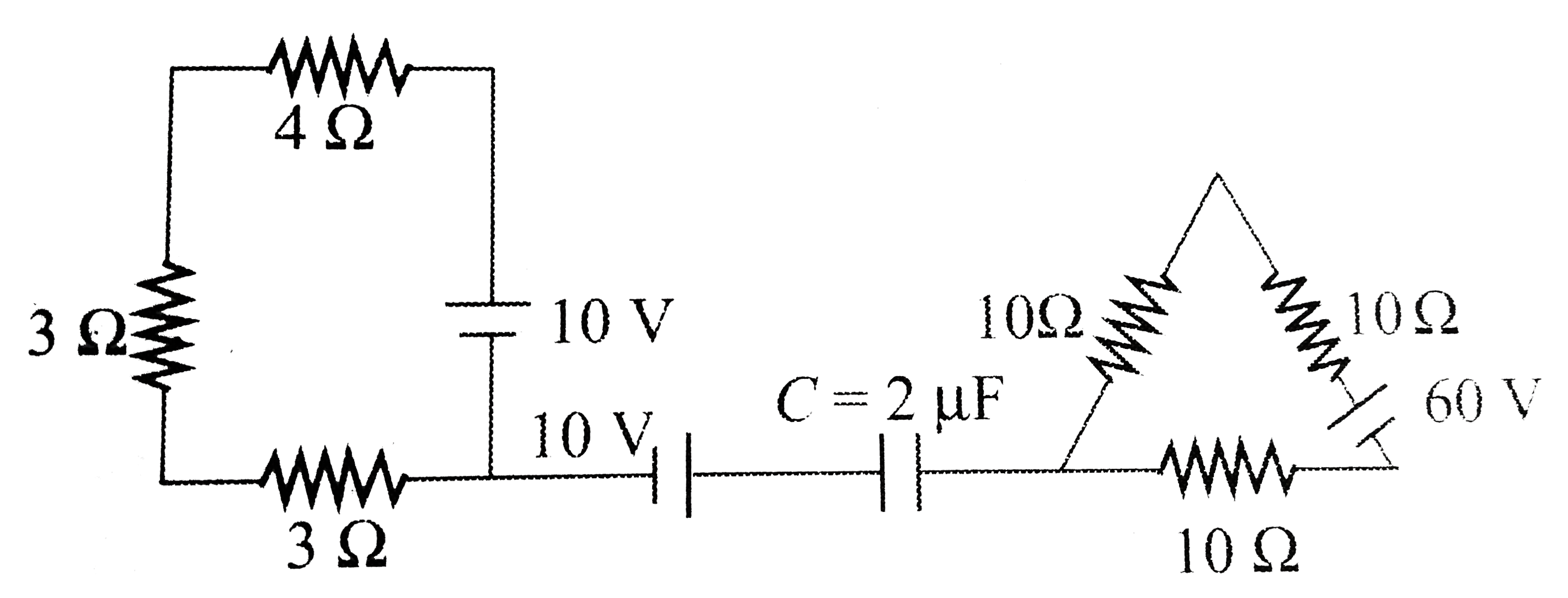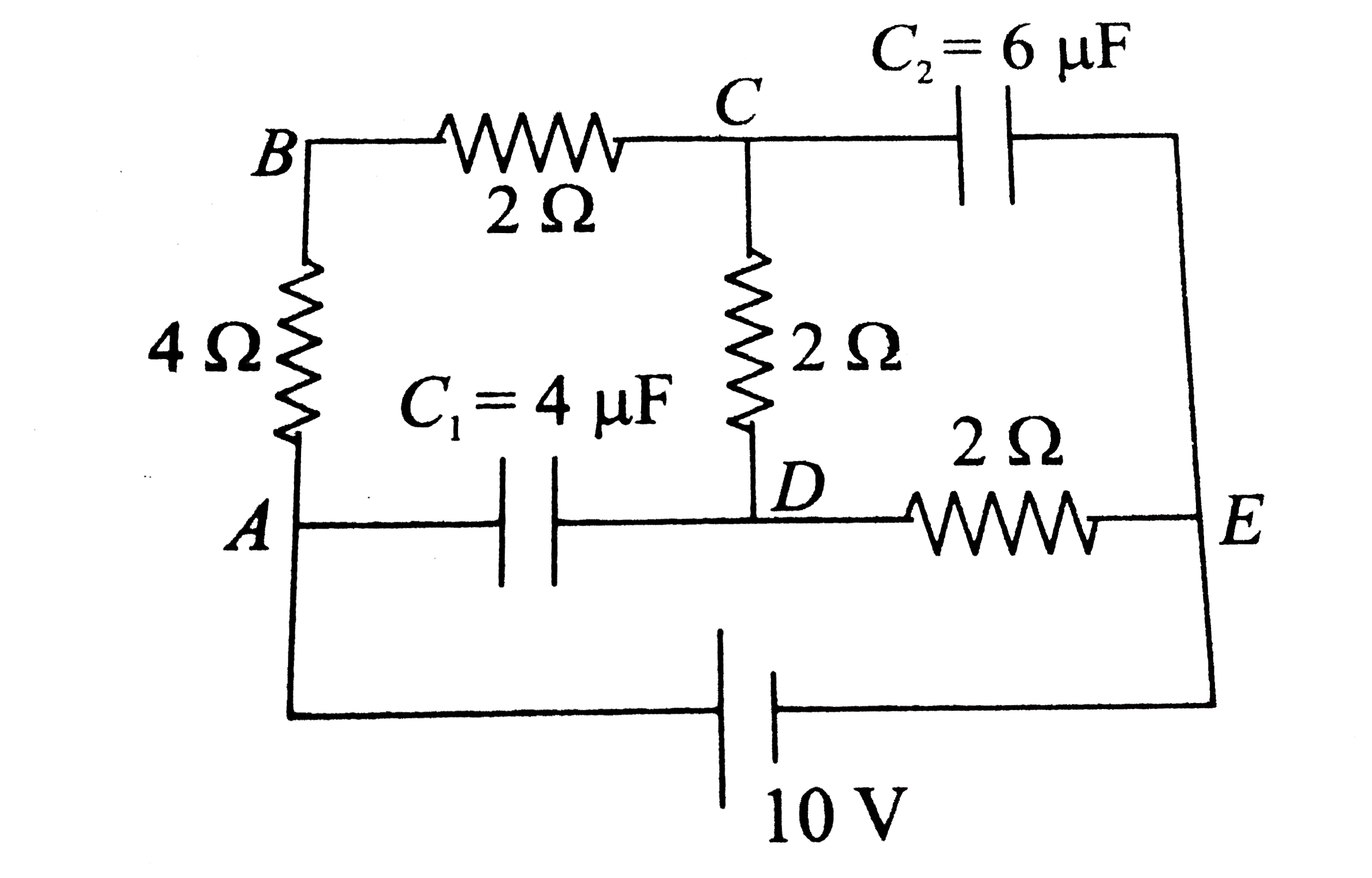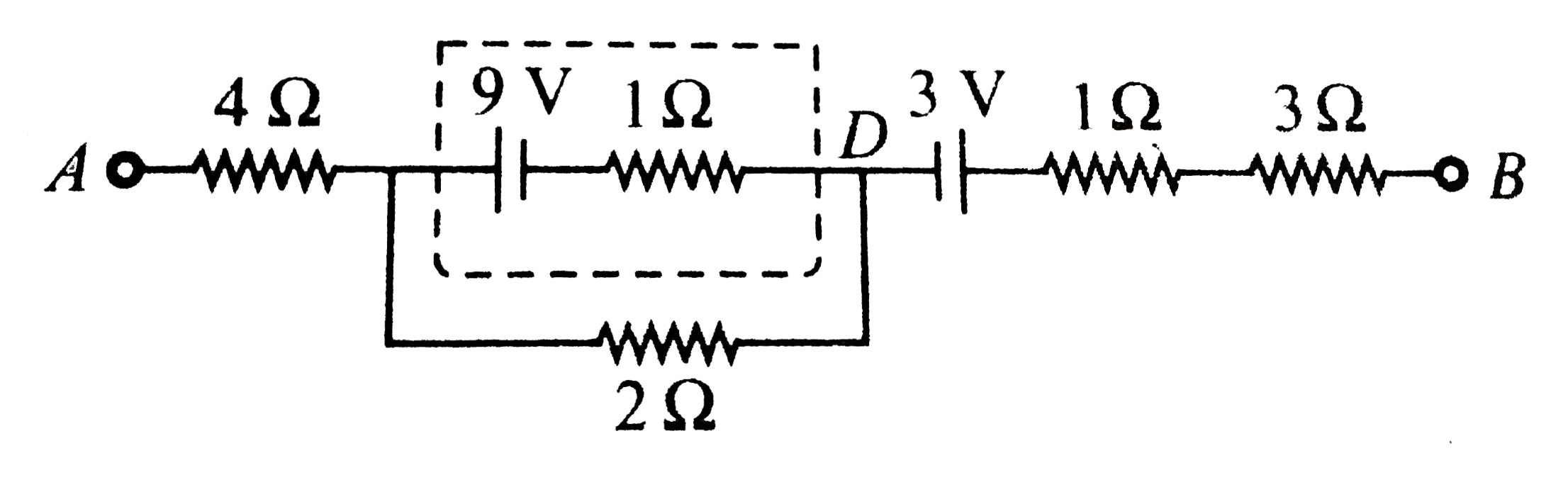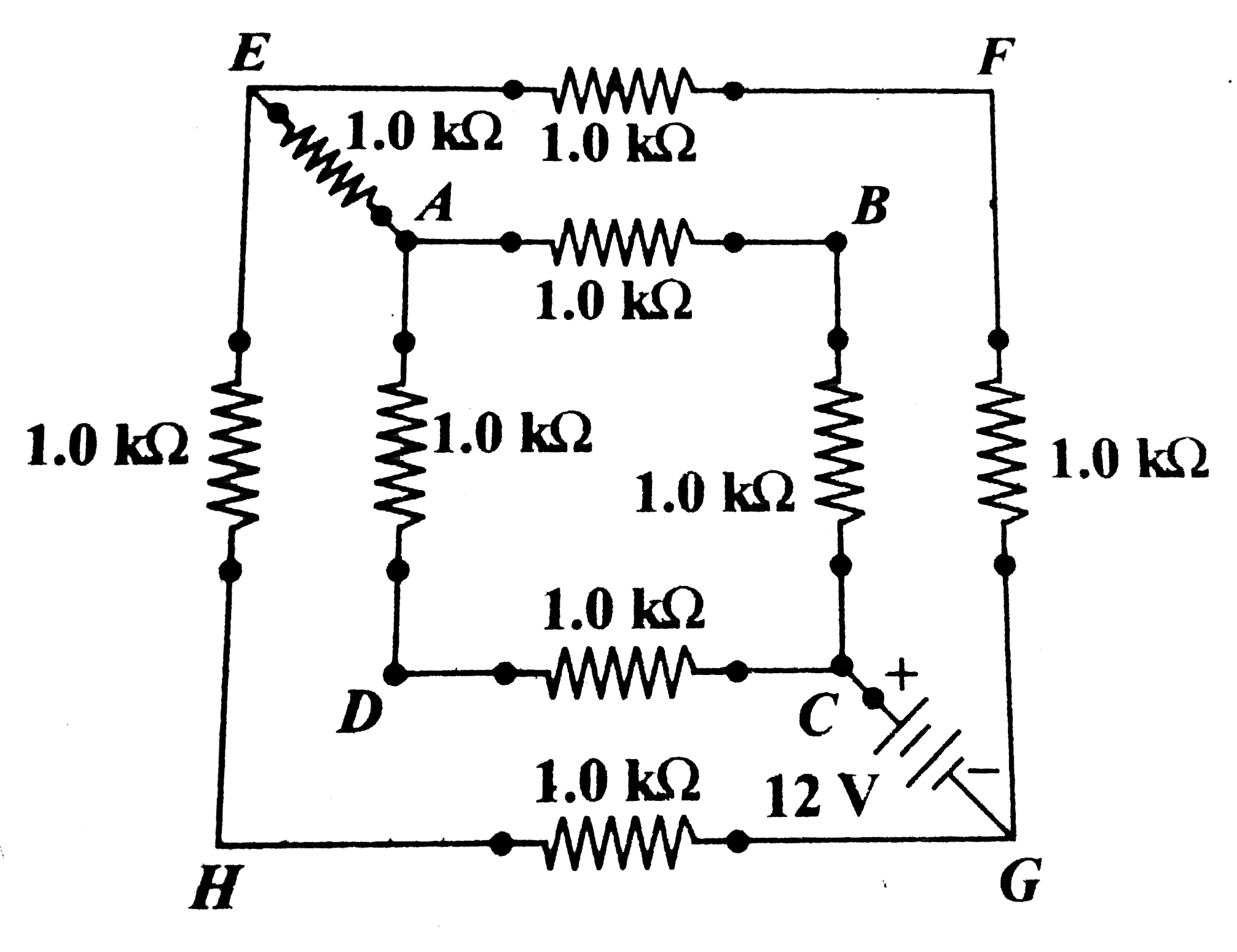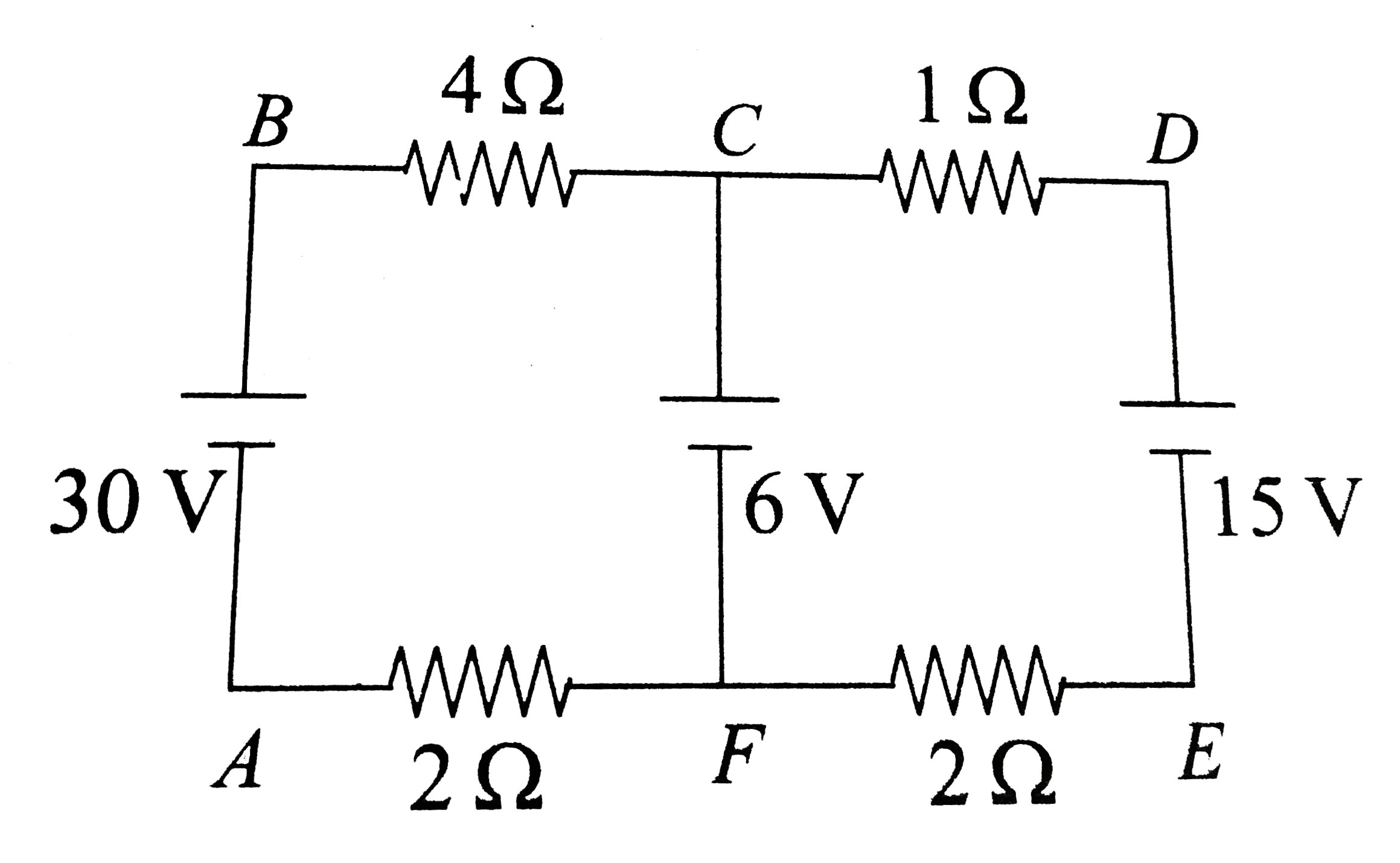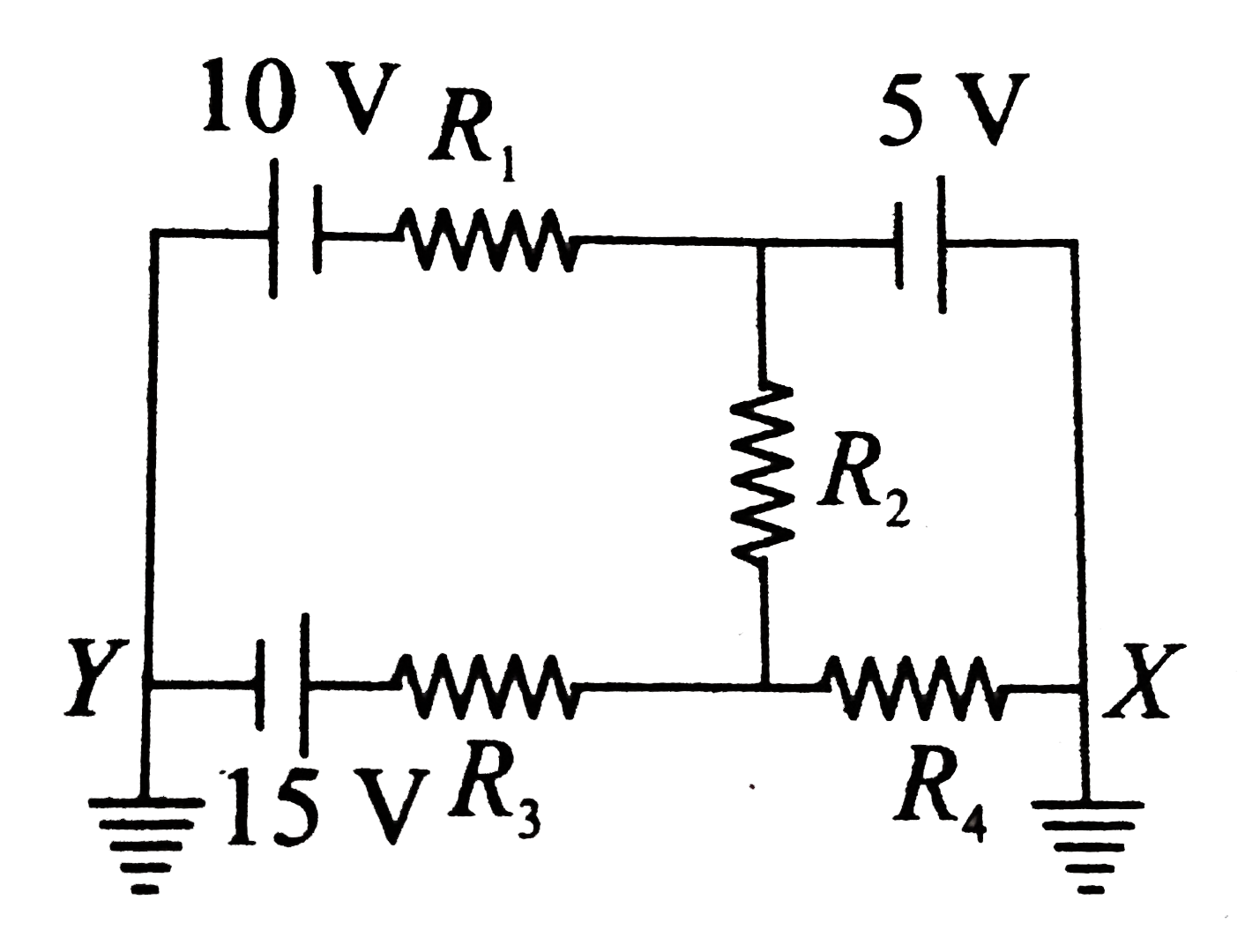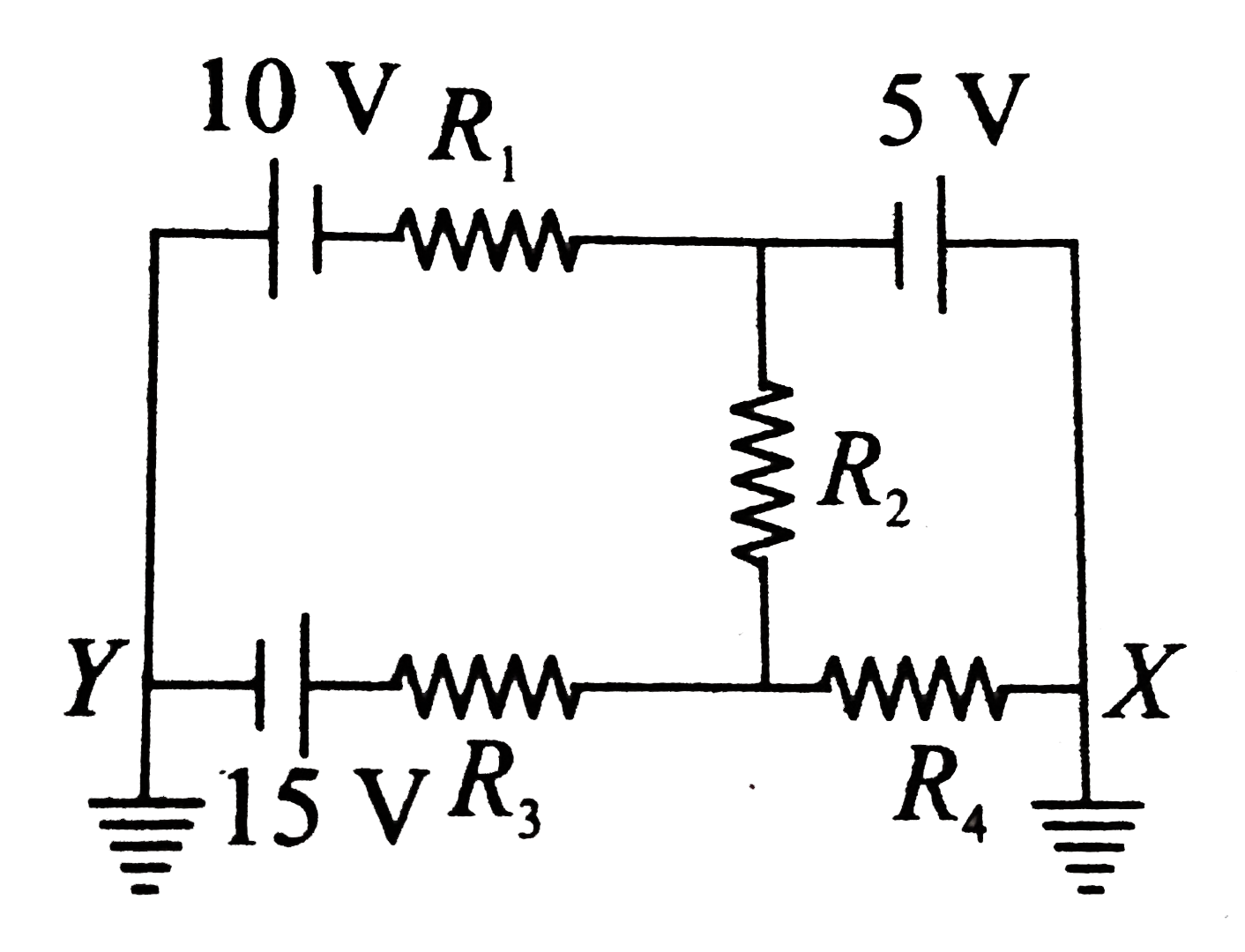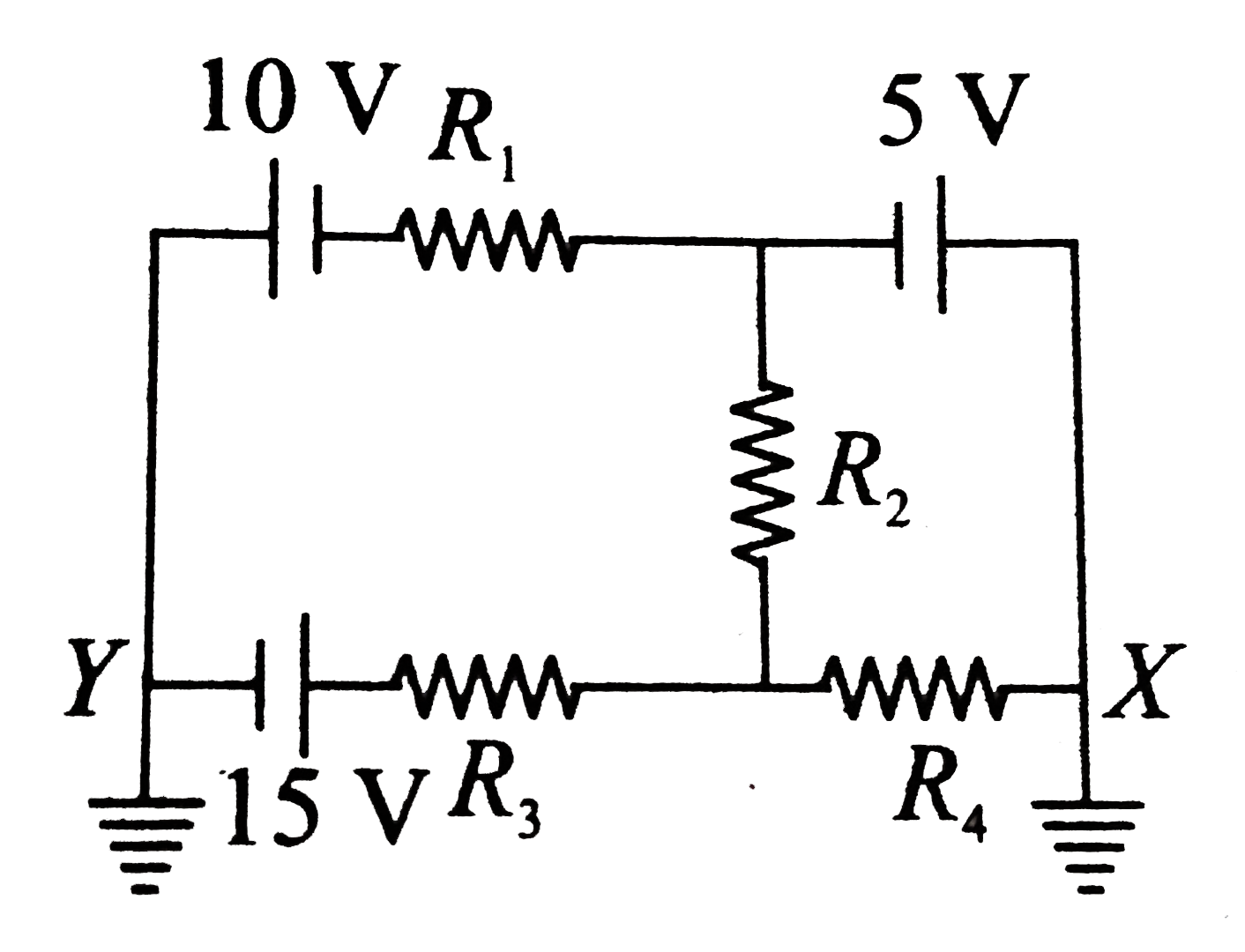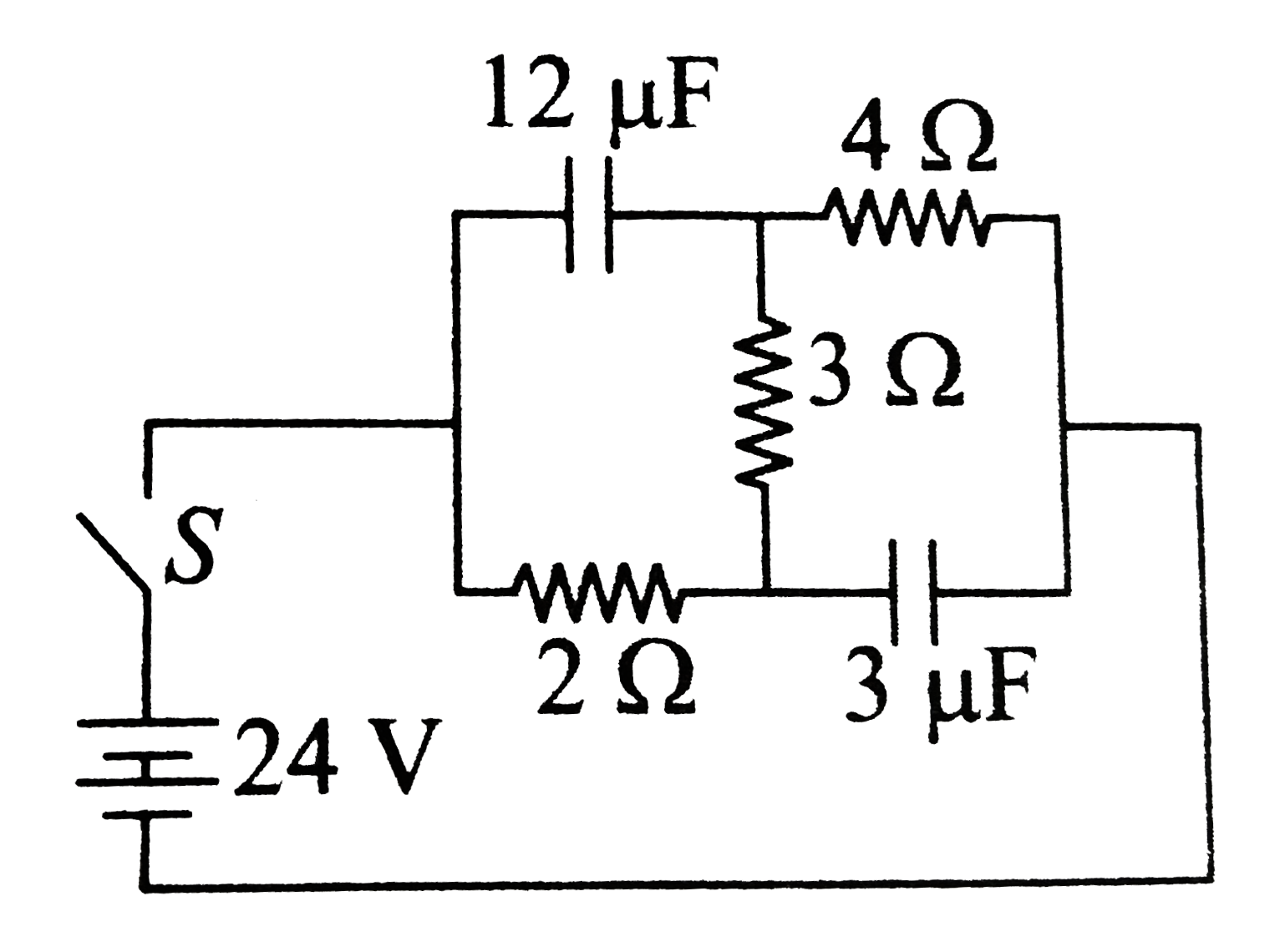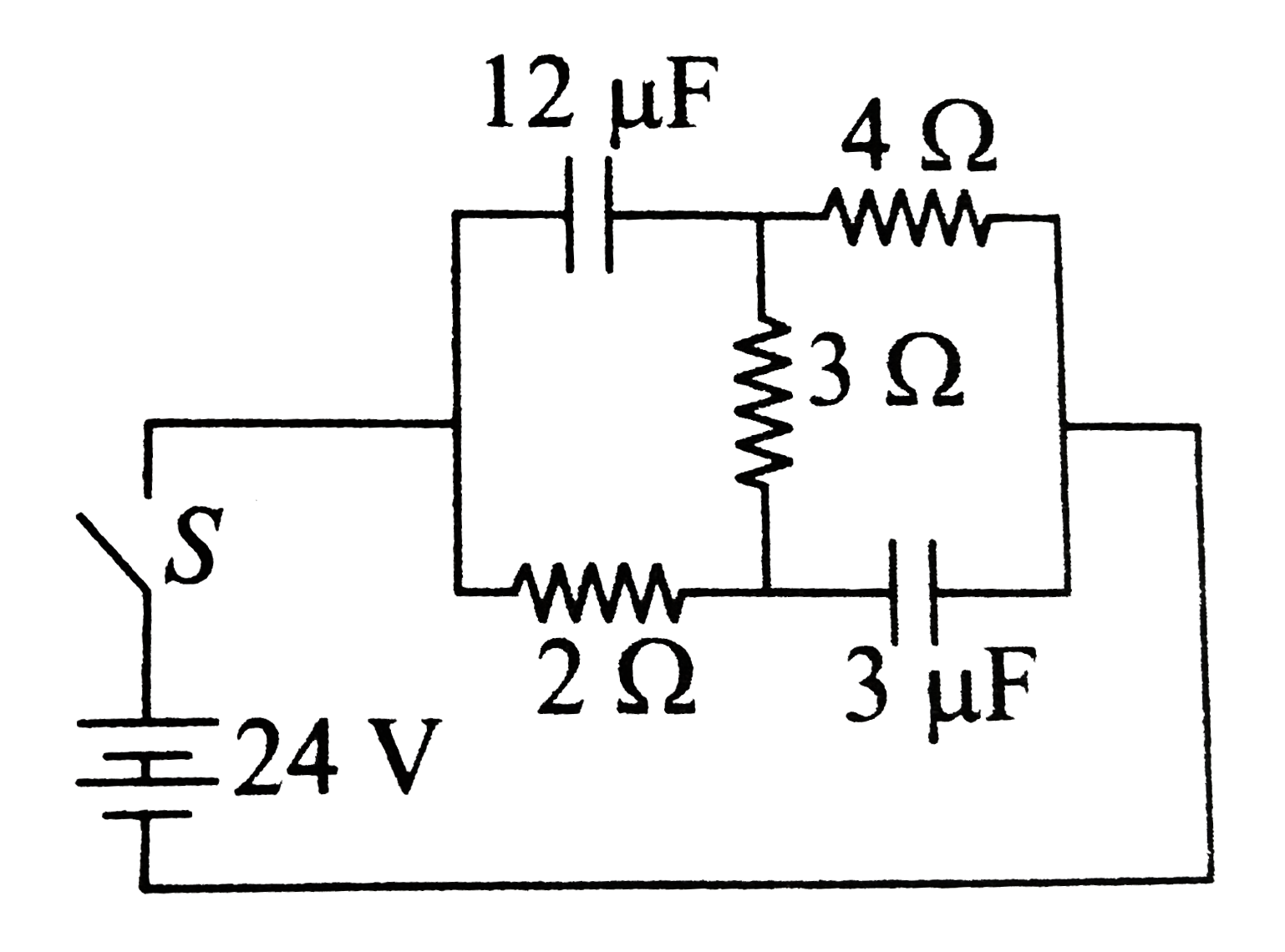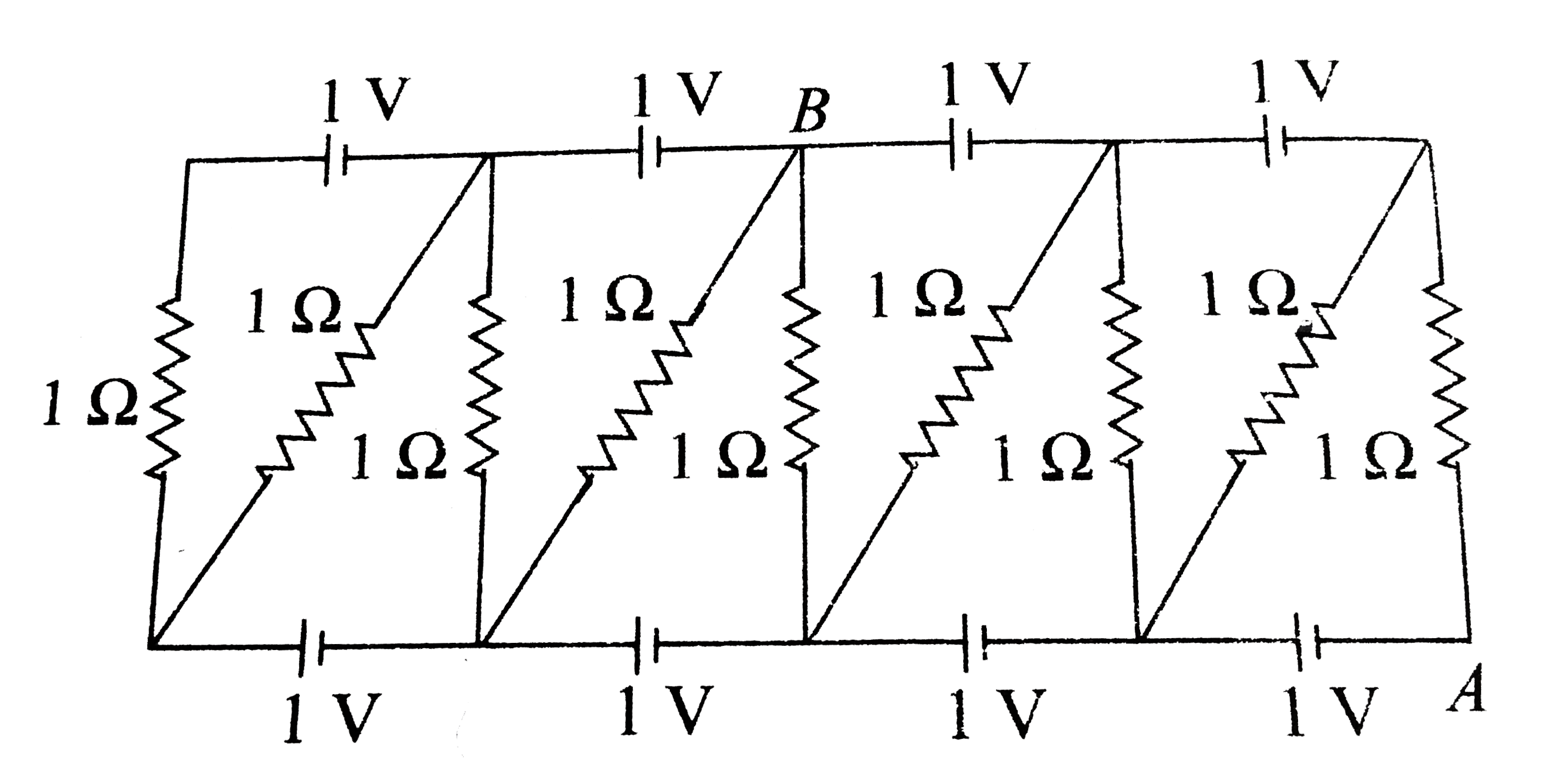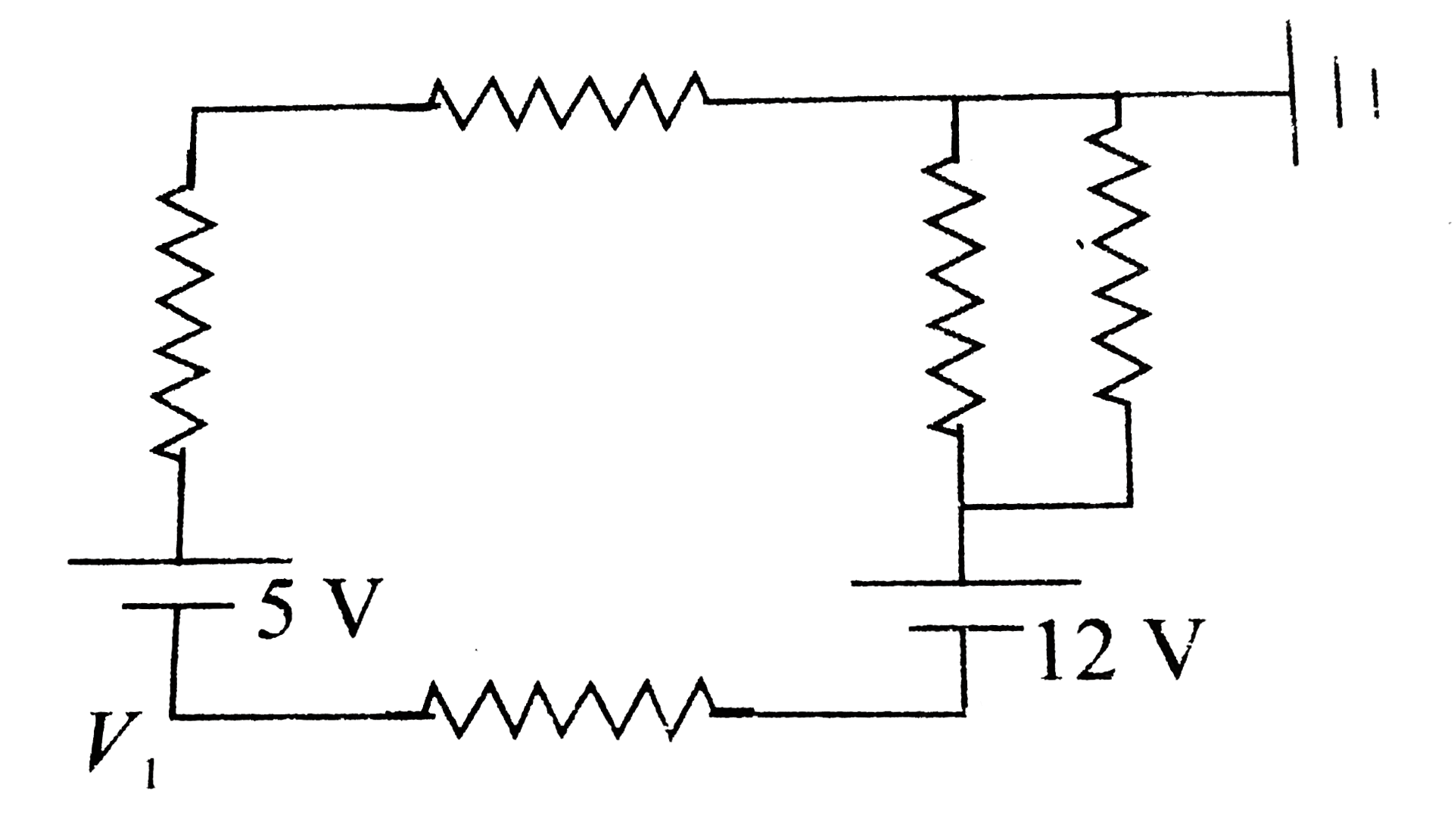Exercise 5.2 from CENGAGE PHYSICS (ENGLISH) ELECTRIC CURRENT AND CIRCUIT for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTRIC CURRENT AND CIRCUIT |
| CENGAGE PHYSICS (ENGLISH) | Exercise 5.2 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 4
A typical copper wire might have 2×1021 free electrons in 1 cm of its length. Suppose that the dirft speed of the electrons along the wire is 0.05cms−1. How many electrons would pass through a given cross section of the wire each second. How large would a current be flowing in the wire?View SolutionQuestion 7
It is desired to make a 20Ω coil of wire, which has a zero thermal coefficient of resistance. To do this, a carbon resitor fo resistane R1 is placed in series with an iron resistor of resistance R2 the proportions of iron and carbon are so chosen that R1+R2=20Ω for all temperatures near 20∘C. How long are R1andR2? αcarbon=−0.5×10−3.∘C−1,αiron=5×10−3.∘C(−1) View SolutionQuestion 10
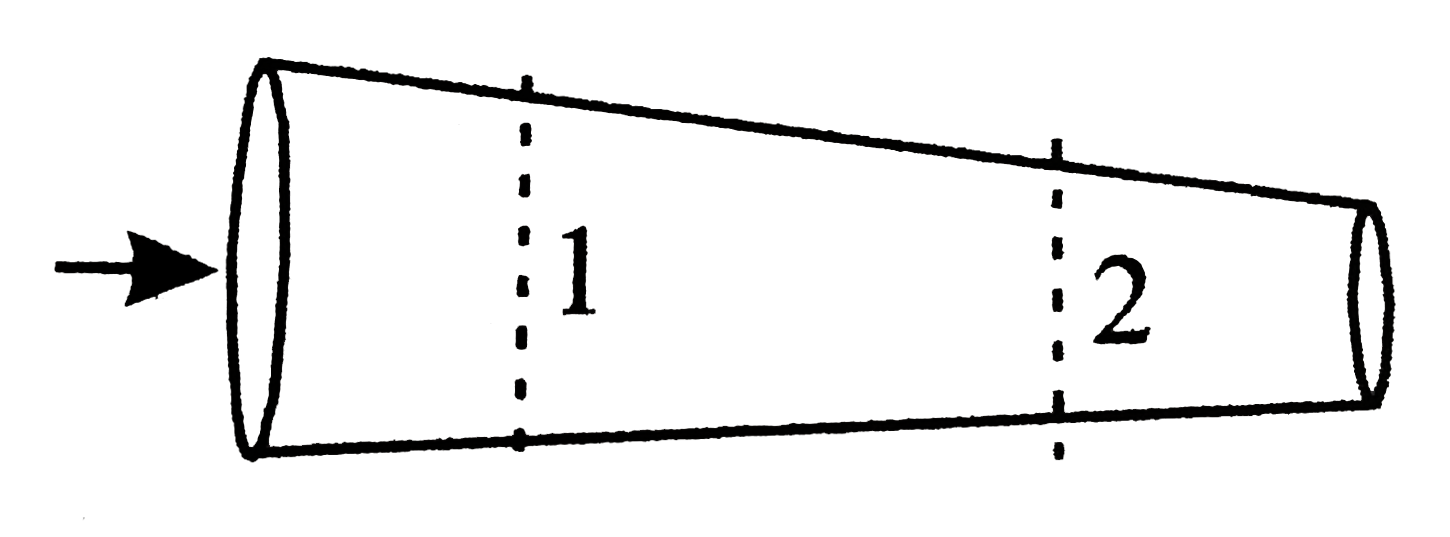
a. A steady current flows in a metallic conductor of non - uniform cross section. State which of the quantities i.e., current density, electric field, and drift velocity remain constant?
b. A steady current passes through a cylindrical conductor. Is there an electorn field inside the conductor?View SolutionQuestion 14
The following table gives the length of three copper rods, their diameters, and the potential differences between their ends. Rank the rods according to (a) the magnitude of the electric field within them, (b) the current density within them, and (c ) the drift speed of electrons through them, greates first.
 View Solution
View SolutionQuestion 17
A beam contains 2.0×108 doubly charged positive ions per cubic centimeter, all of which are moving toward north with a speed of 1.0×105ms−1. (a) what are the magnitude and direction of the current density →J? (b) can you calculate the total current i in this ion beam? If not what additional informaiton in needed.View SolutionQuestion 18
The current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.View SolutionQuestion 21
A copper wire having cross- sectional area of 0.5mm2 and a length of 0.1 m is initially at 25∘C and is thermally insulated form the surrounding. If a current of 10A is set up in this wire, find the time in which the wire will start melting. For copper, resistivity is 1.6×10−8Ωm, density is 9,000kgm−3 and specific heat capacity is 0.09calg−10C−1. Melting temperature fo copper is 1075∘CView SolutionQuestion 22
A copper wire having cross- sectional area of 0.5mm2 and a length of 0.1m is initially at 25∘C and is thermally insulated form the surrounding. If a current of 10A is set up in this wire, (a) find the time in which the wire will start melting. (b) What will be the change of resistance with time, if the length of the wire is doubled? For copper, resistivity is 1.6×10−8Ωm, density is 9,000kgm−3 and specific heat capacity is 0.09calg−1C−1. Melting temperature of copper is 1075∘CView SolutionQuestion 24
What is the drift speed of the conduction electrons in a copper wire with radius r = 900 micrometer when it has a uniform current I = 17mA? Assume that each copper atom contributes one conduction electron to the current and the current density is uniform across the wire's cross section. The density of copper is 9000 kg/m^3 and atomic mass is 63.5u .View SolutionQuestion 26
A potential difference is applied across the filament of a bulb at t =0, and it is maintained at a constant value while the filament gets heated to its equilibrium temperature. We find that the final current in the filament is one sixth of the current drawn at t = 0. if the temperature of the filament at t = 0 is 20∘C and the temperature coefficient of resistivity at 20∘C is 0.0043∘C−1, find the final temperature of the filament.View SolutionQuestion 27
The space between the plates orf a parallel plate capacitor is completely filled with a meterail of resistaivity 2×1011Ωm and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the paltes is 20uF. Find the leakage current if a potential difference 2500 V is applied across the capacitor.View SolutionQuestion 28
A uniform copper wire of mass 2.23×10−3 kg carries a current of 1 A when 1.7 V is applied across it. Calculate the length and the area of cross section. If the wire is uniformly stretched to double its length, calculate the new resistance. Density of copper is 8.92×103kgm−3 and resistivity is 1.7×10−8Ωm.View SolutionQuestion 31
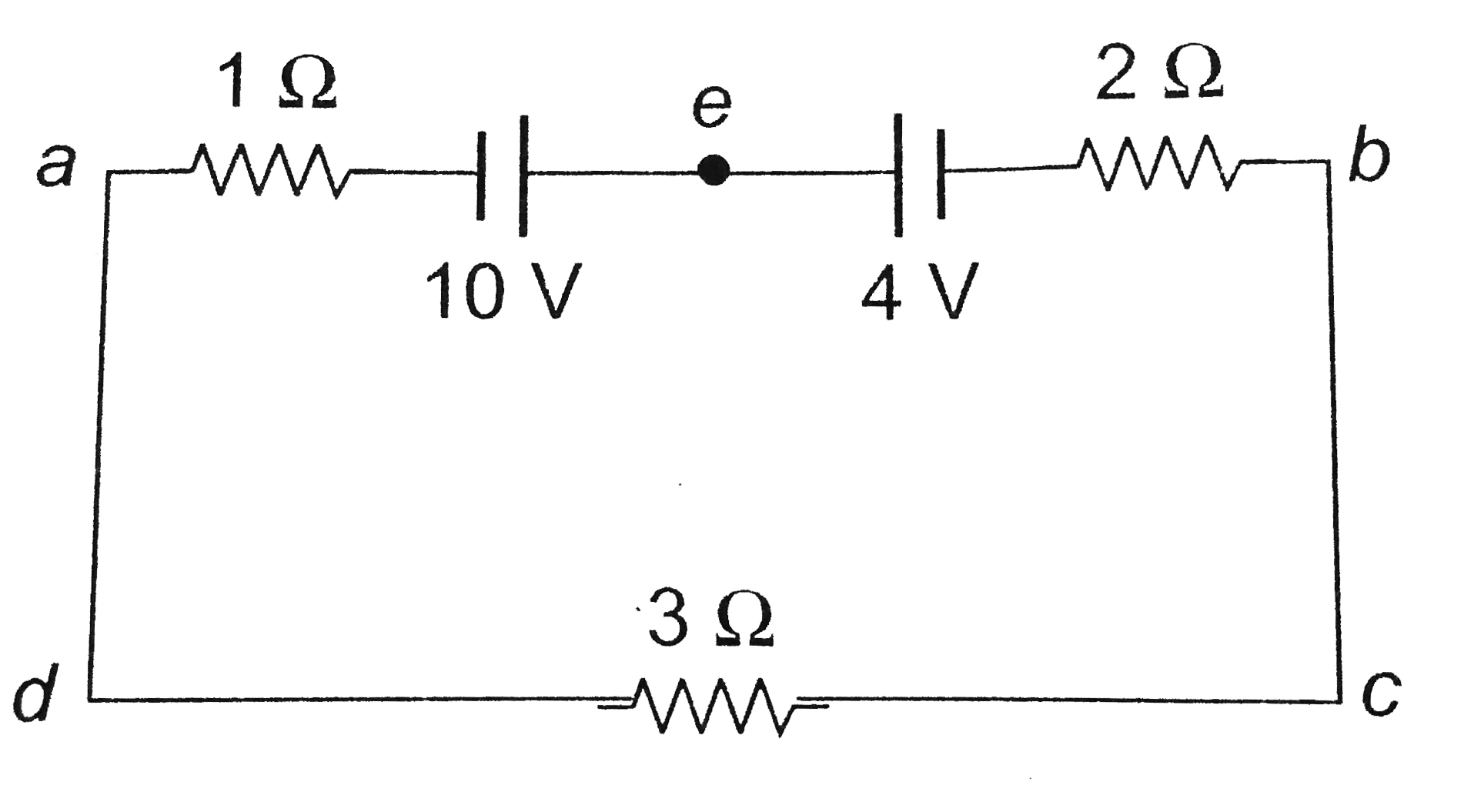
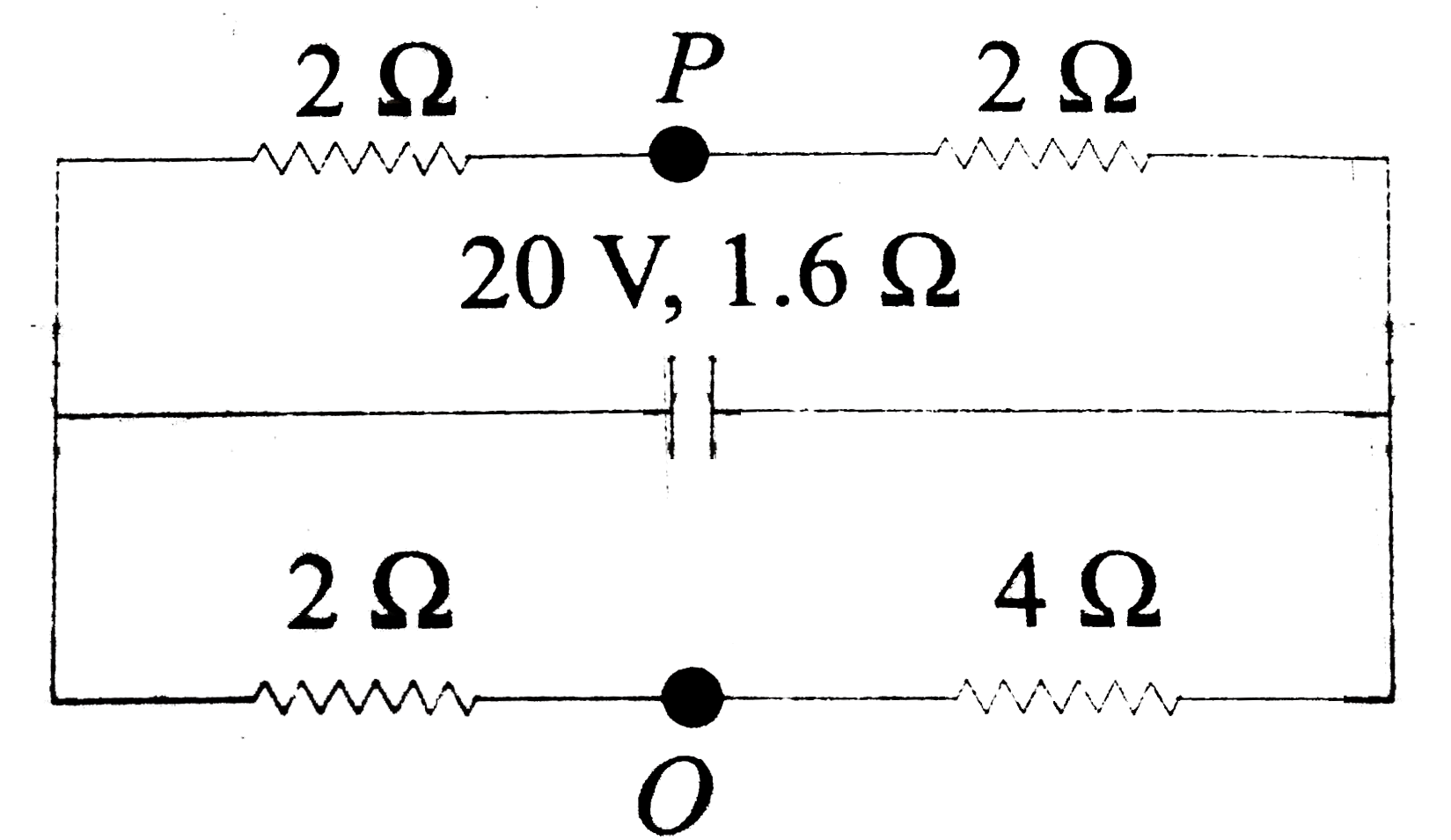
A 20 V battery of internal resistance 1Ω is connected to three coils of 12Ω,6Ω,and4Ω in parallel, a resistor of 5Ω and a reversed battery (emf 8 V and internal resistance 2 Omega) as shown in fig Calculate

a. the current in the circuit,
b. current in resistor of 12Ω coil, and
c. potential difference across each battery.View SolutionQuestion 32
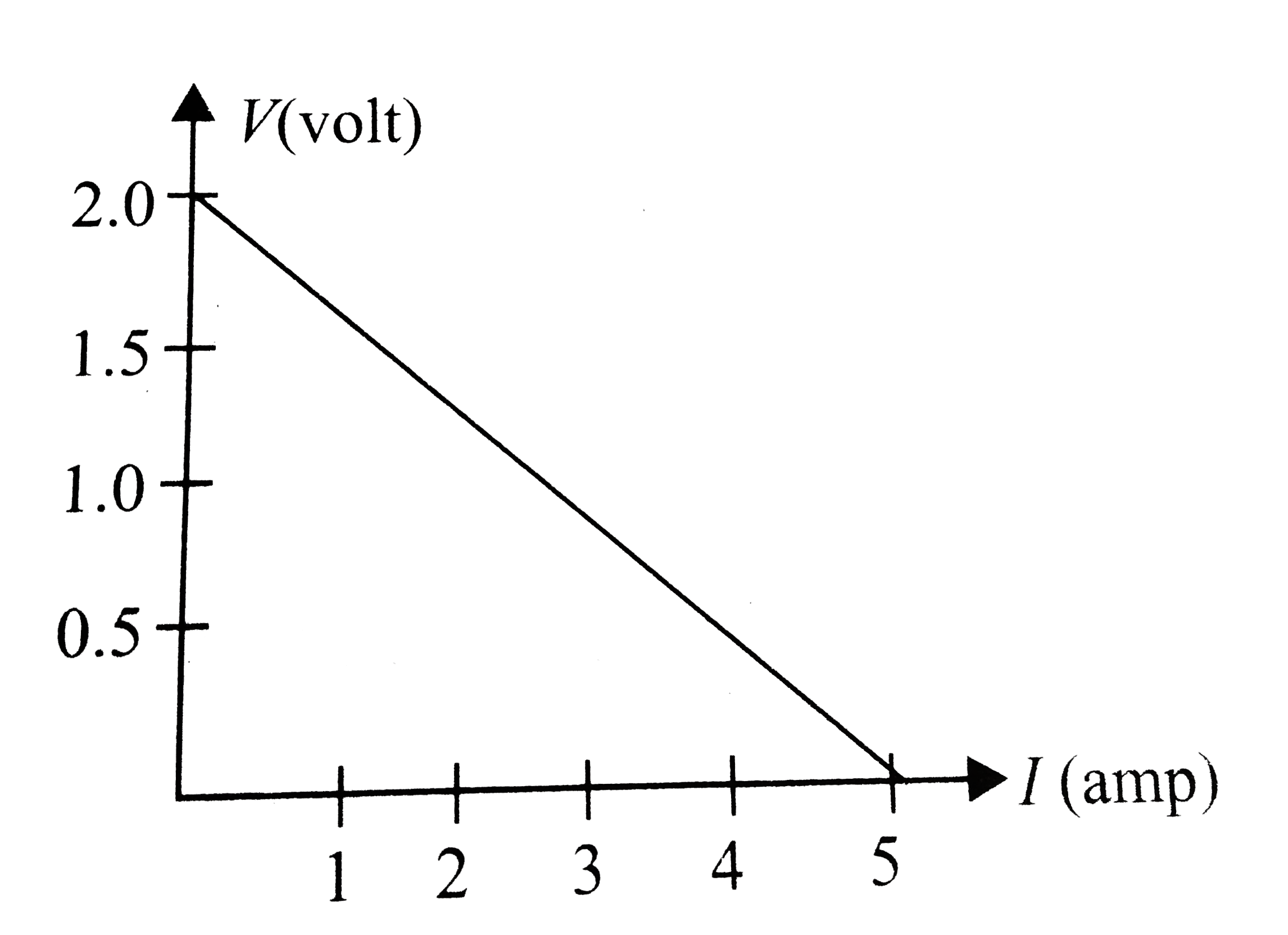
Potential difference across the terminals of a cell was measured (in volts) against different current (in ampere) flowing through the cell. A graph was drawn, which was a straight line ABC. Using the data given in the graph determine a. the emf, and
b. the internal resistance of the cell.View SolutionQuestion 35
When 10 identical cells in sereis are connected to the ends of a resistance of 59Ω, the current is found to be 0.25A. But when the nsame cells, being connected in parallel, are joined to the ends of a resistance of 0.05Omega, the current is 25A. Calculate the internal resistance and the emf of each cell. View Solution
View SolutionQuestion 42
A parallel combination of an 8Ω resistor and an unknown resistor R is connected in series with a 16Ω resistor and a battery. This circuit is then disassembled, and the three resistors are then connected in series with each other oand the same battery. in both arrangements, the current through the 8Ω resistor is the same. What is the unknown resistance R?
 View Solution
View SolutionQuestion 47
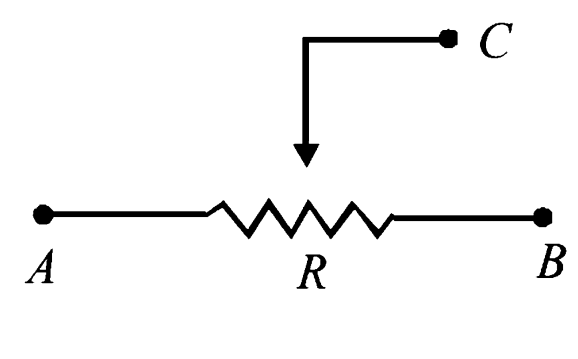
The diagram shows a circuit used in an experiment to determine the emf and internal resistance of the cell C. A graph was plotted of the potential difference V between the terminals of the cell against the current I, which was varied by adjusting the rheostat. What is the internal resistance of the cell?
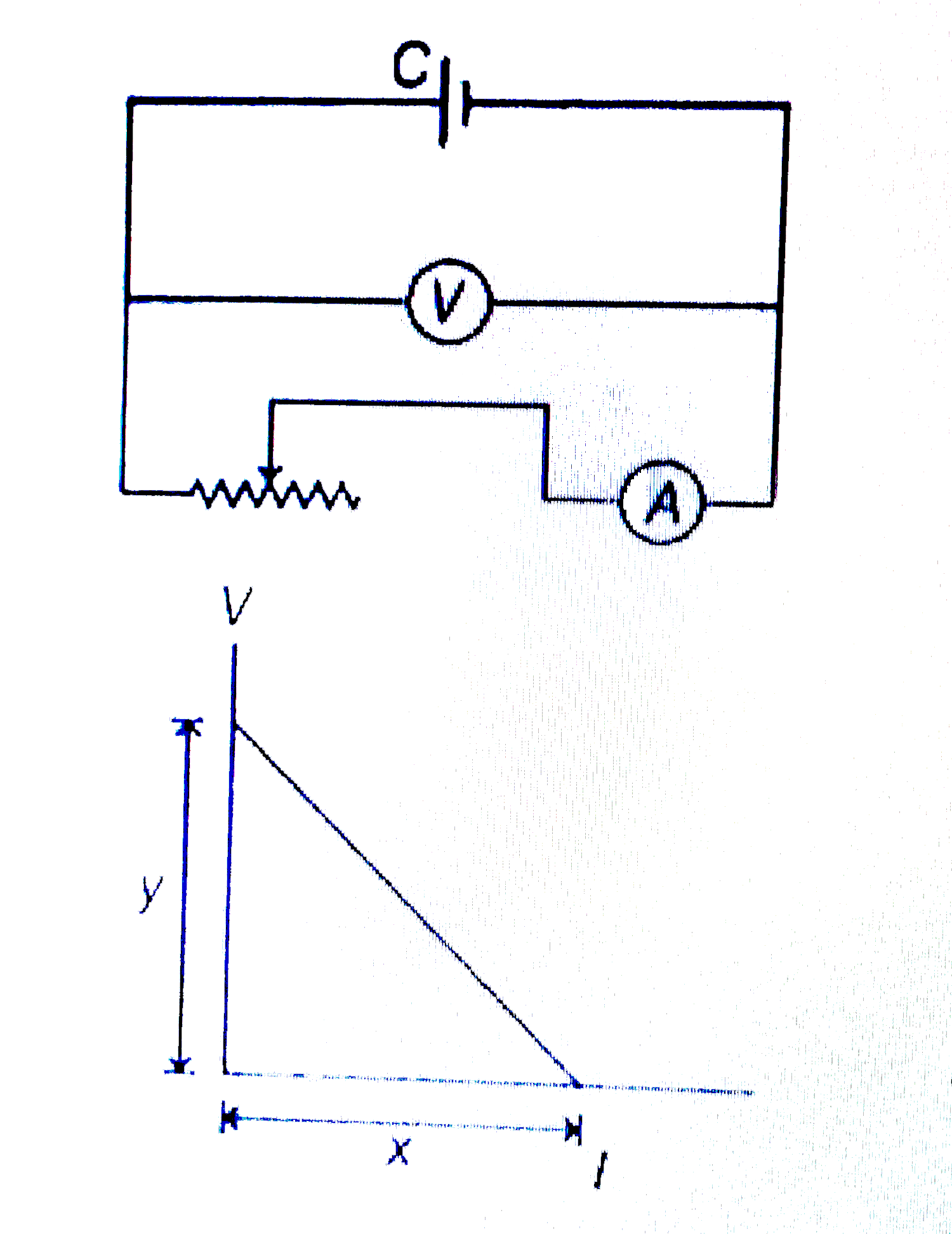 View Solution
View SolutionQuestion 66
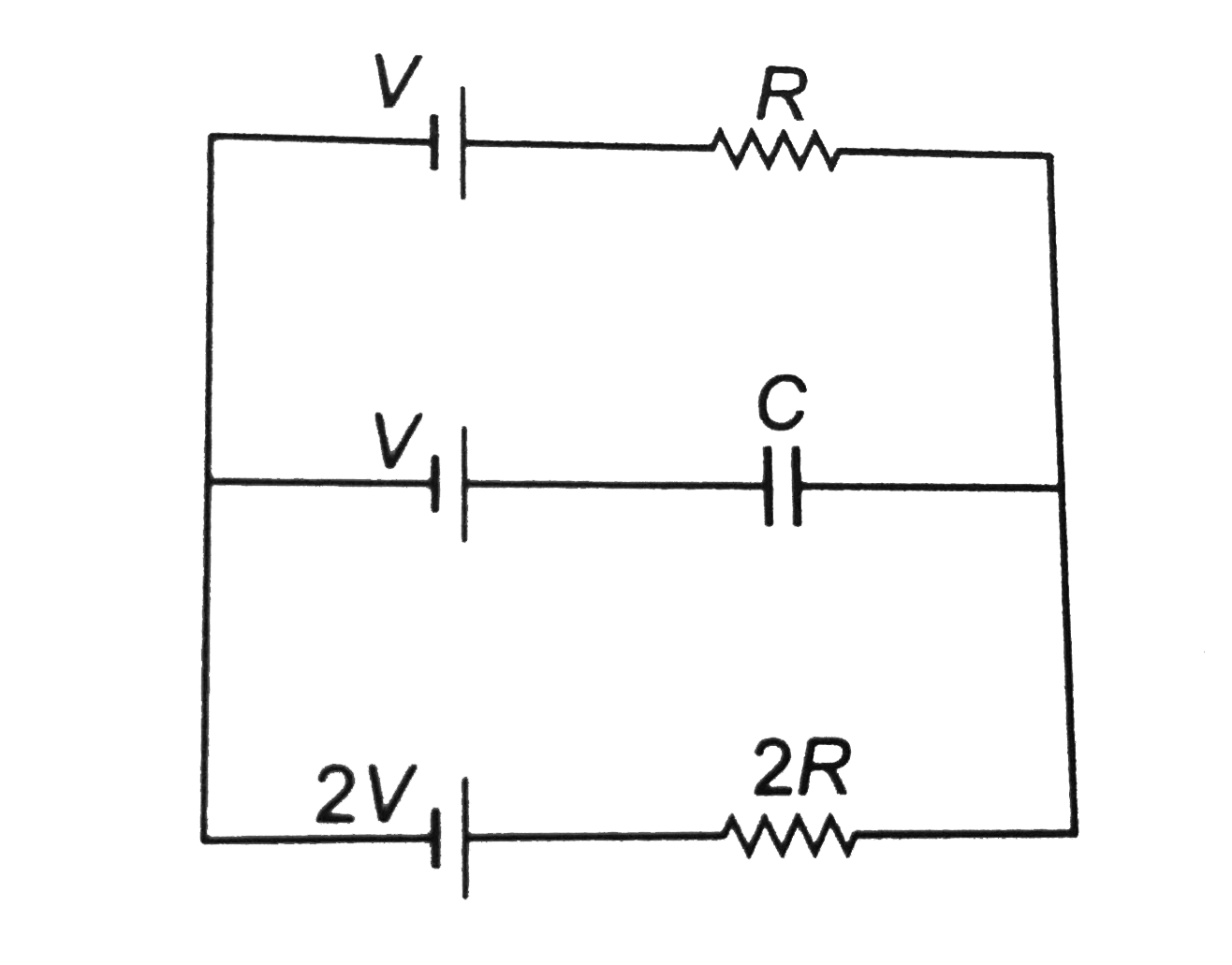
Shown three sections of the circuit that are to be connecte in turn to the same battery via a switch. The resistors are all identical, as are capactiors. Rank the sections according to

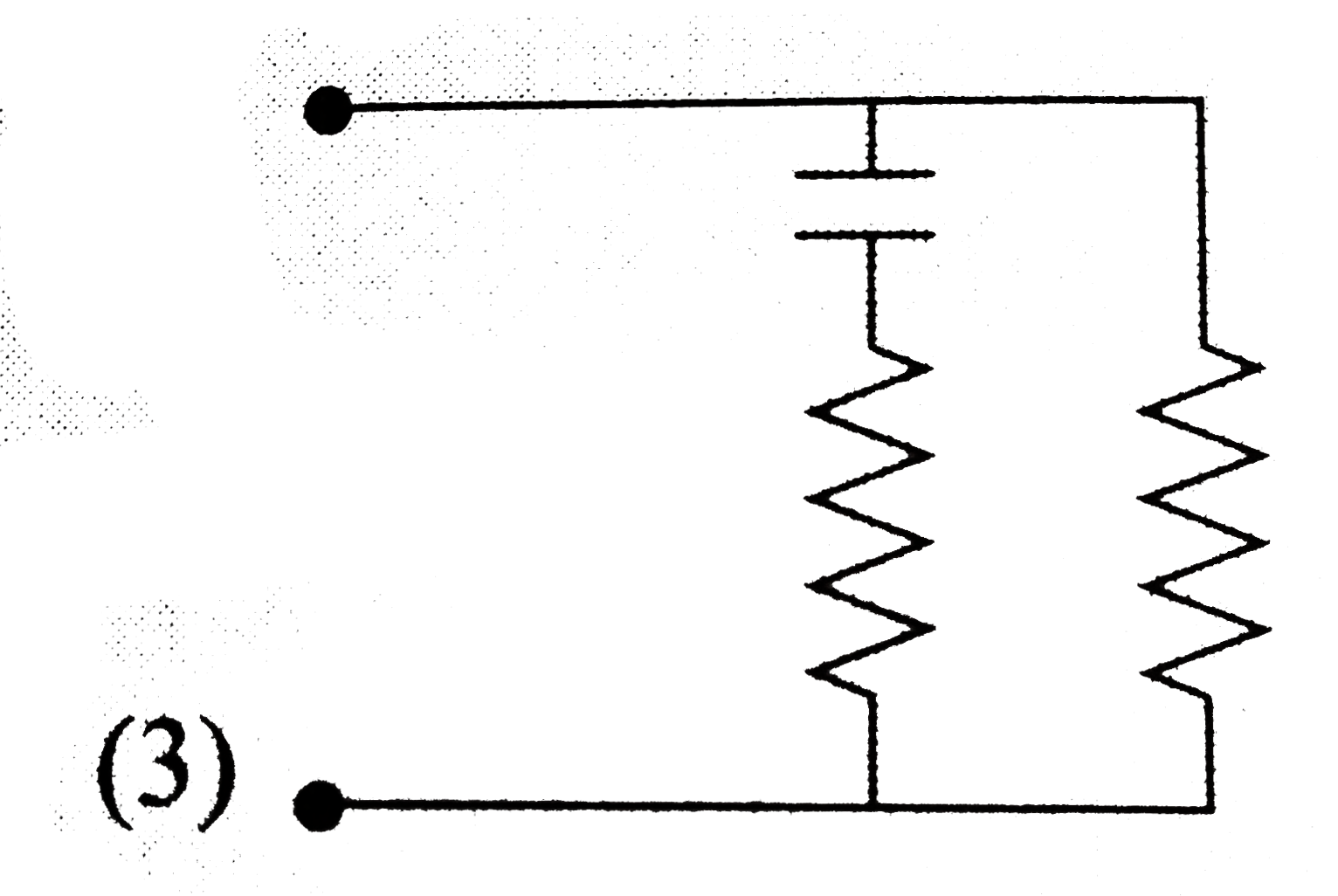
a. the final (equilibrium) charge on the capacitor.........
b. the time required for the capacitor to reah 50% of its final charge, greatest first.......View SolutionQuestion 71
In the circuit shown in fig switch S is closed at time t =0.
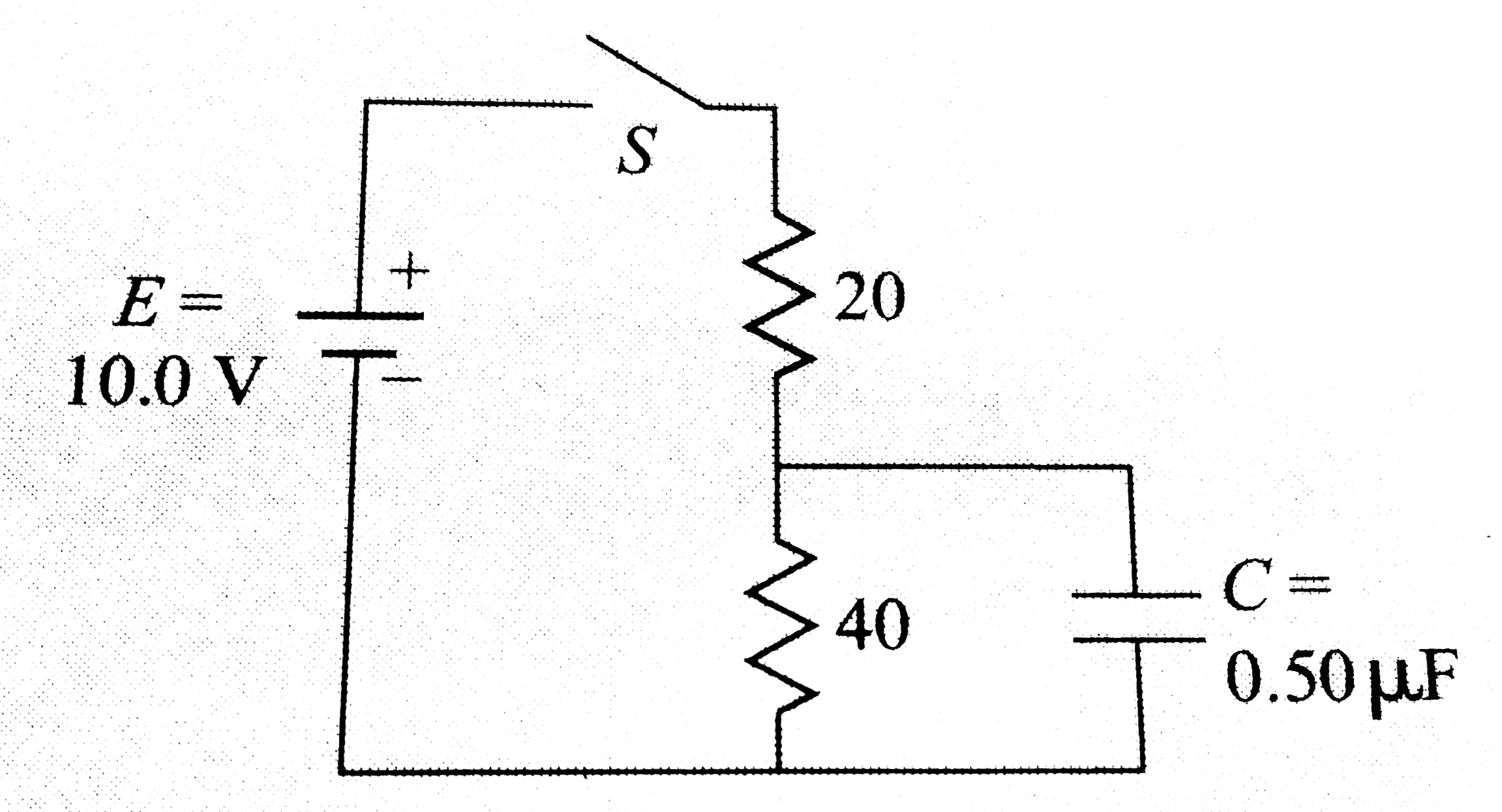
a. What is the current I0 leacing the battery at t=0, immediately after the switch is closed?
b. What is the current I "long time" later?
c. What charge has accmulated on the capacitor after this long time?
d. If, finally, swtich S is opened again, how long will it take after the switch is opened for the capactior to lose 80% of its charge?View SolutionQuestion 85
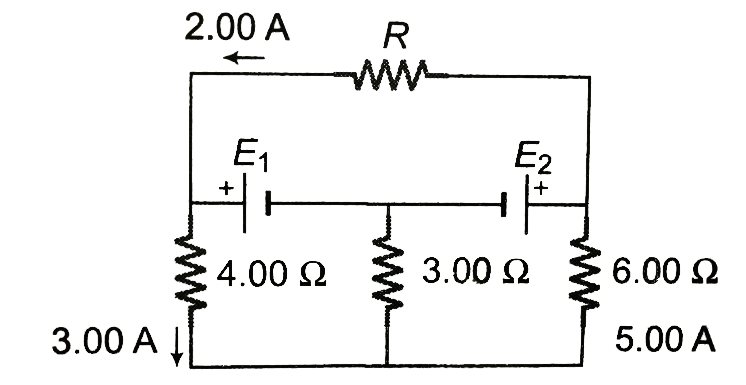
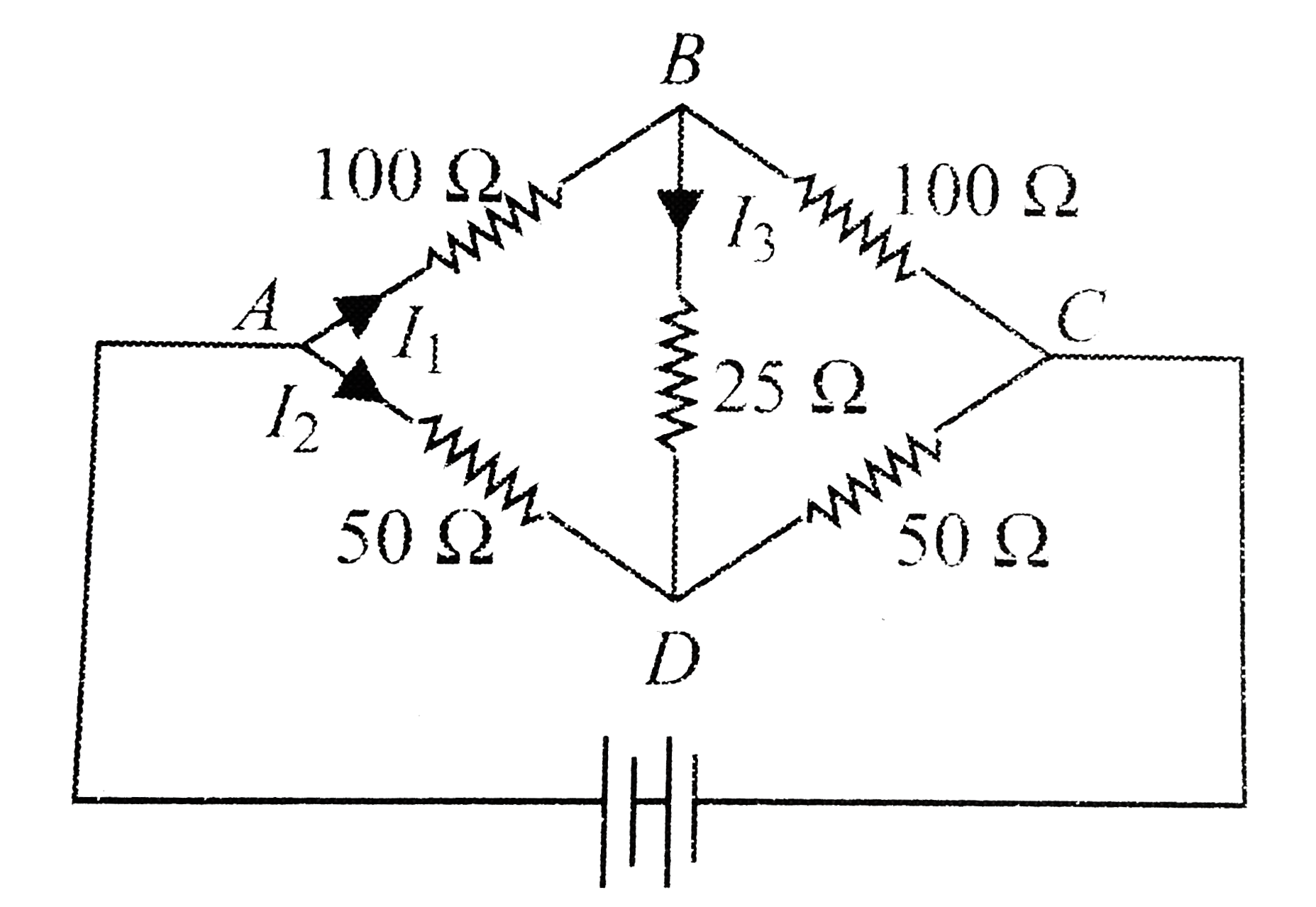
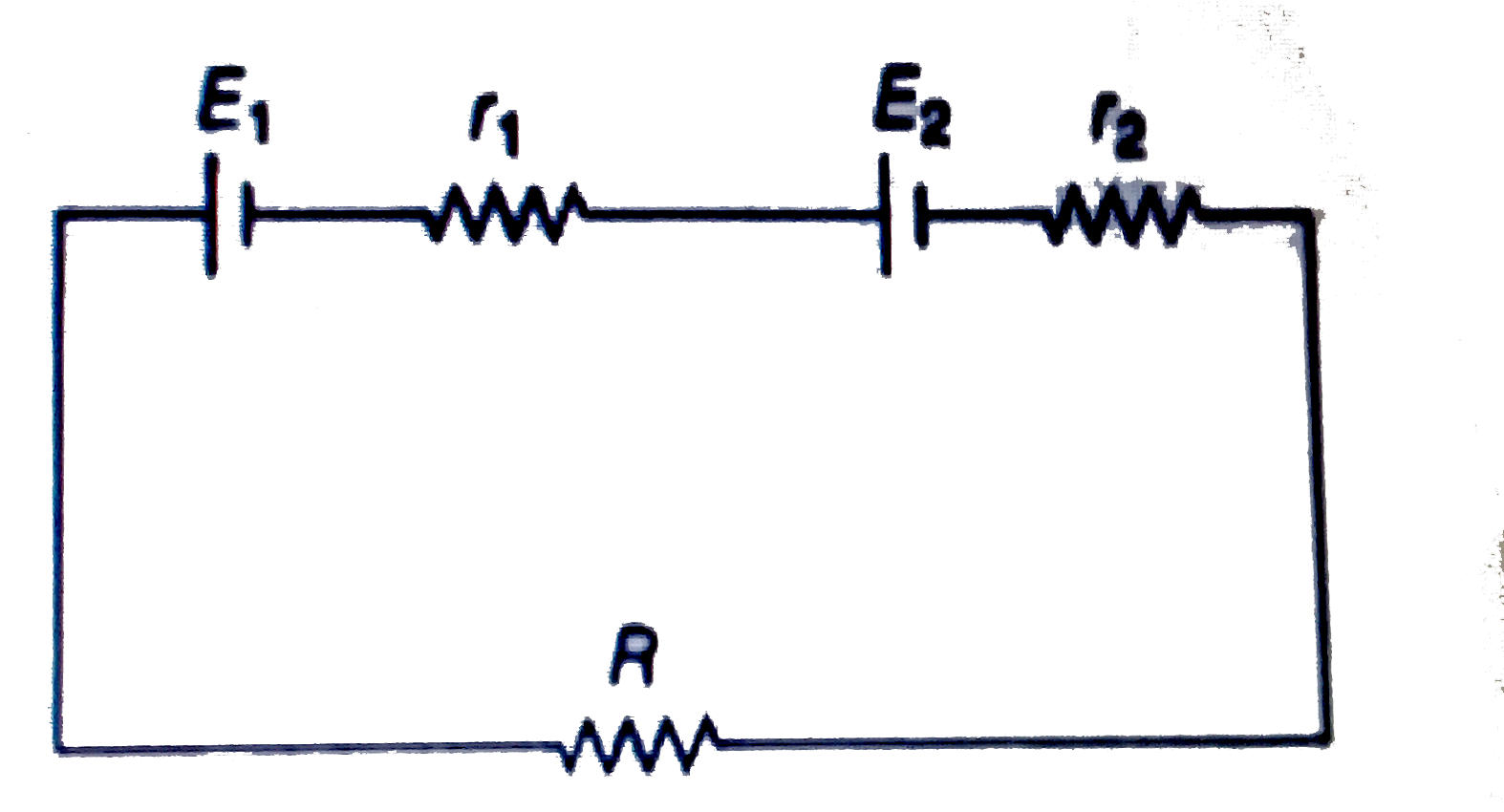
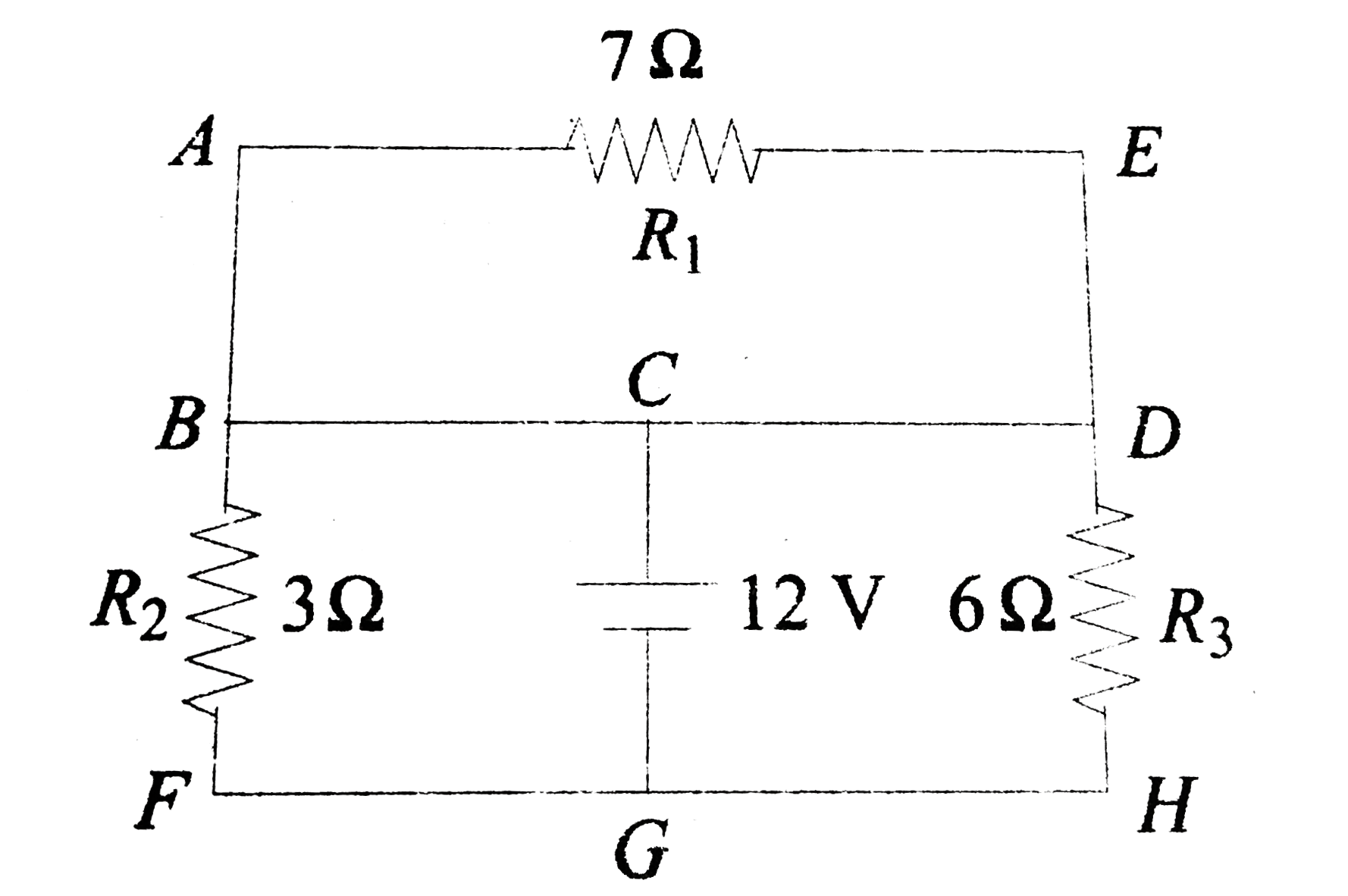
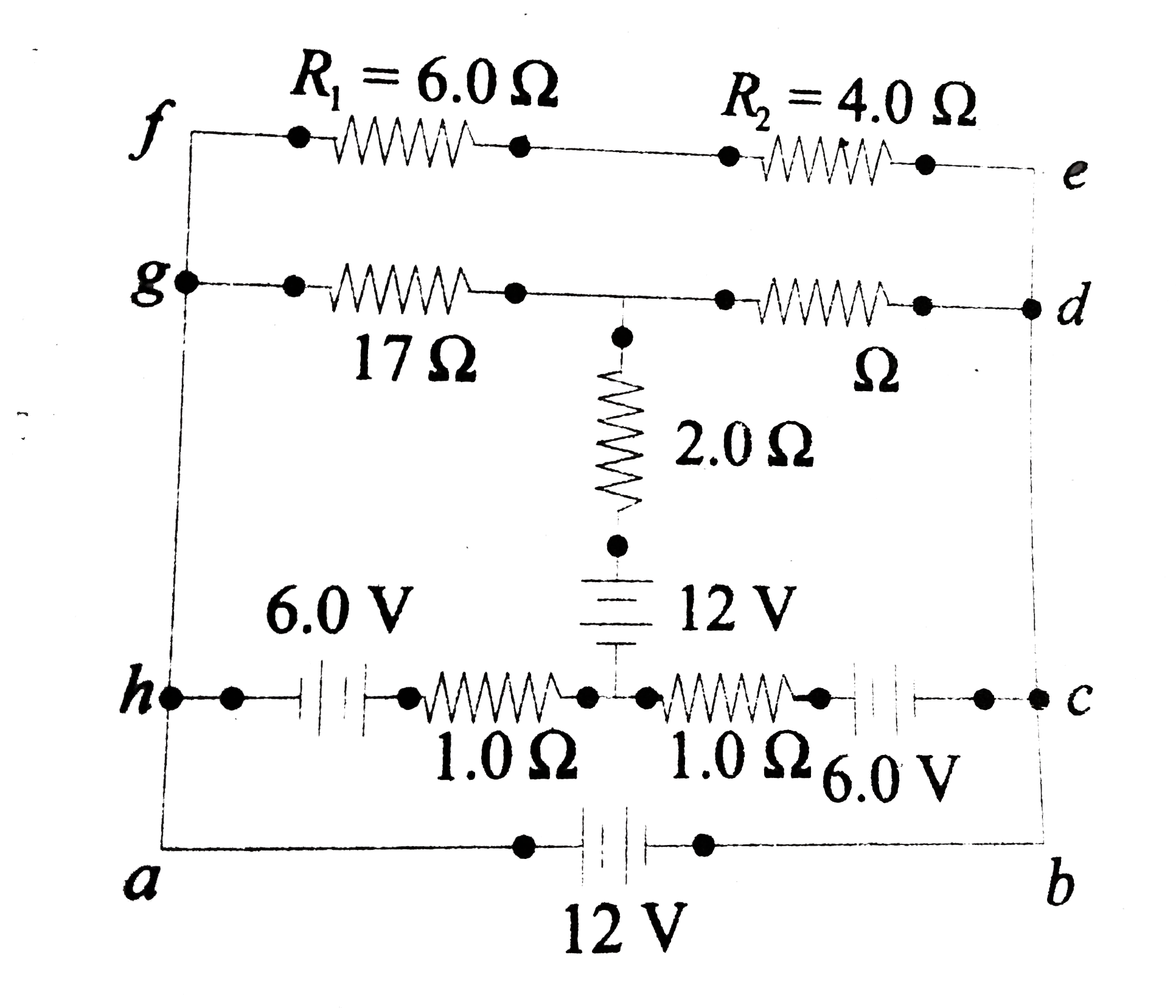
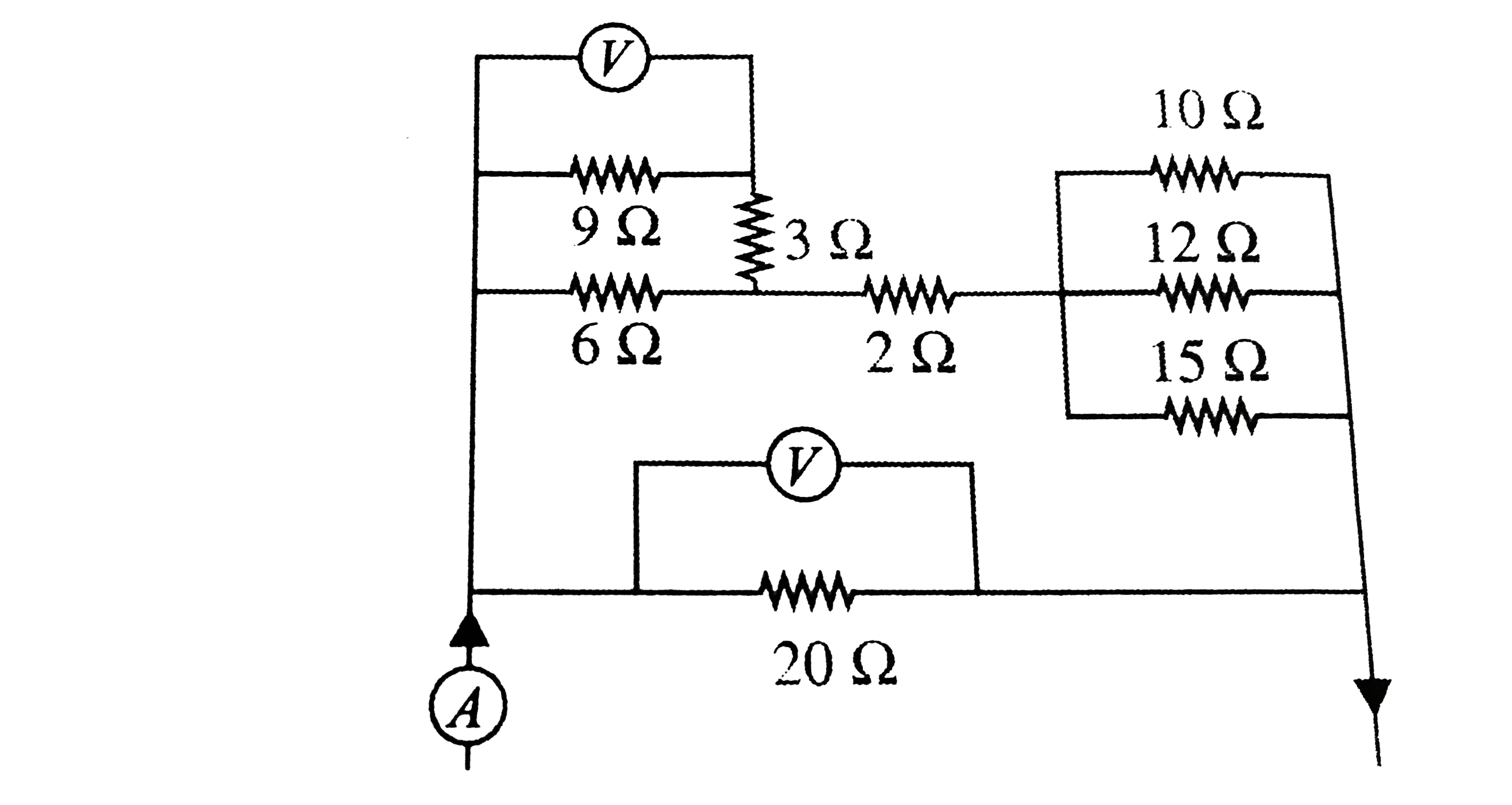
The circuit shown in fig 5.230 contains three resistors R1=100Ω,R=50Ω and R3=20Ω and cells of emfs E12VandE2 The ammeter indicates a current of 50mA. Determina the currents in the resistors and the emf of the second cell. The internal resistance of the ammeter and of the cells shoudl be
 View Solution
View SolutionQuestion 89
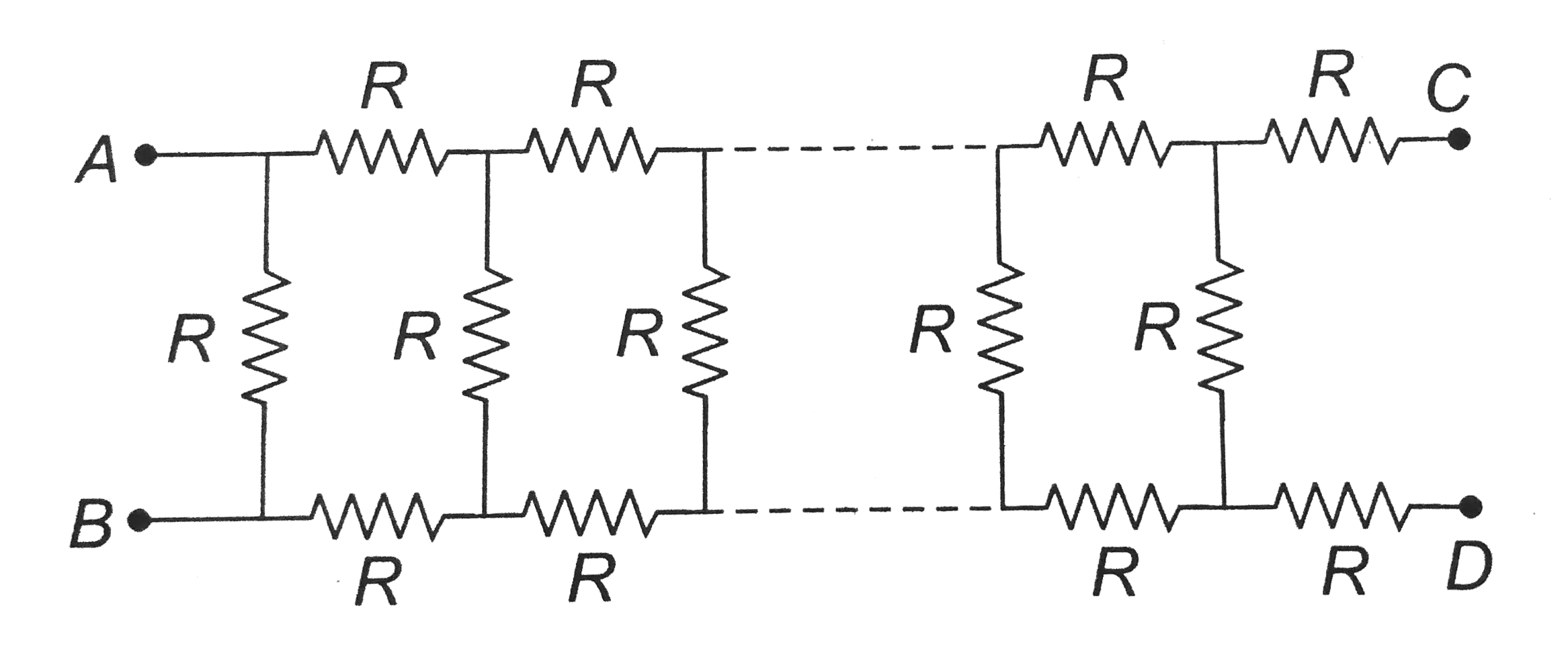
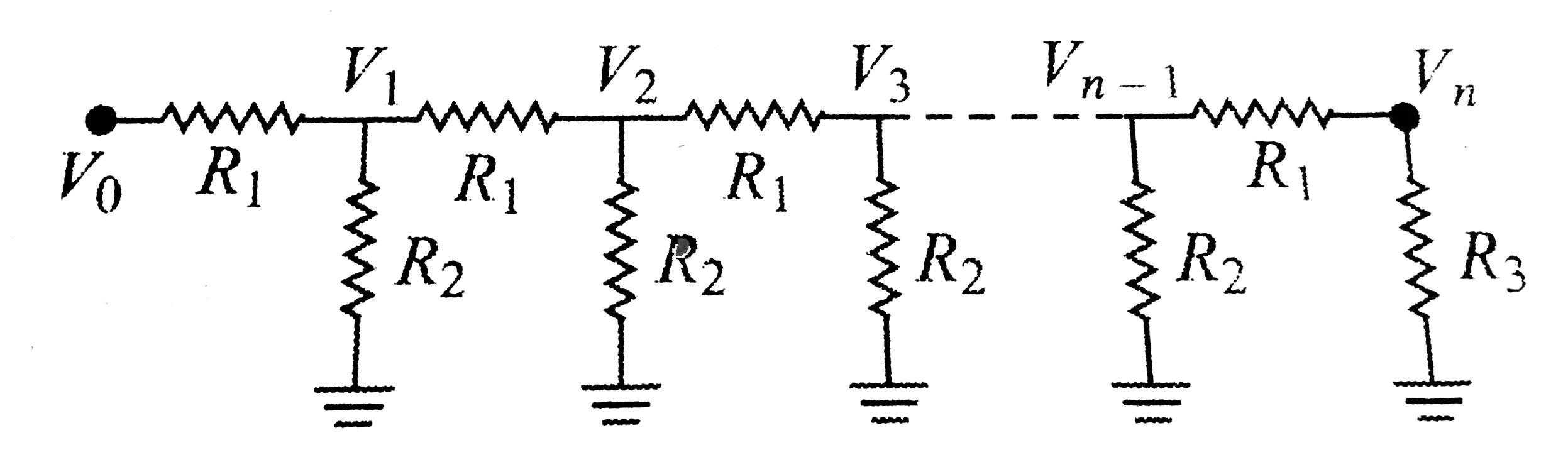
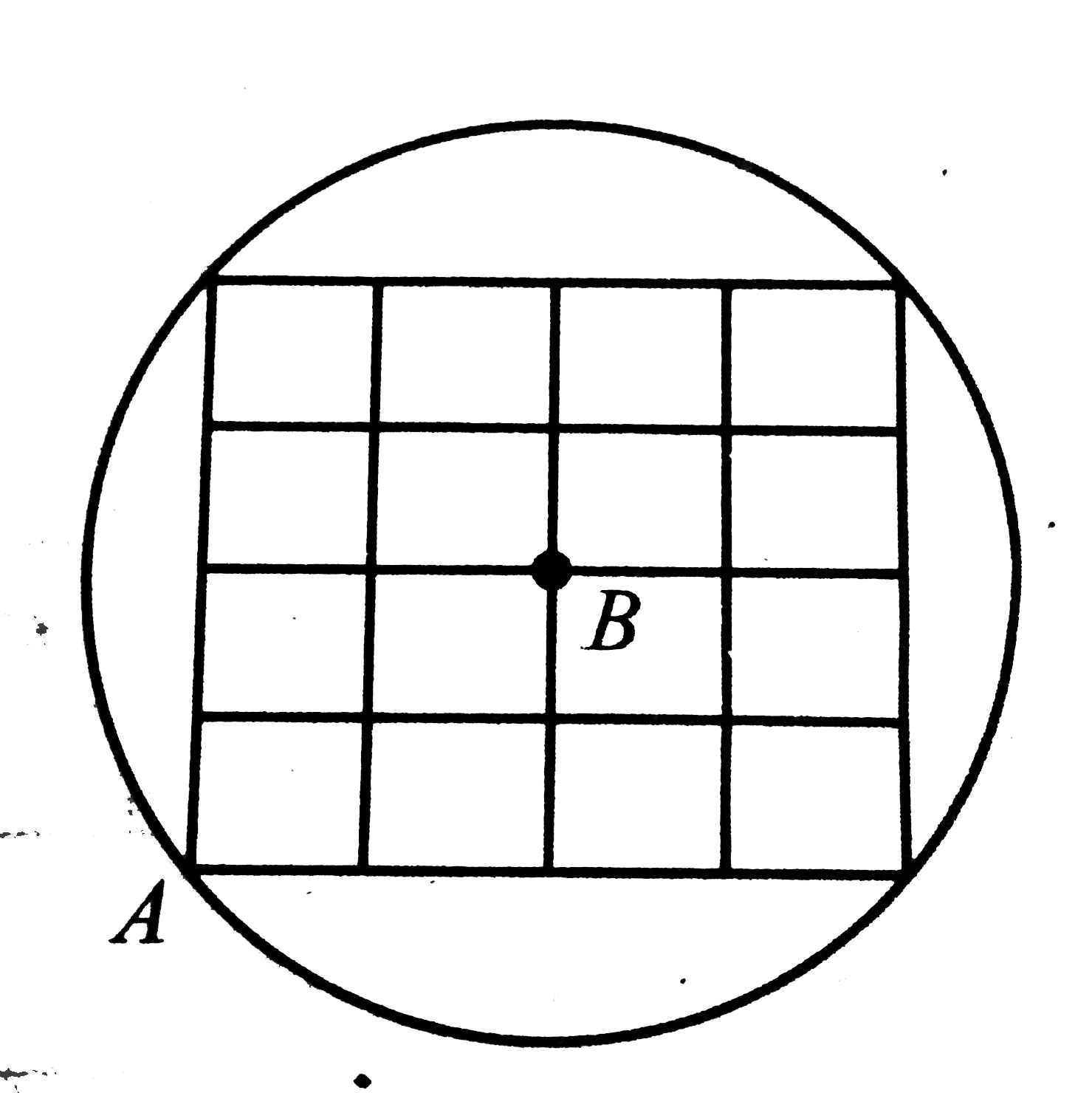
Consider an infinita ladder of network shown In fig 5.223A voltage is applied between points A and B. If the voltage is havled after each seciton, find the raito of R1/R2
Suggest a method to terminate it after a few sections without introducing much error in its attenuation. View SolutionQuestion 92
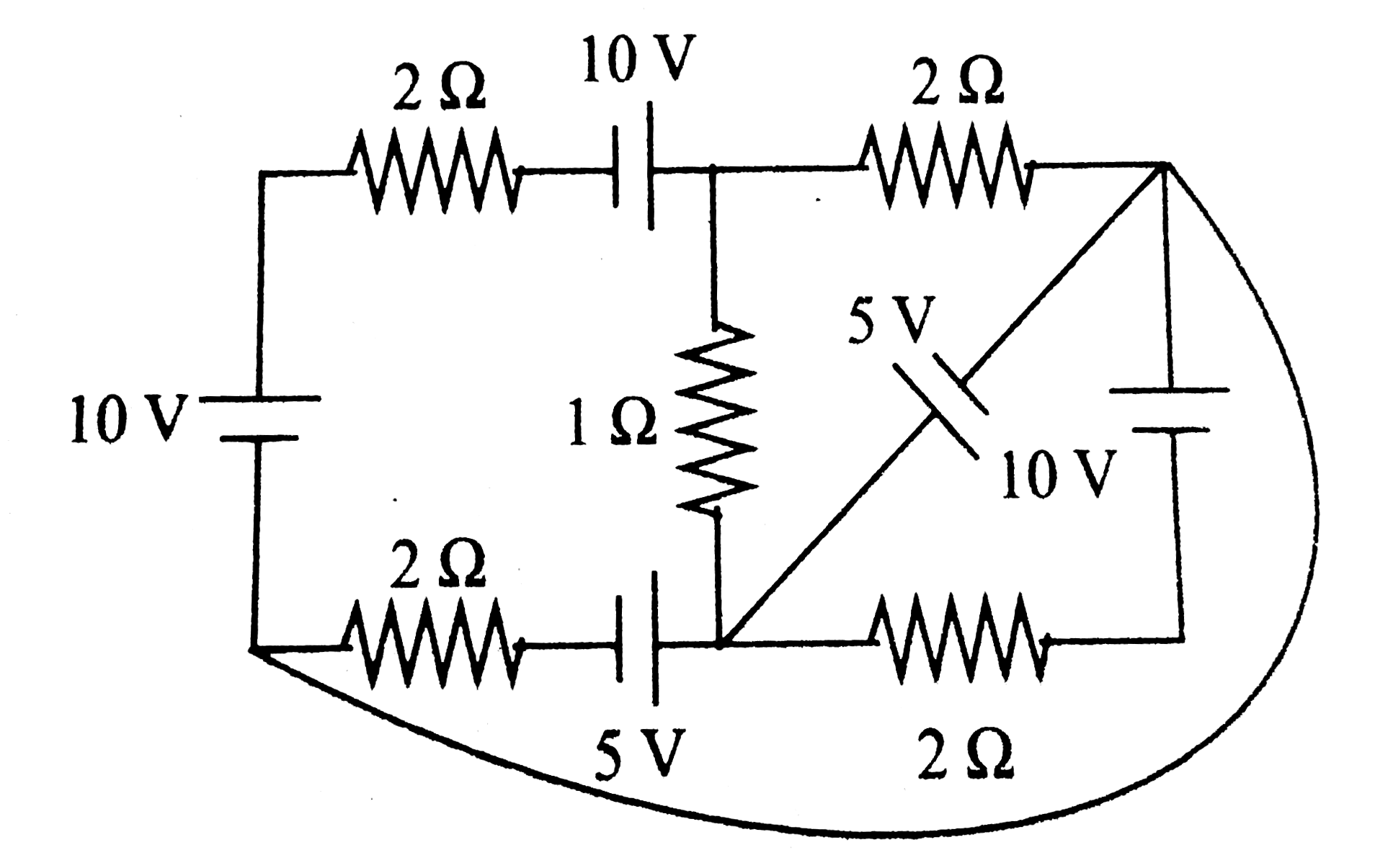
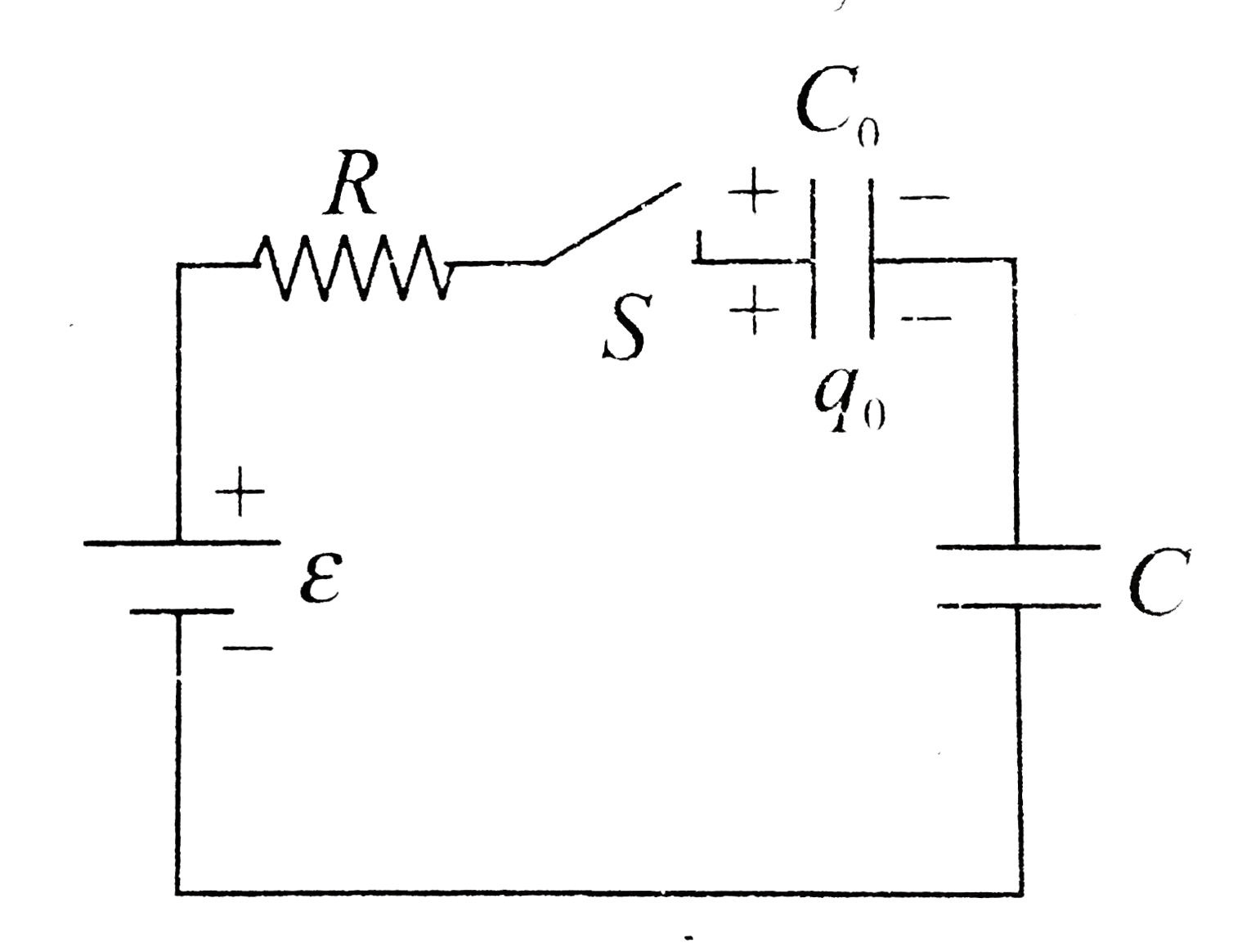
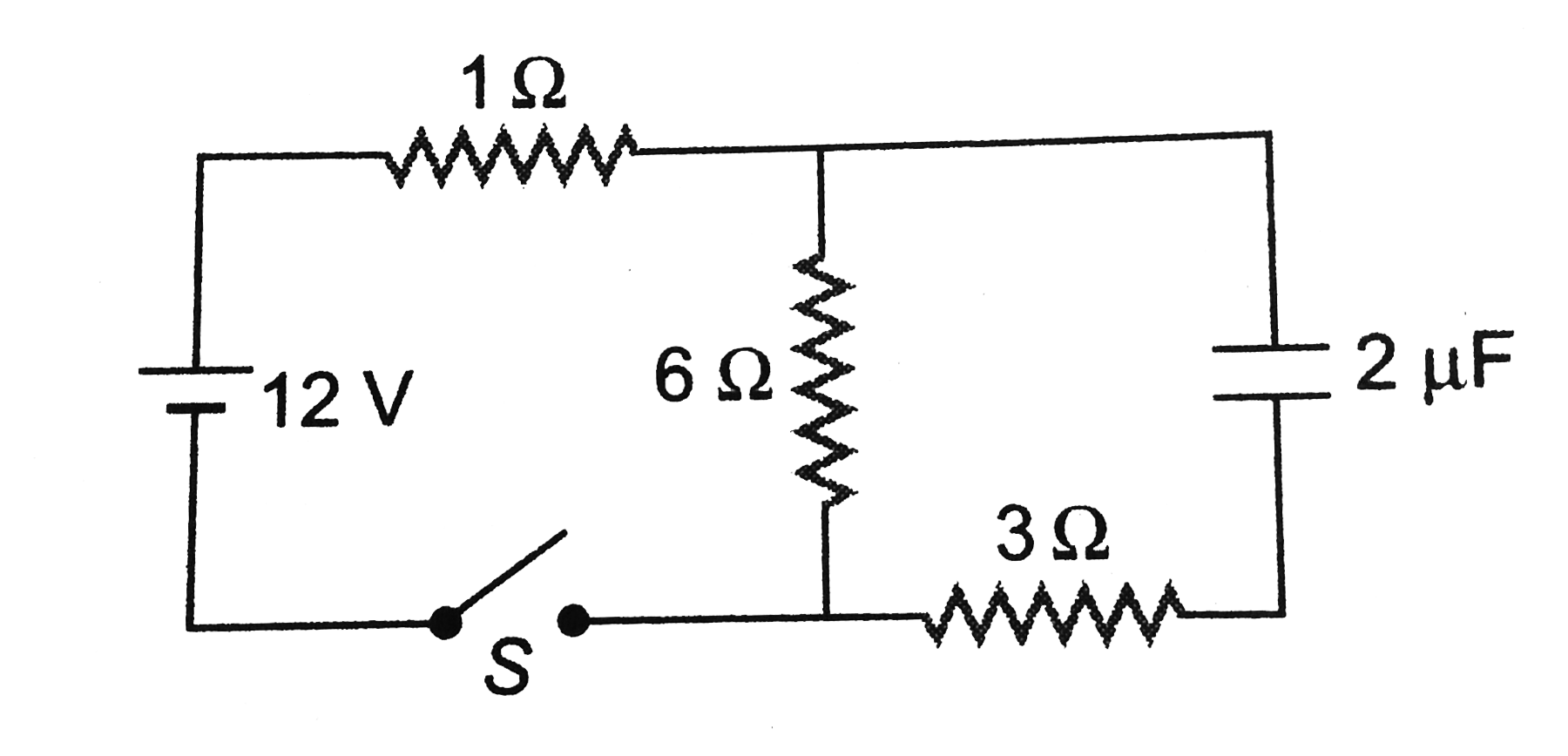
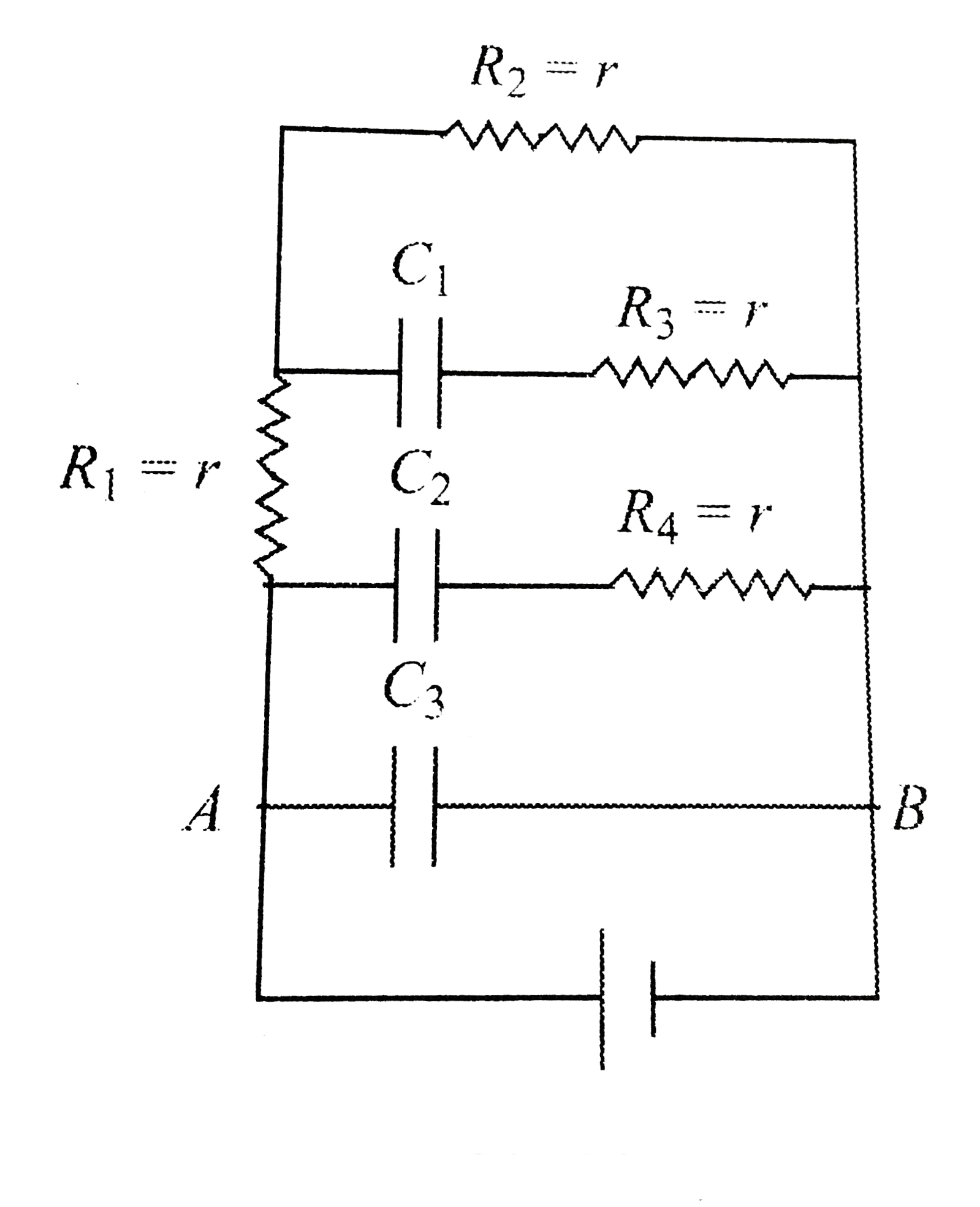
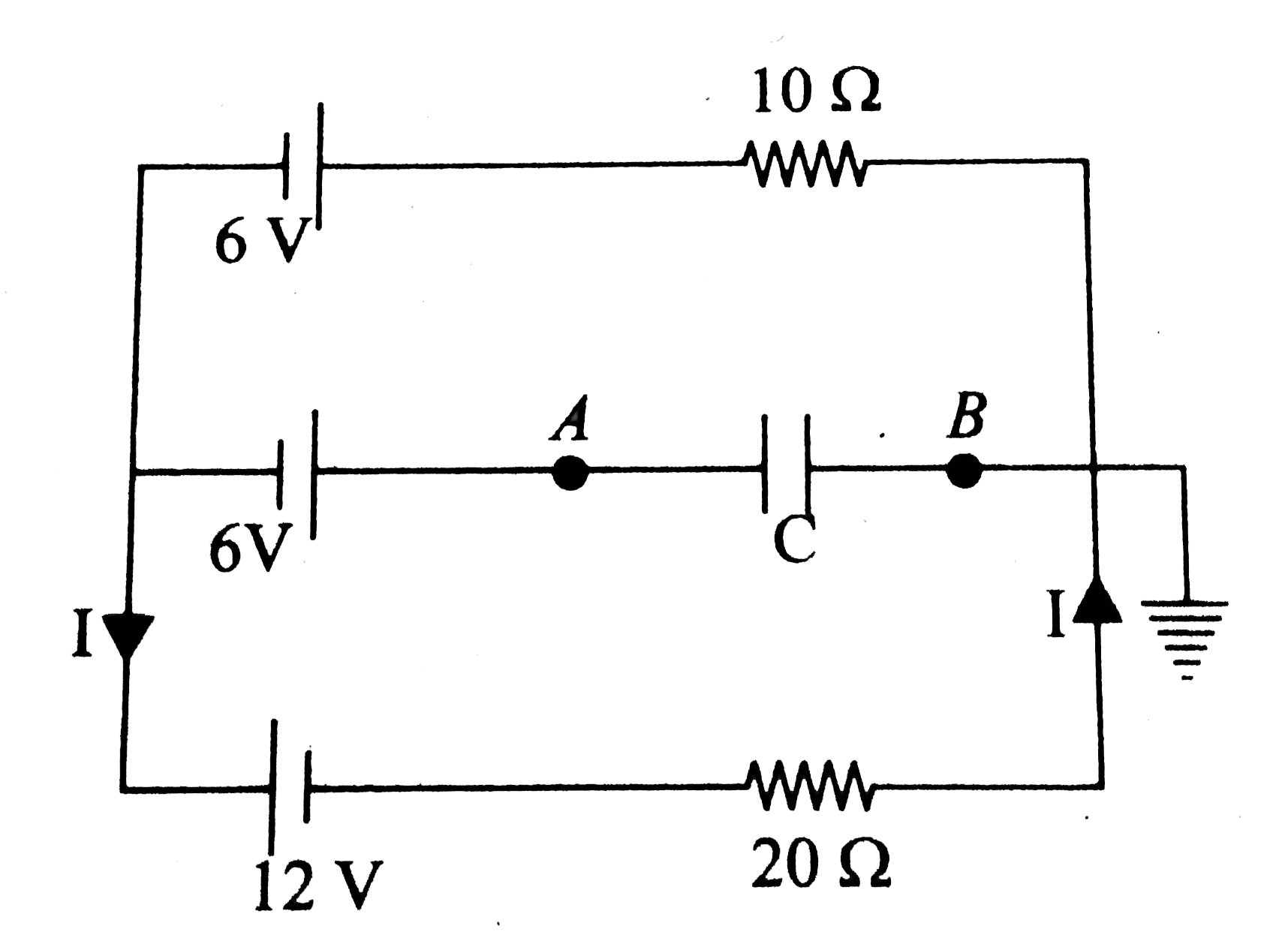
Analyze the given circuit in the steady state condition. Charge on the capacitor isq0=16μC
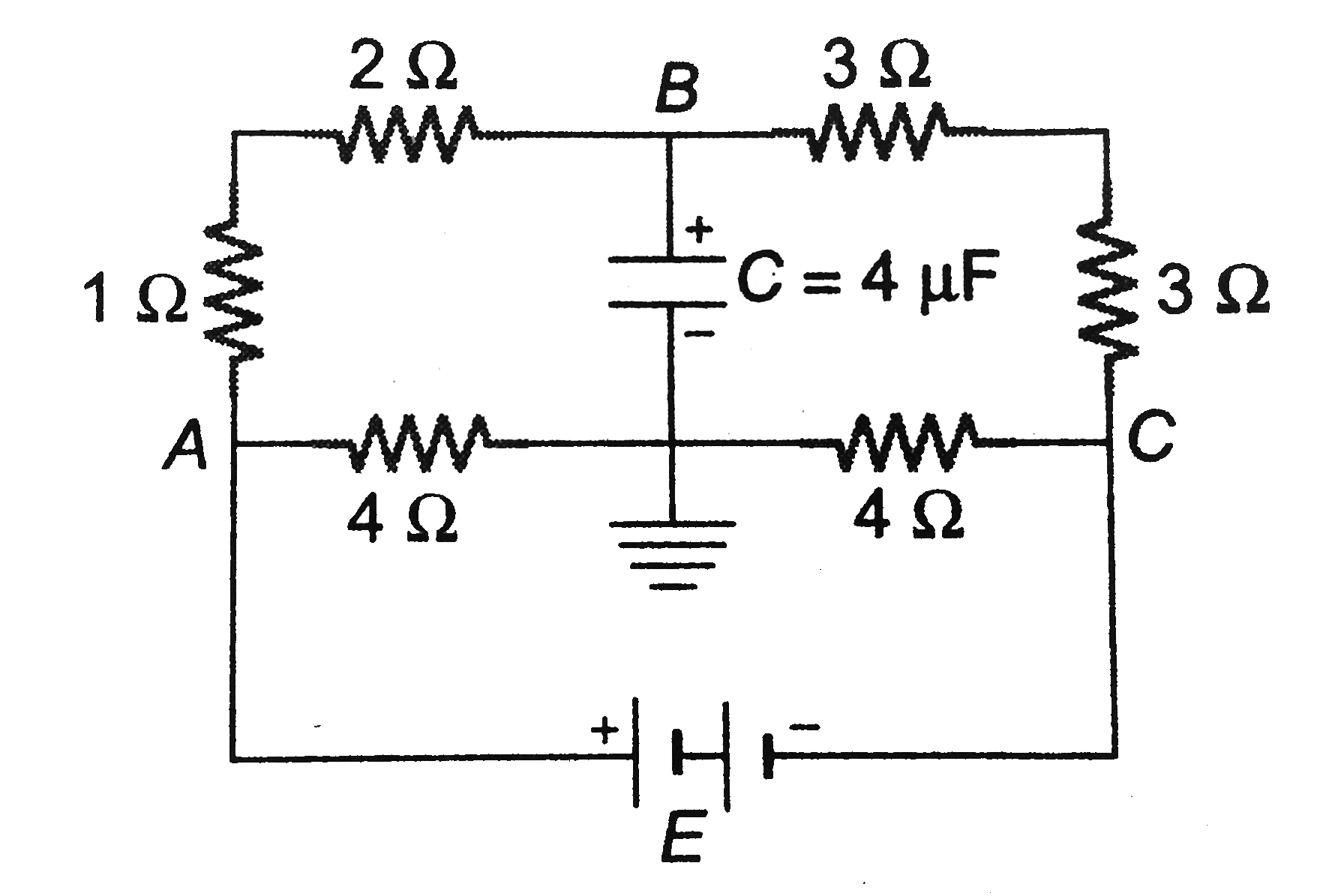
(a) Find the current in each branch
(b) Find the emf of the battery.
(c) If now the battery is removed and the points A and C are shorted. Find the time during which charge on the capacitor becomes
8μCView SolutionQuestion 93
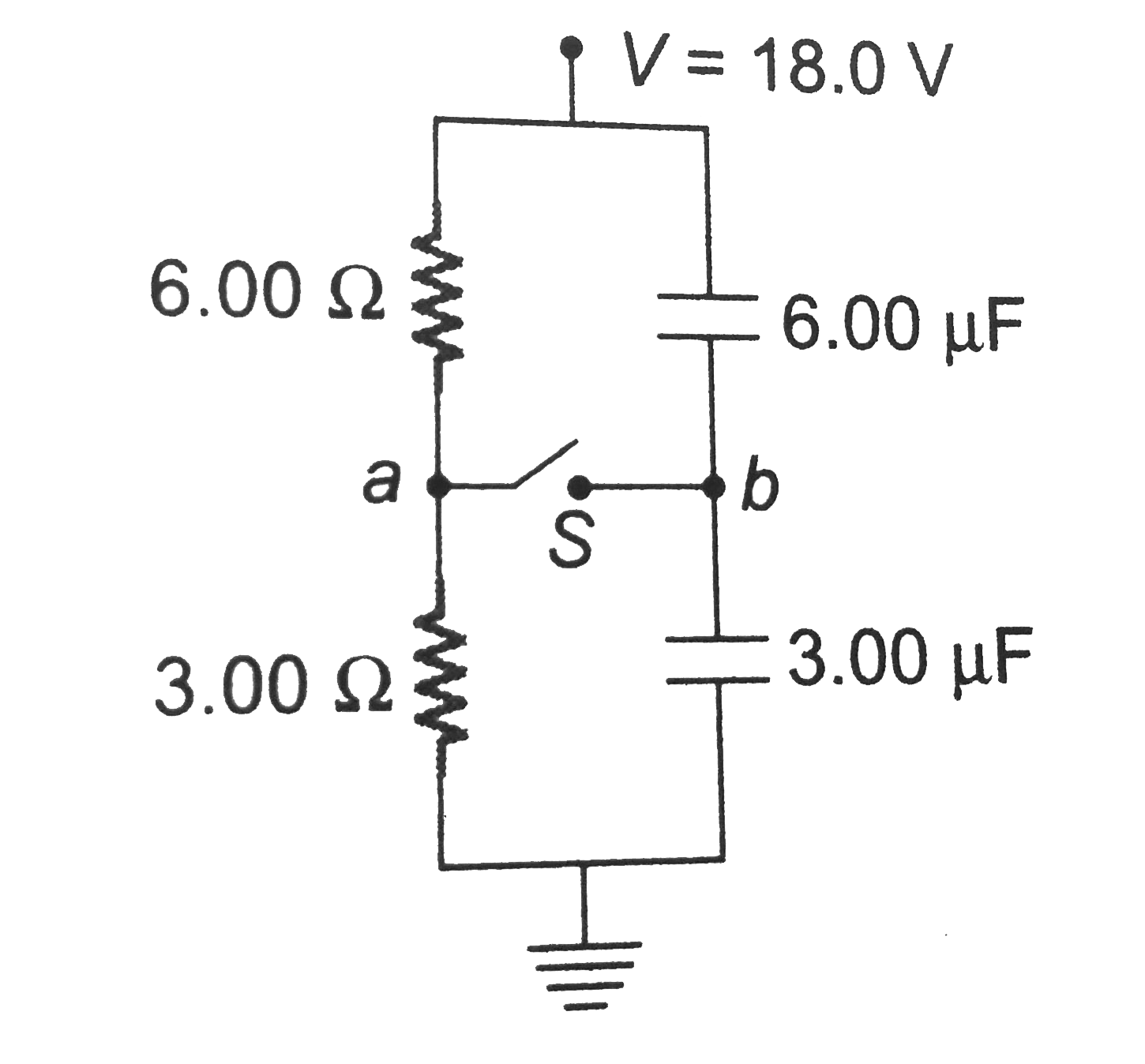
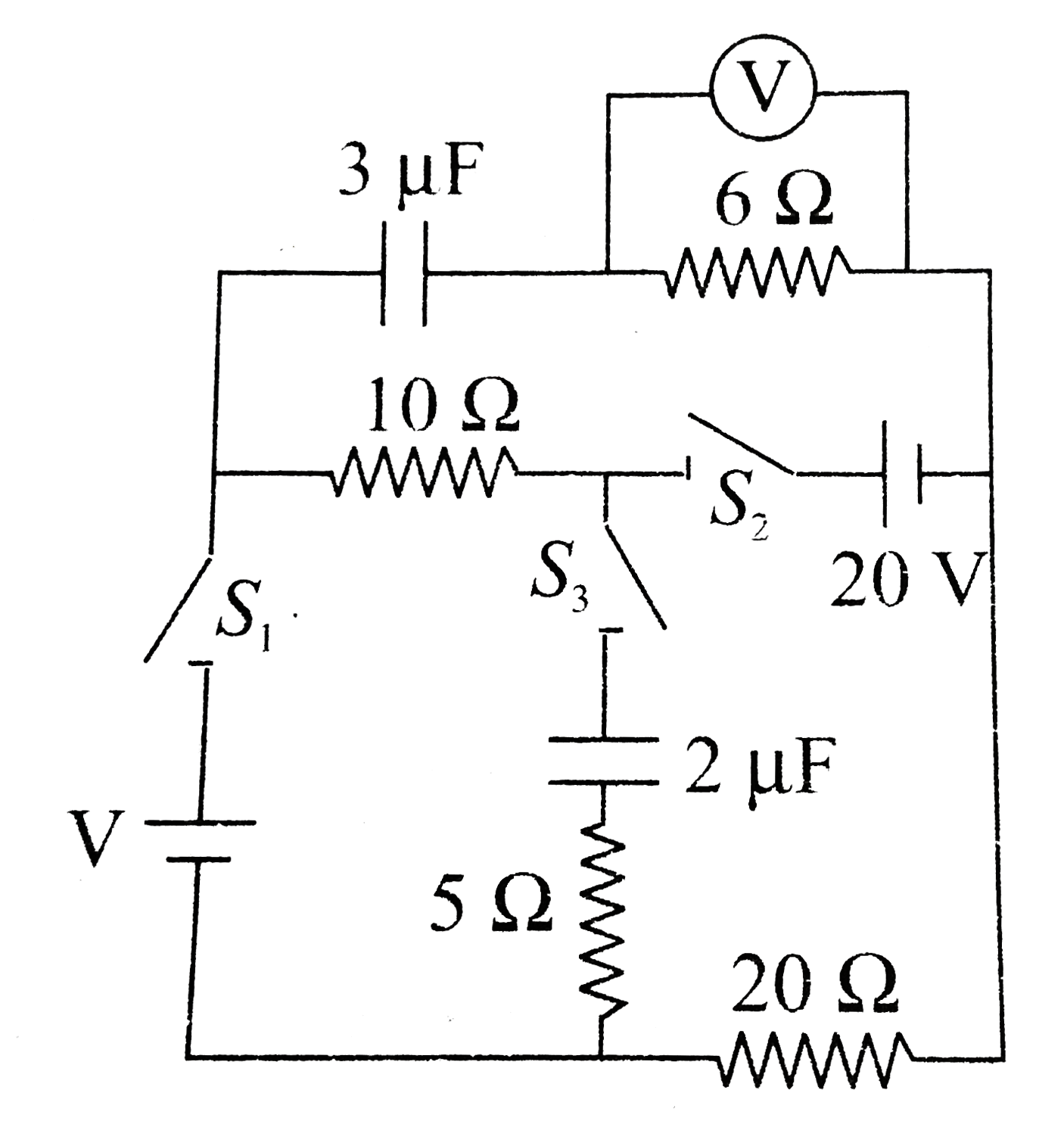
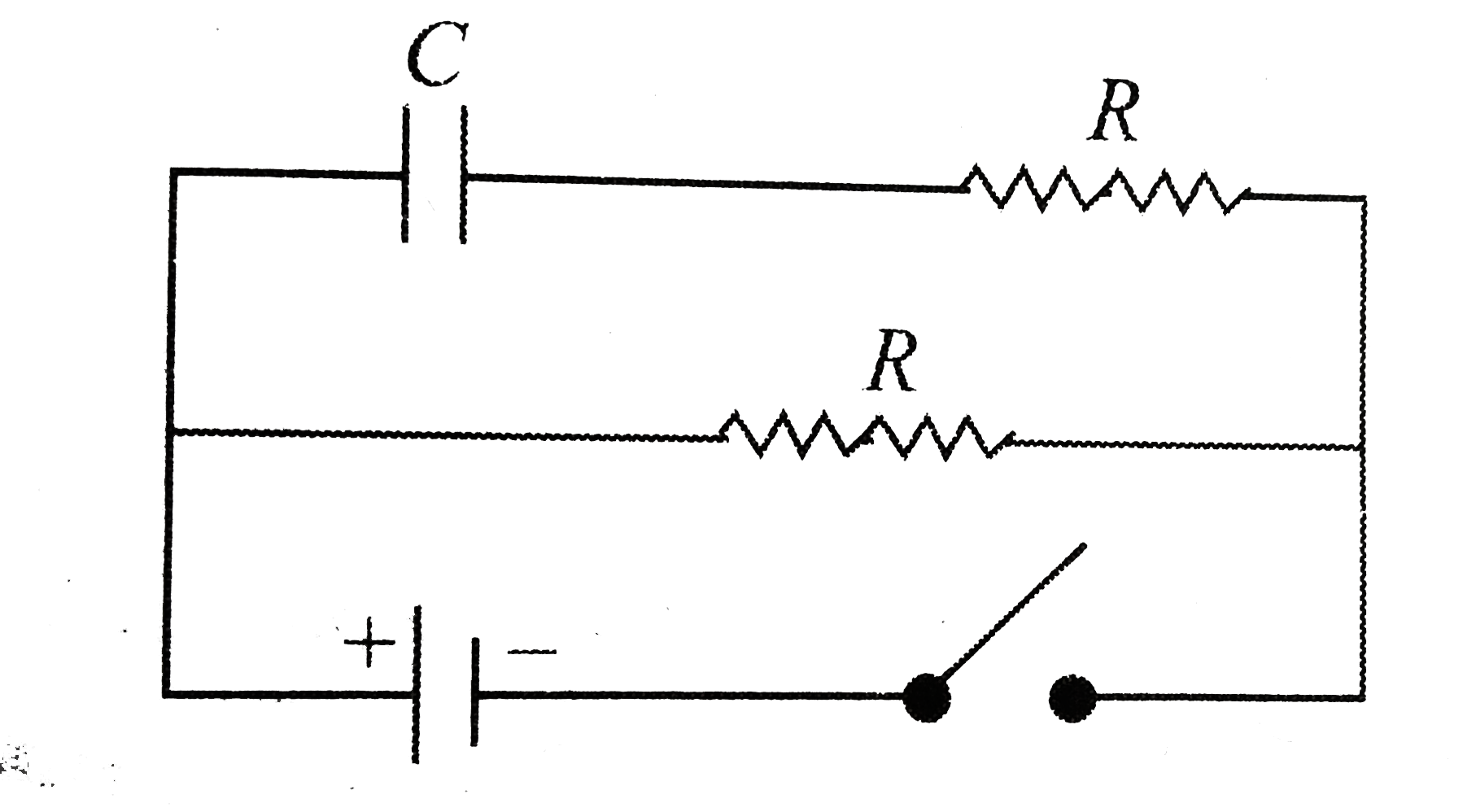
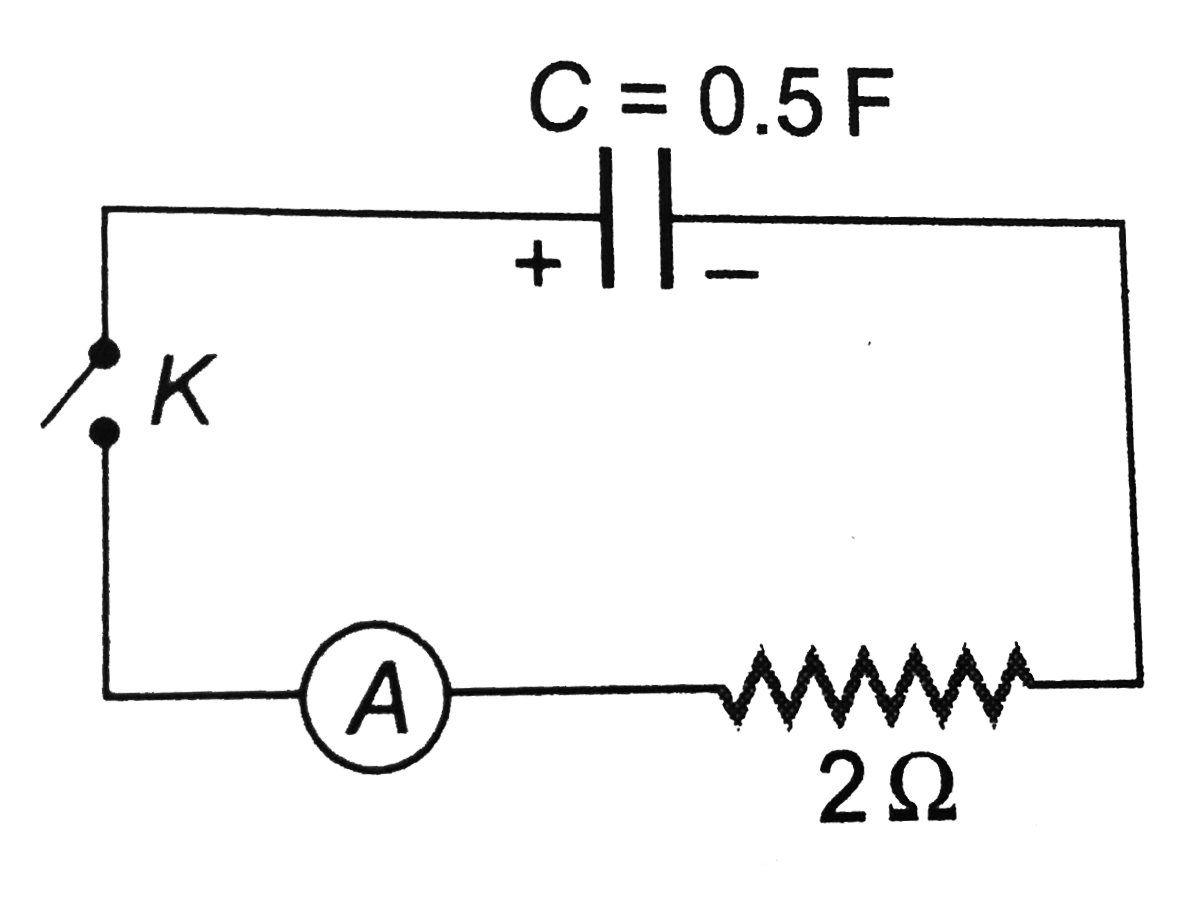
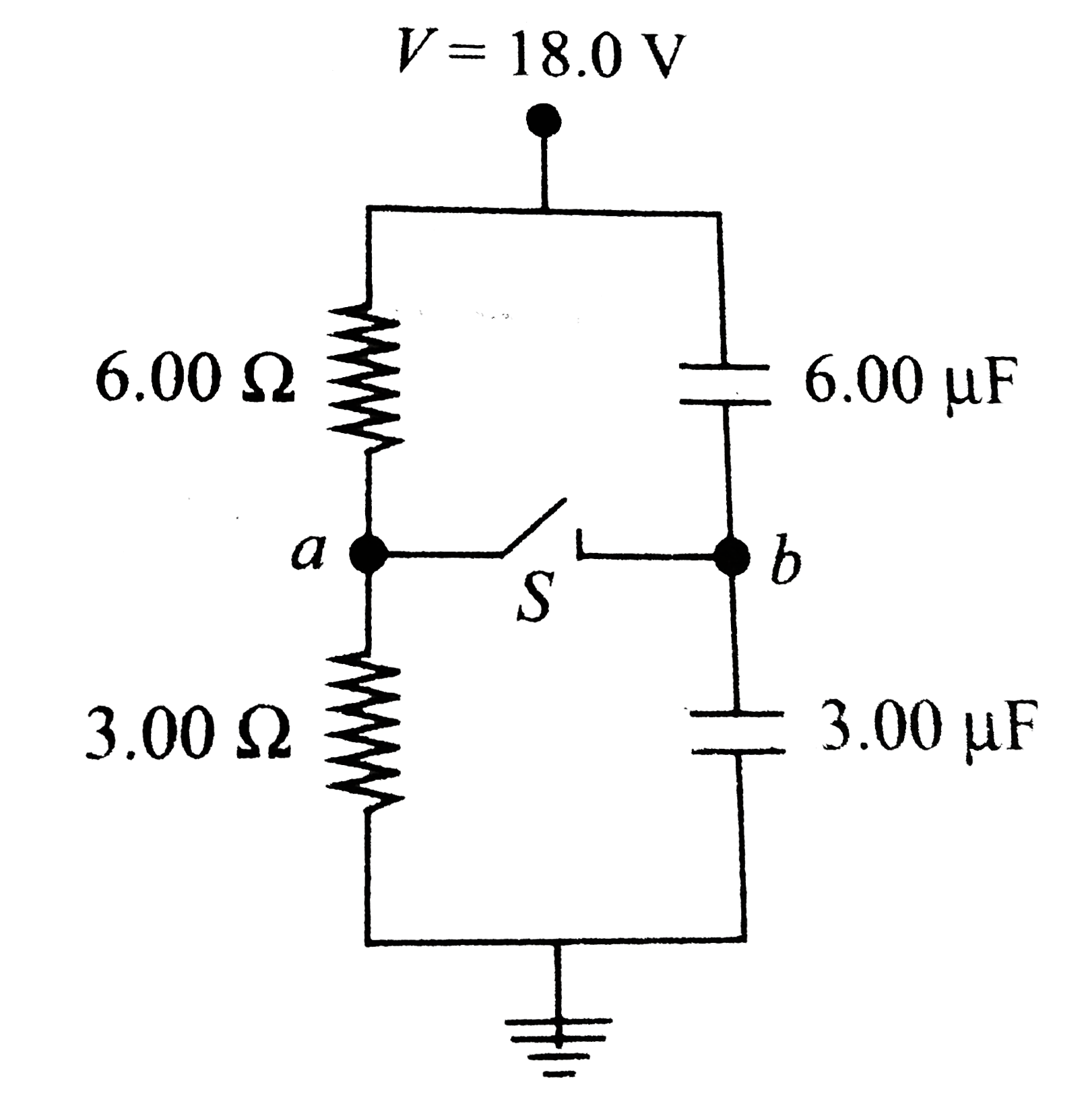
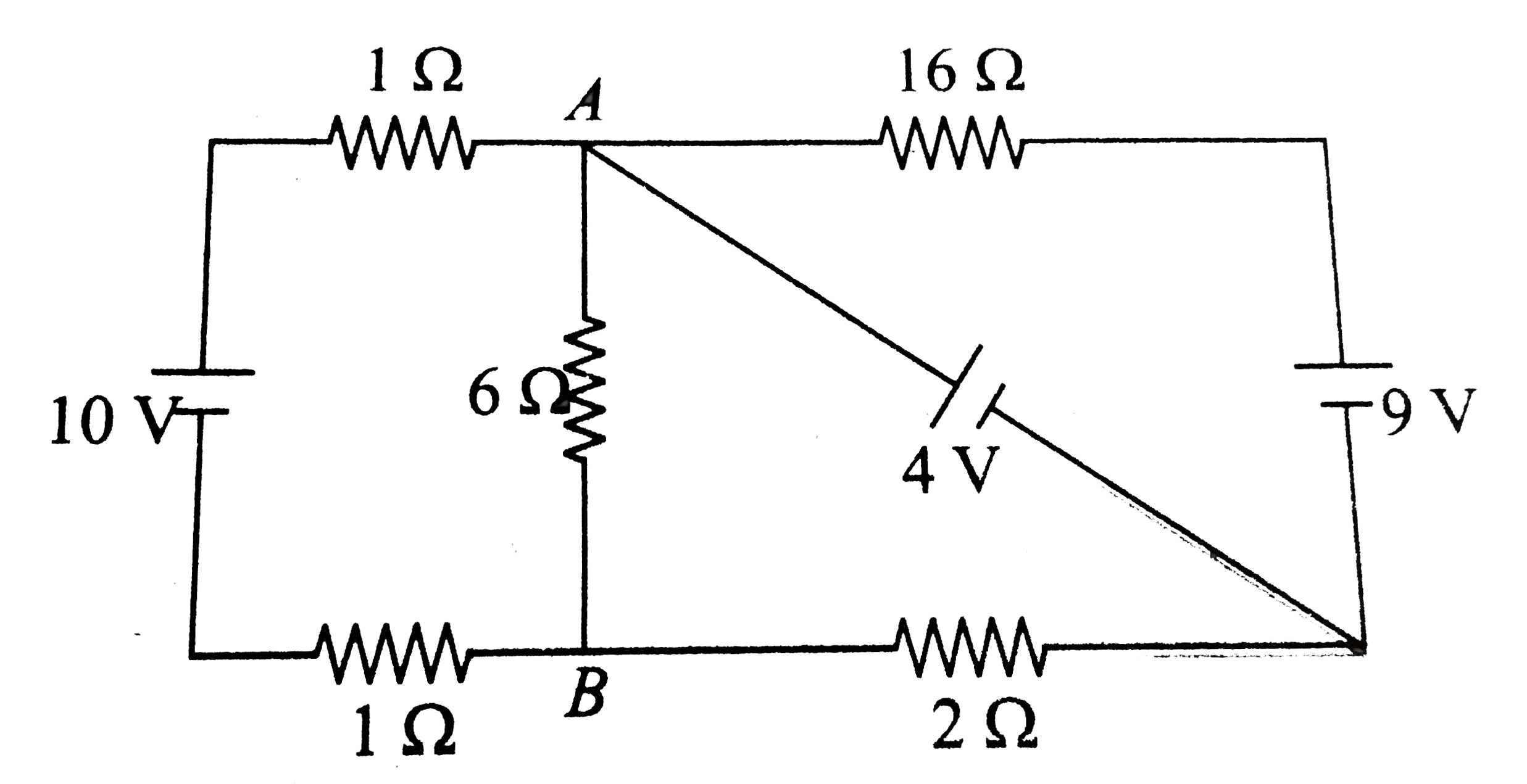
(a) What is the potential of point a with respect to point b in figure, when switch S is open?
(b) Which point, a or b, is at the higher potential?
(c) What is the final potential of point b with respect to ground when switch S is closed?
(d) How much charge flows through switch S when it is closed?View SolutionQuestion 94
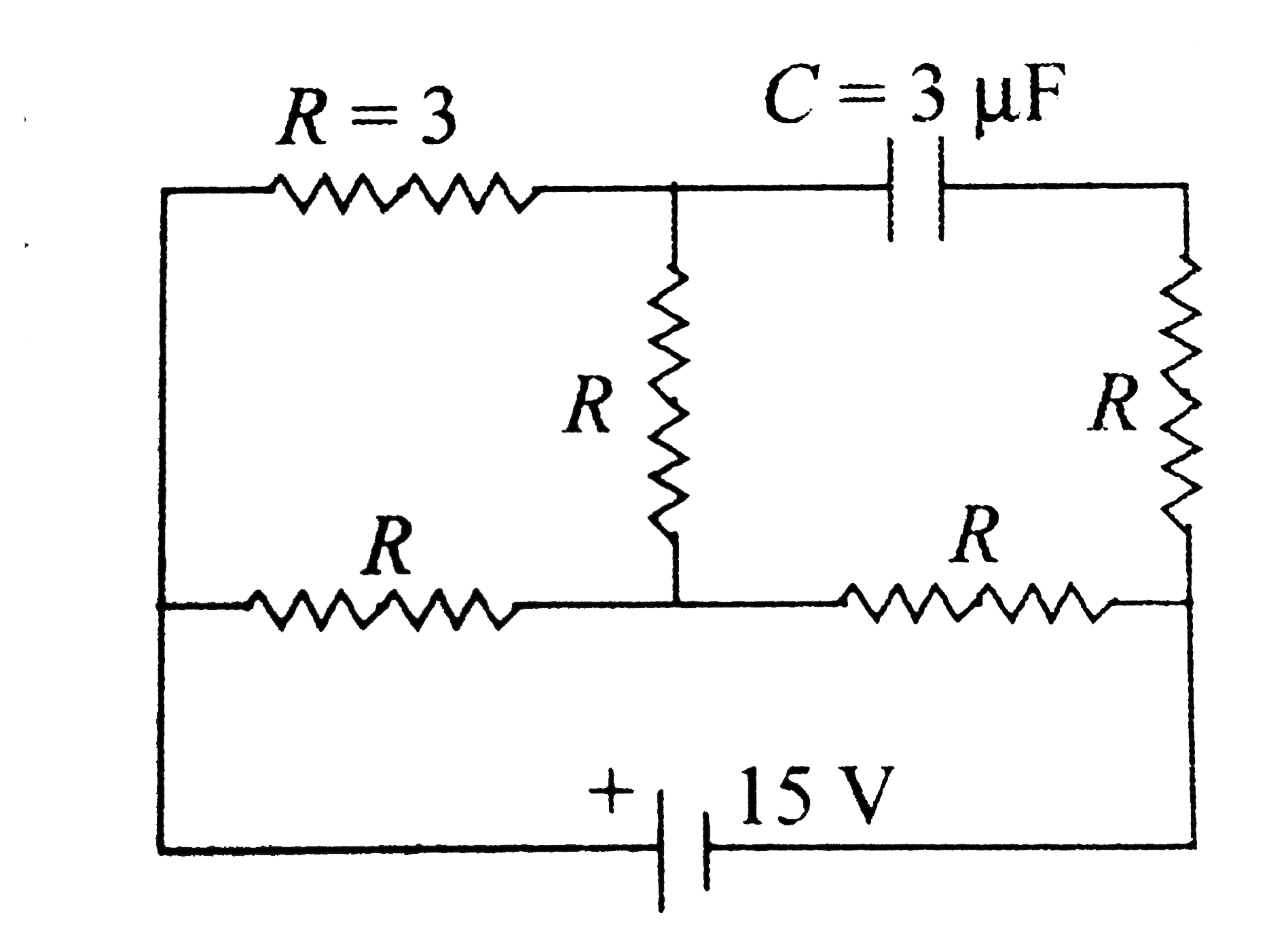
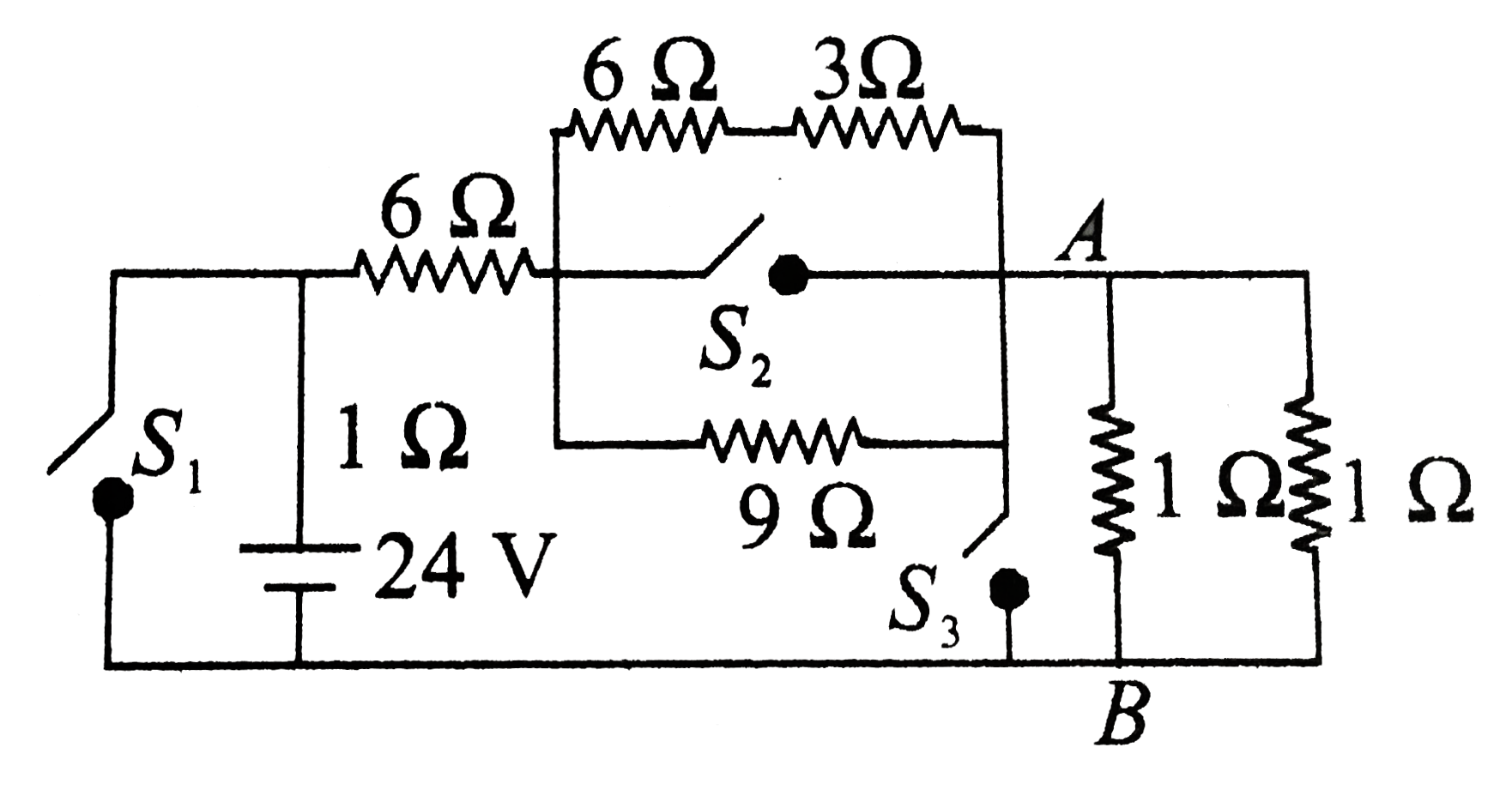
In the cicuit shown in fig. C is a parallel plate air capacitor having plate of area A=50cm2 each and distance d = 1mm apart. R1R2,andR3 are resistors having resistance 3Ω,2Ω,and1Ω respectively. Two identical sources each of emf V and of emf V and of negligible internal resistance are connected as shown in fig. if a dielectric strength of are is E0=3×106Vm−10, calculate the maximum safe value of V.
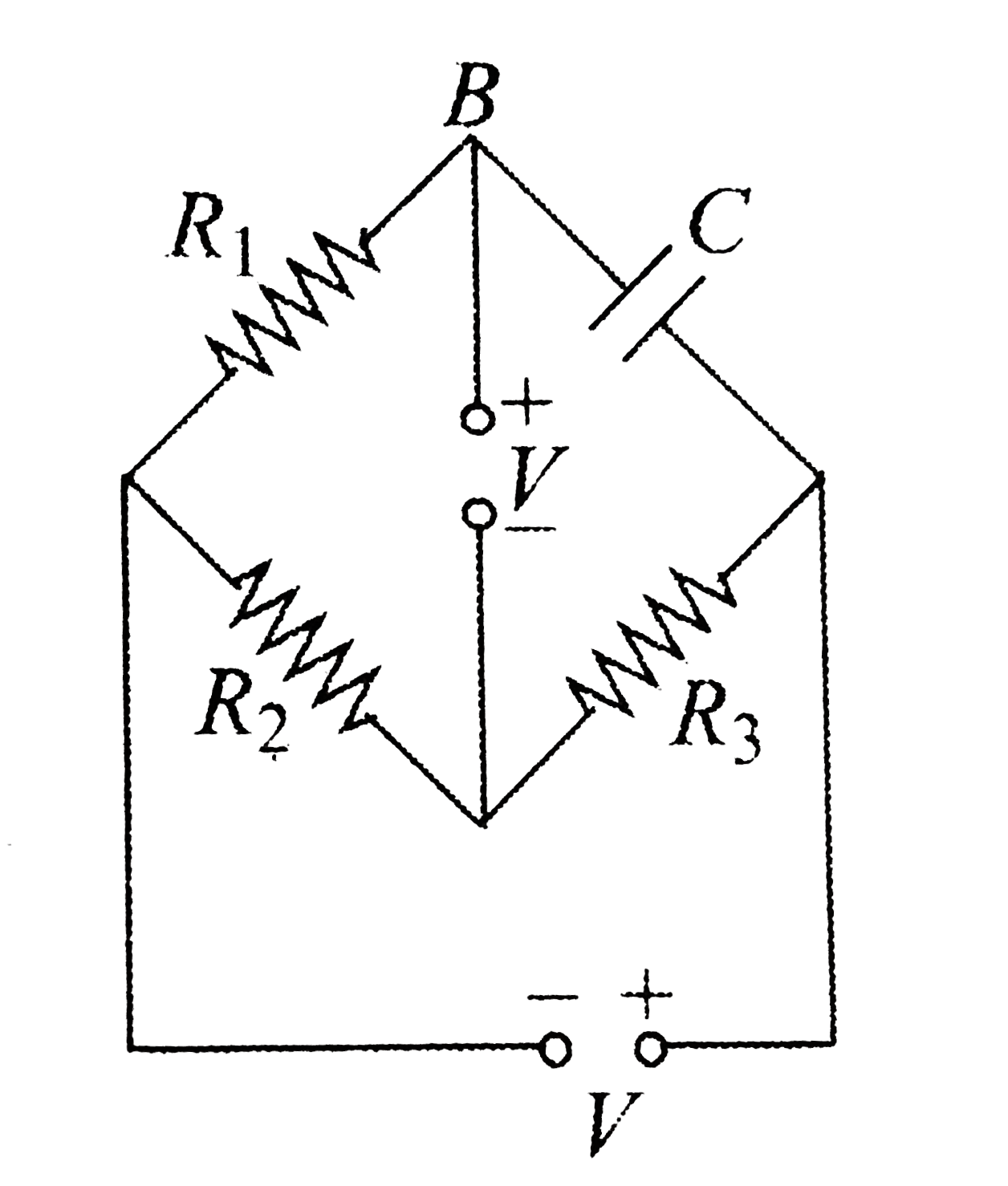 View Solution
View SolutionQuestion 96
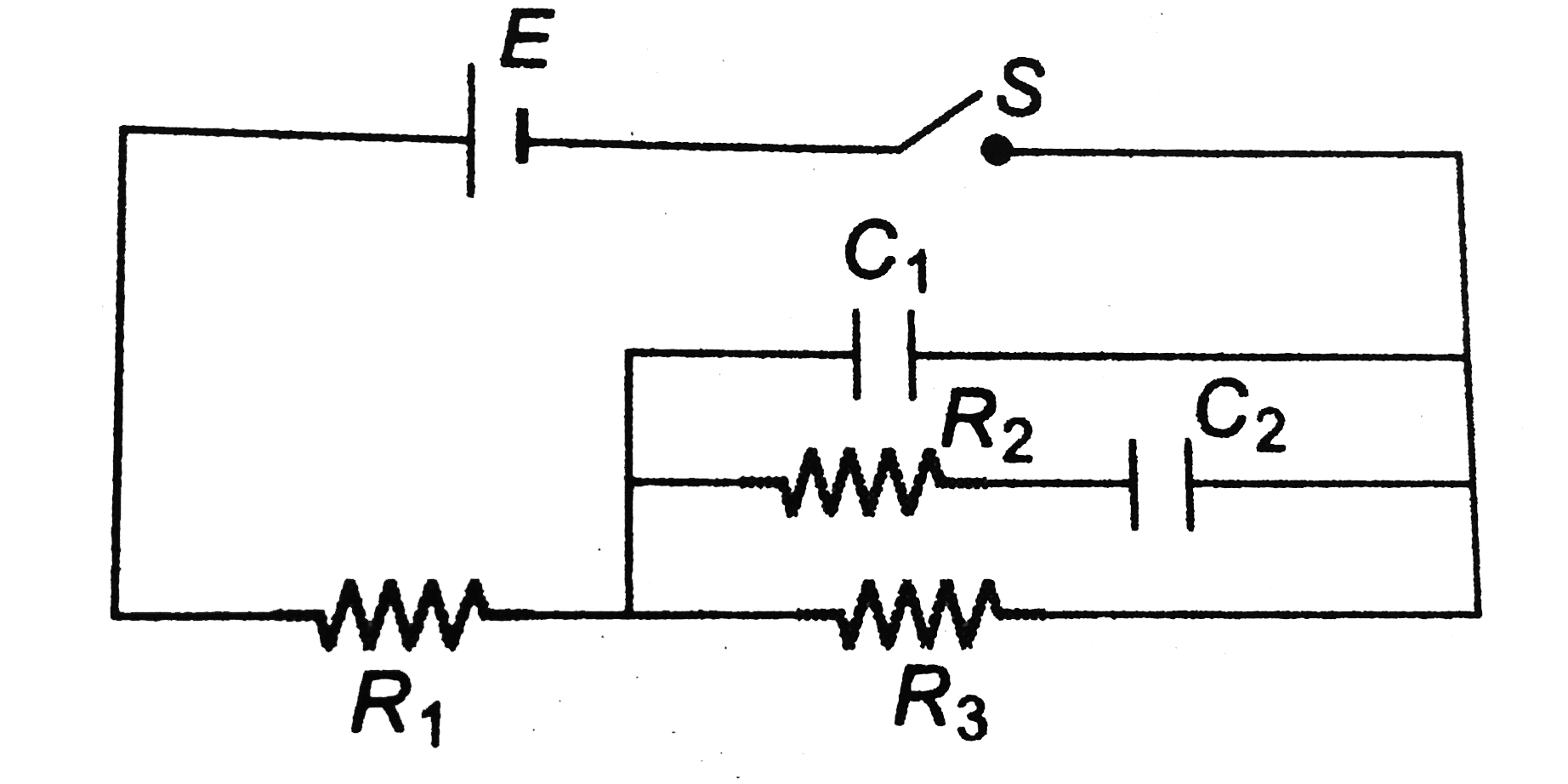
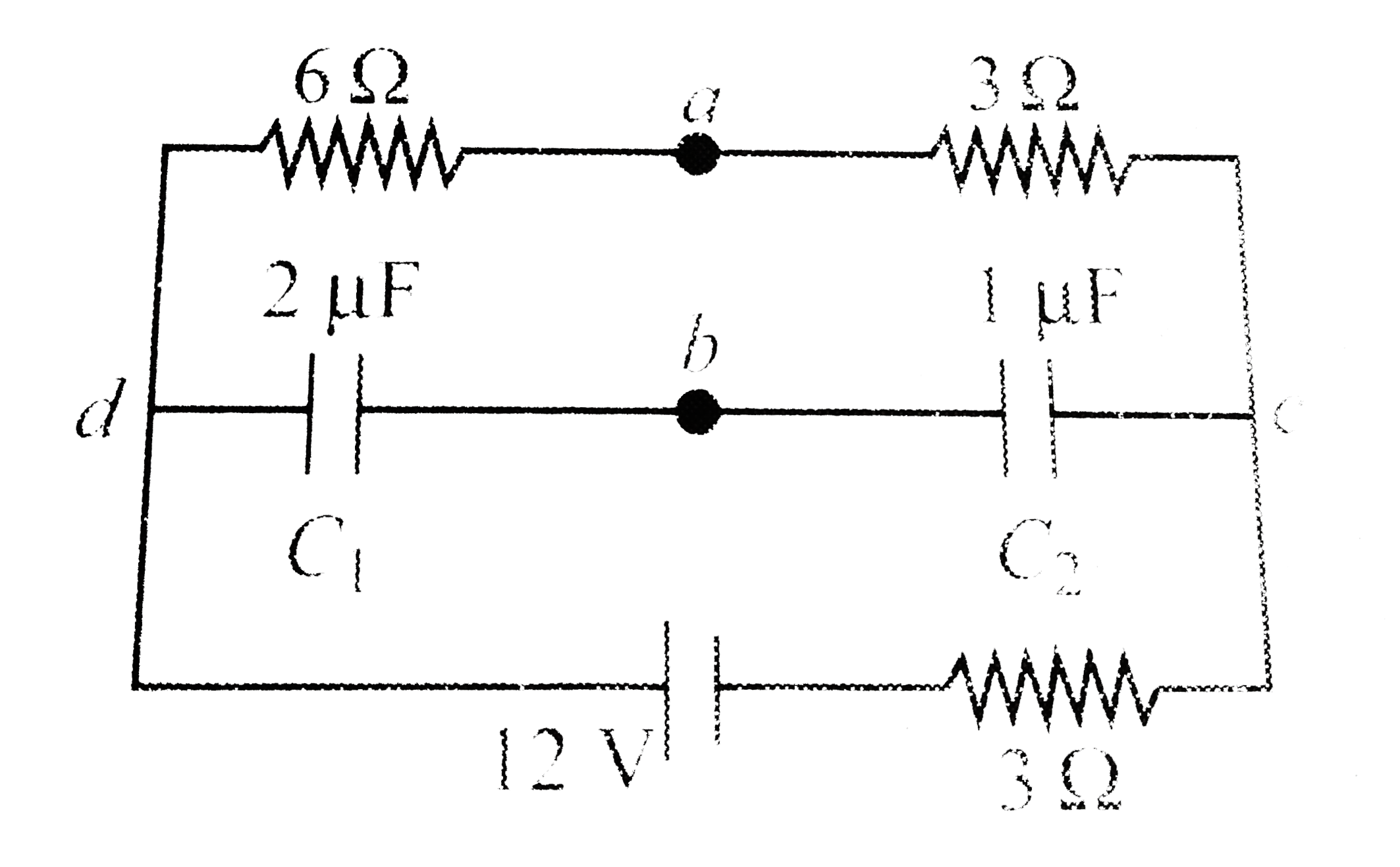
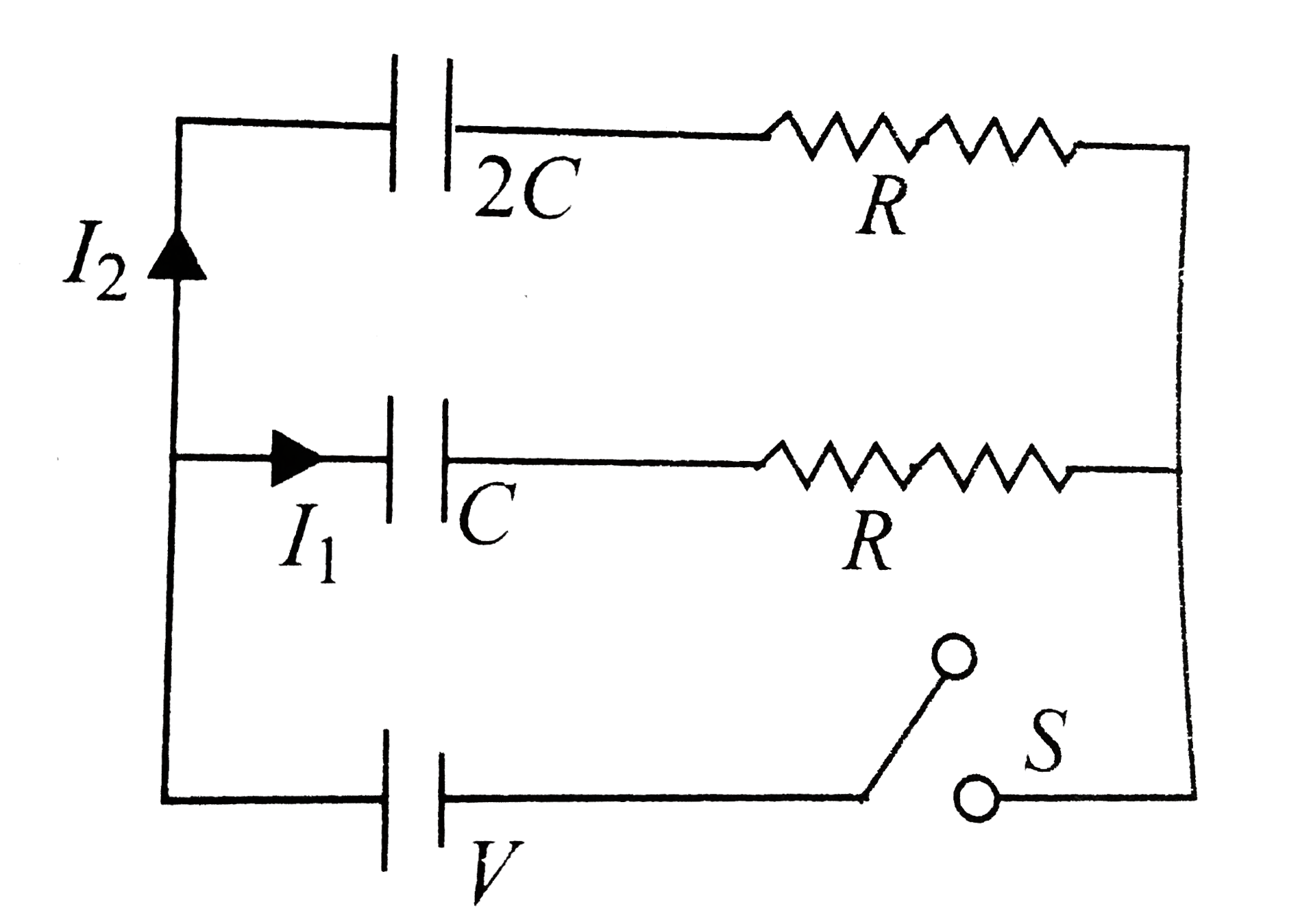
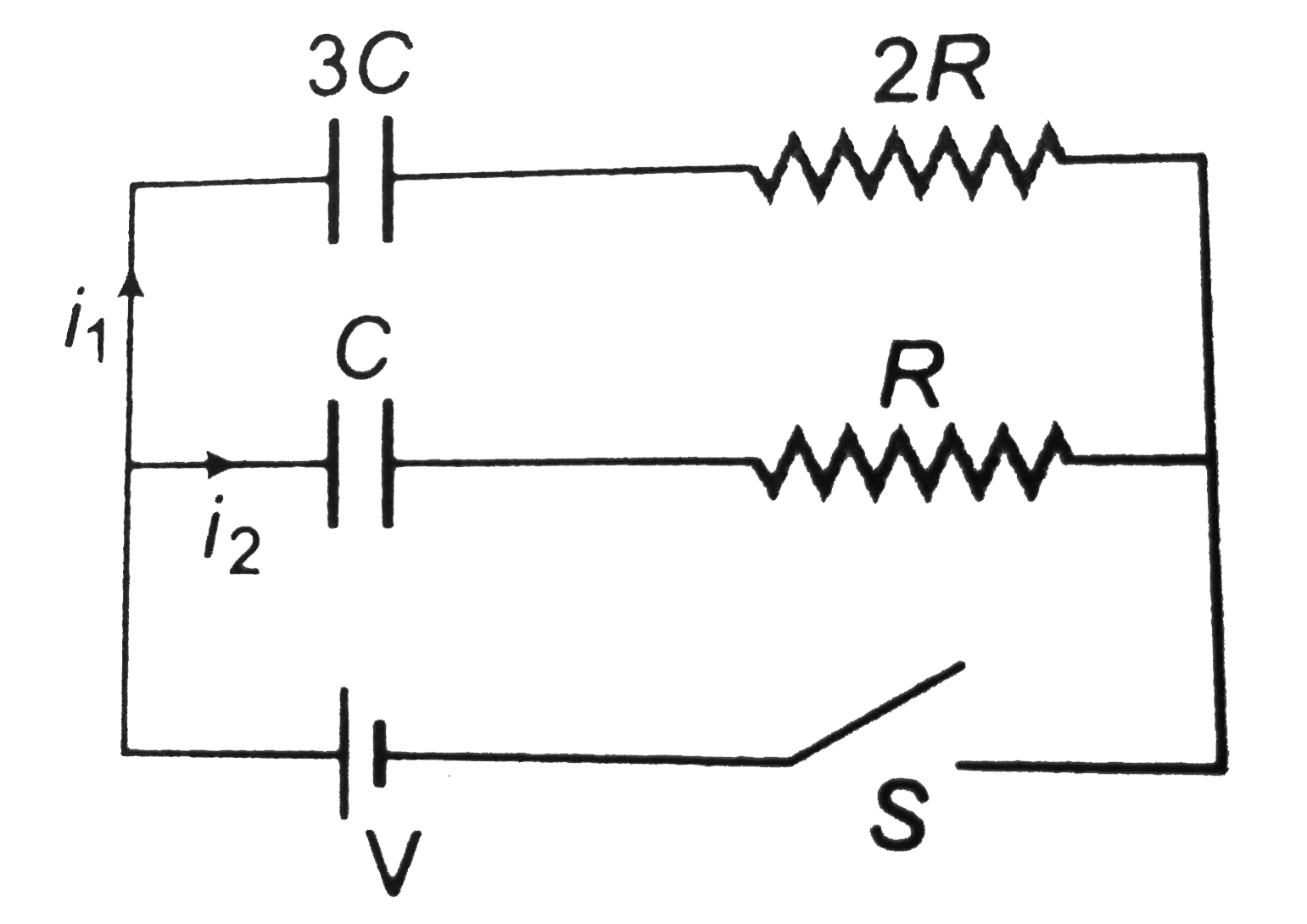
The given R-C circuit has two swithes S1andS2 Swithc S2 is clsoed and S1 is open till the capacitor is fully charged to q0 the S2 is opened and S1 is closed simultaneously till the charge on capacitor remains q0/2 for which it takes time t1. Now S1 is again opened, and S2 is closed till chrage on capacitor becomes 3q04. it takes time t2 (see fig for referecne). Find the raito t1/t2
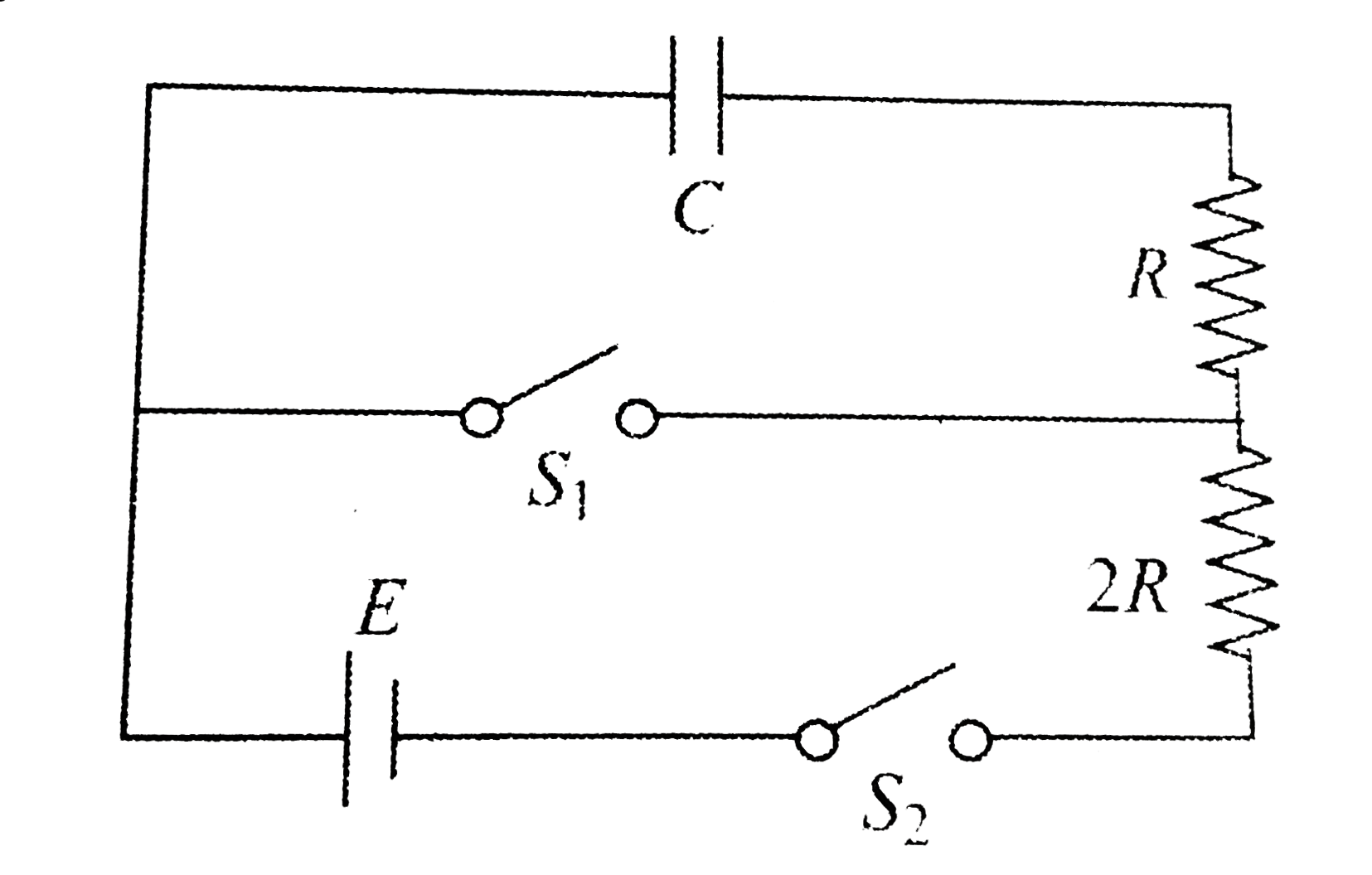 View Solution
View SolutionQuestion 99
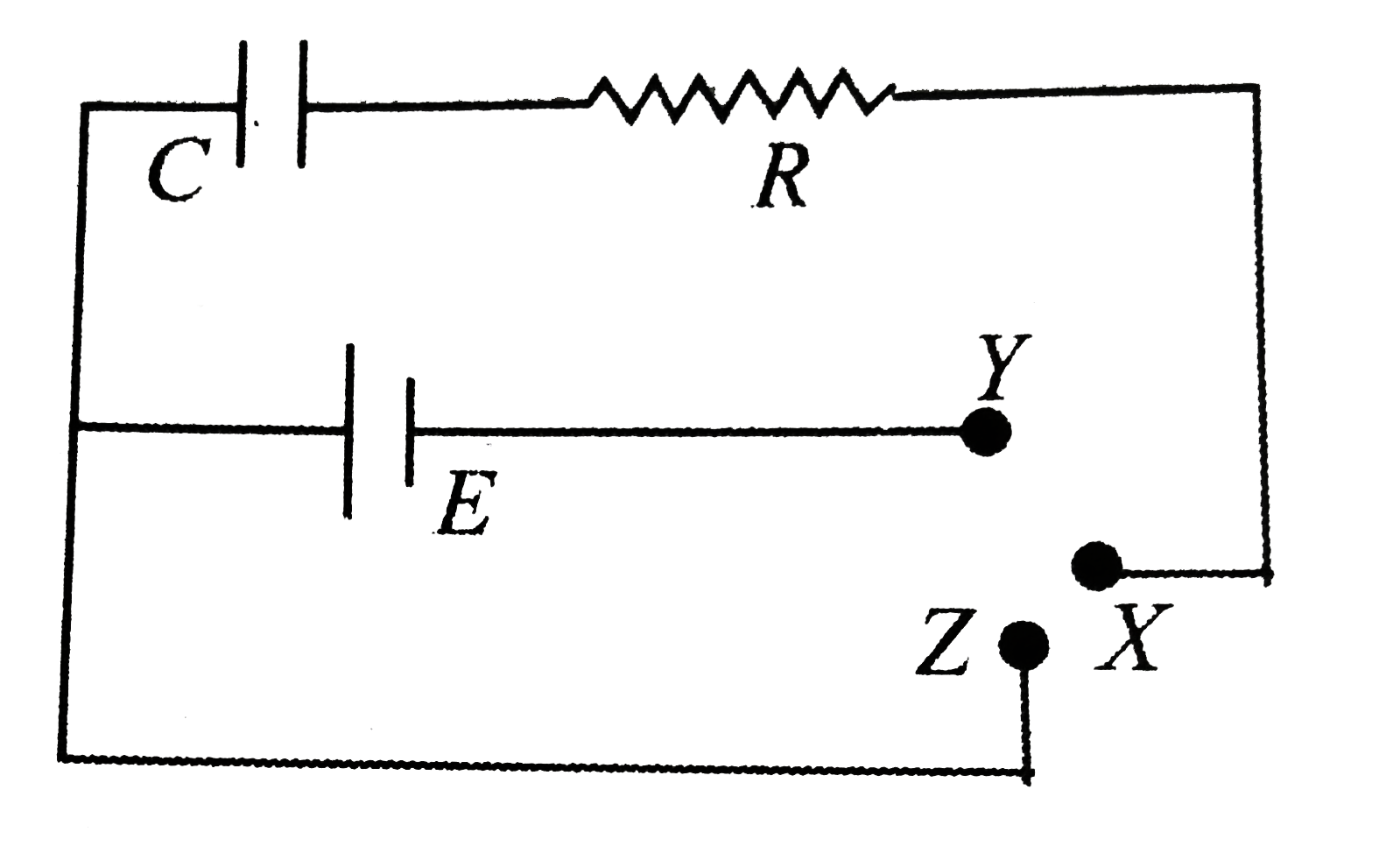
Consider a parallel pate capacitor of capactance C with partially conducting medium between its plates having a resistacne Rc if this capacitor is connected to a battery of emf ε and a resistor R as shown in fig.
a. charge on the capacitor as a function of time.
The switch R as a function of time.
 View Solution
View SolutionQuestion 107
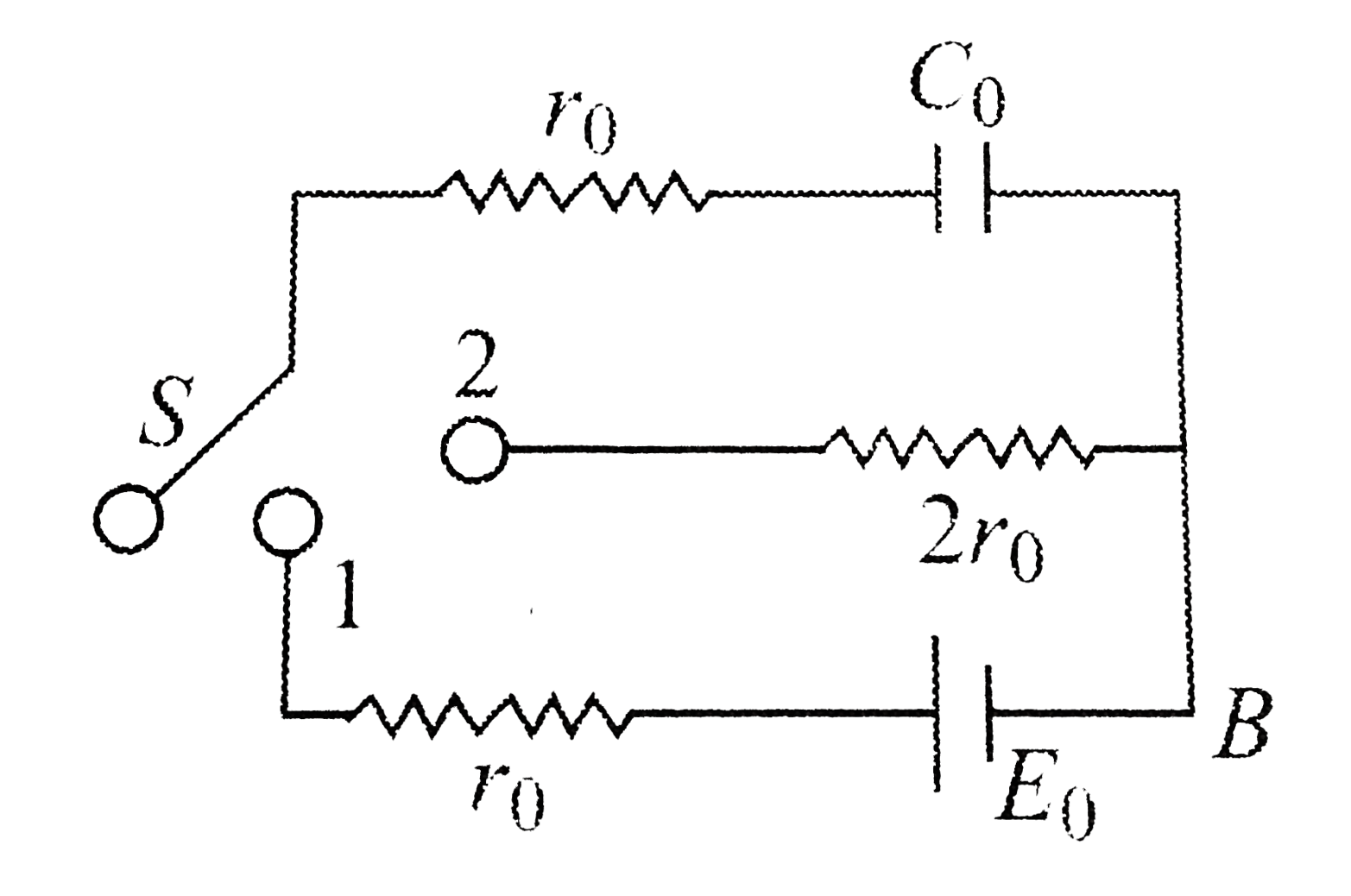
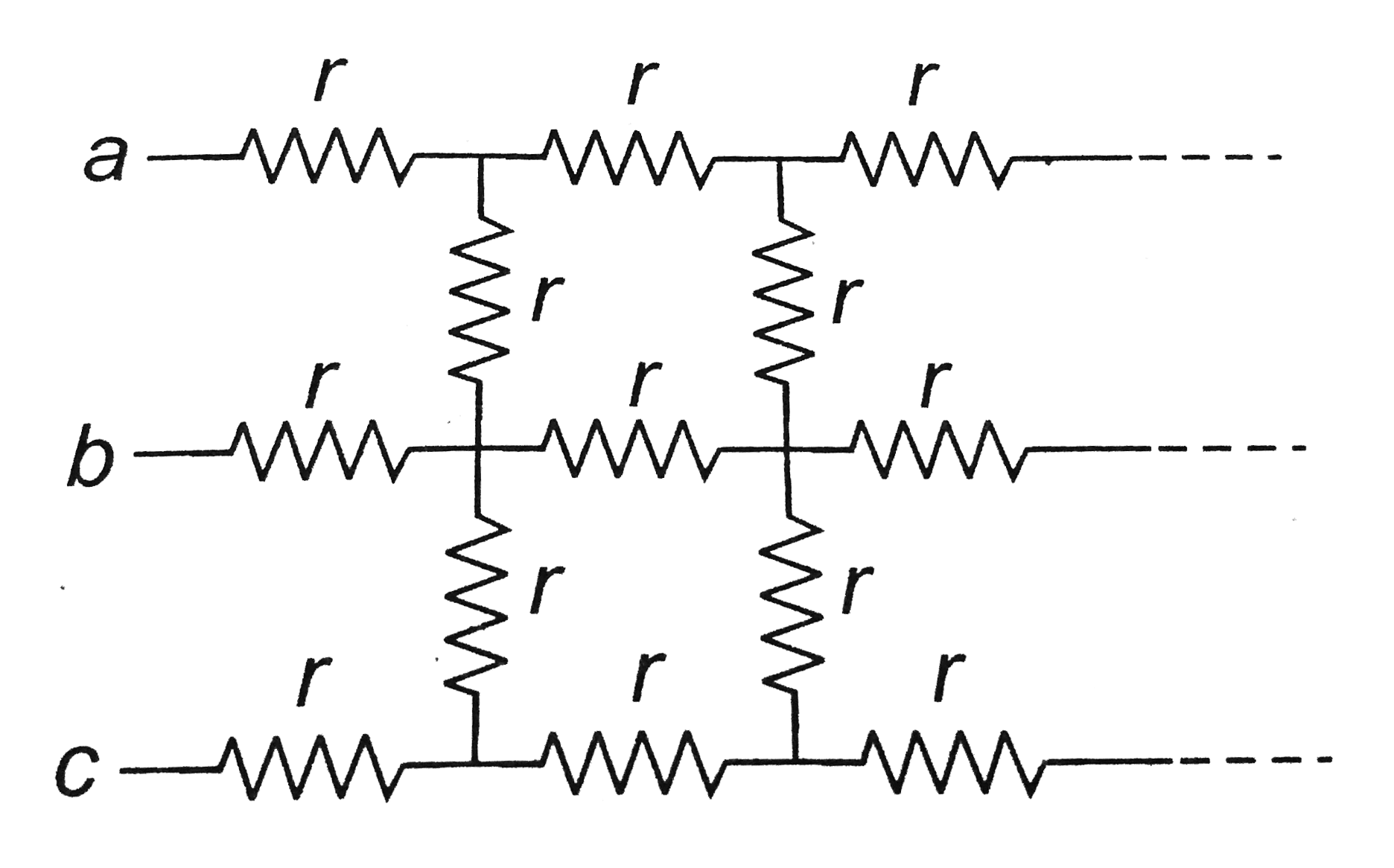
The cirucit shown in fig. extends to the right into infinity. Each battery has the electromotive force V(unknown) and the internal resistance r(known). Each resistor has the resistance 4r. The reading of the idal ammeter shown in the diagram is I. Find the value of V in terms of I and r.
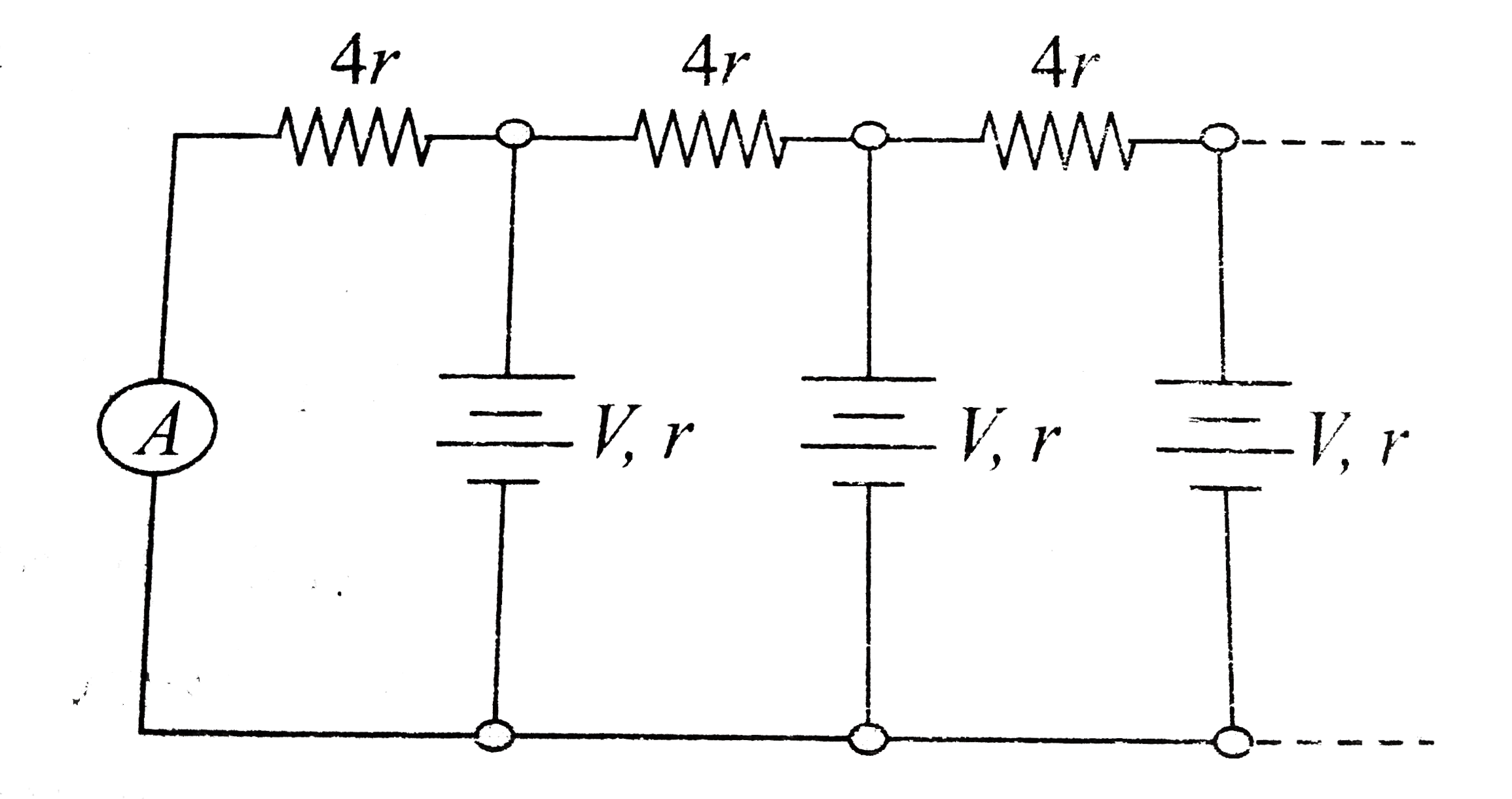 View Solution
View SolutionQuestion 117
A cell ofemf E volt with no internal resistance is connected to a wire whose cross section chages. The wire has three sections of equal length. The middle section has a redius a, whereas the radius of the outer two sections is 2a. The raito of the potential differece across section AB to the potential differecne across section CA is
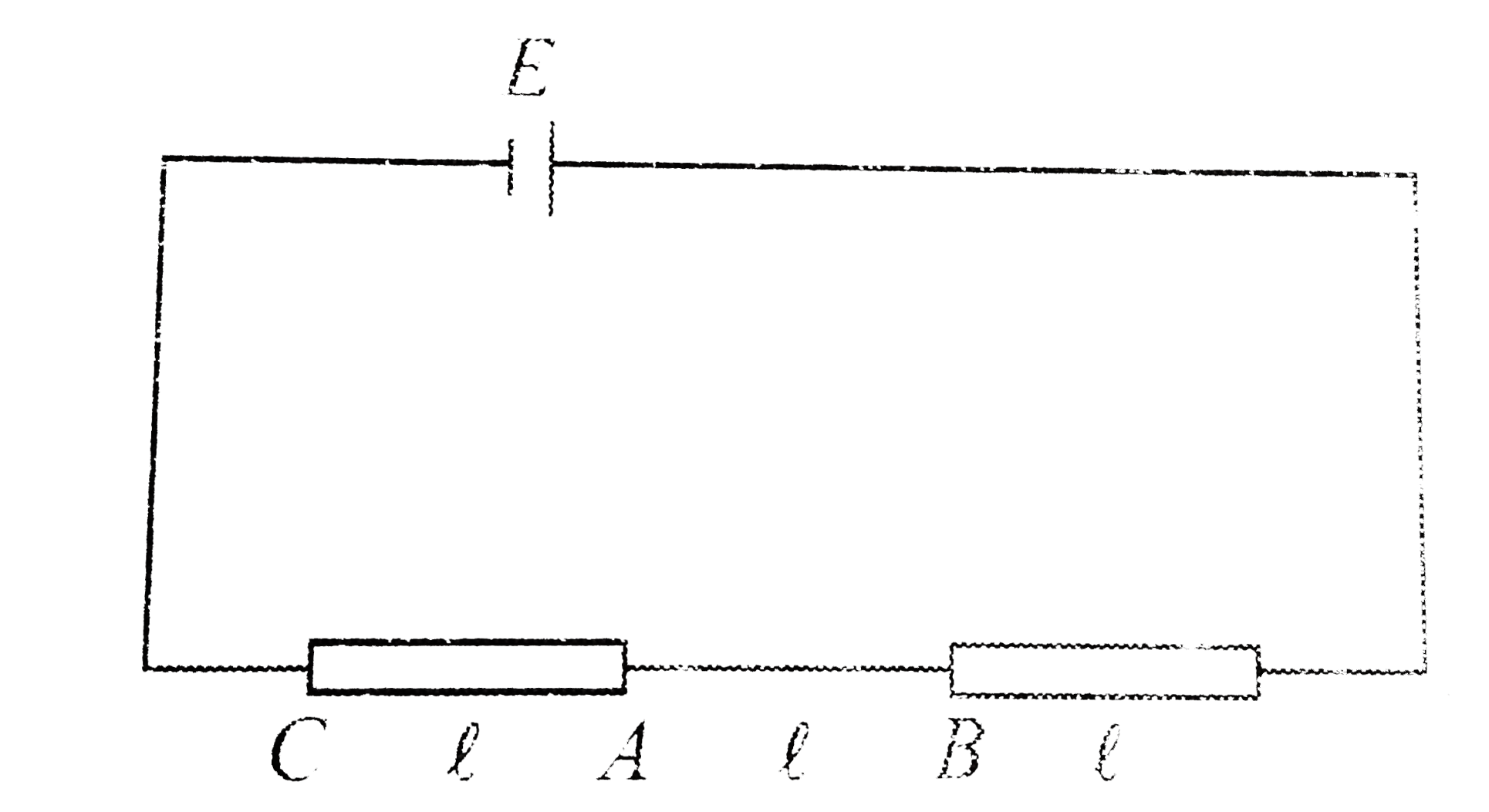 View Solution
View SolutionQuestion 138
A wire of length L and 3 identical cells of negligible internal resistance are connected in series. Due to the current, the temperature of the wire is raised by ΔT in a time t. A number N of similar cells is now connected in series with a wire of the same material and cross-section but of length 2L. The temperature of the wire is raised by the same amount ΔT in the same time t. the value of N is View SolutionQuestion 160
A straight conductor of uniform cross section carries a time varying current, which varies at the rate dI//dt = I. If s is the specific charge that is carried by each charge carries of the conductor and l is the length of the condcutor, then the totalt force experienced by all the charge carries per unit length of the conductor due to their drift velocities only is View SolutionQuestion 162
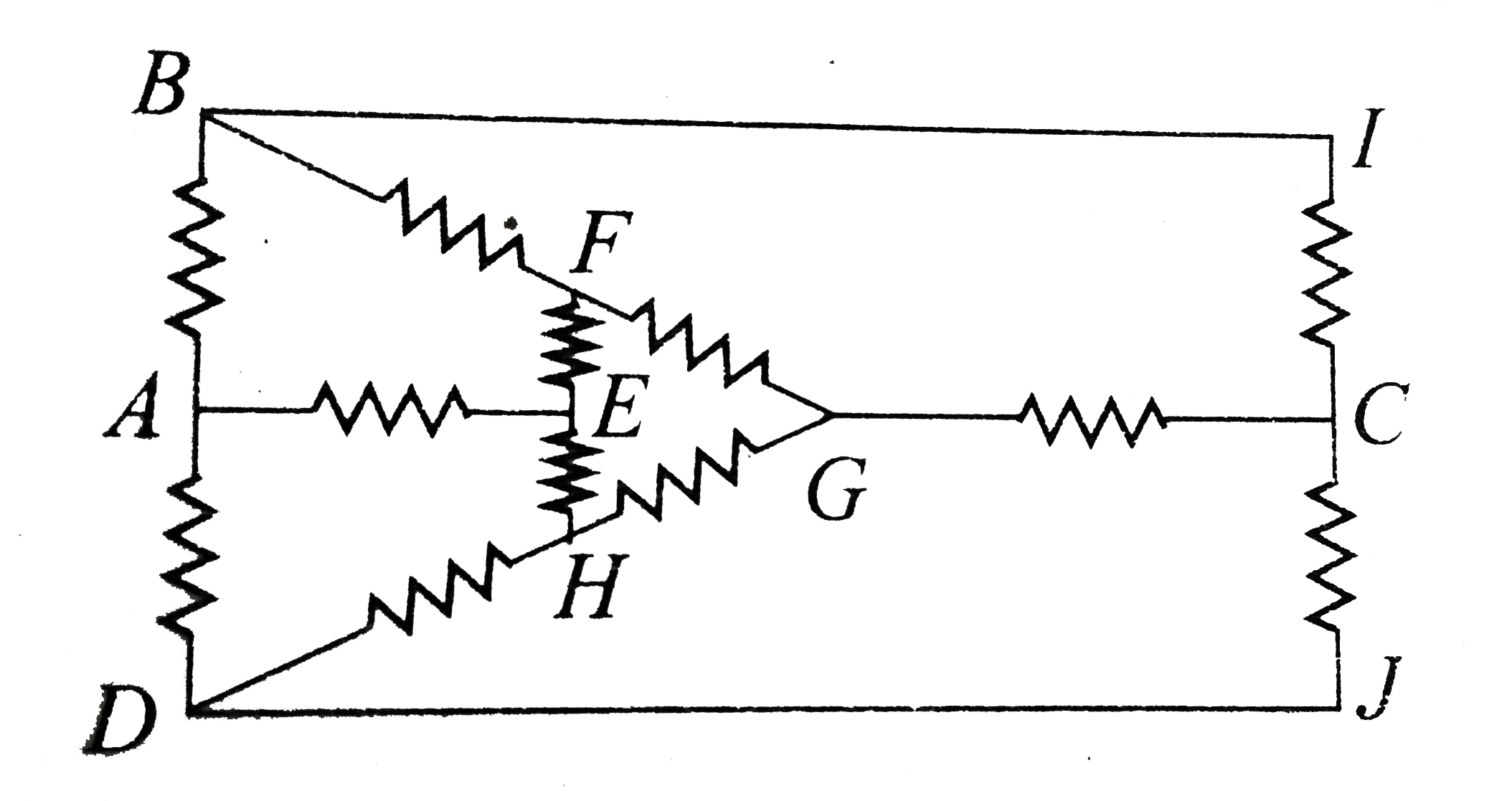
The circuit diagram shwon in the fig consist of a large number of elementws (each element has two resistors R1andR2. The resistance of the resistors in each subsequent element differs by a factor of k=12 from the resistance of the resistors in previous elements find the equivalent resistance between A and B shown in
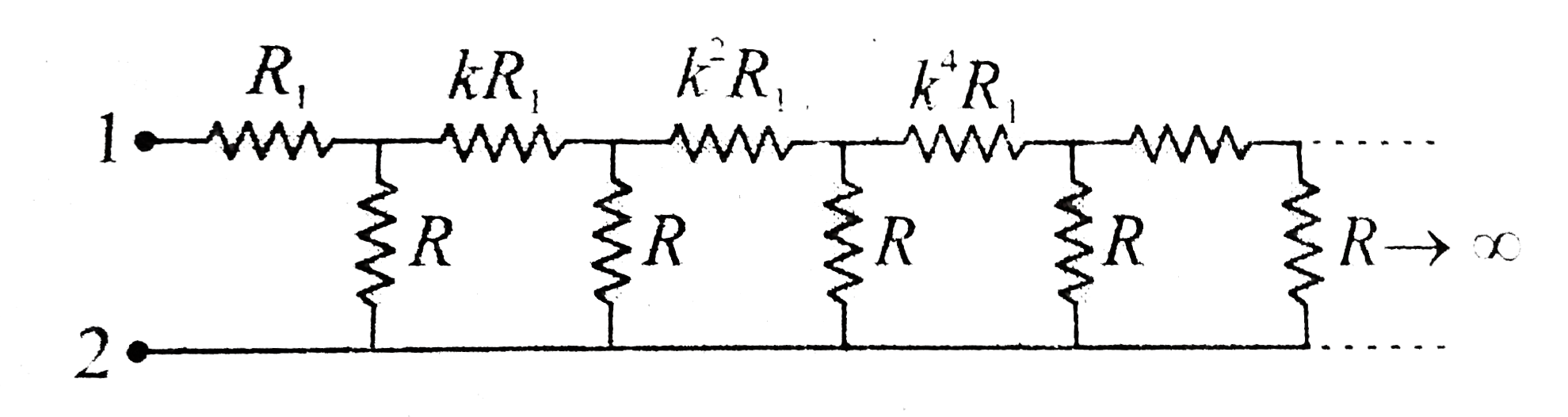 View Solution
View SolutionQuestion 184
A battery of emf E and internal resistance r is connected across a resistance R. Resistance R can be adjusted to any value greater then or equla to zero. A graph is plotted between the current passing through the resistance (I) and potential (V) across it. Select the correct alternatives.
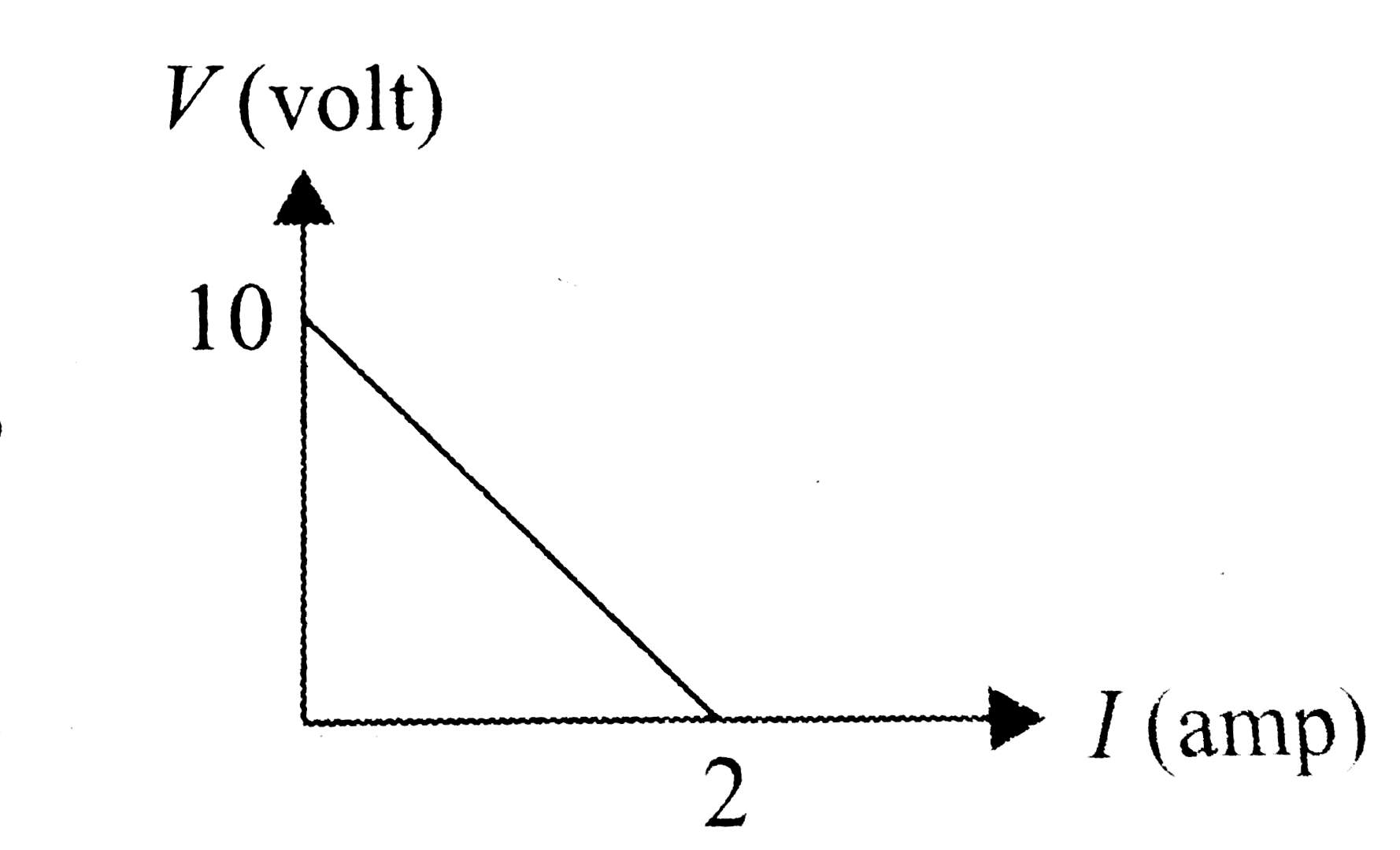 View Solution
View SolutionQuestion 204
A network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.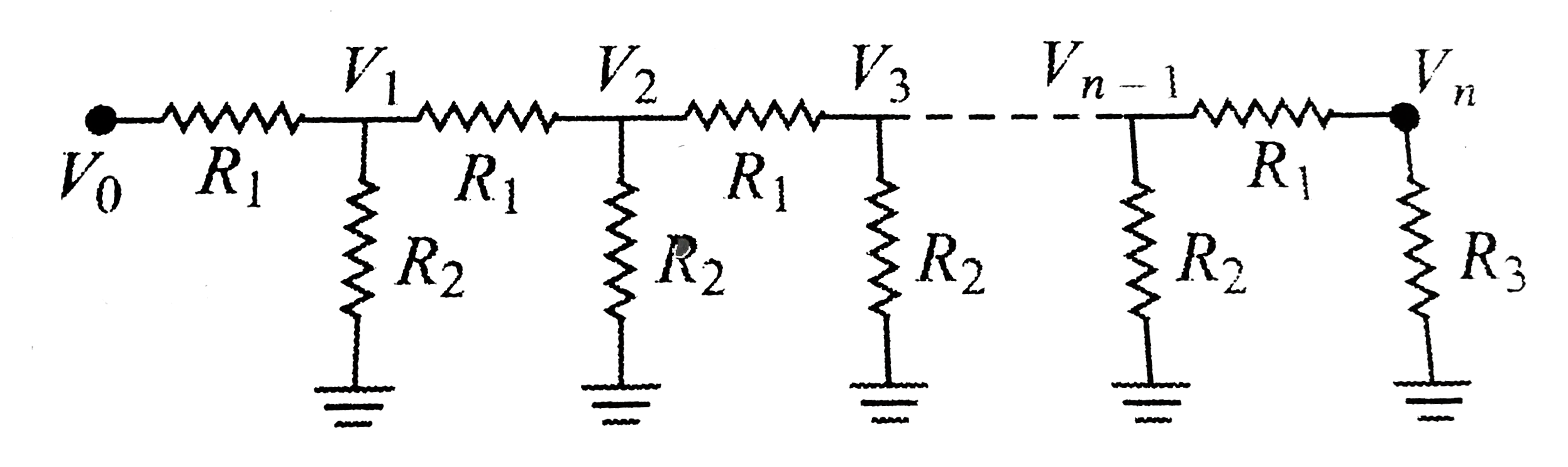
The current that passes through the resistance R2 nearest to the V0 is View SolutionQuestion 214
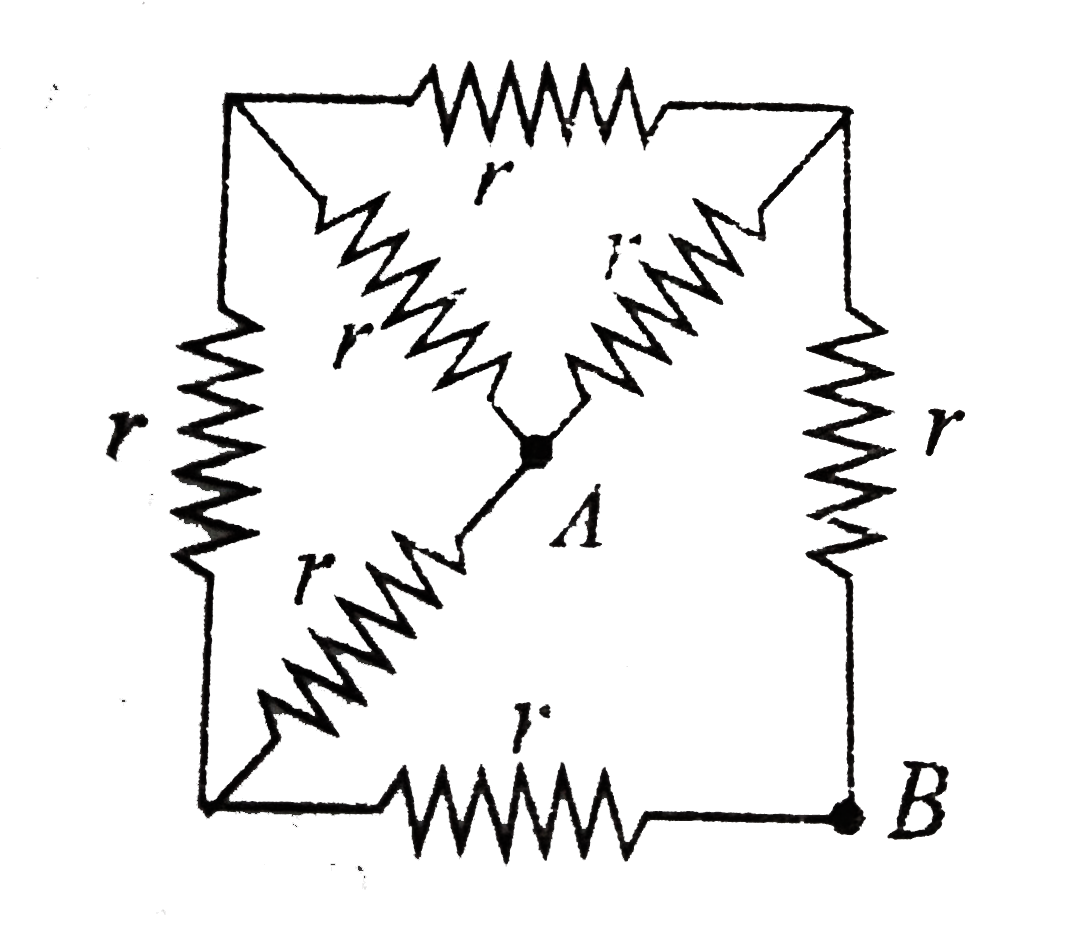
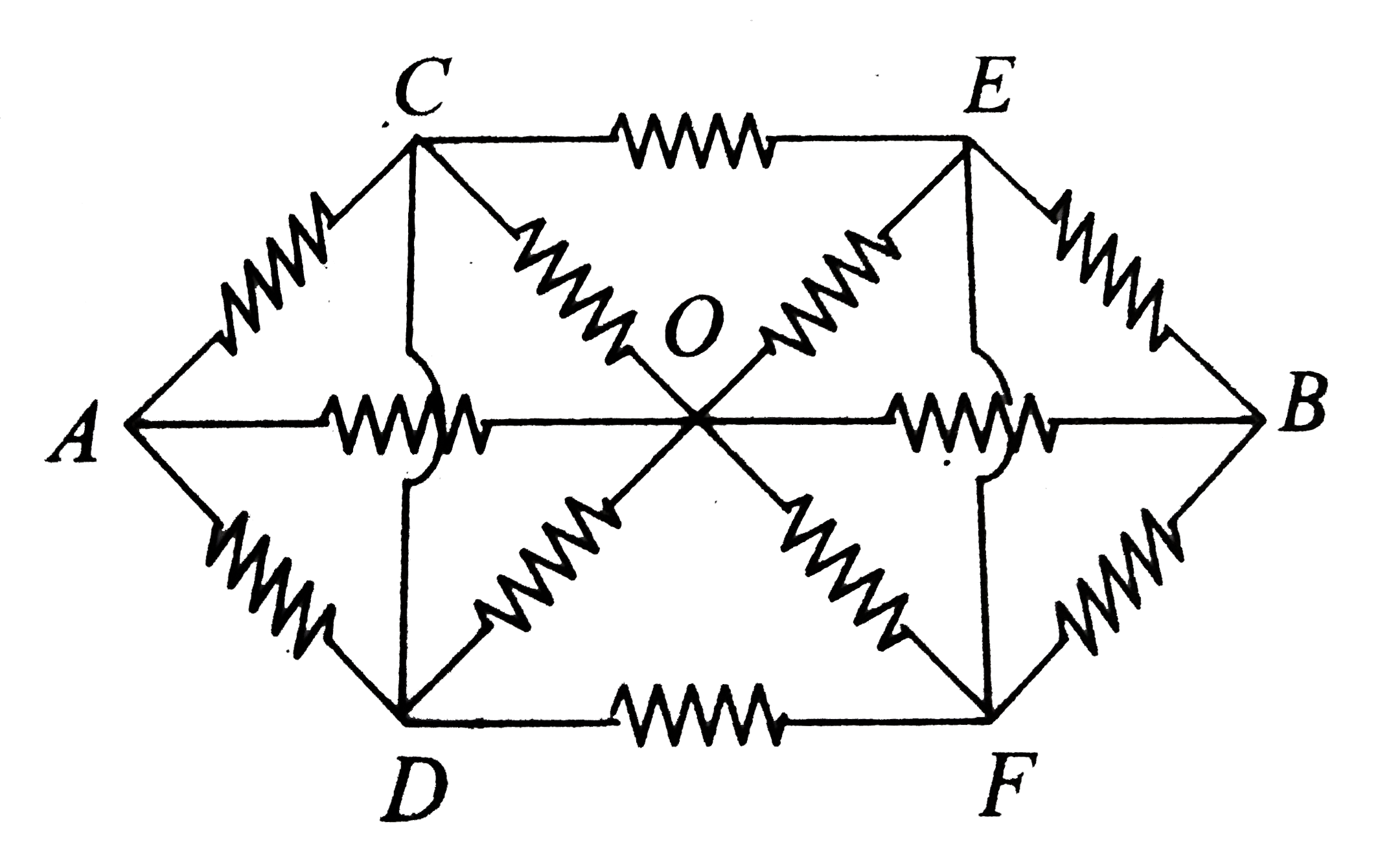
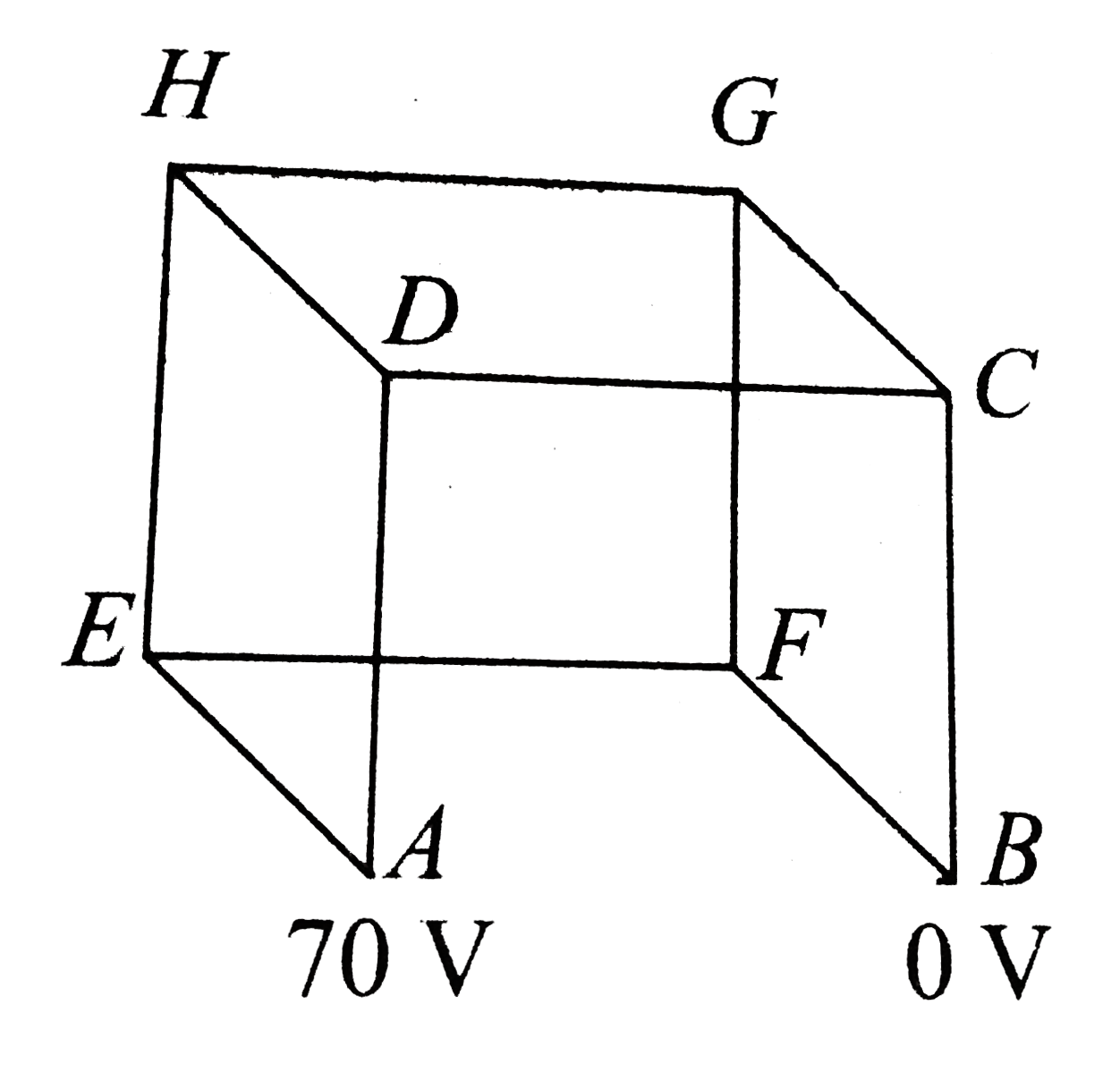
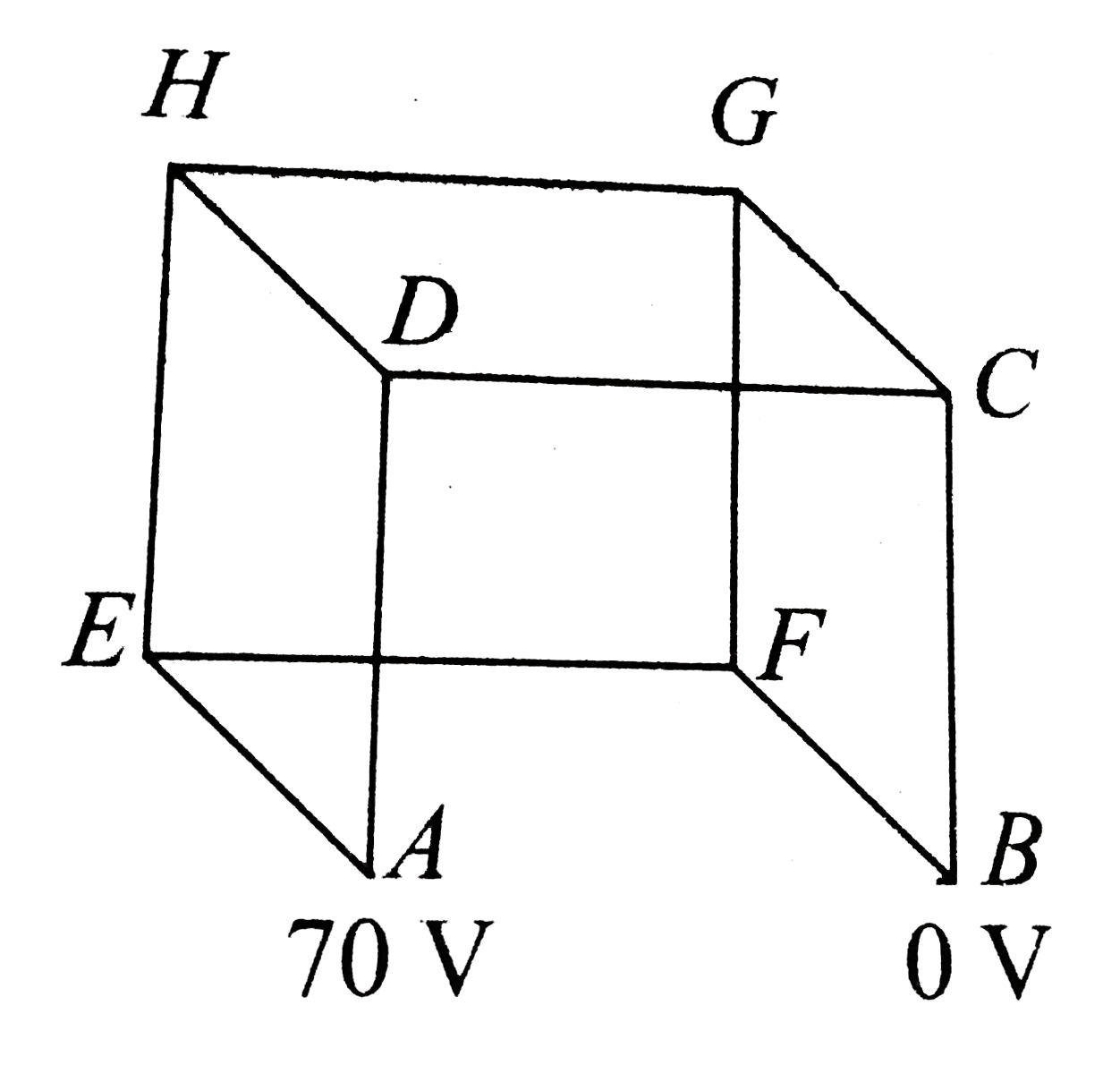
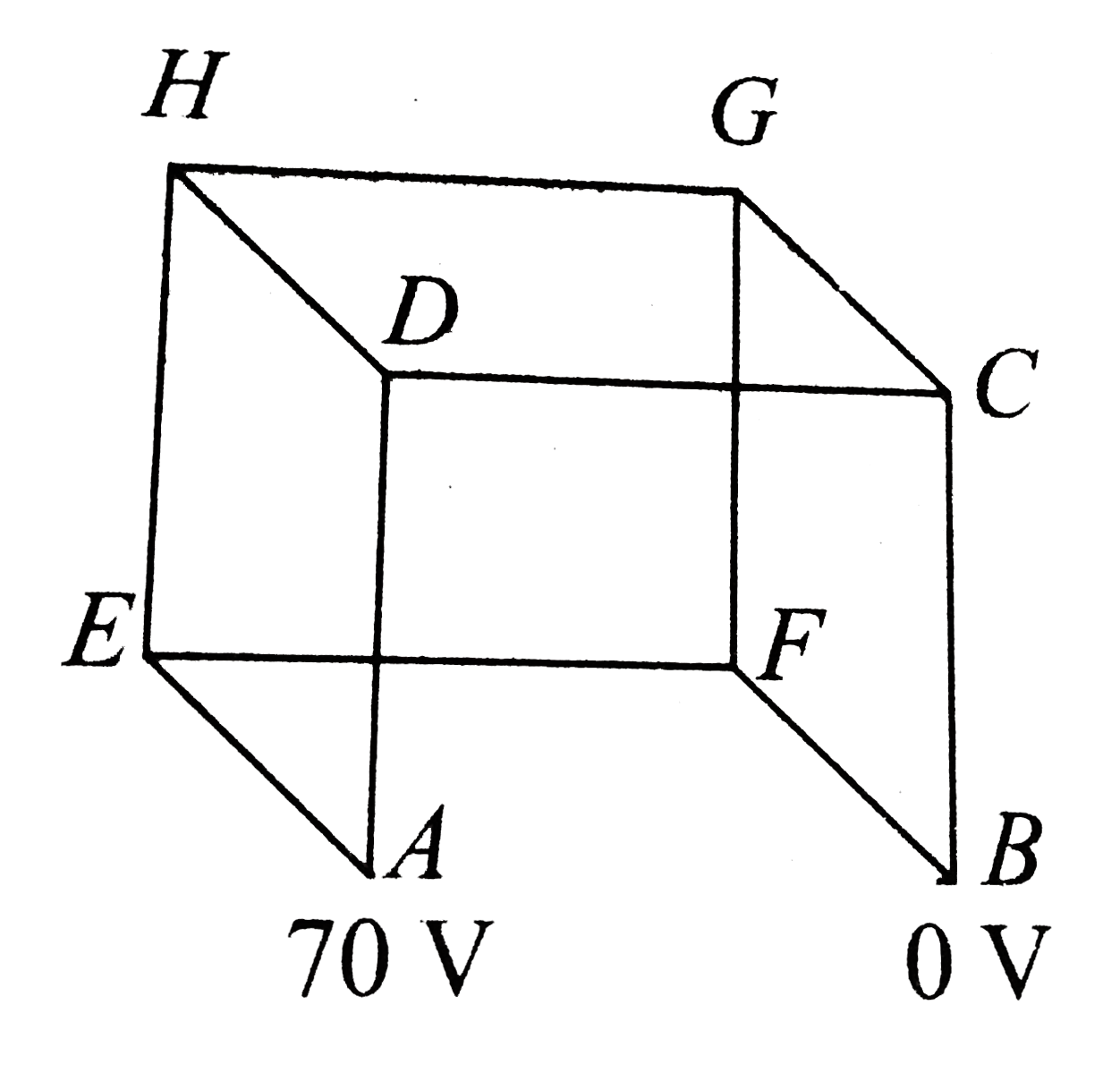
A resistor circuit is constructed such that 12 resistor are arranged to form a cube as shown in fig. Each resistor has a resistance of 2Ω. The potential difference of 30V is applied across two of the opposing points as shown
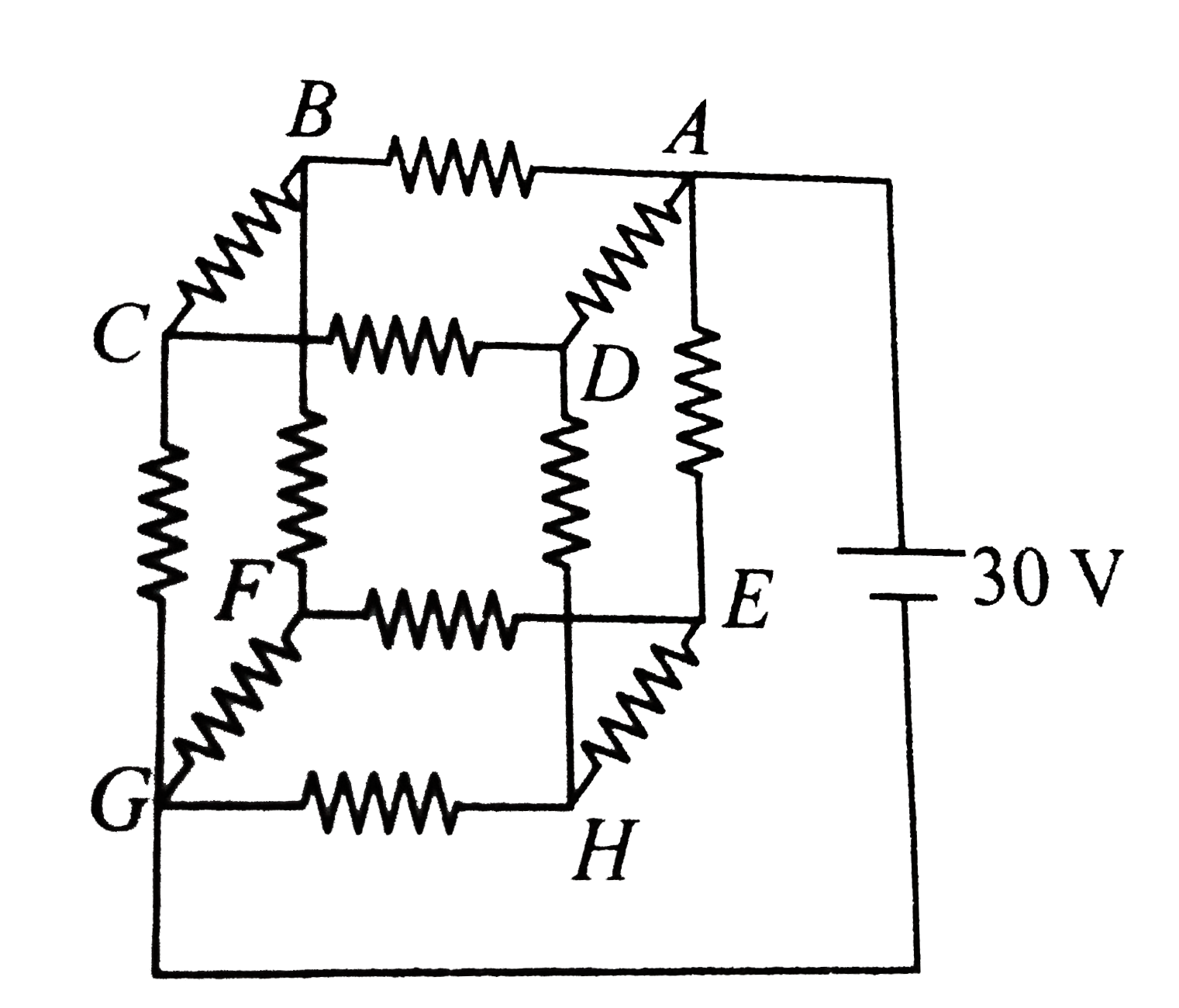
The points having the same potential are
i. B,D,E ,ii. C,F,H ,iii. C,EView SolutionQuestion 215
A resistor circuit is constructed such that 12 resistor are arranged to form a cube as shown in fig. Each resistor has a resistance of 2Ω. The potential difference of 30V is applied across two of the opposing points as shown
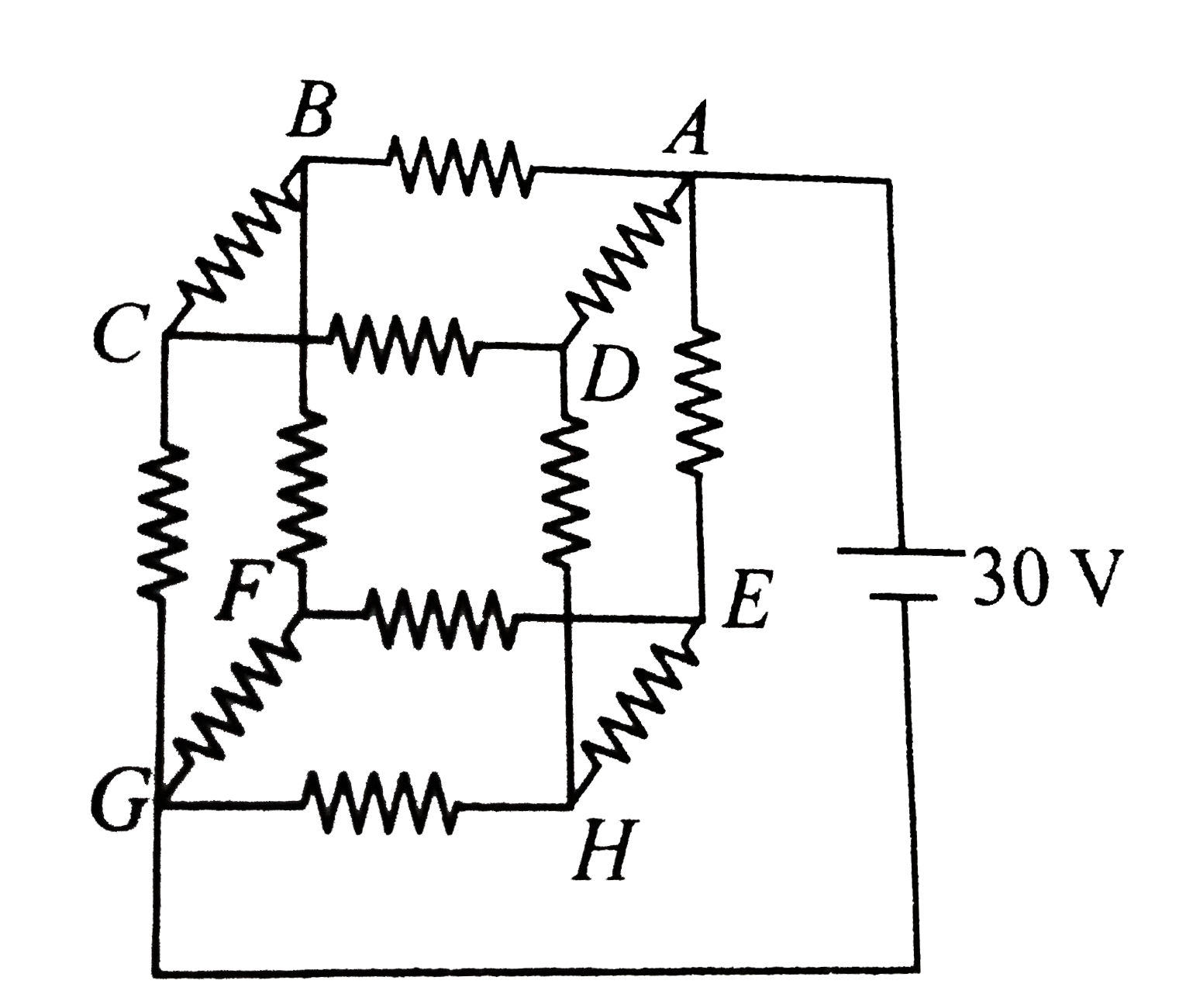
If we replace resistor between A and B and resistors between G and H by wires of zero resistance, then the points having the same potential are
i. D,E,C,F ,ii. A,B ,iii. G,HView SolutionQuestion 216
A resistor circuit is constructed such that 12 resistor are arranged to form a cube as shown in fig. Each resistor has a resistance of 2Ω. The potential difference of 30V is applied across two of the opposing points as shown
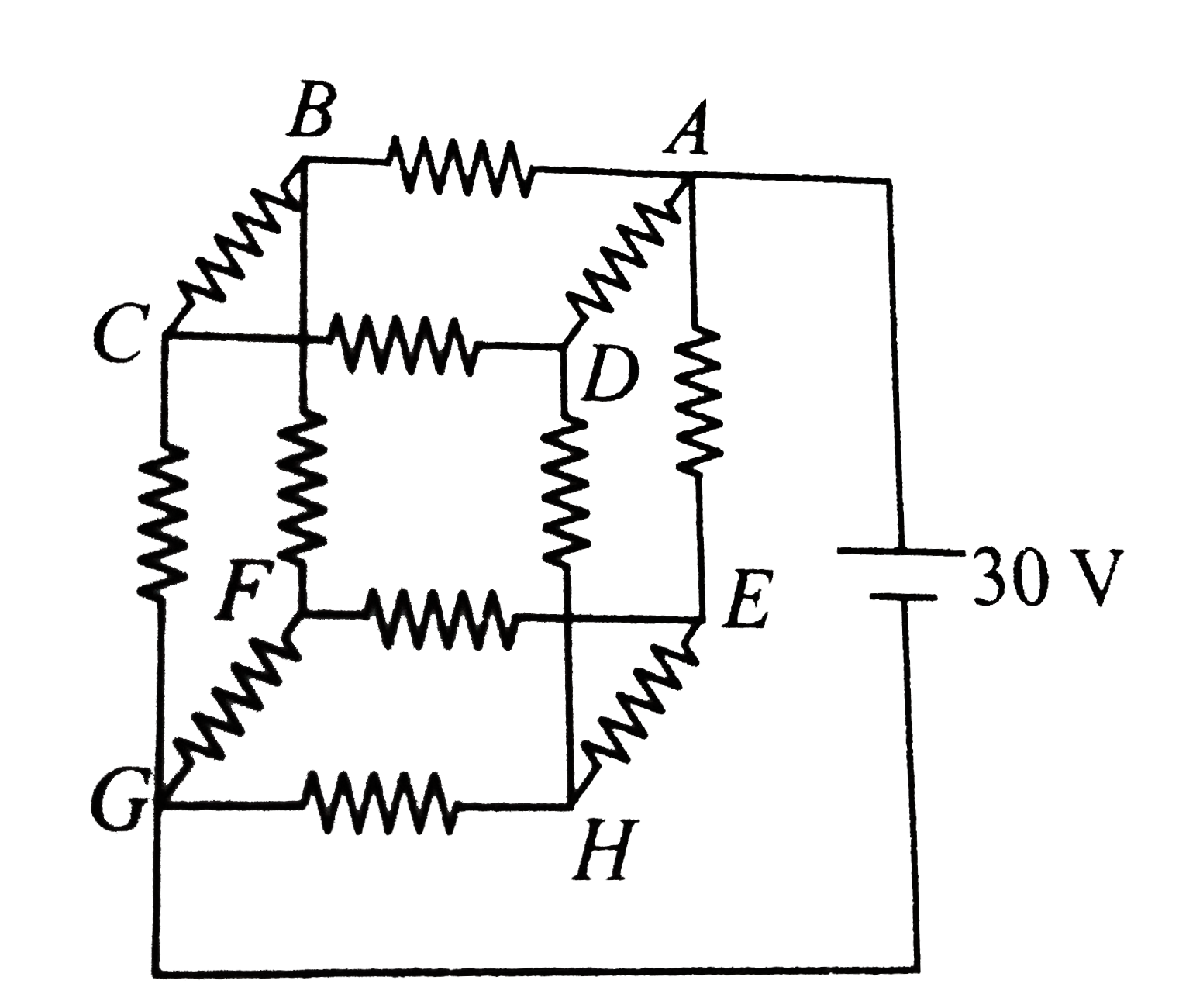
In question 20, the potential difference between the points C and G is View SolutionQuestion 217
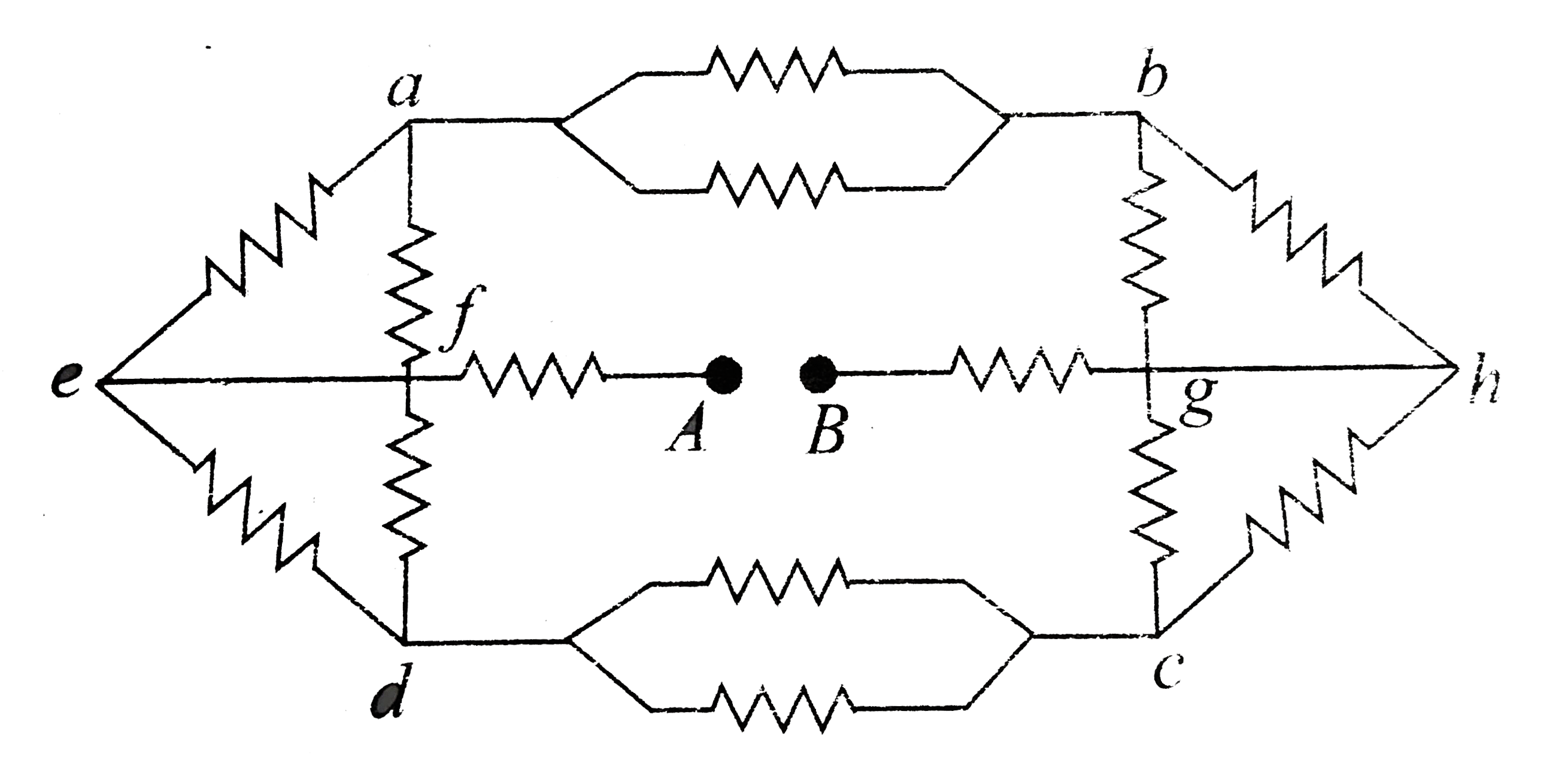
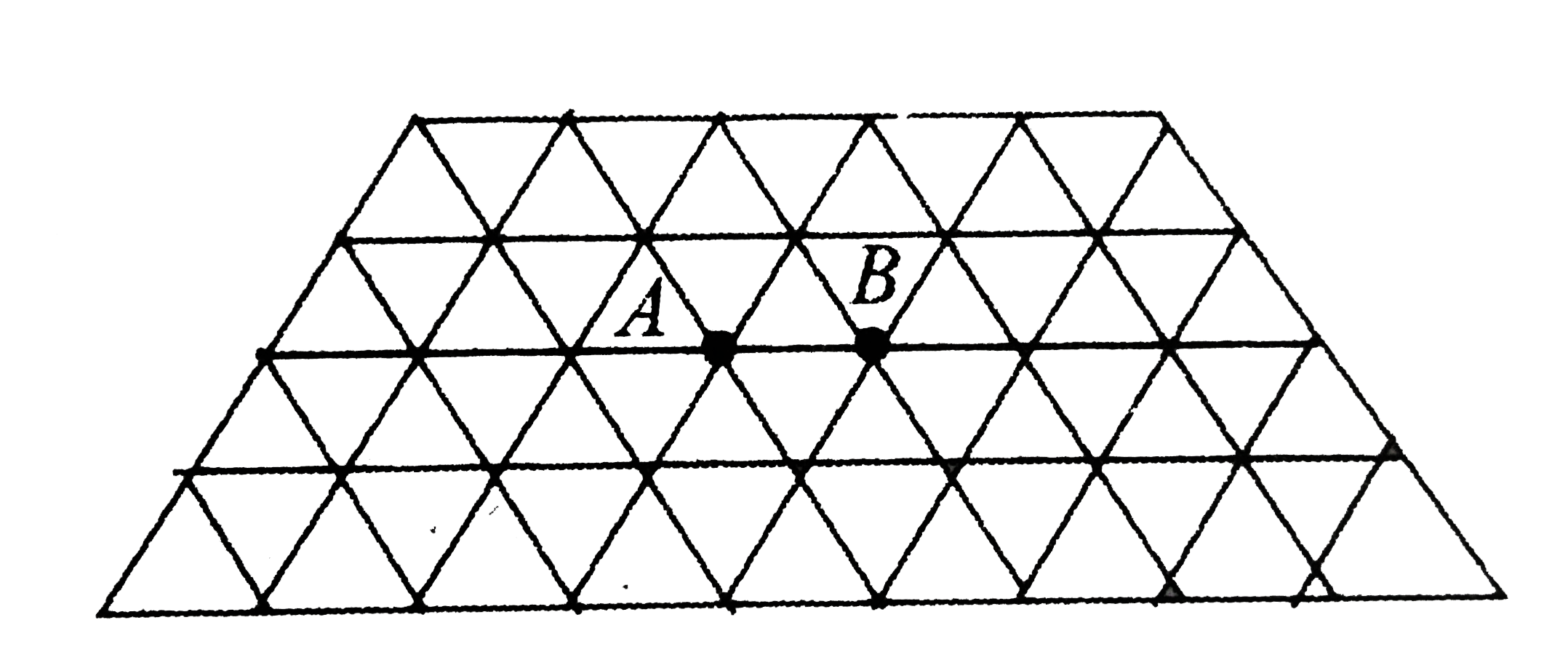
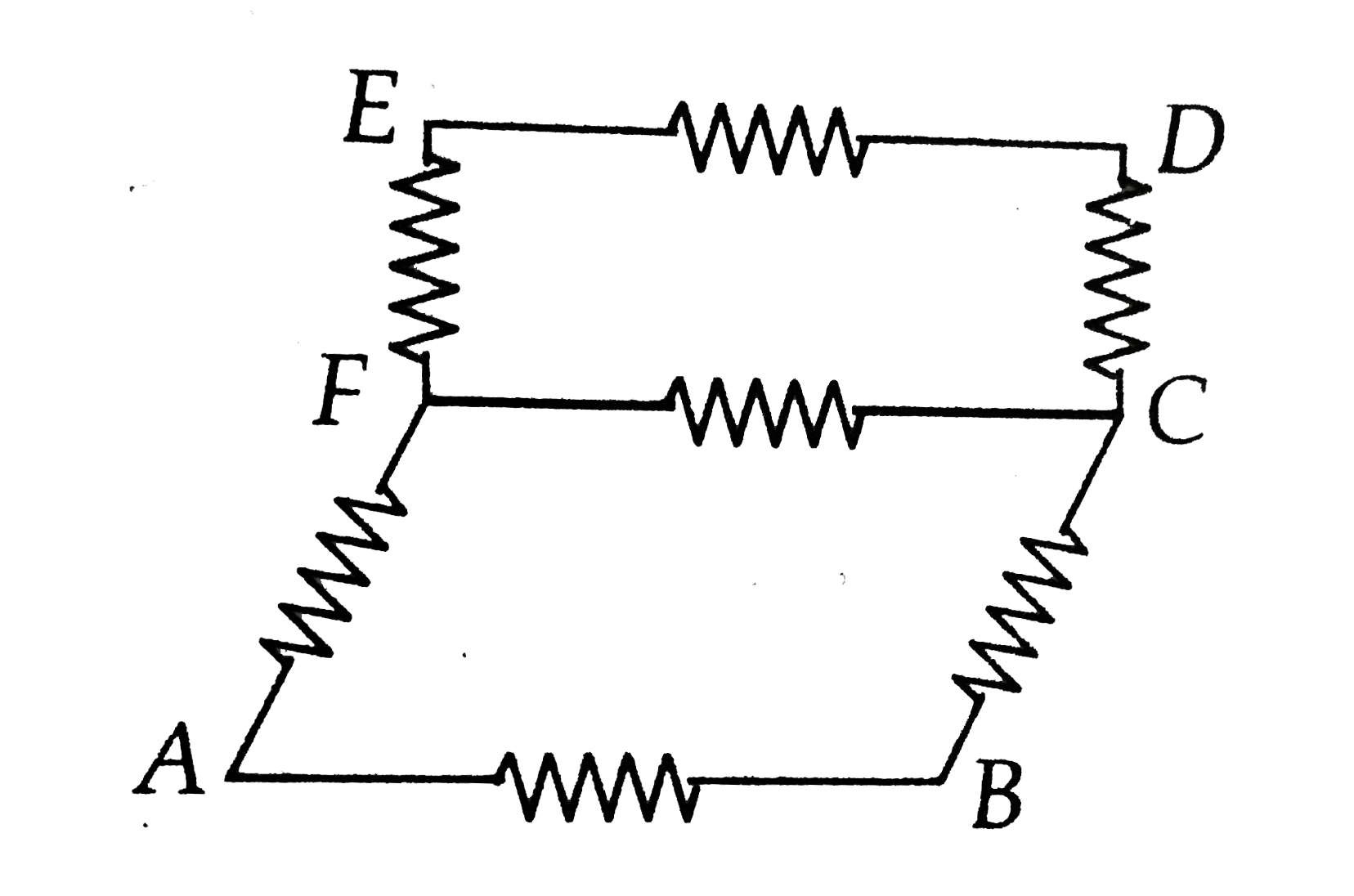
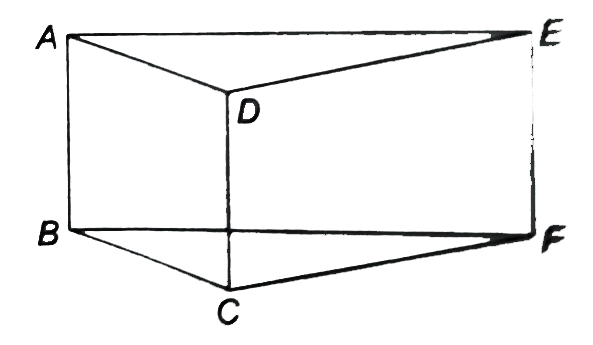
Consider 12 resistor arranged symmetrically in shape of bipyramid ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the plane of squar. The resistance of each resistor is R.
The effective resistance between E and F is View SolutionQuestion 218
Consider 12 resistor arranged symmetrically in shape of bipyraimd ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the plane of square. The resistance of each resistor is R.
The effective resistance between A and C isView SolutionQuestion 219
Consider 12 resistor arranged symmetrically in shape of bipyraimd ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the planw of squar. The resistacne of each resistor is R.
The effective resistance between A and B isView SolutionQuestion 238
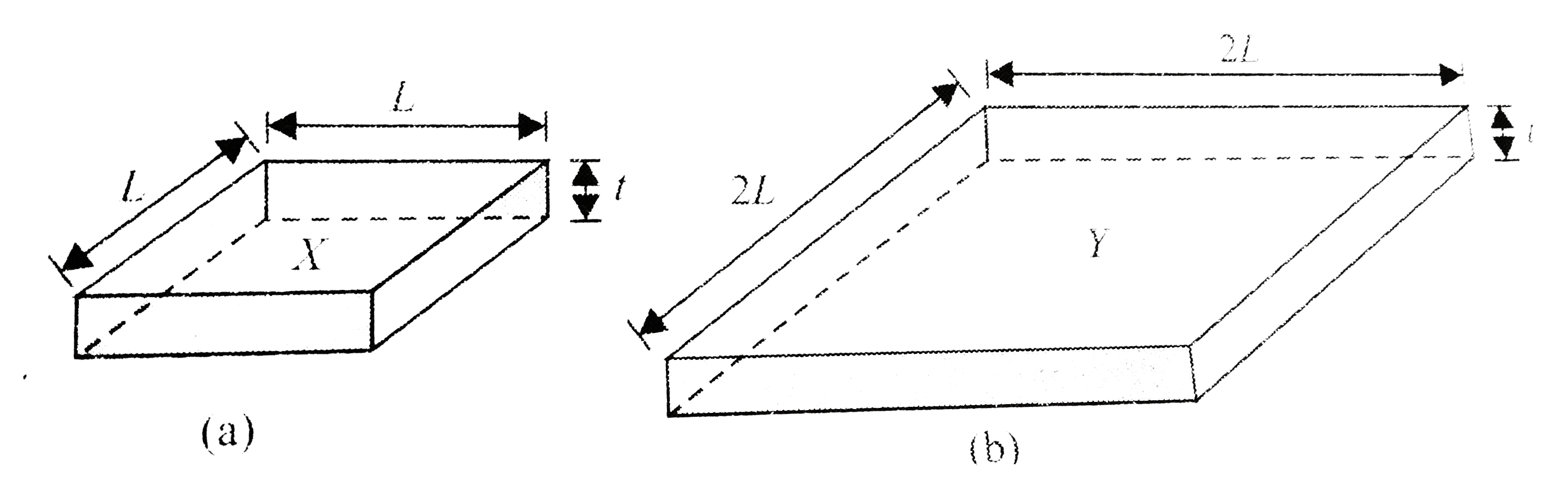
The area of cross-section, length and density of a piece of a metal of atomic weight 60 are 10−6m2, 1.0m and 5×103kg/m3 respectively, every atom contributes one free electron. (Given Avogadro number =6×1023/mol). Find the drift velocity of electrons in the metal when the current of 16A passes through:View Solution

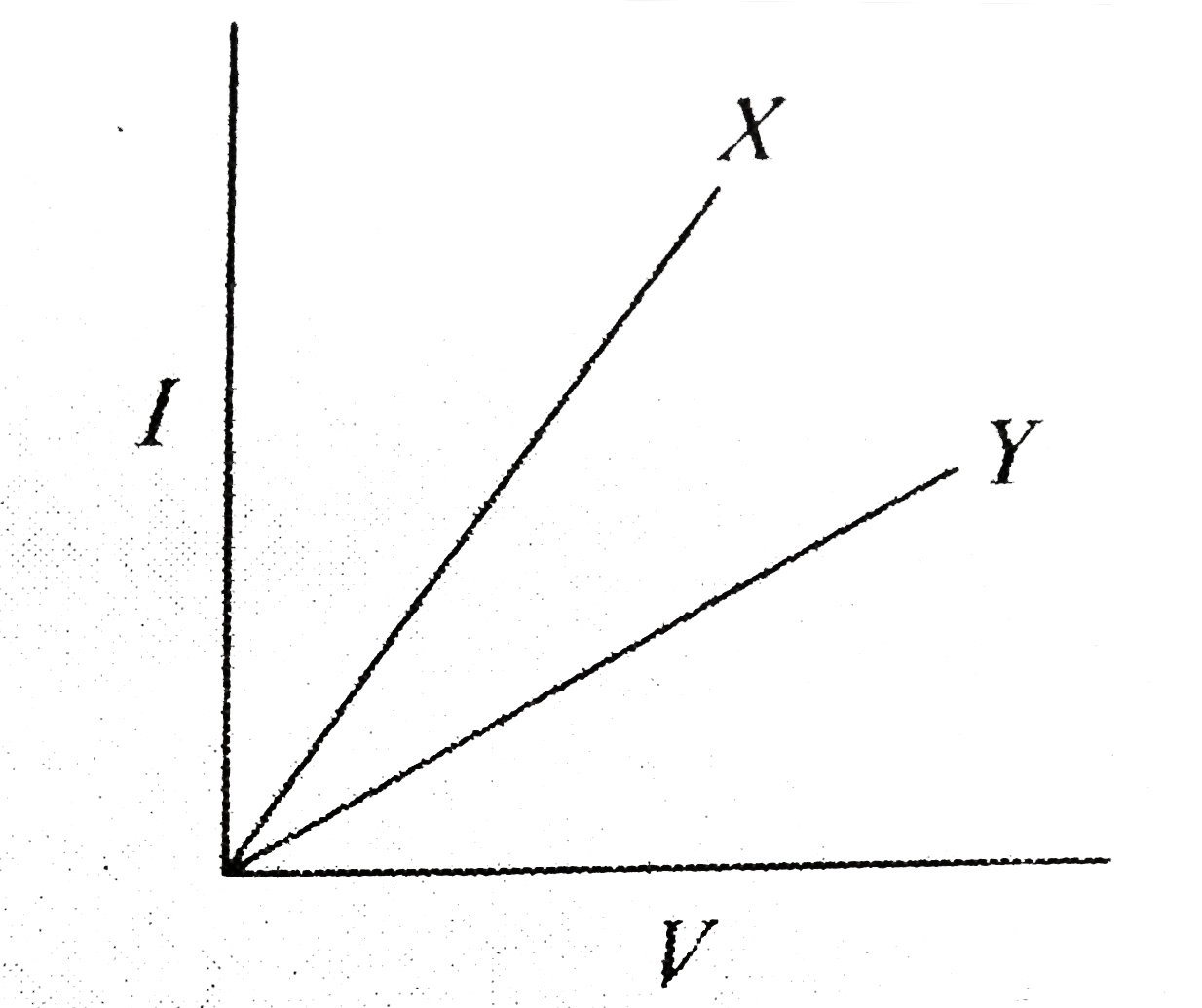




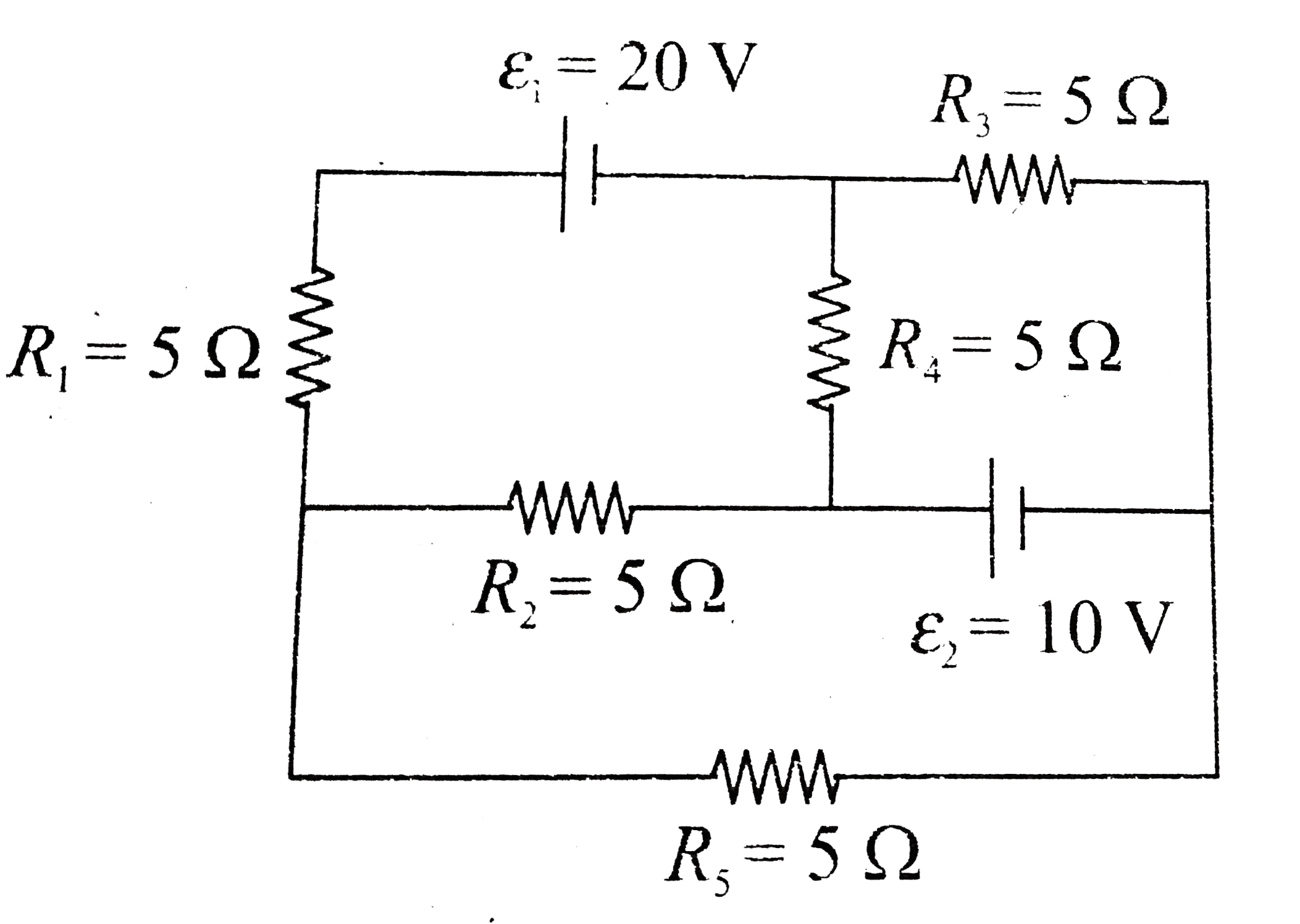
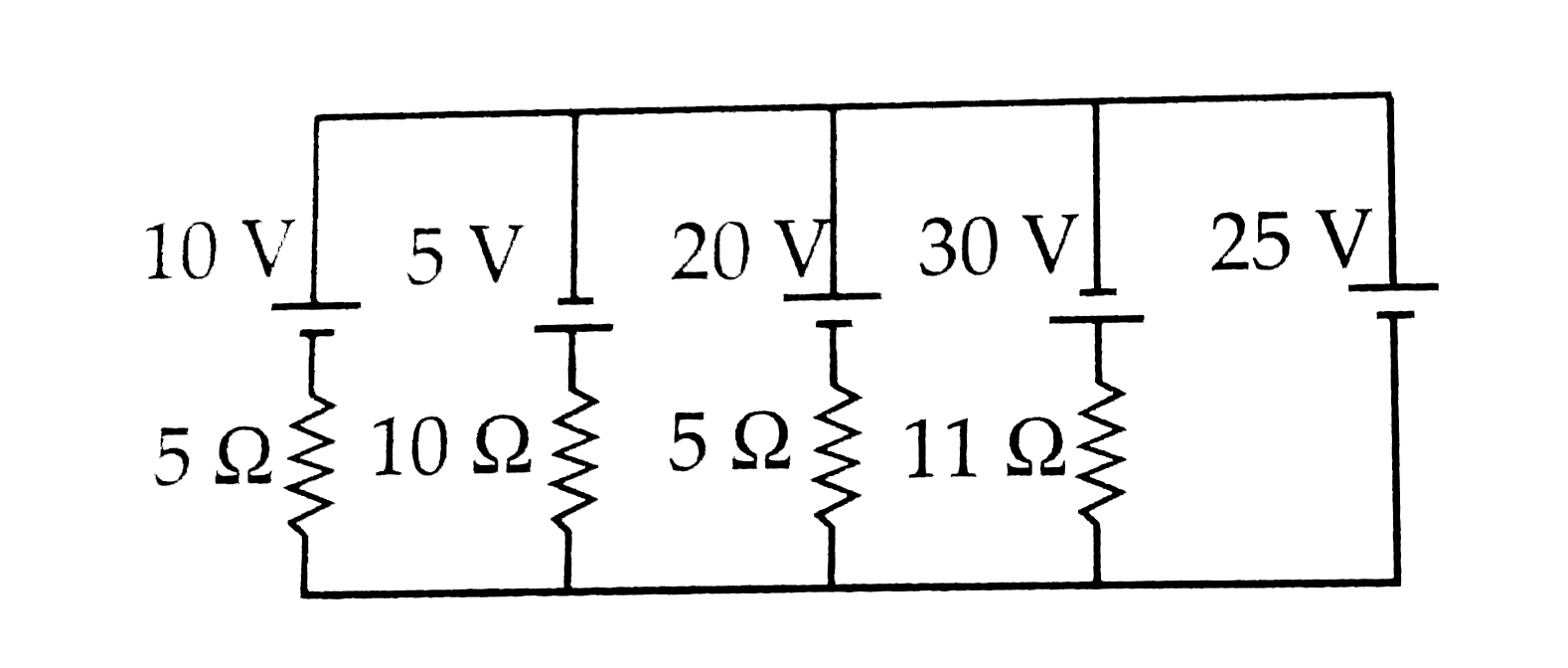
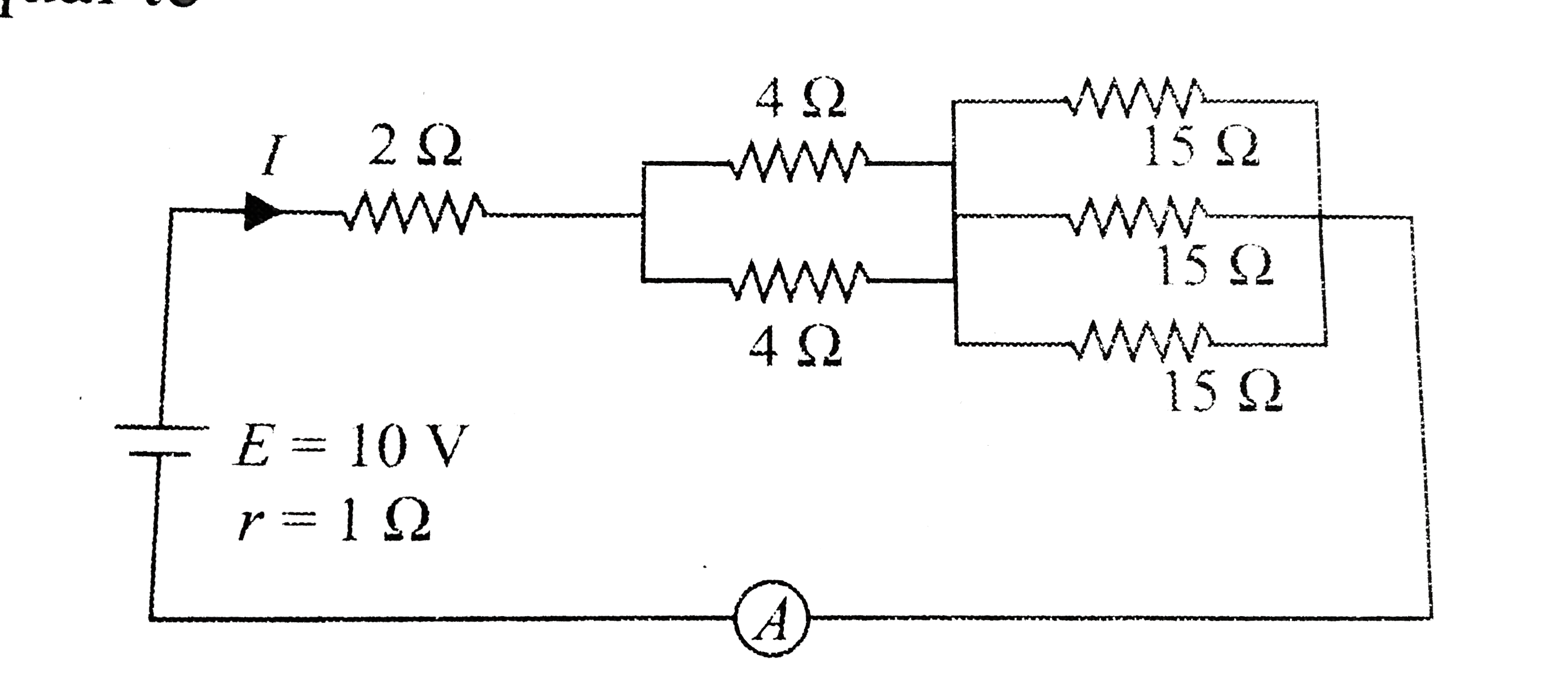
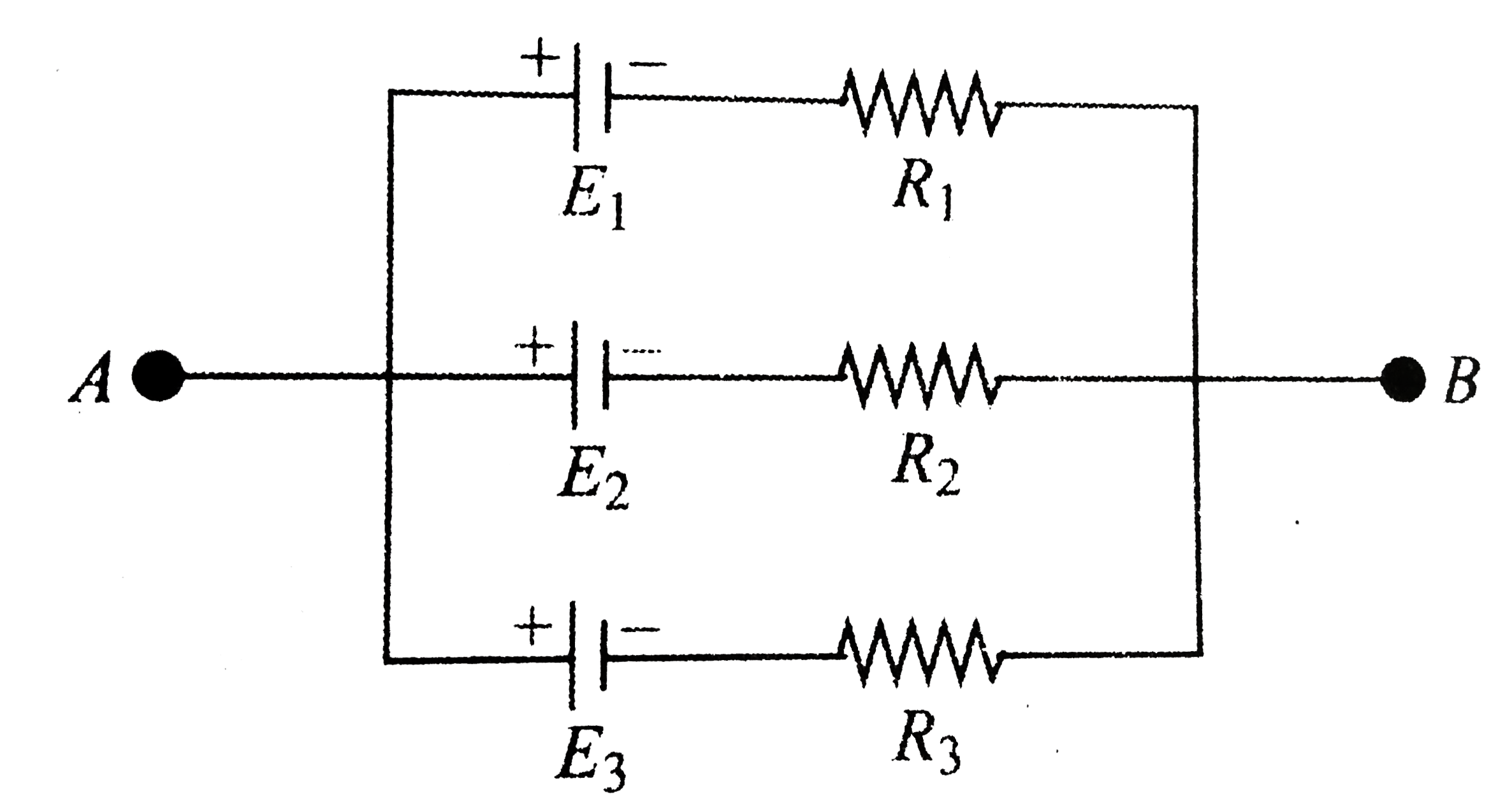
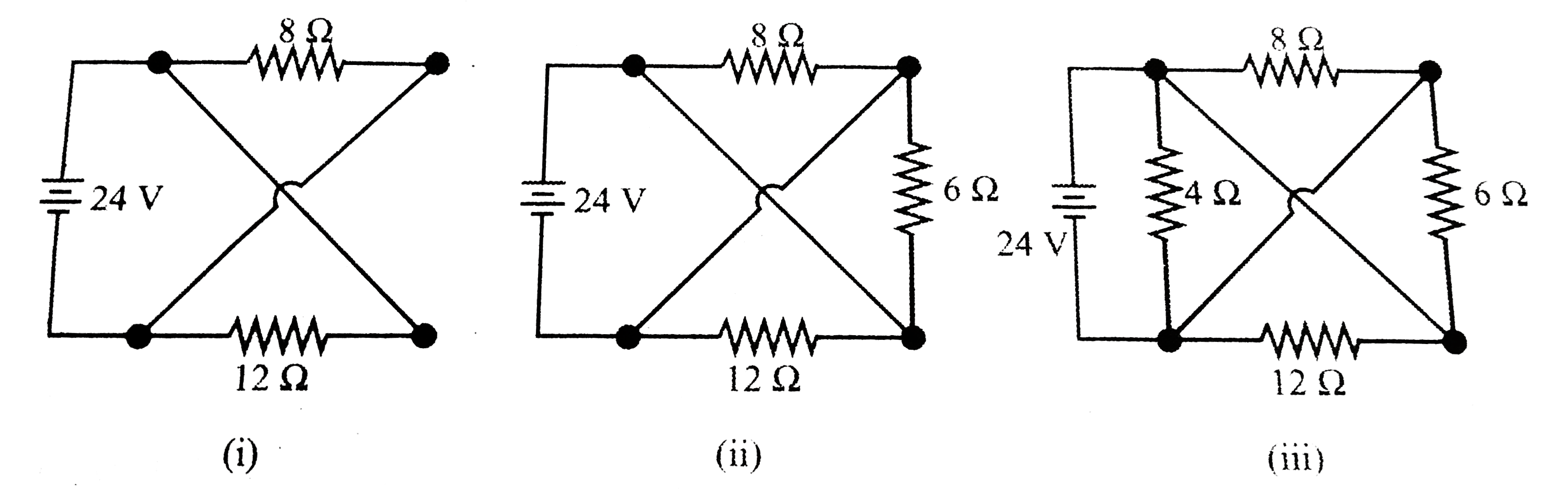
 Find the value of R
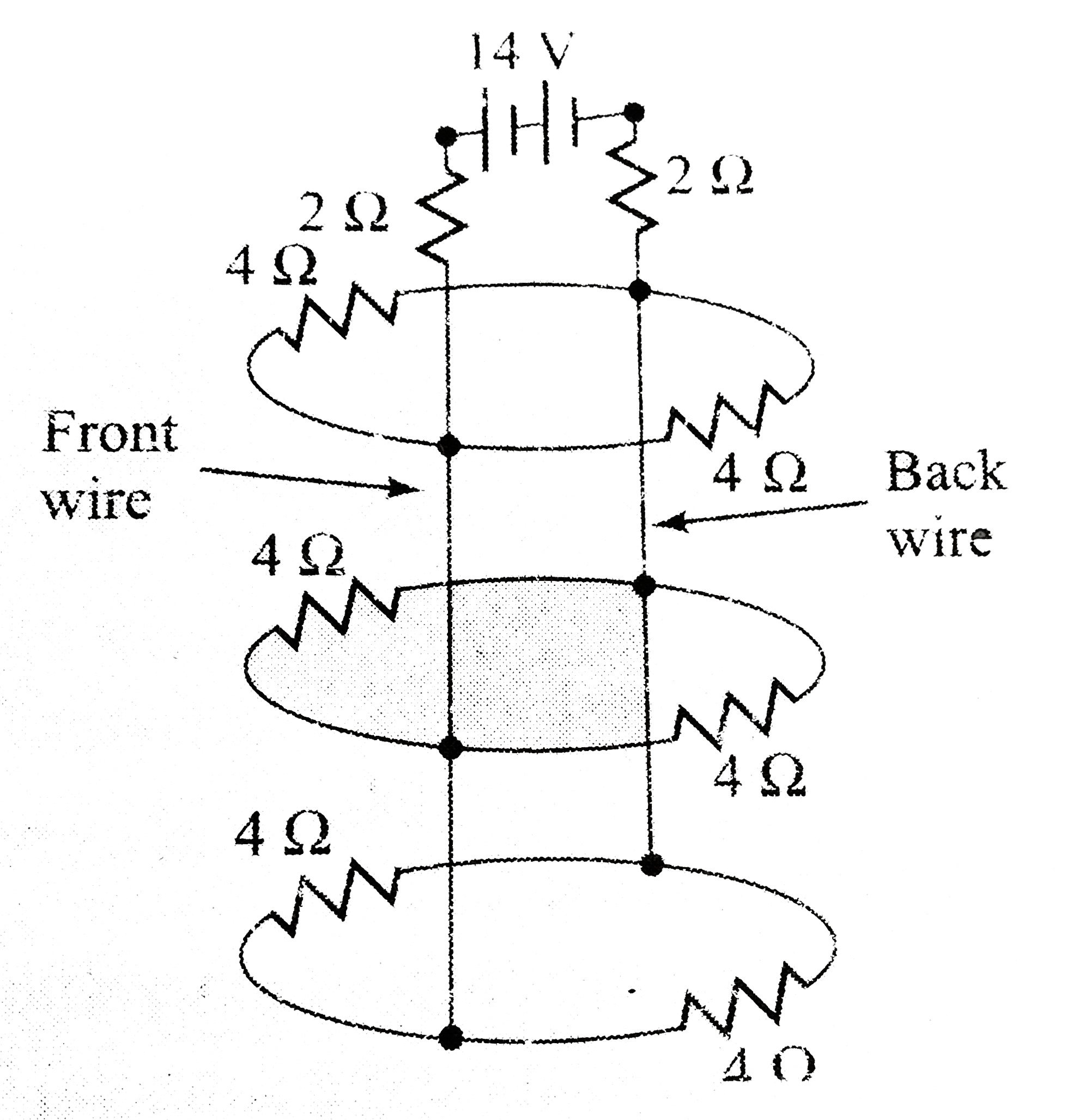
Find the value of R

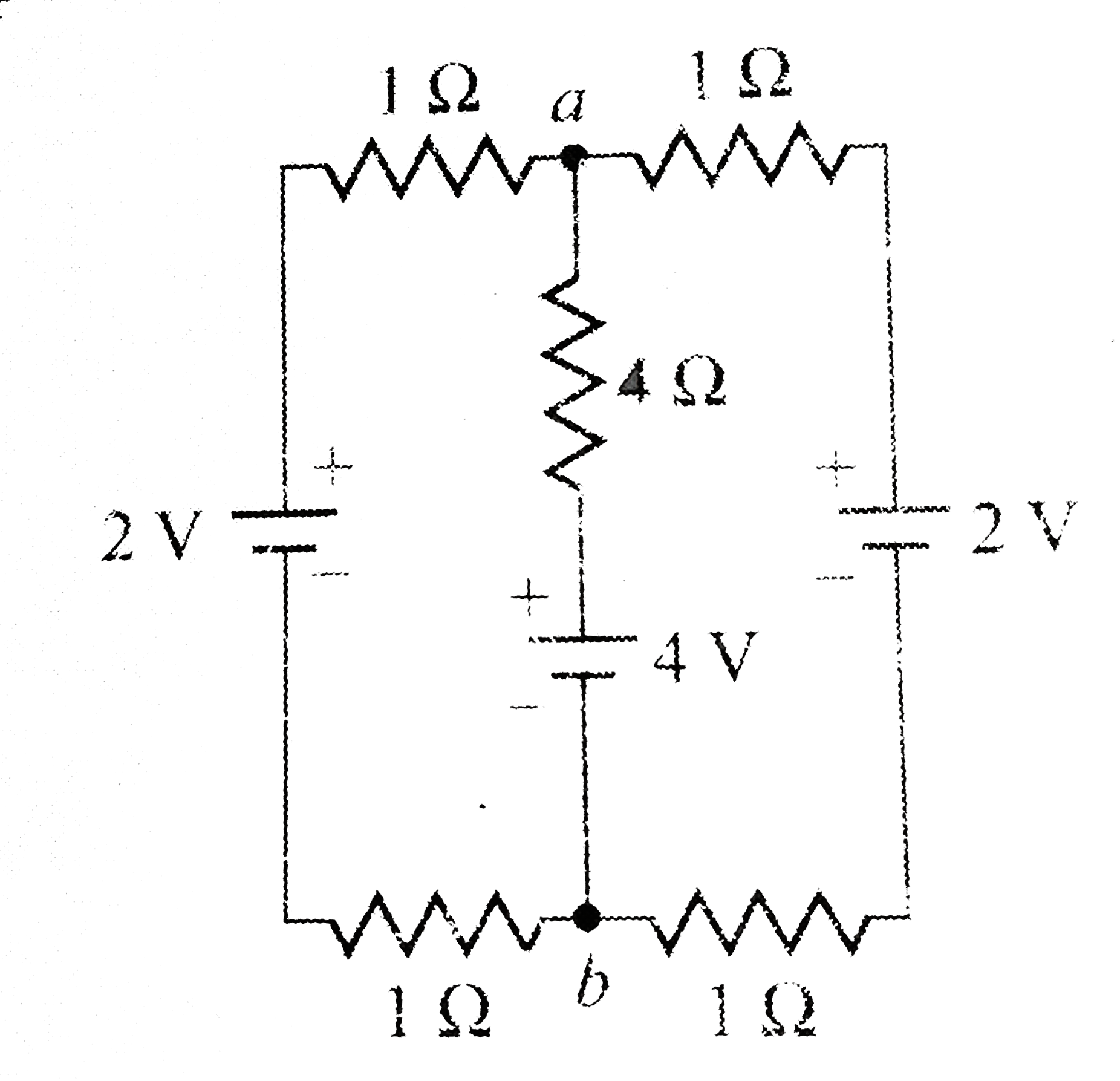
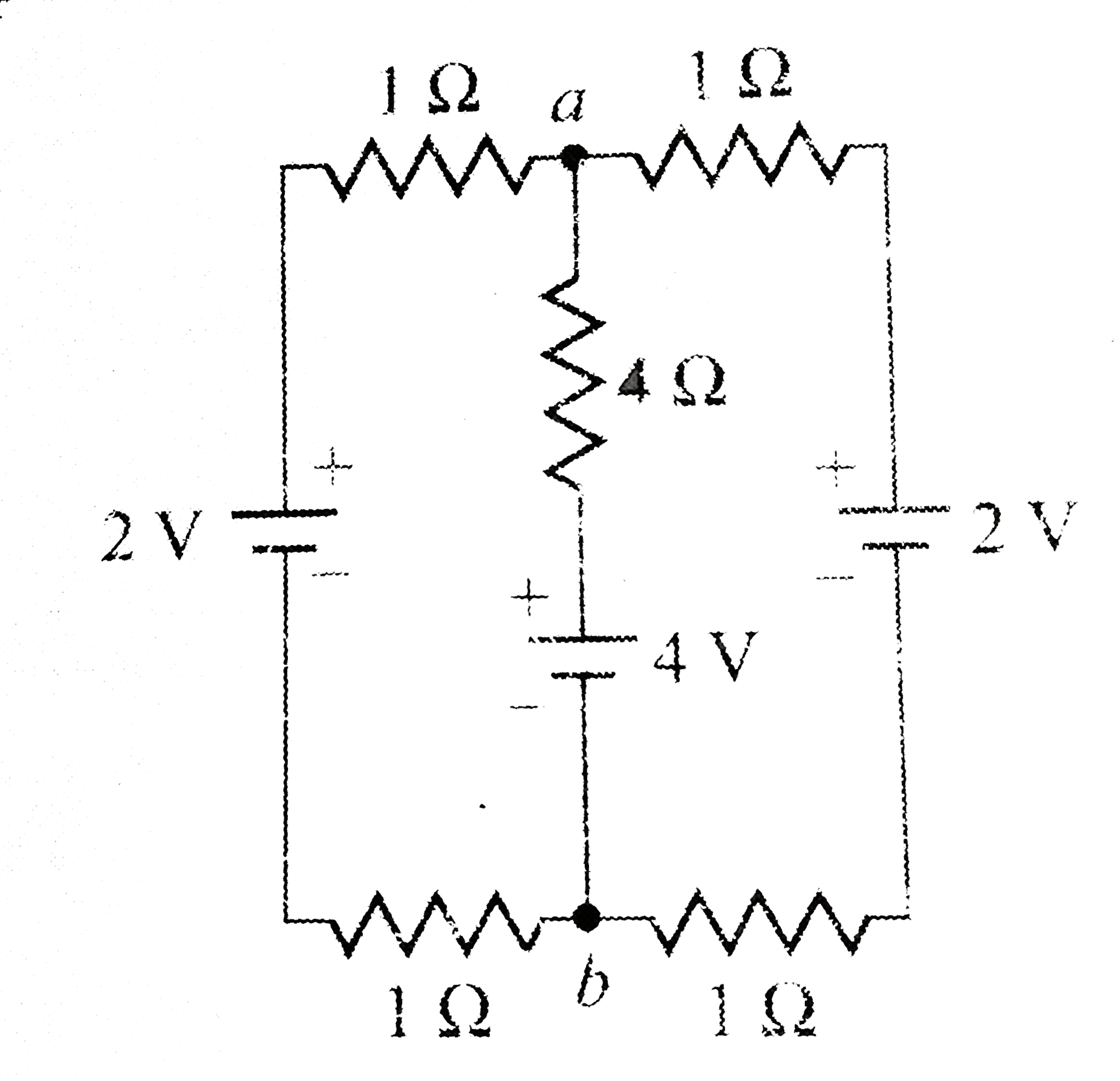
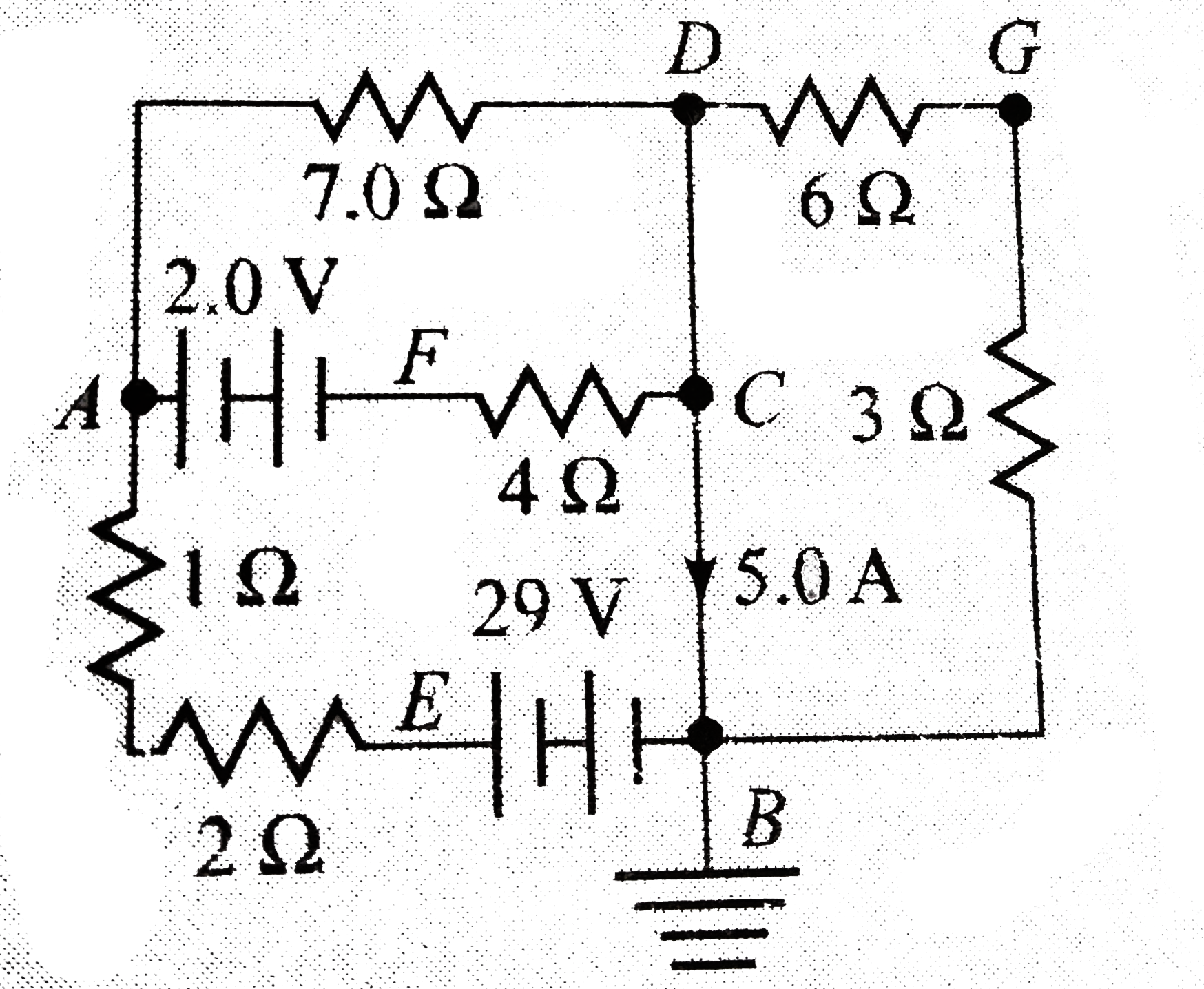
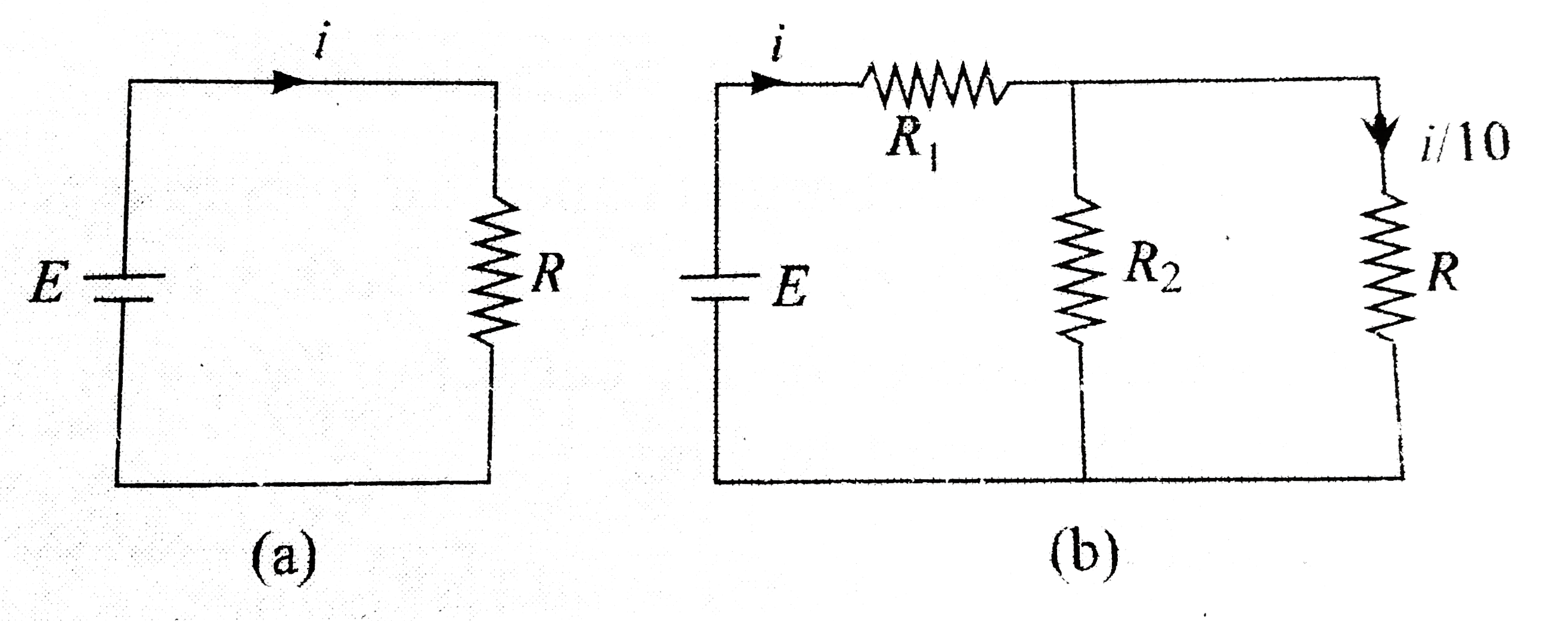
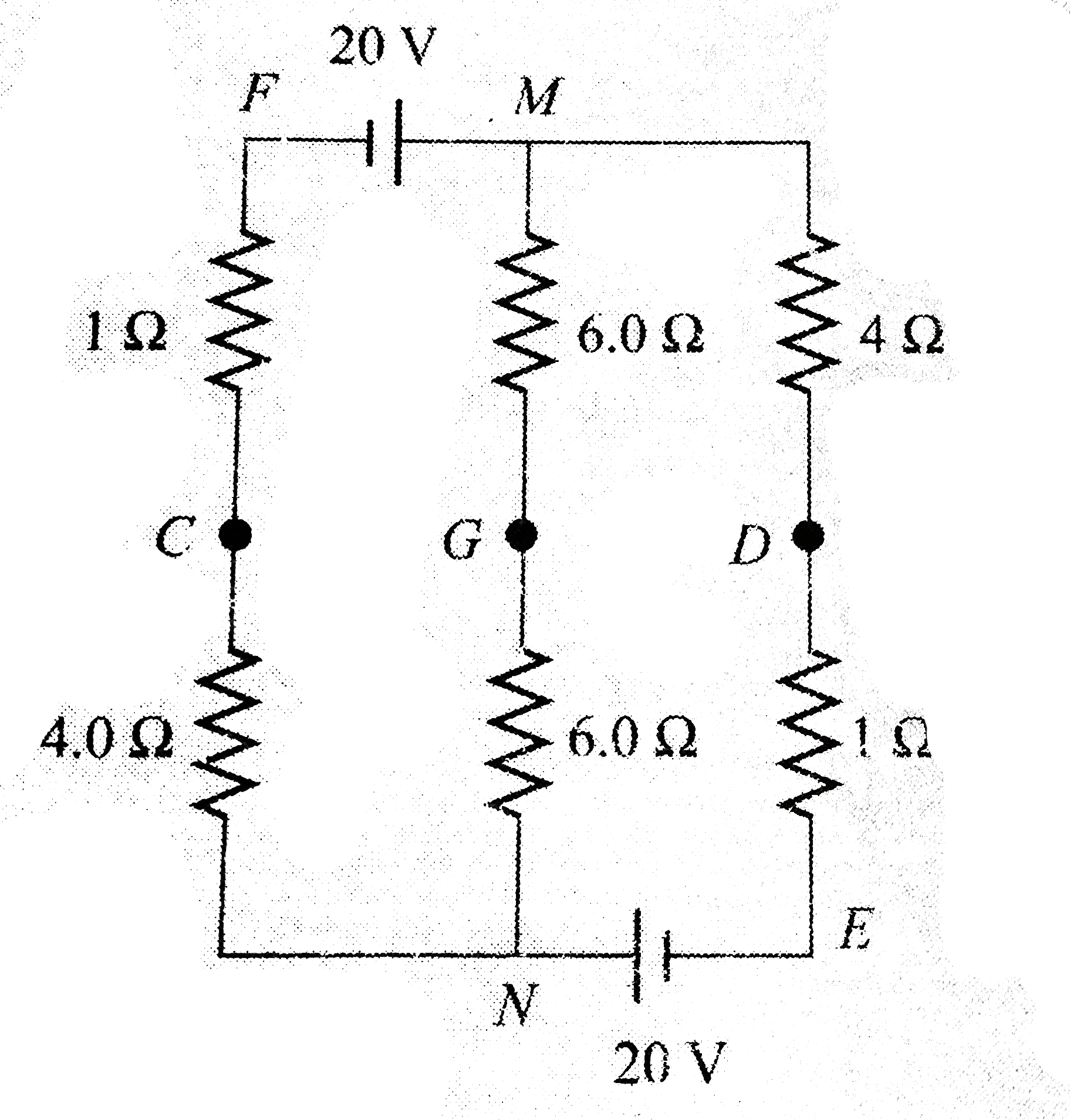


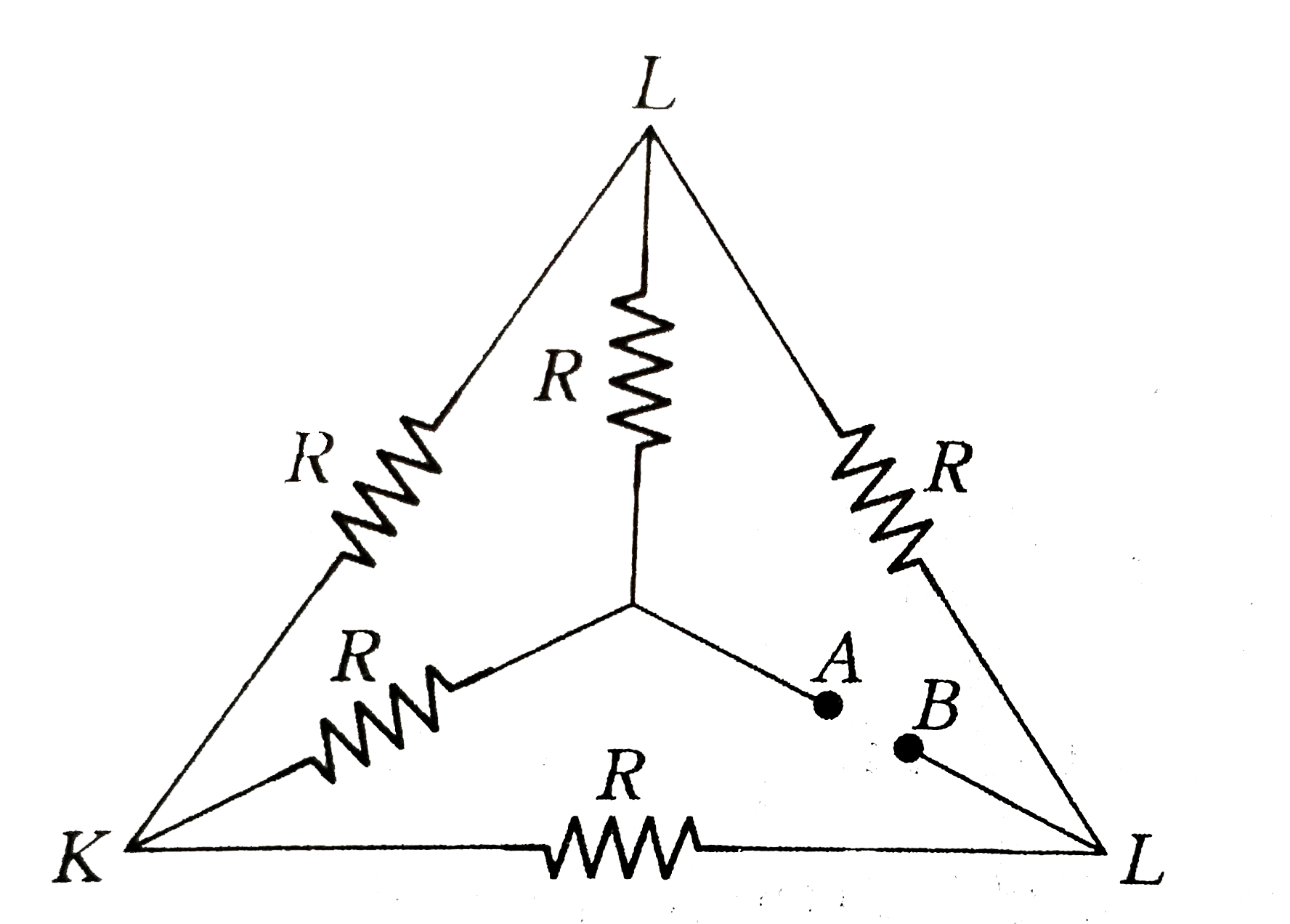
 .
.