An LR circuit constains an inductor of 500 mH, a resistor of 25.OΩ and an emf of 5.00 V in series. Find the potential difference across the resistor at t =(a) 20.0 ms, (b) 100 ms and ( c) 1.00 s.
To solve the problem of finding the potential difference across the resistor in an LR circuit at different time intervals, we can follow these steps:
Given Data:
- Inductance, L=500mH=500×10−3H
- Resistance, R=25.0Ω
- EMF, E=5.00V
Step 1: Calculate the Steady State Current (I0)
The steady state current I0 can be calculated using the formula:
I0=ER
Substituting the values:
I0=5.00V25.0Ω=0.20A
Step 2: Calculate the Time Constant (τ)
The time constant τ is given by:
τ=LR
Substituting the values:
τ=500×10−3H25.0Ω=0.020s=20.0ms
Step 3: Calculate the Current at Different Times
The current I(t) at time t is given by:
I(t)=I0(1−e−tτ)
(a) For t=20.0ms:
I(20.0ms)=0.20(1−e−20×10−320×10−3)=0.20(1−e−1)
Calculating e−1≈0.3679:
I(20.0ms)=0.20(1−0.3679)=0.20×0.6321≈0.1264A
(b) For t=100.0ms:
I(100.0ms)=0.20(1−e−100×10−320×10−3)=0.20(1−e−5)
Calculating e−5≈0.0067:
I(100.0ms)=0.20(1−0.0067)=0.20×0.9933≈0.1986A
(c) For t=1.00s:
I(1.00s)=0.20(1−e−1.000.020)=0.20(1−e−50)
Since e−50 is very close to 0:
I(1.00s)≈0.20×1=0.20A
Step 4: Calculate the Potential Difference Across the Resistor
The potential difference V across the resistor is given by:
V=I(t)×R
(a) For t=20.0ms:
V(20.0ms)=0.1264A×25.0Ω≈3.16V
(b) For t=100.0ms:
V(100.0ms)=0.1986A×25.0Ω≈4.97V
(c) For t=1.00s:
V(1.00s)=0.20A×25.0Ω=5.00V
Final Answers:
- (a) V(20.0ms)≈3.16V
- (b) V(100.0ms)≈4.97V
- (c) V(1.00s)=5.00V
- Inductance, L=500mH=500×10−3H
- Resistance, R=25.0Ω
- EMF, E=5.00V
The steady state current I0 can be calculated using the formula:
I0=ER
Substituting the values:
I0=5.00V25.0Ω=0.20A
The time constant τ is given by:
τ=LR
Substituting the values:
τ=500×10−3H25.0Ω=0.020s=20.0ms
The current I(t) at time t is given by:
I(t)=I0(1−e−tτ)
I(20.0ms)=0.20(1−e−20×10−320×10−3)=0.20(1−e−1)
Calculating e−1≈0.3679:
I(20.0ms)=0.20(1−0.3679)=0.20×0.6321≈0.1264A
I(100.0ms)=0.20(1−e−100×10−320×10−3)=0.20(1−e−5)
Calculating e−5≈0.0067:
I(100.0ms)=0.20(1−0.0067)=0.20×0.9933≈0.1986A
I(1.00s)=0.20(1−e−1.000.020)=0.20(1−e−50)
Since e−50 is very close to 0:
I(1.00s)≈0.20×1=0.20A
The potential difference V across the resistor is given by:
V=I(t)×R
V(20.0ms)=0.1264A×25.0Ω≈3.16V
V(100.0ms)=0.1986A×25.0Ω≈4.97V
V(1.00s)=0.20A×25.0Ω=5.00V
- (a) V(20.0ms)≈3.16V
- (b) V(100.0ms)≈4.97V
- (c) V(1.00s)=5.00V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
100J of heat are produced each second in a 4Ω resistance. Find the potential difference across the resistor.
View SolutionA circuit containing five resistors is connected to a battery with a 12 v emf as shown in figure. The potential difference across 4Ω resistor is

View SolutionA series AC circuit contains an inductor (20mH), a capacitor (100μF), a resistor (50Ω) and an AC source of 12V,50Hz. Find the energy dissipated in the circuit in 1000s.
View SolutionAn inductor of inducance 5.0 H, having a negligible resistance, is connected in series with a 100Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
View SolutionAn L−C circuit consists of a 20.0mH inductor and a 0.5μF capacitor. If the maximum instantaneous current is 0.1A, what is the greatest potential difference across the capacitor?
View SolutionAn inductor-coil of inductance 20 mH having resistance 10Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at t=0, (b) t = 10 ms and (c ) t = 1.0s.
View SolutionAn inductor-coil of inductance 20 mH having resistance 10Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at t=0, (b) t = 10 ms and (c ) t = 1.0s.
View SolutionIn the circuit diagram given below, a cell of 9 V and internal resistance of 0.5(Ω) is connected across a resistor A of 2Ω in series and two resistors of 2Ω and 6Ω in parallel.
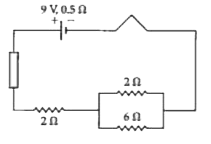
Find
The potential difference across the terminals of the cell.
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View SolutionA constant voltage of 25 V is applied to a series L-R circuit at t = 0, by closing a switch. What is the potential difference across the resistor and the inductor at time t = 0?
View Solution
