An electric field of 105N/C points due west at a certain spot. What are the magnitude and direction of the force that acts on a charge of +2μCand−5μC at this spot?
The correct Answer is:A, B, D
To solve the problem, we need to calculate the force acting on two different charges in an electric field. The electric field is given as E=105N/C and points due west. The two charges are +2μC and −5μC.
Step 1: Convert the charges from microcoulombs to coulombs
The charges are given in microcoulombs (µC). We need to convert them to coulombs (C):
- +2μC=2×10−6C
- −5μC=−5×10−6C
Step 2: Calculate the force on the positive charge +2μC
The force F on a charge in an electric field is given by the formula:
F=Q⋅E
For the positive charge:
F1=(2×10−6C)⋅(105N/C)=2×10−6⋅105=0.2N
Since the electric field points west, the force on the positive charge will also point west.
Step 3: Calculate the force on the negative charge −5μC
Using the same formula for the negative charge:
F2=(−5×10−6C)⋅(105N/C)=−5×10−6⋅105=−0.5N
The negative sign indicates that the force acts in the opposite direction to the electric field. Since the electric field points west, the force on the negative charge will point east.
Summary of Results
- The force on the charge +2μC is 0.2N directed west.
- The force on the charge −5μC is 0.5N directed east.
Final Answer
- Force on +2μC: 0.2N (West)
- Force on −5μC: 0.5N (East)
---
The charges are given in microcoulombs (µC). We need to convert them to coulombs (C):
- +2μC=2×10−6C
- −5μC=−5×10−6C
The force F on a charge in an electric field is given by the formula:
F=Q⋅E
For the positive charge:
F1=(2×10−6C)⋅(105N/C)=2×10−6⋅105=0.2N
Since the electric field points west, the force on the positive charge will also point west.
Using the same formula for the negative charge:
F2=(−5×10−6C)⋅(105N/C)=−5×10−6⋅105=−0.5N
The negative sign indicates that the force acts in the opposite direction to the electric field. Since the electric field points west, the force on the negative charge will point east.
- The force on the charge +2μC is 0.2N directed west.
- The force on the charge −5μC is 0.5N directed east.
- Force on +2μC: 0.2N (West)
- Force on −5μC: 0.5N (East)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 55videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 64videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The electric field due to a point charge at a distance 6 m from it is 630 N/C. The magnitude of the charge is
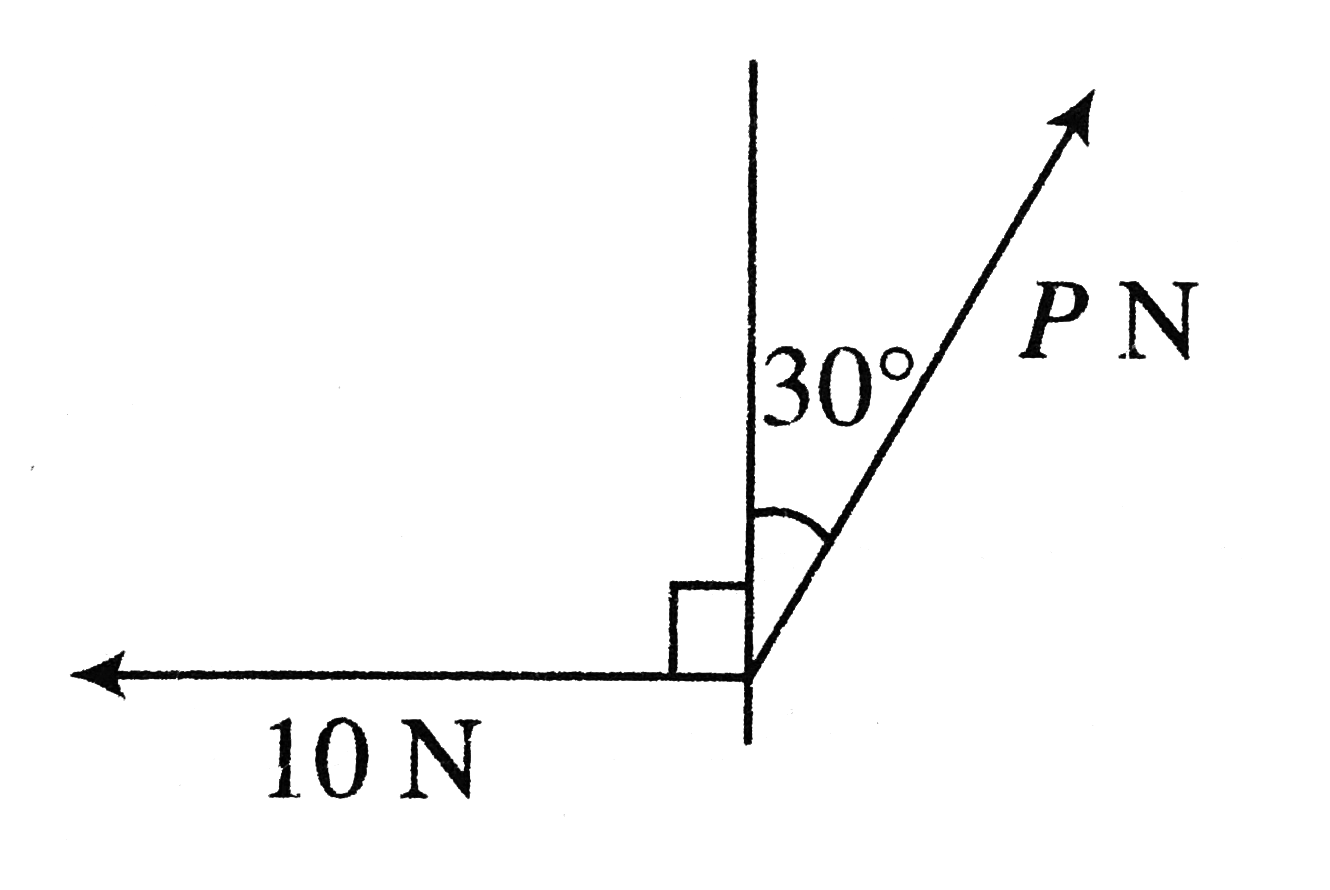
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two point charges of 1μCand−1μC are separated by a distance of 100 Å. A point P is at a distance of 10 cm from the midpoint and on the perpendicular bisector of the line joining the two charges. The electric field at P will be
A9NC−1B0.9NC−1C90NC−1D0.09NC−1
Four point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is
 View Solution
View Solutionfind the electric field strength due to a point charge of 5μC at a distance of 80 cm from the charge.
View SolutionCalculate the magnitude and direction of the electric field at a point P which is 30 cm to the right of a point charge Q=−3.0×10−6C
View SolutionElectric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
View SolutionThe electric force experienced by a charge of 5×10−6C is 25×10−3N. Find the magnitude of the electric field at that position of the charge due to the source charges.
View SolutionThe force of attractions between two charges 8μC and −4μC is 0.2 N. Find the distance of separation.
View SolutionA parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, then force on each capacitor plate is-
View Solution

