Two concentric coducting thin spherical shells A and B having radii rA and rB(rB>rA) are charged to QA and −QB(|QB|>|QA|). The electrical field along a line passing through the centre is
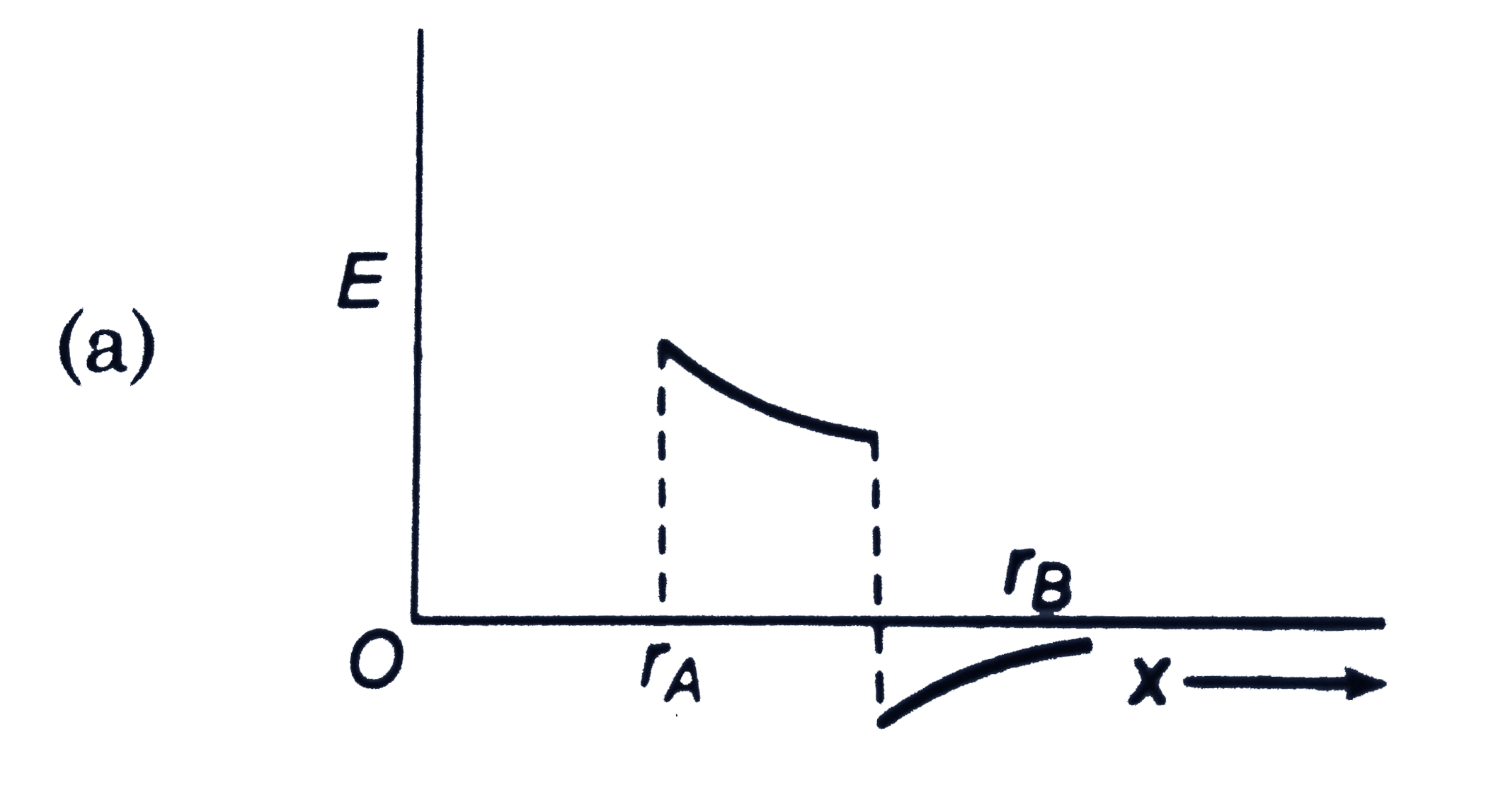
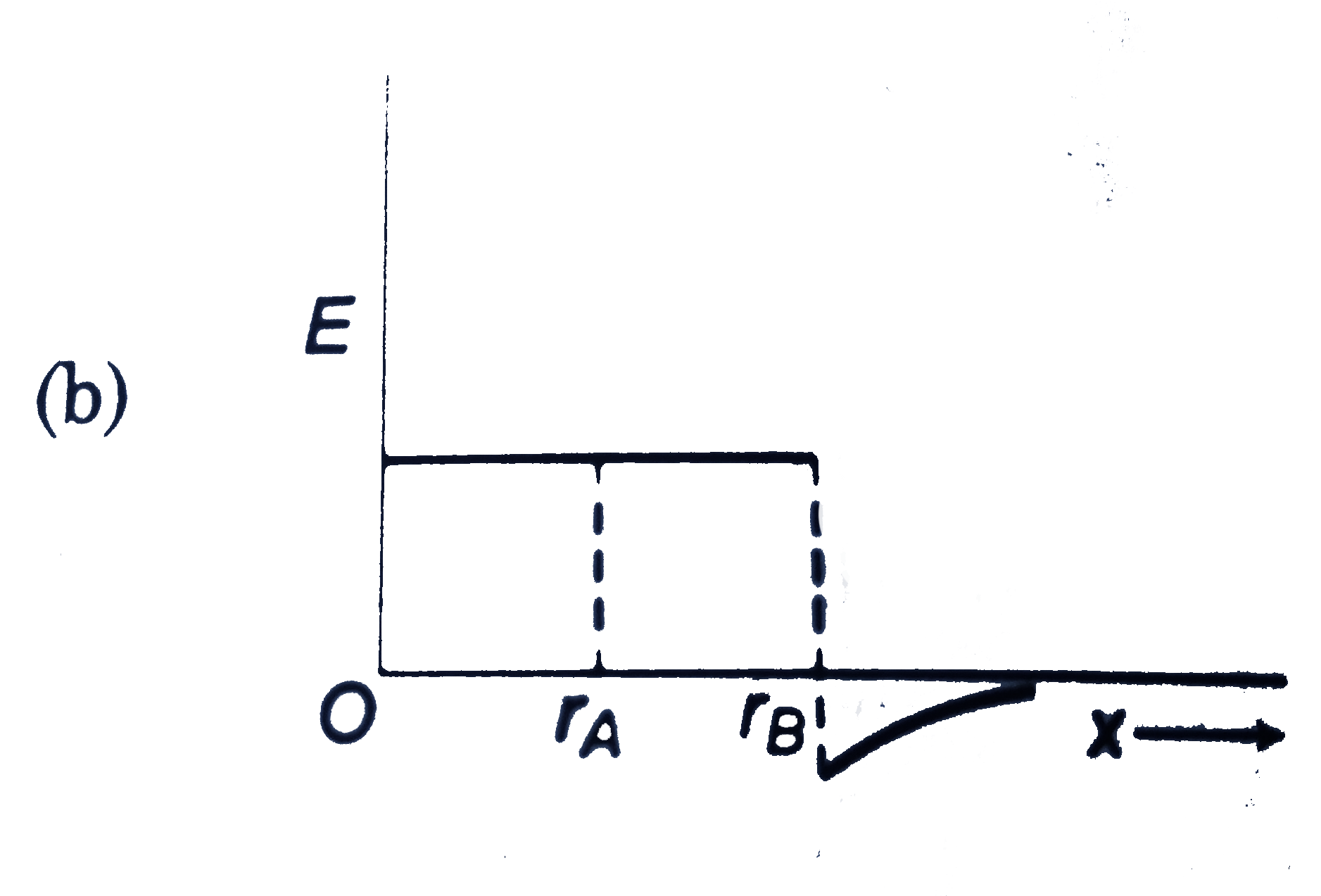

none of these
The correct Answer is:A
To solve the problem of finding the electric field along a line passing through the center of two concentric conducting thin spherical shells A and B, we can break it down into several steps:
Step 1: Understand the Configuration
We have two concentric conducting spherical shells:
- Shell A with radius rA and charge QA
- Shell B with radius rB (where rB>rA) and charge −QB (with |QB|>|QA|)
Step 2: Electric Field Inside Shell A
According to electrostatic principles, the electric field inside a conductor (and thus inside shell A) is zero. Therefore, for any point inside shell A (i.e., for r<rA), the electric field E is:
E=0for r<rA
Step 3: Electric Field Between Shells A and B
For points between the two shells (i.e., for rA<r<rB), we can use Gauss's Law. The charge enclosed by a Gaussian surface in this region is only the charge on shell A, QA. Thus, the electric field E can be calculated as:
E⋅4πr2=QAϵ0
Solving for E:
E=QA4πϵ0r2for rA<r<rB
Step 4: Electric Field Outside Shell B
For points outside shell B (i.e., for r>rB), we consider the total charge enclosed by a Gaussian surface that encompasses both shells. The total charge is:
Qtotal=QA−QB
Since |QB|>|QA|, this results in a net negative charge. Thus, the electric field E is given by:
E⋅4πr2=QA−QBϵ0
Solving for E:
E=QA−QB4πϵ0r2for r>rB
Summary of Electric Field in Different Regions
- For r<rA: E=0
- For rA<r<rB: E=QA4πϵ0r2
- For r>rB: E=QA−QB4πϵ0r2
We have two concentric conducting spherical shells:
- Shell A with radius rA and charge QA
- Shell B with radius rB (where rB>rA) and charge −QB (with |QB|>|QA|)
According to electrostatic principles, the electric field inside a conductor (and thus inside shell A) is zero. Therefore, for any point inside shell A (i.e., for r<rA), the electric field E is:
E=0for r<rA
For points between the two shells (i.e., for rA<r<rB), we can use Gauss's Law. The charge enclosed by a Gaussian surface in this region is only the charge on shell A, QA. Thus, the electric field E can be calculated as:
E⋅4πr2=QAϵ0
Solving for E:
E=QA4πϵ0r2for rA<r<rB
For points outside shell B (i.e., for r>rB), we consider the total charge enclosed by a Gaussian surface that encompasses both shells. The total charge is:
Qtotal=QA−QB
Since |QB|>|QA|, this results in a net negative charge. Thus, the electric field E is given by:
E⋅4πr2=QA−QBϵ0
Solving for E:
E=QA−QB4πϵ0r2for r>rB
- For r<rA: E=0
- For rA<r<rB: E=QA4πϵ0r2
- For r>rB: E=QA−QB4πϵ0r2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Two concentric conducting thin spherical shells A andB having radii rA and r8(r8>rA) are charged to QA and −QB(|QB|>|QA|). The electric field strength along a line passing through the centre varies with the distance x as :
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
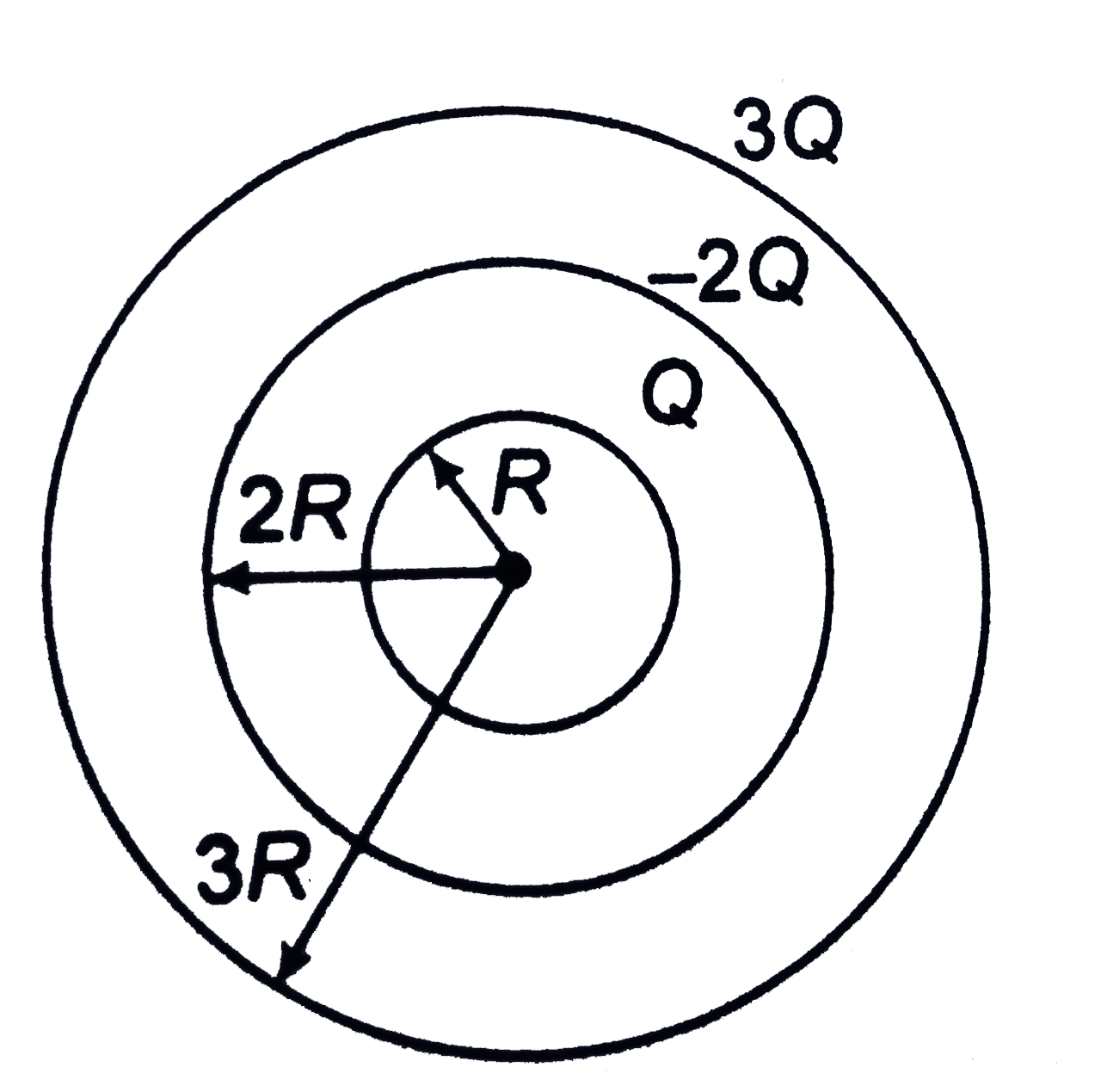
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre . b. Compute the electric field at r=52R
c. Compute the total electrostatic energy stored in the system.
The inner shell is now connected to the external one by a conducting wire, passing through a very small hole in the middle shell.
d. Compute the charges on the spheres of radii R and 3R.
e. Compute the electric field at r=52R
View SolutionThere are two concentric conducting spherical shells of radius rA and rB respectively (rB=2rA). If the inner shell is given a charge Q and outer shell is given a charge 2Q, then the potential difference between the surfaces of the shells will be K=14πε0
View SolutionThree concentric conducting spherical shells of radii R,2R carry charges Q, -2Q and 3Q, respectively. Find the electric potential at r = R and at r = 3 R, where r is the radii distance from the centre.

View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

View SolutionFour concentric conducting spherical shells A, B, C and D of radii a, 2a, 3a and 4a respectively. Shell B and D are given charges q and −q respectively. If shell C is grounded then potential difference (VA — VC) is
View SolutionThree concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
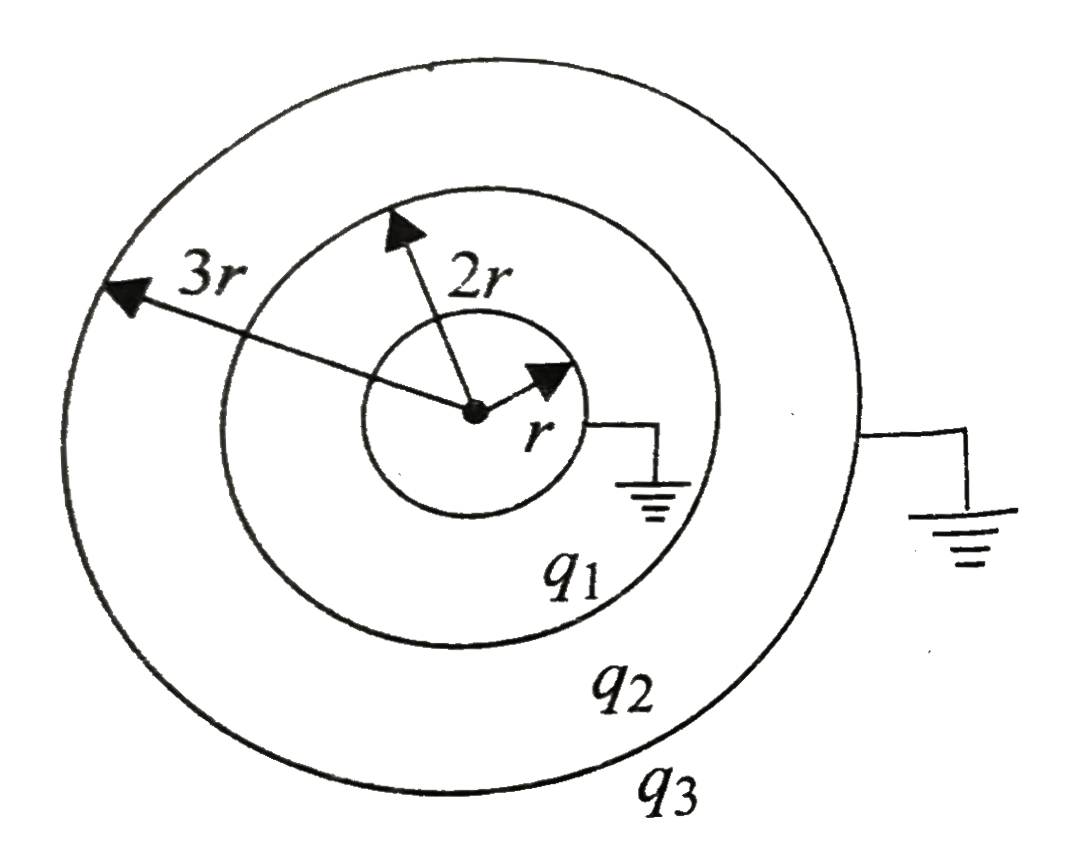
View SolutionTwo concentric conducting shells A and B are of radii R and 2R. A charge +q is placed at the centre of the shells. Shell B is earthed and a charge q is given to shell A. Find the charge on outer surface of A and B.
View SolutionThere are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
View Solution
