Two isolated sphereical conductors have radii 5cm and 0cm, espctively They have charges of 12μC and −3μC. Find the charges after they are connected by a conductng wire. Also find the common potential after resistribution.
To solve the problem, we need to find the charges on the two spherical conductors after they are connected by a conducting wire, as well as the common potential after charge redistribution.
1. Identify the Initial Charges and Radii:
- Let the radius of the first sphere R1=5cm=0.05m
- Let the radius of the second sphere R2=0cm=0m
- Initial charge on the first sphere Q1=12μC=12×10−6C
- Initial charge on the second sphere Q2=−3μC=−3×10−6C
2. Calculate the Total Charge:
- The total charge Qtotal=Q1+Q2=12μC−3μC=9μC
3. Establish the Relationship Between Charges After Connection:
- When the two spheres are connected by a conducting wire, they will reach the same potential. The potential V on a sphere is given by:
V=kQR
- For the two spheres, the potentials must be equal:
kQ′1R1=kQ′2R2
- Since R2=0, we can consider the potential of the second sphere to be effectively zero, which means we only need to find the relationship between the charges:
Q′1R1=Q′2R2
- However, since R2 is zero, we can use the fact that the charge will redistribute such that:
Q′2=2Q′1
4. Use Charge Conservation:
- From charge conservation, we have:
Q′1+Q′2=Qtotal=9μC
- Substitute Q′2=2Q′1 into the equation:
Q′1+2Q′1=9μC
3Q′1=9μC
Q′1=3μC
5. Calculate Q′2:
- Now substitute Q′1 back to find Q′2:
Q′2=2Q′1=2×3μC=6μC
6. Calculate the Common Potential:
- The common potential V after redistribution can be calculated using either sphere's charge and radius:
V=kQ′1R1=k3×10−60.05
- Using k=9×109N m2/C2:
V=9×1093×10−60.05=9×109×6×10−4=5.4×106V
Final Answers:
- Charges after connection:
- Q′1=3μC
- Q′2=6μC
- Common potential after redistribution:
- V=5.4×106V
- Let the radius of the first sphere R1=5cm=0.05m
- Let the radius of the second sphere R2=0cm=0m
- Initial charge on the first sphere Q1=12μC=12×10−6C
- Initial charge on the second sphere Q2=−3μC=−3×10−6C
- The total charge Qtotal=Q1+Q2=12μC−3μC=9μC
- When the two spheres are connected by a conducting wire, they will reach the same potential. The potential V on a sphere is given by:
V=kQR
- For the two spheres, the potentials must be equal:
kQ′1R1=kQ′2R2
- Since R2=0, we can consider the potential of the second sphere to be effectively zero, which means we only need to find the relationship between the charges:
Q′1R1=Q′2R2
- However, since R2 is zero, we can use the fact that the charge will redistribute such that:
Q′2=2Q′1
- From charge conservation, we have:
Q′1+Q′2=Qtotal=9μC
- Substitute Q′2=2Q′1 into the equation:
Q′1+2Q′1=9μC
3Q′1=9μC
Q′1=3μC
- Now substitute Q′1 back to find Q′2:
Q′2=2Q′1=2×3μC=6μC
- The common potential V after redistribution can be calculated using either sphere's charge and radius:
V=kQ′1R1=k3×10−60.05
- Using k=9×109N m2/C2:
V=9×1093×10−60.05=9×109×6×10−4=5.4×106V
- Charges after connection:
- Q′1=3μC
- Q′2=6μC
- Common potential after redistribution:
- V=5.4×106V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two insulated charged conducting spheres of radii 20cm and 15cm respectively and having an equal charge of 10C are connected by a copper wire and then they are separted. Then
View SolutionTwo metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
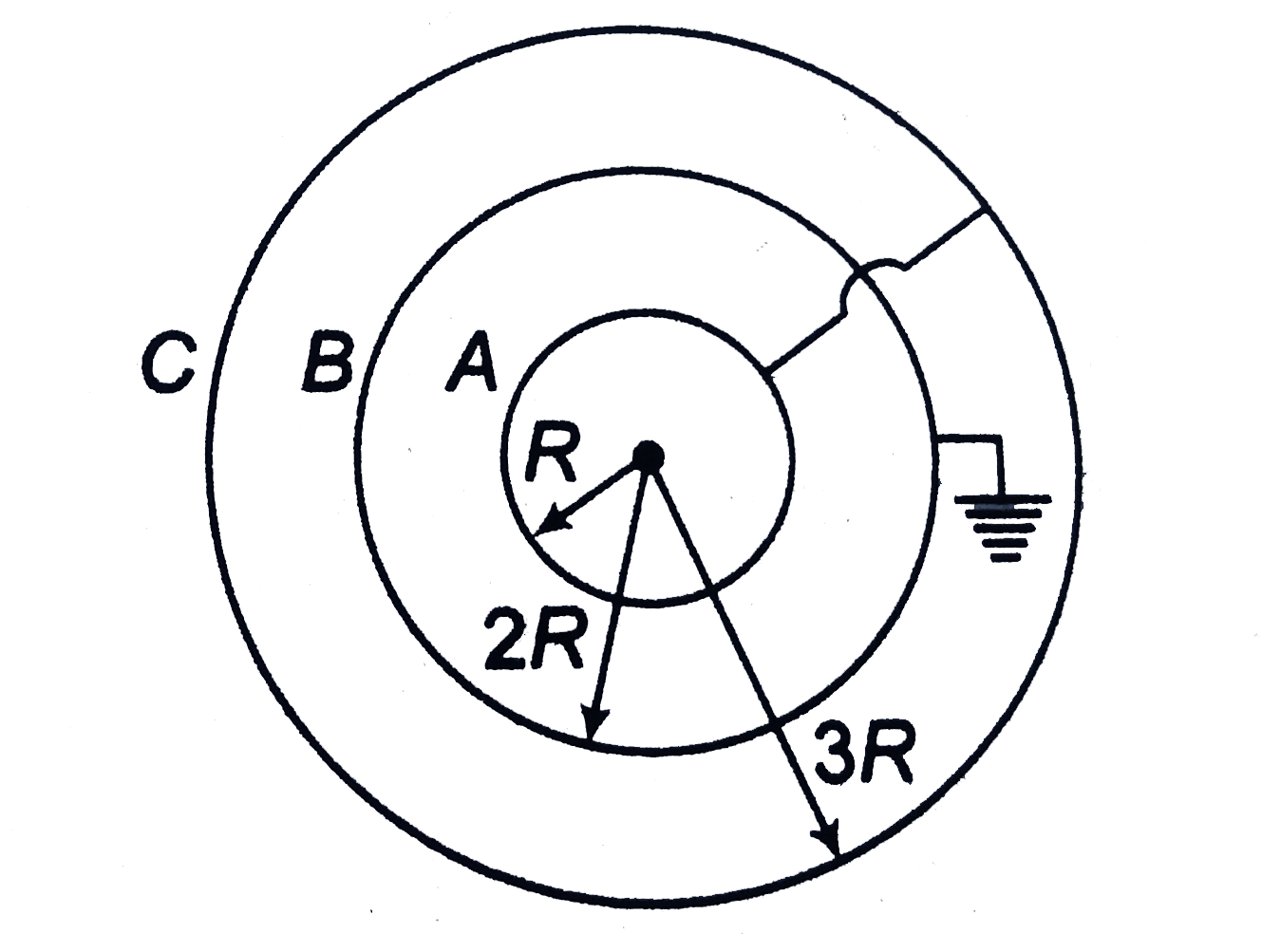
View SolutionThree spherical shells have radii R,2R and 3R respectively. Total charge on A and C is 3q. Find the charges on different surface of A, B and C. The connecting wire does not touch the shell B.
View SolutionTwo spherical conductors A and B of radii 1mm and 2mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is
View SolutionConsider Two metallic charged sphere whose radii are 20 cm and 10 cm respectively each having 150 microcoulomb positive charge. What is their common potential after they are connected by a conducting wire ?
View SolutionConsider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
View SolutionTwo isolated conducting spheres S1andS2 of radius 23Rand13R have 12μC and −3μC charges, respectively, and are at a large distance from each other. They are now connected by a conducting wire . A long time after this is done the charges on S1andS2 are respectively :
View SolutionTwo spheres A and B of radius 4 cm and 6 cm are given charges of 80μCand40μC, respectively. If they are connected by a fine wire, then the amount of charge flowing from one to the other is
View SolutionFigure shows two conducting spheres separated by large distance and of radius 2 cm and 3 cm containing charges 10μC and 20μC respectively. When the spheres are connected by a conducting wire then find out following :
(i) Ratio of the final charge.
(ii) Final charge on each sphere.
(iii) Ratio of final charge densities.
(iv) Heat produced during the process.

View SolutionTwo conductors of capacitance 1μF and 2μF are charged to +10V and −20V They are now connected by a conducting wire. Find
(a) their common potential
(b) the final charges on them
(c) the loss of energy during, redistribution of charges.
View Solution
