A coil having 500 square loops each of side 10cm is placed normal to a magnetic flux which increase at the rate of 1.0teslasecond. The induced r.m.f. in volts is
0.1
0.5
1
5
The correct Answer is:D
To solve the problem, we will use Faraday's law of electromagnetic induction, which states that the induced electromotive force (emf) in a coil is equal to the rate of change of magnetic flux through the coil.
1. Identify the given values:
- Number of loops (N) = 500
- Side length of each loop (s) = 10 cm = 0.1 m
- Rate of change of magnetic field (dB/dt) = 1.0 T/s
2. Calculate the area of one loop:
Area (A)=s2=(0.1m)2=0.01m2
3. Calculate the magnetic flux (Φ) through one loop:
Since the coil is placed normal to the magnetic field, the magnetic flux through one loop is given by:
Φ=B⋅A
Here, B is the magnetic field and A is the area of the loop. The change in magnetic flux (dΦ/dt) can be expressed as:
dΦdt=A⋅dBdt
4. Substituting the values into the equation for dΦ/dt:
dΦdt=0.01m2⋅1.0T/s=0.01Wb/s
5. Calculate the induced emf (E) using Faraday's law:
E=−N⋅dΦdt
Since we are interested in the magnitude, we can ignore the negative sign:
E=500⋅0.01V=5V
Final Answer:
The induced r.m.f. in volts is 5 V.
- Number of loops (N) = 500
- Side length of each loop (s) = 10 cm = 0.1 m
- Rate of change of magnetic field (dB/dt) = 1.0 T/s
Area (A)=s2=(0.1m)2=0.01m2
Since the coil is placed normal to the magnetic field, the magnetic flux through one loop is given by:
Φ=B⋅A
Here, B is the magnetic field and A is the area of the loop. The change in magnetic flux (dΦ/dt) can be expressed as:
dΦdt=A⋅dBdt
dΦdt=0.01m2⋅1.0T/s=0.01Wb/s
E=−N⋅dΦdt
Since we are interested in the magnitude, we can ignore the negative sign:
E=500⋅0.01V=5V
The induced r.m.f. in volts is 5 V.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A coil having 500 square loops each of side 10 cm is placed normal to a magnetic flux which increases at the rate of 1.0 tesla/second. The induced e.m.f. in volts is
View SolutionA 50 turns circular coil has a radius of 3 cm, it is kept in a magnetic field acting normal to the area of the coil. The magnetic field B increased from 0.10 tesla to 0.35 tesla in 2 milliseconds. The average induced e.m.f in the coil is
View SolutionA coil having an area 2m2 is placed in a magnetic field which changes from 1Wb/m2 to 4Wb/m2 in an interval of 2 second. The average e.m.f. induced in the coil will be
View SolutionA current of2⋅00A exists in a square loop of edge 10⋅0cm. Find the magnetic field B at the centre of the square loop.
View SolutionA square wire loop of side 30cm & wire cross section having diameter 4mm is placed perpendicular to a magnetic field changing at the rate 0.2 T/s. Final induced current in the wire loop.
(Given: Resistivity of wire material is (1.23×10−8ohmm)View SolutionA coil of circular cross - section having 1000 turns and 4cm2 face area is placed with its axis parallel to a magnetic field which decreases by 10−2Wb m−2 in 0.01 s. the e.m.f induced in the coil is :
View SolutionA square loop of wire with side length 10 cm is placed at angle of 45∘ with a magnetic field that changes uniformly from 0.1 T to zero in 0.7s. The induced current in the loop (its resistance is 1Ω) is
View SolutionThe side of a square is increasing at the rate of 0.1cm/sec. Find the rate of increase of its perimeter.
View SolutionABCDA is a closed loop of conducting wire consisting of two semicircular sections, the part ABCD lying in the XY plane and the part CDA lying in the YZ plane, both the parts having the centre at origin O (see the diagram). This loop is placed in a uniform field →B which varies with time.
Radius of the semicircular section is 0.5 m
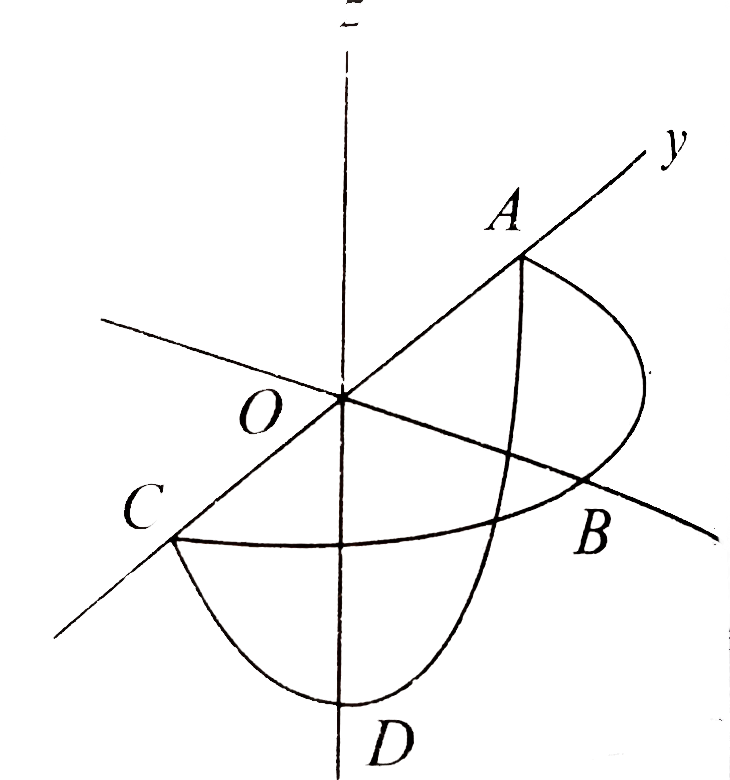
If →B be directed along the +z axis and increases at the rate of 10−2Teslasecond. the magnitude and sense of the induced emf in the loop as seen along the field direction will beView SolutionThe side of a square is increasing at the rate of 0.2 cm/s. The rate of increase of perimeter w.r.t time is :
View Solution

