Find the area of the region bounded by the curve y=|x+1|, lines x=−4,x=2 and X-axis.
y=|x+1|
={x+1,x≥−1−(x+1),x<−1
Its graph is shown in the figure.
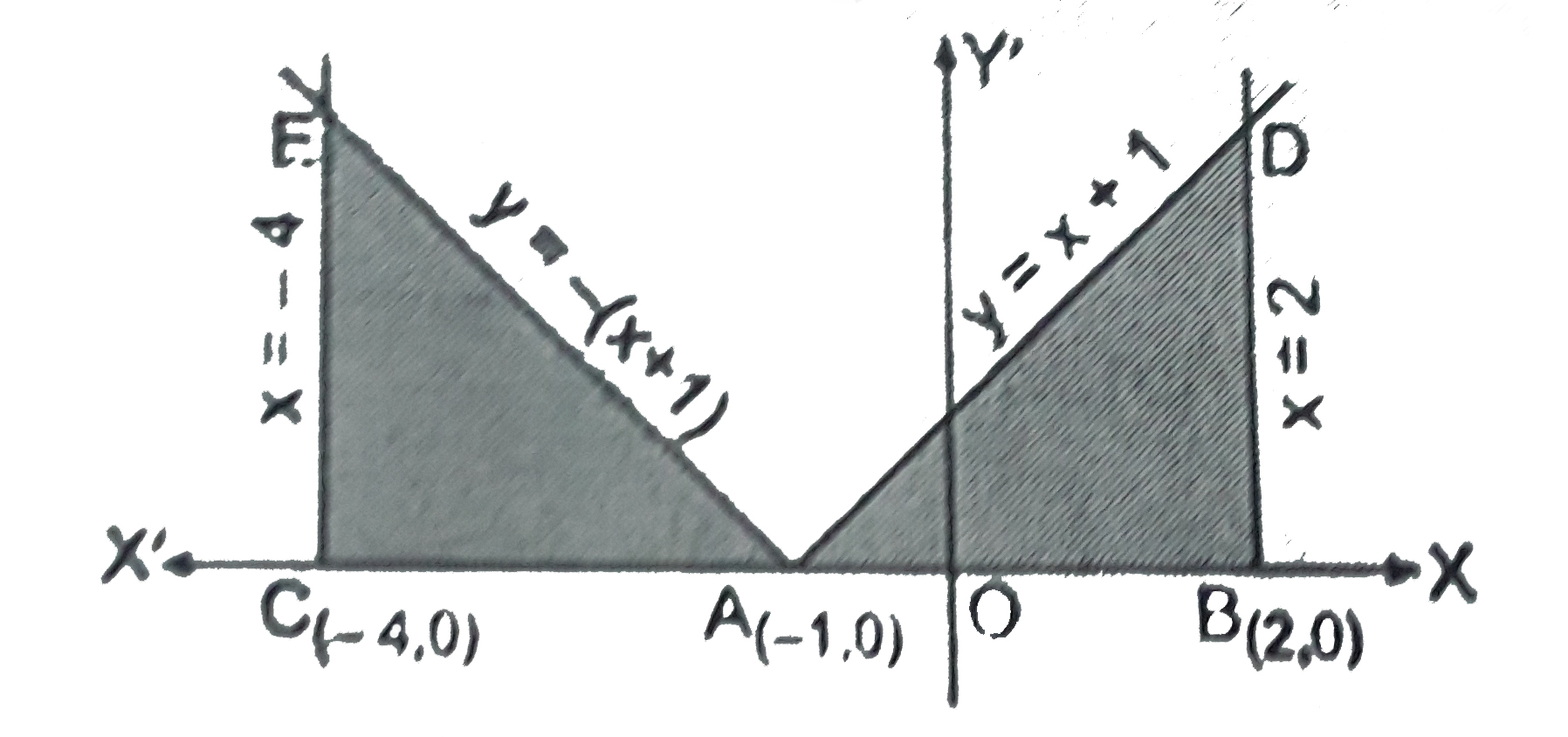
Area of region bounded by the curve y=|x+1|, lines x=−4,x=2 and X-axis
= Area of ACEA + Area of ABDA
=∫−1−4yAEdx+∫2−1yADdx
=∫−1−4−(x+1)dx+∫2−1(x+1)dx
=−[x22+x]−1−4+[x22+x]2−1
=−[(12−1)−(8−4)]+[(2+2)−(12−1)]
=−(−12−4)+(4+12)
=92+92=9sq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8a28videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8 B Multiple Choice Questions10videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Using intergration, find the area of the region bounded by the lines y=|x+1|,x=−3,x=1 and X-axis.
View SolutionFind the area of the region bounded by the curve y2=4xand the line x=3.
View SolutionFind the area of the region bounded by the curve y2=xand the lines x=1,x=4and the x-axis.
View SolutionFind the area of the region bounded by the curve y=x2 and the line y = 4 .
View SolutionFind the area of the region bounded by the curves y=x3 and the lines y=x+6 and y=0.
View SolutionA body weighs w Newton on the surface of the earth. Its weight at a height equal to half the radius of the earth, will be xyw where x and y are coprimes . Find x and y
View SolutionFind the area of the region bounded by the curves 2y2=x,3y2=x+1,y=0.
View SolutionFind the area of the region bounded by the curves x=∣∣y2−1∣∣ and y=x−5.
View SolutionFind the area of the region bounded by the curves x=2y−y2 and y=2+x.
View SolutionFind the area of the region bounded by the curves y=x−1 & (y−1)2=4(x+1).
View Solution
