Let V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)None
The correct Answer is:(A→t,B→t,C→p,q,r,s,D→c)
To solve the problem, we need to match the gravitational potential (V) and gravitational field (E) at specific points with the corresponding descriptions in the columns provided. Here’s a step-by-step breakdown:
Step 1: Understand the Properties of Gravitational Field and Potential
- The gravitational field (E) is defined as the force per unit mass experienced by a small test mass placed in the field.
- The gravitational potential (V) is the work done per unit mass to bring a mass from infinity to a point in the field.
Step 2: Analyze Each Case in Column-I
1. (A) E = 0, V = 0:
- This occurs at the center of a spherical shell. According to Gauss's law, the gravitational field inside a uniform spherical shell is zero. Since the potential is constant throughout the shell and can be taken as zero at infinity, V = 0 at the center.
- Match: (A) → (p)
2. (B) E ≠ 0, V = 0:
- This situation does not occur in classical mechanics. The gravitational field cannot be non-zero while the potential is zero at the same point. Therefore, this option does not match any case.
- Match: (B) → (t)
3. (C) V ≠ 0, E = 0:
- This occurs at the center of a solid sphere. Inside a uniform solid sphere, the gravitational field is zero at the center, but the potential is non-zero and is maximum at the center.
- Match: (C) → (q)
4. (D) V ≠ 0, E ≠ 0:
- This scenario occurs at the center of a circular ring of mass. At the center of the ring, the gravitational field is zero, but the potential is non-zero.
- Match: (D) → (r)
Step 3: Compile the Matches
Based on the analysis:
- (A) → (p)
- (B) → (t)
- (C) → (q)
- (D) → (r)
Final Matches:
- A → p
- B → t
- C → q
- D → r
- The gravitational field (E) is defined as the force per unit mass experienced by a small test mass placed in the field.
- The gravitational potential (V) is the work done per unit mass to bring a mass from infinity to a point in the field.
1. (A) E = 0, V = 0:
- This occurs at the center of a spherical shell. According to Gauss's law, the gravitational field inside a uniform spherical shell is zero. Since the potential is constant throughout the shell and can be taken as zero at infinity, V = 0 at the center.
- Match: (A) → (p)
- This situation does not occur in classical mechanics. The gravitational field cannot be non-zero while the potential is zero at the same point. Therefore, this option does not match any case.
- Match: (B) → (t)
- This occurs at the center of a solid sphere. Inside a uniform solid sphere, the gravitational field is zero at the center, but the potential is non-zero and is maximum at the center.
- Match: (C) → (q)
- This scenario occurs at the center of a circular ring of mass. At the center of the ring, the gravitational field is zero, but the potential is non-zero.
- Match: (D) → (r)
Based on the analysis:
- (A) → (p)
- (B) → (t)
- (C) → (q)
- (D) → (r)
- A → p
- B → t
- C → q
- D → r
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Let V and E denote the gravitational potential and gravitational field at a point. It is possile to have
View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
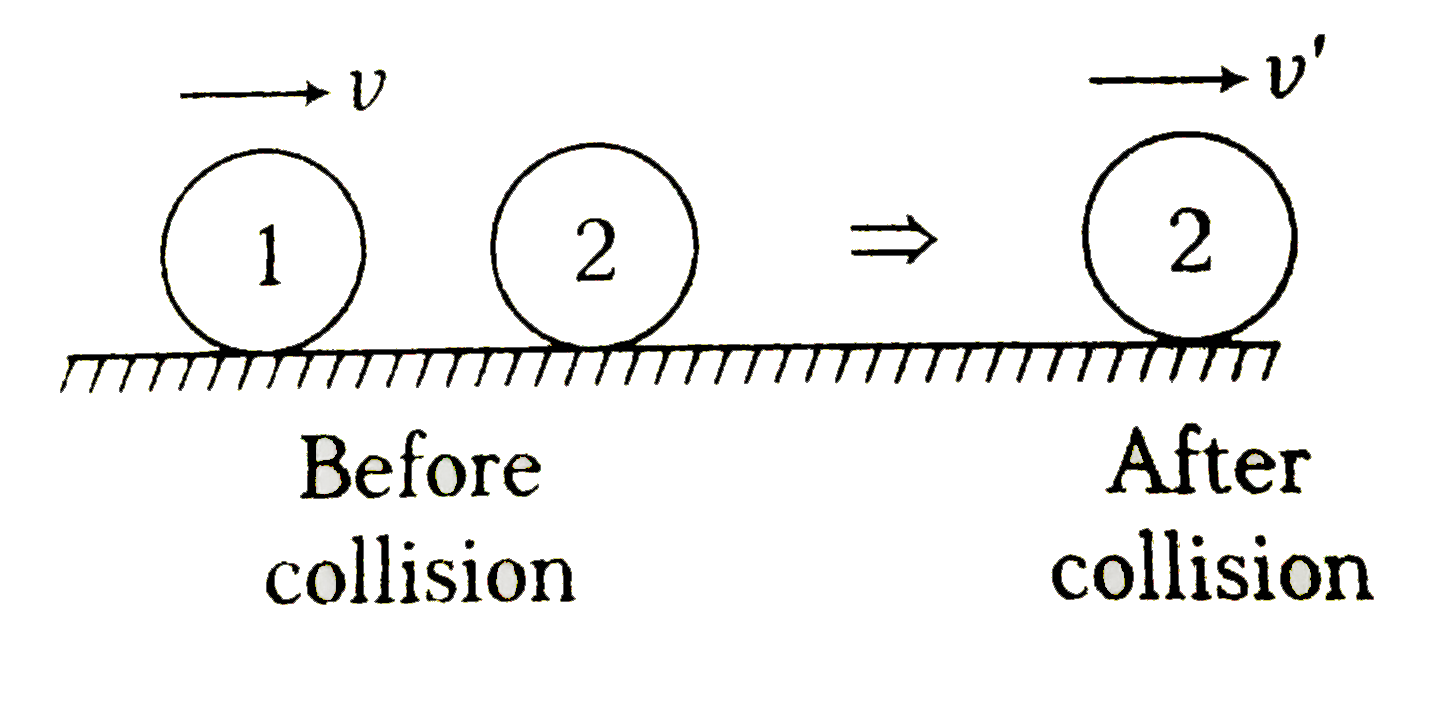
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
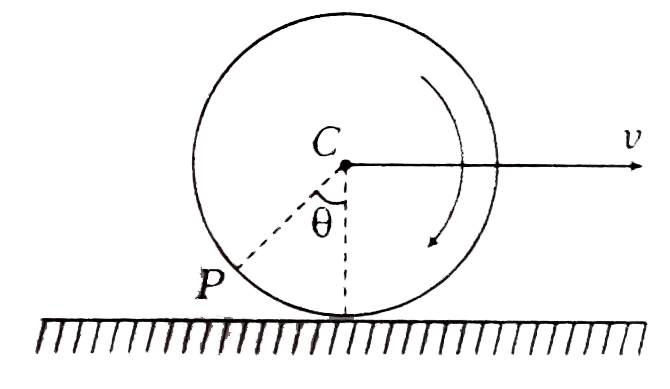
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View SolutionIn the circuit shown in figure, E = 10 V, r = 1Ω,
R = 4Ω and L = 5H. The circuit is closed at time t = 0.
Then, match the following two columns.
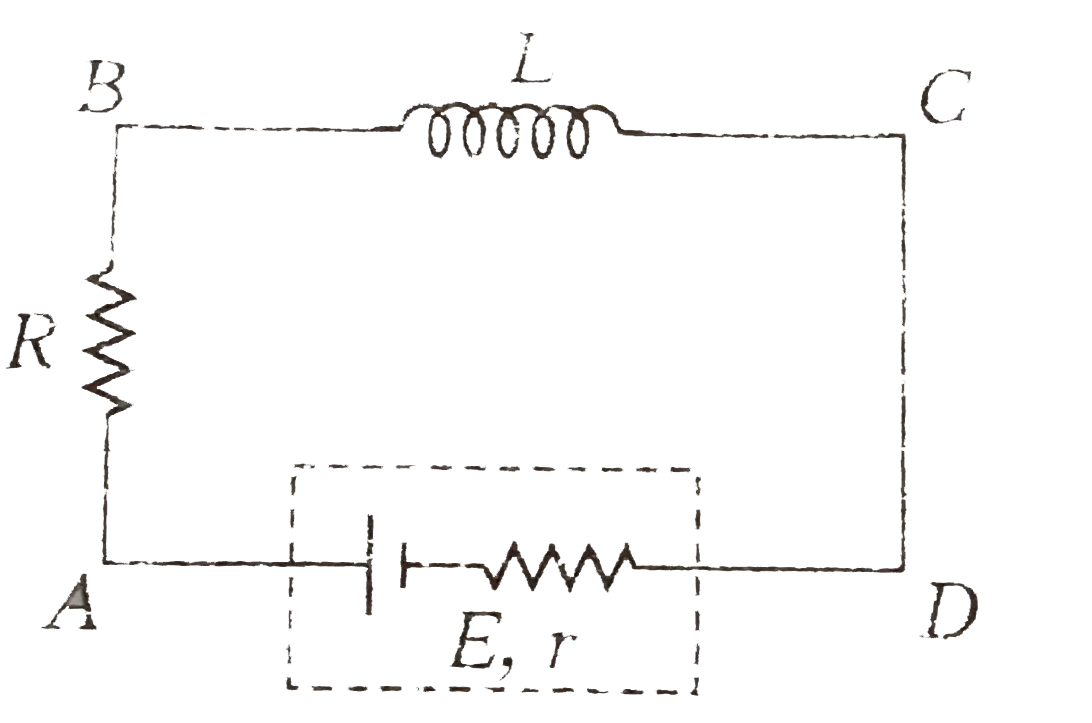
Column IColumn IIA.VAD at t = 0p4VB.VBC at t = 0q8VC.VAB at t =∞r.0VD.VAD at t=∞s.10V
View SolutionLet V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
View SolutionMatch the following
Column IColumn II(A)E∝1r2(p)Point charge(B)E∝r(q)Spherically symmetric charge distribution(C)V∝1r(r)Long line charge(D)V2−V1=f(r2r1)(s)Plane sheet of charge(E)V2−V1∝r2−r1(t)Electric dipole
View SolutionGiven that the gravitation potential on Earth surface is V0. The potential at a point distant half the radius of earth from the cetre will be
View SolutionColumn IColumn II(A)R/L(p)Time(B)C/R(q)Frequency(C)E/B(r)Speed(D)√ε0μ0(s)None
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionColumn I shows charge distribution and column II shows electrostatic field created by that charge at a point r distance from its centre.
(,Column I ,,Column II),((A),A stationary point charge,(p),E∝r0),((B),A stationary uniformly long charge rod,(q),E∝r1),((C),A stationary electric dipole,(r),E∝r⋅−1),,(s),E∝r−2),(,,(t),E∝r−3):}
View Solution
