Three point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
The correct Answer is:A, C
To find the electric potential at the origin due to the three point charges q1,q2, and q3, we can use the formula for electric potential V due to a point charge, which is given by:
V=kQr
where:
- V is the electric potential,
- k is Coulomb's constant (9×109N m2/C2),
- Q is the charge,
- r is the distance from the charge to the point where the potential is being calculated.
Step 1: Calculate the potential due to q1
Given:
- q1=1μC=1×10−6C
- Position of q1 is at (1m,0,0)
- Distance from the origin r1=1m
Using the formula:
V1=kq1r1=9×1091×10−61=9×103V
Step 2: Calculate the potential due to q2
Given:
- q2=−2μC=−2×10−6C
- Position of q2 is at (0,2m,0)
- Distance from the origin r2=2m
Using the formula:
V2=kq2r2=9×109−2×10−62=−9×103V
Step 3: Calculate the potential due to q3
Given:
- q3=3μC=3×10−6C
- Position of q3 is at (0,0,3m)
- Distance from the origin r3=3m
Using the formula:
V3=kq3r3=9×1093×10−63=9×103V
Step 4: Calculate the total potential at the origin
Now, we can find the total potential V at the origin by summing the potentials due to each charge:
V=V1+V2+V3
Substituting the values we calculated:
V=9×103+(−9×103)+9×103
V=9×103−9×103+9×103=9×103V
Final Answer
The electric potential at the origin is:
9000V
- V is the electric potential,
- k is Coulomb's constant (9×109N m2/C2),
- Q is the charge,
- r is the distance from the charge to the point where the potential is being calculated.
- q1=1μC=1×10−6C
- Position of q1 is at (1m,0,0)
- Distance from the origin r1=1m
- q2=−2μC=−2×10−6C
- Position of q2 is at (0,2m,0)
- Distance from the origin r2=2m
- q3=3μC=3×10−6C
- Position of q3 is at (0,0,3m)
- Distance from the origin r3=3m
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Three charges q1=1μC,q2=−2μC,andq3=−1μC are placed at A(0,0,0),B(−1,2,3,)andC(2,−1,1). Find the potential of the system of three charges at P(1,−2,−1).
View SolutionTwo point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionThree charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionTwo point charges of magnitude +qand−q are placed at (−d/2,0,0)and(d/2,0,0) are respectively. Find the equation of the euipotential surface where the potential is zero.
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1

View SolutionTwo point charges q1=20μC and q2=25μC are placed at (-1, 1, 1) m and (3, 1, -2)m, with respect to a coordinate system. Find the magnitude and unit vector along electrostatic force on q2 ?
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).
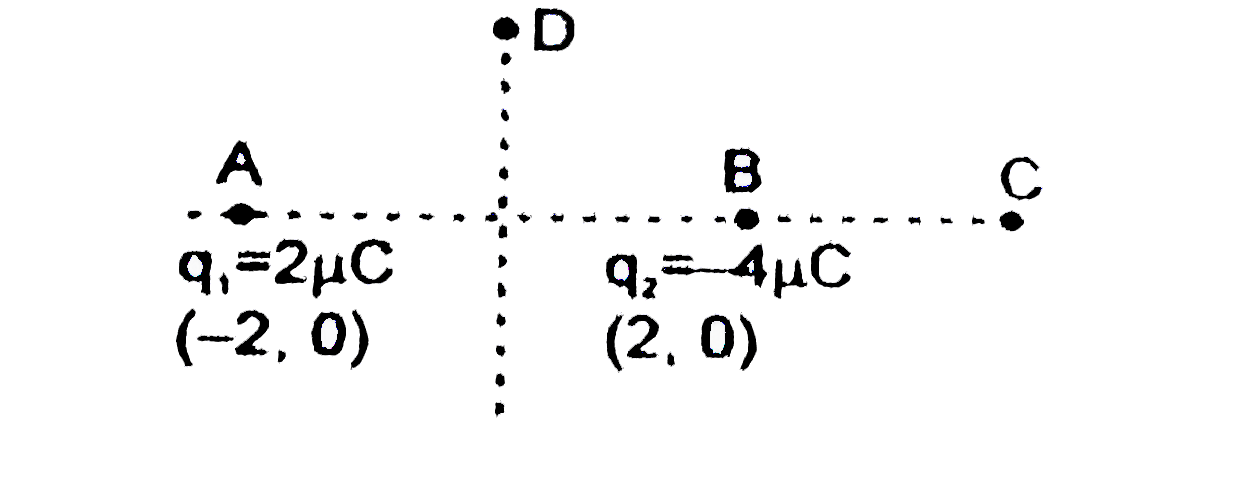
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View Solution
