Two identical electric point dipoles have dipole moments −→P1=pˆiand−→P2=pˆi and are held on the x axis at distance 'a' from each other. When released, they move along the x-axis with the direaction of their dipole moments remaining unchanged. If the mass of each dipole is 'm', their speed when they are infinitely for apart is :
Pa√1π∈0ma
Pa√12π∈0ma
Pa√22π∈0ma
Pa√32π∈0ma
To solve the problem, we will use the concept of conservation of energy. The potential energy of the dipoles when they are at a distance 'a' apart will be converted into kinetic energy when they are infinitely far apart.
1. Identify the Initial Potential Energy:
The potential energy U between two dipoles can be expressed as:
U=−→P1⋅→E2
where →E2 is the electric field due to dipole →P2 at the location of dipole →P1. The electric field →E due to a dipole at a distance r along the axial line is given by:
E=2kpr3
Here, k=14πϵ0 and p is the dipole moment.
2. Calculate the Electric Field at Distance 'a':
At a distance a from dipole →P2, the electric field E is:
E=2kpa3
3. Calculate the Initial Potential Energy:
Since both dipoles have the same dipole moment p, the potential energy when they are at distance a is:
U=−→P1⋅→E=−p⋅2kpa3=−2kp2a3
4. Final Potential Energy at Infinity:
When the dipoles are infinitely far apart, the potential energy Uf becomes zero:
Uf=0
5. Apply Conservation of Energy:
The initial potential energy will be converted into kinetic energy when the dipoles are infinitely far apart. The kinetic energy K of both dipoles can be expressed as:
K=2⋅12mv2=mv2
Setting initial potential energy equal to final kinetic energy:
−2kp2a3=mv2
6. Solve for Velocity v:
Rearranging the equation gives:
v2=2kp2ma3
Taking the square root:
v=√2kp2ma3
7. Substitute the Value of k:
Substitute k=14πϵ0:
v=
⎷2⋅14πϵ0p2ma3=pa√12πϵ0m
Final Answer:
The speed of each dipole when they are infinitely far apart is:
v=pa√12πϵ0m
The potential energy U between two dipoles can be expressed as:
U=−→P1⋅→E2
where →E2 is the electric field due to dipole →P2 at the location of dipole →P1. The electric field →E due to a dipole at a distance r along the axial line is given by:
E=2kpr3
Here, k=14πϵ0 and p is the dipole moment.
At a distance a from dipole →P2, the electric field E is:
E=2kpa3
Since both dipoles have the same dipole moment p, the potential energy when they are at distance a is:
U=−→P1⋅→E=−p⋅2kpa3=−2kp2a3
When the dipoles are infinitely far apart, the potential energy Uf becomes zero:
Uf=0
The initial potential energy will be converted into kinetic energy when the dipoles are infinitely far apart. The kinetic energy K of both dipoles can be expressed as:
K=2⋅12mv2=mv2
Setting initial potential energy equal to final kinetic energy:
−2kp2a3=mv2
Rearranging the equation gives:
v2=2kp2ma3
Taking the square root:
v=√2kp2ma3
Substitute k=14πϵ0:
v=
⎷2⋅14πϵ0p2ma3=pa√12πϵ0m
The speed of each dipole when they are infinitely far apart is:
v=pa√12πϵ0m
Topper's Solved these Questions
Similar Questions
Two electric dipoles, A, B with respective dipole moments −→dA=−4 qa ˆiand−→dB=−2 qa ˆi are placed on the x-axis with a seperation R, as shown in the figure
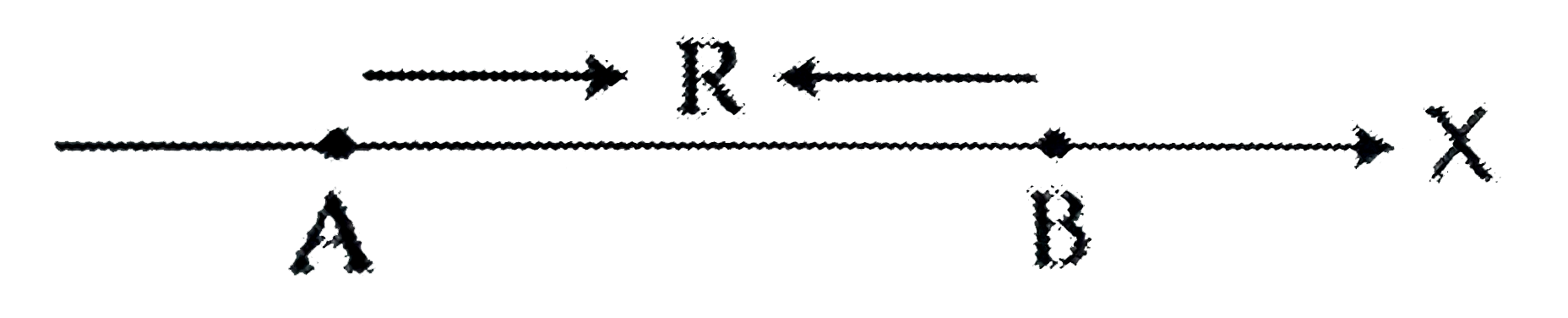
The distance from A at which both of them produce the same potential is :
View SolutionA very small electric dipole with dipole moment p is placed in such in way that it is at a distance r from another point charge +q. The point charge lies on the axis of the dipole . Electric dipole moment is pointing towards the point charge. Determine electric dipole will attract the point charge or repel it ? What will be the magnitude of force between them ?
View Solution
Knowledge Check
Two point dipoles of dipole moment →p1and→p2 are at a distance x from each other and →p1∣∣→p2 . The force between the dipoles is :
A14πε04p1p2x4B14πε03p1p2x3C14πε06p1p2x4D14πε08p1p2x4A dipole of dipole moment →P is placed in uniform electric field →E, then torque acting on it is given by
A→τ=→P.→EB→τ=→P×→EC→τ=→P+→ED→τ=→P−→ETwo short dipoles , each of dipole moment P are placed at a large separation r. The force between them
Ais proportional to product of dipole momentaBis inversely proportional to r4Cthe force is attractive , if direction of dipole momenta are same , repulsive if oppositeDall options are correct
Two small identical electric dipoles AB and CD, each of dipole moment →p are kept at an angle of 120∘ to each other in an external electric field →E pointing along the x-axis as shown in the figure. Find the
(a) dipole moment of the arrangement, and
(b) magnitude and direction of the net torque acting on it.
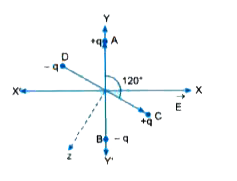
View SolutionTwo short electric dipoles having dipole moment p1 and p2 are placed co-axially and uni-directionally, at a distance r apart. Calculate nature and magnitude of force between them :
View SolutionTwo identical dipoles have their axes at right angles to each other and also bisecting each other . Calculate the field at a distance r from the point of intersection of their axes in a direction θ with the axis of one of the dipoles . The dipole moment of each dipole is equal to p .
View SolutionAn electric dipole is kept on the axis of a uniformly charged ring at distance d from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
View SolutionTwo identical magnetic dipoles of magnetic moments 4A−m2 each, are placed at a separation of 4 m with their axis perpendicular to each other. The resultant magnetic field at a point midway between the dipoles is
View Solution
