Find by integration the area of the region bounded by the curve y=2x−x2 and the x-axis.
y=4x−x2 …(1)
Equation of X-axis y=0 …(2)
Their points of intersection are O(0, 0) and A(4, 0).
Now draw the graph of the curve and shade the common region.
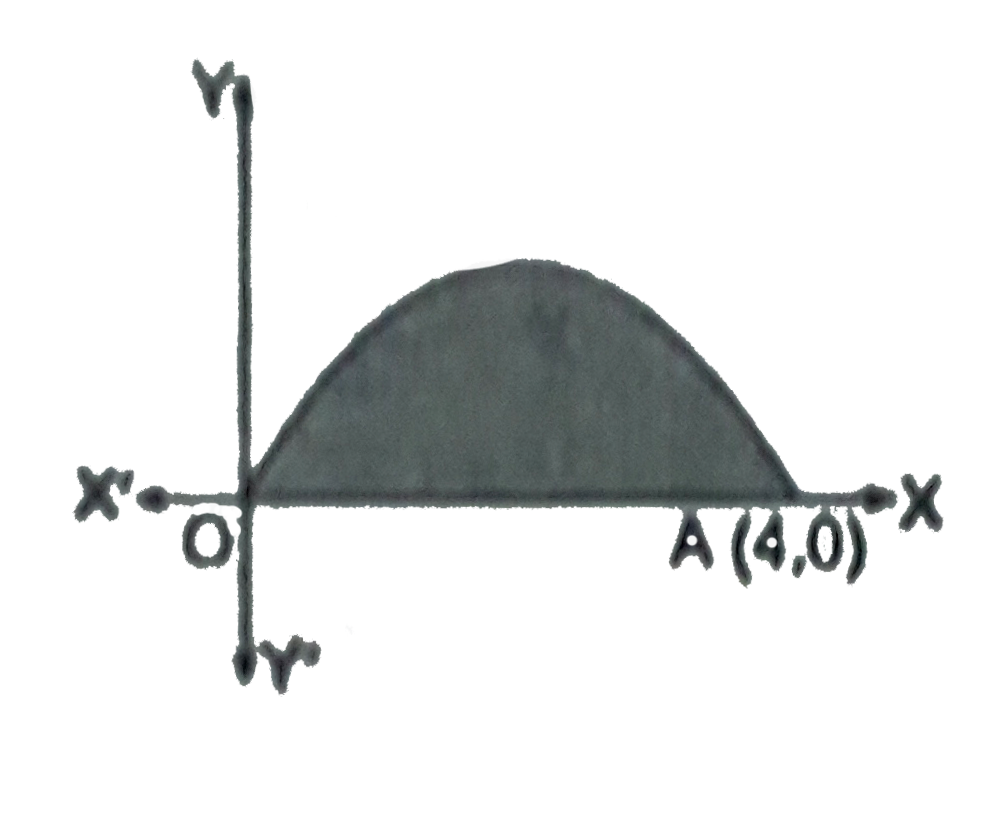
Required area =∫40ydx
=∫40(4x−x2)dx
=[2x2−x33]40
=32−643=323sq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8a28videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8 B Multiple Choice Questions10videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
The area of the region bounded by the curve y=2x−x2 and x - axis is
View SolutionFind the area of the region bounded by the curves x=4y−y2 and the Y-axis.
View SolutionThe area of the region bounded by the curves y=|x−2|,x=1,x=3 and the x-axis is
View SolutionFind the area bounded by the curve y=x3−3x2+2x and the x-axis.
View SolutionThe area bounded by the curve y=4x−x2 and the x-axis is:
View SolutionFind the area of the region bounded by the curves x=2y−y2 and y=2+x.
View SolutionThe area of the region bounded by the curve y=√16−x2 and X-axis is
View SolutionFind the area bounded by the curve y=x(x−1)(x−2) and the x-axis.
View SolutionFind the area of the region bounded by the curve y=|x+1|, lines x=−4,x=2 and X-axis.
View SolutionThe area of the region bounded by the curve y=sin2x, y-axis and y=1 is :
View Solution

