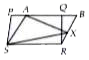
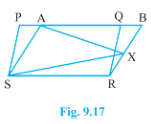
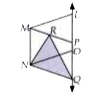
In the adjoining figure, MNPQ and ABPQ are parallelogram and T is any point on the side BP. Prove that
(i) ar(MNPQ)=ar(ABPQ)
(ii)ar(△ATQ)=12ar(MNPQ).
ar(MNPQ)=ar(ABPQ) ( they have same base and lie between same parallels).
ar(△ATQ)=12ar(ABPQ) (they have same base and lie between same parallels).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
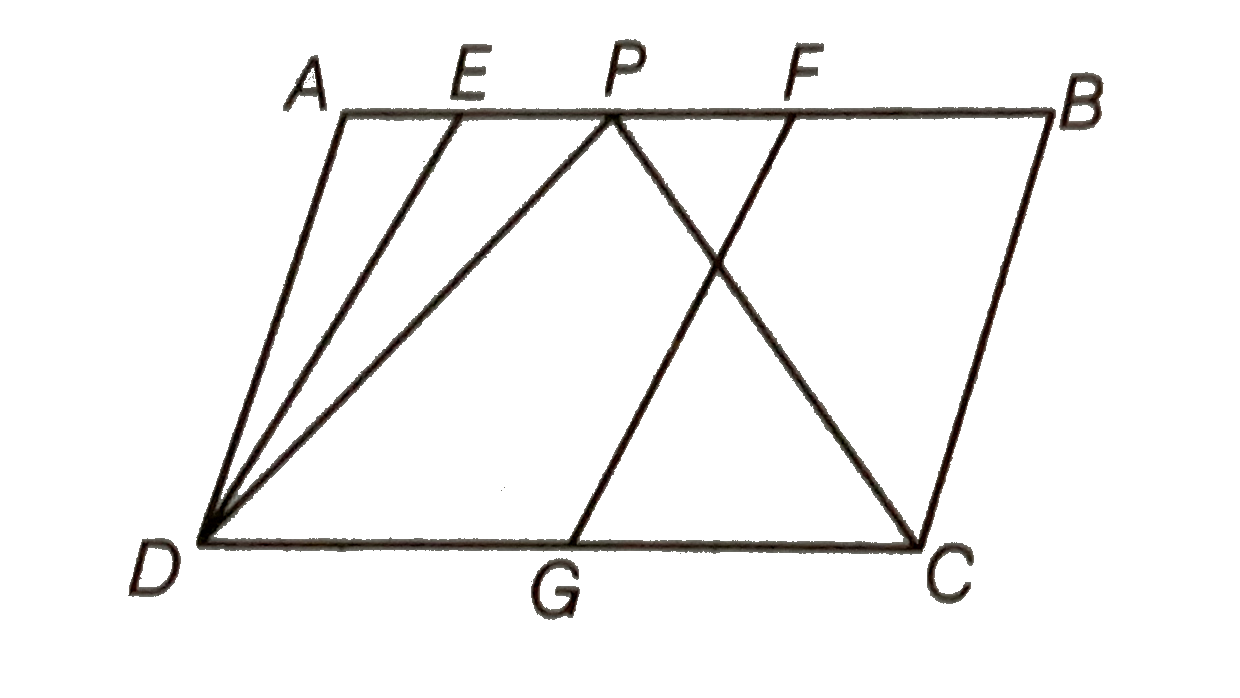
In the given figure, ABCD and AEFD a re two parallelograms.
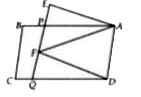
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
 ATrueBFalseCPartially trueDNone of these
ATrueBFalseCPartially trueDNone of these
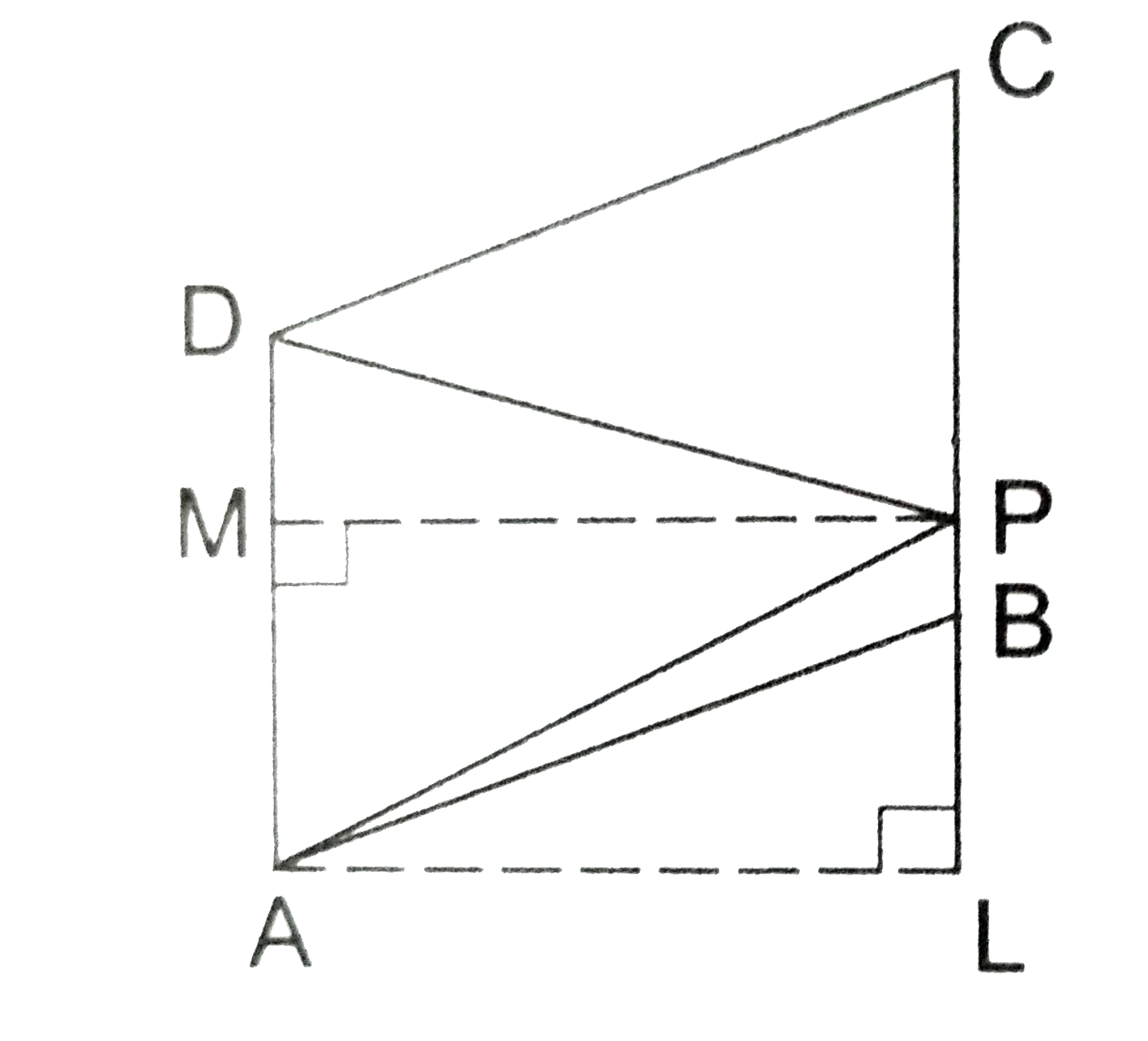
In the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
View SolutionIn the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
ar(△APQ)=ar(△DPQ)=16ar(△ABCD).
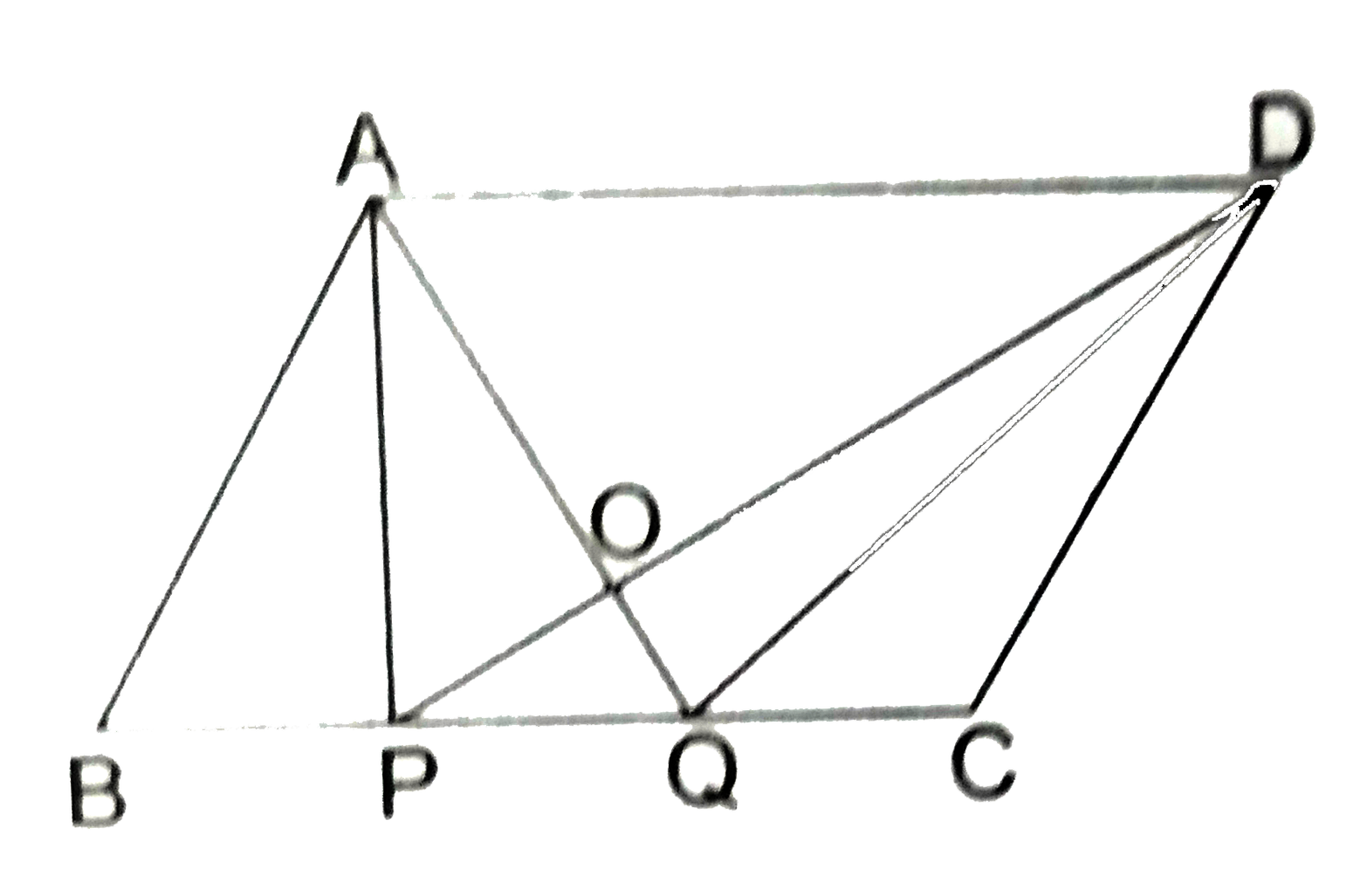
View SolutionIn the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).
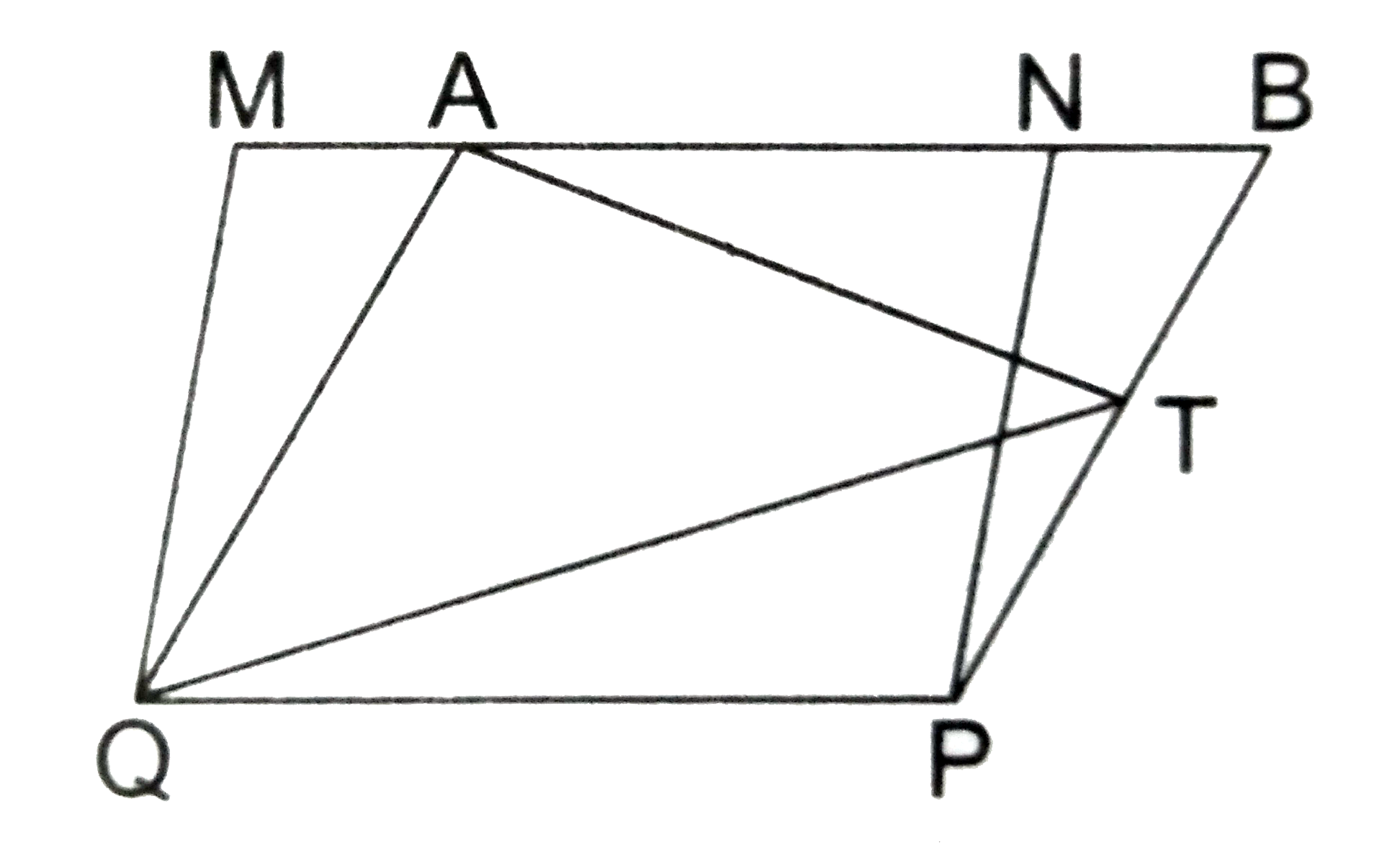
View SolutionIn the given figure LMNO and PMNQ are two parallelograms. R is any point on side MP. If ar(ΔNRQ) = k[ar( IIgm LMNO)] then 2k equals
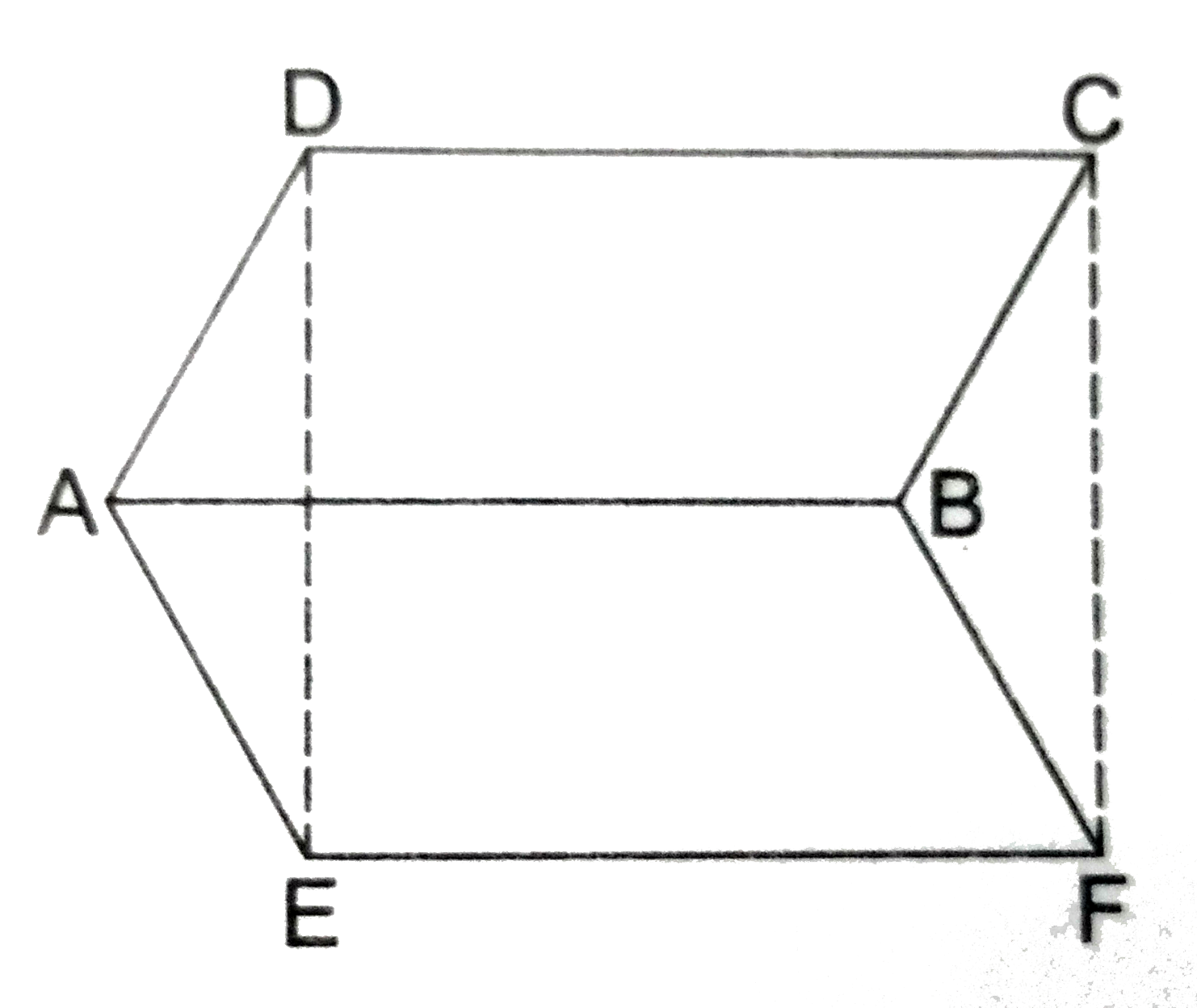
View SolutionIn the adjoing figure, two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that
ar(||gm ABCD)+ar(||gm AEFB)
=ar(||gm EFCD).
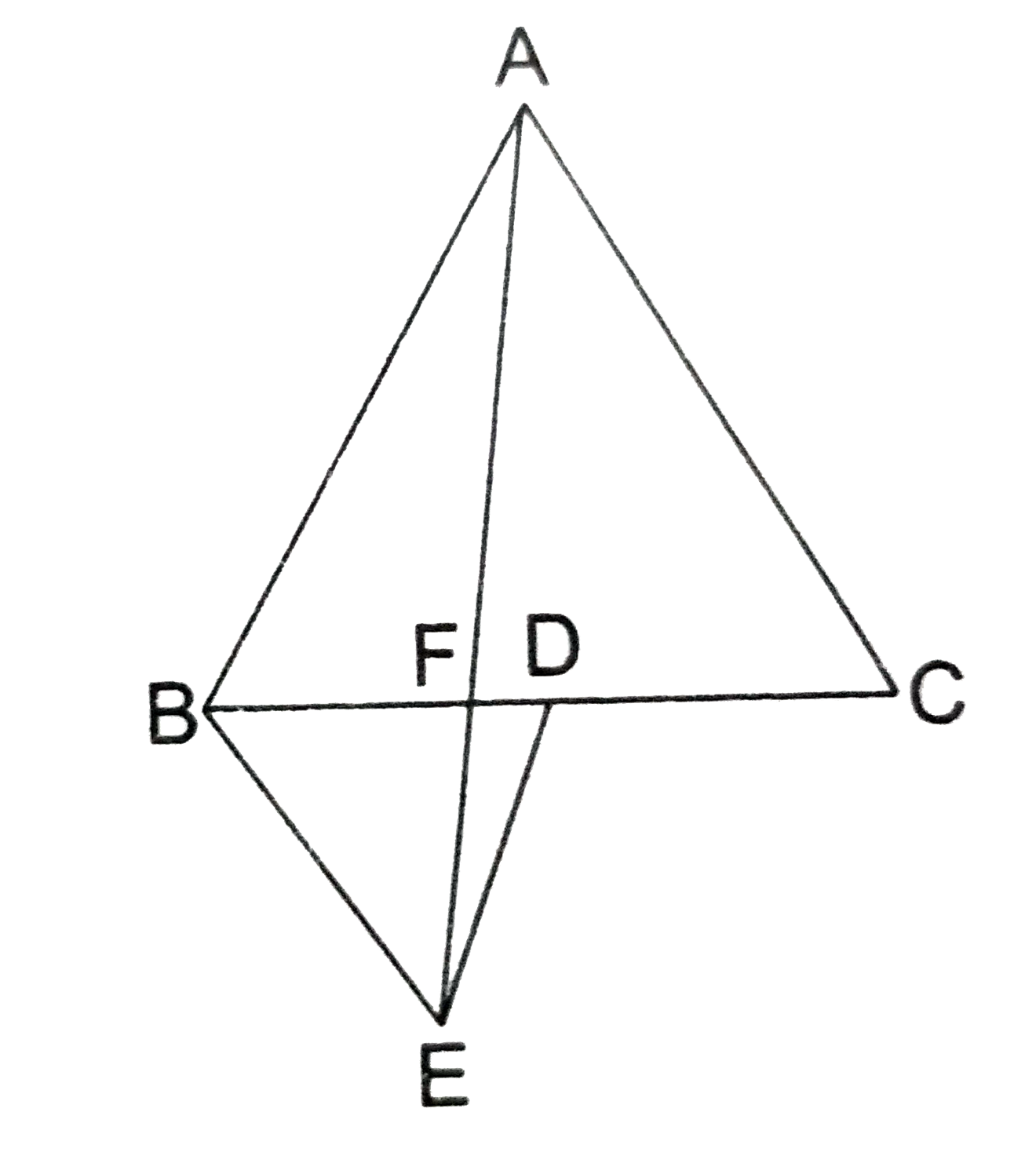
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
View Solution