Complete Solutions to Level 1 Objective of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| DC PANDEY | Level 1 Objective |
| Number Of Questions | 82 |
| Academic Year | 2023-24 |
Identify the correct statement about the charges `q_1` and `q_2` then

View SolutionThree identical charges are placed at corners of a equilateral triangel of side l. If force between any two charges is F, the work required to double the dimensiions of triangle is
View SolutionA proton a deutron and an `alpha` particle are accelerated through potentials of `V, 2V` and `4V` respectively. Their velocity will bear a ratio
View SolutionElectric potential at a point P, r distance away due to a point charge q kept at point A is V. If twice of this charge is distributed uniformly on the surface of a hollow sphere of radius 4r with centre at point A the potential at P now is
View SolutionFour charges `+q, -q, +q` and `-q` are placed in order on the four consecutive corners of a square of side a. The work done in interchanging the positions of any two neighboring charges of the opposite sign is
View SolutionTwo concentric spheres of radii `R` and `2R` are charged. The inner sphere has a charge if `1muC` and the outer sphere has a charge of `2muC` of the same sigh. The potential is `9000 V` at a distance `3R` from the common centre. The value of R is
View SolutionA ring of radius R is having two charges `q` and `2q` distributed on its two half parts. The electric potentiasl at a point on its axis at a distance of `2sqrt2 R` from its centre is `(k=1/(4piepsilon_0))`
View SolutionA particle A having charge of `2.0xx10^-6C` and a mass of 100 g is fixed at the bottom of a smooth inclined plane of inclination `30^@`. Where should another particle B having same charge and mass, be placed on the inclined plane so that B may remain in equilibrium?
View SolutionFour positive charges `(2sqrt2-1)Q` are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
View SolutionA proton is released from rest, 10 cm from a charged sheet carrying charged density of `-2.21xx10^-9C//m^2`. It will strike the sheet after the time (approximately)
View SolutionTwo point charges `+q` and `-q` are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View SolutionCharge `2q and -q` are placed at `(a,0) and (-a, 0)` as shown in the figure. The coordinates of the point at which electric field intensity is zero will be `(x,0)` where

View SolutionFive point charge (`+q` each) are placed at the five vertices of a regular hexagon of side `2a`.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionTwo identical small conducting spheres having unequal positive charges `q_1` and `q_2` are separated by a distance r. If they are now made to touch each other and then separated again to the same distance, the electrostatic force between them in this case will be
View SolutionThree concentric conducting sphereical shells carry charges `+4Q` on the inner shell `-2Q` on the middle shel and `+6Q` on the outer shell. The charge on the inner surface of the outer shell is
View Solution1000 drops of same size are charged to a potential of 1 V each. If they coalesce to form in single drop, its potential would be
View SolutionTwo concentric conducting spheres of radii `R` and `2R` are crrying charges `Q` and `-2Q`, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
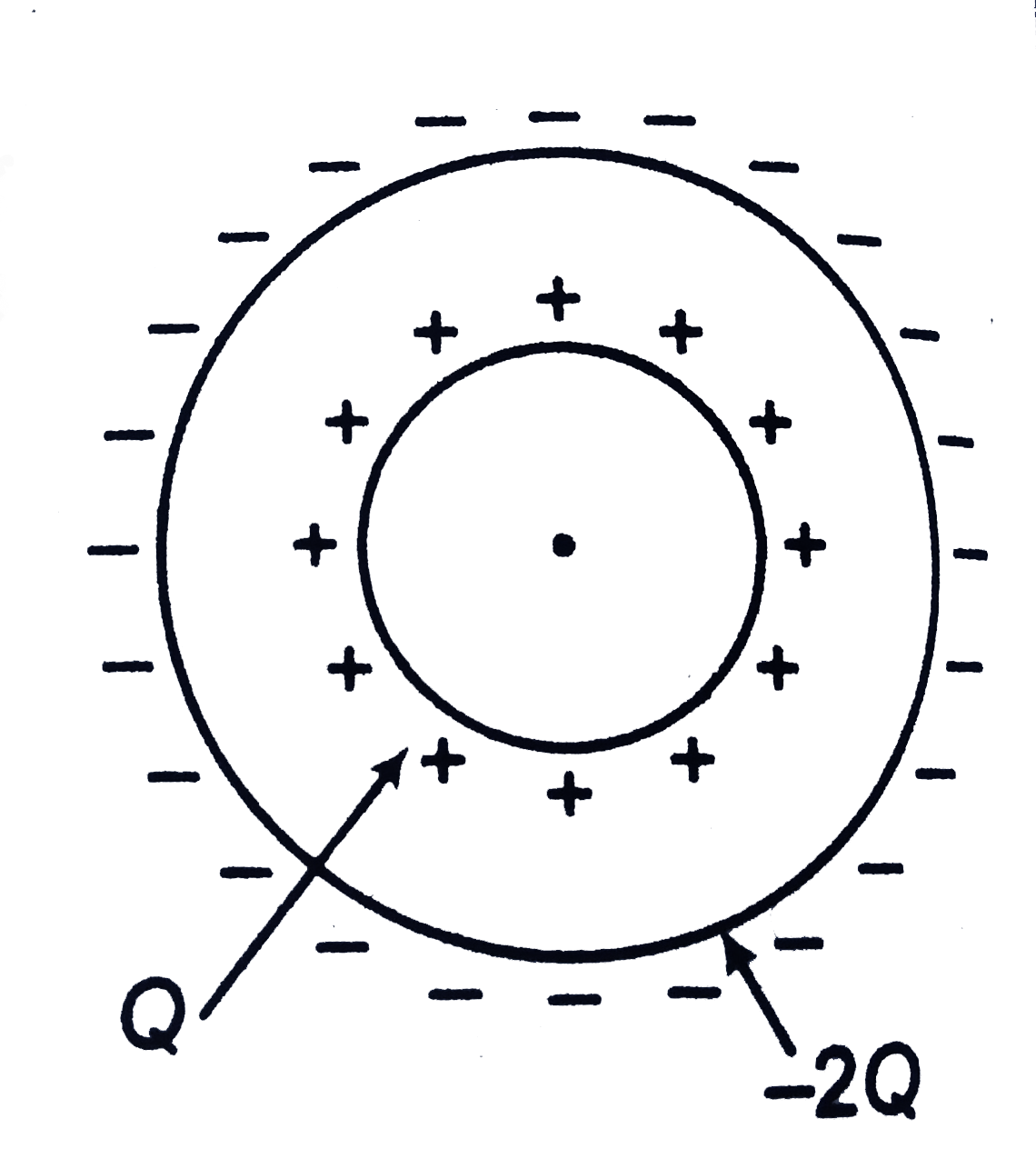
View SolutionCharges `Q, 2Q`, and `-Q` are given to three concentric conducting sphereical shells `A, B` and `C` respectively as shown in figure. The ratio of charge on the inner and outer surface of shell C will be

View SolutionThe electric field in a region of space is given by `E=5hati+2hatjN//C`. The flux of E due ot this field through an area `1m^2`lying in the y-z plane, in SI units is
View SolutionA charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
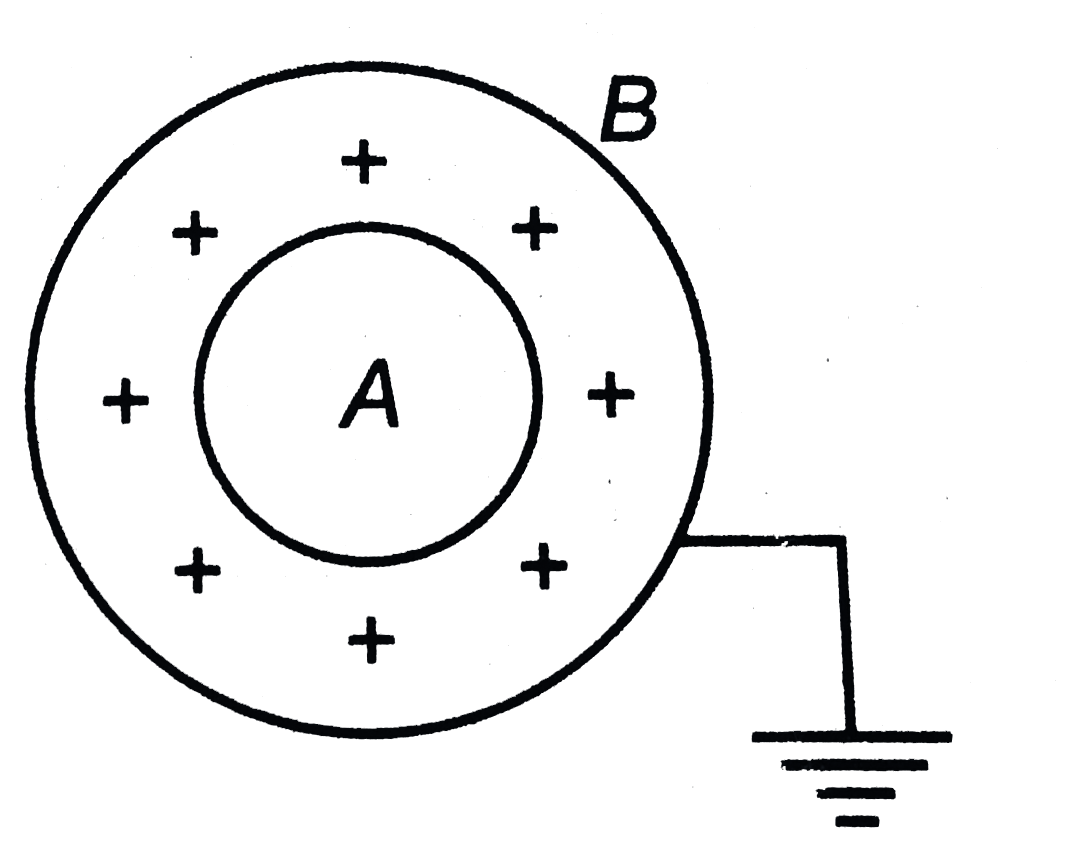
View SolutionA and B are two concentric spherical shells. If A is given a charge `+q` while B is earthed as shown in figure then
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from its surface at which the electrostatic potential is equal to half of the potential at the centre is
View SolutionFour dipoles each of magnitudes of charges `+-e` are placed inside a sphere. The total flux of E coming out of the sphere is
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle `theta` with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionTwo isolated charged conducting spheres of radii a and b produce the same electric field near their surface. The ratio of electric potentials on their surfaces is
View SolutionTwo point charges +q and -q are held fixed at `(-a,0)` and `(a,0)` respectively of a x-y coordinate system then
View SolutionA conducting shell `S_1` having a charge Q is surrounded by an uncharged concentric conducting spherical shell `S_2`. Let the potential difference between `S_1` and that `S_2` be V. If the shell `S_2` is now given a charge `-3Q`, the new potential difference between the same two shells is
View SolutionAt a certain distance from a point charge, the field intensity is `500 V/m` and the potential is `-3000 V`. The distance to the charge and the magnitude of the charge respectively are
View SolutionTwo points charges `q_1 and q_2` are placed at a distance of 50 m from each each other in air, and interact with a certain force. The same charges are now put in oil whose relative permittivity is 5. If the interacting force between them is still the same, their separation now is
View SolutionAn infinite line of charge `lamda` per unit length is placed along the y-axis. The work done in moving a charge q from `A(a,0)` to `B (2a,0)` is
View SolutionAn electric dipole is placed perpendicular to an infinite line of charge at same distance as shown in figure. Identify the correct statement.

View SolutionAn electrical charge `2xx10^-8` C is placed at the point `(1,2,4)` m. At the point `(4,2,0) `m, the electric
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be `(rgtR)`.

View SolutionThere is an electric field E in x-direction. If the work done on moving a charge of `0.2C` through a distance of 2 m along a line making an angle `60^@` with x-axis is 4 J, then what is the value of E?
View SolutionTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are `+Q` and `-Q`. The potential difference between the centre so the two rings is
View SolutionThe electric field at a distance 2 cm from the centre of a hollow sphereical coducting shell of radIus 4 cm having a charge of `2xx10^-3` C on its surface is
View SolutionCharge Q is given a displacement `r=ahati+bhatj` in electric field `E=E_1hati+E_2hatj`. The work done is
View SolutionA certain charge Q is divided into two parts q and `Q-q`, which are then separated by a certain distance. What must q be in terms of Q to maximum the electrostatic repulsion between the two charges?
View SolutionAn `alpha`- particle is the nucleus of a helium atom. It has a mas `m=6.64xx10^-27` kg and as charge `1=+2e=3.2xx10^-19`c. compare the force of the electric repulsion between two `alpha`-particles with the force of gravitational attraction between them.
View SolutionWhat is the charge per unit area in `C//m^2` of an infinite plane sheet of charge if the electric field produced by the sheet of charge has magnitude `3.0 N//C`?
View SolutionA circular wire loop of radius R carries a total charge q distributed uniformly over its length. A small length `x (ltlt R)` of the wire is cut off. Find the electric field at the centre due to the remaining wire.
View SolutionTwo identical conducting spheres, fixed in space, attract each other with an electrostatic force of `0.108 N` when separated by `50.0 cm`, centre-to-centre. A thin conducting wire then connects the spheres. When the wire is removed, the spheres repel each other with an electrostatic force of `0.0360 N`. What were the initial charges on the spheres?
View SolutionShow that the torque on an electric dipole placed in a uniform electric field is `tau=pxxE` independent of the origin about which torque is calculated.
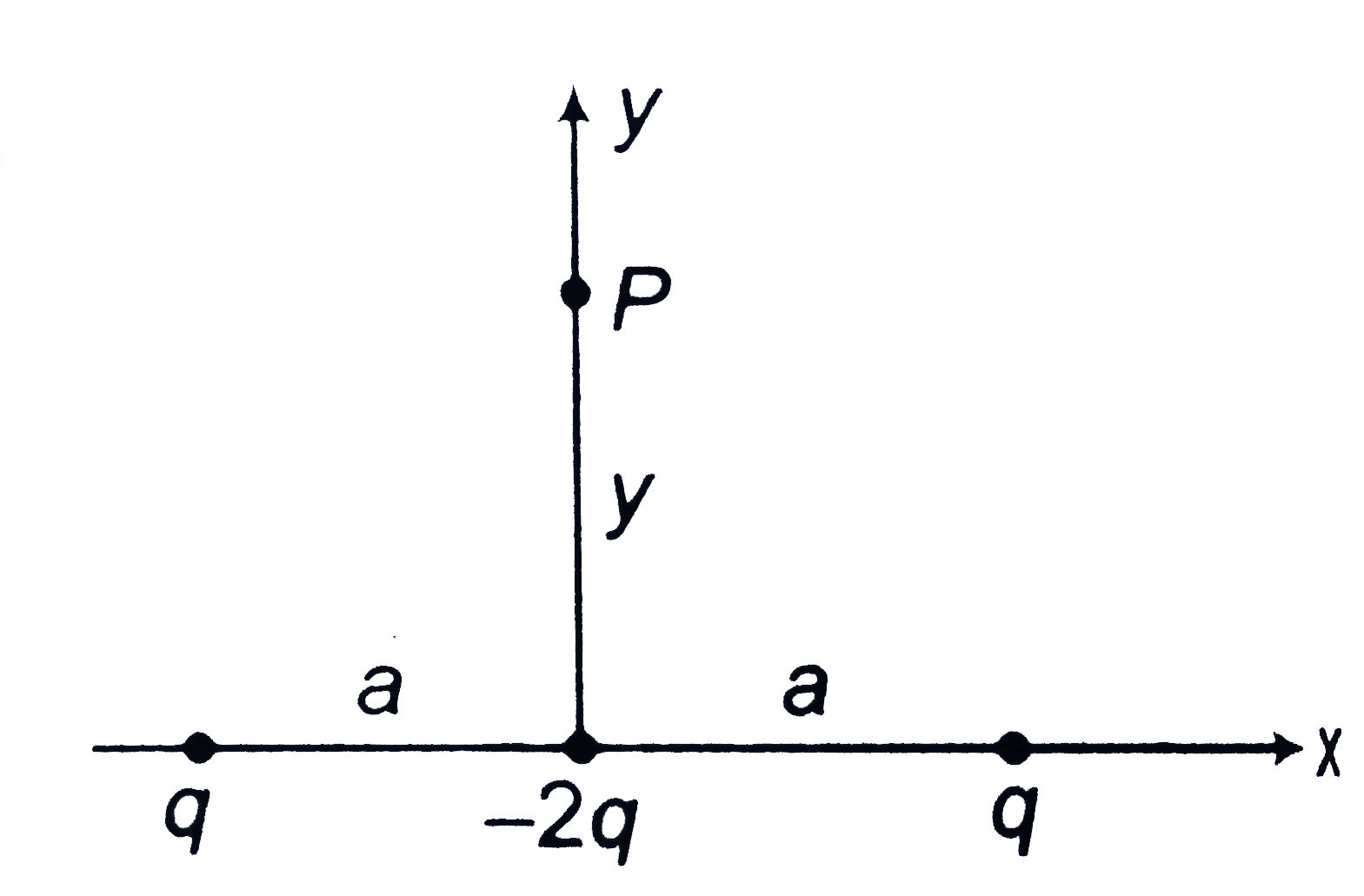
View SolutionThree point charges `q,-2q` and q are located along the x-axis a s shown in figure. Show that the electric field at `P (y gtgta)` along the y-axis is,
`E=-1/(4piepsilon_0) (3qa^2)/y^4 hatj`
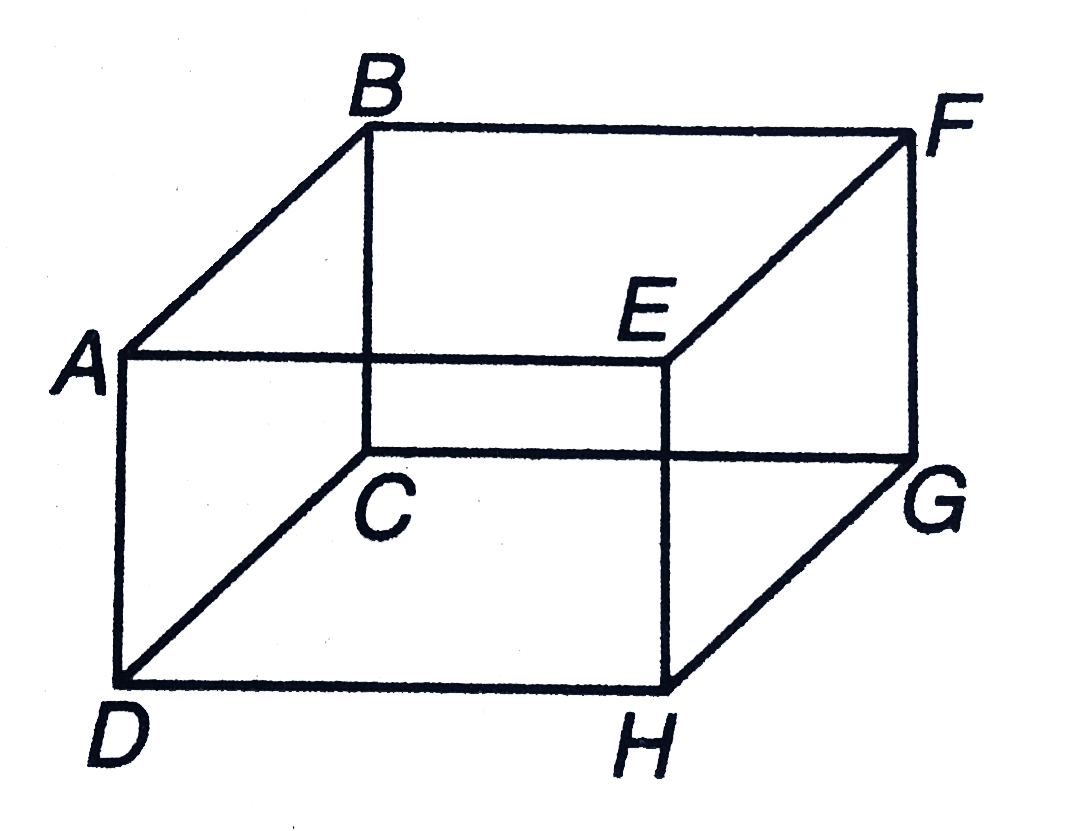
View SolutionA charge q is placed at point D of the cube. Find the electric flux passing through the `EFGH` and face `AEHD`.
View SolutionPoint charges `q_1` and `q_2` lie o the x-axis at points `x=-a` and `x=+a` respectively.
a. How must `q_1` and `q_2` be related for the net electrostatic force on point charge `+Q`, placed at `x=+a/2, ` to be zero?
b. With the same point charge `+Q` now placed ate `x=+3a//2`
View SolutionTwo particles (free to move) with charges `+q` and `+4q` are a distance L apart. A third charge is placed so that the entire system is in equilibrium.
(a) Find the location, magnitude and sign of the third charge.
(b) Show that the equilibrium is unstable.
View SolutionTwo identical beads each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, non-conducting walls, the beads move, and at equilibrium they area distance R apart (figure). Determine the charge on each bead.
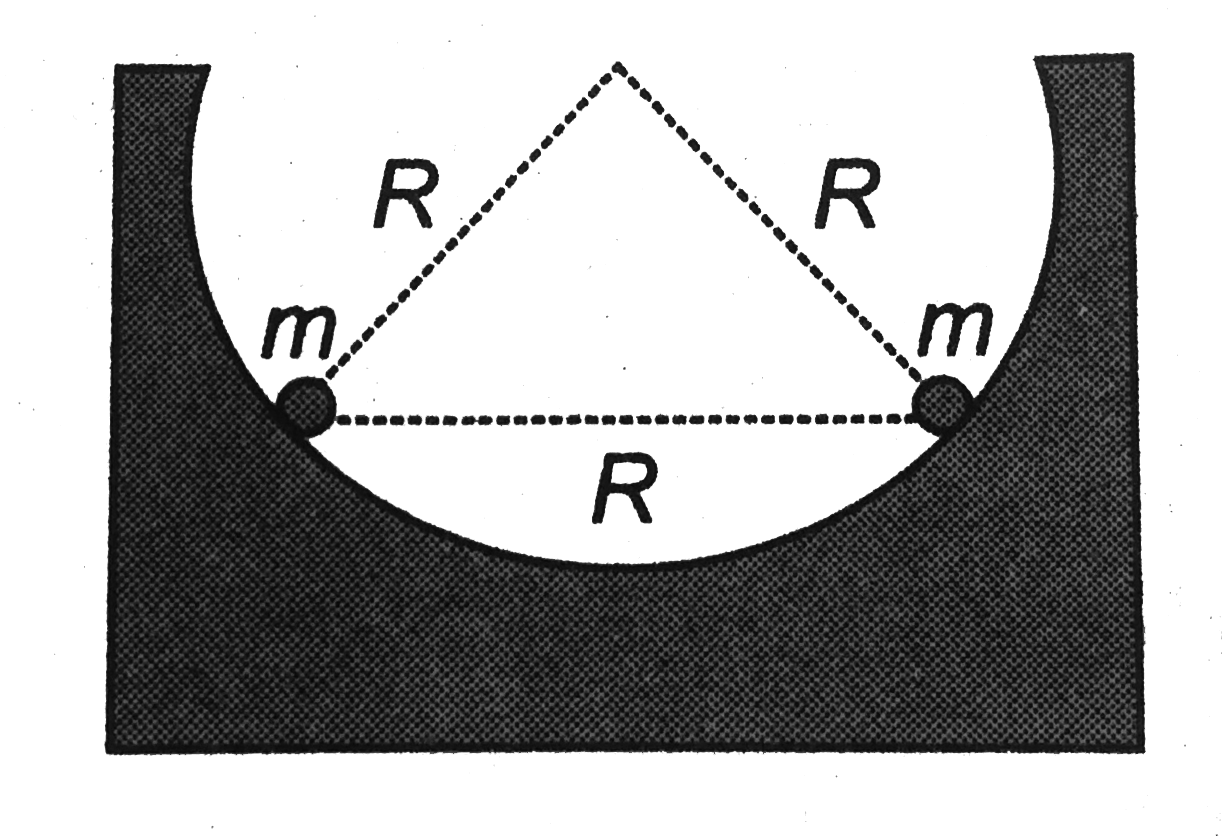
View SolutionThree identical small balls, each of mass 0.1 g, are suspended at one point on silk thread having a length of `l = 20cm` . What charges should be imparted to the balls for each thread to form an angle of `alpha = 30^@` with the vertical?
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionA point charge `q = - 8.0 nC` is located at the origin. Find the electric field vector at the point `x = 1.2 m, y = -1.6 m. `
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is `lamda`
View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionFind the direction of electric field at P for the charge distribution as shown infigure.
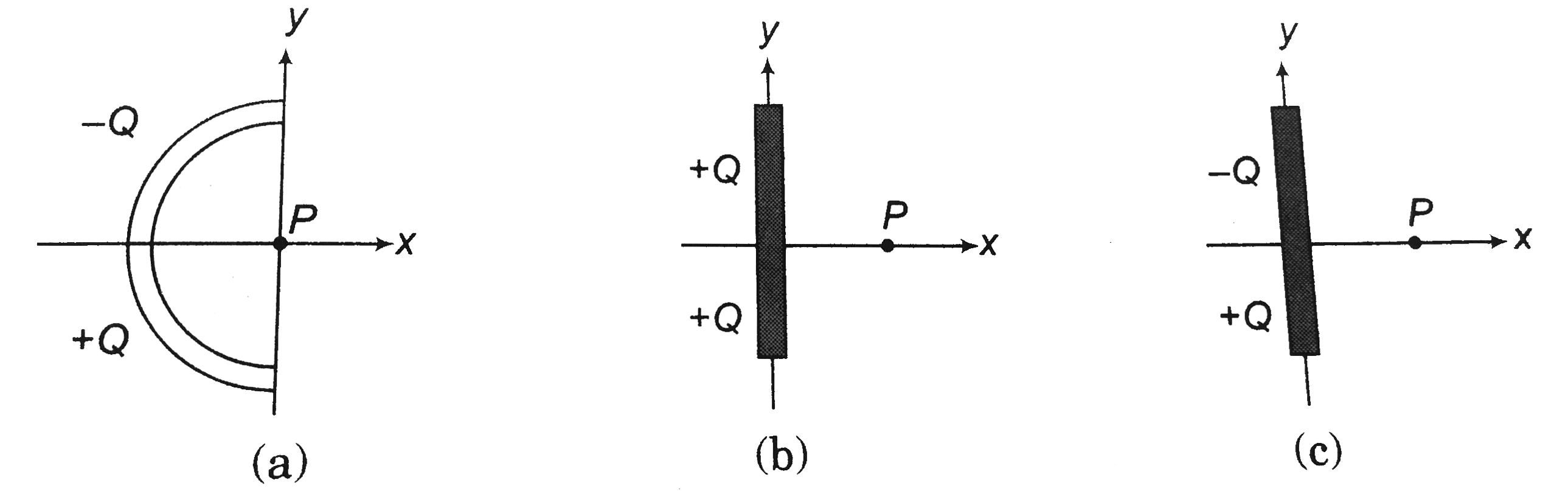
View SolutionA clock face has charges `-q, -2q, ,.....-12q` fixed at the position of the corresponding numerals on the dial. The clock hands do not disturb the net field due to point charges. At what time does the hour hand point in the direction of the electric field at the centre of the dial.
View SolutionA charged particle of mass `m = 1` kg and charge `q = 2muC` is thrown from a horizontal ground at an angle `theta = 45^@` with the speed `25 m//s`. In space, a horizontal electric field `E = 2 xx 10^7` V/m exists in the direction of motion. Find the range on horizontal ground of the projectile thrown. Take `g = 10 m//s^2`.
View SolutionProtons are projected with an initial speed `v_i = 9.55 xx 10^3 m//s` into a region where a uniform electric field `E = (-720hat j`) N/C is present, as shown in figure. The protons are to hit a target that lies at a horizontal distance of 1.27 mm from the point where the protons are launched. Find
(a) the two projection angles 0 that result in a hit and
(b) the total time of flight for each trajectory.

View SolutionAt some instant the velocity components of an electron moving between two charged parallel plates are `v_x=1.5xx10^5m//s` and `v_y=3.0xx10^6 m//s`.Suppose that the electric field between the plates is given by `E = (120 N//C) hatj`
. (a) What is the acceleration of the electron?
(b) What will be the velocity of the electron after its x-coordinate has changed by 2.0 cm?
View SolutionA point charge `q_1 = + 2muC` is placed at the origin of coordinates. A second charge, `q_2 = - 3muC`, is placed on the x-axis at `x = 100cm`. At what point (or points) on the x-axis will the absolute potential be zero?
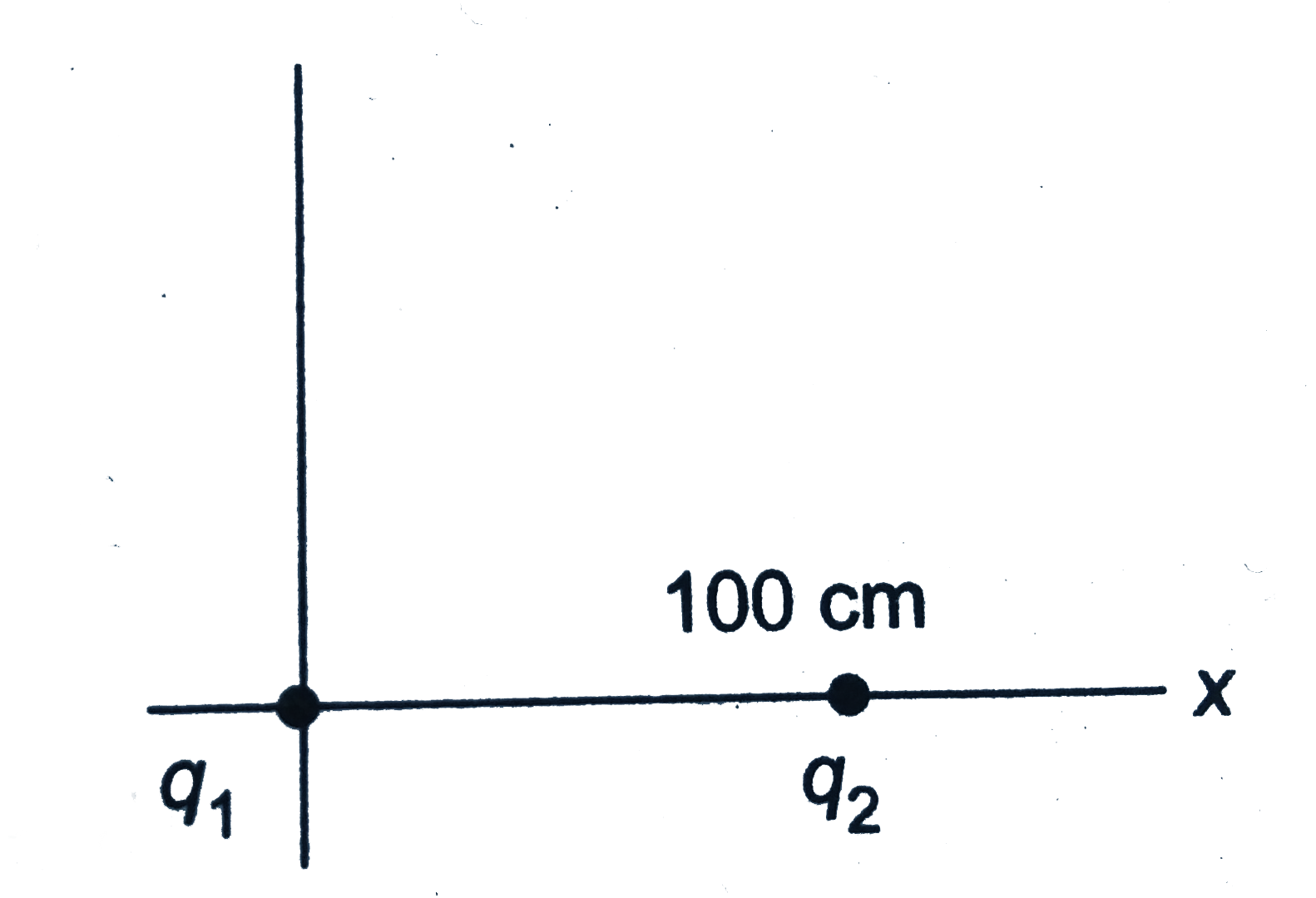
View SolutionA charge Q is spread uniformly in the form of a line charge density `lamda=Q/(3a)` on the sides of an 3a equilateral triangle of perimeter 3a. Calculate the potential at the centroid C of the triangle.
View SolutionA uniform electric field of magnitude `250 V// m` is directed in the positive x-direction. `A+12muC` charge moves from the origin to the point `(x, y) = (20.0 cm, 5.0 cm).`
(a) What was the change in the potential energy of this charge?
(b) Through what potential difference did the charge move?
View SolutionA small particle has charge `-5.00muC` and mass `2.00 xx 10-4` kg. It moves from point A where the electric potential is `V_A = +200 V`. to point B, where the electric potential is `V_B=+ 800 V`. The electric force is the only force acting on the particle. The particle has speed `5.00 m/s` at point A. What is its speed at point B? is it moving faster or slower at B than at A. Explain,
View SolutionA plastic rod has been formed into a circle of radius R. It has a positive charge `+Q` uniformly distributed along one-quarter of its circumference and a negative charge of ` -6Q` uniformly distributed along the rest of the circumference (figure). With V = 0 at infinity, what is the electric potential `-6Q`
(a) at the centre C of the circle and
(b) at point P, which is on the central axis of the circle at distance z from the centre?
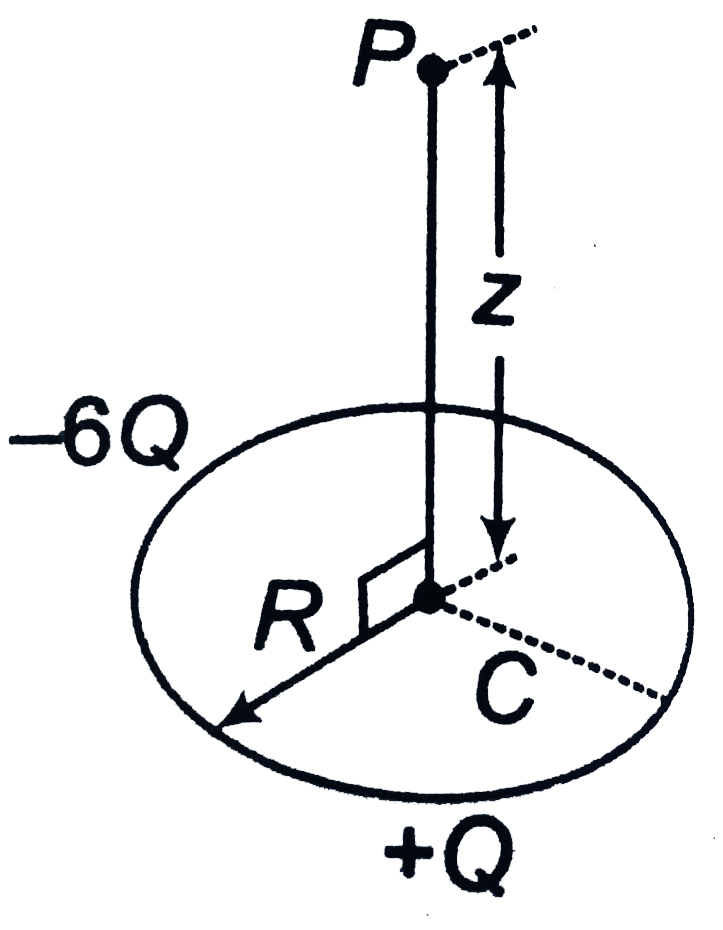
View SolutionA point charge `q_1=+2.40muC` is held stationary at the origin. A second point charge `q_2=-4.30muC` moves from the point x=0.150 m, y=0 to the point x=0.250 m, y=0.250 m. How much work is done by the electric force on `q_2`?
View SolutionA point charge `q_1 = 4.00 nC` is placed at the origin, and a second point charge `q_2 = -3.00 nC`, placed on the x-axis at x = + 20.0 cm. A third point charge `q_3 = 2.00 nC` is placed on the X-axis between `q_1, and q_2`. (Take as zero the potential energy of the three charges when they are infinitely far apart).
(a) What is the potential energy of the system of the three charges if `q_3` is placed at x= + 10.0 cm?
(b) Where should `q_3` be placed to make the potential energy of the system equal to zero?
View SolutionThree point charges, which initially are infinitely far apart, are placed at the corners of an equilateral triangle with sides d. Two of the point charges are identical and have charge q.If zero net work is required to place the three charges at the corners of the triangles, what must the value of the third charge be?
View SolutionThe electric field in a certain region is given by `E=(5hati-3hatj)kV//m`. Find the difference in potential `V_B-V_A`. If A is at the origin and point B is at a. (0,0,5)m, b. (4,0,3) m.`
View SolutionIn a certain region of space, the electric field is along `+y`-direction and has a magnitude of 400 V/m . What is the potential difference from the coordinate origin to the following points?
`a. x=0,y=20cm, z=0`
b. `x=0, y=-30cm, z=0`
`c. x=0, y=0, z=15cm`
View SolutionAn electric field of `20 N//C` exists along the x-axis in space. Calculate the potential difference `V_B - V_A` where the points A and B are given by
a. `A=(0,0), B=(4m, 2m)`
b. `A=(4m,2m),B=(6m,5m)`
View SolutionThe electric potential existing in space is `V(x,y,z)=A(xy+yz+zx)`
(a) Write the dimensional formula of A.
(b) Find the expression for the electric field.
(c) If A is 10 SI units, find the magnitude of the electric field at `(1 m, 1 m, 1 m)`
View SolutionAn electric field `E = (20hati + 30 hatj)` N/C exists in the space. If the potential at the origin is taken be zero, find the potential at `(2 m, 2 m)`.
View SolutionIn a certain region of space, the electric potential is `V (x, y, z) = Axy - Bx^2 + Cy`, where A, B and C are positive constants.
(a) Calculate the x, y and z- components of the electric field.
(b) At which points is the electric field equal to zero?
View SolutionA sphere centered at the origin has radius `0.200 m. A-500muC` point charge is on the x-axis at `x = 0.300 m`. The net flux through the sphere is `360 N-m^2//C`. What is the total charge inside the sphere?
View SolutionA closed surface encloses a net charge of `-3.60 muC`. What is the net electric flux through the surface?
(b) The electric flux through a closed surface is found to be `780 N-m^2//C`. What quantity of charge is enclosed by the surface?
(c) The closed surface in part (b) is a cube with sides of length 2.50 cm. From the information given in part (b), is it possible to tell where within the cube the charge is located? Explain.
View SolutionThe electric field in a region is given by `E = 3/5 E_0hati +4/5E_0j` with `E_0 = 2.0 × 10^3 N//C`. Find the flux of this field through a rectangular surface of area `0.2 m^2` parallel to the y-z plane.
View SolutionThe electric field in a region is given by `E = (E_0x)/lhati`. Find the charge contained inside a cubical 1 volume bounded by the surfaces `x=0, x=a, y=0, yh=, z=0` and z=a. Take `E_0=5xx10^3N//C` l=2cm and a=1m.
View SolutionA point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then `R=sqrt3b`.
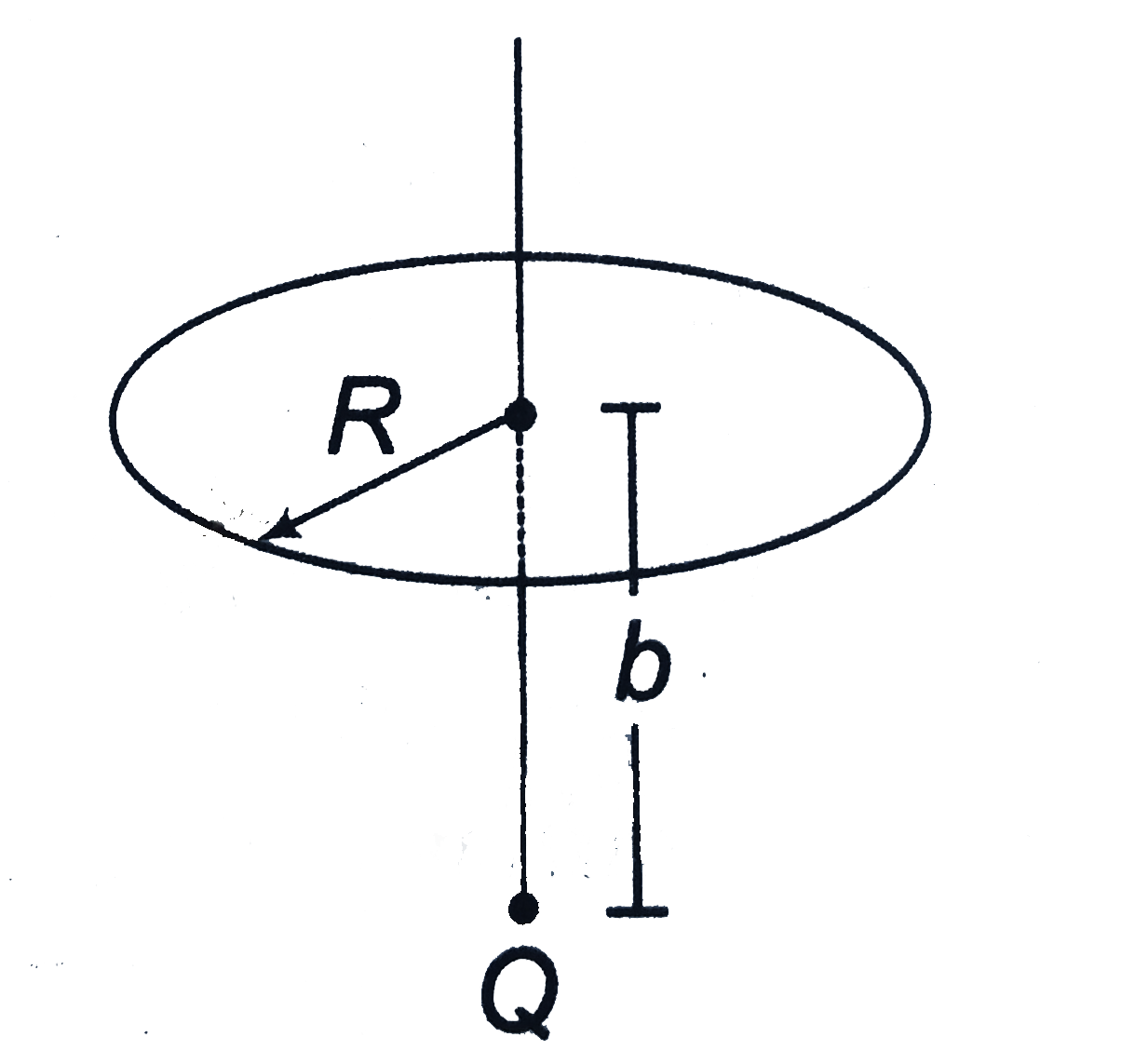
View SolutionA cube has sides of length L. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by `E = - B hati + Chatj - Dhatk`, where B, C and D are positive constants.
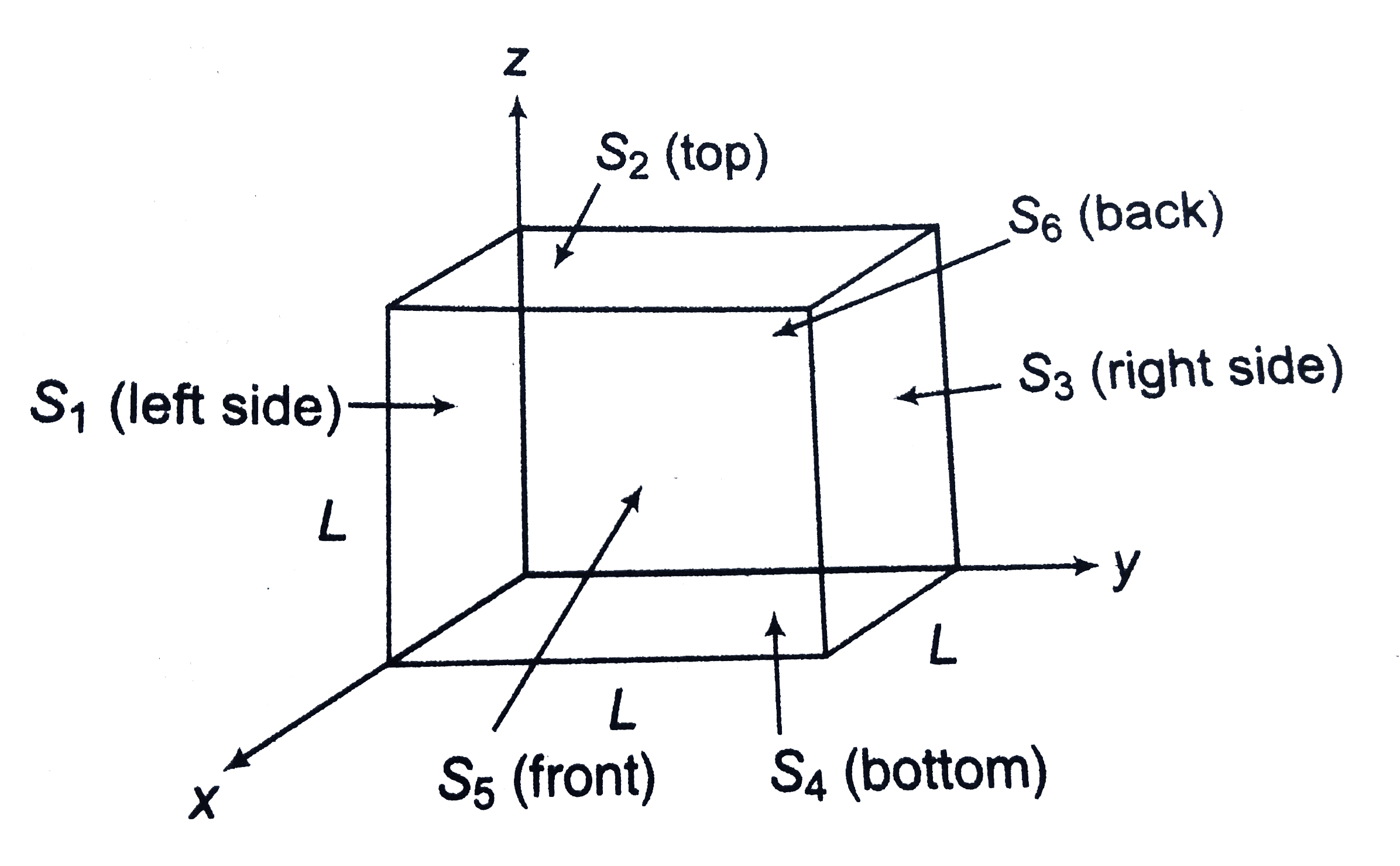
(a) Find the electric flux through each of the six cube faces `S_1, S_2, S_3 , S_4 and S_5 and S_6`.
(b) Find the electric flux through the entire cube.
View SolutionTwo point charges `q` and `-q` are separated by a distance `2l`. Find the flux strength vector across the circle of radius R placed with its centre coinciding with the of line joining the two charges in the perpendicular plane.
View SolutionA point charge q is placed at the origin. Calculate the electric flux through the open hemispherical surface `(x-a)^2+y^2+z^2=a^2,xgea`
View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and `R (gt r)` such that the surface charge densities are equal. Find the potential at the common centre.
View SolutionA charge `q_0` is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View Solution
Level 1 Objective questions and complete solutions for chapter ELECTROSTATICS of DC PANDEY ENGLISH of Class 12
All Exercises from DC PANDEY Class 12 PHYSICS ELECTROSTATICS
- Assertion and Reason
- Check point 1.1
- Check point 1.2
- Check point 1.3
- Check point 1.4
- Check point 1.5
- Example
- Example Type 5
- Example Type 6
- Example Type 8
- Exercise 24.1
- Exercise 24.2
- Exercise 24.3
- Exercise 24.4
- Exercise 24.5
- Exercise 24.6
- Exercise 24.7
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Single Correct
- Match the columns
- Medical entrances gallery
- SUBJECTIVE_TYPE
- Taking it together