Complete Solutions to Level 2 Single Correct of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| DC PANDEY | Level 2 Single Correct |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
The nuclear charge (`Ze`) is non uniformlly distribute with in a nucleus of radius `r`. The charge density `rho(r)` (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
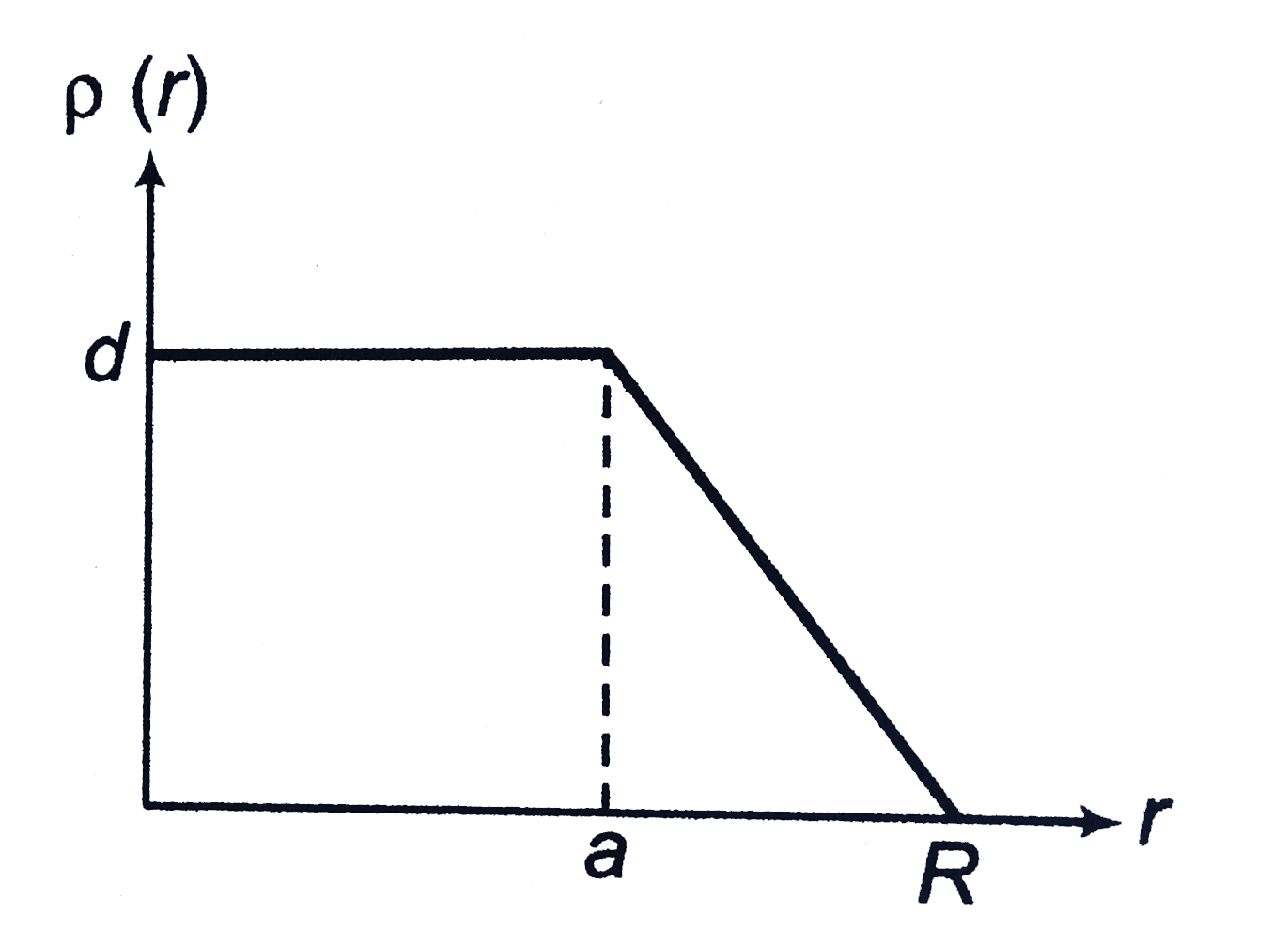
For a=0 the value of d (maximum value of `rho` as shown in the figure) is
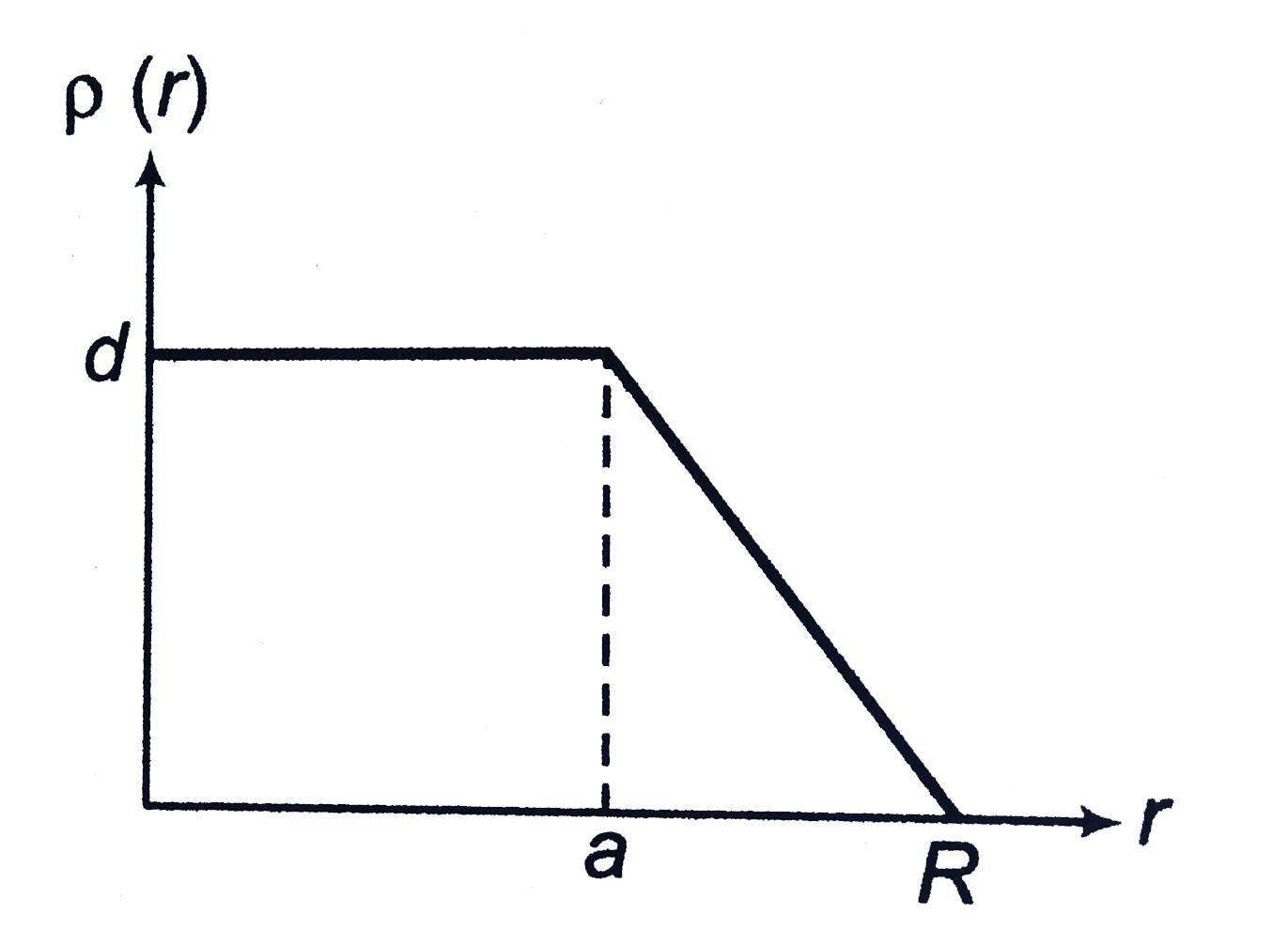
View SolutionThe nuclear charge (`Ze`) is non uniformlly distribute with in a nucleus of radius r. The charge densilty `rho(r)` (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
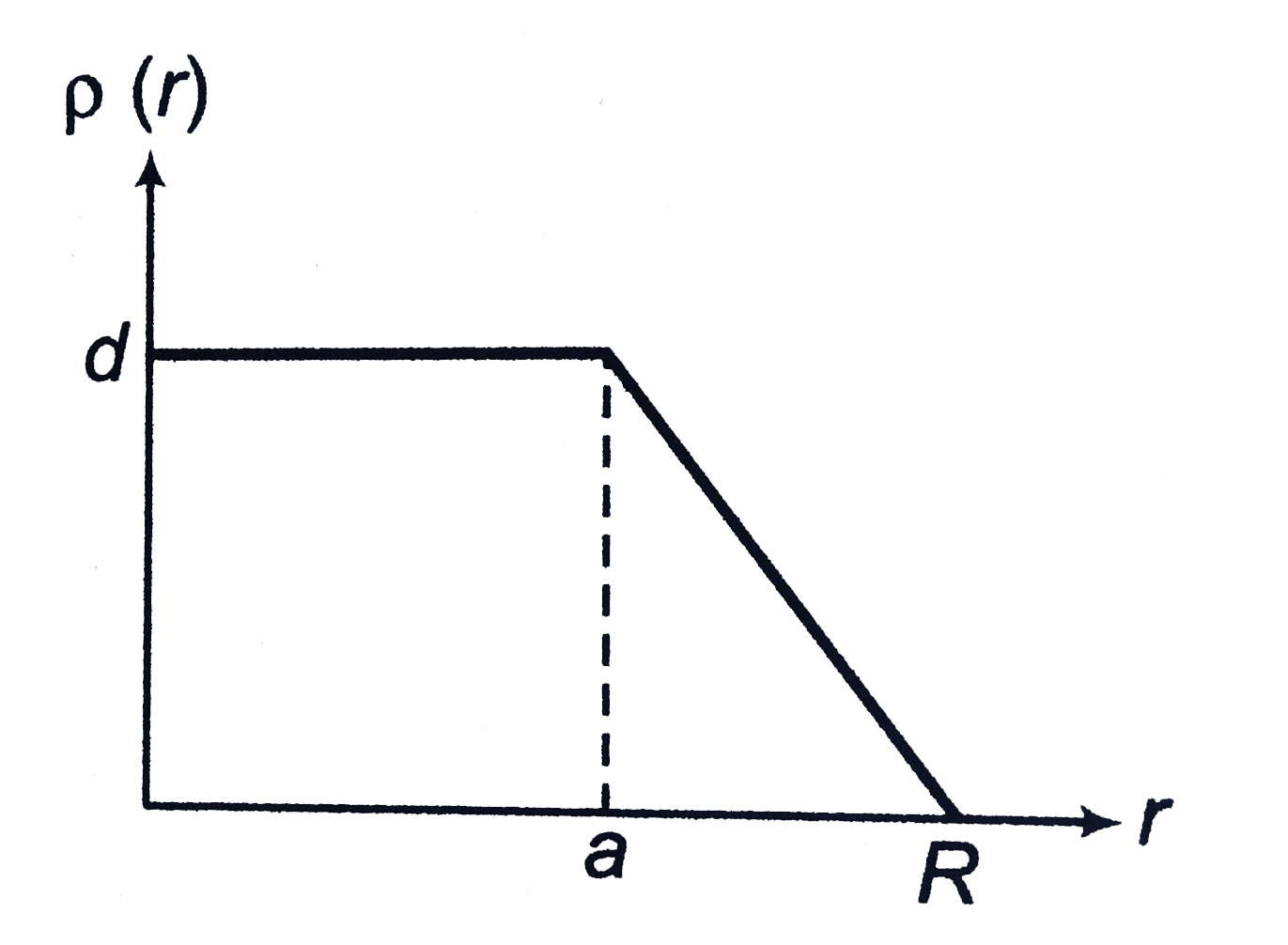
The electric field within the nucleus is generaly observed to be linearly dependent on r. This implies
View SolutionThe electric field in a region is given by `E=ahati+bhatj`. Hence as and b are constants. Find the net flux passing through a square area of side `I` parallel to y-z plane.
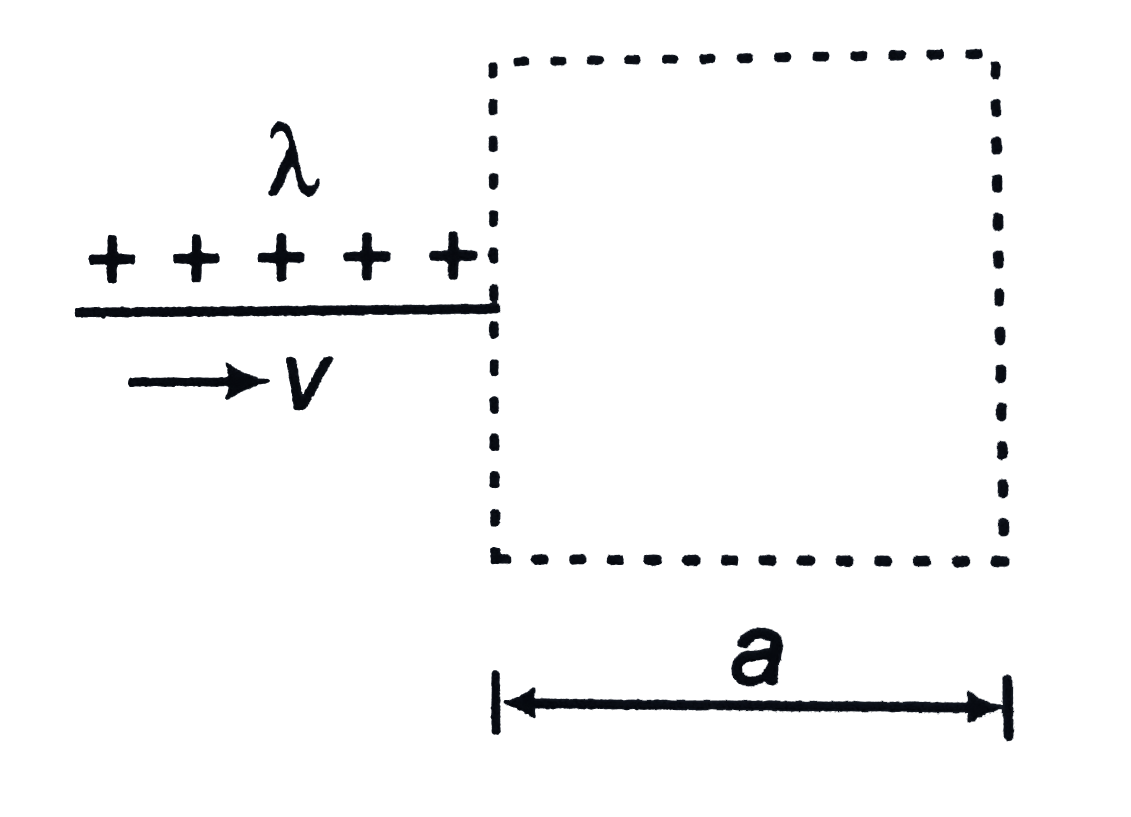
View SolutionFigure shows an imaginary cube of side a. A uniformly charged rod of length a moves towards right at a constant speed v. At `t=0` the right end of the just touches the left face of the cube. Plot a graph between electric flux passing through the cube versus time.
View SolutionThe electric field in a region is given by `E=alphaxhati`. Here `alpha` is a constant of proper dimensions. Find
a. the total flux passing throug a cube bounded by the surface `x=l, x=2l, y=0, y=l, z=0, z=l`.
b. the charge contained inside in above cube.
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
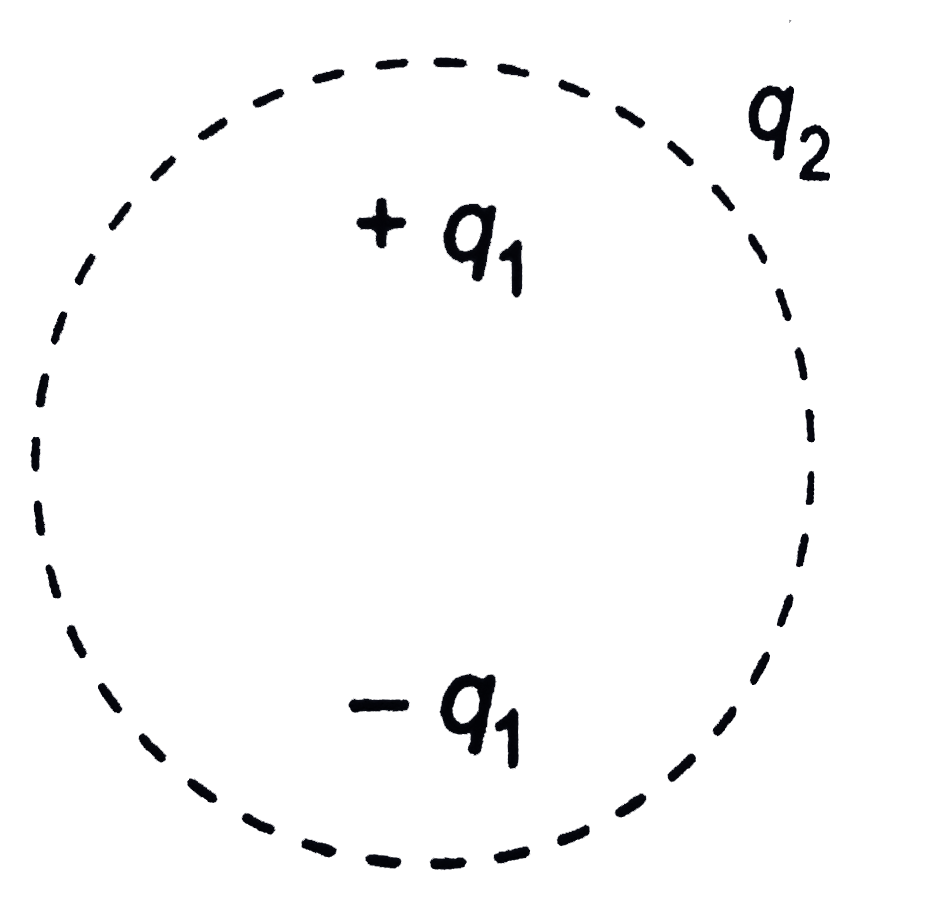
View SolutionA point charge q is placed on the top of a cone of semi vertex angle `theta`. Show that the electric flux through the base of cone is `(q(1-costheta))/(2epsilon_0)`
View SolutionDraw `E-r` and `V-r` graphs due to two point charges `+ q` and `-2q` kept at some along the line joining these two charges.
View SolutionDraw E-r and V-r graphs due to two charged spherical shells as shown in figure (along the line between `C` and `prop`)

View SolutionAn electron with a speed `5.00xx10^6` m/s enters an electric field of magnitude `10^3` N/C, travelling along the field lies in the direction that retards its motion.
a. How far will the electron travel in the field before stopping momentarily?
b. How much time will have elapsed?
c. If the regin with the electric field is only 8.00 mm long (too short from the electronn to stop with in it), what fraction of the elctron's initial kinetic energy wil be lost in that region.
View SolutionA charged particle of mass `m=1` kg and charge `q=2muC` is thrown for a horizotal ground at an angle `theta=45^@` with speed `20 m//s`. In space a horizontal electric field `E=2xx10^(7)` V/m exist. Find the range on horizontal ground of the projectile thrown.
View SolutionFind the potential difference `V_(AB)` between `A(2m, 1m, 0)` and `B(0, 2m, 4m)` in an electric field,
`E=(xhati-2yhatj+zhatk)V/m`
View SolutionFind potential difference `V_(AB)` between `A(0,0,0) and `B(1m,1m,1m) in an electric field a. `E-yhati+xhatj` b. `E=3x^2yhati+x^3hatj`
View SolutionAn electric dipole of dipole moment p is placed in a uniform electric field E in stable equilibrium position. Its moment of inertia about the centroidal axis is I . If it is displaced slightly from its mean position, find the period of small oscillations.
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If `Q_1` coulomb, and `Q_2` coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionFive point charges, each of value +q coul, are placed on five vertices of a regular hexagon of isde L meters. The magnitude of the force on the point charge of value -q coul, placed at the centre of the hexagen is…………….
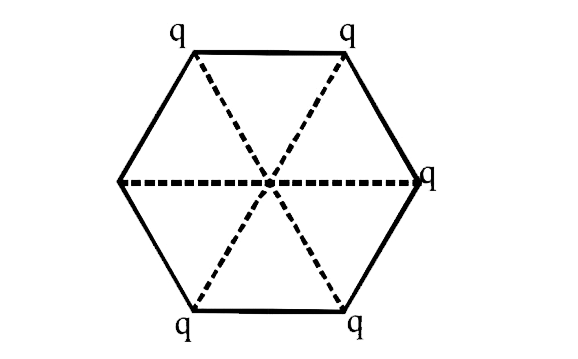
View SolutionA point charge `q_1=9.1muC` is held fixed at origin. A second point charge `q_2=-0.42muC` and `a` mass `3.2xx10^-4kg` is placed on the x-axis, `0.96m` from the origin. The second point charge is released at rest. What is its speed when it is `0.24m` from the origin?
View SolutionA point charge `q_1 =-5.8muC` is held stationary at the origin. A second point charge `q_2=+4.3muC` moves from the point `(0.26m 0,0)` to `(0.38m, 0, 0)`. How much work is done by the electric force on `q_2`?
View SolutionA uniformly charged thin ring has radius `10.0 cm` and total charge `+12.0muC`. An electron is placed on the ring's axis a distance `25.0 cm` from the centre of the ring and is constrained to stay on the axis of the ring. The electron is then released from rest.
a. describe the subsequent motion of the electron
b. find the speed of the electron when it reaches the centre of the ring
View SolutionTwo points A and B are 2 cm apart and a uniform electric field E acts along the straight line `AB` directed A to B with `E=200N//C`. A particle of charge `+10^-6C` is taken from A to B along AB, Calculate
a. the force on the charge
b. the potential difference `V_A -V_B` and
c.the work done on the charge by E
View SolutionAn alpha particle with kinetic energy `10 Me V` is heading toward a stationary tin nuclcus of atomic number 50. Calculate the distance of closest approach (Fig . 3.23).
 .
.
View SolutionThree point charges `1C, 2C` and `3C` are placed at the corners of an equilaternal triangle of side `1m`. The work required to move these charges to the corners of a smaller equilaternal triangle of side `0.5 m` in two differenct ways as in fig. `(A)` and fig. `(B)` are `W_(a)` and `W_(b)` then:
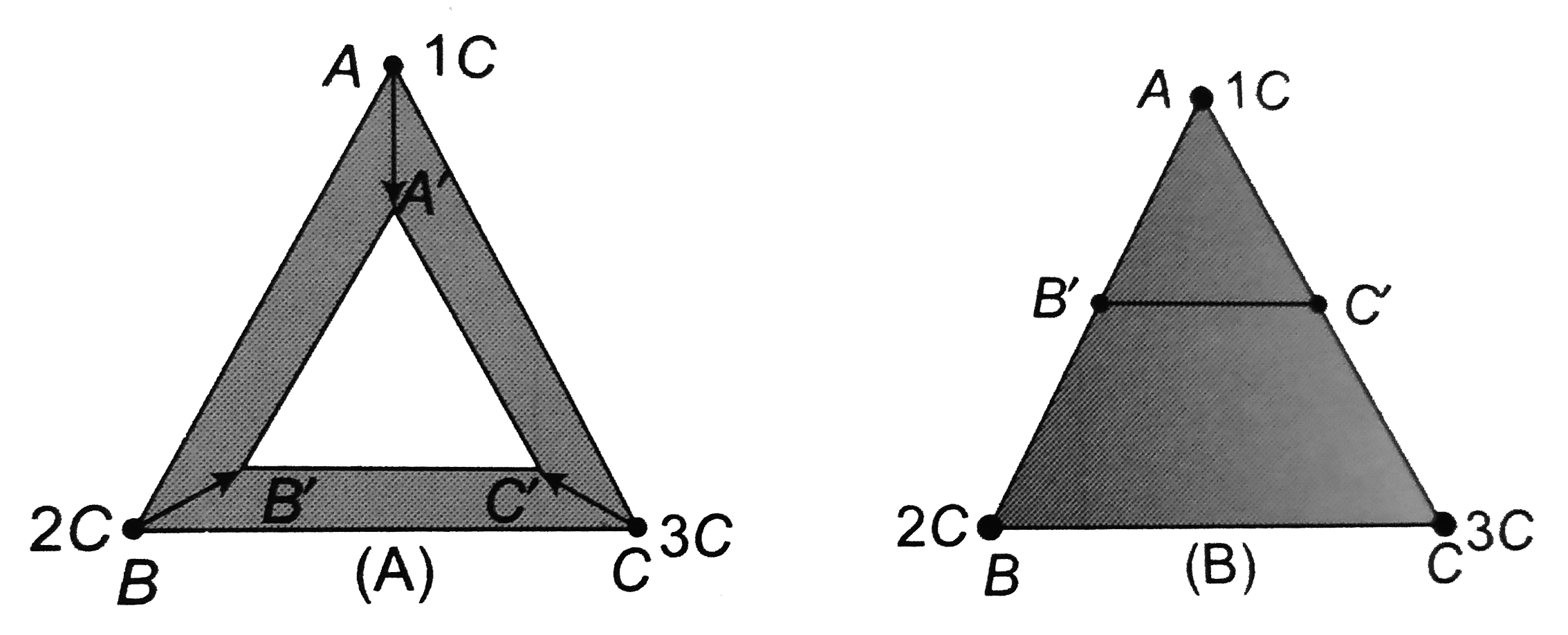
View SolutionConsider a spherical surface of radius 4 m cenred at the origin. Point charges +q and - 2q are fixed at points A( 2 m, 0,0) and B( 8 m, 0, 0), respectively. Show that every point on the shperical surface is at zero potential.
View SolutionThe intensity of an electric field depends only on the coordinates x and y as follows,
`E = (a(xhati +y hatj))/(x^(2)+y^(2))` where, a is constant and `hati` and `hatj` are the unit vectors of the x and y axes. Find the charges within a sphere of radius R with the centre at the origin.
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density `sigma` (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionA nonconducting disk of radius a and uniform positive surface charge density `sigma` is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disk, from a height H with zero initial velocity. The particle has `q//m = 4 epsilon_(0) g// sigma`.
(i) Find the value of H if the particle just reaches the disk.
(ii) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
View SolutionFour point charges `+8muC,-1muC,-1muC` and , `+8muC` are fixed at the points `-sqrt(27//2)m,-sqrt(3//2)m,+sqrt(3//2)m`
and `+sqrt(27//2)m` respectively on the y-axis. A particle of mass `6xx10^(-4)kg` and `+0.1muC` moves along the x-direction. Its speed at `x=+ infty` is `v_(0)`. find the least value of `v_(0)` for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.
View SolutionPotential difference beween centre and surface of the sphere of radius R and uniorm volume charge density `rho` within it will be
View SolutionA positively charged disc is placed on a horizontal plane. A charged particle is released from a certain height on its axis. The particle just reaches the centre of the disc. Select the correct alternative.
View SolutionThe curve represents the distribution of potential along the staight line joining the two charges `Q_1 and Q_2` (separated by a distance r) then which of the following statements are correct?
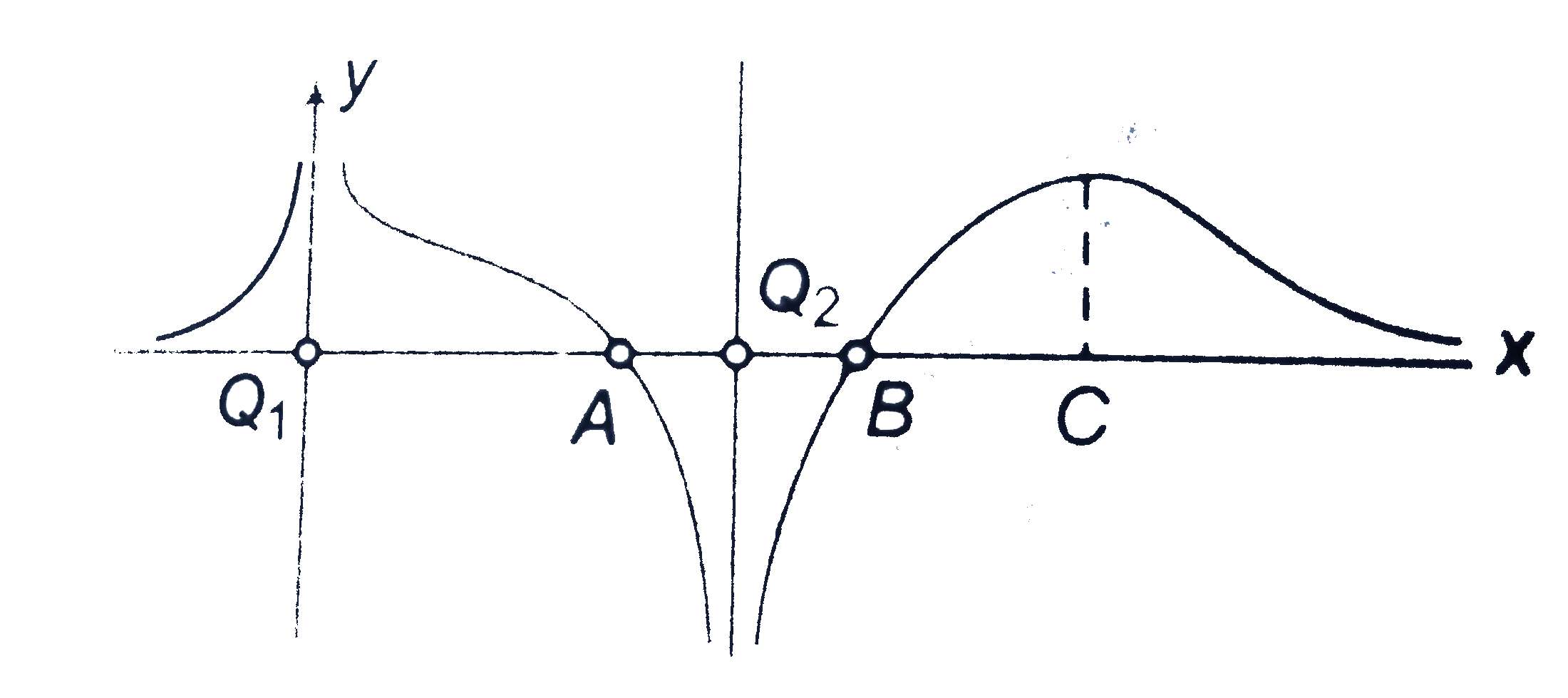
1. `|Q_1|gt|Q_2|`
2. `Q_1` is positive in nature
3. A and B are equilibrium points
4. C is a point of unstabkle equilibrium
View SolutionA point charge `q_1=q` is placed at point P. Another point charge `q_2=-q` is placed at point Q. At some point `R(R!=P, R!=Q)`, electric potential due to `q-1 is V_1` and electric potential due to `q_2` is `V_2`. Which of the following is correct
View SolutionThe variation of electric field between two charge `q_1` and `q_2` along the line joining the charges is plotted against distance from `q_1` (taking rightward direction of electric field as positive) as shown in the figure. Then the correct statement is
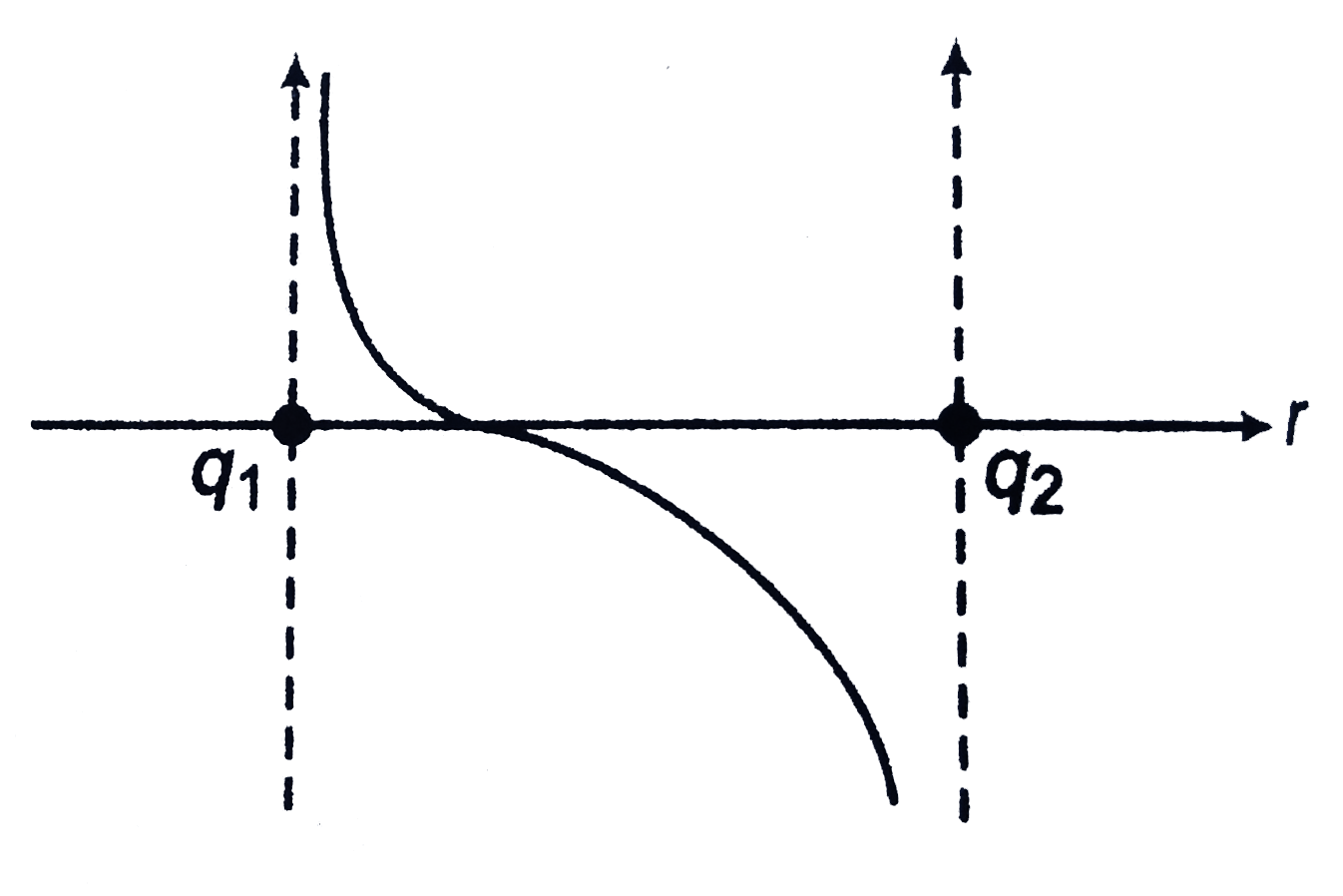
View SolutionA charge q is placed at O in the cavity in a sphereical uncharged conductor. Points S is outside the conductor. If q is displaced from O towards S (still remaining within the cavity)

View SolutionA uniform electric field of `400 V/m` is directed at `45^@` above the x-axis as shown in the figure. The potential difference `V_A-V_B` is given by
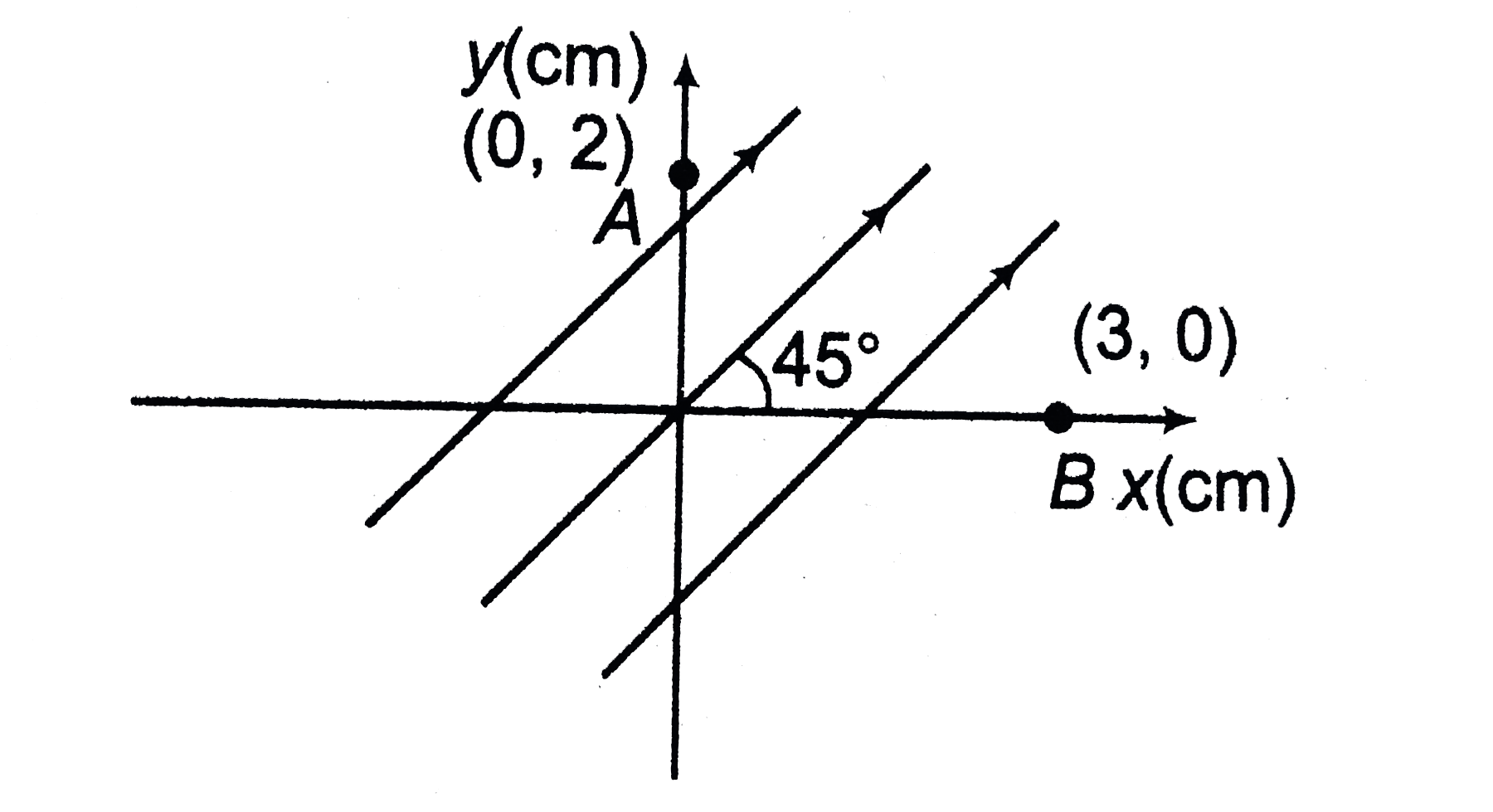
View SolutionInitially the spheres A and B are at potentials `V_A` and `V_B`. Find the potential of A when sphere B is earthed.
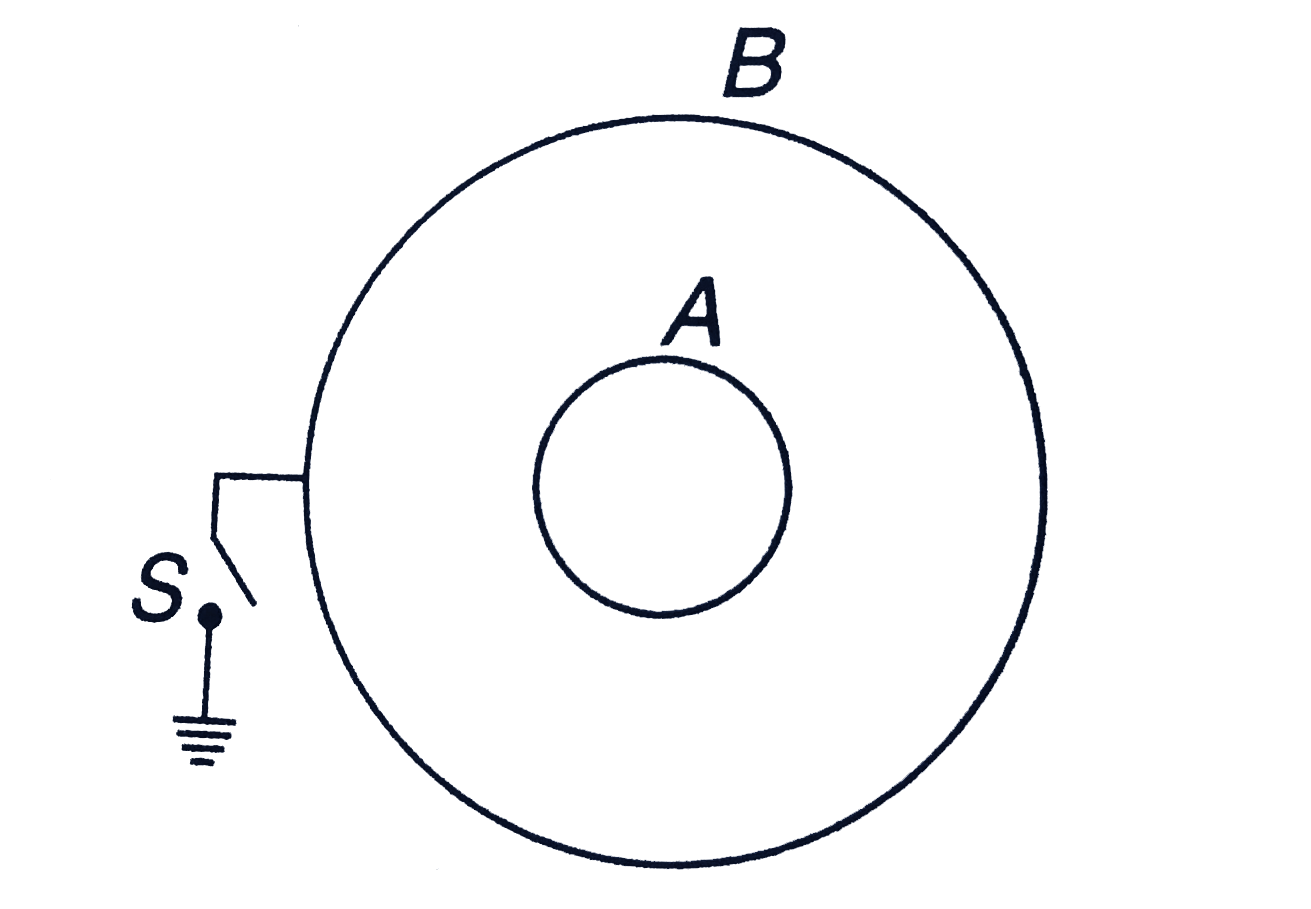
View SolutionA particle of mass `m` and charge `q` is fastened to one end of a string fixed at point O. The whole system lies on a frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown is then switched on. Then

View SolutionA charged particle of mass m and charge q is released from rest the position `(x_0,0)` in a uniform electric field `E_0hatj`. The angular momentum of the particle about origin.
View SolutionA charge `+Q` is uniformly distributed in a spherical volume of radius R. A particle of charge `+q` and mass m projected with velocity `v_0` the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of `v_0` such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is
View SolutionTwo identical coaxial rings each of radius R are separated by a distance of `sqrt3R`. They are uniformly charged with charges `+Q` and `-Q` respectively. The minimum kinetic energy with which a charged particle (charge `+q`) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
View SolutionA uniform electric fied exists in x-y plane. The potential of ponts `A(2m,2m),B(-2m,2m)` and `C(2m,3m)` are `4V, 16V` and `12V` respectively. The electric field is
View SolutionTwo fixed charges `-2Q` and `+Q` are located at points `(-3a,0)` and `(+3a,0)` respectively. Then which of the following statement is correct?
View SolutionA particle of mass m and charge `-q` is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity
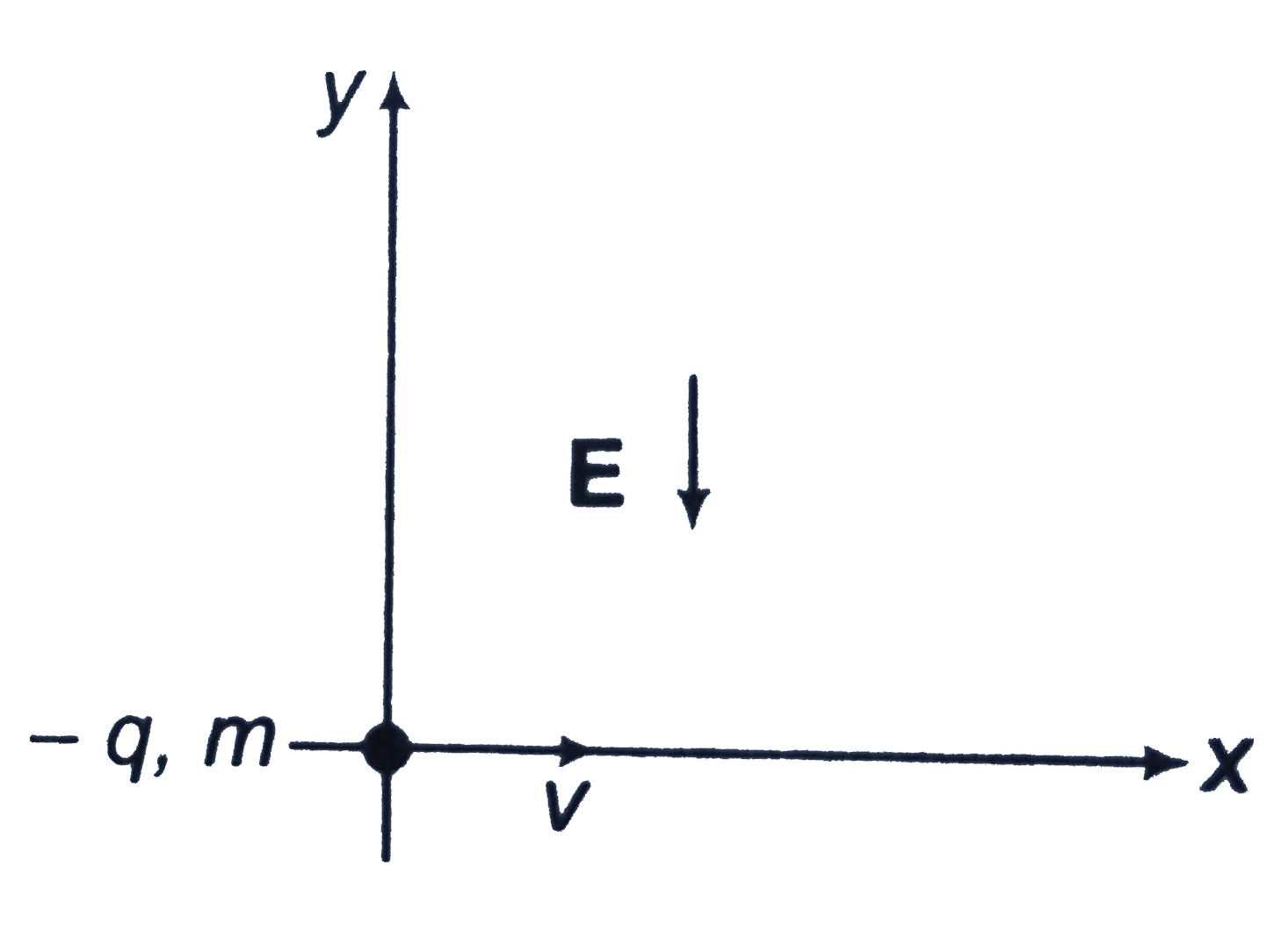
View SolutionA particle of charge `-q` and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density `+lamda`. Then, time period will be
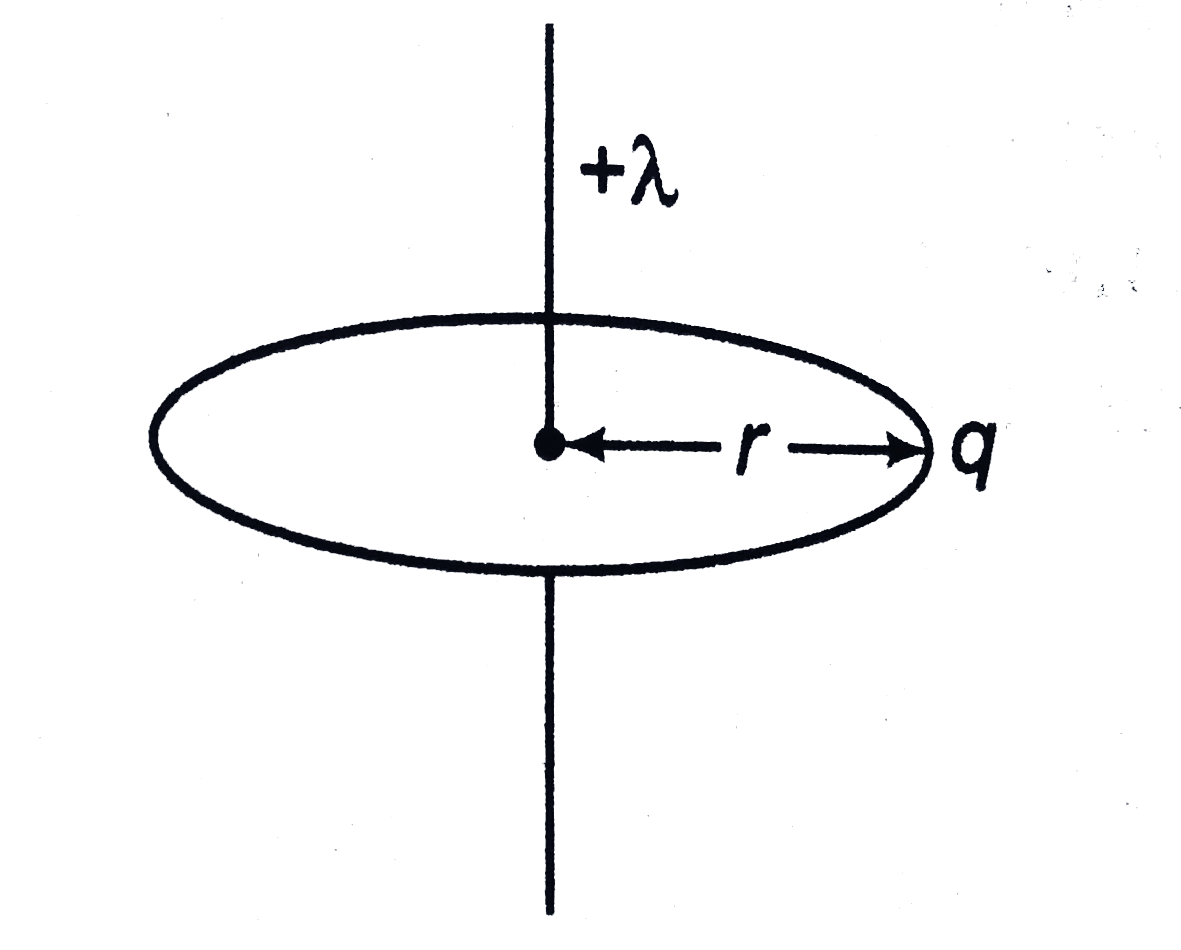 where , `k=1/4piepsilon_0)`
where , `k=1/4piepsilon_0)`
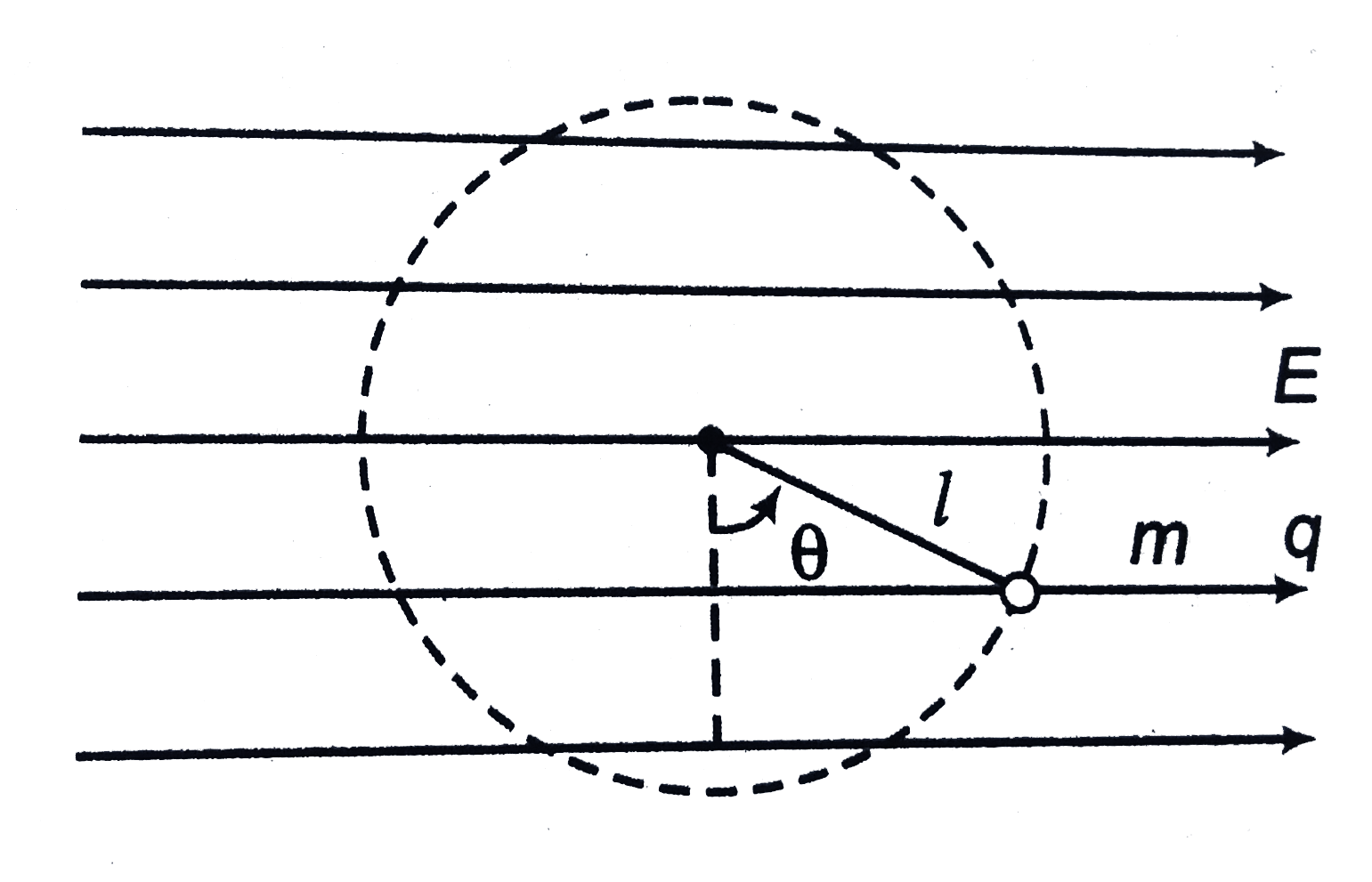
View SolutionA small ball of masss m and charge +q tied with a string of length l, rotating in a veticle circle under gravity and a uniform horizontal electric field E as shown. The tension in the string will be minimum for
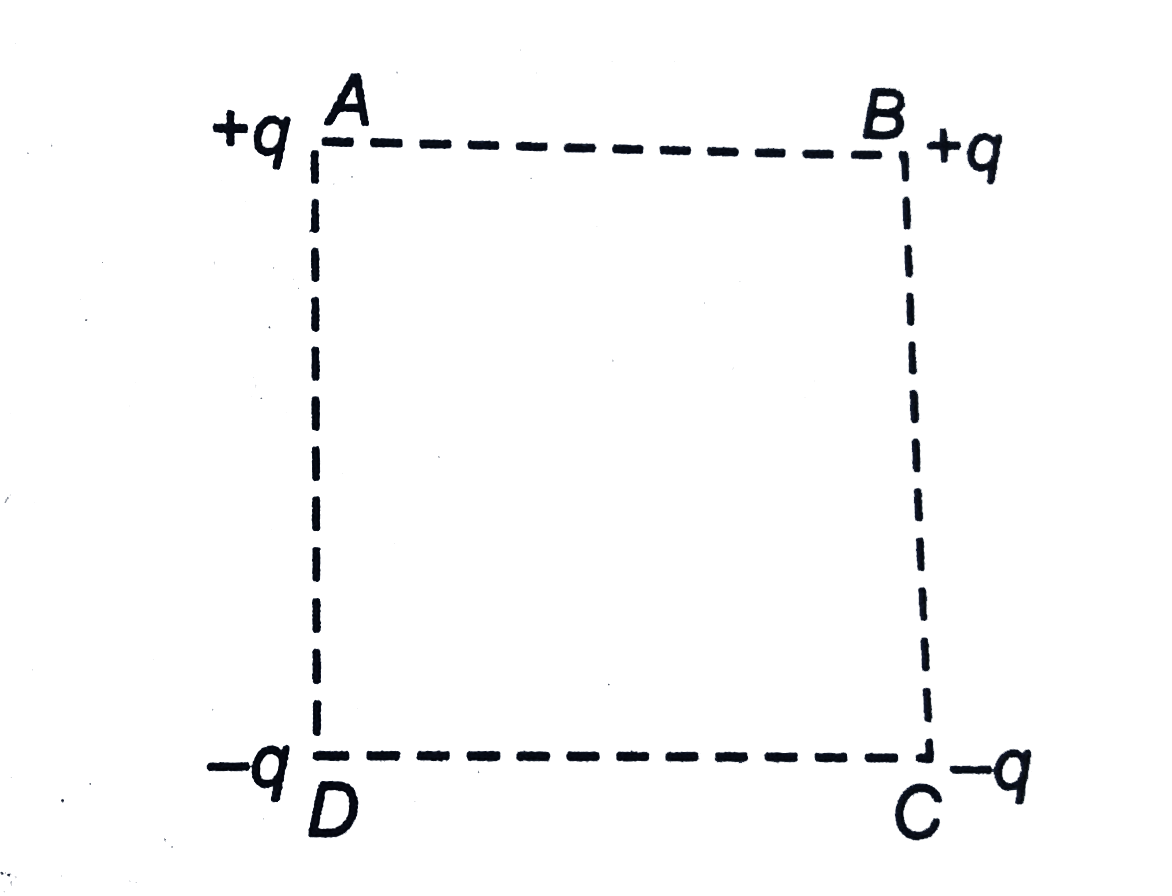
View SolutionFor charges A,B,C and D are plasced at the four corners of a squre of a side a. The energy required to take the charges C and D to infinity (they are also infinitely separated from each other )is
View SolutionTwo identical positive charges are placed at `x=-a` and `x=a`. The correct variation of potential V along the x-axis is given by
View SolutionTwo identical charges are placed at the two corners of an equilateral triangle. The potential energy of the system is U. The work done in bringing an identical charge from infinity to the third vertex is
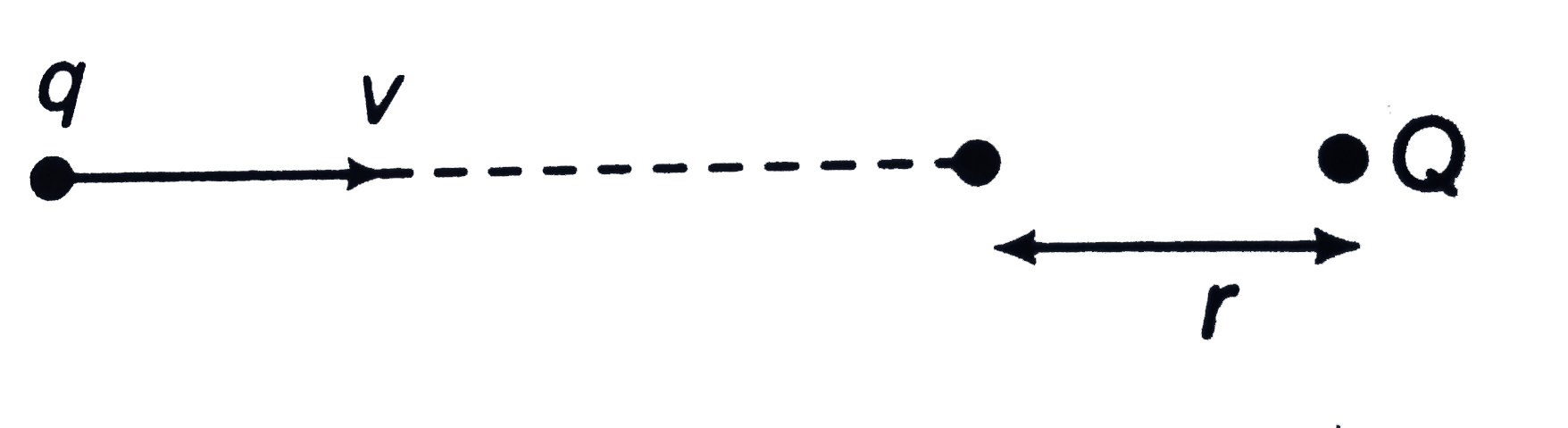
View SolutionA charged particle q is shot from a large distance towards another charged particle Q which is fixed, with speed v. It approaches Q up to as closed distance r and then returns. If q were given a speed 2v, the distasnce of approach would be
View SolutionTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of `30^@` with each other. When suspended in a liquid of density `0.8gcm^-3`, the angle remains the same. If density of the material of the sphere is `1.6gcm^-3`, the dielectric constant of the liquid is
View SolutionThe electrostatic potential due to the charge configuration at point P as shown in figure for b << a is
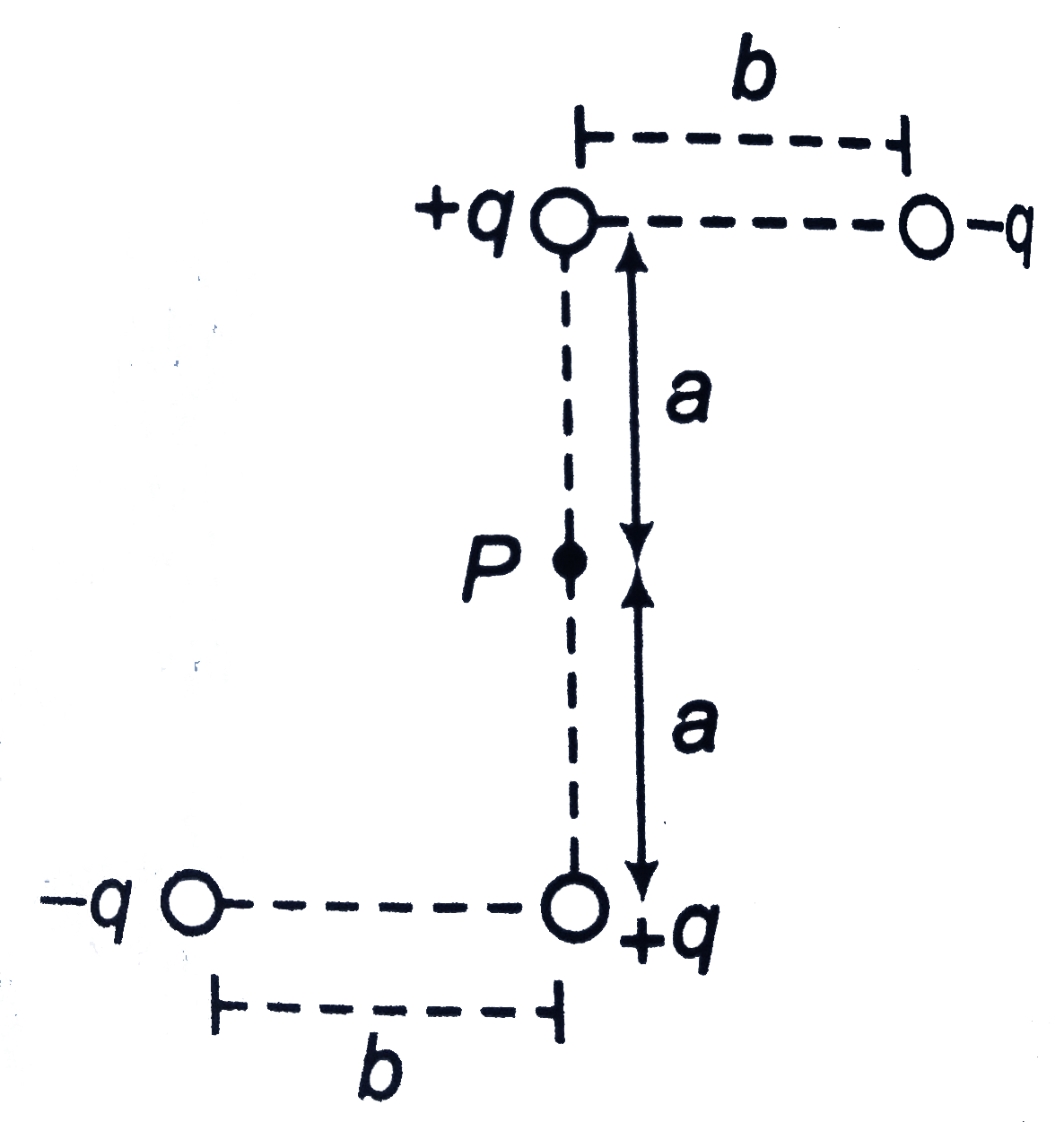
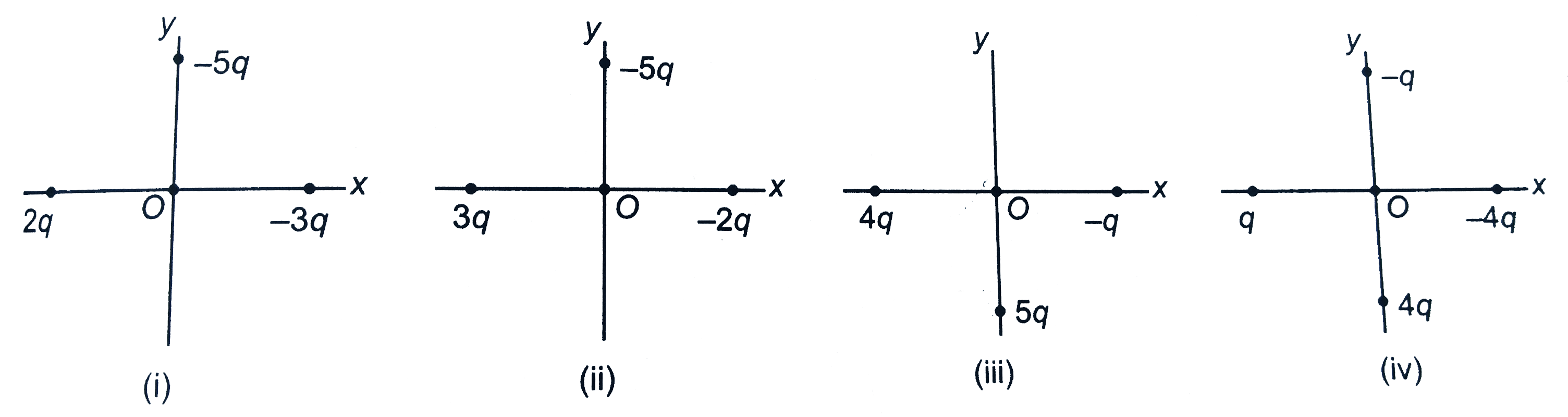
View SolutionThe figure show four situations in which charged particles are at equal distances from the origin. If `E_1,E_2,E_3 and E_4` be the magnitude of the net electic field at the origin in four situations i, ii, iii and iv respectively then
View SolutionAn isolated conduction sphere sphere whose radius `R=1` m has a charge `q=1/9nC.` The energy density at the surfasce of the sphere is
View SolutionTwo conducting concentric, hollow spheres A and B have radii a and b respectively, with A inside B. Their common potentials is V. A is now given some charge such that its potential becomes zero. The potential of B will now be
View SolutionIn a uniform electric field, the potential is ` 10V` at the origin of coordinates , and ` 8 V` at each of the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). The potential at the point (1, 1,1 ) will be .
View SolutionThere are two uncharged identicasl metallic spheres 1 and 2 of radius r separated by a distance `d(dgtgtr)`. A charged metalllic sphere of same radius having charge q is touched with one of the sphere. After some time it is moved away fom the system. Now, the uncharged sphere is earthed. Charge on earthed sphere is
View SolutionFigure shown a closed surface which intersects a conducting sphere. If a positive charge is placed at the point P, the flux of the electric field through the closed surface

View SolutionTwo concentric coducting thin spherical shells A and B having radii `r_A` and `r_B(r_Bgtr_A)` are charged to `Q_A` and `-Q_B(|Q_B|gt|Q_A|)`. The electrical field along a line passing through the centre is
View SolutionThe electric potential at a point `(x,y)` in the x-y plane is given by `V=-kxy`. The field intentisy at a distance r in this plane, from the origin is proportional to
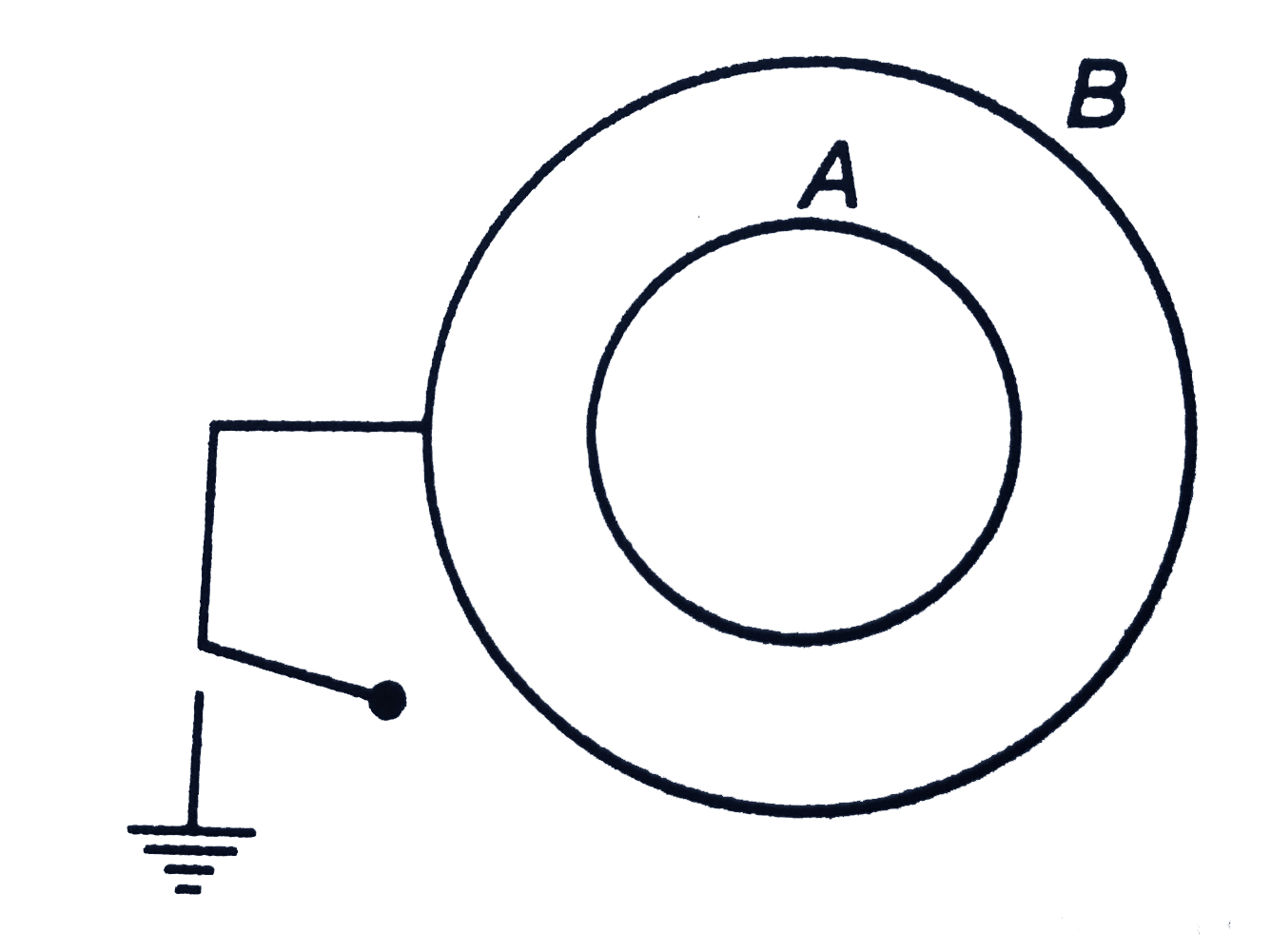
View SolutionTwo concentric shells have radii R and `2R` charges `q_A` and `q_B` and potentials `2V` and `(3/2)V` respectively. Now, shell B is earthed and let charges on them become `q_A'` and `q_B'`. Then,
View SolutionA particle of mass 2 kg charge 1 mC is projected vertially with velocity k`10 ms^-1`. There is as uniform horizontal electric field of `10^4N//C,` then
View SolutionAt a distance of `5 cm and 10 cm` outward from the surface of a uniformly charged solid sphere, the potentials are `100 V and 75 V`, repectively. Then.
View SolutionThree charged particle sare in equilibrium under their electrostatic forces only. Then
View SolutionCharges `Q_1 and Q_2` lie inside and outside, respectively, of a closed surface S. Let E be the field at any point on S and `phi` be the flux of E over S.
View SolutionAn electric dipole is placed at the centre of a sphere. Mark the correct options:
View SolutionMark correct options
View SolutionTwo concentric spherical shells have charges `+q` and `-q` as shown in figure. Choose the correct options.

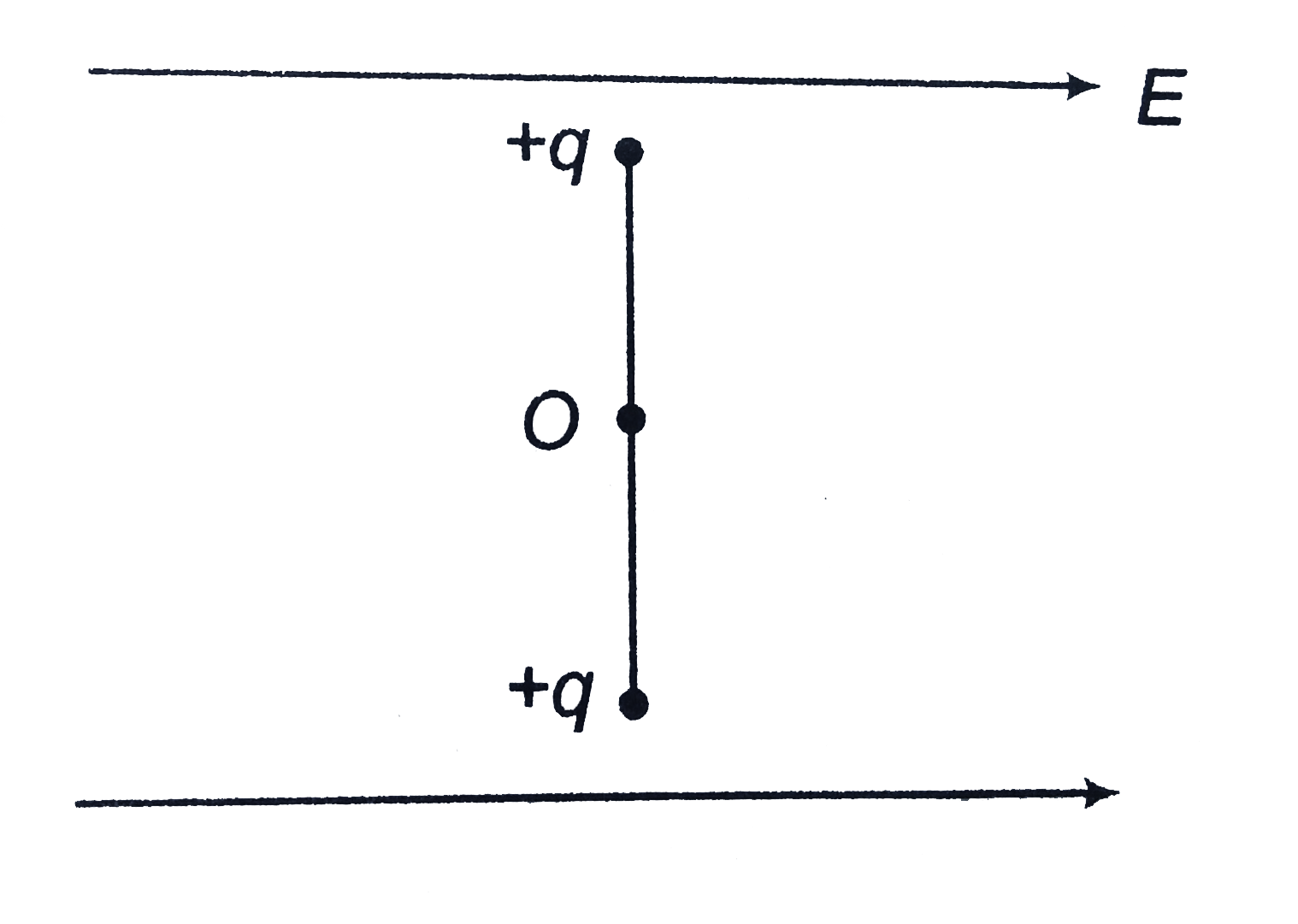
View SolutionA rod is hinged (free to rotate) ast its centre O as shown in figue. Two point charge `+q` and `+q` are kept at its two ends. Rod is placed in uniform electric field E as shown. Space is gravity free. Choose the correct options.
View SolutionTwo charges `+Q` each are fixed at points C and D. Line AB is the bisector line of CD. A third charge `+q` is moves from A to B, then from B to C
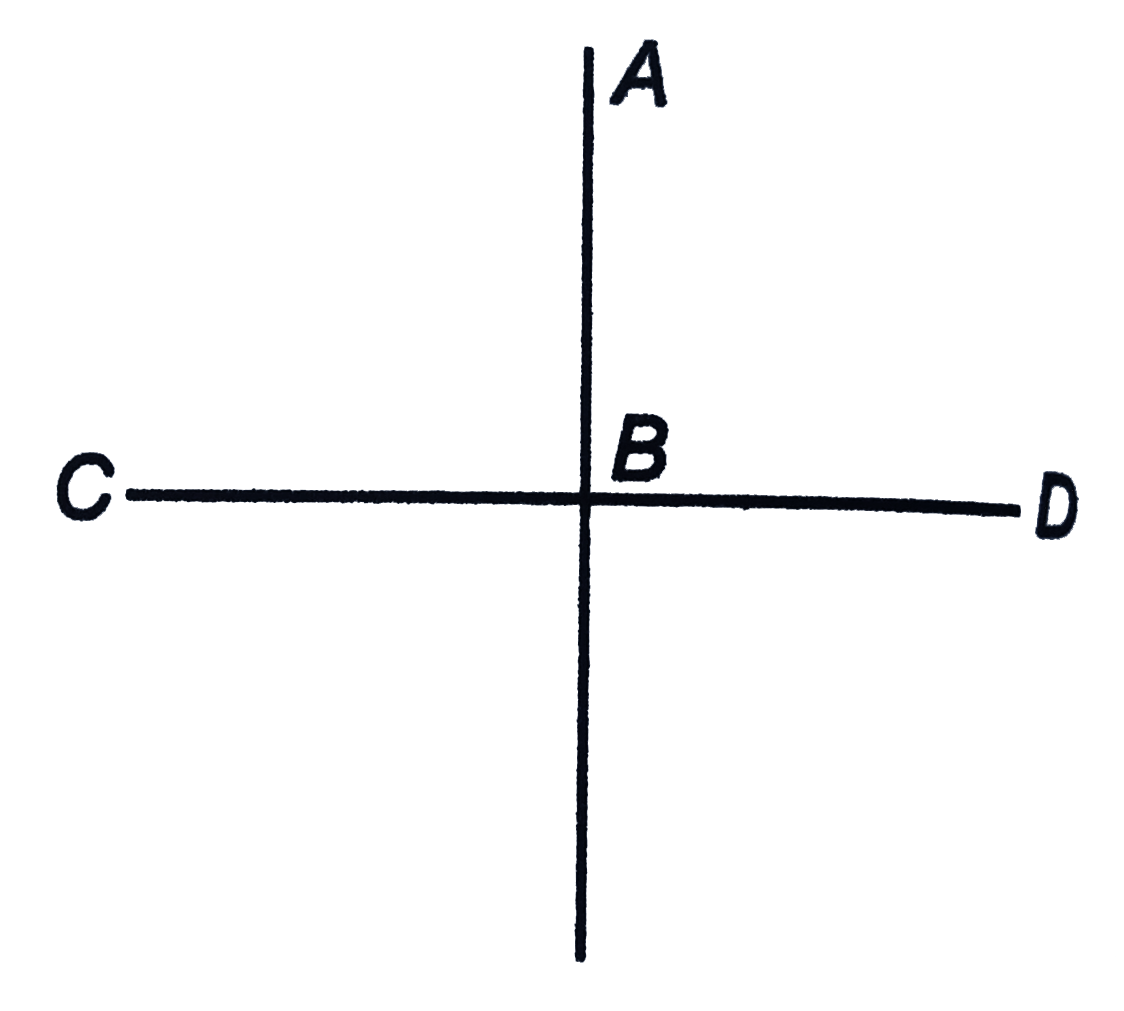
View SolutionThere are two concentric spherical shell of radii r and `2r`. Initially, a charge Q is given to the inner shell and both the switches are open.

If switch `S_1` is closed and then opened, charge on the outer shell will be
View SolutionThere are two concentric spherical shell of radii r and `2r`. Initially, a charge Q is given to the inner shell and both the switches are open.

Now, `S_2` is closed and opened. The charge flowing through the swithc `S_2` in the process is
View SolutionThere are two concentric spherical shell of radii r and `2r`. Initially, a charge Q is given to the inner shell and both the switches are open.

The two steps of the above two problems are repeated b times, the potential differences between the shells will be
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as `rho=rho_0(1-r/R),` where `rho_0` is constant. Assume epsilon as theh permittivity of space.
The magnitude of electric field as a function of the distance r inside the sphere is given by
View SolutionA sphere of charges of radius R carries a positive charge whose volume charge density depends only on the distance r from the ball's centre as `rho=rho_0(1-r/R)`, where` rho_0` is constant. Assume epsilon as theh permittivity of space.
The magnitude of the electric field as a functiion of the distance r outside the balll is given by
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as `rho=rho_0(1-r/R)`, where `rho_0` is constant. Assume epsilon as theh permittivity of space.
The value of distance `r_m` at which electric field intensity is maximum is given by
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as `rho=rho_0(1-r/R),` where `rho_0` is constant. Assume epsilon as theh permittivity of space.
the maximum electric field intensity is
View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius `b(bgt a`). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as `V_b`. After taking these readings, he decides . to put charge of `-4Q` on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is `/_\V` .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as `q_2`. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as `q_3`.
Potential difference `(/_\CV)` measured by the student between the inner solid shere and outer shell after putting a charge `-4Q` is
View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius `b(bgt a)`. The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as `V_b`. After taking these readings, he decides . to put charge of `-4Q` on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is `/_\V` .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as `q_2`. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as `q_3`.
`q_2` is
View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius `b(bgt a)`. The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as `V_b`. After taking these readings, he decides . to put charge of `-4Q` on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is `/_\V` .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as `q_2`. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as `q_3`.
`q_3` is
View SolutionA `4.00 kg` block carrying a charge `Q = 50.0muC` is connected to a spring for which k = 100 N/ m. The block lies on a frictionless horizontal track, and the system is immersed in a uniform electric field of magnitude `E = 5.00 xx 10^5 V/m`, directed as shown in figure. If the block is released from rest when the spring is unstretched (at x = 0).

(a) By what maximum amount does the spring expand?
(b) What is the equilibrium position of the block?
(c) Show that the block's motion is simple harmonic and determine its period.
(d) Repeat part (a) if the coefficient of kinetic friction between block and surface is 0.2.
View SolutionA particle of mass m and charge `-Q` is constrained to move along the axis of a ring of radius a. The ring carries a uniform charge density `+lamda` along its length. Initially, the particle is in the centre of the ring where the force on it is zero. Show that the period of oscillation of the particle when it is displaced slightly from its equilibrium position is given by
`T=2pisqsqrt((2epsilon_0ma^2)/(lamdaQ))`
View SolutionThree identical conducting plain parallel plates, each of area A are held with equal distance between successive surfaces. Charges`Q`, `2Q`, and `3Q` are placed on them.Neglecting edge effects, find the distribution of charges on the six surfaces.
View SolutionA long non-conducting, massless rod of length L pivoted at its centre and balanced with a weight w at a distance x from the lefrt end. At the left and right ends fo the rod are attached small conducting sphers with positive charfges q and `2q` respectively. A distance h directly beneath each of these spheres is a fixed sphere with positive charge Q.
(a) Find the distance x where the rod is horizontal and balanced.b. What valueshold h have so that the rod exerts no vertical force on the bearing when the rod is horizontal and balanced?
View SolutionThe electric potential varies in space according to the relation `V = 3x + 4y`. A particle of mass 10 kg starts from rest from point `(2, 3.2)` m under the influence of this field. Find the velocityr,f the particle when it crosses the x-axis. The charge on the particle is `+1muC`. Assume V (x, y)are in SI units.
View SolutionA simple pendulum with a bob of mass `m = 1` kg, charge `q = 5muC` and string length imis given a horizontal velocity a in a uniform electric field `E = 2 xx 10^6 V/m` at its bottommost point A, as shown in figure. It is given that the speed a is such that the particle leaves the circle at point C. Find the speed a (Take `g = 10 m/ s^2`)
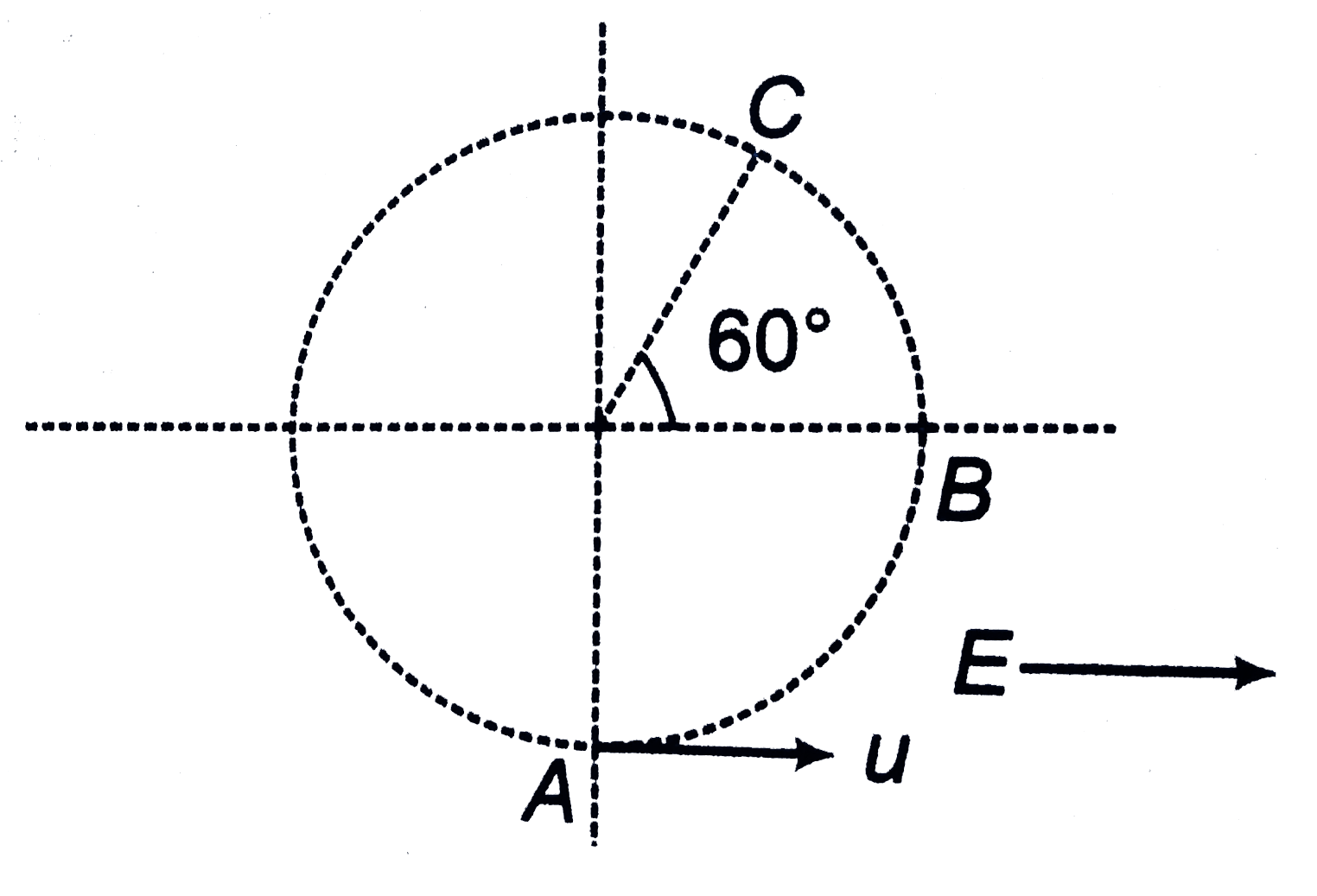
View SolutionThere are two concentric spherical shell of radii r and `2r`. Initially, a charge Q is given to the inner shell and both the switches are open.

The two steps of the above two problems are repeated b times, the potential differences between the shells will be
View SolutionTwo point like charges `Q_(1)` and `Q_(2)` are positioned at point 1 and 2. The firld intensity to the right of the chaege `Q_(2)` on the line that passes through the two charges varies accoreing to a law that is represented schematically in fig. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
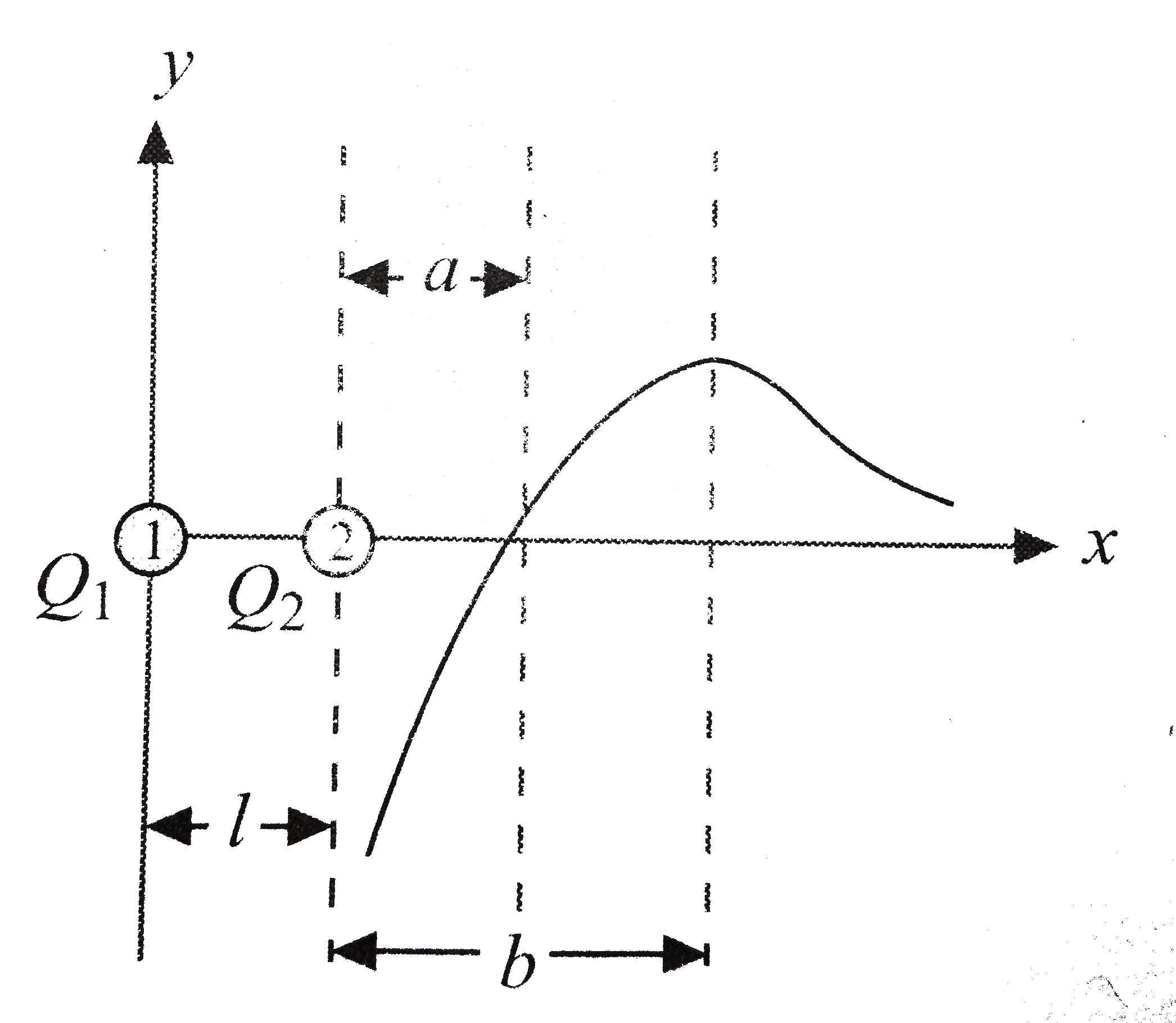
The ratio of the absolute values of the charges `|Q_(1)//Q_(2)|` is
View SolutionA conducting sphere `S_1` of radius `r` is attached to an insulating handle. Another conduction sphere `S_2` of radius `R` is mounted on an insulating stand. `S_2` is initially uncharged. `S_1` is given a charge `Q` brought into contact with `S_2` and removed. `S_1` is recharge such that the charge on it is again `Q` and it is again brought into contact with `S_2` and removed. This procedure is repeated `n` times.
a. Find the electrostatic energy of `S_2` after `n` such contacts with `S_1`.
b. What is the limiting value of this energy as `nrarroo` ?
View SolutionTwo fixed, equal, positive charges, each of magnitude `5xx10^-5` coul are located at points A and B separated by a distance of 6m. An equal and opposite charge moves towards them along the line COD, the perpendicular bisector of the line AB.
The moving charge, when it reaches the point C at a distance of 4m from O, has a kinetic energy of 4 joules. Calculate the distance of the farthest point D which the negative charge will reach before returning towards C.
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance `r (r gt R)` from the center of the sphere. Find the minimum velocity v so that it can penetrate `(R//2)` distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

View SolutionA point charge `–q` revolves around a fixed charge `+Q` in elliptical orbit. The minimum ar.d maximum distance of q from Q are `r_1` and `r_2`, respectively. The mass of revolving particle is `Q gt q` and assume no gravitational effects. Find the velocity of q at positions when it is at `r_1` and `r_2` distance from Q.
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density `p =(A)/(r)`, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
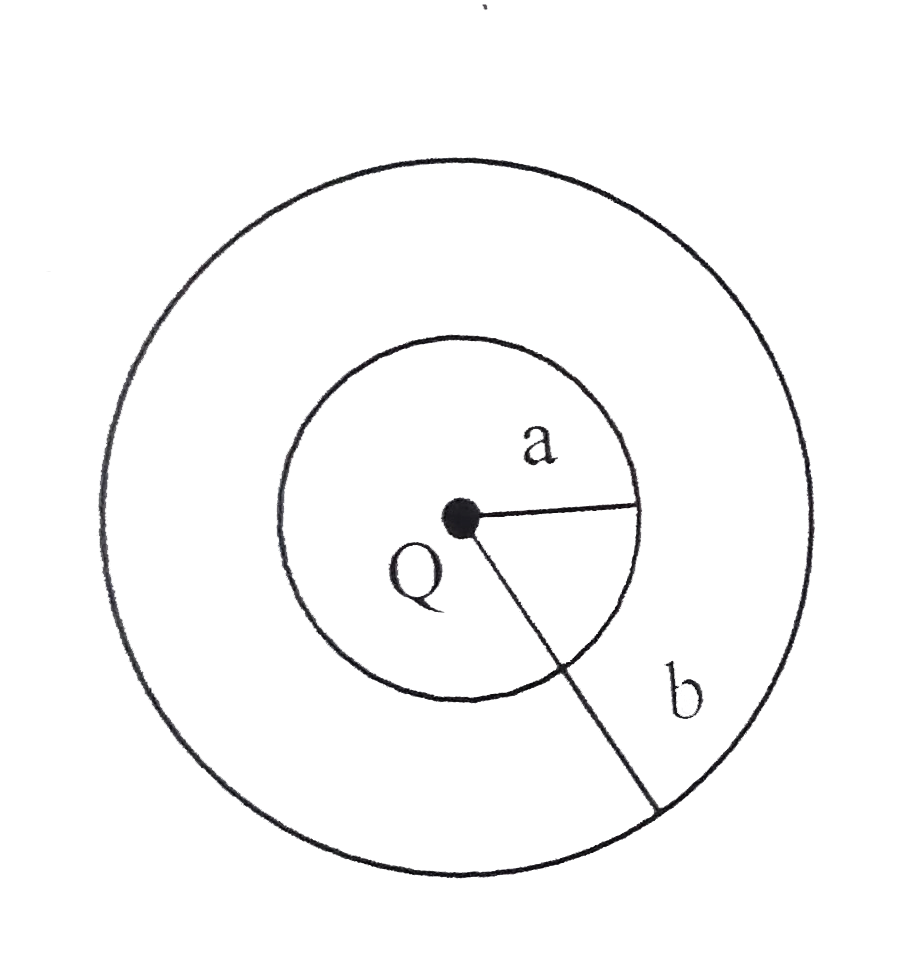
View SolutionA nonconducting ring of mass m and radius R, with charge per unit length `lambda` is shown in fig. It is then placed on a rough nonconducting horizontal plane. At time t=0, a uniform electric field `vecE =E_(0)hati` is switched on and the ring starts rolling without sliding. Determine the friction force (magnitude and direction ) acting on the ring.

View SolutionA rectangular tank of mass `m_(0)` and charge Q is placed over a smooth horizontal floor. A horizontal electric field E exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second. Mass of each drop is m. Find velocity of tank as function of time.
View SolutionIn a region an electric field is setu!l with its strength `E = 15 N//C` and it makes an angle of `30°` with the horizontal plane as shown in figure. A ball having a charge 2C, mass 3kg and coefficient of restitution with ground 0.5 is projected at an angle of `30°` with the horizontal along the direction of electric field with speed 20 m/s. Find the horizontal distance travelled by ball from first hit with the ground to the second time when it hits the ground.
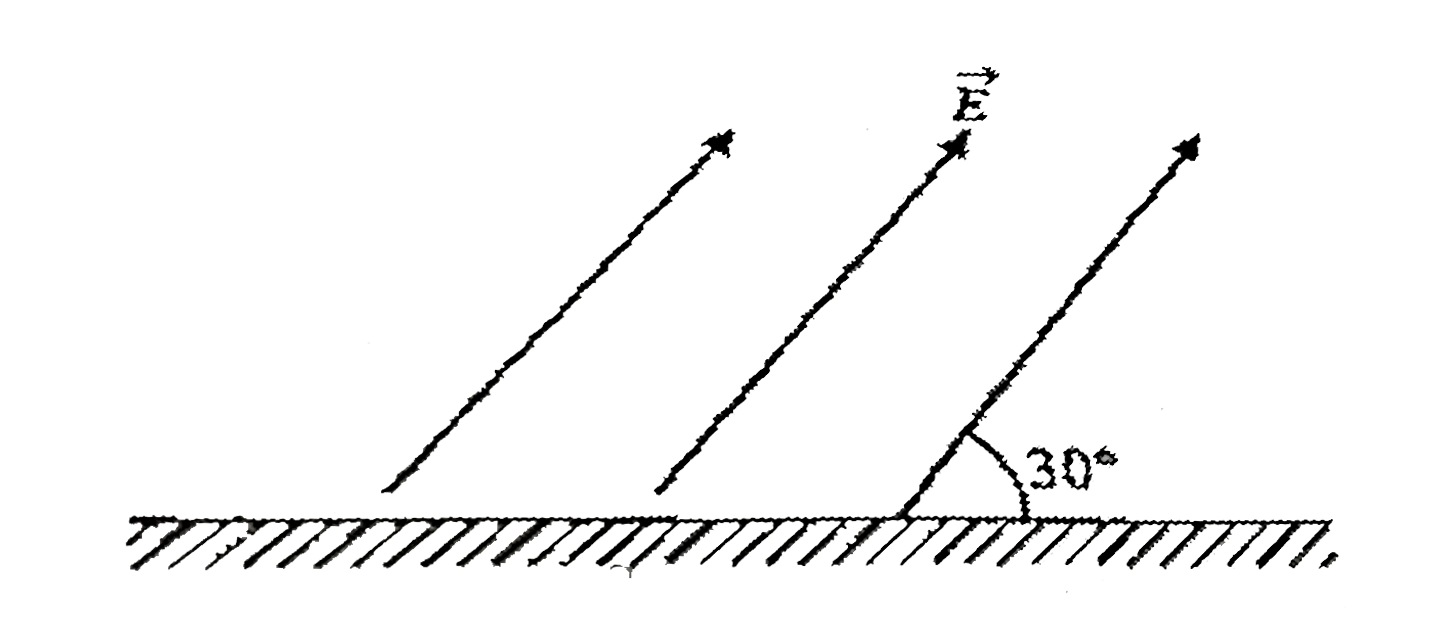
View Solution
Level 2 Single Correct questions and complete solutions for chapter ELECTROSTATICS of DC PANDEY ENGLISH of Class 12
All Exercises from DC PANDEY Class 12 PHYSICS ELECTROSTATICS
- Assertion and Reason
- Check point 1.1
- Check point 1.2
- Check point 1.3
- Check point 1.4
- Check point 1.5
- Example
- Example Type 5
- Example Type 6
- Example Type 8
- Exercise 24.1
- Exercise 24.2
- Exercise 24.3
- Exercise 24.4
- Exercise 24.5
- Exercise 24.6
- Exercise 24.7
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Single Correct
- Match the columns
- Medical entrances gallery
- SUBJECTIVE_TYPE
- Taking it together