In Figure, AC=BC,∠DCA=∠ECB and ∠DBC=∠EAC. Prove that triangles DBC and EAC are congruent, and hece DC=EC and BD=AE
To prove that triangles DBC and EAC are congruent, we will use the criteria for congruence of triangles.
Given:
1. AC=BC (Given)
2. ∠DCA=∠ECB (Given)
3. ∠DBC=∠EAC (Given)
To Prove:
1. △DBC≅△EAC
2. Hence, DC=EC and BD=AE
Proof:
1. Identify the triangles: We are working with triangles DBC and EAC.
2. Use the given information:
- We know that AC=BC (Given).
- We also know that ∠DCA=∠ECB (Given).
- Lastly, we have ∠DBC=∠EAC (Given).
3. Apply the Angle-Side-Angle (ASA) Congruence Criterion:
- In triangle DBC:
- Side BC is common to both triangles.
- We have AC=BC (Given).
- We have ∠DBC=∠EAC (Given).
- In triangle EAC:
- Side AC is equal to BC.
- We have ∠EAC=∠DBC (Given).
- We have ∠DCA=∠ECB (Given).
4. Conclude the congruence:
- By the ASA criterion, since we have two angles and the included side equal in both triangles, we can conclude that:
△DBC≅△EAC
5. State the corresponding sides:
- From the congruence of triangles, we can say that:
DC=ECandBD=AE
Conclusion:
Thus, we have proved that triangles DBC and EAC are congruent, and therefore DC=EC and BD=AE.
---
1. AC=BC (Given)
2. ∠DCA=∠ECB (Given)
3. ∠DBC=∠EAC (Given)
1. △DBC≅△EAC
2. Hence, DC=EC and BD=AE
1. Identify the triangles: We are working with triangles DBC and EAC.
- We know that AC=BC (Given).
- We also know that ∠DCA=∠ECB (Given).
- Lastly, we have ∠DBC=∠EAC (Given).
- In triangle DBC:
- Side BC is common to both triangles.
- We have AC=BC (Given).
- We have ∠DBC=∠EAC (Given).
- In triangle EAC:
- Side AC is equal to BC.
- We have ∠EAC=∠DBC (Given).
- We have ∠DCA=∠ECB (Given).
- By the ASA criterion, since we have two angles and the included side equal in both triangles, we can conclude that:
△DBC≅△EAC
- From the congruence of triangles, we can say that:
DC=ECandBD=AE
Thus, we have proved that triangles DBC and EAC are congruent, and therefore DC=EC and BD=AE.
Topper's Solved these Questions
Similar Questions
In Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE
 View Solution
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
 View Solution
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
 View Solution
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
 View Solution
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
 View Solution
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
 View Solution
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure, it is given that AB=EF,BC=DE,AB⊥BD and FE⊥CE. Prove that ABD≅FEC.
 View Solution
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
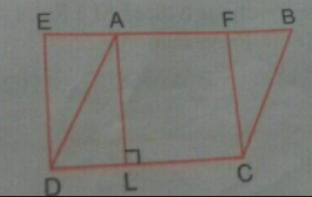 View Solution
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14ACView Solution

