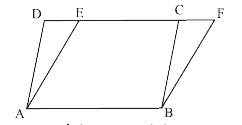
ABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
The correct Answer is:36cm2
ar(△ACD)=ar(△ABC)=12ar(||gm ABCD),
ar(△AMC)=ar(△MBC)=12ar(△ABC).
∴ar(AMCD)=3ar(△AMC)⇒24=3ar(△AMC)
⇒(△AMC)=8cm2.
And so, ar(△ABC)=2ar(△AMC)=16cm2.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
Knowledge Check
- Question 1 - Select One
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC - Question 2 - Select One
In the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
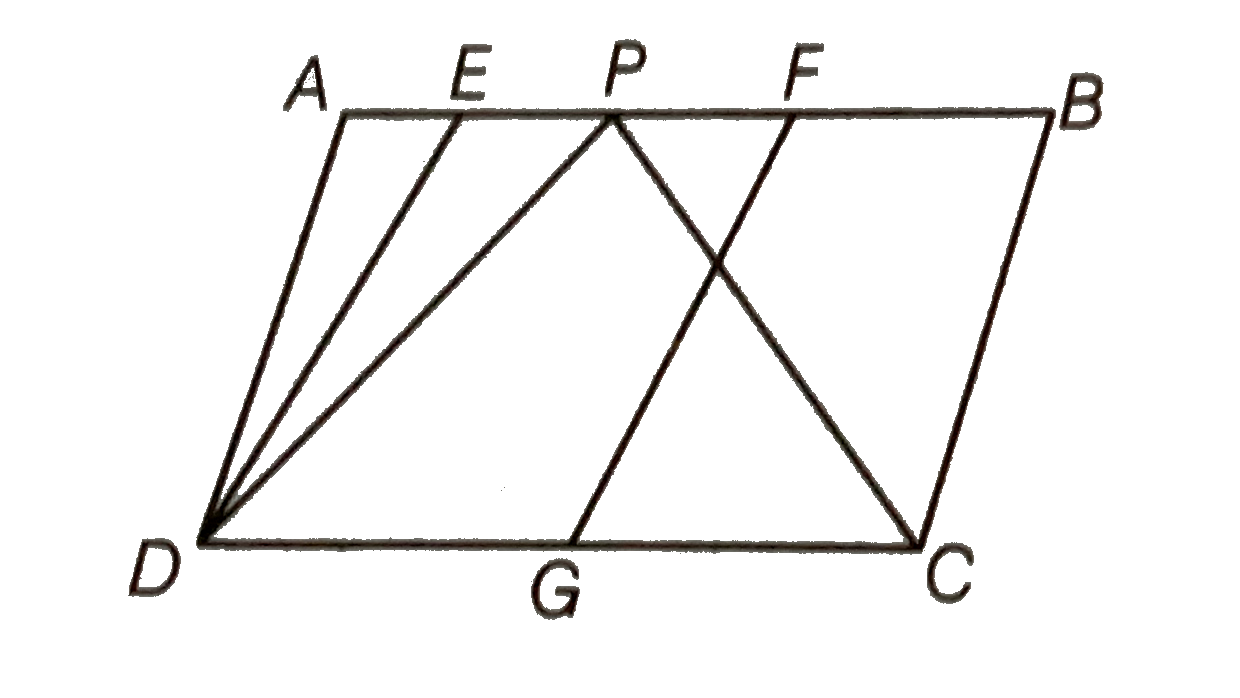 ATrueBFalseCPartially trueDNone of these
ATrueBFalseCPartially trueDNone of these - Question 3 - Select One
In the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
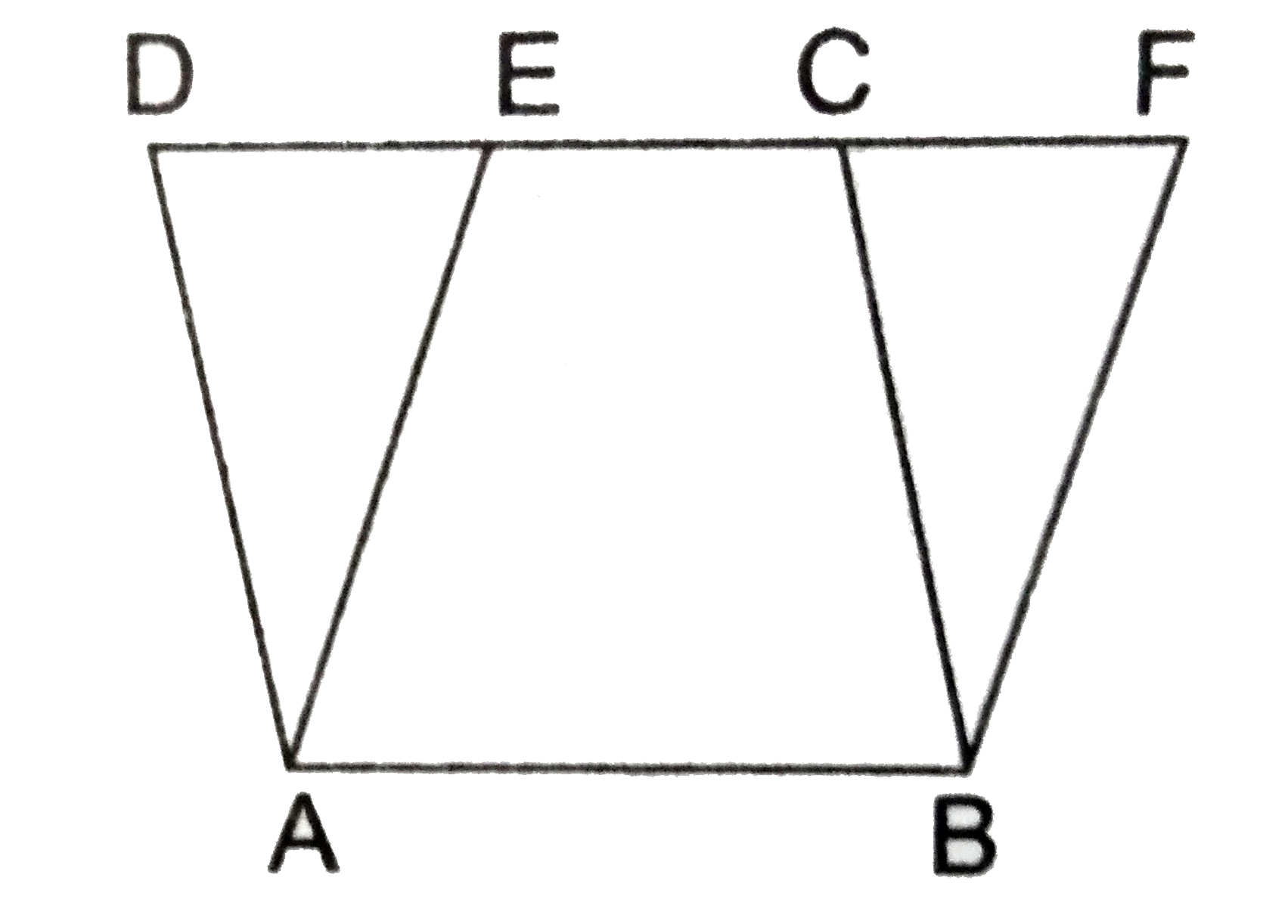 A4cm2B4.8cm2C6cm2D8cm2
A4cm2B4.8cm2C6cm2D8cm2
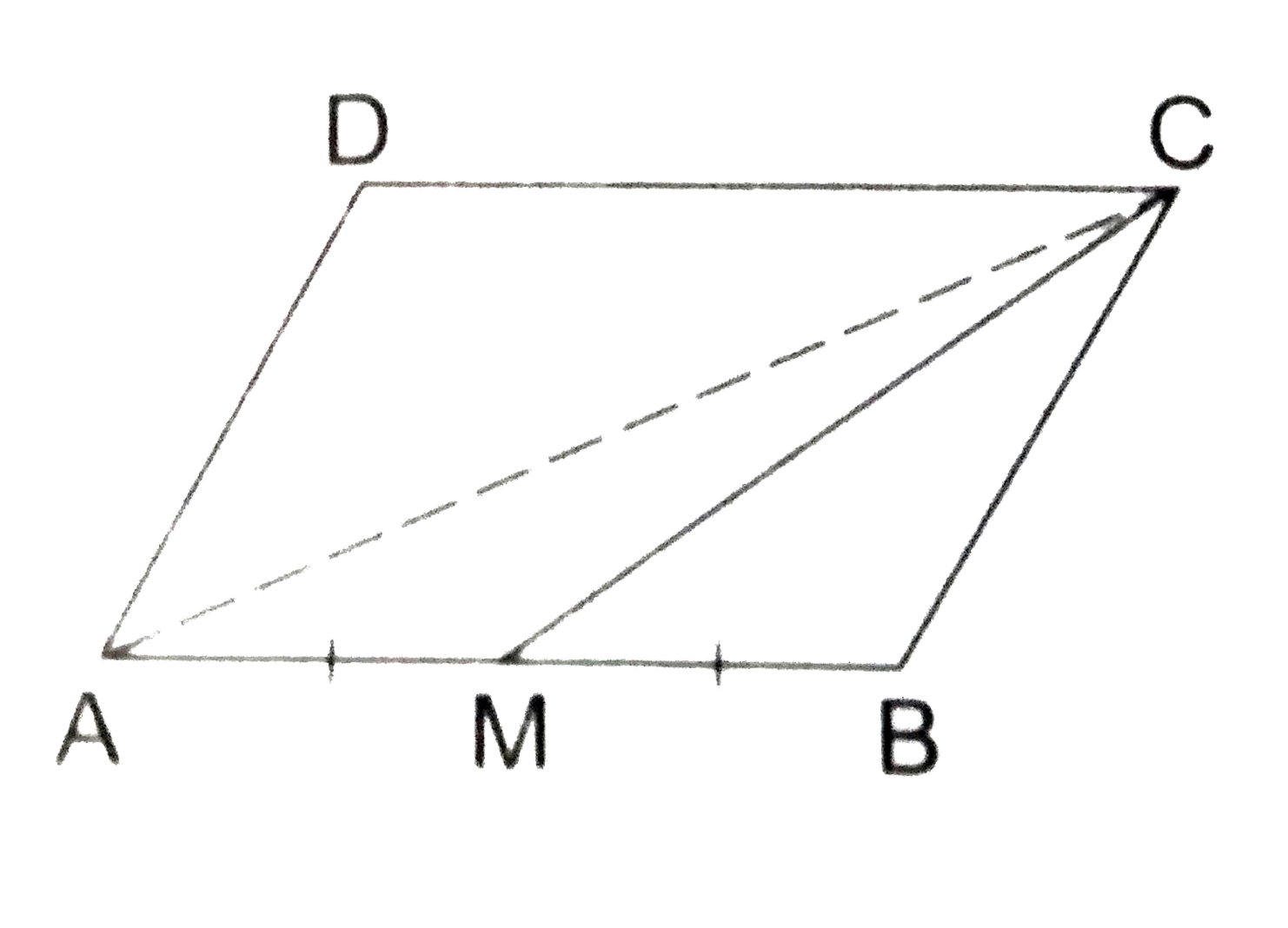
ABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
 View Solution
View SolutionABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
View Solution