A resistance is connected to a capacitor in AC are the phase differece is π4 between current and voltage. Whe the same resistance is connected to an inductor, phase difference becomes tan−1(2). Power factor of the circuit when both capacitor and inductor are connect to the resistance will be
1
1√2
1√3
12
The correct Answer is:B
To solve the problem step by step, we will analyze the given information regarding the phase differences when a resistance is connected to a capacitor and an inductor, and then find the power factor when both are connected.
Step 1: Understand the Phase Difference with the Capacitor
When the resistance R is connected to a capacitor, the phase difference ϕC is given as π4 (or 45 degrees). The power factor cos(ϕC) can be expressed as:
cos(π4)=RZC
where ZC is the impedance of the circuit with the capacitor.
Step 2: Calculate the Capacitive Reactance
From the above equation, we can express the impedance ZC:
ZC=Rcos(π4)=R√2
Now, we know that:
ZC=√R2+X2C
where XC is the capacitive reactance. Since ZC=R√2, we can set up the equation:
R√2=√R2+X2C
Squaring both sides:
2R2=R2+X2C
This simplifies to:
X2C=R2⟹XC=R
Step 3: Understand the Phase Difference with the Inductor
When the same resistance R is connected to an inductor, the phase difference ϕL is given by:
tan(ϕL)=2
This implies:
tan(ϕL)=XLR=2⟹XL=2R
Step 4: Calculate the Impedance with Both Capacitor and Inductor
When both the capacitor and inductor are connected to the resistance, the total impedance Z can be calculated using the formula:
Z=√R2+(XL−XC)2
Substituting the values of XL and XC:
Z=√R2+(2R−R)2=√R2+R2=√2R2=R√2
Step 5: Calculate the Power Factor
The power factor PF is given by:
PF=RZ
Substituting the value of Z:
PF=RR√2=1√2
Final Answer
Thus, the power factor of the circuit when both the capacitor and inductor are connected to the resistance is:
Power Factor=1√2
When the resistance R is connected to a capacitor, the phase difference ϕC is given as π4 (or 45 degrees). The power factor cos(ϕC) can be expressed as:
cos(π4)=RZC
where ZC is the impedance of the circuit with the capacitor.
From the above equation, we can express the impedance ZC:
ZC=Rcos(π4)=R√2
Now, we know that:
ZC=√R2+X2C
where XC is the capacitive reactance. Since ZC=R√2, we can set up the equation:
R√2=√R2+X2C
Squaring both sides:
2R2=R2+X2C
This simplifies to:
X2C=R2⟹XC=R
When the same resistance R is connected to an inductor, the phase difference ϕL is given by:
tan(ϕL)=2
This implies:
tan(ϕL)=XLR=2⟹XL=2R
When both the capacitor and inductor are connected to the resistance, the total impedance Z can be calculated using the formula:
Z=√R2+(XL−XC)2
Substituting the values of XL and XC:
Z=√R2+(2R−R)2=√R2+R2=√2R2=R√2
The power factor PF is given by:
PF=RZ
Substituting the value of Z:
PF=RR√2=1√2
Thus, the power factor of the circuit when both the capacitor and inductor are connected to the resistance is:
Power Factor=1√2
Topper's Solved these Questions
Similar Questions
A series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View SolutionA resistance is connected to a n AC source. If a capacitor is induced in the series cirucit, the average power absorbed by the resistance
View Solution
Knowledge Check
The phase relationship between current and voltage in a pure resistive circuit is best represented by
A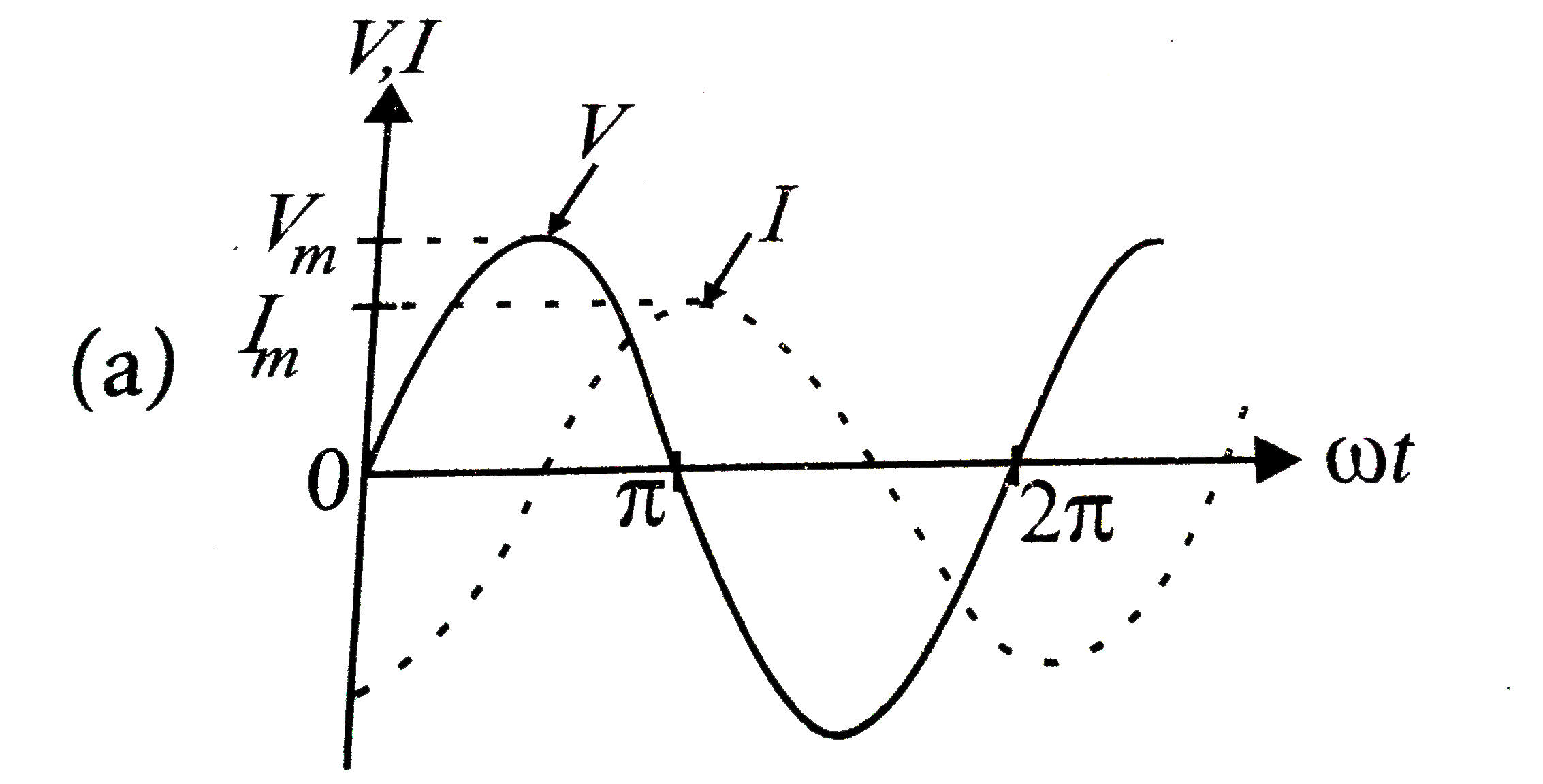 B
B C
C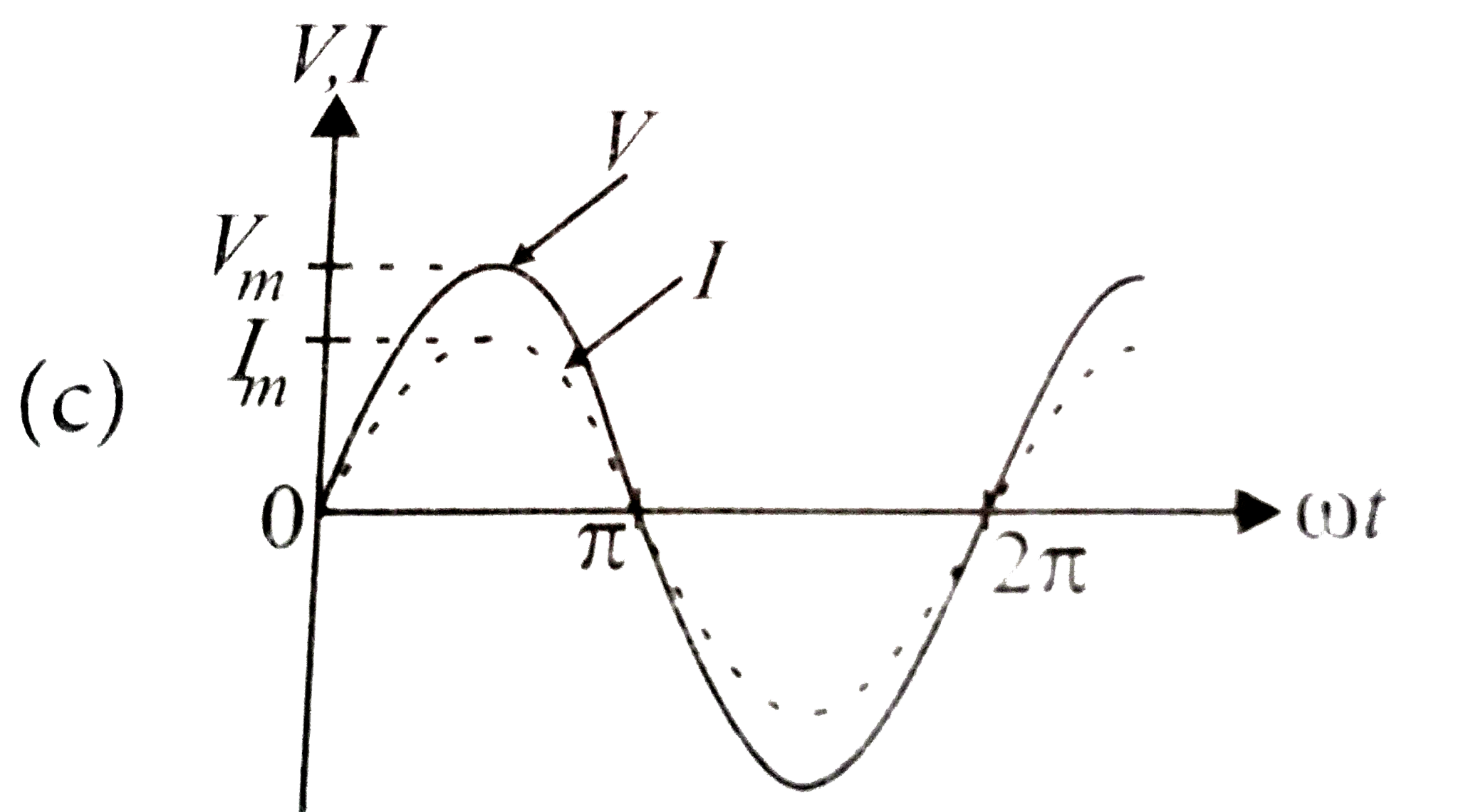 D
D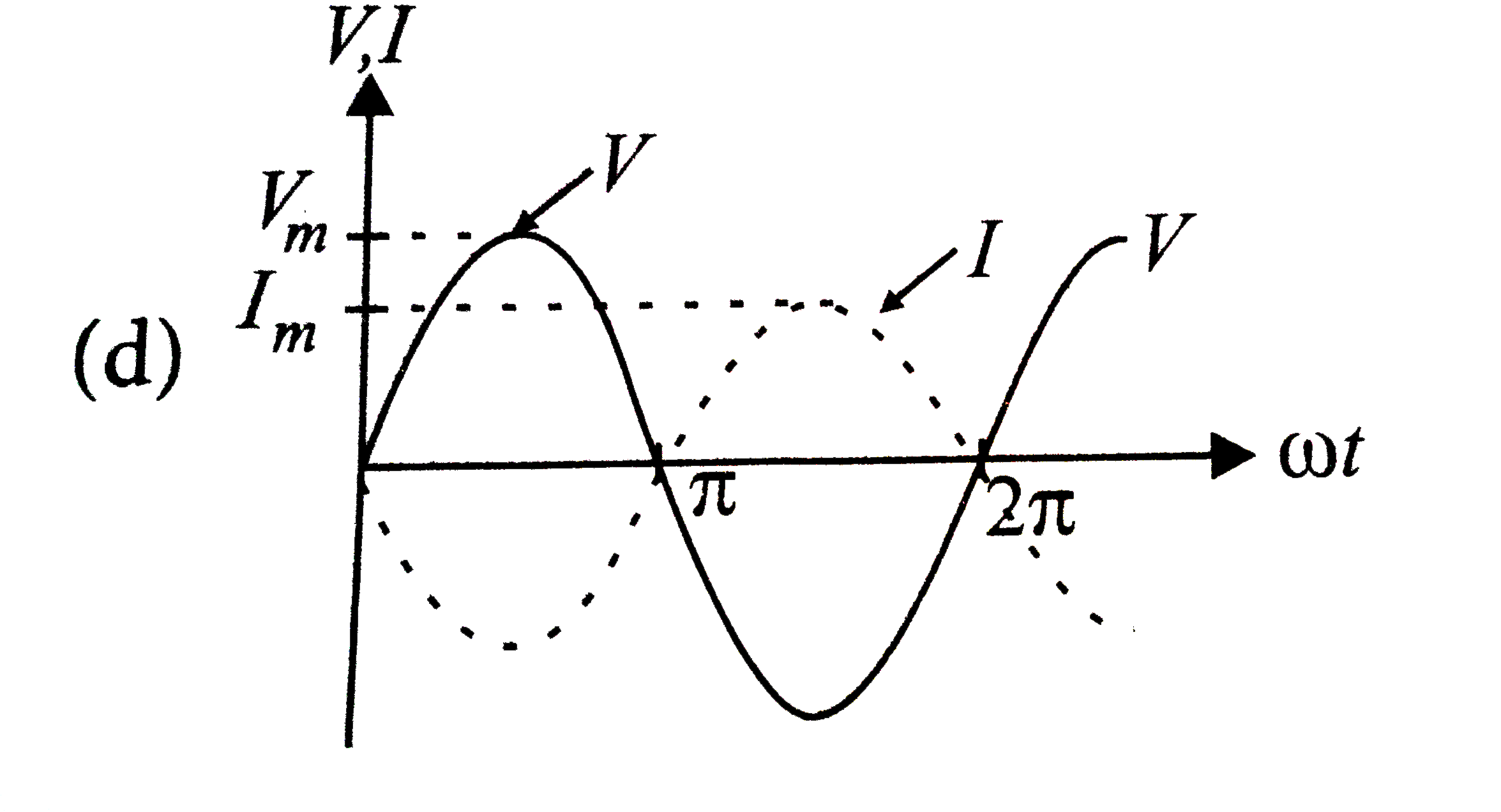
Phase difference between voltage and current in a capacitor in an ac circuit is
AπBπ/2C0Dπ/3
A seriesLCR circuit is connected to an ac voltage source. When L is removed from the circuit, the phase difference between current and voltage is π3. If instead C is removed from the circuit phase difference is again π3 between current and voltage. Power factor of circuit is:
View SolutionA resistance is connected to an AC source. If a capacitor is included in the series circuit, will the average power absorbed by the resistance increase or decrease? If an inductor of small inductance is also included in the series circuit, will the average power absorbed increase or decrease further?
View SolutionThe power factor of an AC circuit having resistance (R) and inductance (L) connected in series and an angular velocity ω is
View SolutionIn the LCR circuit shown in figure unknown resistance and alternating voltage source are connected.When swith S is closed then there is a phase difference of π4 between current and applied voltage and voltage across resister is 100√2V.When switch is open current and applied voltage are in same phase.Neglecting resistance of connecting wire answer the following questions :
Average power consumption in the circuit when S is open:

View SolutionIn the LCR circuit shown in figure unknown resistance and alternating voltage source are connected.When swith S is closed then there is a phase difference of π4 between current and applied voltage and voltage across resister is 100√2V.When switch is open current and applied voltage are in same phase.Neglecting resistance of connecting wire answer the following questions :
Resonance frequency of circuit is:

View SolutionA 220-V, 50 Hz, ac generator is connected to an inductor and a 50Ω resistance in series. The current in the circuit is 1.0A. What is the PD across inductor?
View Solution
