The current in an L−R circuit builds upto 3/4th of its steady state value in 4sec. Then the time constant of this circuit is
1ln 2s
2ln 2s
3ln 2s
4ln 2s
The correct Answer is:B
To find the time constant of the L-R circuit where the current builds up to 34 of its steady state value in 4 seconds, we can follow these steps:
1. Understand the Formula:
The current I(t) in an L-R circuit is given by the equation:
I(t)=I0(1−e−tτ)
where I0 is the steady state current and τ is the time constant.
2. Set Up the Equation:
We know that at t=4 seconds, the current I(4) is 34I0. Therefore, we can set up the equation:
34I0=I0(1−e−4τ)
3. Simplify the Equation:
Dividing both sides by I0 (assuming I0≠0):
34=1−e−4τ
4. Rearranging the Equation:
Rearranging gives:
e−4τ=1−34=14
5. Taking the Natural Logarithm:
Taking the natural logarithm of both sides:
−4τ=ln(14)
6. Simplifying the Logarithm:
We can express ln(14) as:
ln(14)=ln(1)−ln(4)=0−ln(4)=−ln(4)
Thus, we have:
−4τ=−ln(4)
7. Solving for the Time Constant τ:
Rearranging gives:
4τ=ln(4)
Therefore, solving for τ:
τ=4ln(4)
8. Expressing ln(4):
We can express ln(4) as:
ln(4)=ln(22)=2ln(2)
Substituting this back into the equation for τ:
τ=42ln(2)=2ln(2)
Final Answer:
Thus, the time constant τ of the circuit is:
τ=2ln(2) seconds
The current I(t) in an L-R circuit is given by the equation:
I(t)=I0(1−e−tτ)
where I0 is the steady state current and τ is the time constant.
We know that at t=4 seconds, the current I(4) is 34I0. Therefore, we can set up the equation:
34I0=I0(1−e−4τ)
Dividing both sides by I0 (assuming I0≠0):
34=1−e−4τ
Rearranging gives:
e−4τ=1−34=14
Taking the natural logarithm of both sides:
−4τ=ln(14)
We can express ln(14) as:
ln(14)=ln(1)−ln(4)=0−ln(4)=−ln(4)
Thus, we have:
−4τ=−ln(4)
Rearranging gives:
4τ=ln(4)
Therefore, solving for τ:
τ=4ln(4)
We can express ln(4) as:
ln(4)=ln(22)=2ln(2)
Substituting this back into the equation for τ:
τ=42ln(2)=2ln(2)
Thus, the time constant τ of the circuit is:
τ=2ln(2) seconds
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
The time constant of C-R circuit is
View SolutionThe time constant of L-R circuit is doubled if
View SolutionThe value of time constant for the given circuit is
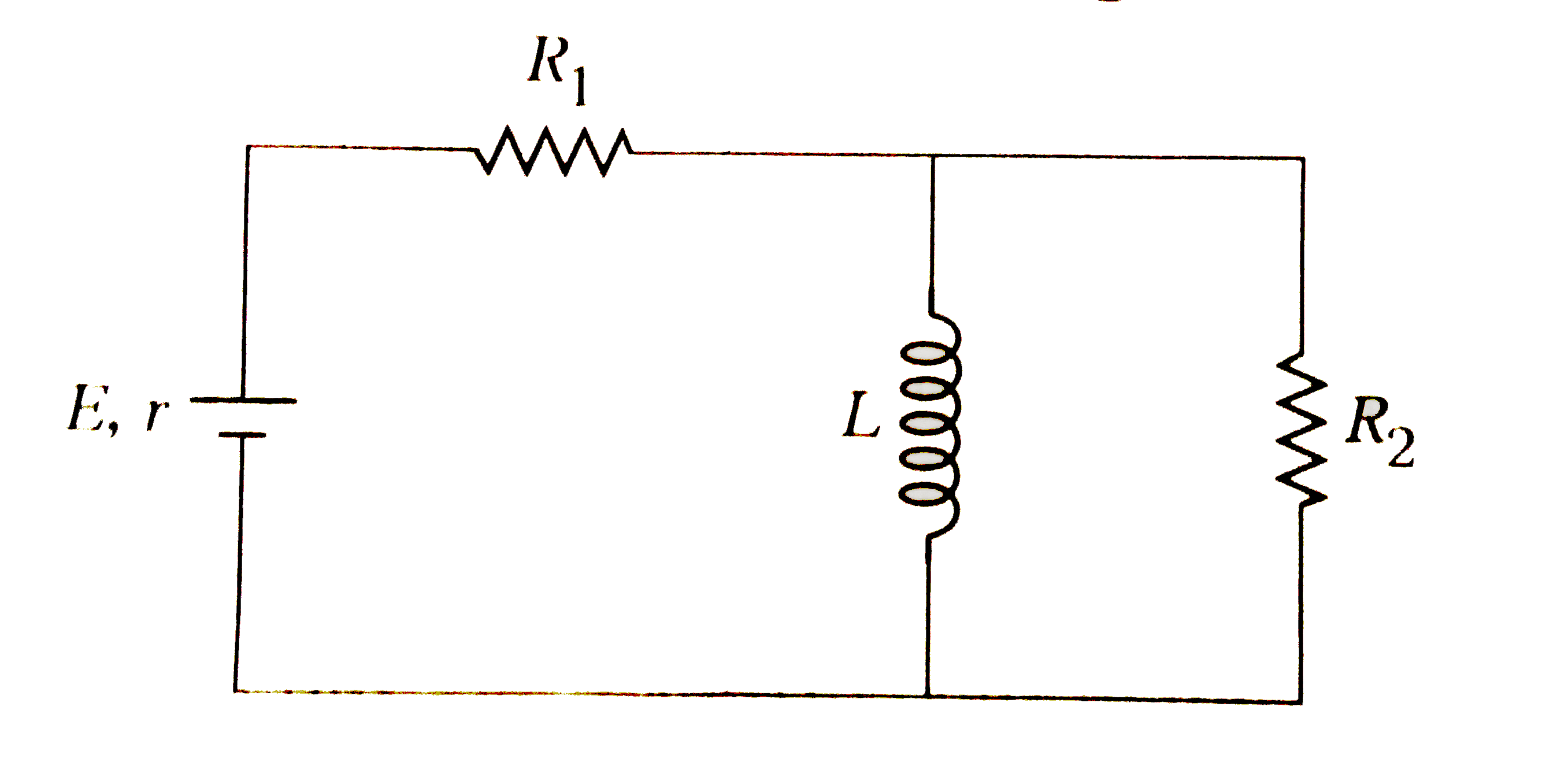 View Solution
View SolutionThe figure shows an L−R circuit the time constant for the circuit is
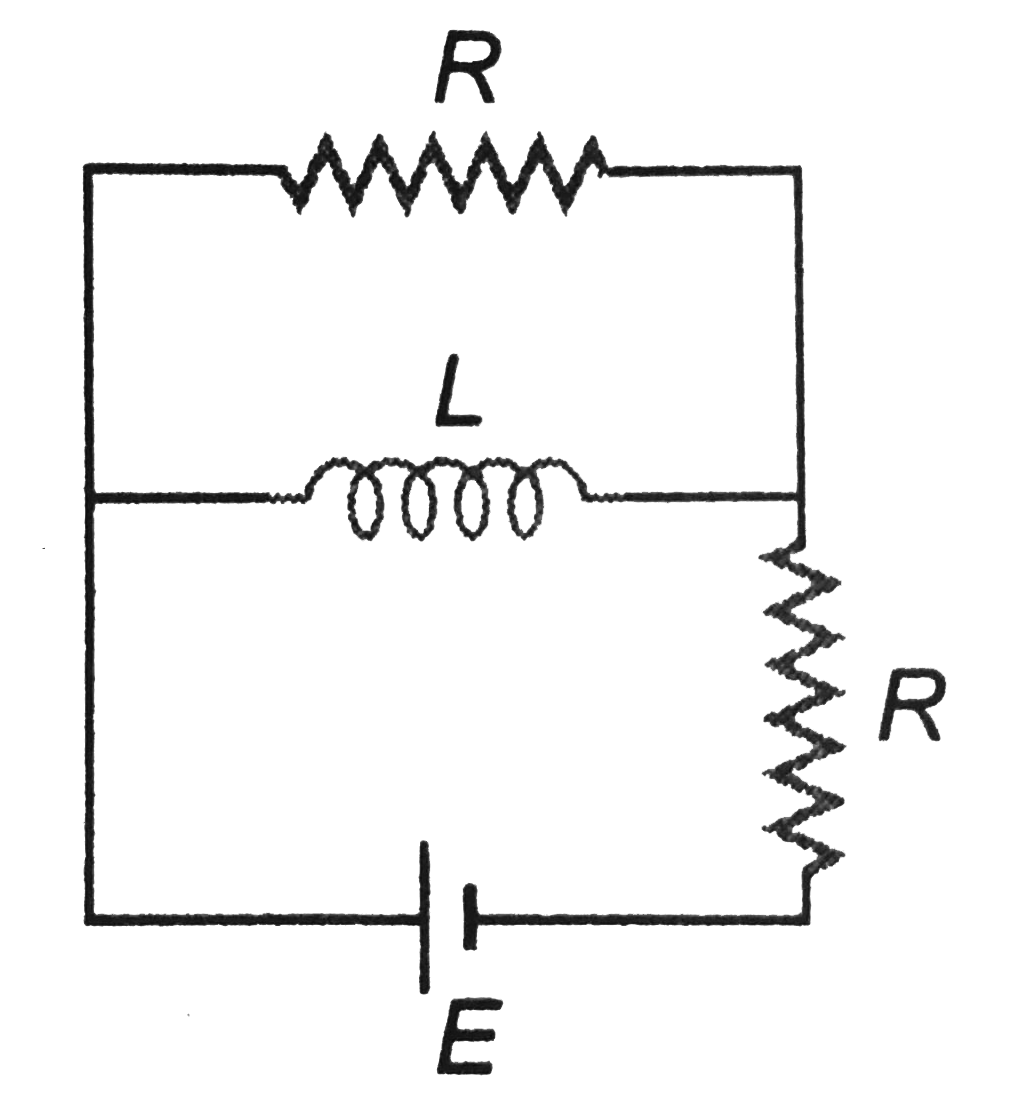 View Solution
View SolutionA coil carrying a steady current is short-circuited. The current in it decreases α times in time t0. The time constant of the circuit is
View SolutionThe current in a discharging LR circuit without the battery drops from 2.0 A to 1.0A in 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?
View SolutionIn a series L-R growth circuit, if maximum current and maximum voltage across inductor of inductane 3mH are 2A and 6V respectively, the the time constant of the circuit is
View SolutionIn a series L-R growth circuit, if maximum current and maximum voltage across inductor of inductane 3mH are 2A and 6V respectively, the the time constant of the circuit is
View SolutionIn an LR circuit, current at t=0 is 20A . After 2s it reduced to 18A. The time constant of the circuit is (in second)
View SolutionHow many time constants will elapse before the current in a charging RC circuit drops to half of its initial value?Answer the same question for a discharging RC circuit.
View Solution

