Two identical circular loops of metal wire are lying on a table without touching each other. Loop-A carries a current which increases with time. In response, the loop-B
remains stationary
is attracted by loop A
is repelled by loop A
rotates about its centre of mass with CM fixed
The correct Answer is:C
To solve the problem, we will analyze the situation step by step using the principles of electromagnetic induction, specifically applying Faraday's law and Lenz's law.
1. Identify the Setup: We have two identical circular loops of wire, Loop-A and Loop-B, placed on a table without touching each other. Loop-A carries a current that is increasing with time.
2. Determine the Magnetic Field: When current flows through Loop-A, it generates a magnetic field around it. The direction of the magnetic field can be determined using the right-hand rule. If the current in Loop-A is flowing in a certain direction (let's assume counterclockwise), the magnetic field lines will point upwards through the center of the loop.
3. Change in Magnetic Flux: As the current in Loop-A increases, the strength of the magnetic field produced by Loop-A also increases. This leads to an increase in the magnetic flux through Loop-B, which is positioned nearby.
4. Apply Faraday's Law of Induction: According to Faraday's law, a change in magnetic flux through a loop induces an electromotive force (EMF) in that loop. The induced EMF in Loop-B is proportional to the rate of change of magnetic flux through it.
5. Determine the Direction of Induced Current: According to Lenz's law, the direction of the induced current in Loop-B will be such that it opposes the change in magnetic flux. Since the magnetic flux through Loop-B is increasing (due to the increasing current in Loop-A), the induced current in Loop-B will flow in a direction that creates a magnetic field opposing the increase.
6. Conclusion on Induced Current Direction: If the magnetic field from Loop-A is directed upwards (due to the current in Loop-A), Loop-B will induce a current that flows in the same direction as Loop-A to oppose the increase in upward magnetic flux. Therefore, the induced current in Loop-B will also flow counterclockwise.
7. Determine the Interaction Between the Loops: Since the currents in Loop-A and Loop-B are in the same direction (both counterclockwise), they will attract each other. This is due to the fact that parallel currents attract each other.
Final Answer:
The induced current in Loop-B will flow in the same direction as the current in Loop-A (counterclockwise), and Loop-B will be attracted to Loop-A.
The induced current in Loop-B will flow in the same direction as the current in Loop-A (counterclockwise), and Loop-B will be attracted to Loop-A.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
Two identical coils A and B are kept on a horizontal tube side by side without touching each other. If the current in the coil A increases with time, in response, the coil B
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionTwo identical coaxial circular loops carry a current i each circulating int the same direction. If the loops approch each other the current in
View SolutionTwo different wire loops are concentric and lie in the same plane. The current in the outer loop is clockwise and increasing with time. The induced current in the inner loop then is
View SolutionConsider a circular loop of wire lying in the plane of the table. Let the current pass through the loop clockwise. Apply the right hand rule out the direction of magnetic field inside and outside the loop.
View SolutionA circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop
 View Solution
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
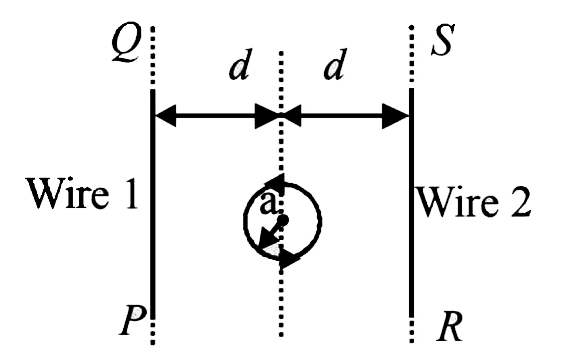
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that caseView SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseView Solution

