ABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
the triangles ADX and BAY are congruent.
To prove that triangles ADX and BAY are congruent, we will use the Side-Angle-Side (SAS) congruence criterion. Here are the steps:
Step 1: Identify the square and midpoints
We start with square ABCD. Let:
- A(0, 0)
- B(1, 0)
- C(1, 1)
- D(0, 1)
The midpoints are:
- X, the midpoint of AB, which is at (0.5, 0)
- Y, the midpoint of BC, which is at (1, 0.5)
Step 2: Show that AX = BX and BY = CY
Since X is the midpoint of AB:
- AX = BX = AB/2 = 1/2 (because AB = 1)
Since Y is the midpoint of BC:
- BY = CY = BC/2 = 1/2 (because BC = 1)
Step 3: Show that AD = AB
In square ABCD, all sides are equal:
- AD = AB = 1
Step 4: Show that angles A and B are right angles
Since ABCD is a square:
- ∠A = ∠B = 90 degrees
Step 5: Apply the SAS criterion
Now we have:
1. AD = AB (1 = 1)
2. AX = BY (1/2 = 1/2)
3. ∠A = ∠B (90° = 90°)
By the SAS congruence criterion, we can conclude that:
- Triangle ADX is congruent to triangle BAY.
Conclusion
Thus, we have proven that triangles ADX and BAY are congruent.
---
We start with square ABCD. Let:
- A(0, 0)
- B(1, 0)
- C(1, 1)
- D(0, 1)
- X, the midpoint of AB, which is at (0.5, 0)
- Y, the midpoint of BC, which is at (1, 0.5)
Since X is the midpoint of AB:
- AX = BX = AB/2 = 1/2 (because AB = 1)
- BY = CY = BC/2 = 1/2 (because BC = 1)
In square ABCD, all sides are equal:
- AD = AB = 1
Since ABCD is a square:
- ∠A = ∠B = 90 degrees
Now we have:
1. AD = AB (1 = 1)
2. AX = BY (1/2 = 1/2)
3. ∠A = ∠B (90° = 90°)
- Triangle ADX is congruent to triangle BAY.
Thus, we have proven that triangles ADX and BAY are congruent.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - INEQUALITIES
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - LOGARITHM
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
ABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYB
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
DX is perpendicular to AY.
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
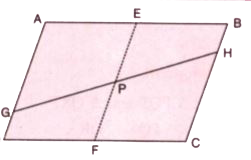
View SolutionABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14area of△ABC. GIVEN : A △ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
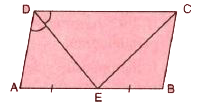
BC= BE
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
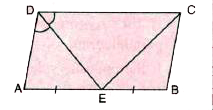
CE bisects angle C
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionE is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD . Prove that AEFD is a parallelogram.
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View Solution
