Complete Solutions to Triangles of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| NCERT EXEMPLAR | Triangles |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
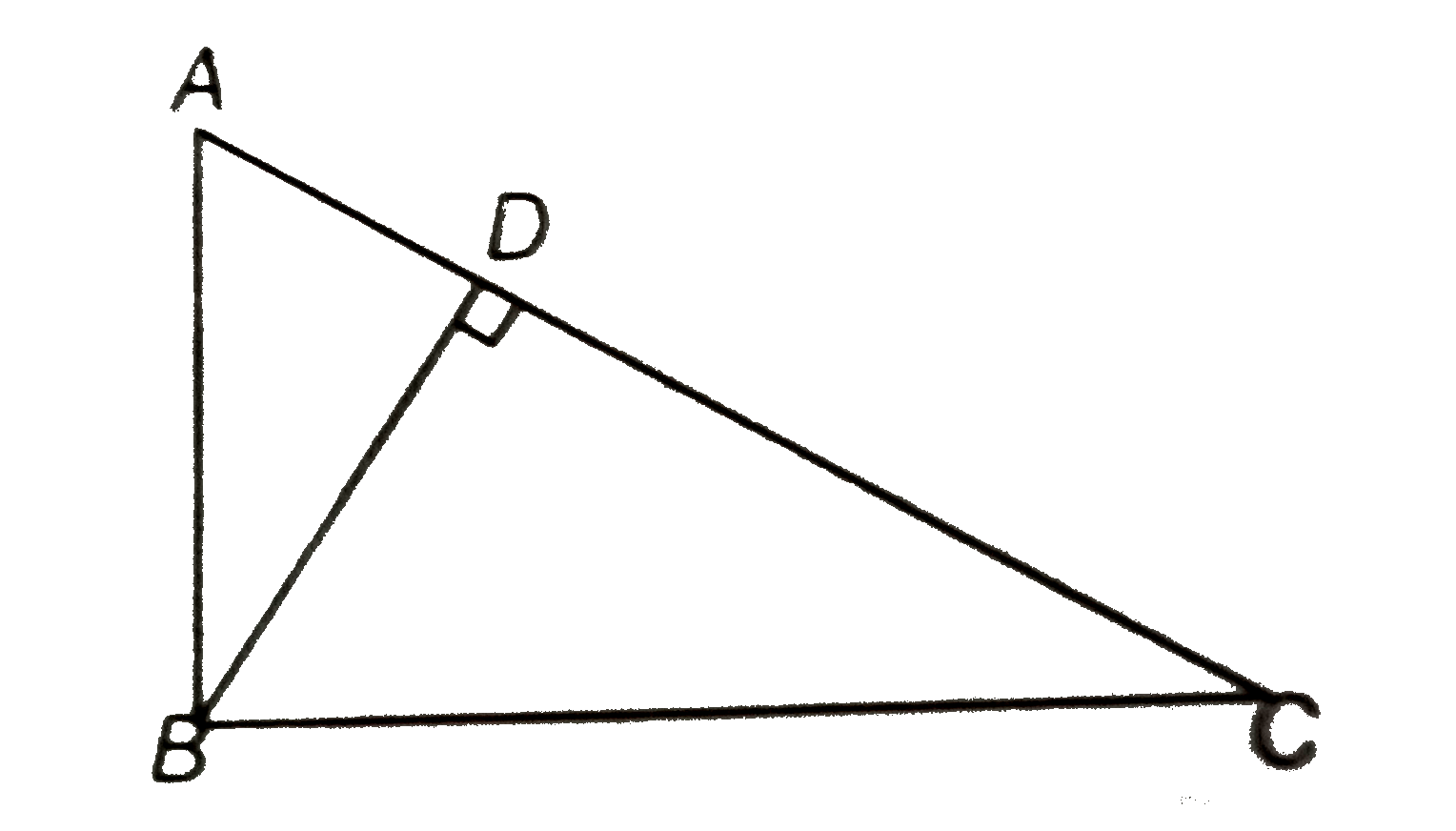
In figure, if `angleBAC=90^(@)` and `ADbotBC`. Then,

View SolutionIf the diagonals of a rhombus are 12cm and 16cm, find the length of each side.
View SolutionIf `DeltaABC~DeltaEDF` and `DeltaABC` is not similar to `DeltaDEF`, then which of the following is not true?
View SolutionIf in two `DeltaABC` and `DeltaPQR`, `(AB)/(QR)=(BC)/(PR)=(CA)/(PQ)`, then
View SolutionIn figure, two line segments `AC` and `BD` intersects each other at the point `P` such that `PA` = 6 cm, `PB` = 3 cm, `PC` = 2.5 cm, `PD`=5 cm, `angleAPB=50^(@)` and `angleCDP=30^(@)`. Then, `anglePBA` is equal to
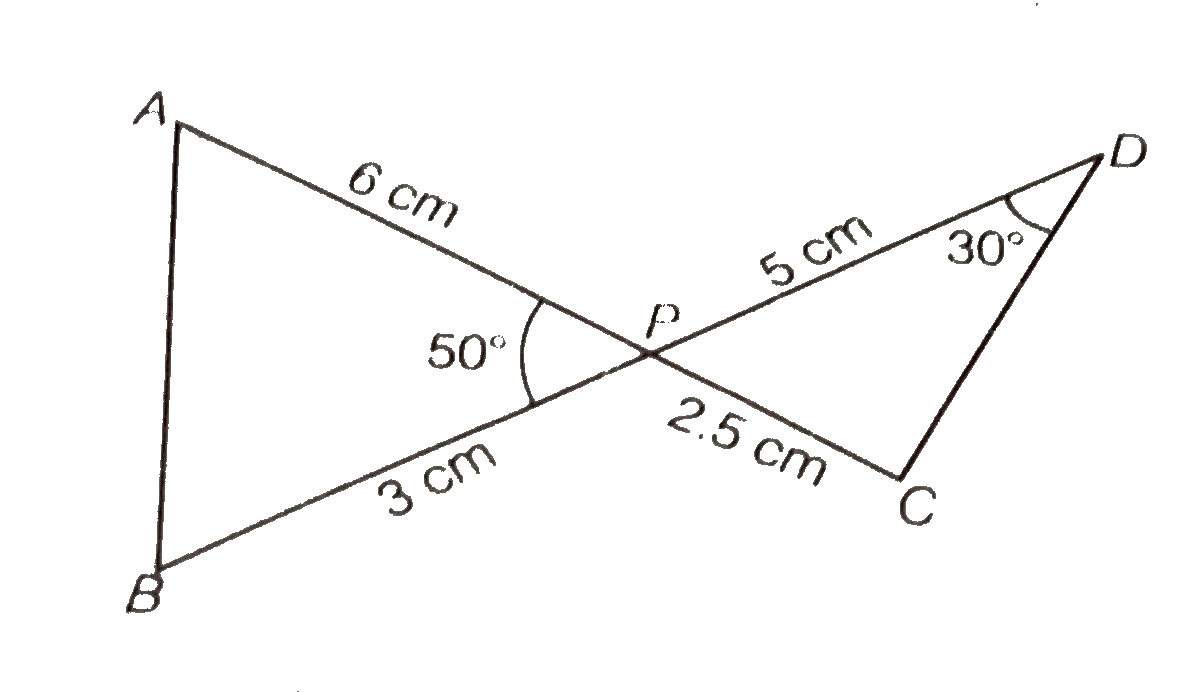
View SolutionIn `Delta DEF and Delta PQR`, it is given that `angle D=angle Q and angle R= angleE`, then which of the following is not true?
View SolutionIn `DeltaABC and DeltaDEF`, `angleB=angleE,angleF=angleC` and AB=3DE. Then, the two triangles are
View SolutionIf `DeltaABC~DeltaPQR` with `(BC)/(QR)=1/3`,then `(ar(DeltaPRQ))/(ar(DeltaBCA))` is equal to
View SolutionIf `DeltaABC~DeltaDFE,angleA=30^@,angleC=50^(@)`,AB=5 cm,AC=8 cm and DF=7.5 cm. Then, which of the following is true?
View SolutionIf in `DeltaABC and DeltaDEF` , `(AB)/(DE)=(BC)/(FD)`, then they will be similar, when
View SolutionIf `DeltaABC~DeltaQRP,(ar(DeltaABC))/(ar(DeltaPQR))=9/4`, AB=`18` cm and BC=`15` cm, then PR is equal to
View SolutionIf S is a point on side PQ of a `DeltaPQR` such that PS=QS=RS, then
View SolutionIs the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reason for your answer.
View SolutionIt is given that `DeltaDEF~DeltaRPQ`. Is it true to say that `angleD = angleR` and `angleF= angleP`? Why?
View SolutionA and B are respectively the points on the sides PQ and PR of a `Delta PQR` such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB `abs` QR? Give reason for your answer.
View SolutionIn figure BD and CE intersect each other at the point P. Is`DeltaPBC~DeltaPDE`? Why?

View SolutionIn `DeltaPQR` and `DeltaMST`, `angleP=55^(@),angleQ=25^(@),angleM=100^(@)and angleS=25^(@)`. Is `DeltaQPR~DeltaTSM`? Why ?
View SolutionIs the following statement true? Why? "Two quadrilaterals are similar, if their corresponding angles are equal".
View SolutionTwo sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
View SolutionIf in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle. Can you say that two triangles will be similar? Why?
View SolutionThe ratio of the corresponding altitudes of two similar triangles is `3/5`. Is it correct to say that ratio of their areas is `6/5`? Why?
View SolutionD is a point on side QR of `DeltaPQR` such that PD`bot`QR. Will it be correct to say that `DeltaPQD~DeltaRPD`? Why?
View SolutionIn figure, if `angleD=angleC`, then it is true that `DeltaADE~DeltaACB`? Why?

View SolutionIs it true to say that, if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reason for your answer.
View SolutionIn ` P Q R ,\ \ Q M_|_P R` and `PR^2-P Q^2=Q R^2`.Prove that `Q M^2=P MxxM R`
View SolutionFind the value of x for which DE`abs()`AB in given figure.
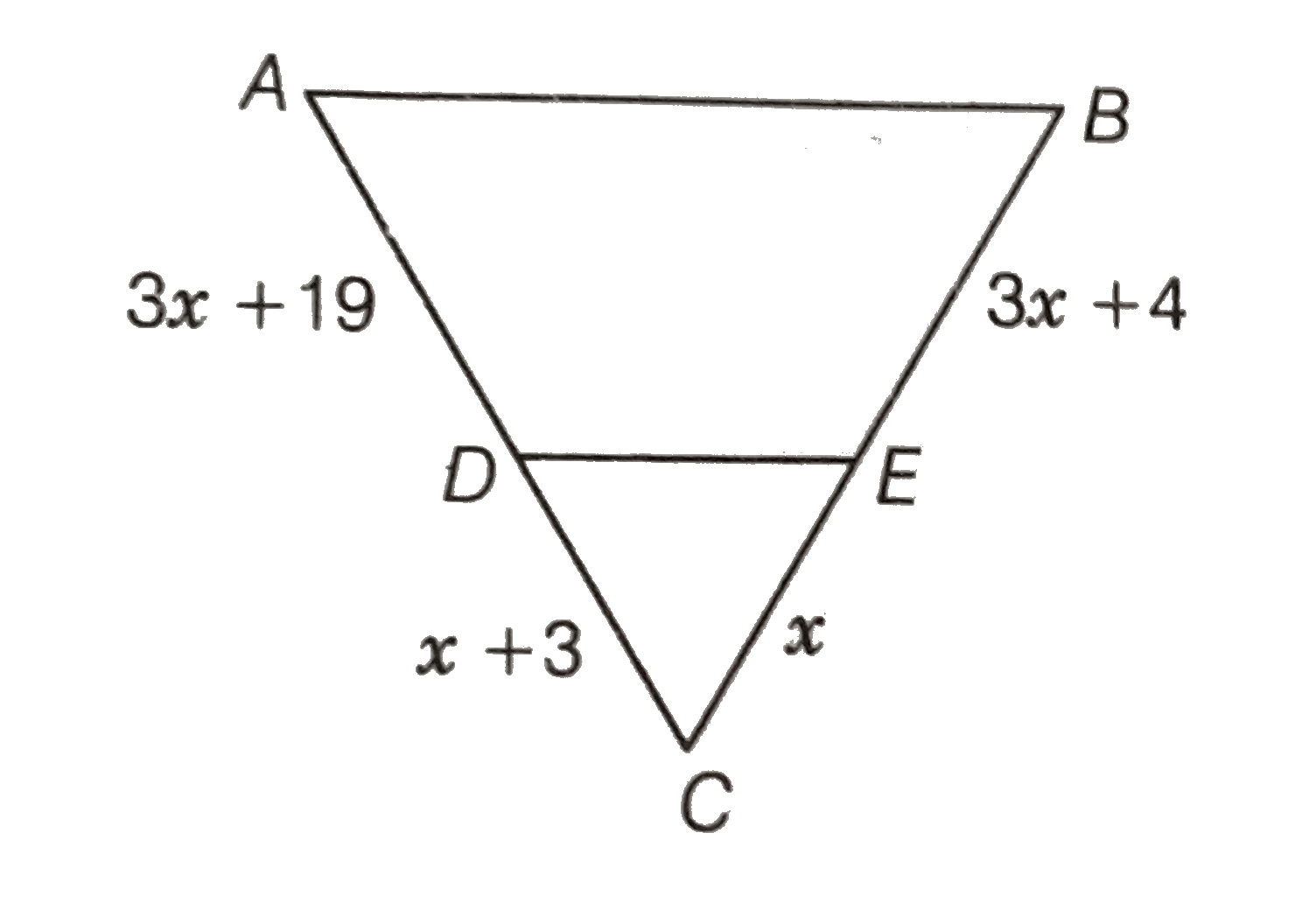
View SolutionIn figure, if `angle1=angle2` and `DeltaNSQ=DeltaMTR`, then prove that `DeltaPTS~DeltaPRQ`.
View SolutionDiagonals of a trapezium PQRS intersect each other at the point 0 ,PQ`abs()`RS and PQ=3 RS. Find the ratio of the areas of `DeltaPOQ` and `DeltaROS`.
View SolutionIn figure , if `ABabs()DC` and AC, PQ intersect each other at the point O. Prove that OA.CQ=OC.AP.

View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View SolutionIf `DeltaABC~DeltaDEF`, AB=4cm, DE=6,EF=9 cm and FD=12 cm, then find the perimeter of `DeltaABC`.
View SolutionIn figure, if DE`abs()`BC, then find the ratio of ar (`DeltaADE`) and ar(DECB).
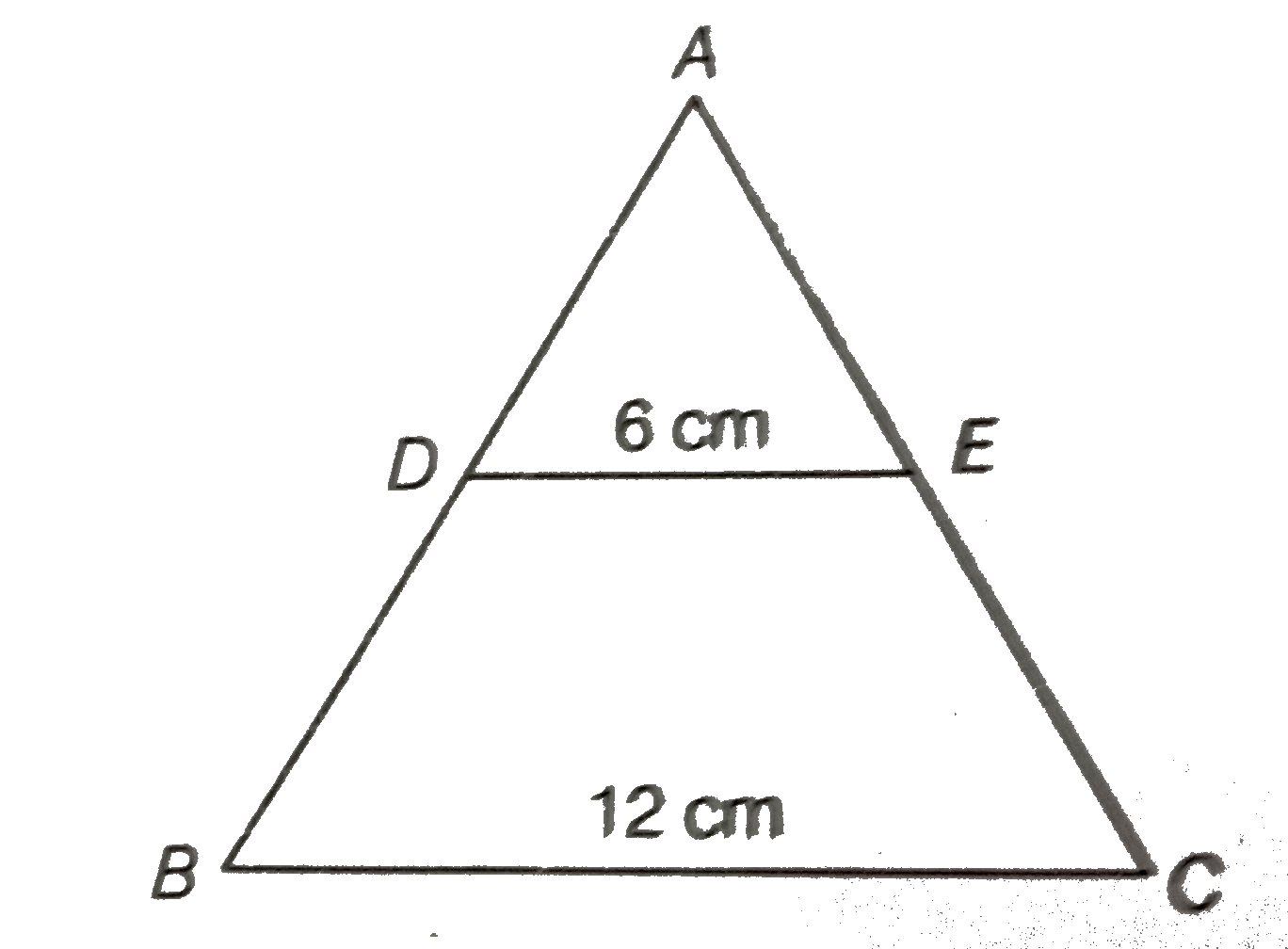
View SolutionABCD is a trapezium in which AB`abs()`DC and P,Q are points on AD and BC respectively, such that PQ`abs()`DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
View SolutionCorresponding sides of two triangles are in the ratio `2\ :3` . If the area of the smaller triangle is `48\ c m^2` , determine the area of the larger triangle.
View SolutionIn a `Delta PQR`, N is a point on PR, such that QN`bot`PR. If PN`cdot`NR=`QN^(2)`, then prove that `anglePQR=90^(@)`.
View SolutionThe areas of two similar triangles are `36\ c m^2` and `100\ c m^2` . If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
View SolutionIn given figure, if `angleACB=angleCDA,AC=8cm` and `AD=3 cm`, then find BD.
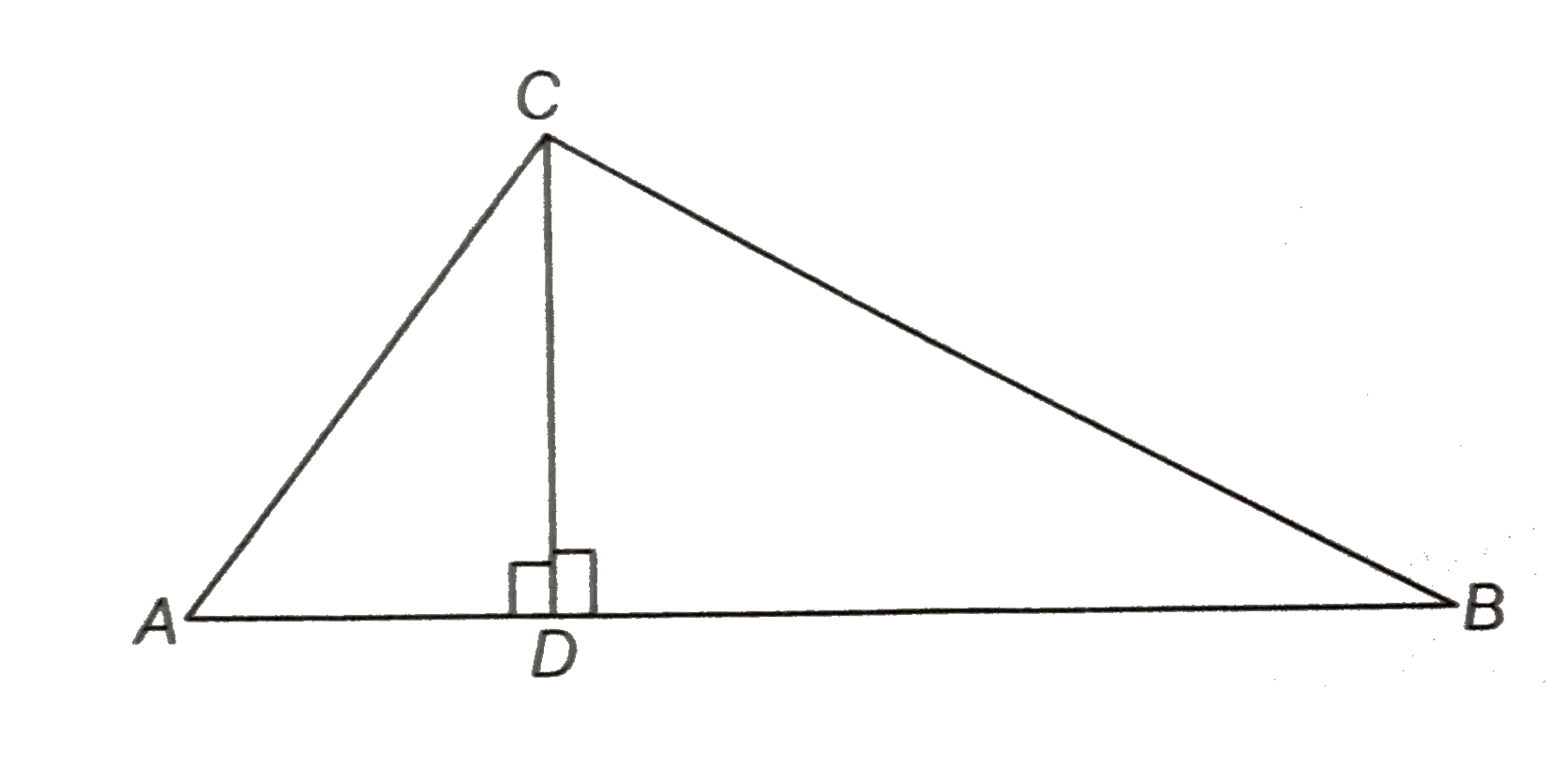
View SolutionA 15 high tower casts a sshadow 24 long at a certain time at the same time, a telephone pole casts a shadow 16 long. Find the height of the telephone pole.
View SolutionFoot of a 10 m long ladder leaning against a verticle wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
View SolutionIn given figure, if `angleA=angleC`, AB= 6 cm, BP = 15 cm, AP = 12 cm and CP= 4 cm, then find the lengths of PD and CD.

View SolutionIt is given that `DeltaABC~DeltaEDF` such that AB=5 cm, AC=7 cm, DF= 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
View Solution`If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIn the given figures, if PQRS is a parallelogram and `ABabs()PS`, then prove that `OCabs()SR`.
View SolutionA 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on teh wall.
View SolutionFor going to a city B from city A there is a route via city C such that `AC botCB`, AC =2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
View SolutionA flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
View SolutionA street light bulb is fixed on a pole 6 m above the level of the street. If a women of height 1.5 m casts a shadow of 3 m, then find how far she is away from the base of the pole.
View SolutionIn given figure, ABC is a triangle right angled at B and BD`bot`AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
View SolutionIn given figure PQR is a right angled triangle, right angled at Q and QS`bot`PR. If PQ=6 cm and PS=4cm, then find QS, RS and QR.

View SolutionIi `DeltaPQR`, PD`bot`QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
View SolutionIn a quadrilateral ABCD, `angleA+angleD=90^(@)`. Prove that
`AC^(2)+BD^(2)=AD^(2)+BC^(2)`
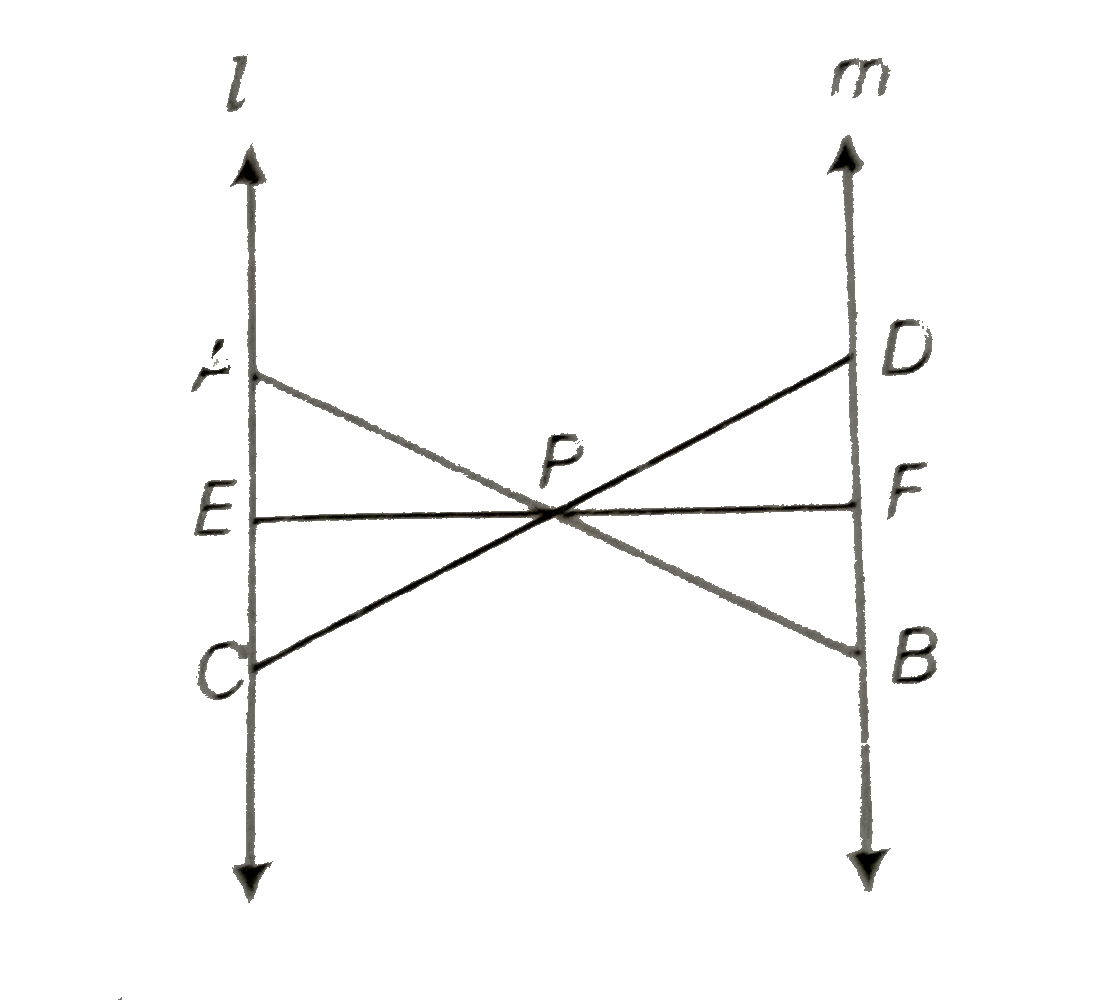
View SolutionIn given figure,l`abs()`m and liner segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF)=(AC)/(BD)=(CE)/(FD)`
View Solution14 In Fig. 6.21, PA, QB Rc and SD are all perpendiculars to a line l, AB 6 cm, Bc 9 cm, CD g cm and SP 36 om Find PO, QR an RS. Fig. 6.21
View SolutionO is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB`abs()`DC. Through O , aline segment PQ is drawn parallel to AB meeting AD in P and BC in Q, prove that PO=QO.
View SolutionIn figure, line segment DF intersects the side AC of a `DeltaABC` at the point E such that E is the mid-point of CA and `angleAEF-angleAFE`. Prove that `(BD)/(CD)=(BF)/(CE)`

View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionEquilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View Solution
Triangles questions and complete solutions for chapter TRIANGLES of NCERT EXEMPLAR MATHS (HINGLISH) of Class 10