Complete Solutions to Subjective of chapter MASTER PRACTICE PROBLEM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MASTER PRACTICE PROBLEM |
| BANSAL | Subjective |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In a given system of unit standard measurement of mass is 100 gm standard measurement of length is 200 cm and standard measurement of time is 5 sec 10 J energy in the given system of unit has value N, then value of N is
View SolutionRain is falling with speed `12sqrt(2)` m//s at an angle of `45^(@)` with vertical line A man in a glider going at a speed of v at angle of `37^(@)` with respect to ground find the speed (in m//s) of glider so that rain apears to him falling vertically Consider motion of glider and rain drops in same vertical plane.

View SolutionTwo balls are fired form ground level,`a` distance `d` apart. The right one is fired vertically with speed `v`. You wish to simultancously fire the left one at appropriate velocity `u` so that collides with the right ball when they reach their highest point. Value of horizontal `(u_(x))` and vertical `(u_(y))`components of `u` are respectively`:-`
 .
.
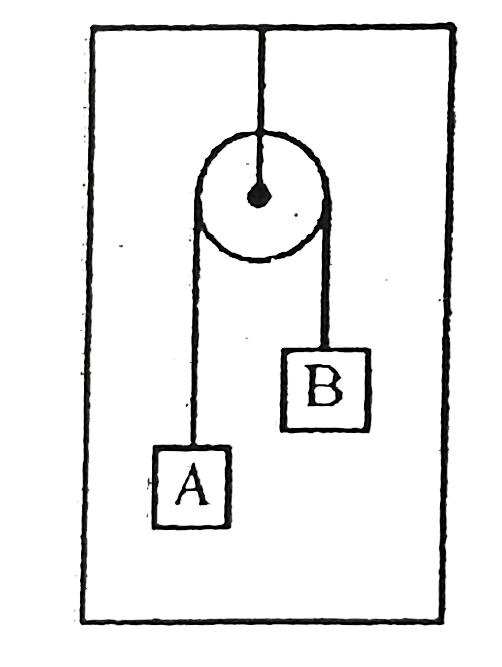
View SolutionAn atwood machine is setup in an elevator moving upward at `5 m//s` and slowing down at `2m//s^(2)` The initial velocity of block B is `2m//s` upward and the acceleration of block A is `3 m//s^(2)` downwards Find the time (in sec) at which block B will return to its initial position. Assume the string remains taut and the acceleration of the elevator does not change during the required time interval
View SolutionA car is travelling in steady rain with constant acceleration in a straight line When is begins to move the driver sees that the raindrops make track at an angle of `37^(@)` with the vertical on the side window. After 20 sec., the raindrops make track at an angle of `53^(@)` with vertical in same direction Find the acceleration of the car in `cm//s^(2)` Rain is falling at `3 m//s`.
View SolutionThe acceleration - time graph of a particle is as shown in figure Initial velocity of particle is `10 m//s` Displacement of the particle (in m) at the end of 8 sec is ___ Round off to nearest integer.

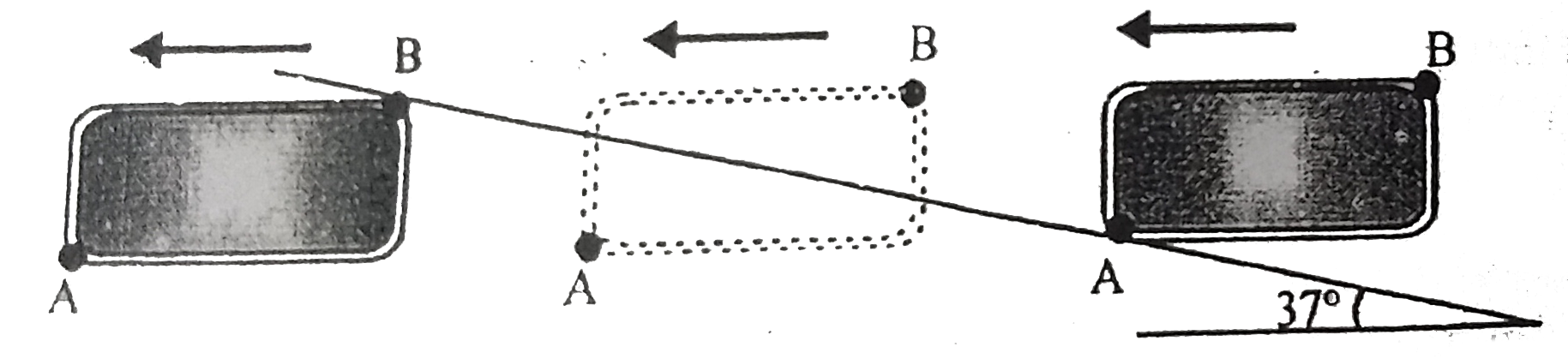
View SolutionA train is travelling at vm//s along a level straight track Very near and parallel to the track is a wall On the wall a naughty boy has drawn a straight line that slopes upward at a `37^(@)` angle with the horizontal A passanger in the train is observing the line out of window (`0.90` m high `1.8` wide as shown in figure) The line first appears at window corner A and finally disappears at window corner B if it takes `0.4` sec between appearance at A and disappearance of the line at B what is the value of v (in cm//s)?
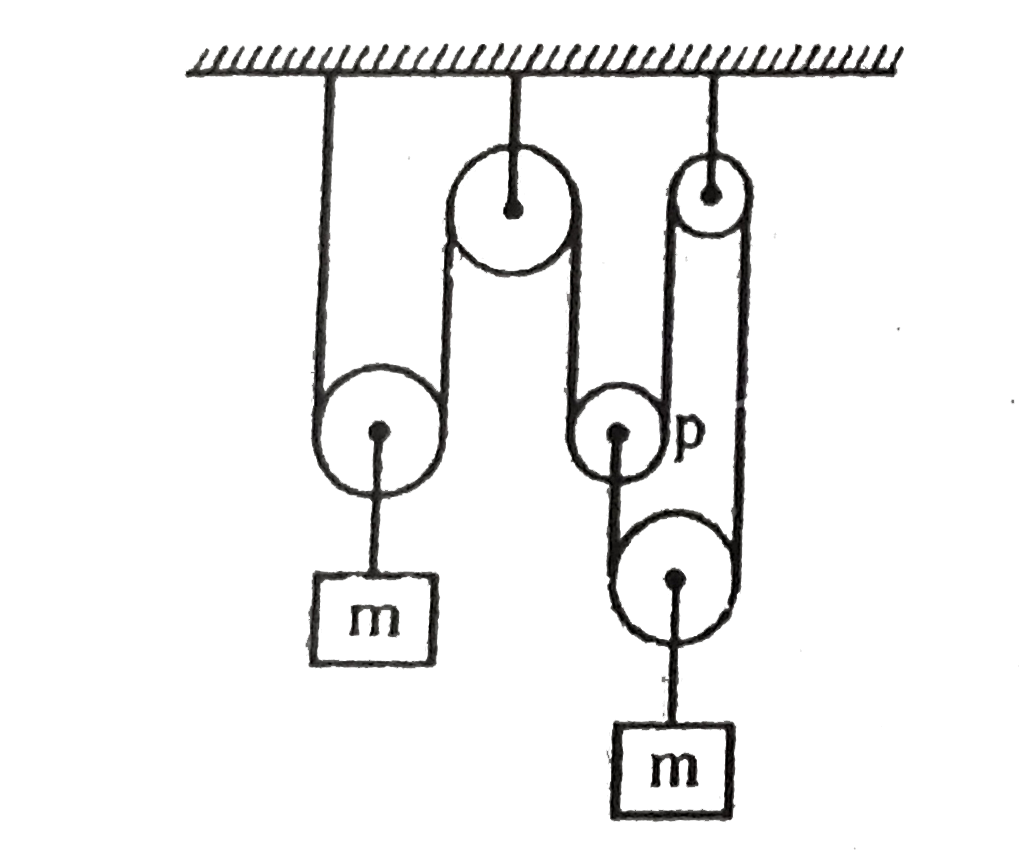
View SolutionAll pulleys are massless The string is light and inextensible Find acceleration of centre of pulley `'p' in m//s^(2)`
View SolutionA certain person nicknamed "Raju" encountered an automatic staircase (i.e. escalator) at a shopping complex, which was moving upward at a constant rate. Just for the fun of it he decided to walk up this escalator at the rate of one step a second Twenty steps brings him to the top Next day he goes up at two steps a second and reaches the top in 32 steps How many steps are there in the escalator?
View SolutionA man of mass 50 kg is standing on one end of a stationary wooden plank resting on a frictionless surface. The mass of the plank is 100 kg its length is 75 m and the coefficient of friction between the man the plank is `0.2` Find the least possible time (in sec) in which the man reach the other end starting from rest and stopping at the other end.
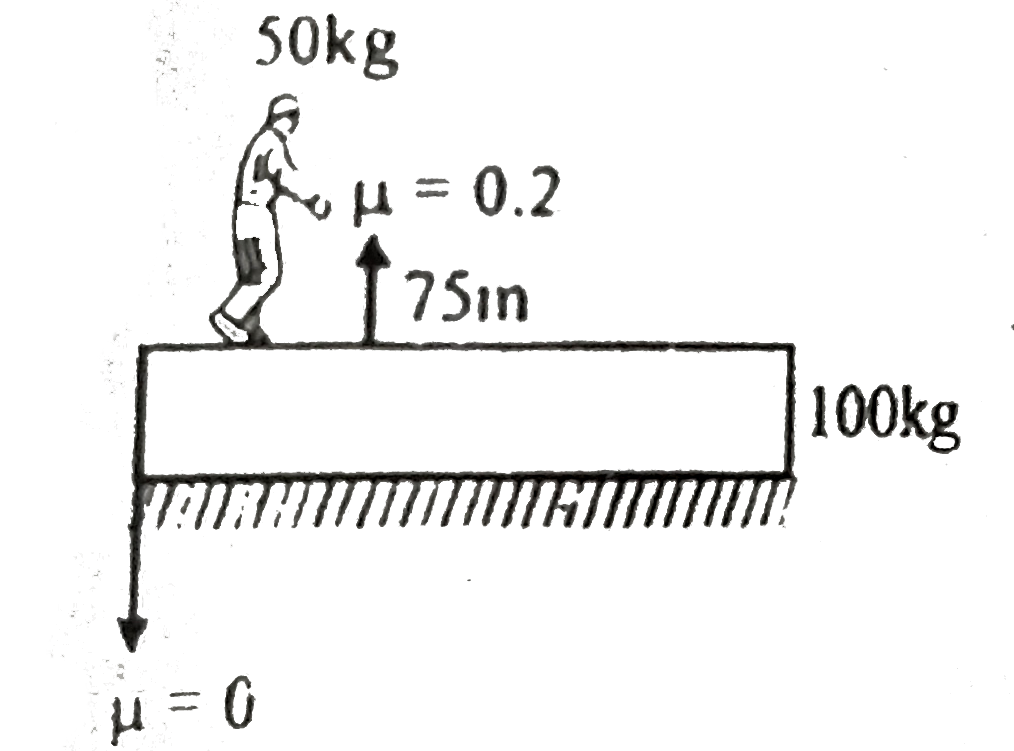
View SolutionA vertical rod of mass 4 kg is hanging on a rope and a 3kg cat is grasping the bottom end of the rod The rope is cut off and the frightened cat begins to run up on the rod. While the rod is falling vertically the cat remains at the same height with respect to the ground. If the acceleration of the rod is n (g//4) m//s^(2) then what is value of n.
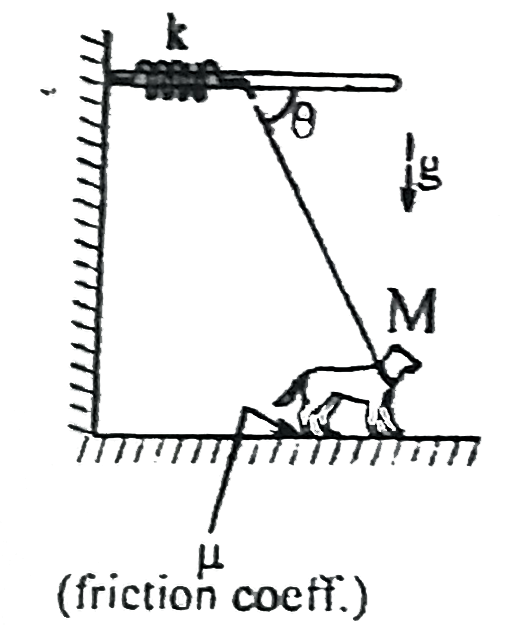
View SolutionA dog with mass M has its string attached to one end of a spring which runs without friction along a horizontal overhead rod. The other end of the springs is fixed to a wall The spring constant is K. The string is massless and inextensible and it maintains a constant angle `theta` with the overhead rod, even when the dog moves. There is friction with coefficient mu between the dog and the gound What is the maximum distance (in cm) that the dog moving slowly can stretch the spring beyond its natural length? Use M=30 kg,`theta=400N//m and mu=1/3`
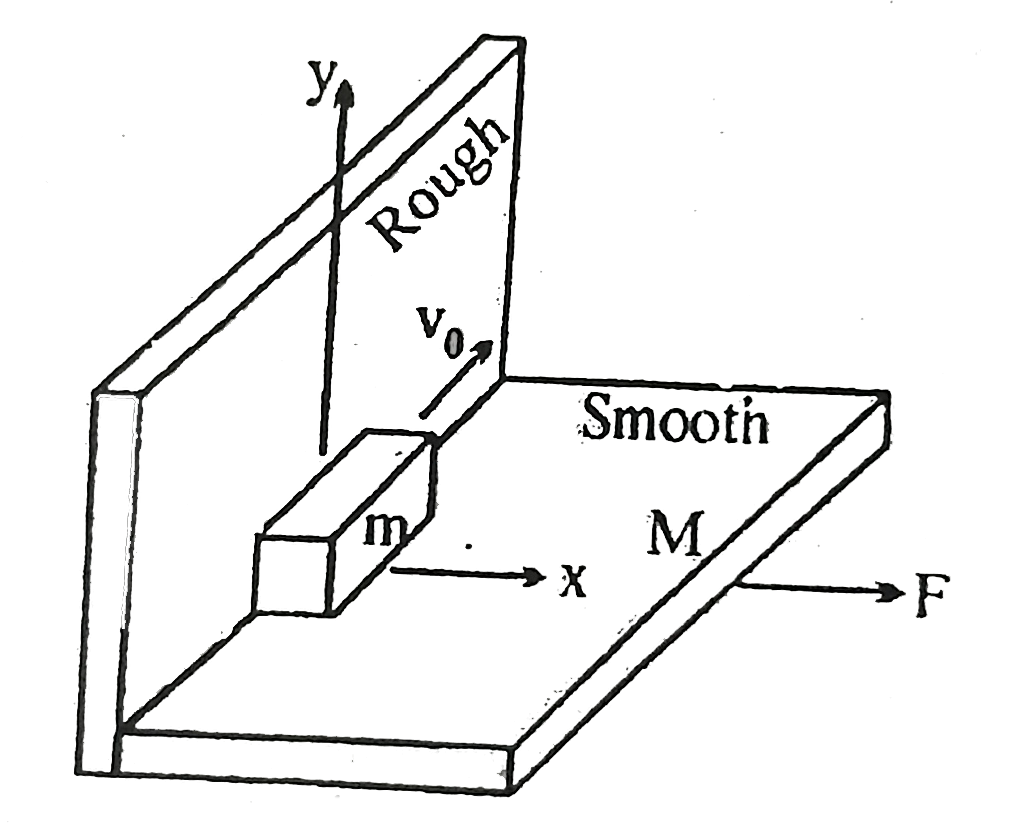
View SolutionFigure shows a block placed on a bracket. Bracket is placed on a smooth floor, it is pulled by a force F=6N horizontally Block is projected with velocity v_(0) relative to bracket as shown in figure. Find time in second after which it stops relative to bracket. Horizontal surface of bracket is smooth while vertical surface is rough (Given `m=1 kg M=5 kg v_(0)=5 m //s mu =0.5)` (Round off nearest integer)
View SolutionTwo identical cubes of mass `1.5` M each are kept almost touching the faces on a smooth horizontal surface On top of them we neatly placed a smooth ball of mass M, which begins to move vertically downwards, pushing the cubes sideways. Find the velocity of the ball `(in m//s)` just before impact on the horizontal surface The initial velocity of the ball is negligible Radius of the ball is 5m side of cube `2.5` m
View SolutionA ring of mass `m=1kg` can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of `L=0.7m` from the rod as shown in figure.
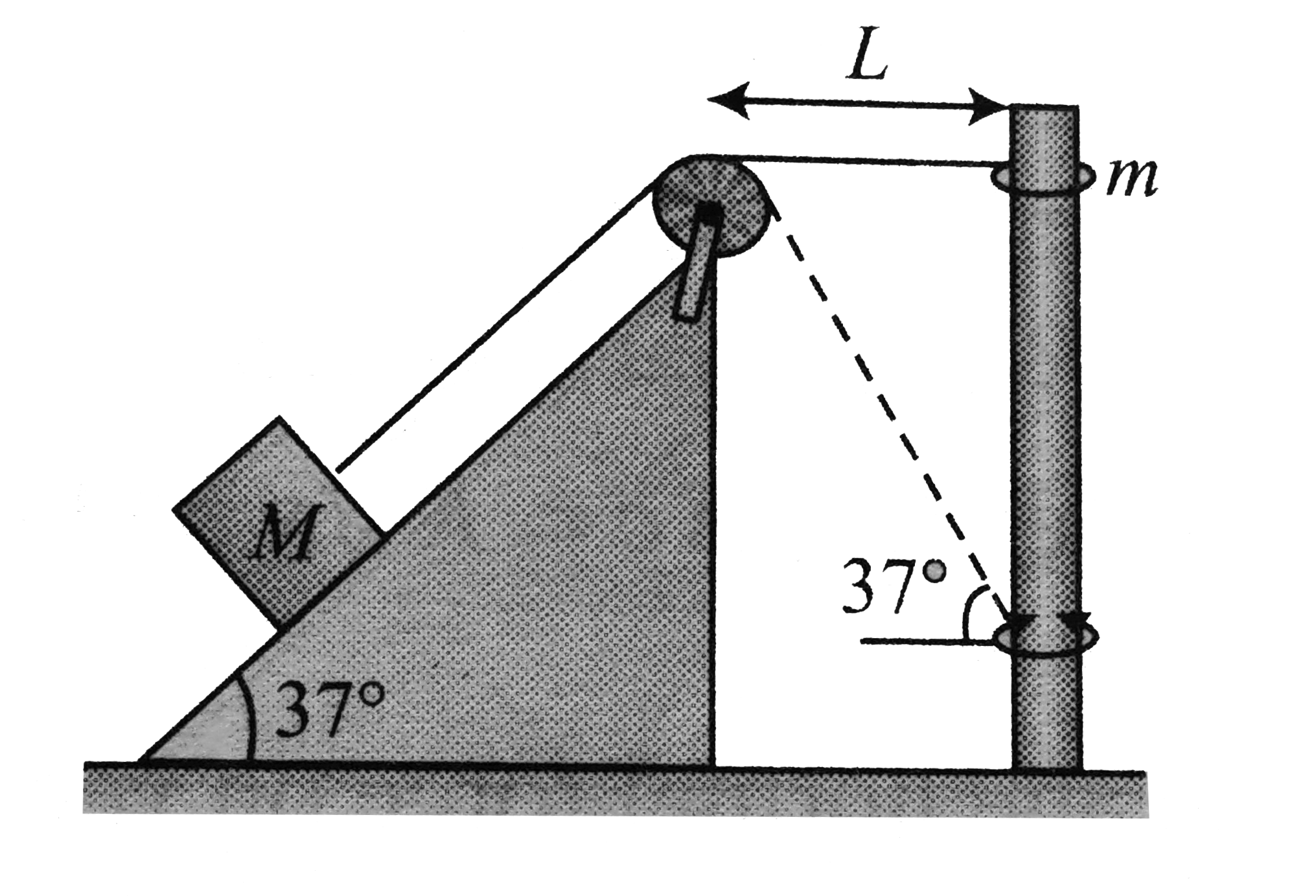
At the other end of the string mass `M=5kg` is attached, lying over a smooth fixed inclined plane of inclination angle `37^@`. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle `(alpha=37^@)` with the horizontal. `[sin 37^@=0.6]`
View SolutionA man of height `h_(0)=2 m` is bungee jumping from a platform situated at a height h = 25 m above a lake One end of an elastic rope is attached to his foot and the other end is fixed to the platform He starts falling from rest in vertical position. The length and elastic properties of the rope are chosen so that his speed will have been reduced to zero at instant when his head reaches the surface of water. Ultimetely the jumper is hanging from the rope with his head 8m above the water. Find the maxima acceleration acheived during the jump in `m//s^(2))`

View SolutionAt what angle `theta_(0)` with the horizontal, should a shell be fired if at the top of its trajectory its path has a radius of curvature equal to twice the maximum height of the trajectory
View SolutionTwo beads connected by a light inextensible string are placed over fixed vertical rings as shown in figure If mass of each bead is 100 gms and all surfaces are frictionless if the tension (T) in the string just after the beads are released from the shown position, then find `100T^(2) (in N^(2))`

View SolutionAn object A of mass 2 kg is moving on a frictionless horizontal track has perfectly inelastic collision with another object B of mass 3 kg made of the same material and moving in front of A in same direction their common speed after the collision is `4 m//s` Due to the collision the temperature of the two objects which was initially the same, is increased though only by `0.006^(@)` C What was the initial speed `(in m//s)` of the colliding object A before the collision?
View SolutionA cart of mass M has a pole on it from which a ball of mass mu hangs from a thin string attached at point P the cart and ball have initial velocity V the cart crashes onto another cart of mass m and sticks to it (figure) If the length of the string is R, the smallest initial velocity (in m//s) for which the ball can go in circles around point P is Neglect friction and assume M, `m gtgt mu` Given `m=1kg M=2 kg R=2m`
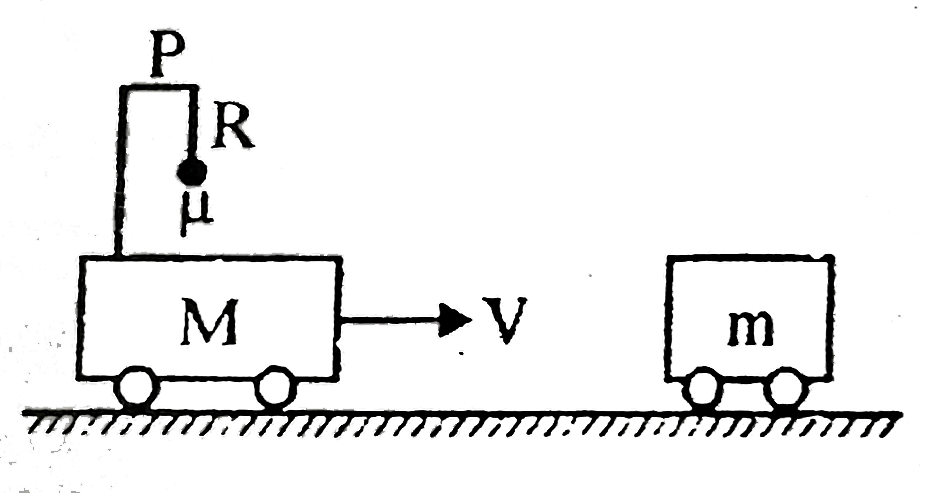
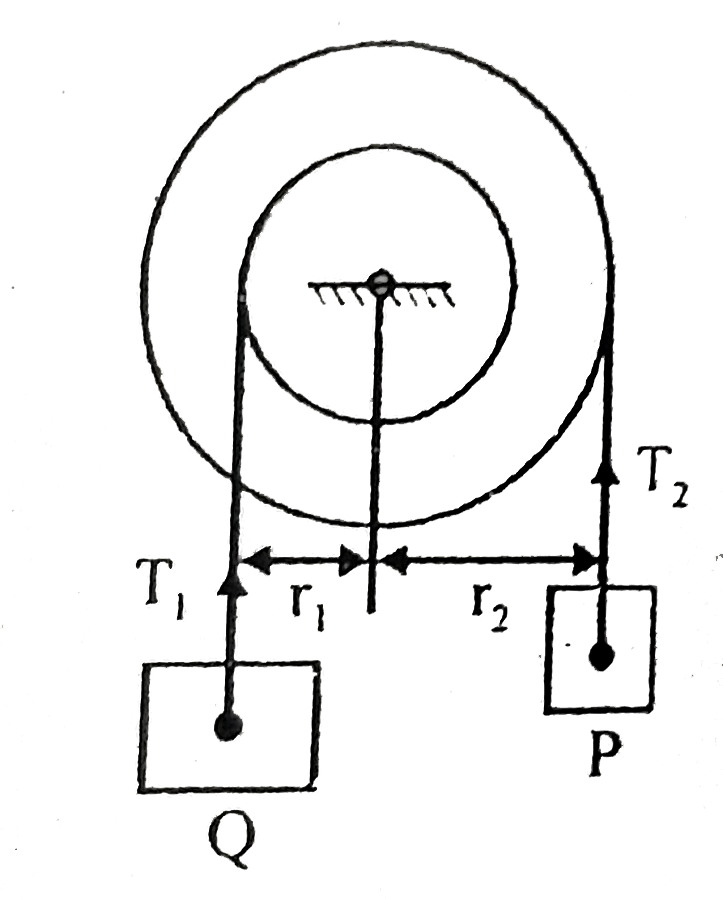
View SolutionNeglecting friction at the axle and the inertia of the two step pulley shown in figure find the acceleration 'a' of the falling weight P in `(m//s^(2))` (assume P=2 kg Q=2 kg & `r_(2)=2r_(1))`
View SolutionA uniform stick of mass m and length l with `I=1/12 ml^(2)` spins around on a frictionless horizontal plane, with its CM stationary A mass M is placed on the plane, and the stick collides elastically with it, as shown (with the contact point being the end of the stick) What should be the ratio of m//M be so that after the collision the stick has translational motion but no rotational motion?
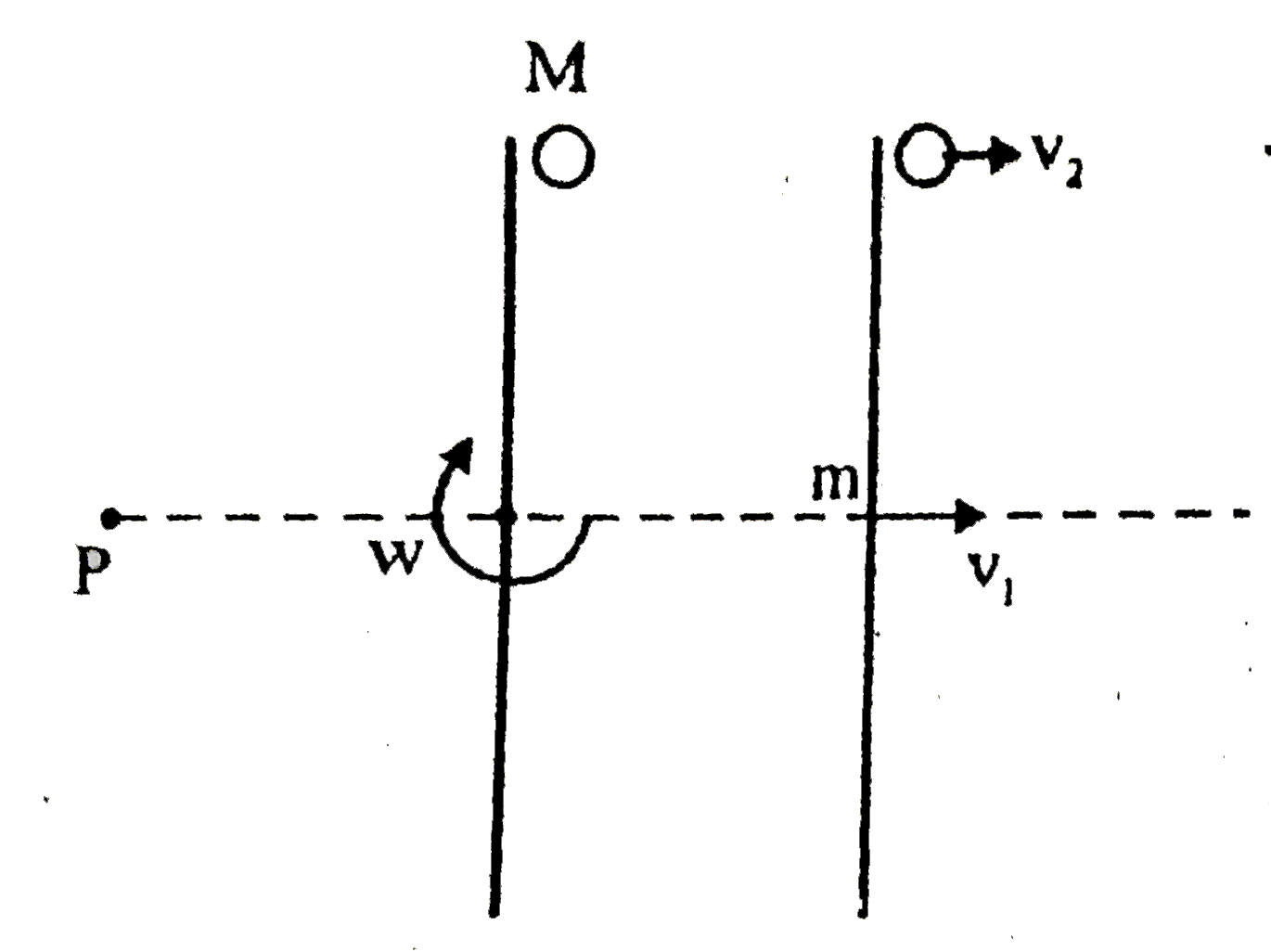
View SolutionTwo equal masses are situated at a separation `r_(0)` One of them is imparted a velocity `v_(0)=sqrt((GM)/r_(0))` perpendicular to the line joining them both are free to move Treating motion only under mutual gravitational force find the ratio of maximum and minimum separation between them. [Hint Solve in CM frame]

View SolutionA spherical planet has uniform density `pi/2xx10^(4)kg//m^(3)`. Find out the minimum period for a satellite in a circular orbit around it in seconds (Use `G=20/3xx10^(-11) (N-m^(2))/(kg^(2))`).
View SolutionTwo particles of mass 'm' and 3 m are initially at rest an infinite distance apart. Both the particles start moving due to gravitational attraction. At any instant their relative velocity of approach is `sqrt((ne Gm)/d` where 'd' is their separation at that instant. Find ne.
View SolutionTwo objects of equal volume `V=1 m^(3)` and different densities `d_(1) =500kg//m^(3)` and `d_(2) =1000kg // m^(3)` are gluod to each other so that their contact surface is flat and has an area `A=0.1 m^(2)` When the objects are submerged in a certain liquid they float in stable equilibrium the contact surface being parallel to the surface of the liquid (see the diagram) How deep (H in meters) can the contact surface be in the liquid so that the objects are not torn apart? The maximum force that the glue can with stand is `F=250 N (Neglect atmospheric pressure)

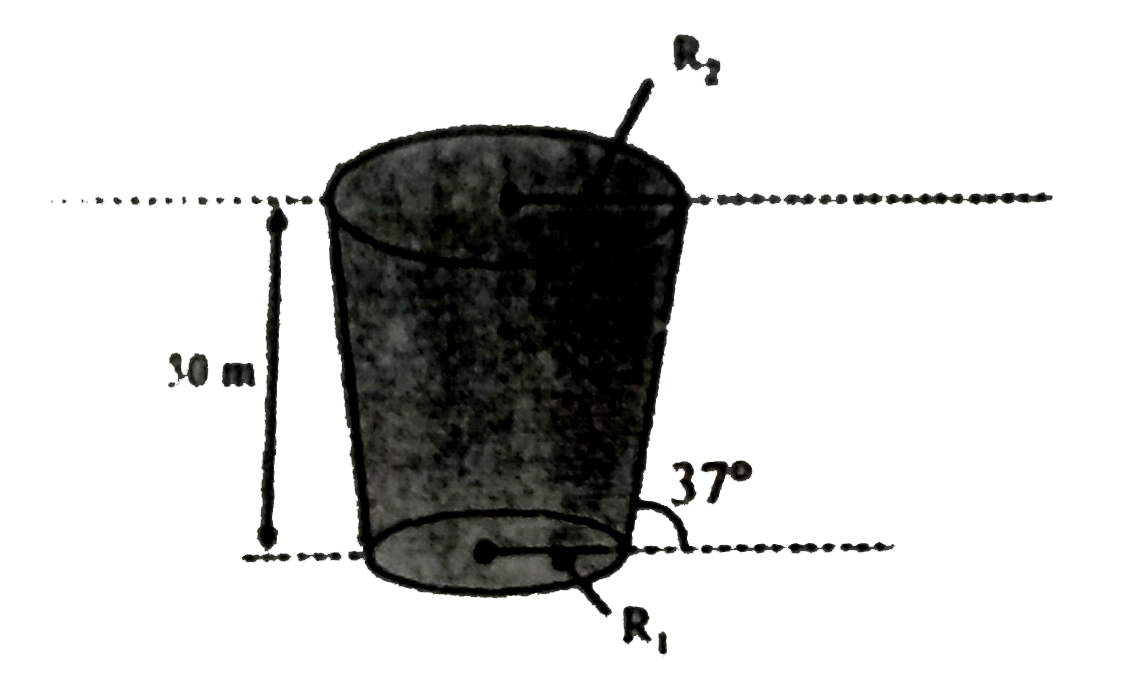
View SolutionThe figure shows a pond full of water having the shape of a truncated cone. The depth of the pond is 30 m. The atmospheric pressure above the pond is `1.0xx10^(5)` Pa. The circular top surface `(radius=R_(2))` and circular bottom surface `(radius = R_(1))` of the pond are both parallel to the ground The magnitude of the force acting on the top surface is the same as the magnitude of the force acting on the bottom surface. Obtain
View SolutionA block of wood weights 16 kg in air. A lead block which has apparent weight of 28 kg in water is attached to the block of wood, and both of them are submerged in water If their combined apparent weight in water is 19 kg find the density of wooden block in `kg//m^(3)` Take density of water `=1000 kg//m^(3)` .
View SolutionWater (density `1 gm//c)` is to be sucked upto point A. The area of the barrow tube is `1 cm^(2)`. In this situation, minimum work required to be done is `w_(1)`. When the tube is inverted and water is to be sucked upto point B, the minimum work required to be done is `w_(2)`. Find (`w_(2)-w_(1))` in Joule Fill 100 `(w_(2)-w_(1))` in OMR sheet.
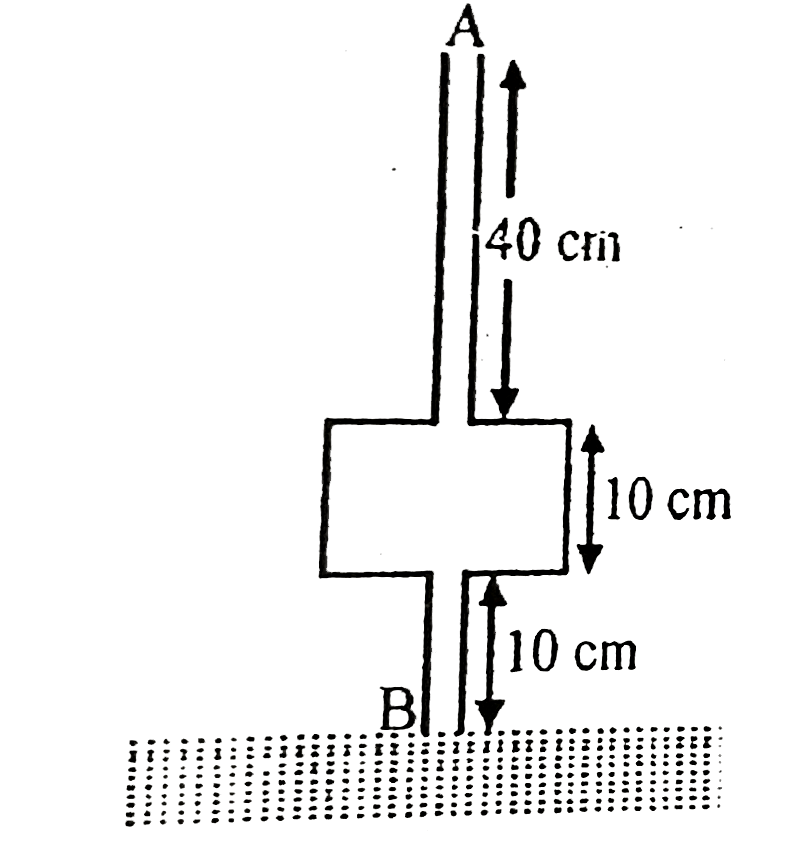
View SolutionA block of wood is floating in water such that `1//2` of it is submerged in water when the same block is floated in alcohol, `1//3^(rd)` of it's volume is submerged Now a mixture of water and alcohol is made taking equal volume of both and block is floated in it. What is the % of it's volume that is now submerged?
View SolutionA hole in the horizontal bottom of the container is closed by a hemispherical cap of radius R (see figure) The vessel is filled with liquid of density d. Bottom is at a depth of H. Find the force with which the cap presses down on the bottom of the vessel. Neglect atmospheric pressure. If the force is api N, fill 'a' in the OMR sheet (Take `d=10^(3)kg//m^(3), H=1m, R=30cm)`

View SolutionTwo solid balls have different radii but are made of same material. The balls are linked together with a long thin thread and released from a large height. At the terminal velocity, the thread is under tension. The larger ball has a fixed mass, but we have choice of the smaller ball with different masses. At what ratio of larger and smaller mass will this tension be maximum?
View SolutionA U-tube having uniform cross-section but unequal arm length `I_(1)=100` cm and `I_(2)=50` cm has same liquid of density `rho_(1)` filled in it upto a height h=30 cm as shown in figure. Another liquid of density `rho_(2)=rho_(1)//2` is poured in arm. A Both liquids are immiscible What length of the second liquid (in cm) should be poured in A so that second overtone of A is in unison with fundamental tone of B. (Neglect end correction)
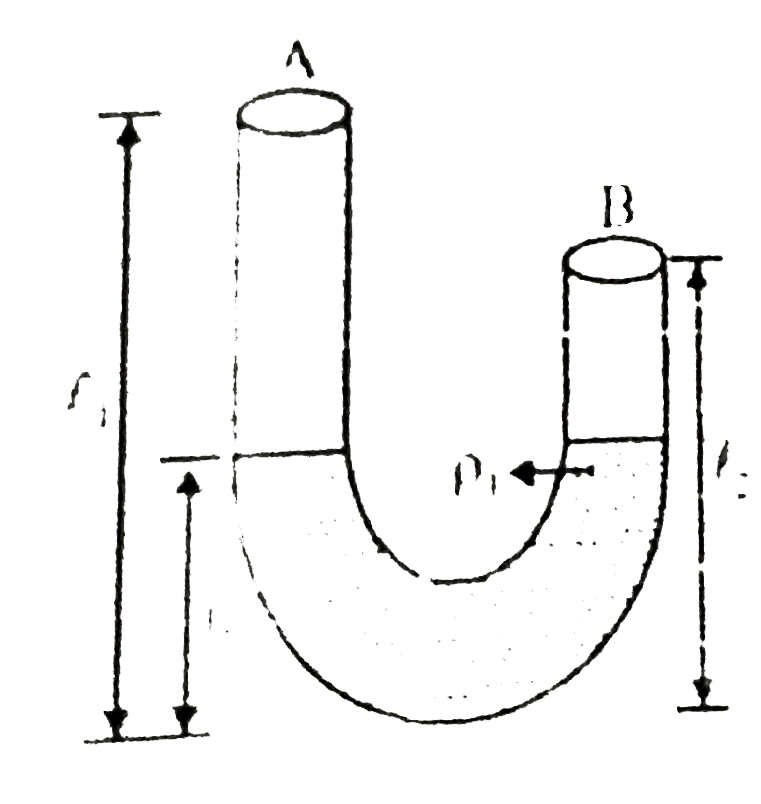
View SolutionA point source of sound is located somewhere along the x-axis. Experiments show that the same wave front simultaneously reaches listeners at x=-8 m and `x=+2.0 m` A third listener is positioned along the positive y-axis What is her y-coordinate (in m) if the same wave front reaches her at the same instant as it does the first two listeners?
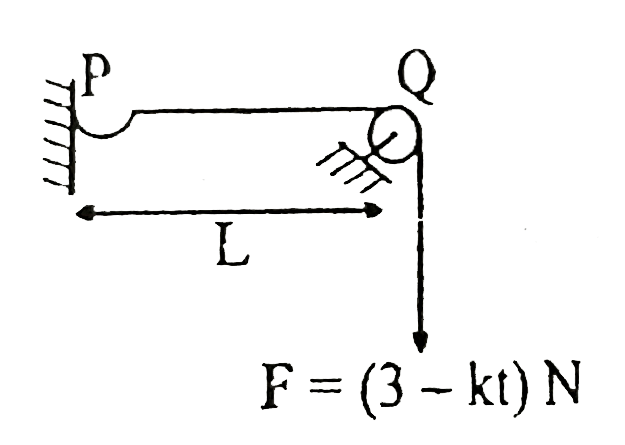
View SolutionIn the given figure a string of linear mass density `3xx10^(-2)` kg//m and length `L=1` m, is stretched by a froce `F=(3-kt)N`, where k is a constant and t is time in sec. At the time `t=0`, a pulse is generated at the end P of the string Find the value of k (in N//s) if the value of force becomes zero as the pulse reaches point Q.
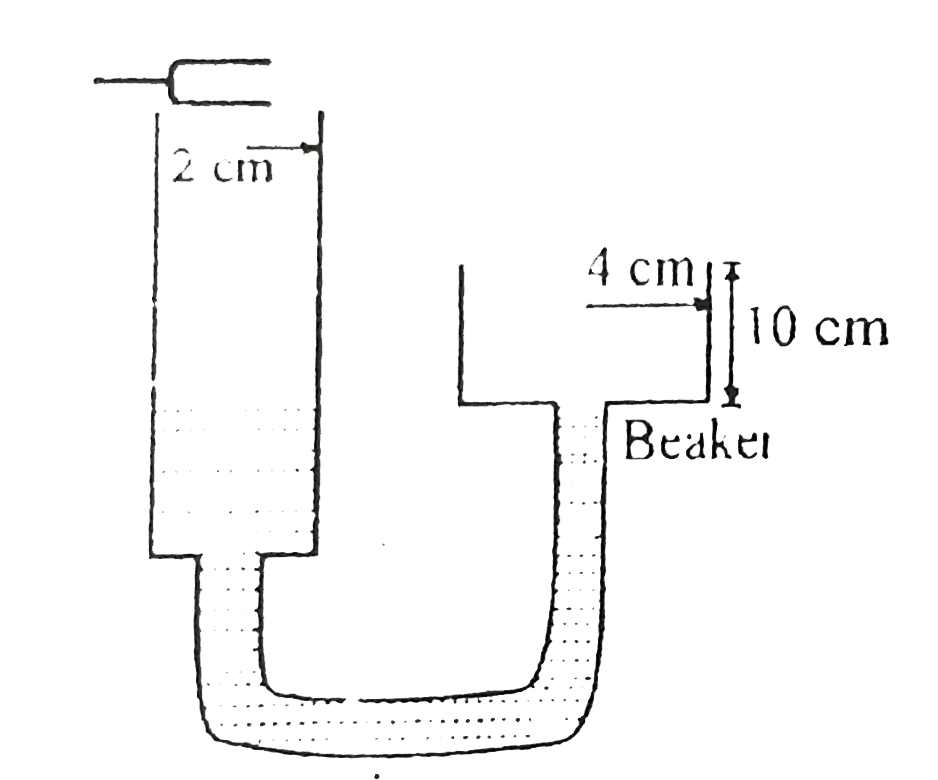
View SolutionIn a resonance column apparatus, first resonance is obtained when the water filling beaker (of cylindrical shape) is just empty as shown The water filling beaker is lowered down and it is seen that second resonance is obtained when beaker is filled upto brim. If the tunning fork has a frequency 420 Hz What is the velocity (in m//s) of sound in air ?
View SolutionShin Chan and his mother have a tin whistle each. The pipe length of Shin chan's tin whistle is 52 cm long while the pipe length of mother's tin whistle is 50 cm long. They both play at the same time, sounding the whistles at their fundamental resonant frequencies. They note that they are not in tune with each other. The velocity of sound in air is `325 m//s`. Assume the whistle is a pipe with one end open find the beat frequency (in Hz) that is heard when both whistles are playing simultaneously. (Round off to nearest integer)
View SolutionIf the kinetic energy of pulse travelling in a taut string is `Kxx10^(-2)` mJ then find the value of K (Given `T=10 N & mu=0.1 kg//m`
View SolutionTwo cylinders of equal masses, one made of material A and the other of material B, are heated to `50^(@)` C and placed on two large blocks of ice at `0^(@)` C If both the cylinders have the same height, find the ratio `(h_(A)//h_(B))` of their maximum depth of penetration in the ice. Assume that no heat is lost to the surroundings and change in gravitational potential energy is not considered `S_(A)=0.2cal g^(-1)(C^(@)),rho_(A) = 4 g cm^(-3)`
`S_(B) = 0.1 cal g^(-1) (C^(@)), rho_(B)=2 g cm^(-3)`
View SolutionIn two calorimeters we poured 200 g of water each- at temperatures of `+30^(@)` C and `+40^(@)` C. From the "hot" calorimeter 50 g of water, is poured into "cold" calorimeter and stirred. Then, from "cold" calorimeter 50 g of water is poured in "hot" and again stirred. How many times do you have to pour the same portion of water back and forth so that the temperature difference between water in the calorimeters becomes less than `3^(@)` C? Heat loss during the transfer and heat capacity of calorimeters is neglected.
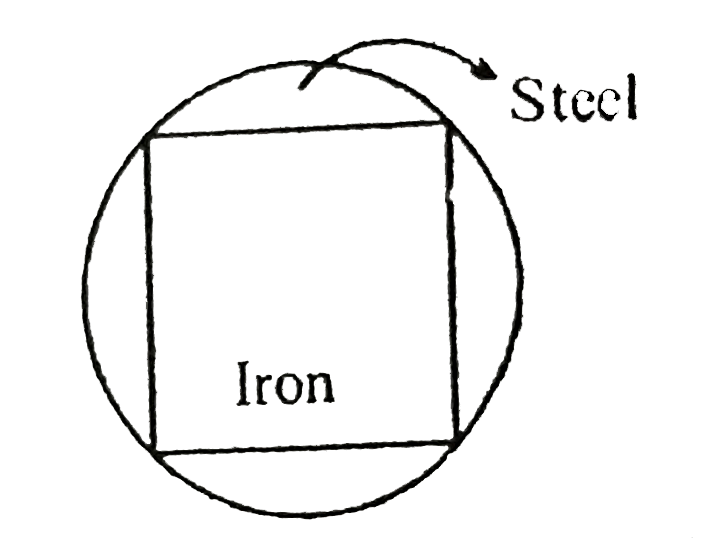
View SolutionA composite rod is made from stainless steel and iron and has a length of `0.5` m The cross-section of this composite rod consists of a square within a circle. The square is 1 cm on a side `k_(steel)=14 W//m^(@)` C, `k_(iron)=80 W//m^(@)` C One end of the rod is at `78^(@)` C and other end is in melting ice. Find the amount of ice melted in 7 minutes (in gm). (Take `pi=22//7`)
View SolutionA small sphere (emissivity`=0.9, radius =r_(1)`) is located at the centre of a spherical asbestos shell (thickness`=5.0` cm , outer radius `=r_(2)`) The thickness of the shell is small compared to the inner and outer radii of the shell. The temperature of the small sphere is 800 K while the temperature of the inner surface of the shell is 600 K The temperature of small sphere is maintained constant. Assuming that `r_(2)/r_(1)=10.0` and ignoring any air inside the shell, find the temperature (in k) of the outer surface of the shell Take : `K_(asbestor)=0.085 W//m^(@)` C `sigma = 17/3 xx10^(-8) W//m^(2)k^(4)`
View SolutionA room is heated by a radiator that has a constant temperature T (unknown). When the outside temperature is 260 K, the room temperature is 300 K. However, when the outside temperature drops to 240 K, the room temperature is only 290 K. Estimate the radiator temperature T.
View SolutionOne mole of an ideal monoatomic gas is taken from state A to state B through the process `P=3/2 T^(1//2)` It is found that its temperature increases by 100 K in this process. Now it is taken from state B to C through a process for which internal energy is related to volume as `U= 1/2 V^(1//2)` Find the total work performed by the gas (in Joule) if it is given that volume at B is `100 m^(3)` and at C it is `1600m^(3)` [Use `R= 8.3 J //mol-K`]
View Solution`0.5` mole of an ideal gas at constant temperature `27^(@)C` kept inside a cylinder of length `L` and cross-section area A closed by a massless piston The cylinder is attached with a conducting rod of length `L` cross-section area `(1//9)m^(2)` and thermal conductivity k whose other end is maintained at `0^(@)C` If piston is moved such that rate of heat flow through the conducing rod is constant then find velocity of piston when it is at height `L//2` from the bottom of cylinder [Neglect any kind of heat loss from system
 .
.
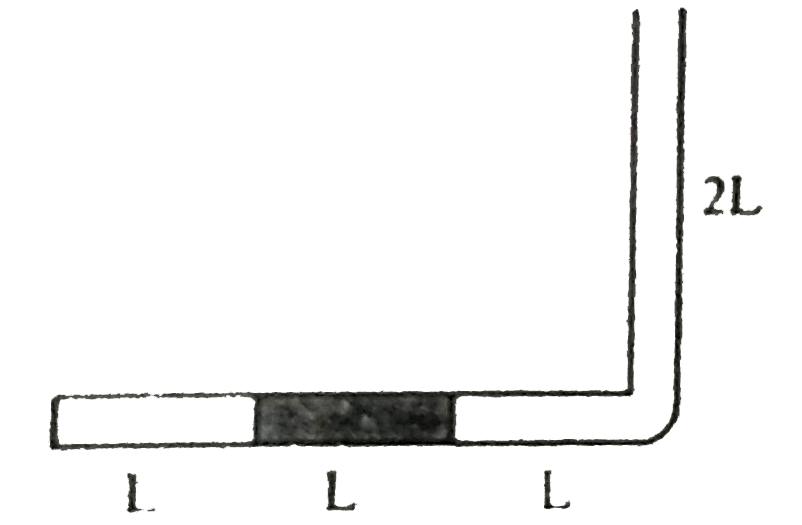
View SolutionThe narrow tube with one of its ends sealed as shown in the figure, is in a vertical plane. In the 3L long horizontal part of the tube a mercury column of length L blocks some oxygen gas of length L. The outside air - pressure of `p_(0)` equals with the pressure of a mercury column of height L. Increasing the temperature of the surrounding, the volume of the blocked gas doubles while the gas absorbs `Q=7J` of heat from its surroundings. How much work (in Joule) is done by the expanding gas?
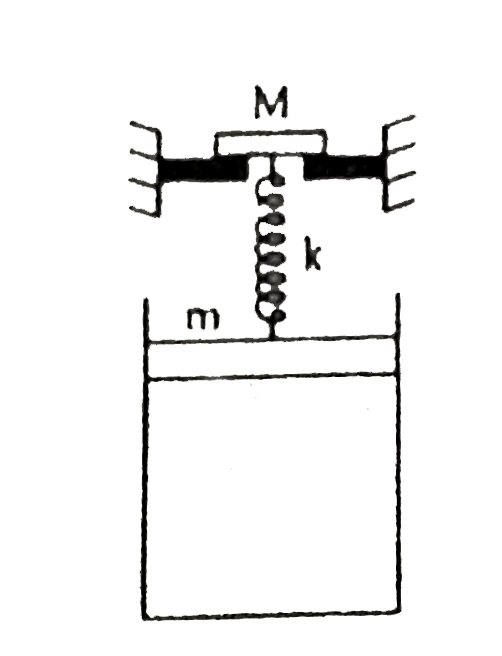
View Solution`0.01` moles of an ideal diatomic gas is enclosed in an adiabatic cylinder of cross-sectional area `A=10^(-4)m^(2)` In the arrangement shown, a block of mass `M= 0.8` kg is placed on a horizontal support, and piston of mass `m=1` kg is suspended from a spring of stiffness constant `k=16 N//m` Initially, the springs is relaxed and the volume of the gas is `V= 1.4 xx10^(-4)m^(3)` When the gas in the cylinder is heated up the piston starts moving up and the spring gets compressed so that the block M is just lifted up. Determine the heat supplied (in Joule) Take atmospheric pressure `P_(0)=10^(5) Nm^(-2) , g=10 m//s^(2)`
View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is `T_(A)` =200 K. In states B and C the temperature of the gas is the same.

What is the greastes temperature of the gas during the cyclic process ?
View SolutionA diatomic ideal gas is taken through the cyclic process shown in the figure in state 1 the pressure of the gas is 100 kPa and its temperature is 350 K in state 2 the pressure is 300 kPa What is the efficiency of the cycle in percent rounded to nearest integer` [Take l n 3=12//11]`
View SolutionIn a linear particle accelerator two large plane uniformly charged are placed parallel to each other as shown in the figure.
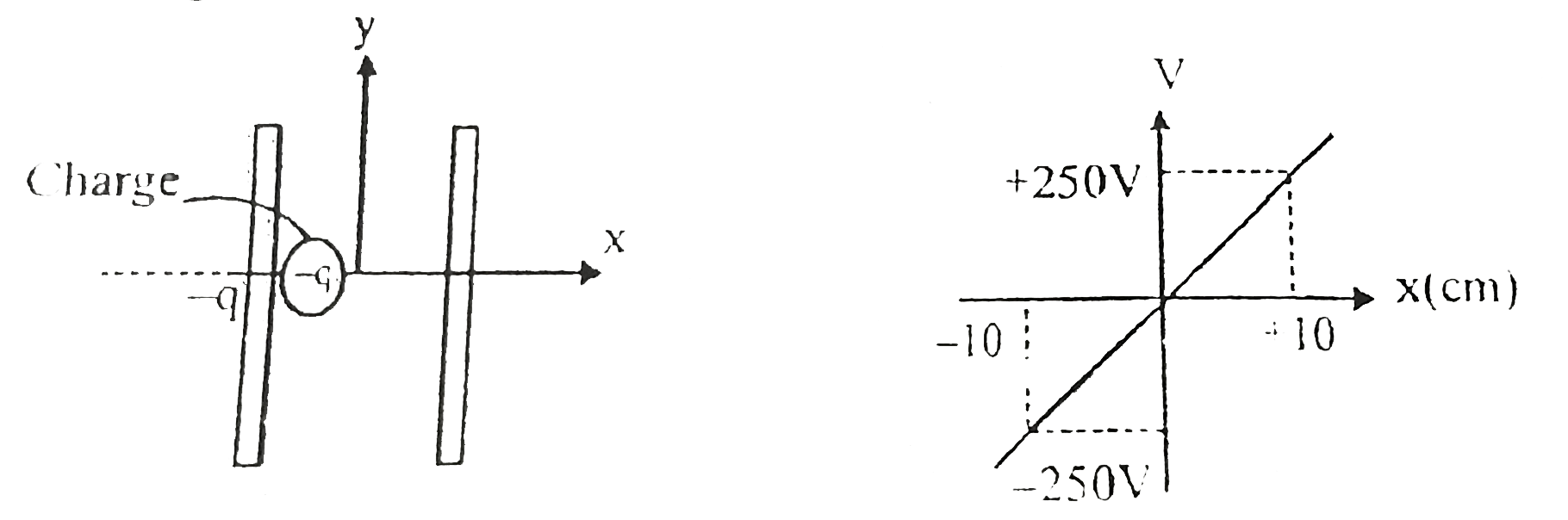
figure also shows variation of potential between planes A charged particle carrying a charge `q=1.6xx10^(-19)` C and having mass m `=16xx10^(-31)` kg is released from rest at `x=-10` cm determine time taken (in ns ) by particle to strike the other plane Neglect relativistic considerations.
View SolutionA thin spherical soap bubble has surface tension S . It's surface is charged with charge Q, its's volume is V it is found that when `Q^(2)=npi varepsilon_(0) SV` the excees pressure inside the bubble becomes zero find n.
View SolutionThe visible portion of a lightning strike is preceded by an invisible stage in which a column of electrons extends downward from a cloud to the ground Assume the linear charge density along the column is `1.00xx10^(-3)C//m` Treat the column of charge as if it were straight and infinitely long. At what distance (in m) from the column of electrons does the electric field have a magnitude of `3.00xx10^(6) V//m` the dielectric strength for air? This is an estimate of the radius of a visible lightning bolt. (Round off to nearest integer) (value of `in_(0)is 8.85xx10^(-12) C^(2)//Nm^(2))`
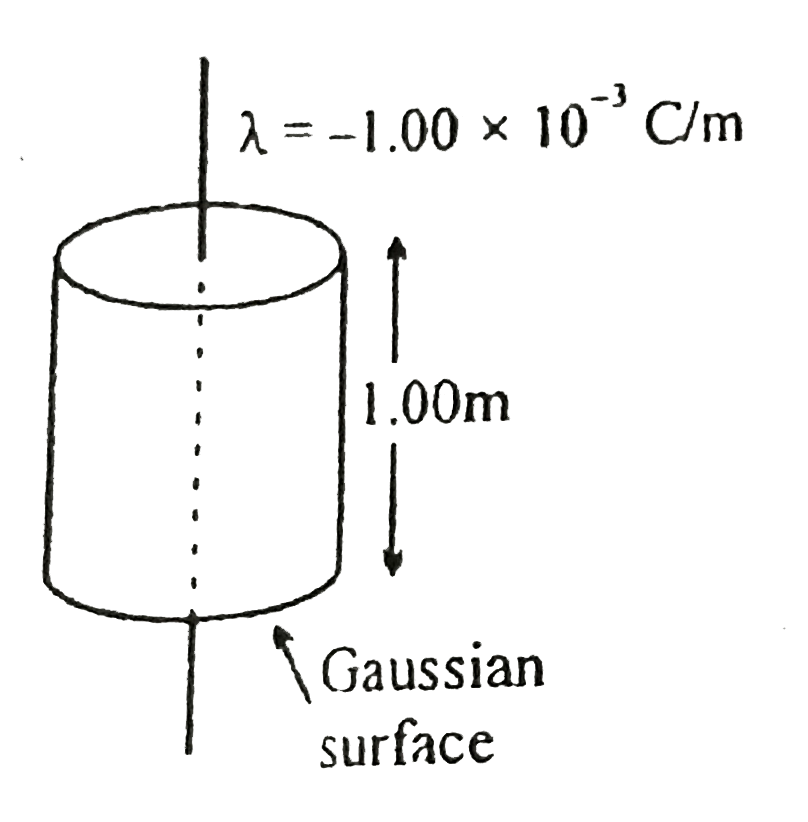
View SolutionAn electric field is given by `vec(E)=4hat(i)+3(y^(2)+2)hat(j)` pierces gaussian cube of side 1 m placed at origin such that one of its corners is at origin & rest of sides are along positive side of coordinate axis. If the magnitude of net charge enclosed is n `varepsilon_(0)` then n (in SI units) will be equal to
View SolutionThe diagram shows a semicircular ring carrying uniformly distributed charge `+2muC` on it. The radius of the ring is 4 cm A point charge `+2muC` is taken slowly from the point (0,0,8cm) to (0,8cm,0). The manitude of work done is equal to 4J After fixing the charge at its new position, the ring is rotated in anticlockwise sense about the x-axis as seen from (16cm,0,0) by an angle `pi//2` What is the magnitude of work done by electric field during the rotation of the ring?

View SolutionA particle is unchanged and is thrown vertically upward from ground level with a speed of `5sqrt(5)` m//s in a region of space having uniform electric field As a result, it attains a maximum height h. The particle is then given a positive charge +q and reaches the same maximum height h when thrown vertically upward with a speed of `13 m//s` Finally the particle is given a negative charge -q Ignoring air resistance determine the speed (in m//s) with which the negatively charged particle must be thrown vertically upward, so that it attains exactly the same maximum height h.
View SolutionA square loop of side 'l' each side having uniform linear charge density 'lambda' is placed in 'xy' lane as shown in the figure There exists a non uniform electric field `vec(E)=a/l(x+l)hat(i)` where a and l are constants and x is the position of the point from origin along x-axis. Find the resultant electric force on the loop (in Newtons) if `l=10 cm lambda=20 muC//m and a=5 xx 10^(5) N//C`.

View SolutionA positive charge `+q_(1)` is located to the left of a negative charge `-q_(2)` On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00cm to the right of the negative charge if `q_(2)=-12muC` , what is the value of charge `q_(1) in muC`
View SolutionThe two ends of a rubber string of negligible mass and having unstretched length `24cm` are fixed at the some height as shown. A small object is attached to the string in its midpoint due to which the depression `h` of the object in equilibrium is `5cm`. Then the small object is charged and a vertical electric field `E_(1)` is switched on in the region. The equilibrium depression of the object increases to `9cm`, now the electric field is changed to `E_(2)` and the depression of object in equilibrium increases to `16cm`. What is the ratio of electric field in the second case to that of in the first case ?

View Solution2 conducting objects one with charge of +Q and another with -Q are kept on x-axis at `x=-3` and `x -+4` respectively. The electric field on the x - axis is given by `3Q(x^(2)+4/3)` What is the capacitance C of this configuration of objects. Fill `1/C` (in `F^(-1))` in OMR sheet.
View SolutionIn the connection shown in the figure the switch K is open and the capacitor is uncharged. Then we close the switch and let the capacitor charge up to the maximum and open the switch again. Then
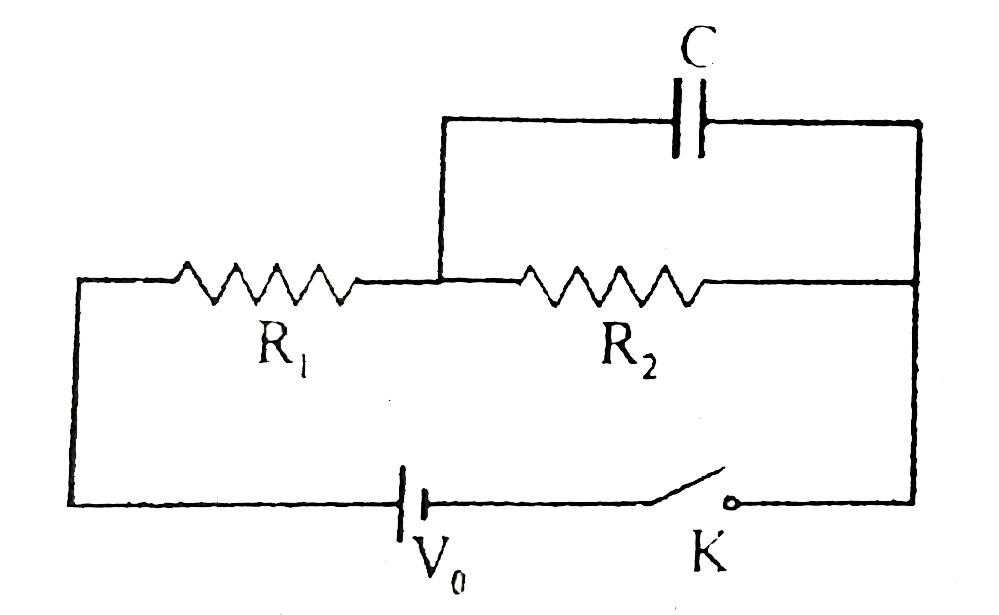
(a) the current through `R_(1)` be `I_(1)` immediately after closing the switch,
(b) the current through `R_(2)` be `I_(3)` immediately after reopening the switch, Find `I_(1)/(I_(2) I_(3))` (in `ampere^(-1)`) (Use the following data: `V_(0)=30VR_(1)=10 K Omega R_(2) = 5 k Omega)`
View SolutionAn electrometer is charged to 3 kV. Then the electrometer is touched with a neutral metal ball, mounted on an isulating rod and then the metal ball is taken away and earthed The process is done for 10 times and finally the electrometer reads 1.5 kV. After this, at least how many times must the above process be repeated in order that the electrometer reads less than 1 kV?
View SolutionFour uncharged capacitors are charged by `24V` battery as shown in the figure. How much charge flows through switch `S` when it is closed?
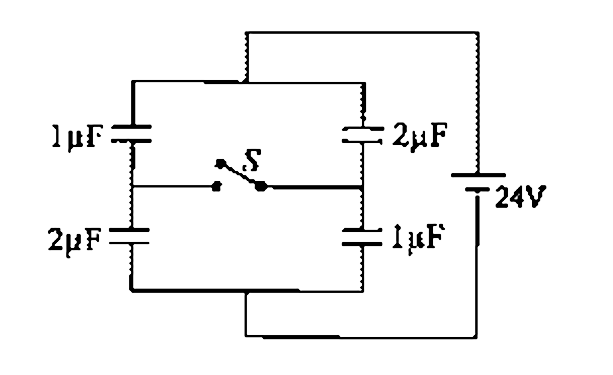
View SolutionThe figure shows four identical conducting plates each of area A the seperation between the consecutive plates is equal to L. When both the switches are closed, if charge present on the upper surface of the lowest plate from the top is written as `(xV_(0)vareosilon_(0)A)/L` then what is the value of x? Treat symbols as having usual meaning

View SolutionTwo potentiometer wires `w_(1)` and `w_(2)` of equal length `l` connected to a battery of emf `epsilon_(P)` and internal resistance 'r' as shown through two switches `s_(1)` and `s_(2)`. A battery of emf `epsilon` is balanced on these potentiometer wires. if potentiometer wire `w_(1)` is of resistance 2r and balancing length on `w_(1)` is `l//2` when only `s_(1)` is closed and `s_(2)` is open. On closing `s_(2)` and opening `s_(1)` the balancing length on `w_(2)` is found to be `((2l)/(3))` then find the resistance of potentiometer wire `w_(2)`
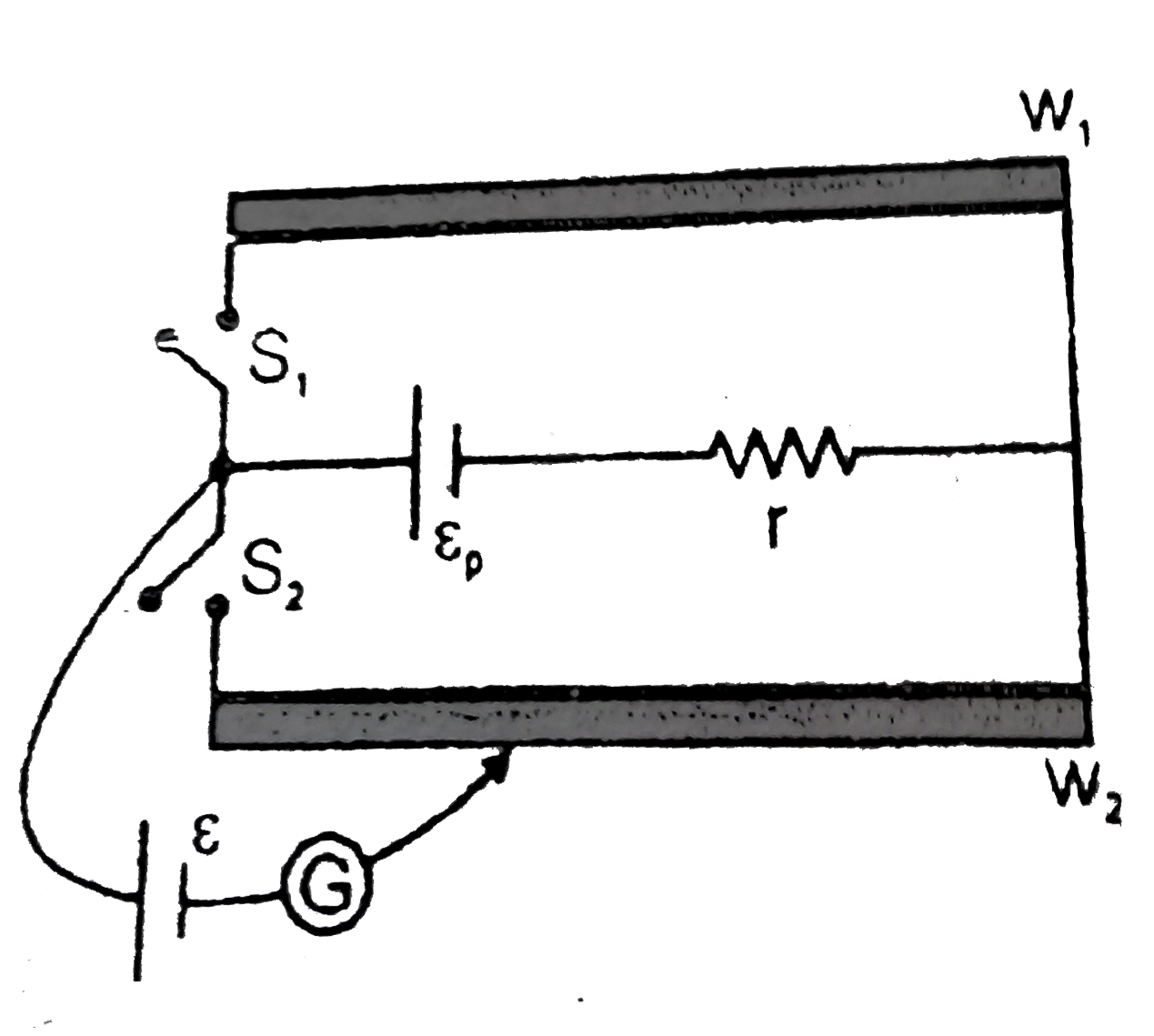
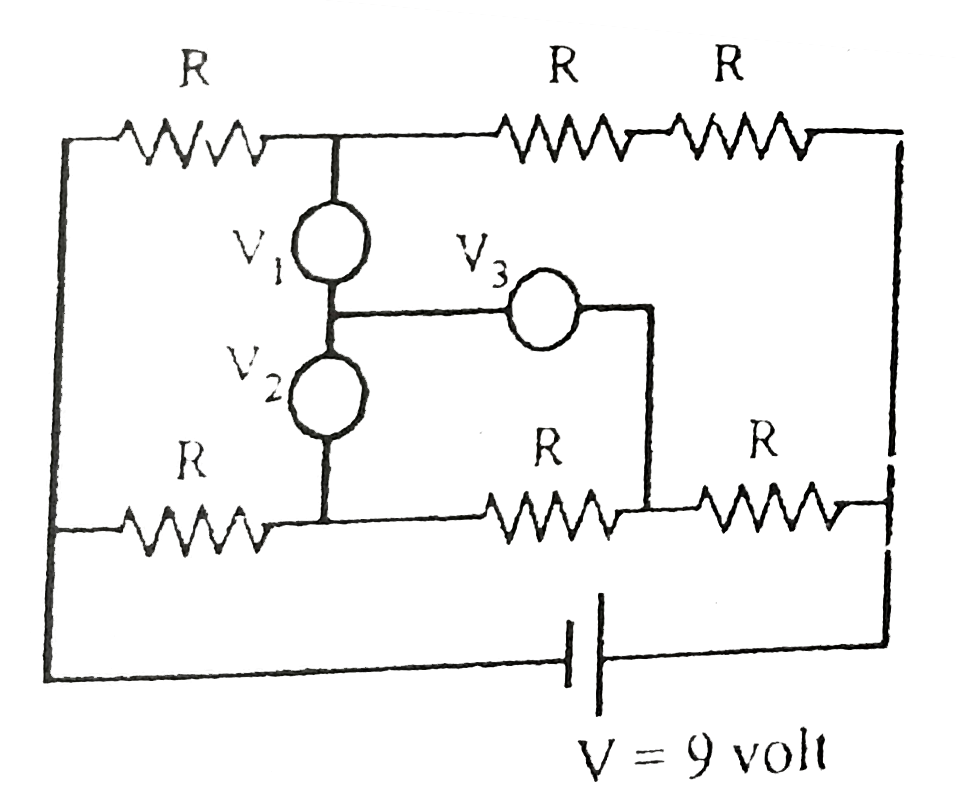
View SolutionIn the circuit shown below, all the three voltmeters are identical and have very high resistance. Each resistor has the same resistance The voltage of the ideal battery shown is 9 V Find the reading of voltmeter `V_(3)` (in volts)
View SolutionFigure shows a square loop `10cm` on each side in the `x-y` plane with its centre at the origin. An infinite wire is at `z=12cm` above `y`-axis.
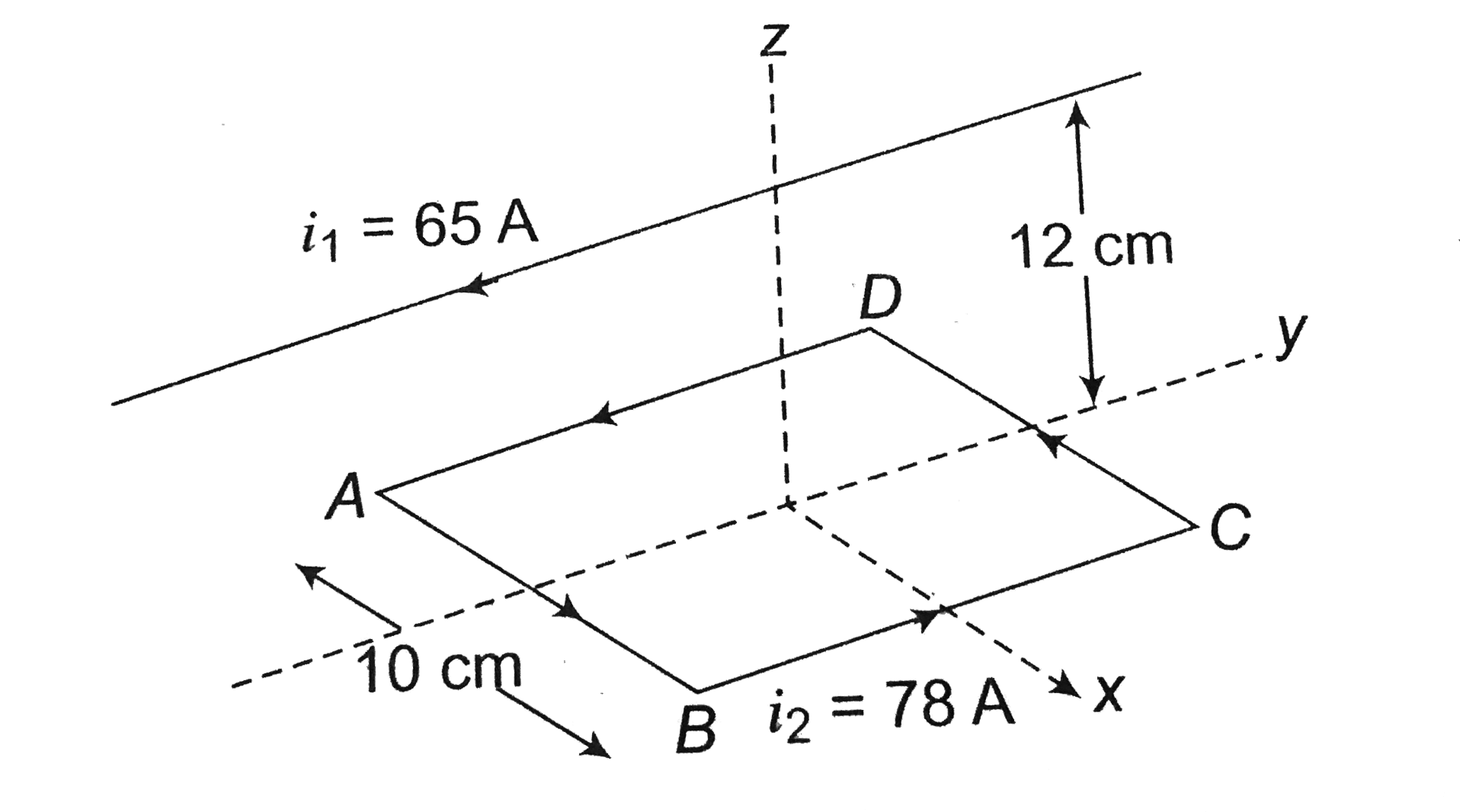 What is torque on loop due to magnetic force?
What is torque on loop due to magnetic force?
View SolutionA long straight wire lies on y-axis and carries a current of 8 A in - y direction. In addition to the magnetic field produced by the wire, a uniform magnetic field of `1.4xx10^(-6)T hat(i)` is also present. What is the magnitude of net magnetic field at (1,1,1) Express your answer in `axx10^(-7)T` and fill a in OMR sheet.
View SolutionAt a certain place, the angle of dip is `tan^(-1)(4//5)` and angle of declination is `37^(@)` The earth's magnetic field has a horizontal component of `0.1` T at that point. A square coil of side 2m is kept in a vertical plane such that its normal points in the true north direction. If the coil is made of 4 rods each of mass 3 kg and the coil is free to rotate about any axis. If the angular acceleration `(in rad //s^(2))` of the coil is `kxx10^(-2)` when a current of 1A passes through it. Find the value of k.
View SolutionThe diagram shows a circuit having a coil of resistance `R=10Omega` and inductance L connected to a conducting rod PQ which can slide on a perfectly conducting circular ring of radius 10 cm with its centre at 'P' Assume that friction & gravity are absent and a constant uniform magnetic field of 5 T exists as shown in figure. At `t=0` the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40 rad//s Find magnitude of this torque (in mu Nm) when current reaches half of its maximum value. Neglect the self inductance of the loop formed by the circuit.

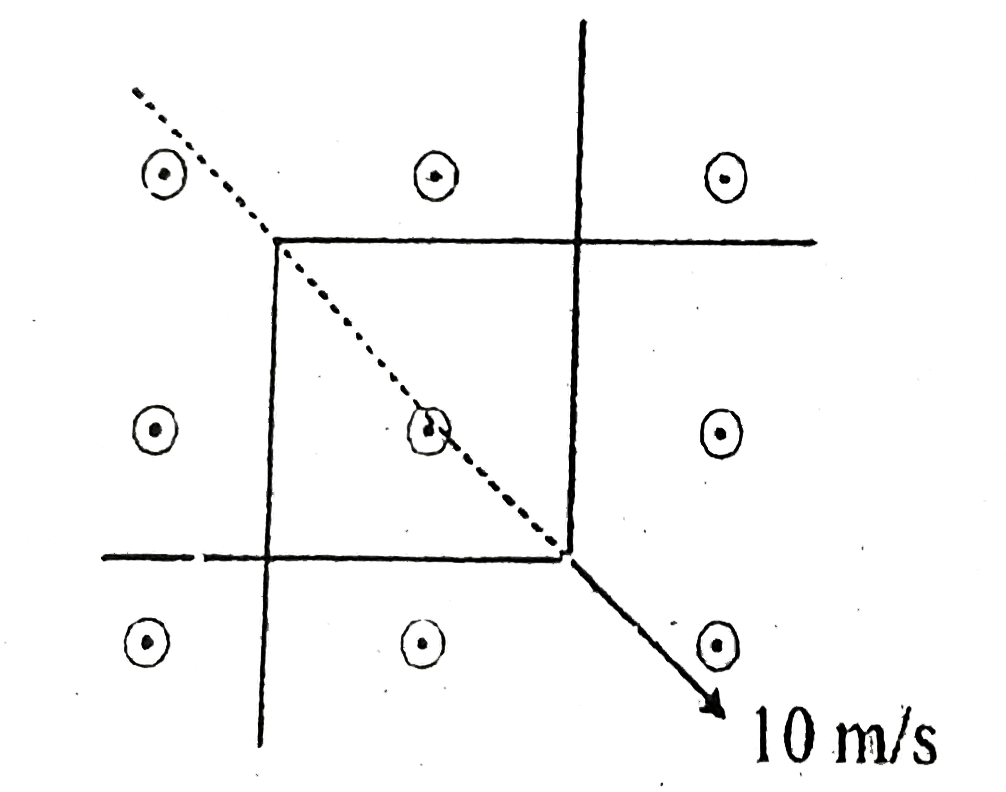
View SolutionThe L-shaped conductor as shown in figure moves a `10 m//s` across a stationary L-shaped conductor in a `0.10` T magnetic field. The two vertices overlap so that the enclosed area is zero at `t-0` The conductor has resistance of `0.010` ohms per meter. What is current (in Amp) at `t=0` 10 sec (Round off to nearest integer)
View SolutionThe long, horizontal pair of rails shown in the figure is connected using resistance R. The distance between the rails is l, the electrical resistance of the rails is negligible. A conducting wire of mass m and length l can slide without friction on the pair of rails, in a vertical, homogeneous magnetic field of induction B.
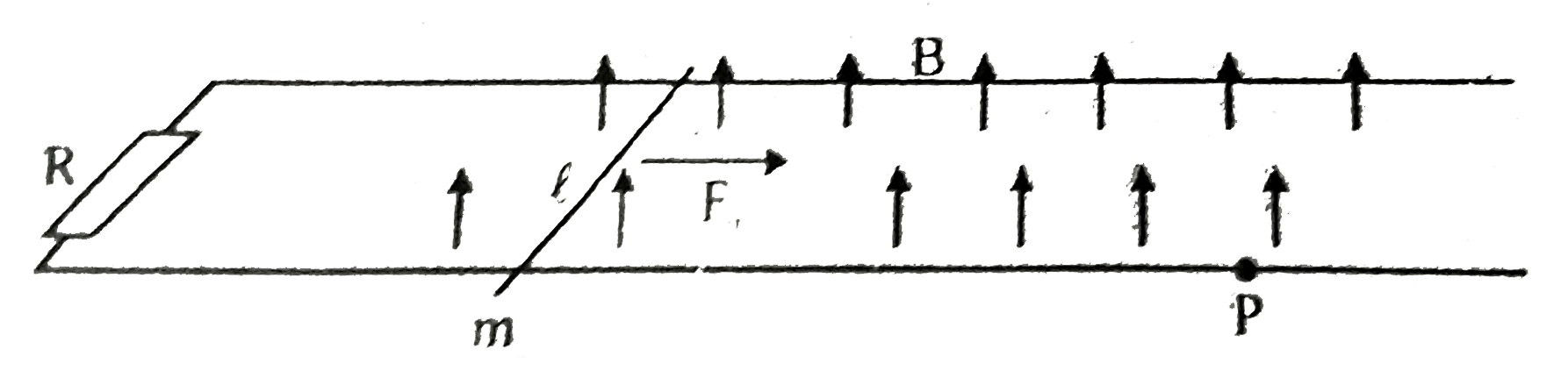 A force of magnitude `F_(0)` is exerted for sufficiently long time onto the conducting wire, so that the speed of the wire becomes nearly constant. The force `F_(0)` is now removed at a certain point P What distance (inm) does the conducting wire cover on rails from point P before stopping? (Given `F_(0)=20N, m=1.6 gm, R= 0.01 Omega l=19 cm, B=0.1 T)`
A force of magnitude `F_(0)` is exerted for sufficiently long time onto the conducting wire, so that the speed of the wire becomes nearly constant. The force `F_(0)` is now removed at a certain point P What distance (inm) does the conducting wire cover on rails from point P before stopping? (Given `F_(0)=20N, m=1.6 gm, R= 0.01 Omega l=19 cm, B=0.1 T)`
View SolutionA thin conducting rod of length `l=5m` is moved such that its end B moves along the X-axis while end A moves along the Y-axis A uniform magnetic field `B=6hat(k)` T exists

View SolutionA conducting frame is placed in a horizontal plane as shown in the figure. The two sides are parallel and separated by a distance of `0.25` m. A massless conducting rod can slide without friction on the frame. The total resistance of the circuit is 40 Omega. The rod is connected to a `0.2` kg mass by a massless cord which passes over a massless and frictionless pulley. A uniform magnetic field of 2T points vertically upward. The voltage of the bettery is 100 V. Find the constant velocity in m//s with which the rod and mass eventually move.
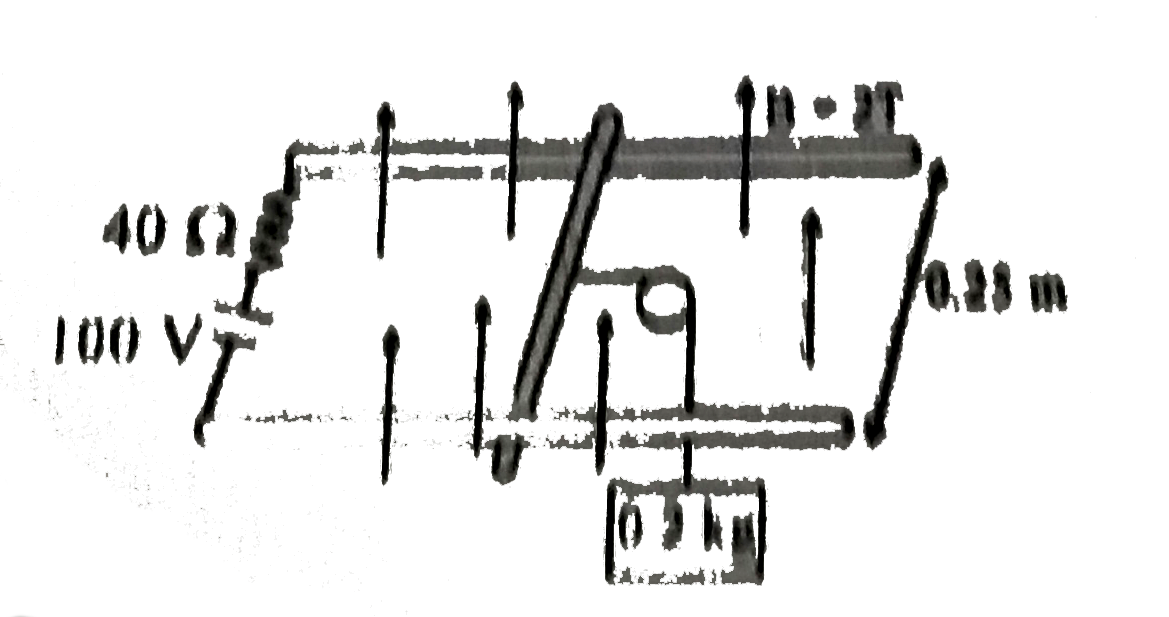
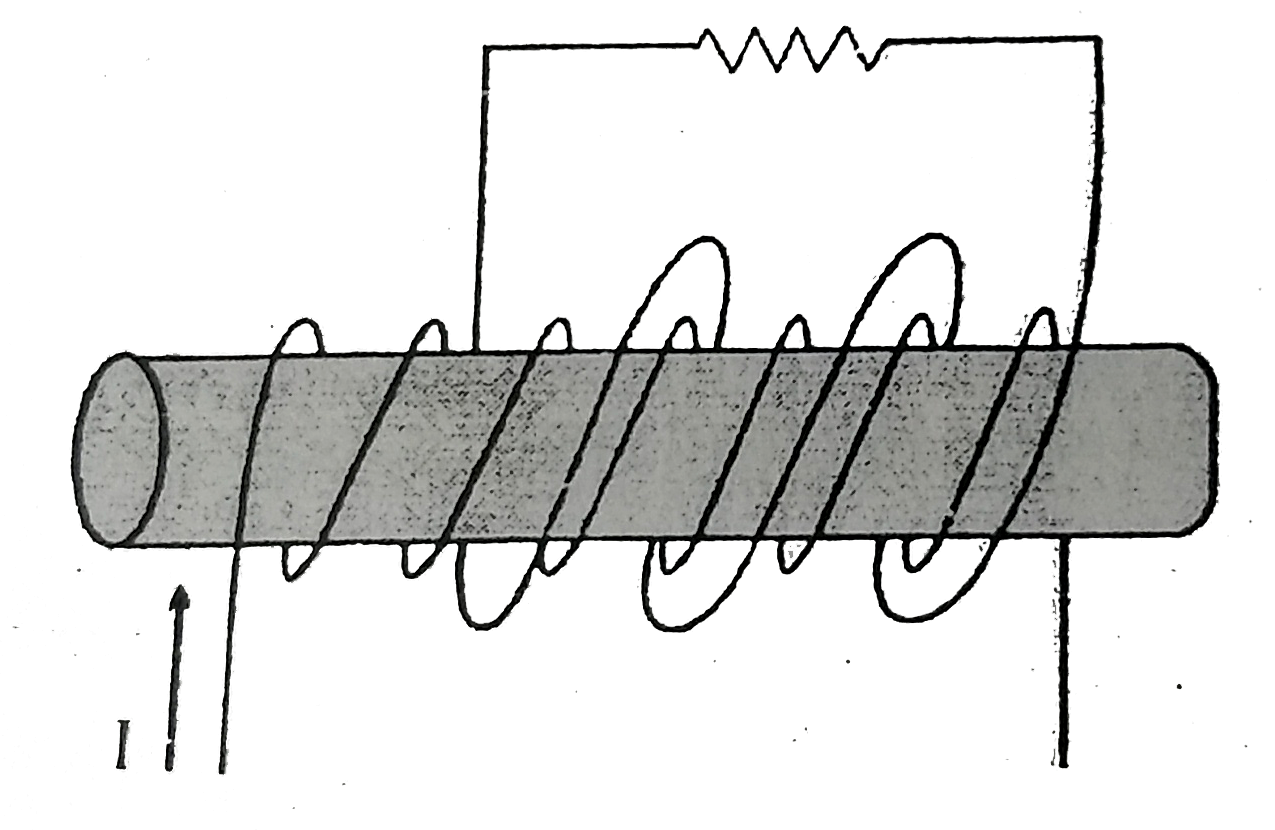
View SolutionA coil with 1500 turns, a radius of `5.0` cm and a resistance of `12 Omega` surrounds a solenoid with `240 turns // cm` and a radius of 4 cm , see figure. The current in the solenoid changes at a constant rate from 0 to 20 A in `0.10` s. Calculate the magnitude of the induced current (in mA) in the 1500 turn coil (`pi^(2)=10` Neglect self inductance of the coil).
View SolutionAn RLC circuit includes a `1.6` H inductor and a `250 muF` capacitor rated at 400 V. The circuit is connected across a sine - wave generator whose peak voltage is 32 V. What minimum resistace must the circuit have to ensure that the capacitor voltage does not exceed its rated value when the generator is at the resonant frequency? Fill 10 R in OMR sheet.
View SolutionIf an AC voltage 100 V is applied between points A and B, then current of 1 A and phase difference between current and voltage will be `Deltaphi=37^(@)` . IF the same voltage is applied between points B and C, then current of 5 A and `Deltaphi =53^(@)` What will be the impedance `(in Omega)` in the chain, if the same voltage is applied between points A and C? Round off to nearest integer.

View SolutionIn the given LCR series circuit find the reading (in A) of the hot wire ammeter. (there all hot wire meters are ideal)
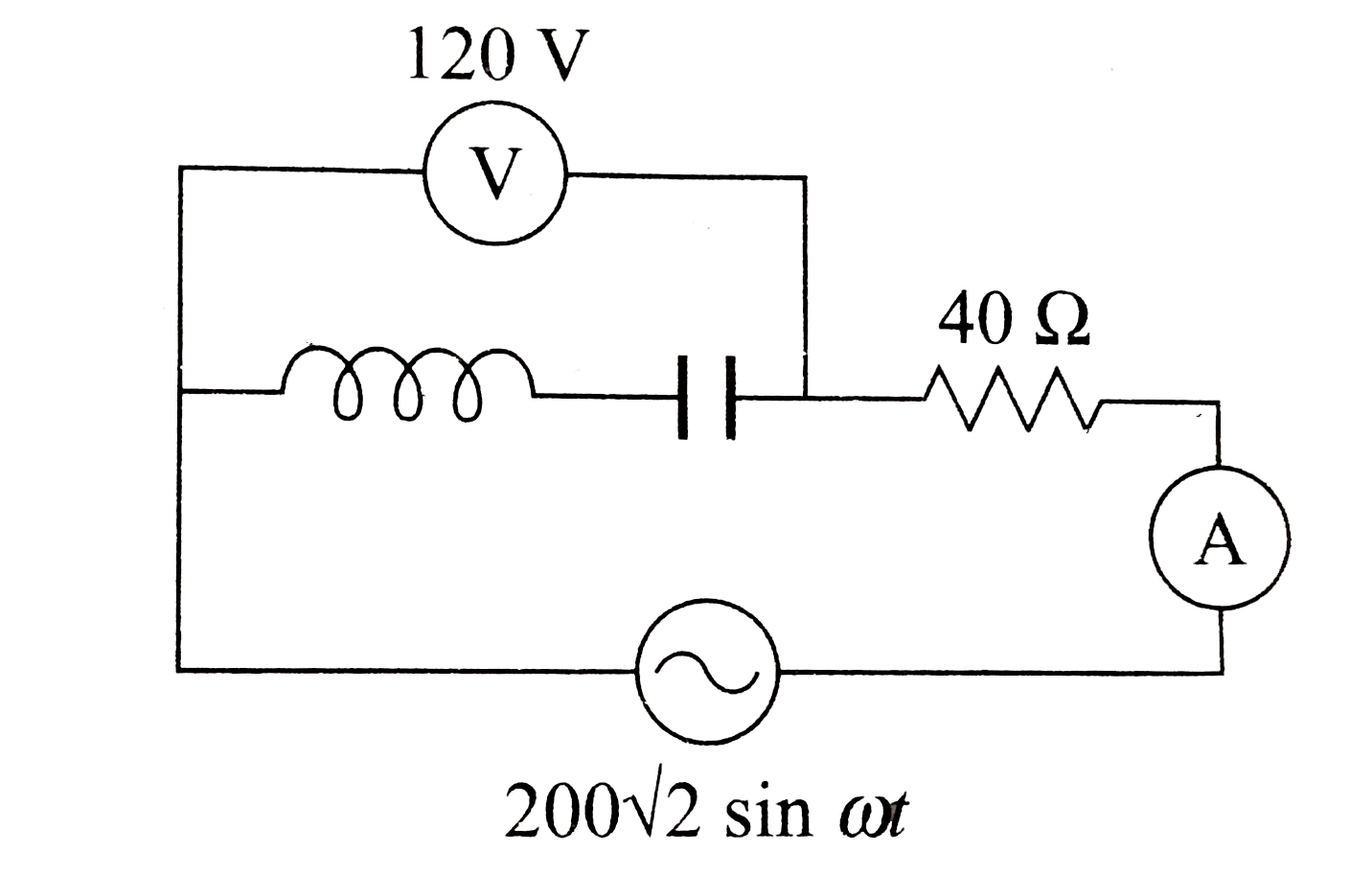
View SolutionA beam of light parallel to the principal axis is focused on a screen with the help of lens, forming a circular spot with a diameter of A. If we put a plane - parallel glass plate of thickness h and refractive index n between the lens and the screen, the diameter of the bright spot on the screen increases. The diameter of the lens is d and focal length F. Find the new diameter in mm. (Take F=10 cm, A = 1 cm, n=1.5,d=2 cm, h=3 cm)
View SolutionFigure shows the path of a light beam in an isosceles prism with apex angle `delta=60^(@)` (inside the prism beam is parallel to the base). Find the angle of deflection in degrees. The refractive index of prism material is `1.732`

View SolutionAlong the main optical axis of a converging lens with focal length F = 5 cm two fireflies are moving towards each other. They are on opposite sides of the lens. The speed of the fireflies is the same `V=2 cm//sec` After what minimum time (in sec) does the first firefly meet the image of the second, if at the initial time they were at distances 20 cm and 30 cm from the lens repectively? Round off to nearest integer.
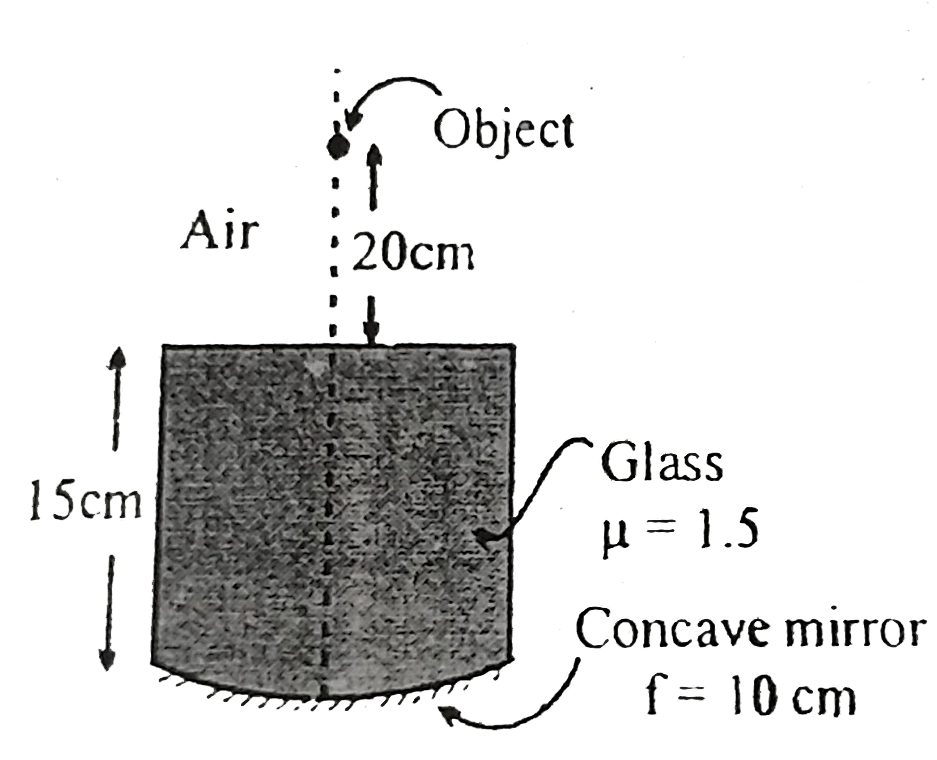
View SolutionAfter all possible reflection and refractions the final image is located at a distance 'x' cm from air-glass interface. Then value of 7x is
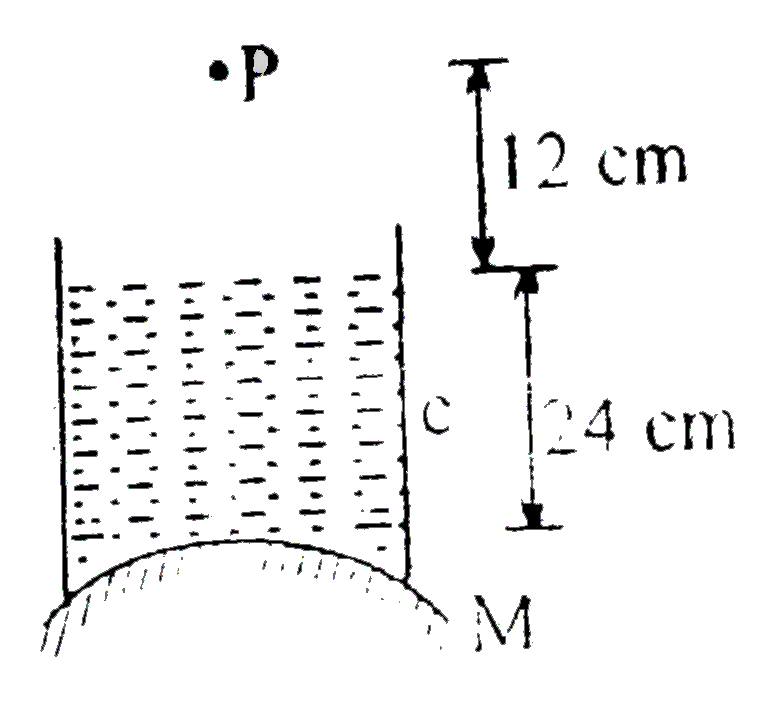
View SolutionAn insect at point 'P' sees its two images in the water mirror system as shown in the figure. One image is formed due to direct partical reflection from water surface and the other image is formed due to refraction, reflection & again refraction by water mirror system in order. Find the separation (in cm) between the two images. Mirror M has focal length 60 cm `[Take mu_(w)=4//3]`
View SolutionA plane mirror is suspended vertically at the center of a large thin-walled spherical flask filled with water. The diameter of the flask is 10 inches. An observer whose eye is 35 inches from the mirror as shown in figure tries to see an image of his own eye. What is distance of the image from the eye (in inches). The effect of the thin glass walls of the flask may be neglected. Take `mu_(water)=4/3`

View SolutionA light ray parallel to the x-axis strikes the outer reflecting surface of a sphere at a point (2,2,0). Its center is at the point (0,0,-1). The unit vector along the direction of the reflected is `xhat(i)+yhat(j)+zhat(k)` Find the value of `yz/x^(2)`
View SolutionA block of mass 'm' is attached to a spring. Block is released from rest, when spring is in natural length. Block is along the pricipal axis of concave mirror and size of block is very small. When spring is in natural length then block is at a distance of 20 cm from the mirror, distance (in cm) in which the image formed by mirror oscillates is (mass of the block `=5xx10^(-2)` kg, spring constant k=20 N//m)

View SolutionA vessel, whose bottom is flat and perfectly reflecting, is filled with water `(index=4//3)` upto a height = 40 cm . A point object in air above is moving towards the water surface with a constant speed `=4 m//s` What is the relative speed of its final image `(in m//s)`, as seen by the object itself, at a moment when the object is 30 cm above the water surface?
View SolutionInterference frings of yellow light of wavelength 6000 A are formed by Billet split lenses. The distance from source to lens is 24 cms. The focal length of lens is 15 cm The lens halves are separated by `0.06` mm. The distance of source to screen is 200 cms. Calculate the fringe width (in mm) Round off the answer to nearest integer.

View SolutionFor an achromatic combination, three different lenses are combined. Dispersive power of their material are `0.066,0.055 and 0.040` and their main focal length are - 22 cm, -11cm, and 'f' respectively then find the value of 'f' (in cm.)
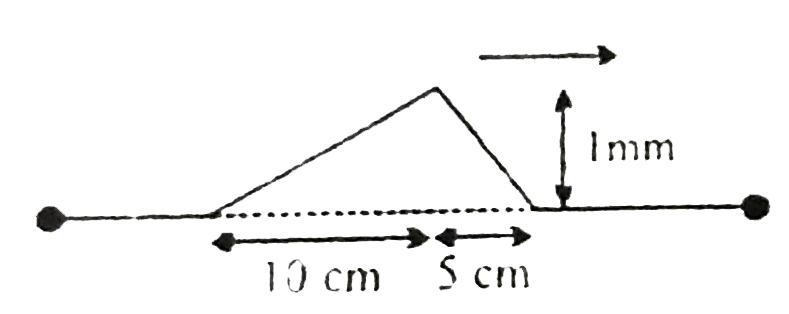
View SolutionFind the total number of fringes formed on screen in the L loyd's mirror arrangement shown.

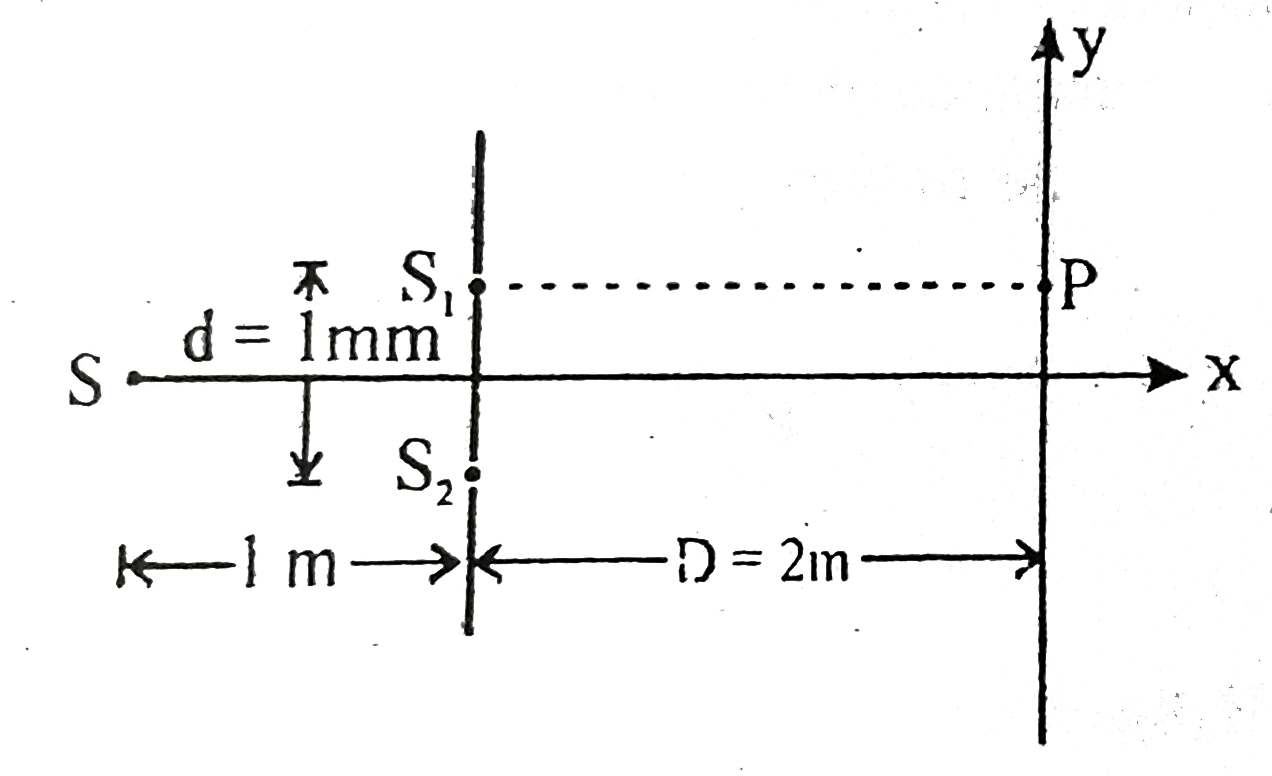
View SolutionIn a modified YDSE the sources S of wavelength 5000 A oscillates about axis of setup according to the equation `y=0.5 sin(pi/6)t` where y is in millimeter and t in second. At what time ti will the intensity at P, a point exactly in front of slit `S_(1)` be maximum for the first time?
View SolutionA thin film of plastic `(n=1.56)` is `0.25mum` thick. It is sandwiched between two glass slabs with refractive indice of `1.58` and `1.52` respectively White light (400-700nm) is first incident normally on the slab for which `n=1.58` Which visible wavelength (in nm) is missing in the reflected light?

View SolutionVisible light of variable wavelength is incident normally on a thin sheet of plastic in air. The reflected light has a minima only for `lamba=512` nm and `lambda=640` nm in the visible spectrem. What is the minimum thickness (in mum) of the film `(mu=1.28)` ?
View SolutionVisible light of variable wavelength is incident normally on a thin sheet of plastic in air. The reflected light has a minima only for `lamba=512` nm and `lambda=640` nm in the visible spectrem. What is the minimum thickness (in mum) of the film `(mu=1.28)` ?
View SolutionA very fine hair-like fiber is stuck between two microscope slides. As a result of this, there is a wedge of air between them. When the slides are illuminated normally (from above) with light of wavelength 550 nm. Bright and dark interference bands are formed. The fiber is seen to lie at the position of fifth dark band counting from the common edge. What is the diameter ( in nm) of the fiber?

View SolutionA flat bottomed metal tank filled with water is dragged along a horizontal floor at the rate of `20 m//s` The tank is of mass 100 kg and contains 900 kg of water and all the heat produced in the dragging is conducted to the water through the bottom plate of the tank. If the bottom plate has an effective area of conduction `1m^(2)` and thickness 5 cm and the temperature of water in the tank remains constant at `50^(@)` C, calculate the temperature of the bottom surface of the tank. Given the coefficient of friction between the tank and the floor is `0.5` and K for the material of the tank is `100 J//m sec` K.
View SolutionA rod PQ of length l=1 m is pivoted at an end P and is freely rotating in a horizontal plane at an angular speed `omega` about a vertical axis passing through P. If coefficient of linear expansion of material of rod is `alpha=2xx10^(-4)//^(@)C` then calculate percentage change in its angular speed (in multiple of `10^(-1))` if the temperature of system is increased by `DeltaT=10^(@)` C.
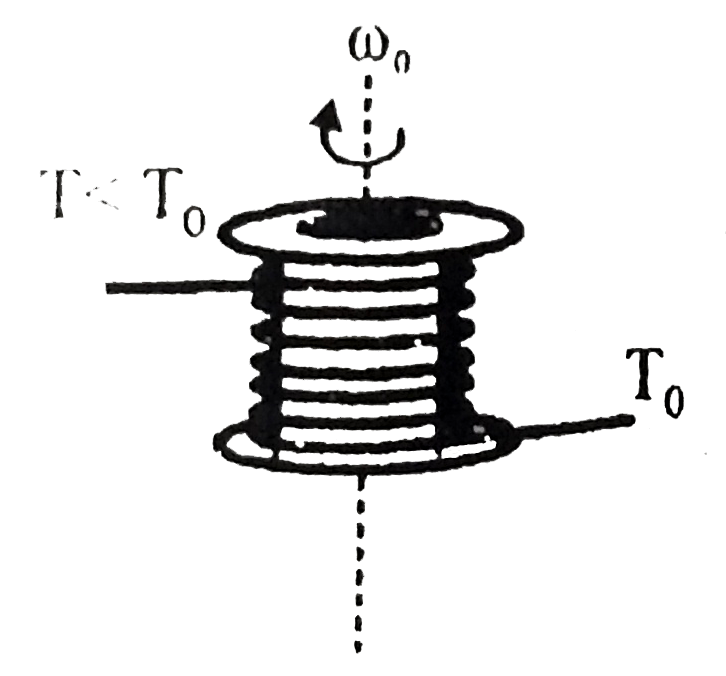
View SolutionA capstan is a rotating drum (cylinder) over which a rope or cord slides in order to increase the tension due to friction. If the difference in tension between the two ends of the rope is 500 N and the capstan has a diameter of 10 cm and rotates with angular velocity `10 rad//s`. Capstan is made of iron and has mass 5 kg, specific heat `1000 J//kg` K. At what rate does temperature rise? Assume that the temperature in the capstan is uniform and all the thermal energy generated flows into it. Express your answer as `xxx10^(-4)^(@)C` Fill up value of x.
View SolutionIn a slow reaction, heat is being evolved at a rate about 10 m W in a liquid. If the heat were being generated by the decay `of ^(32)` P, a radioactive isotope of phosphorus that has half-life of 14 days and emits only beta-particles with a mean energy of 700KeV, estimate the number `of ^(32)` P atoms in the liquid. Express your answer in form of `Axx10^(15)` and fill A in OMR sheet. Round off A to nearest integer [Take:l n`2=0.7`]
View SolutionIn a sample initially there are equal number of atoms of two radioactive isotopes A and B. 3 days later the number of atoms of A is twice that of B. Half life of B is `1.5` days. What is half life of isotope A? (in days)
View SolutionThe reaction `_(3)^(7)Li+_(1)^(1)H rightarrow _(4)^(7)Be + _(0)^(1)n` is endothermic. Assuming that Li nuclei is free and at rest. What is the minimum kinetic energy ( in keV) of incident proton so that this reaction occurs? Take Q value of this reaction as -1645 keV.
View Solution
Subjective questions and complete solutions for chapter MASTER PRACTICE PROBLEM of BANSAL PHYSICS (HINGLISH) of Class 12