Complete Solutions to Subjective Type of chapter GRAPHICAL INTERPRETATION of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | GRAPHICAL INTERPRETATION |
| GRB PUBLICATION | Subjective Type |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
For adsorption of a gas on solid surface, following isotherm was obtained. Where P is pressure of gas in atm, x represents amount of gas adsorbed and m represents mass of adsorbent, calculate the value of `(x)/(m)` of the gas at same temperature and at a pressure of 81 atm.
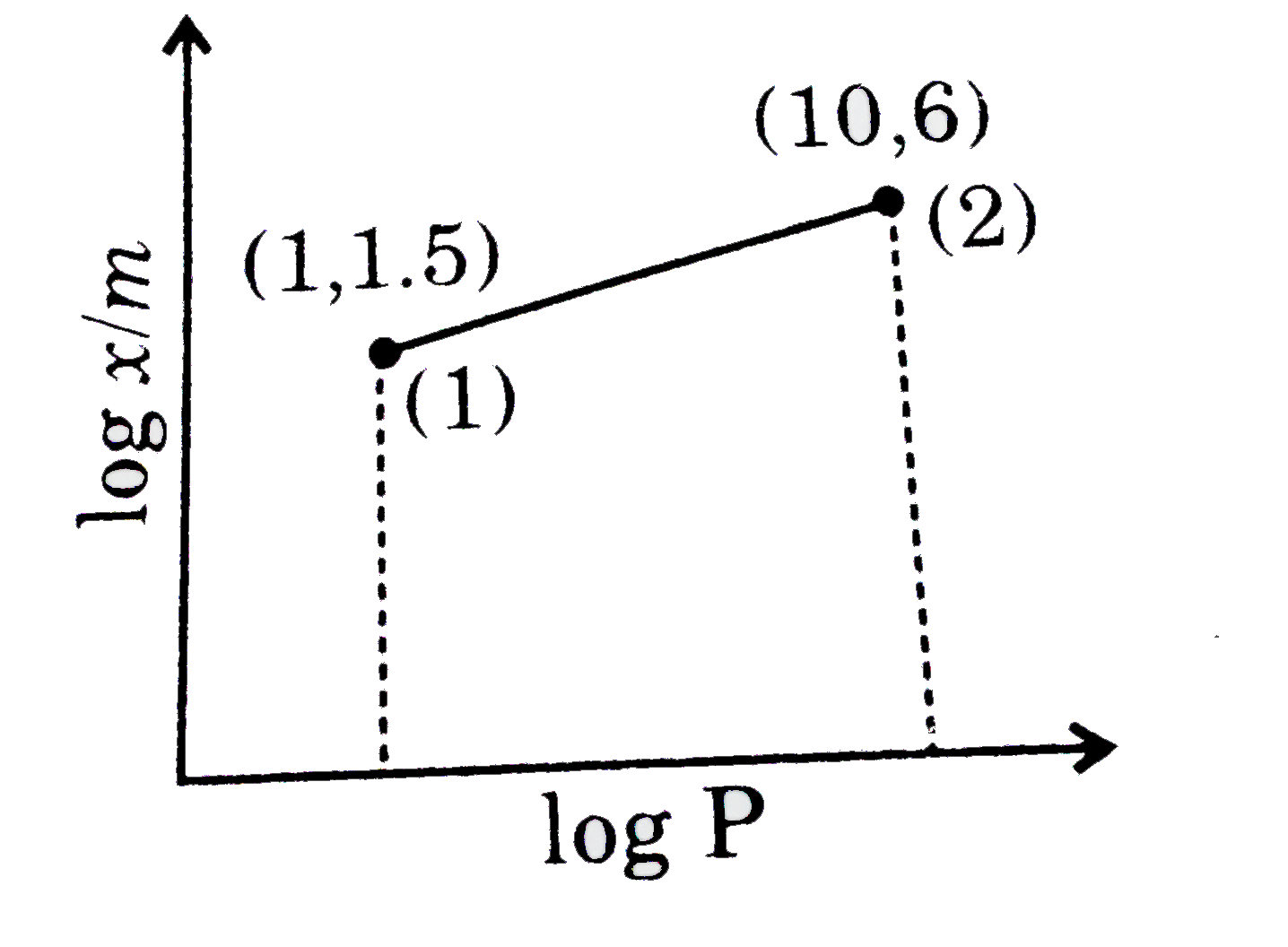
View SolutionFrom the following graph of log `x//m` us log P, calculate mass of `H_(@)` gas adsorped on the surface of 1gm palladium at pressure of `81 xx 10^(-4)atm`.
[Express answer in gm)

`(x)(M) =` Mass of gas absorbed per unit mass of absorbent.
P = Partial pressure of gas in atm.
View SolutionCalculate magnitude of work involved in the reversible cyclic process ABCD if a diatomic ideal gas is involved.
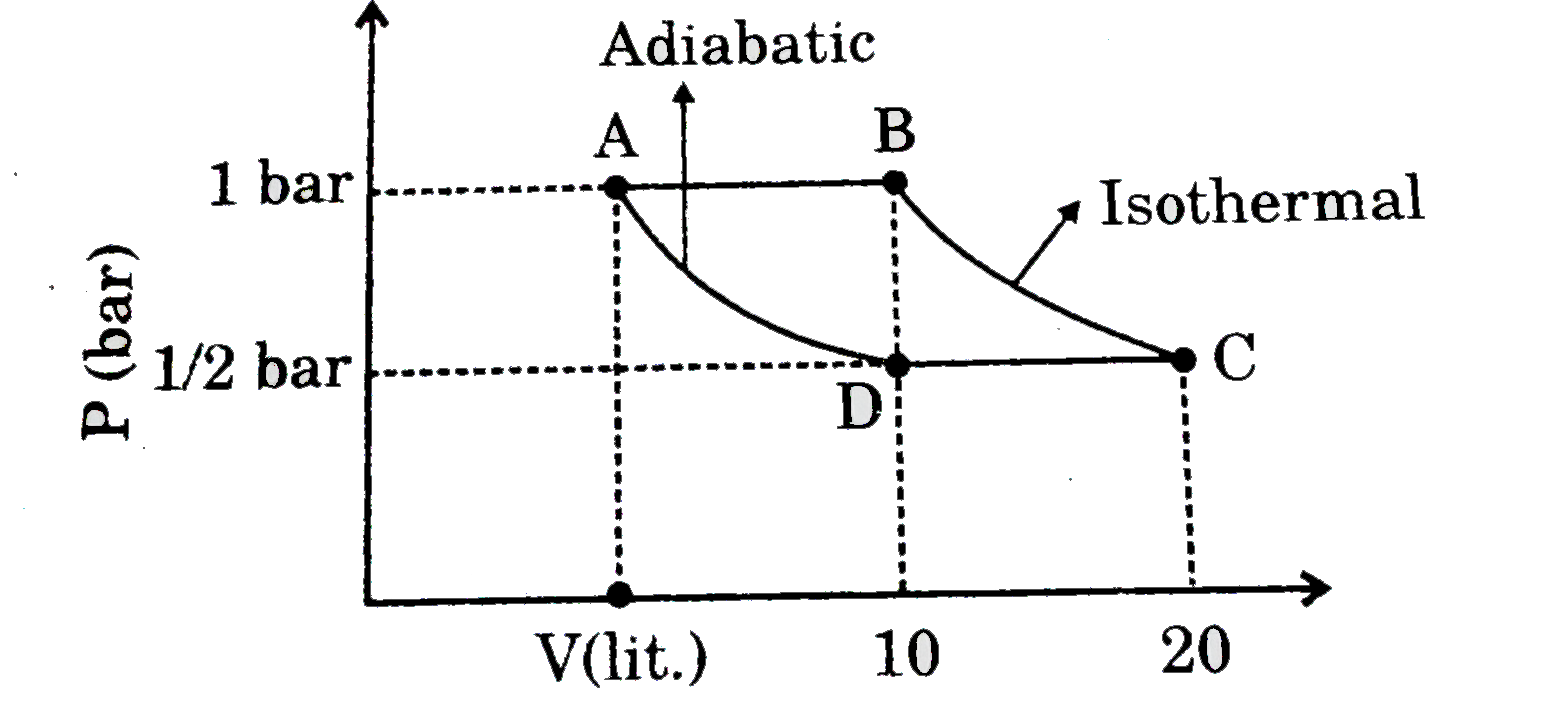
[Given `2^(5/7) = 1.6, ln 2 = 0.7]`
Express answers in bar-lit and round off to next integer.
View SolutionFrom the graph of `(d)/(P)` us P at a constant temperature of 300 K. calculate molar mass of the gas.

View SolutionFor adsorption of gas over solid surface following data is obtained at 300 K.
`{:("Pressure of gas (mm of Hg)",100,25),("Amount adsorbed per Kg of charcoal",3gm,1.5gm):}`
The slope of the graph between log P us log `x//m` will be:
[`x//m` and P are in same units as given in question.]
View SolutionFor a fixed amount of a real gas when a graph of Z us P was plotted then at very high pressure slope was observed to be `0.01 atm^(-1)`. At the same temperature if a graph is plotted between PV us P then for 2 moles of the gas the y intercept is found to be 40 atm-litre. Calculate excluded volume in litres for 20 moles of the real gas/
View Solution10 moles of an ideal gas is subjected to an isochoric process (volume constant) and a graph of log P us log T is plotted where P is in 'atm' and is in 'Kelvin'. If volume of the container is 82.1 ml then calculate sum of a,b and c.
Where : a = slope of the graph
b = x intercept of the graph
c = y intercept of the graph
View SolutionFor `O_(2)` gas at `T_(1)` and `T_(2)` following Maxwell speed distribution is observed [not to be scale]

Ratio `A_(1)//A_(2)` is equal to
View SolutionTwo moles of an ideal gas undergoes the process depicted below. Given that `((deltaP)/(deltaT))_(v)` is `x xx 10^(-y)`, then calculate the value of (y-x).
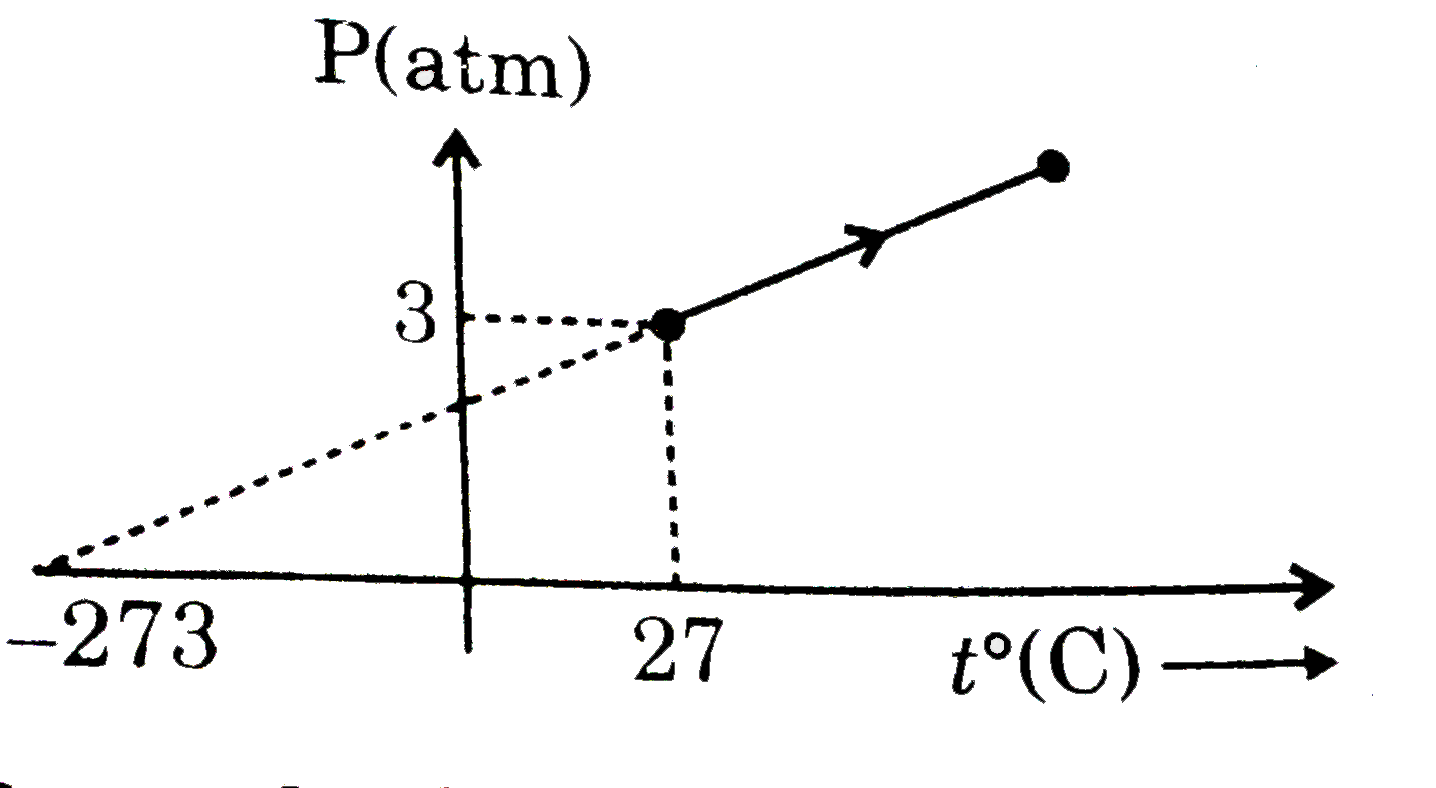
View SolutionOne mole of an ideal gas is subjected to a two step reversible process A-B and B-C. The volume at A and C is same. Find the value of the ratio
`("Pressure of gas at C")/("Pressure of gas at A")`
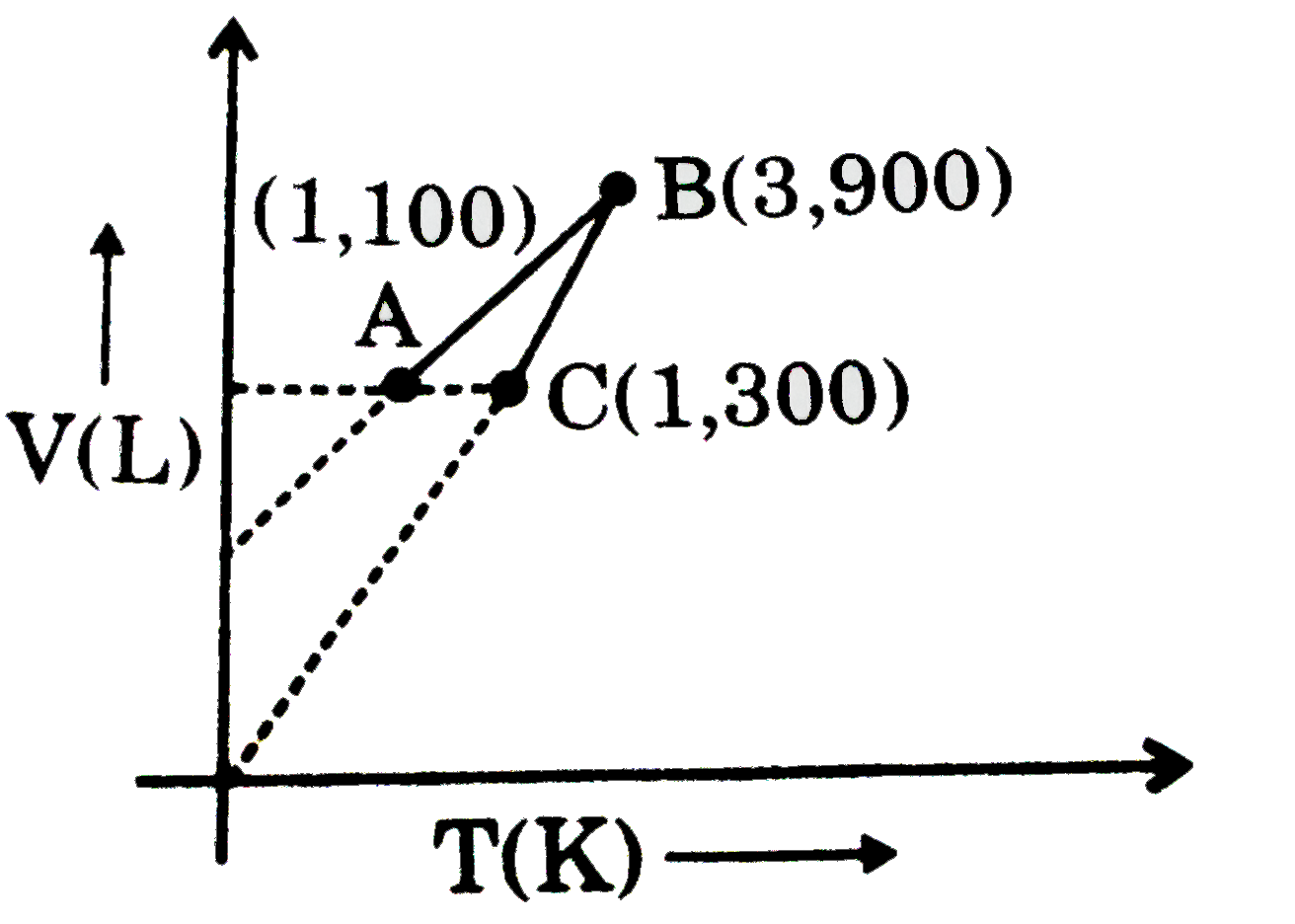
View SolutionCalculate `DeltaG` (in L atm) from the graph of an ideal gas undergoing process AB. [Take: ln 2 = 0.7]
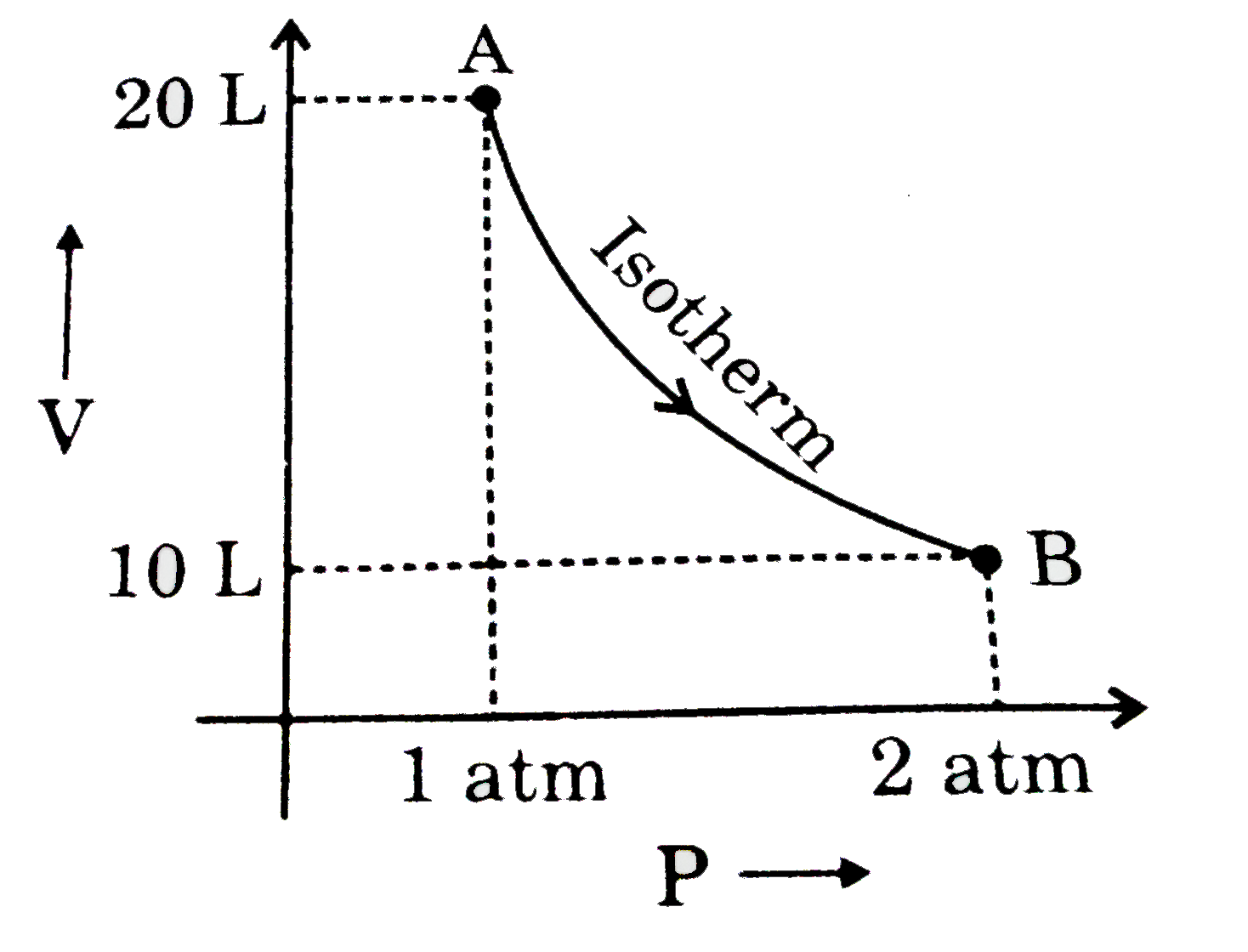
View SolutionOne mole of an ideal monoatomic gas undergoes the following cyclic process. Calculate the magnitude of work (in cal) in a cycle. (Use: ln 2 = 0.7)

View SolutionOne mole of a monoatomic ideal gas is taken through a cycle ABCDA as shown in the P-V diagram. A student wants to determine sign of measurable quantities `DeltaU, q, W` and `DeltaS` for reach process separately. If x is the total number of negative values of measurable quantities in overall cycle, then calculate x.
View SolutionOne mole of a gas is taken from state A to state B as shown in figure. Work done by the gas is `alpha xx 10^(beta) J`. Find the value of `alpha + beta`. (Given: `T_(1) = 320 K, R = (25)/(3))`
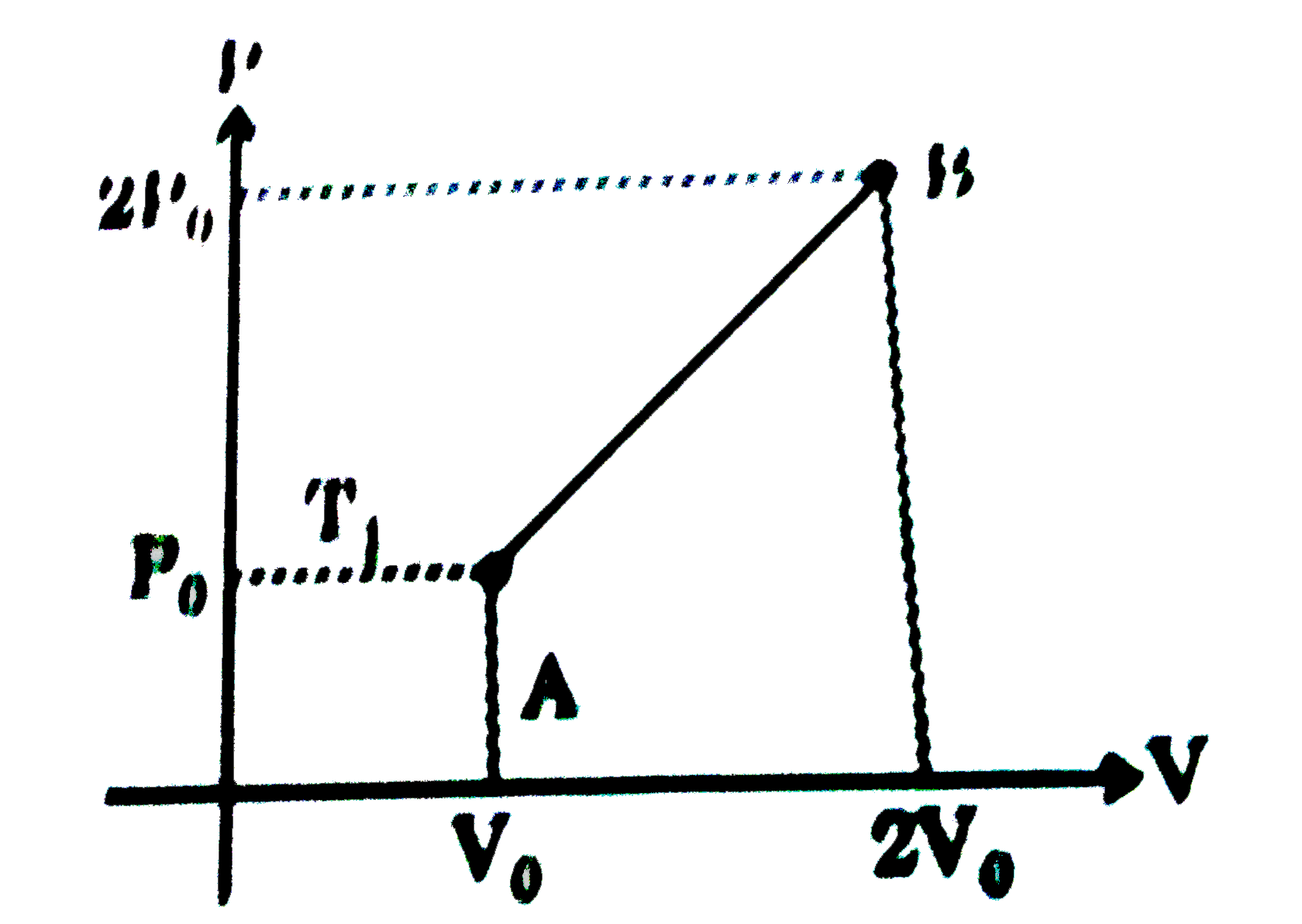
View SolutionOne mole of an ideal monoatomic gas is heated according to path AB and AC. If temperature of state B and C are equal then calculate `(q_(AC))/(q_(AB)) xx 10`.
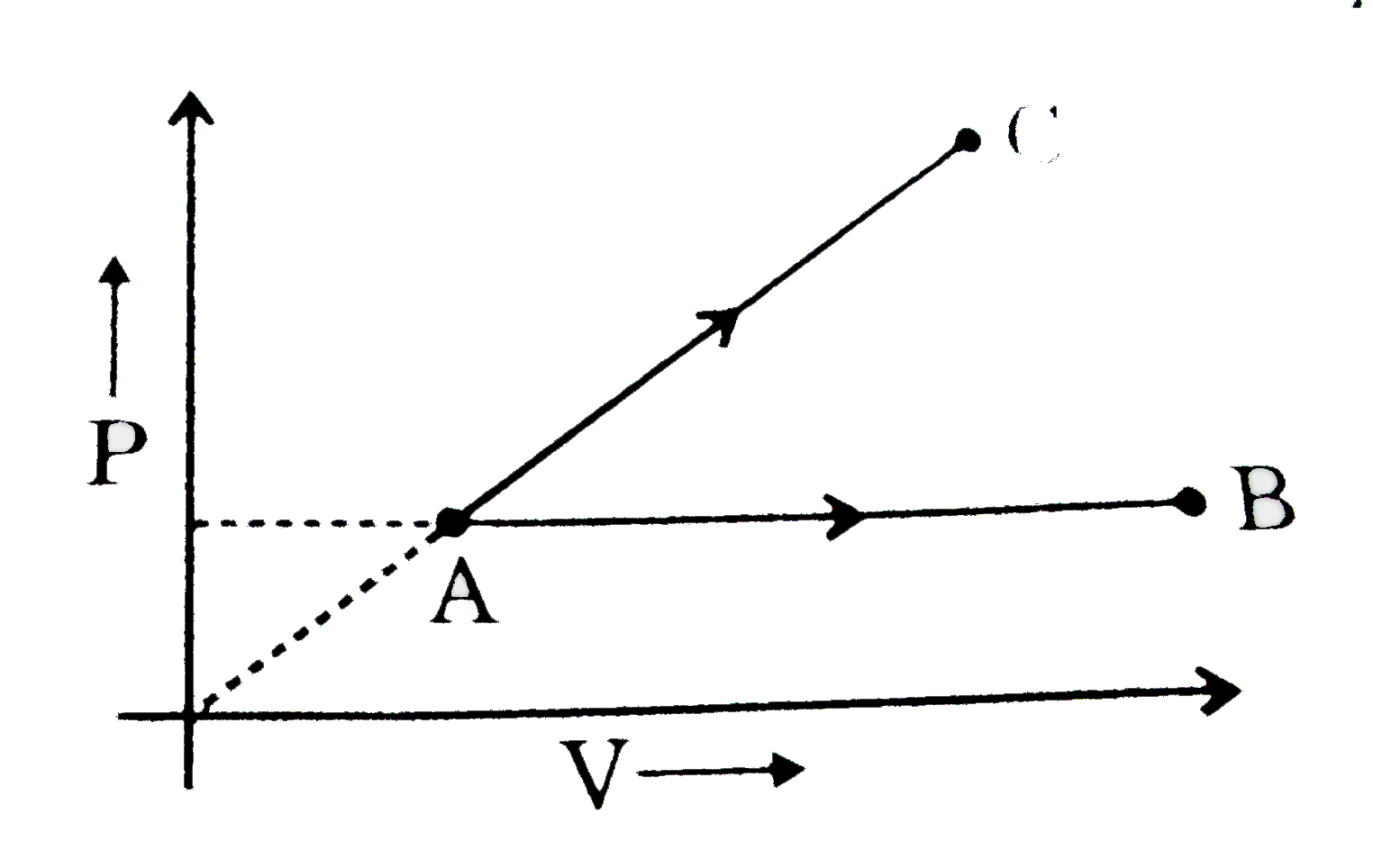
View SolutionFind the heat absorbed by an ideal gas (in kJ)w it follows the graph (given below) during isothermal expansion [ln 2 = 0.7]
[Tale: 1 litre-bar = 0.1 kJ]
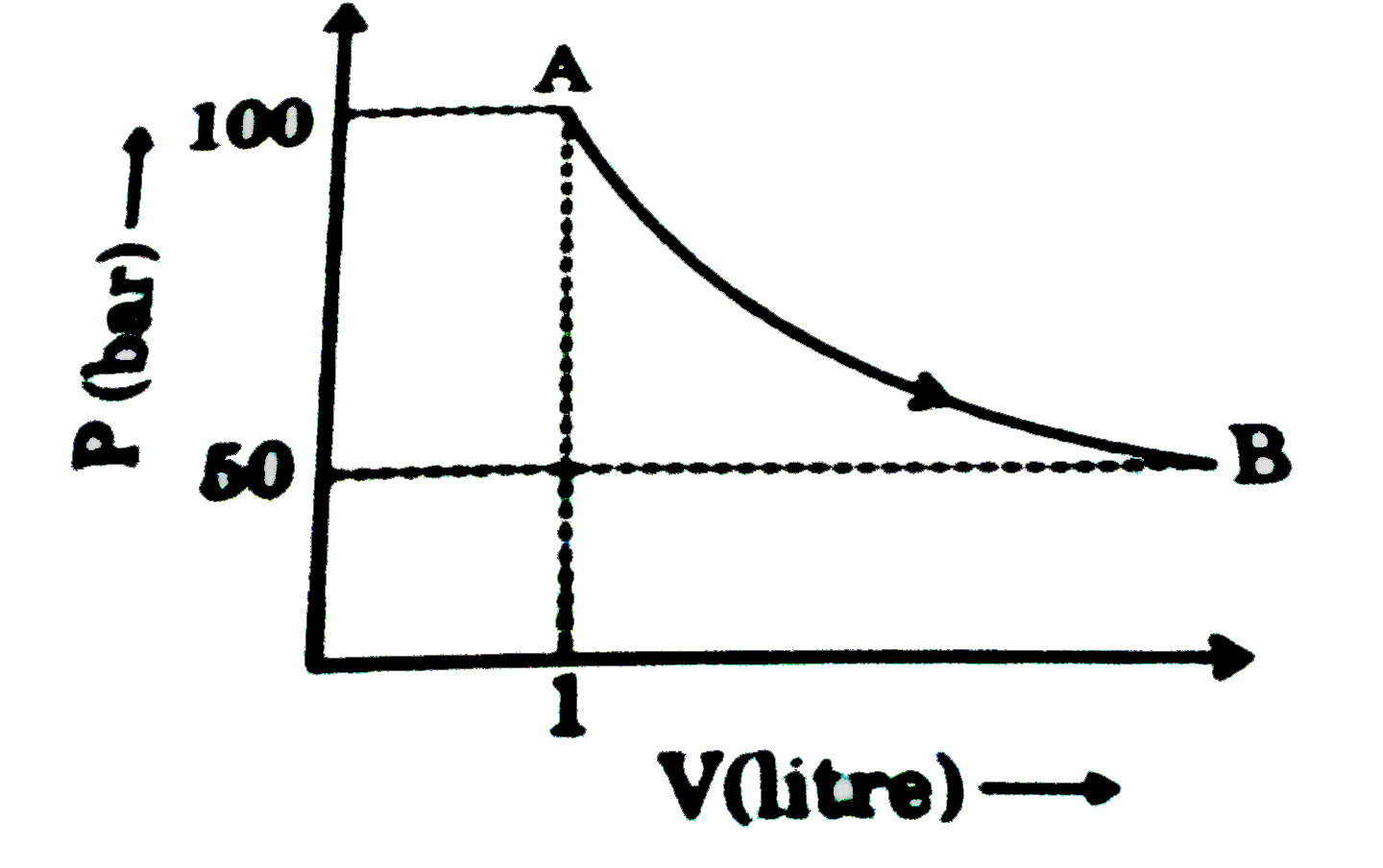
View SolutionIf work done by an ideal gas in process 1-2 on the given graph is 0.4 kJ then product of pressure and volume at point B (in bar-L) is (Enthalpy of gas in process 3-4 is constant) (1 bar-L = 100 J)
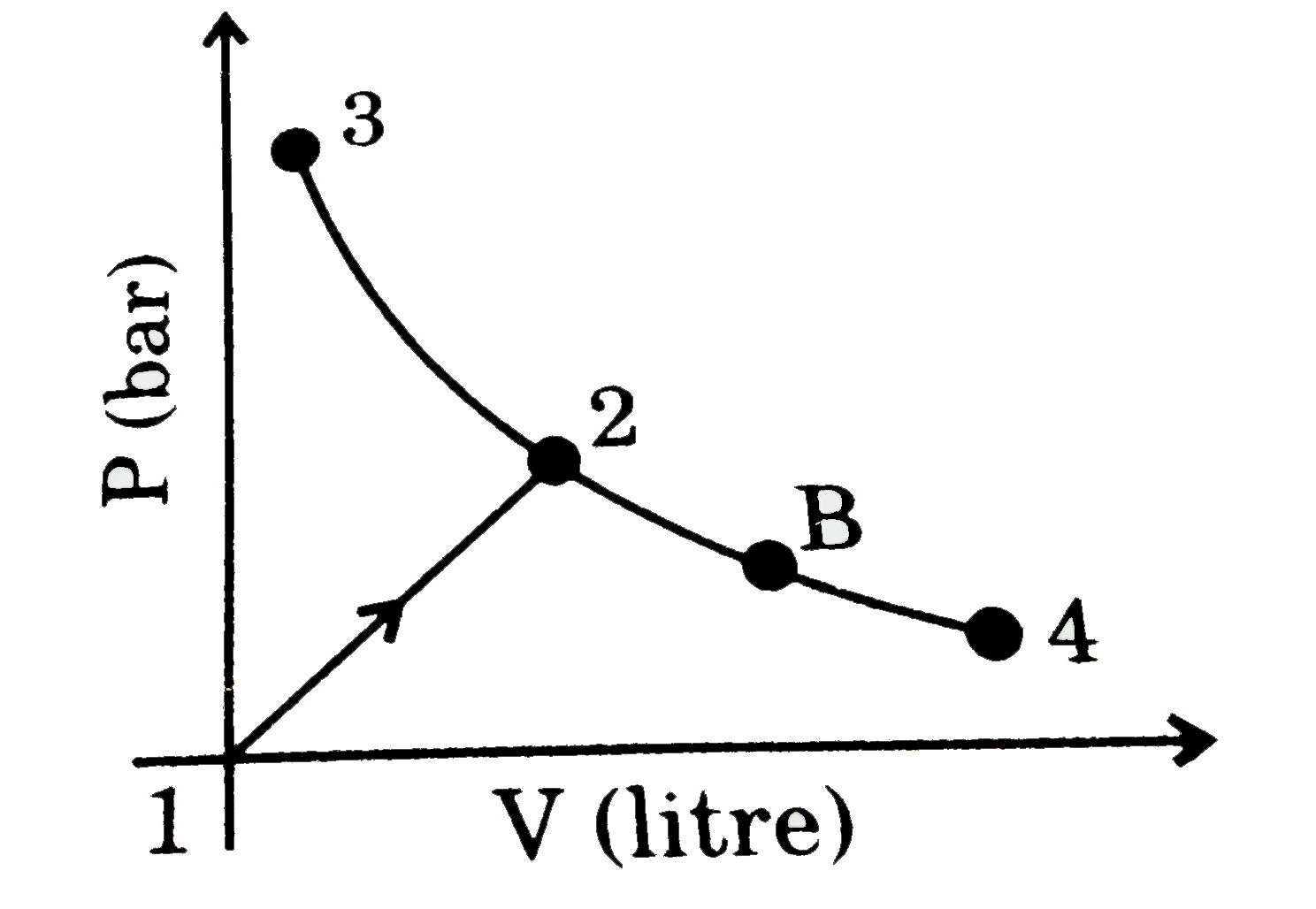
View SolutionBetween two isotherms we have a cycle as shown. Find the work done by the gas during the cycle in (J). [Take: `T_(1) = 127^(@)C, T_(2) = 16^(@)C, n = 1` mole]

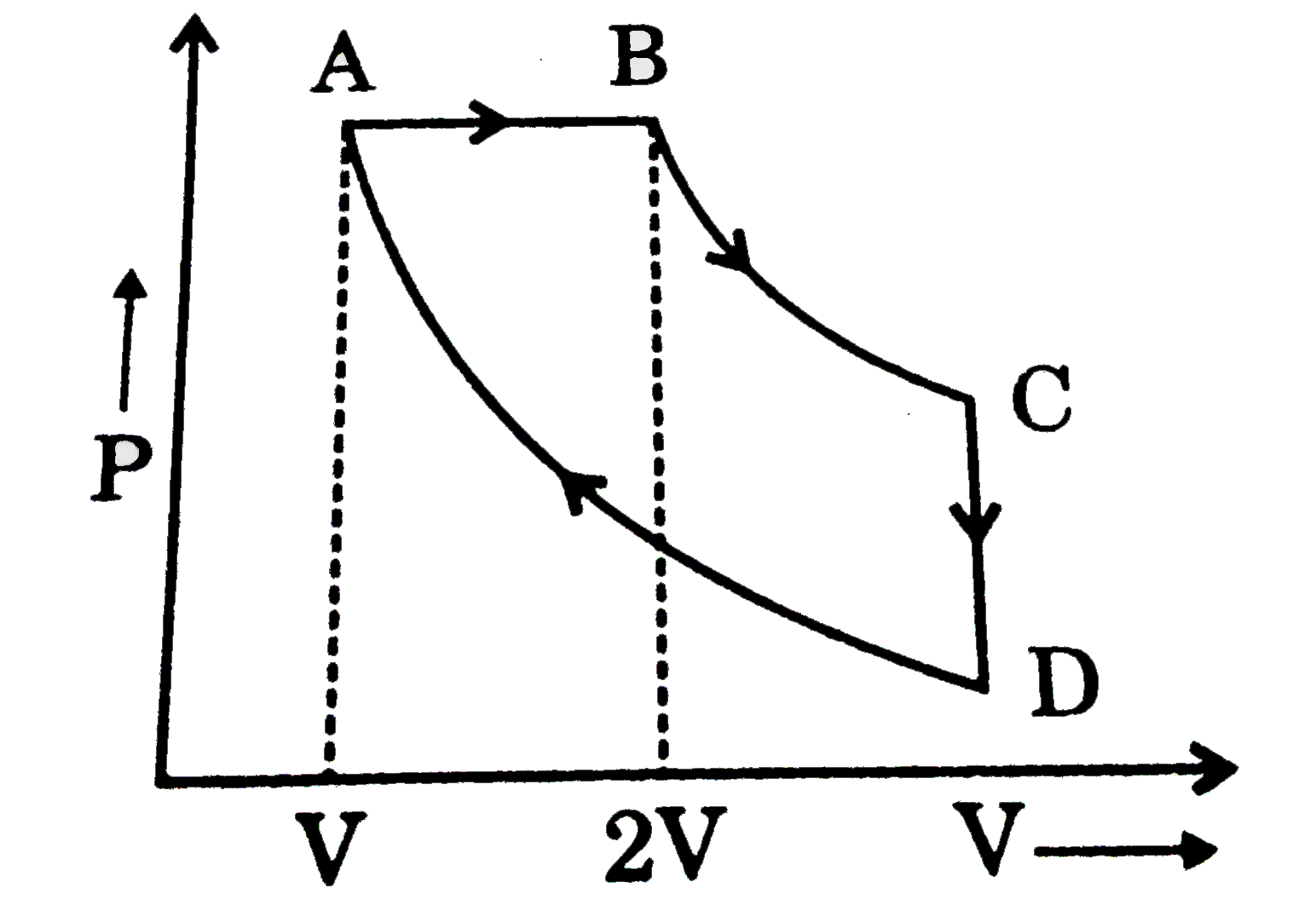
View SolutionCalculate magnitude of net work in following cyclic process for 1 mole of an ideal monoatomic gas (in cal).
(Given: `B rarr C` isothermal process: `D rarr A` adiabatic process : `T_(A) = 300 K, T_(D) = 75, T_(D) = 75 K, R = 2cal//"mole"-K: "ln" 2 = 0.7)`
View SolutionOne mole of monoatomic gas taken through a cyclic process as shown in figure.
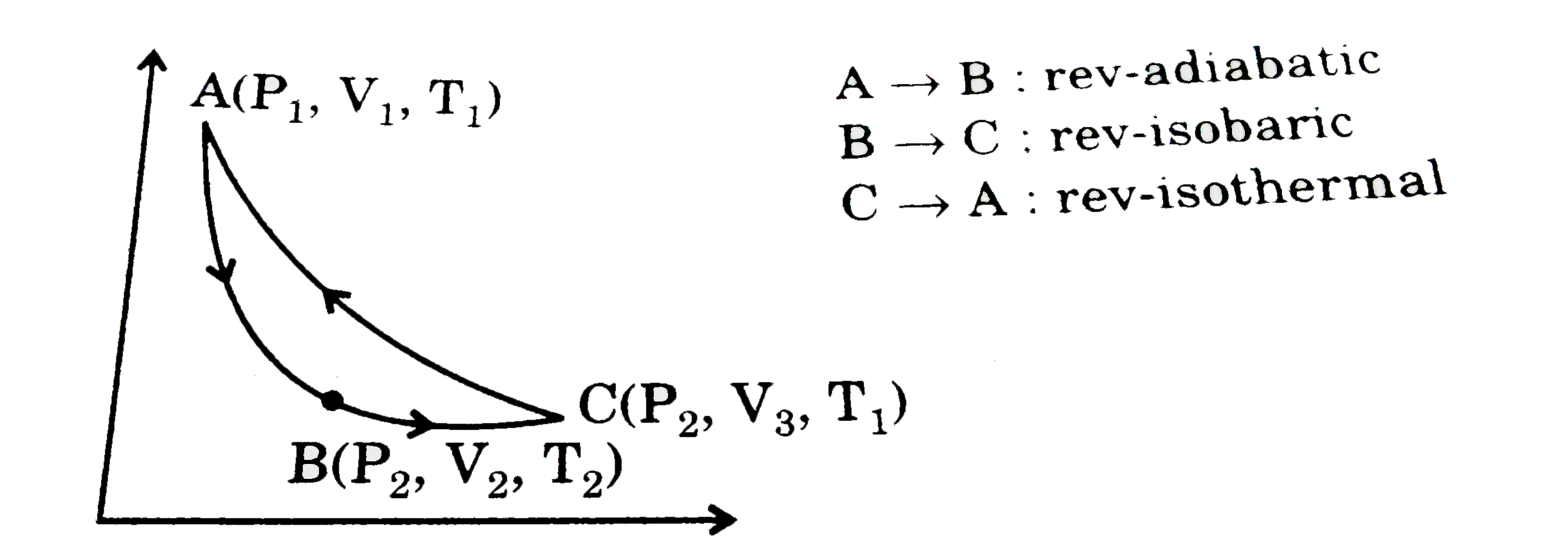
Calculate `sum_(ABCA) = (dq_(rev))/(T)`.
View SolutionFor the reaction `A(s) rarr A(g)`, the variation of log `K_(P)^(@)` us `(1)/(T)` is given by:
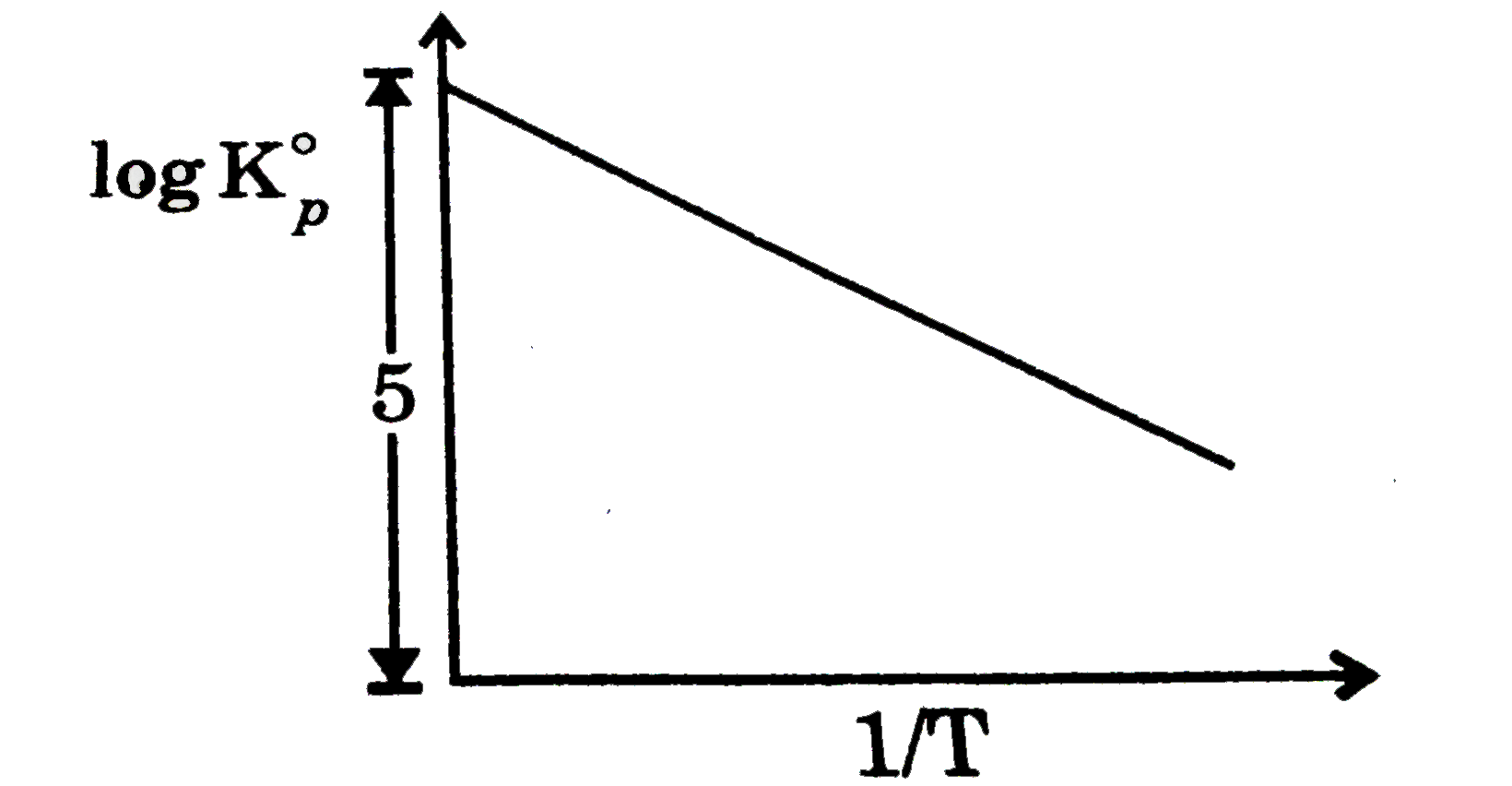
If `S_(m)^(@), A(g)` is `31.78 cal//K` mole, then calculate `S_(m)^(@) A(s)` in cal/K mole.
View SolutionAn ideal gas is subjected to the following changes. Answer the following questions:
(a) A curve showing the dependence of pressure on absolute temperature was obtained for a certain gas. Does compression or expansion takes place when the gas is being heated [constant moles]?
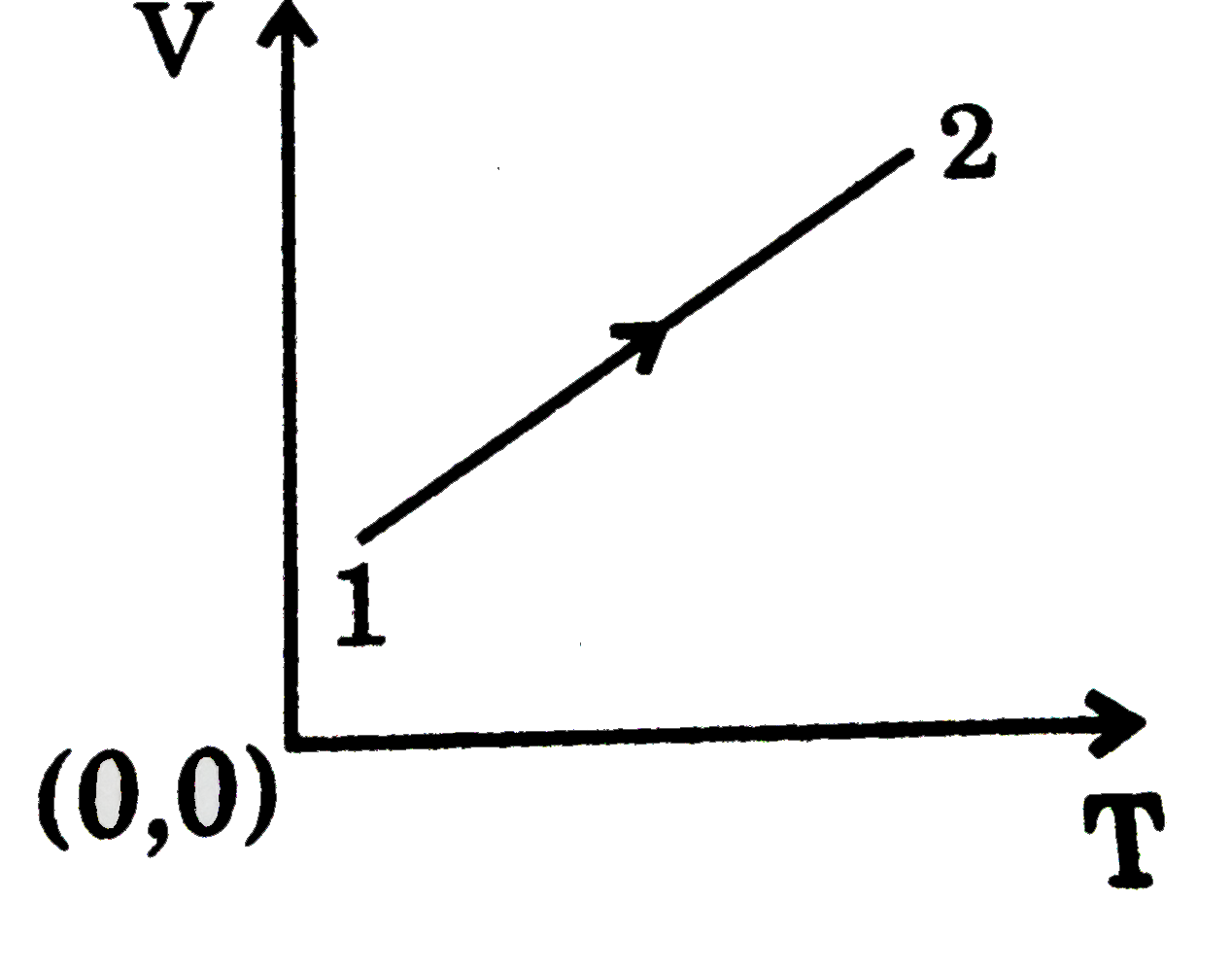
`{:("Code","Process"),(1,"Compression"),(2,"Expansion"):}`
(b) Use the volume temperature curve to find graphically the nature of change in the pressure of a gas during heating [constant moles.]
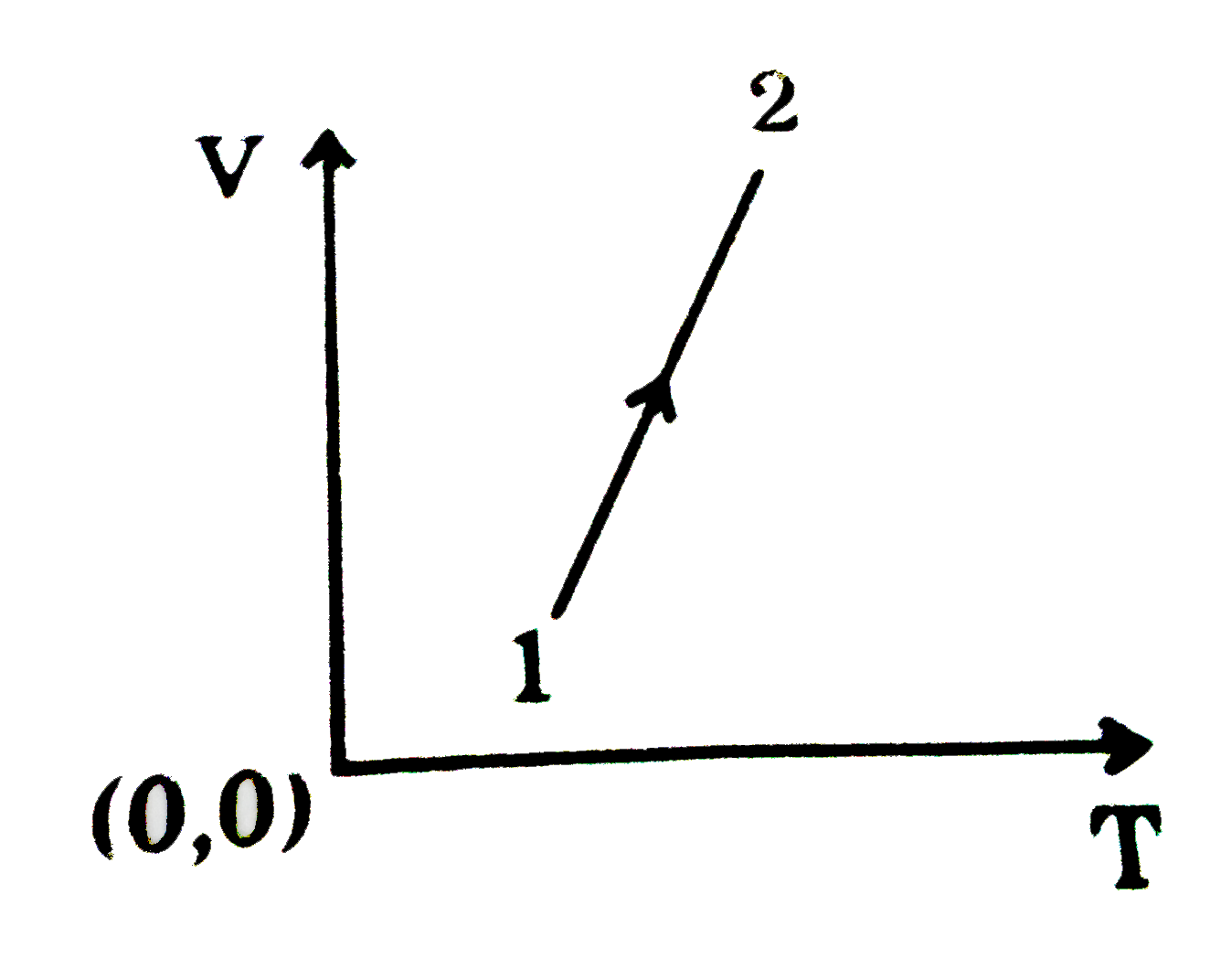
`{:("Code","Process"),(3,"Increases"),(4,"Decreases"),(5,"Remains constant"):}`
(c) The piston in a gas filled cylinder is lossely fitted aganist the wall of the cylinder and can slowly let the gas go past it. The volume temperature curve for the gas at constant pressure has the form shown in the figure. Use this curve to determine whether the amount of gas in the cylinder has increased or decreased.

`{:("Code","Amount of Gas"),(6,"Increases"),(7,"Decreases"),(8,"Remains constant"):}`
Write your answer as "abc", for example if your answer is code: 1,4,8 the, write your answer as 148.
View SolutionFor calculation of molecular weight of a dibasic acid using silver salt method, when a graph is plotted between weight of silver salt and weight of Ag, a straight line is obtained as shown:
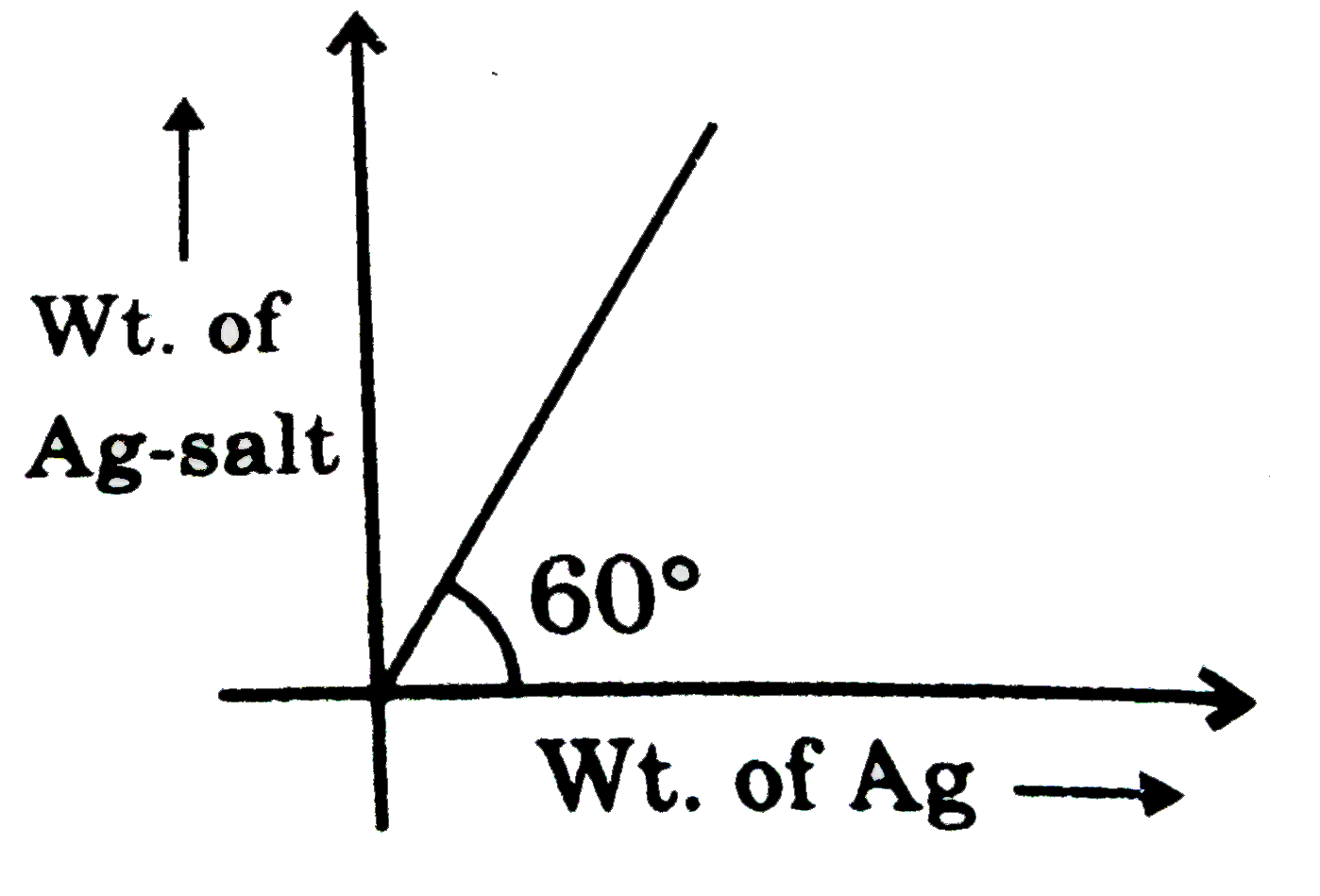
Find molecular weight of acid. (Take, `sqrt(3) = 1.7)` Give your answer after multiplying by 10.
View Solution
Subjective Type questions and complete solutions for chapter GRAPHICAL INTERPRETATION of GRB CHEMISTRY (HINGLISH) of Class 12
All Exercises from GRB PUBLICATION Class 12 CHEMISTRY GRAPHICAL INTERPRETATION
- A. Thermodynamics
- Atomic Sturcture
- B. Gaseous State
- C. Atomic Sturcture
- Chemical Equilibrium
- Chemical Kinetics
- Comprehension
- Comprehension 1
- Comprehension 10
- Comprehension 11
- Comprehension 12
- Comprehension 13
- Comprehension 14
- Comprehension 15
- Comprehension 16
- Comprehension 17
- Comprehension 18
- Comprehension 19
- Comprehension 2
- Comprehension 20
- Comprehension 21
- Comprehension 22
- Comprehension 23
- Comprehension 24
- Comprehension 25
- Comprehension 26
- Comprehension 27
- Comprehension 28
- Comprehension 29
- Comprehension 3
- Comprehension 4
- Comprehension 5
- Comprehension 6
- Comprehension 7
- Comprehension 8
- Comprehension 9
- D. Liquid Solutions
- E. Surface Chemistry
- Electrochemistry
- F. Ionic Equilibrium
- G. Chemical Equilibrium
- Gaseous State
- H. Chemical Kinetics
- I.Electrochemistry
- Ionic Equilibrium
- Liquid Solutions
- Match The Column Type
- Multiple Objective Type
- Subjective Type
- Surface Chemistry
- Thermodynamics