Complete Solutions to Comprehension of chapter GRAPHICAL INTERPRETATION of Class 12 book with complete answers and questions

Every reaction whether started by taking only reactants or by taking only products or any other combination always has a tendency to move towards equilibrium. Hence, equilibrium state can be considered as the one with most stable composition. In case of isomers, based on stability data position of equilibrium can als be decided.
Which of the following graphs are correct for the isomeric conversions at 1 bar and 298 K?

One mole of an ideal gas undergoes a process (10L, 4atm) to (4L, 10 atm ). The process may be represented by straight line in P-V diagram
The only incorrect statement is :
(R = 0.08 L-atm/K-mol)

One mole of an ideal gas undergoes a process (10L, 4atm) to (4L, 10 atm ). The process may be represented by straight line in P-V diagram
The incorrect graph regarding the process is ltbgt

In order to perdict variation of Gibbs free energy with progress of reaction at constant temperature and 1 bar pressure, it is important to know realtive stability of the components involved in chemical reaction at standard useful work then the change in Gibbs free energy should be calculated
In the thermite reaction used obtaining energy, aluminium oxide. From the given data identify the option 9s) which is (are) correct.
[Given : `DeltaH_(f)^(@)Al-(2)O_(3)=-390kj//mol,`
`DeltaH_(f)^(@)Fe_(2)O_(3)=-176kj//mol,`
Density of aluminimum = 2/7 gm/ml, Density of `Fe_(2)O_(3)=3.2gm//ml`

One of the important approach of the study of real gases involves the analysis of a parameter Z called the compressibility factor `Z=(PV_(m))/(RT)` where P is pressure, `V_(m)` is molar volume ,T is absolute temperature and R is the universal gas constant .Such a relation can also be expressed as `Z=((V_(" m real"))/(V_("m ideal")))` (where `V_("m ideal")` and V_("m real")` are the moler volume for ideal and real gas respectively tendencies among constituent particles.As pressure is force among is lowered or temperature is increased the value of Z approaches ideal behaviour
For a real gas 'G', `Zgt1` at STP, then for 'G' which of the following is true ?

One of the important approach of the study of real gases involves the analysis of a parameter Z called the compressibility factor `Z=(PV_(m))/(RT)` where P is pressure, `V_(m)` is molar volume ,T is absolute temperature and R is the universal gas constant .Such a relation can also be expressed as `Z=((V_(" m real"))/(V_("m ideal")))` (where `V_("m ideal")` and V_("m real")` are the moler volume for ideal and real gas respectively tendencies among constituent particles.As pressure is force among is lowered or temperature is increased the value of Z approaches ideal behaviour
Following graph represents a pressure (P) volume (V) relationship at a fixed temperature (T) for moles of a real gas.The graph has two regions masked (I) and (II). Which of the folloing option true ?

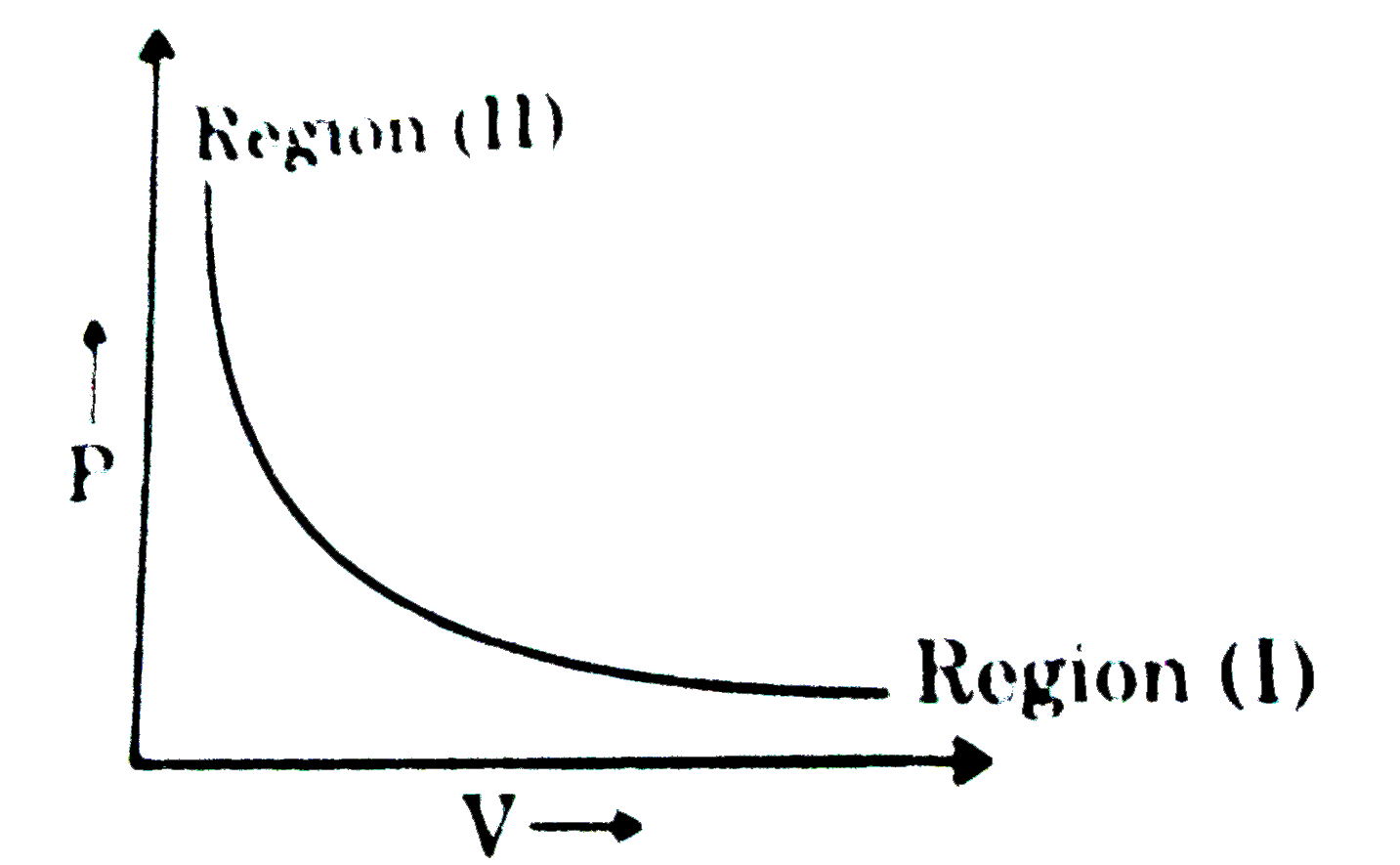
When perssure is increase at constant temperature, volume of gas decreases, AB `to` gases,Bc `to` vapour + liquid ,CD `to`liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
`T_(e)` or critical temp : Temperature above which a gas can not be liquified
`V_(e)` or critical volume : Volume occupied by one mole of gas at `T_(e)` abd `P_(e).`

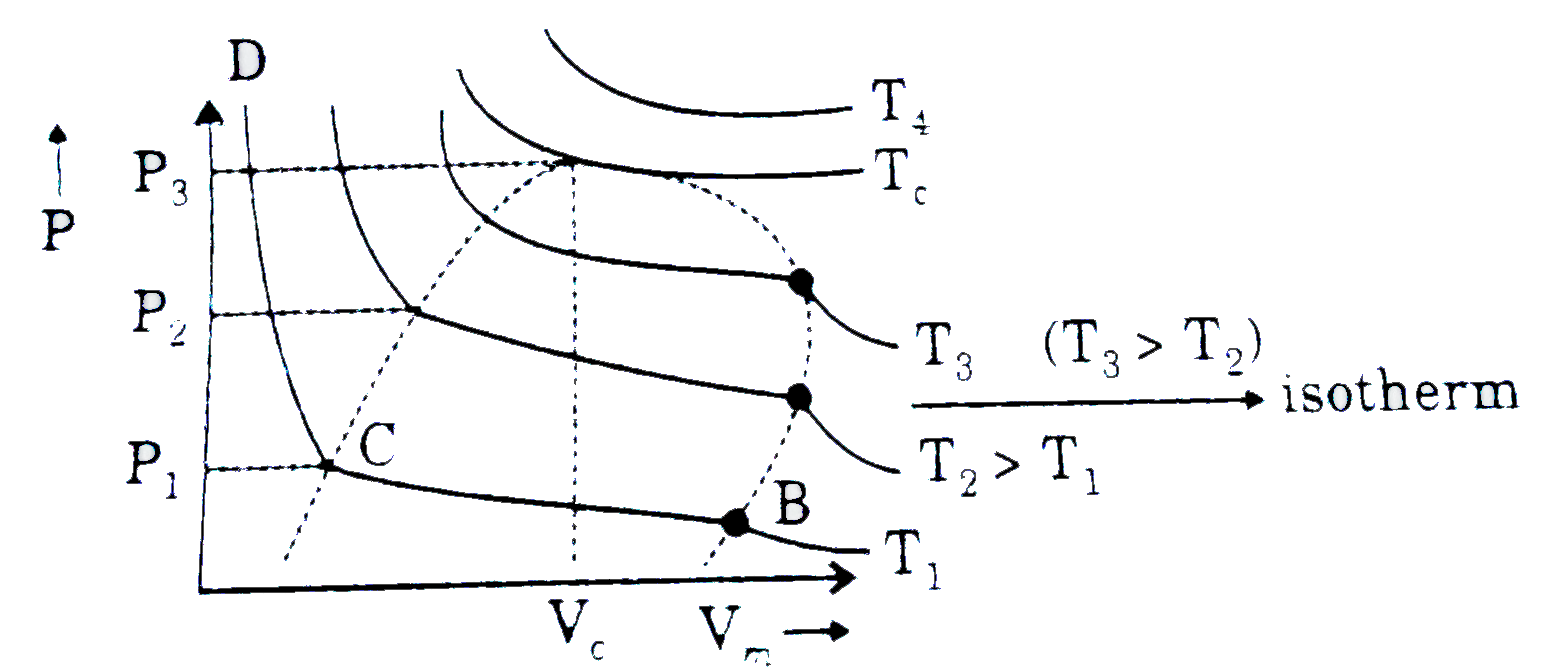
Critical constant Using van der Waals' Equations
`(P+(a)/(V_(m)^(2)))(V_(m)-b)=RT`
`implies(PV_(m)^(2)+a)(V_(m)-b)=RTV_(m)^(2)`
`PV_(m)^(3)+aV_(m)-PbV_(m)^(2)=ab-RTV_(m)^(2)=0`
`impliesV_(m)^(3)-V_(m)^(2)(b+(RT_(e))/(P))+(a)/(p)(V)/(m)-(ab)/(p)=0`
Since equation is cubic in `V_(m)` hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
`V_(m)^(3)-V_(m)^(2)(b+(RT_(c))/(P_(c)))+(a)/(p_(c))V_(m)-(ab)/(p_(c))=0" " ....(i)`
But at critical point all three roots of the equation should be equal, hence equation should be :
`V_(m)=V_(c)`
`(V_(m)-V_(c))^(3)=0`
`V_(m)-3V_(m)^(2)V_(c)+3V_(m)V_(c)^(2)-V_(c)^(3)=0`....(ii)
Comparing with equation (i)
`b+(RT_(c))/(p_(c))=3V_(c)` ...(iii)
`(a)/(p_(c))=3V_(e)^(2)`...(iv)
`(ab)/(p_(c))=V_(c)^(3)`....(v)
from eqns.(iv) and (v0, `V_(c)=3b`
from eq. (iv) `p_(c)=(a)/(3V_(c)^(2))` substituting `p_(c)=(a)/(3(3b)^(2))=(a)/(27b^(2))`
from e.q (iii) `(RT_(c))/(p_(c))=3V_(c)-b=9b-b=8b`
`impliesT_(c)=(8a)/(27Rb)`
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
`((delP)/(delV_(m)))_(Tc)=0`...(iv)
`(del)/(delV_(m))((delP)/(delV_(m)))_(Tc)=0`
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two `T_(c)P_(c)` and `V_(c)` can be calculated
If the critical constants for a hypothetical van der Waals' gas are `V_(c)=150cm^(2)mol^(-1),p_(c)=300K` Then the approxomate radius of the molecule is :
`("Take"R=(1)/(12)Latmmol^(-1)K^(-1)]`

When perssure is increase at constant temperature, volume of gas decreases, AB `to` gases,BC `to` vapour +liquid ,CD `to` liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
`T_(e)` or critical temp : Temperature above which a gas can not be liquified
`V_(e)` or critical volume : Volume occupied by one mole of gas at `T_(e)` abd `P_(e).`

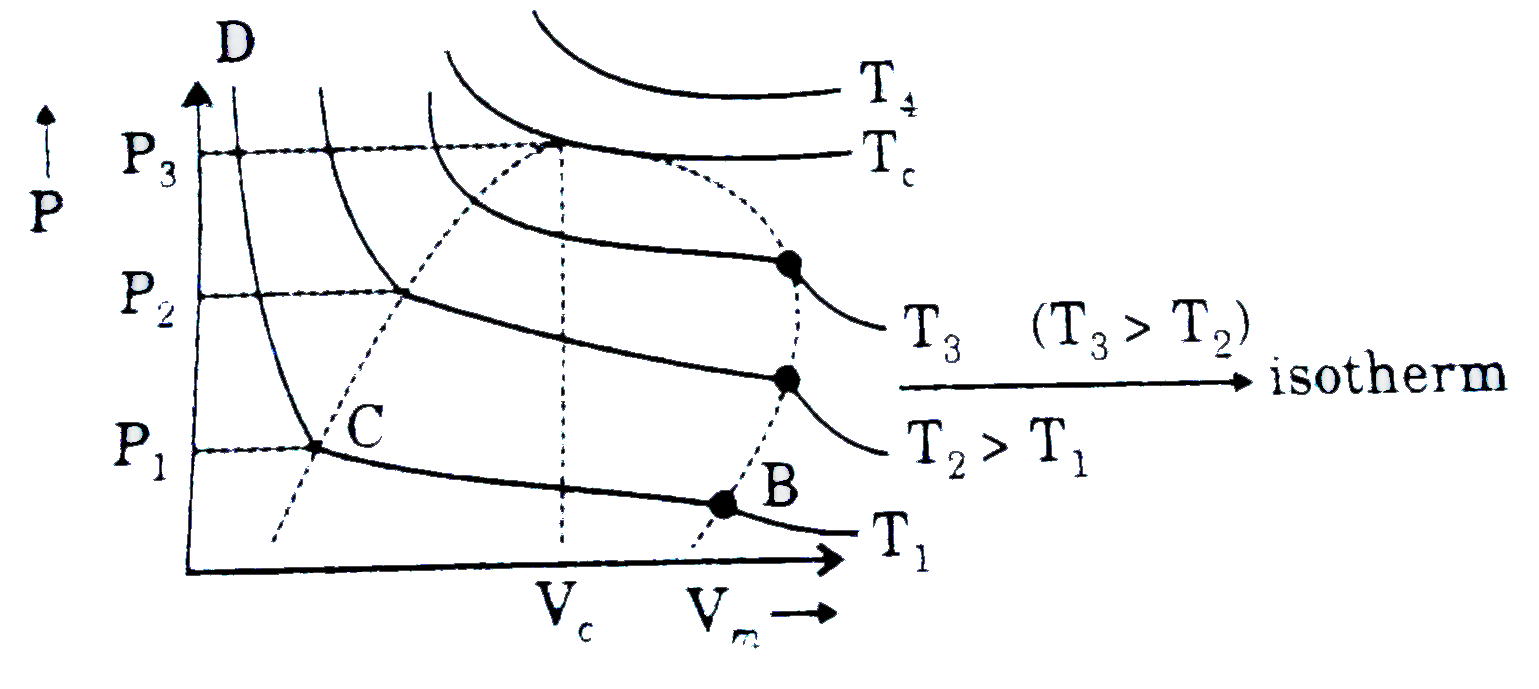
Critical constant Using van der Waals' Equations
`(P+(a)/(V_(m)^(2)))(V_(m)-b)=RT`
`implies(PV_(m)^(2)+a)(V_(m)-b)=RTV_(m)^(2)`
`PV_(m)^(3)+aV_(m)-PbV_(m)^(2)=ab-RTV_(m)^(2)=0`
`impliesV_(m)^(3)-V_(m)^(2)(b+(RT_(e))/(P))+(a)/(p)(V)/(m)-(ab)/(p)=0`
Since equation is cubic in `V_(m)` hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
`V_(m)^(3)-V_(m)^(2)(b+(RT_(c))/(P_(c)))+(a)/(p_(c))V_(m)-(ab)/(p_(c))=0" " ....(i)`
But at critical point all three roots of the equation should be equal, hence equation should be :
`V_(m)=V_(c)`
`(V_(m)-V_(c))^(3)=0`
`V_(m)-3V_(m)^(2)V_(c)+3V_(m)V_(c)^(2)-V_(c)^(3)=0`....(ii)
Comparing with equation (i)
`b+(RT_(c))/(p_(c))=3V_(c)` ...(iii)
`(a)/(p_(c))=3V_(e)^(2)`...(iv)
`(ab)/(p_(c))=V_(c)^(3)`....(v)
from eqns.(iv) and (v0, `V_(c)=3b`
from eq. (iv) `p_(c)=(a)/(3V_(c)^(2))` substituting `p_(c)=(a)/(3(3b)^(2))=(a)/(27b^(2))`
from e.q (iii) `(RT_(c))/(p_(c))=3V_(c)-b=9b-b=8b`
`impliesT_(c)=(8a)/(27Rb)`
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
`((delP)/(delV_(m)))_(Tc)=0`...(iv)
`(del)/(delV_(m))((delP)/(delV_(m)))_(Tc)=0`
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two `T_(c)P_(c)` and `V_(c)` can be calculated
Identify the wrong statement related to the following graph

In the photoelectric effect the eletrons are emiited intantaneously from a given matal plate when it is irradiated with radiation of frequency equal to or greater then some minimum ferquency, is called the threshold frequency.According to Planck's idea, light may be considered to be made up discrete particles called photons.Each photon carries energy equal ti hv.When this photon cllides with the electron of the metal, the electron acquires energy of the emitted electron is given by :
`hv=K.E_("maximum")+PE=(1)/(2)m u^(2)+PE`
If the incident rediation is of threshold frequency the electron will be emitted without any kinetic energy
i.e `hv_(0)`
`:.(1)/(2)m u^(2)=hv-hv_(0)`
A plot of kinetic energy of the emitted electron versus frequency of the incident radiation yields a straight line given as :

A laser producting monochromatic lights of different wavelenght is uesd to eject electrons from the sheet of glod having threshold frequency `6.15xx10^(14)s^(-1)` Which of the following incident rediation will be suitable for the ejecting of electrons ?

In the photoelectric effect the eletrons are emiited intantaneously from a given matal plate when it is irradiated with radiation of frequency equal to or greater then some minimum ferquency, is called the threshold frequency.According to Planck's idea, light may be considered to be made up discrete particles called photons.Each photon carries energy equal ti hv.When this photon cllides with the electron of the metal, the electron acquires energy of the emitted electron is given by :
`hv=K.E_("maximum")+PE=(1)/(2)m u^(2)+PE`
If the incident rediation is of threshold frequency the electron will be emitted without any kinetic energy
i.e `hv_(0)`
`:.(1)/(2)m u^(2)=hv-hv_(0)`
A plot of kinetic energy of the emitted electron versus frequency of the incident radiation yields a straight line given as :

The number of photoelectrons emitted depends upon :

Effect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
`DeltaG^(@)=-2.30RTlogk`
`DeltaG^(@):` Standing free energy change
`DeltaG^(@)=DeltaH^(@)-TDeltaS^(@)`…(ii)
`DeltaH^(@) :`Standard heat of the reaction gt
From eqns.(i) and(ii)
`-2RTlogk=DeltaH^(@)=TDeltaS^(@)`
`DeltaS^(@)` : standard entropy change
`implies" "logK=-(DeltaH^(@))/(2.3RT)+(DeltaS^(@))/(2.3R)`
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope `=(-DeltaH^(@))/(2.3R)` amd y intercept `=(DeltaS^(@))/(2.3R)`
If at temperature `T_(1)` equilibrium constant be `k_(1)` and at temperature `T_(2)`equilibrium constant be `k_(2)` then :
`implies" "logK_(1)=-(DeltaH^(@))/(2.3RT_(1))+(DeltaS^(@))/(2.3R)`..(iv)
`implies" "logK_(2)=-(DeltaH^(@))/(2.3RT_(2))+(DeltaS^(@))/(2.3R)`...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
For exothermic reaction if `DeltaS^(@)lt0` then the sketch of log k vs `(1)/(T)` may be

Effect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
`DeltaG^(@)=-2.30RTlogk`
`DeltaG^(@):` Standing free energy change
`DeltaG^(@)=DeltaH^(@)-TDeltaS^(@)`…(ii)
`DeltaH^(@) :`Standard heat of the reaction gt
From eqns.(i) and(ii)
`-2RTlogk=DeltaH^(@)=TDeltaS^(@)`
`DeltaS^(@)` : standard entropy change
`implies" "logK=-(DeltaH^(@))/(2.3RT)+(DeltaS^(@))/(2.3R)`
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope `=(-DeltaH^(@))/(2.3R)` amd y intercept `=(DeltaS^(@))/(2.3R)`
If at temperature `T_(1)` equilibrium constant be `k_(1)` and at temperature `T_(2)`equilibrium constant be `k_(2)` then :
`implies" "logK_(1)=-(DeltaH^(@))/(2.3RT_(1))+(DeltaS^(@))/(2.3R)`..(iv)
`implies" "logK_(2)=-(DeltaH^(@))/(2.3RT_(2))+(DeltaS^(@))/(2.3R)`...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If for a particular reversible reaction
`K_(C)=57` abd `355^(@)C` and `K_(C)=69` at `450^(@)C` then

The variation of rate constant with temperature can be explained by Arrhenius equation. However , the can be explained by Activation energy is found to be temperature dependent/In such cases`(d"in"K)/(dT)=(E_(a))/(RT^(2))` should be used to predict variation of rate constant with tempreature. On the basic of this information , answer the question that follow :
If for a reaction in `K=20-(20)/(T)+3` in T then `E_(a)` at 300 K will be

The variation of rate constant with temperature can be explained by Arrhenius equation. However , the can be explained by Activation energy is found to be temperature dependent/In such cases`(d"in"K)/(dT)=(E_(a))/(RT^(2))` should be used to predict variation of rate constant with tempreature. On the basic of this information , answer the question that follow :
Which if the following statement is not correct ?

If an element can exist in several oxidation states, it is convenient to display the reduction potentials corresponding to the various half reactions in diagrammatic from, known as Latimer diagram. The Latimer diagram for chlorine in acid solution is
`Cl_(4)^(-)overset(+1.20V)toClO_(3)^(-)overset(+1.60V)toClO_(2)^(-)overset(+1.60V)to`
`ClO^(-)overset(+1.67V)toCl_(2)overset(+1.36V)toCl^(-)`
In basic solution is :
`ClO_(4)^(-)overset(+0.37V)toClO_(3)^(-)overset(+0.30V)toClO_(2)^(-)overset(+0.68)to`
`ClO^(-)overset(+0.42V)toCl_(2)overset(+1.36)toCl^(-)`. The standard potentials for two nonadjacent species can also be calculated by using the concept that `DeltaG^(@)` is an additive property but using potential is not an assitive property and `DeltaG^(@)=-nFx^(0),` If a given oxidation state is a the next higher oxidation state disproportionation can occur. The reverse of relative stabilities of the oxidation state can also be understood by drawing a graph of `DeltaG^(@)//F` against oxidation state, known as Frost diagram, Choosing the stability of zero oxidation state arbitrery as zero. The most stable oxidation state of a apecies lies lowest in the digram Disproportionation is spontaneous if the species lies above a straight line joining its two product species.
What is the potential of couple `(ClO^(-))/(Cl^(-))` at pH = 14 14?

If an element can exist in several oxidation states, it is convenient to display the reduction potentials corresponding to the various half reactions in diagrammatic from, known as Latimer diagram. The Latimer diagram for chlorine in acid solution is
`Cl_(4)^(-)overset(+1.20V)toClO_(3)^(-)overset(+1.60V)toClO_(2)^(-)overset(+1.60V)to`
`ClO^(-)overset(+1.67V)toCl_(2)overset(+1.36V)toCl^(-)`
In basic solution is :
`ClO_(4)^(-)overset(+0.37V)toClO_(3)^(-)overset(+0.30V)toClO_(2)^(-)overset(+0.68)to`
`ClO^(-)overset(+0.42V)toCl_(2)overset(+1.36)toCl^(-)`. The standard potentials for two nonadjacent species can also be calculated by using the concept that `DeltaG^(@)` is an additive property but using potential is not an assitive property and `DeltaG^(@)=-nFx^(0),` If a given oxidation state is a the next higher oxidation state disproportionation can occur. The reverse of relative stabilities of the oxidation state can also be understood by drawing a graph of `DeltaG^(@)//F` against oxidation state, known as Frost diagram, Choosing the stability of zero oxidation state arbitrery as zero. The most stable oxidation state of a apecies lies lowest in the digram Disproportionation is spontaneous if the species lies above a straight line joining its two product species.
Which of the following statement s correct ?

If an element can exist in several oxidation states, it is convenient to display the reduction potentials corresponding to the various half reactions in diagrammatic from, known as Latimer diagram. The Latimer diagram for chlorine in acid solution is
`Cl_(4)^(-)overset(+1.20V)toClO_(3)^(-)overset(+1.60V)toClO_(2)^(-)overset(+1.60V)to`
`ClO^(-)overset(+1.67V)toCl_(2)overset(+1.36V)toCl^(-)`
In basic solution is :
`ClO_(4)^(-)overset(+0.37V)toClO_(3)^(-)overset(+0.30V)toClO_(2)^(-)overset(+0.68)to`
`ClO^(-)overset(+0.42V)toCl_(2)overset(+1.36)toCl^(-)`. The standard potentials for two nonadjacent species can also be calculated by using the concept that `DeltaG^(@)` is an additive property but using potential is not an assitive property and `DeltaG^(@)=-nFx^(0),` If a given oxidation state is a the next higher oxidation state disproportionation can occur. The reverse of relative stabilities of the oxidation state can also be understood by drawing a graph of `DeltaG^(@)//F` against oxidation state, known as Frost diagram, Choosing the stability of zero oxidation state arbitrery as zero. The most stable oxidation state of a apecies lies lowest in the digram Disproportionation is spontaneous if the species lies above a straight line joining its two product species.
For a hypothetical element, the Frost diagram is shown in figure

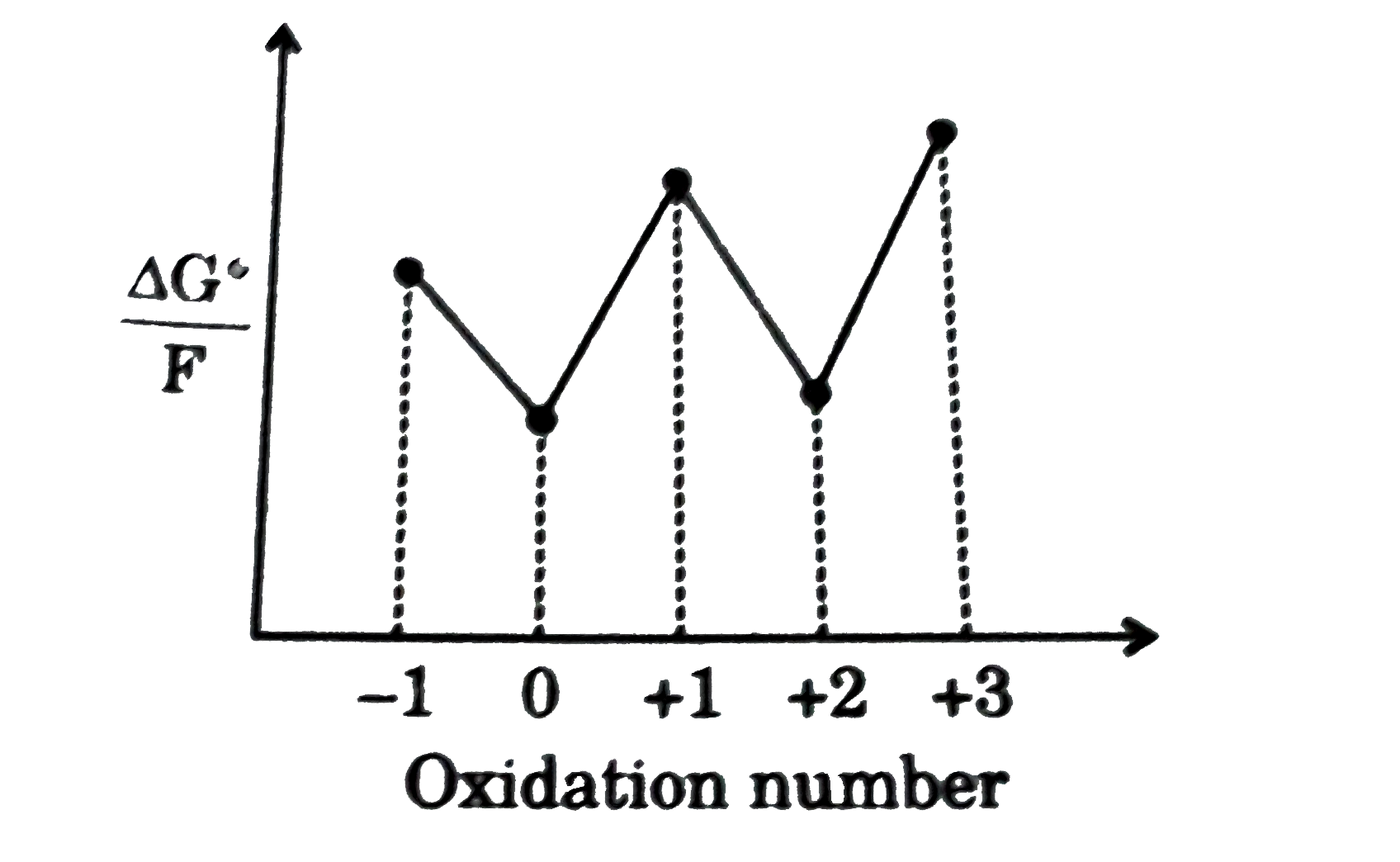
Which of the following oxidation state is least stable ?

If an element can exist in several oxidation states, it is convenient to display the reduction potentials corresponding to the various half reactions in diagrammatic from, known as Latimer diagram. The Latimer diagram for chlorine in acid solution is
`Cl_(4)^(-)overset(+1.20V)toClO_(3)^(-)overset(+1.60V)toClO_(2)^(-)overset(+1.60V)to`
`ClO^(-)overset(+1.67V)toCl_(2)overset(+1.36V)toCl^(-)`
In basic solution is :
`ClO_(4)^(-)overset(+0.37V)toClO_(3)^(-)overset(+0.30V)toClO_(2)^(-)overset(+0.68)to`
`ClO^(-)overset(+0.42V)toCl_(2)overset(+1.36)toCl^(-)`. The standard potentials for two nonadjacent species can also be calculated by using the concept that `DeltaG^(@)` is an additive property but using potential is not an assitive property and `DeltaG^(@)=-nFx^(0),` If a given oxidation state is a the next higher oxidation state disproportionation can occur. The reverse of relative stabilities of the oxidation state can also be understood by drawing a graph of `DeltaG^(@)//F` against oxidation state, known as Frost diagram, Choosing the stability of zero oxidation state arbitrery as zero. The most stable oxidation state of a apecies lies lowest in the digram Disproportionation is spontaneous if the species lies above a straight line joining its two product species.
Which of the following statement is correct according to above question ?

The principle on conductometric titration is based in the fact that during the titration, one of the ions is replaced by the other and invariably thses two ions differ in the ionic conductivity with the result that the conductivity of the solution varies during the course of the titration.Take,for example,the titration between strong acid, say HCl. and a strong base, say NaOH.Before NaOH is added the conuctance of HCl solution has a high value due ti the persence if highly hydrogen ions.As NaOH is added,`H^(+)` ions are the replaced by relatively slower moving `Na^(+)` ions.Consequently, the conductance of the solution decrease and this continues right upto the enuivalence point where the solution contains only NaCL.Beyond the equivalence point if more of NaOH is added, then the solution contains an excess of the fast moving `OH^(-)` with the result that its as more of NaoH added, we plot the conductance value vs the amount of NaOH added we get curve of the type shown in figure.The descending portion AB represents the conductance before the equivalence point (solution cintains a mixture if acid HCl and the salt NaCL and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCL and the excess of NaOH). The point E which repersents only the minimum conductance is alkali and thus repersents the equivalence point.This point can, however, be obtained by the extrapoltion of the lines AB and CD and therefore one is not very particular in location this point experimentally as it is in the case of ordinary acid -base involving the acid base indicators
LET us take the specific exaanple of acetic acid being titration against NaOH.Before the addition the of alkali, the solution shows poor conductance due to feeble inization of acetic acid.Initially the addtion of alkali causes not only the replacement of `H^(+)` by `Na^(+)` but also suppresses the thus the conductance of the solution decrease in the begnning .But very soon the conductance starts increasing as addetion NaOH thus causing neutralizes the undissociated HAc to HAc with strong condutance eletroyte `Na^(+)Ac^(-)`.The increase in conducting `OH^(-)` ions gtthe graph near the highly equivalence point actual equivalence point can as usual be ontained by the extrapoiation method
In all thses graphs it been assumed that the vloume change due addition of solution from burette in negligible heane vloume change of the sloution in beaker the conuctance of which is measured is almost constant throughout the measurement
The most appropriate titration curve ibtained when a mixture of a strong acid (say HCl) and a weak acid (say`CH_(3)`COOH0 is titration with (say NaOH) will be

The principle on conductometric titration is based in the fact that during the titration, one of the ions is replaced by the other and invariably thses two ions differ in the ionic conductivity with the result that the conductivity of the solution varies during the course of the titration.Take,for example,the titration between strong acid, say HCl. and a strong base, say NaOH.Before NaOH is added the conuctance of HCl solution has a high value due ti the persence if highly hydrogen ions.As NaOH is added,`H^(+)` ions are the replaced by relatively slower moving `Na^(+)` ions.Consequently, the conductance of the solution decrease and this continues right upto the enuivalence point where the solution contains only NaCL.Beyond the equivalence point if more of NaOH is added, then the solution contains an excess of the fast moving `OH^(-)` with the result that its as more of NaoH added, we plot the conductance value vs the amount of NaOH added we get curve of the type shown in figure.The descending portion AB represents the conductance before the equivalence point (solution cintains a mixture if acid HCl and the salt NaCL and the ascending portion CD represents the conductances after the equivalence point (solution contains the salt NaCL and the excess of NaOH). The point E which repersents only the minimum conductance is alkali and thus repersents the equivalence point.This point can, however, be obtained by the extrapoltion of the lines AB and CD and therefore one is not very particular in location this point experimentally as it is in the case of ordinary acid -base involving the acid base indicators
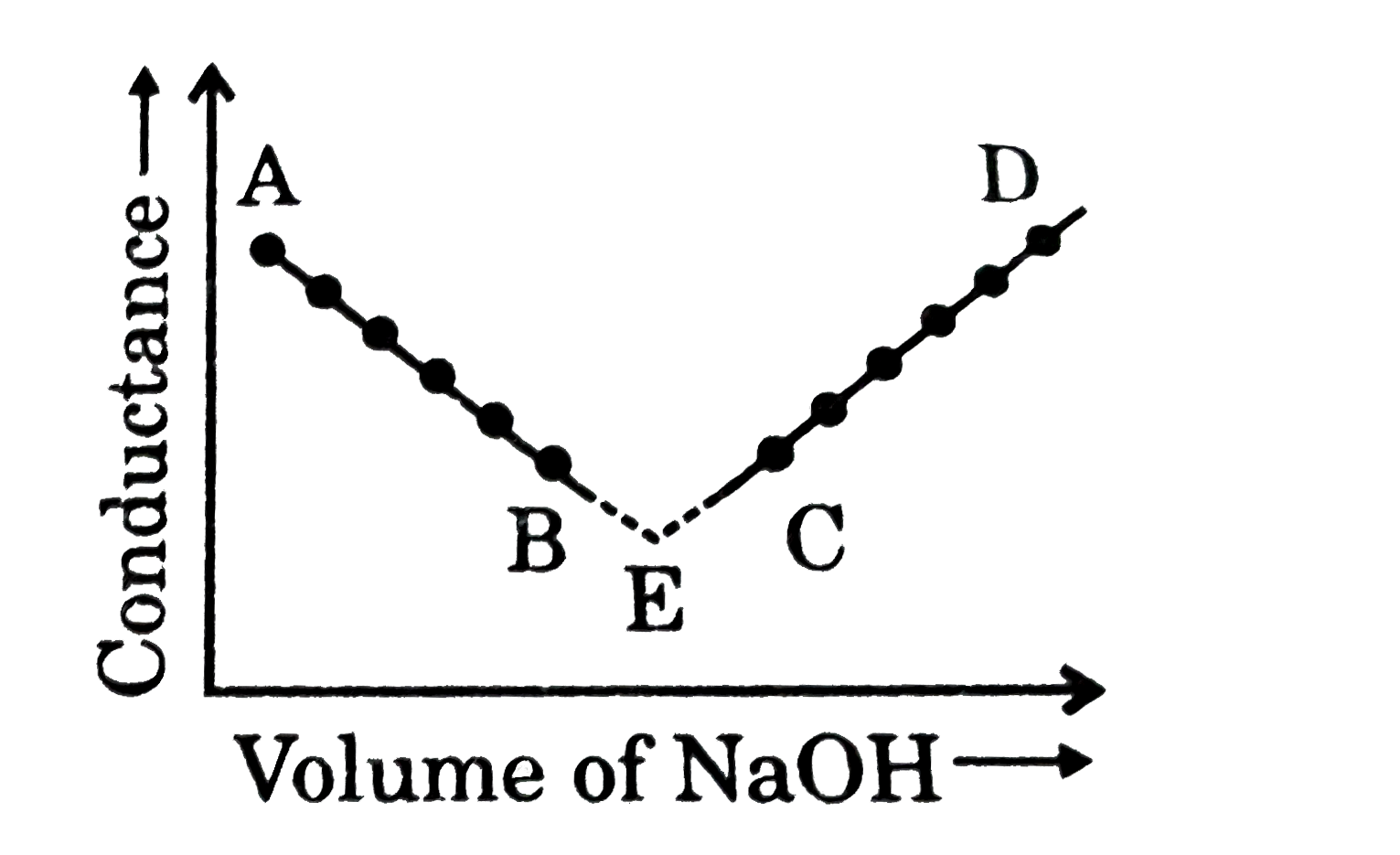
LET us take the specific exaanple of acetic acid being titration against NaOH.Before the addition the of alkali, the solution shows poor conductance due to feeble inization of acetic acid.Initially the addtion of alkali causes not only the replacement of `H^(+)` by `Na^(+)` but also suppresses the thus the conductance of the solution decrease in the begnning .But very soon the conductance starts increasing as addetion NaOH thus causing neutralizes the undissociated HAc to HAc with strong condutance eletroyte `Na^(+)Ac^(-)`.The increase in conducting `OH^(-)` ions gtthe graph near the highly equivalence point actual equivalence point can as usual be ontained by the extrapoiation method
In all thses graphs it been assumed that the vloume change due addition of solution from burette in negligible heane vloume change of the sloution in beaker the conuctance of which is measured is almost constant throughout the measurement
If a 100 ml solution of 0.1 MHBr is titration using a very concentrated solution of NaOH then the conductivity (specific conductance0 of this solution at the equivalence wil be (assume volume change is negligible due addition of NaOH). Report your answer after mulitiplying it with 100 in`Sm^(-1)`
[Given : `lambda_((Na^(+)))^(@)=8xx10^(-3)Sm^(2)mol^(-1), lambda_((Br^(-)))^(@) = 4 xx 10^(-3) Sm^(2)mol^(-1)]`

Titration are one of the methods we can use to discover the precise concentration of solutions. A typical titration involves adding a solution from a burette to another solution in a flask. The end point of the titration is found by watching a colour change taking place.However, a problem arises when a suitable indicator cannot be found, or when the colour change involved are unclear. In these cases, redox potential may sometimes come to the rescue.

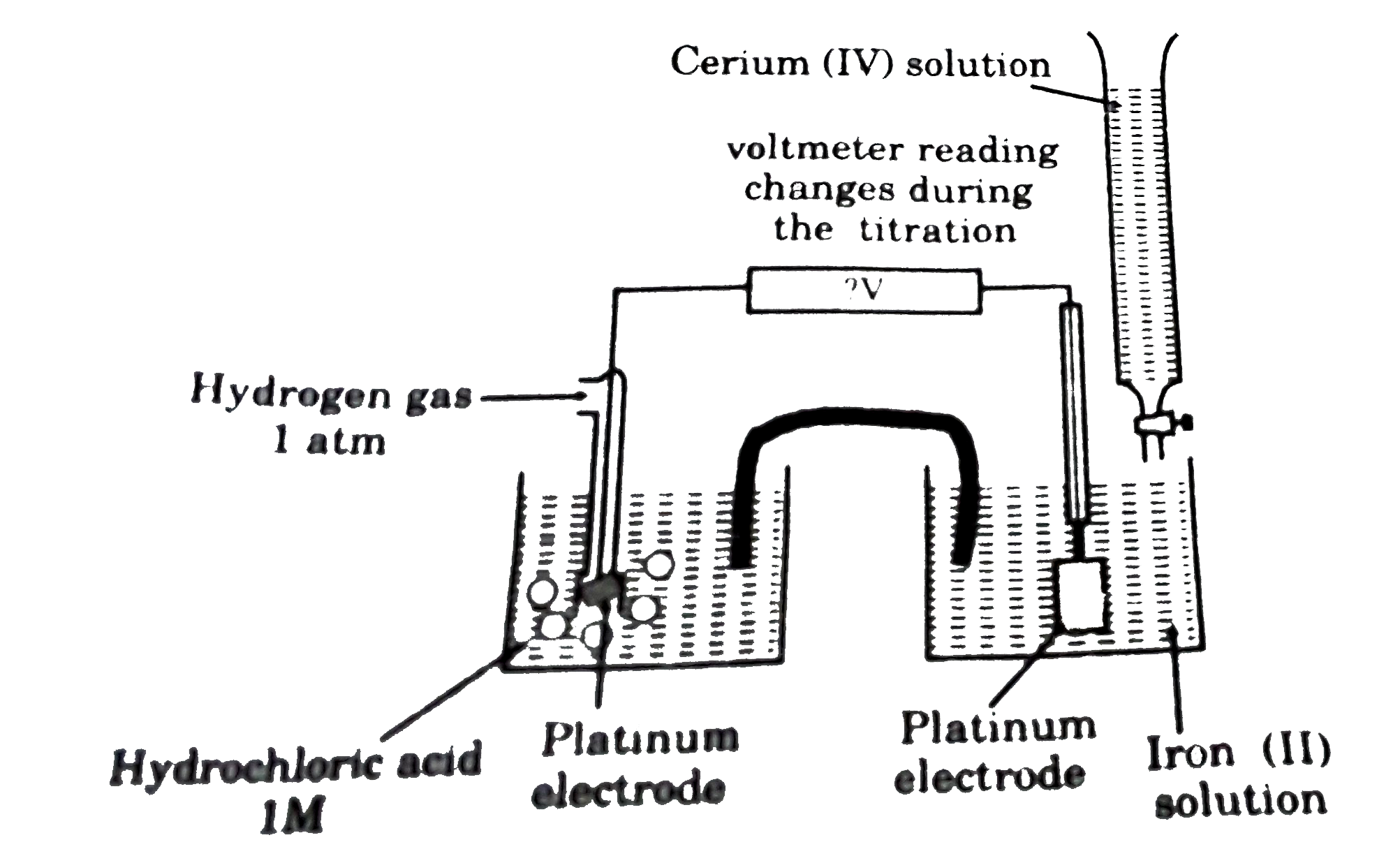
A perticularly well known example (Fig.) is a method of discovering then concentration of iron (II) ions in a solution by titrating them with a solution of cerium (IV). The redox potential that are of interest here are`E_(Fe^(3+)|Fe^(2+))^(@)=0.77 V "and"E_(Ce^(4+|Ce^(3+)))^(@)=1.61V.` These tell us that cerium (IV) ions are the oxidising agents. They should react according to the equation
`Fe^(2+) (aq) + Ce^(4+) (aq) to Fe^(3+) (aq) + Ce^(3+) (aq)`.
Now imagine that we know the concentration of the cerium (IV) ions solution in the burette. We want to measure the concentration of the cerium (IV) solution from the burette, some of the iron (II) ions are will be oxidised. As a consequence the beaker would now contain large number of unreacted iron (II) ions , but also some iron (III) ions as well. All of the cerium (III). The solution in the beaker now represents an iron `(III)//iron(II)` half cell although not at standard conditions.Thus , the emf of the cell will be near, but not equal to `E_(Fe^(3+|Fe^(2+.)))^(@)`

If we continue to add cerium (IV) solution , the number of iron (II) ions is gradually reduced and eventually only a very few are left (Table).At this stage the next few drops of cerium (IV) solution convert all the remaining irom (II) ions into iron (III), and some of the cerium (IV) ions are left unreacted. Once this happens we no longer have an iron `(III)//"iron"(II)` half-cell. Instead we have a solution in which there is a large number of cerium (III) ions and a smaller number of cerium (IV) ions. The solution in the beaker now behaves as a cerium `(IV)//"cerium"(III)`half-cell (although not a standard one.)
Just before all the iron (II) ions are converted into iron (III) we have a cell with an EMF of around `+0.77V.` After all the iron (II) ions are oxidised we have a cell with an emf of about `+1.61 V. ` This rapid rise in emf occurs with the addition of just one drop of cerium (IV) solution. You should be able to understand why a graph of cell emf against volume of cerium (IV) solution of the iron (II) solution calculated in the usual way.
The cell shown below was set up
`Pt|underset(1"mol dm"^(-3))(Fe^(3+)(aq),Fe^(2+)(aq)),||underset(1"mol dm"^(-3)) (Br^(-)(aq)|Br_(2)(l)),|Pt(s)`
what would be the cell emf? If potassium cyanide solution were added to the left hand half cell (with due care!) what would you expect to happen to the emf of the cell ? `E_(Br_(2)//Br^(-))^(@)= 1.07 V` and use data of previous question, if required.

Titration are one of the methods we can use to discover the precise concentration of solutions. A typical titration involves adding a solution from a burette to another solution in a flask. The end point of the titration is found by watching a colour change taking place.However, a problem arises when a suitable indicator cannot be found, or when the colour change involved are unclear. In these cases, redox potential may sometimes come to the rescue.

A perticularly well known example (Fig.) is a method of discovering then concentration of iron (II) ions in a solution by titrating them with a solution of cerium (IV). The redox potential that are of interest here are`E_(Fe^(3+)|Fe^(2+))^(@)=0.77 V "and"E_(Ce^(4+|Ce^(3+)))^(@)=1.61V.` These tell us that cerium (IV) ions are the oxidising agents. They should react according to the equation
`Fe^(2+) (aq) + Ce^(4+) (aq) to Fe^(3+) (aq) + Ce^(3+) (aq).`
Now imagine that we know the concentration of the cerium (IV) ions solution in the burette. We want to measure the concentration of the cerium (IV) solution from the burette, some of the iron (II) ions are will be oxidised. As a consequence the beaker would now contain large number of unreacted iron (II) ions , but also some iron (III) ions as well. All of the cerium (III). The solution in the beaker now represents an iron `(III)//iron(II)` half cell although not at standard conditions.Thus , the emf of the cell will be near, but not equal to `E_(Fe^(3+|Fe^(2+.)))^(@)`

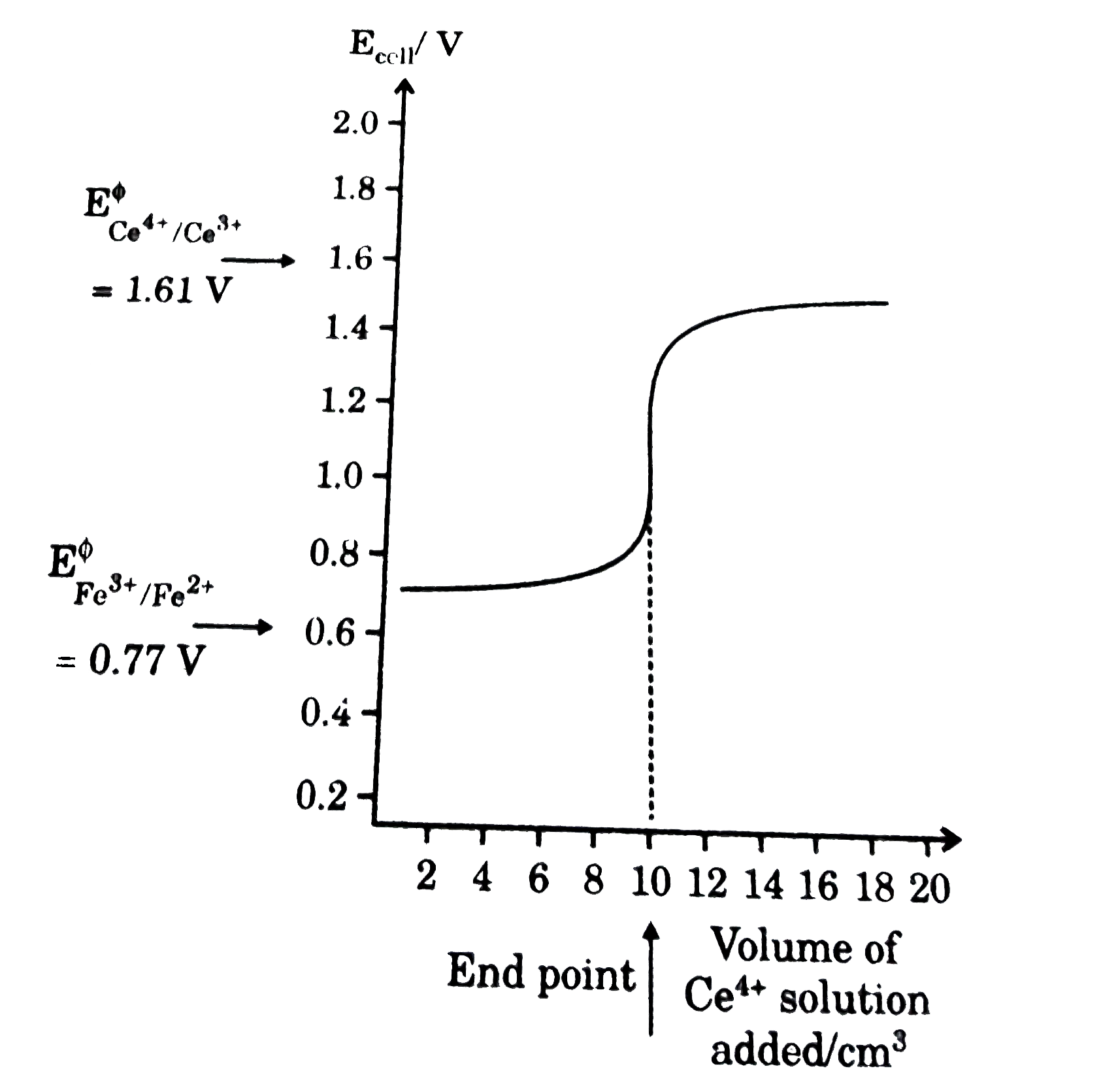
If we continue to add cerium (IV) solution , the number of iron (II) ions is gradually reduced and eventually only a very few are left (Table).At this stage the next few drops of cerium (IV) solution convert all the remaining irom (II) ions into iron (III), and some of the cerium (IV) ions are left unreacted. Once this happens we no longer have an iron `(III)//"iron"(II)` half-cell. Instead we have a solution in which there is a large number of cerium (III) ions and a smaller number of cerium (IV) ions. The solution in the beaker now behaves as a cerium `(IV)//"cerium"(III)`half-cell (although not a standard one.)
Just before all the iron (II) ions are converted into iron (III) we have a cell with an EMF of around `+0.77V.` After all the iron (II) ions are oxidised we have a cell with an emf of about `+1.61 V. ` This rapid rise in emf occurs with the addition of just one drop of cerium (IV) solution. You should be able to understand why a graph of cell emf against volume of cerium (IV) solution of the iron (II) solution calculated in the usual way.
Imagine you were given a solution of potassium dichromate (VI) in a beaker and a solution of iron (II) sulphate in a burette. You do not know the concentration of dichromate (VI) ions , but the concentration of the iron (II) solution is known. Your task it to carry out a redox titration using the two solutions in order to determine the concentration of dichromate (VI) ions. Sketch a graph showing how the emf changes in the course of the above titration.
`E_(Cr_(2)O_(7)^(2-)//Cr^(3+)) = 1.33 V, E_(Fe^(3+)//Fe^(2+)) = 0.77 V`

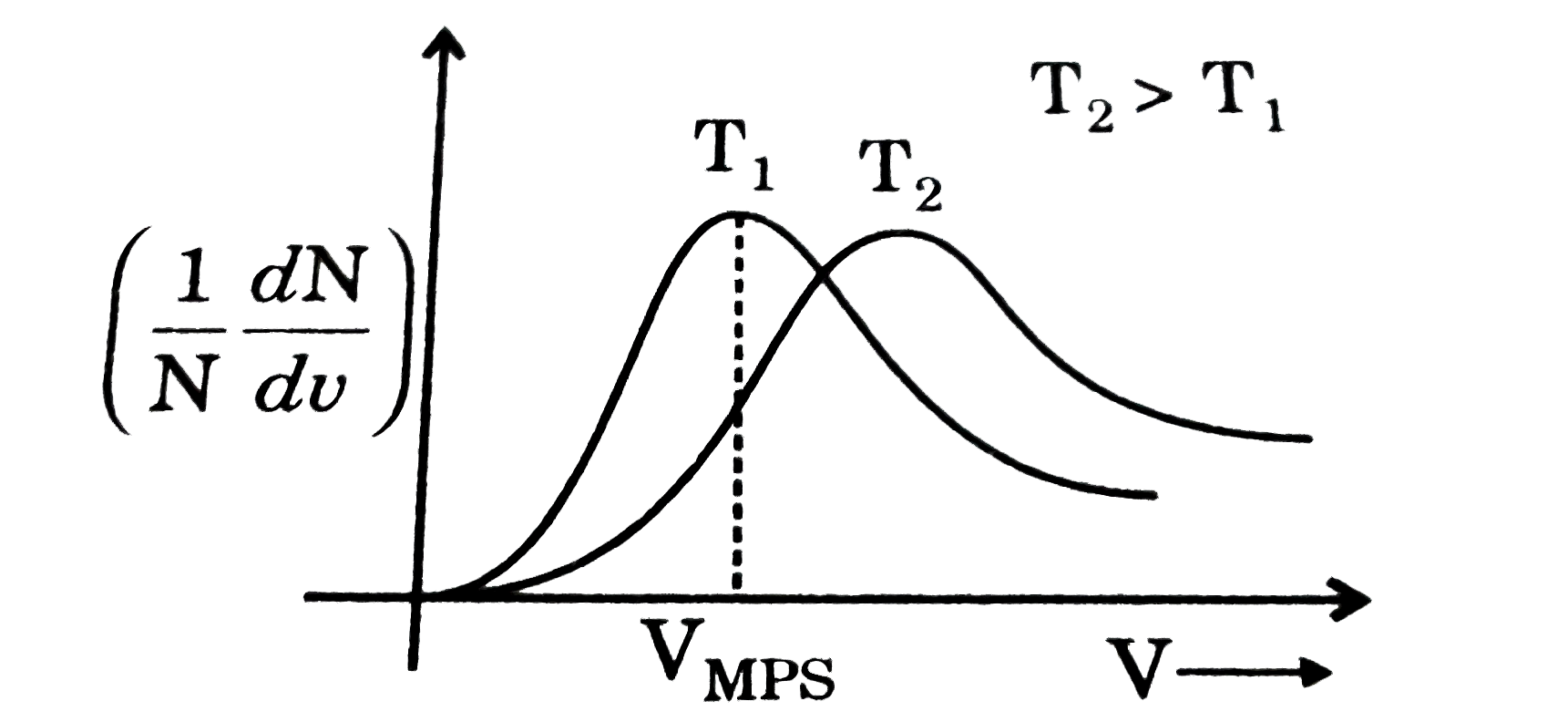
The speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
`bar(KE) =1/N((1)/(2)m underset(i)SigmadN_(i)u_(1)^(2)) = 1/2 m(underset(i)Sigma(dN_(i))/(N).u_(1)^(2))`
where `(dN)/(N)` is the fraction of molecules having speeds between `u_(i)` and `u_(i) + du` and as proposed by maxwell `(dN)/(N) = 4pi ((m)/(2pi KT))^(3//2) exp (-("mu"^(2))/(2KT)).u^(2).du`
The plot of `((1)/(N) (dN)/(du))` is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around `"v"_("MPS")` in the middle of the range of v. There area under the curve between any two speeds `V_(1) "and" V_(2)` is the fraction of molecules having speeds between`V_(1) "and" V_(2).`
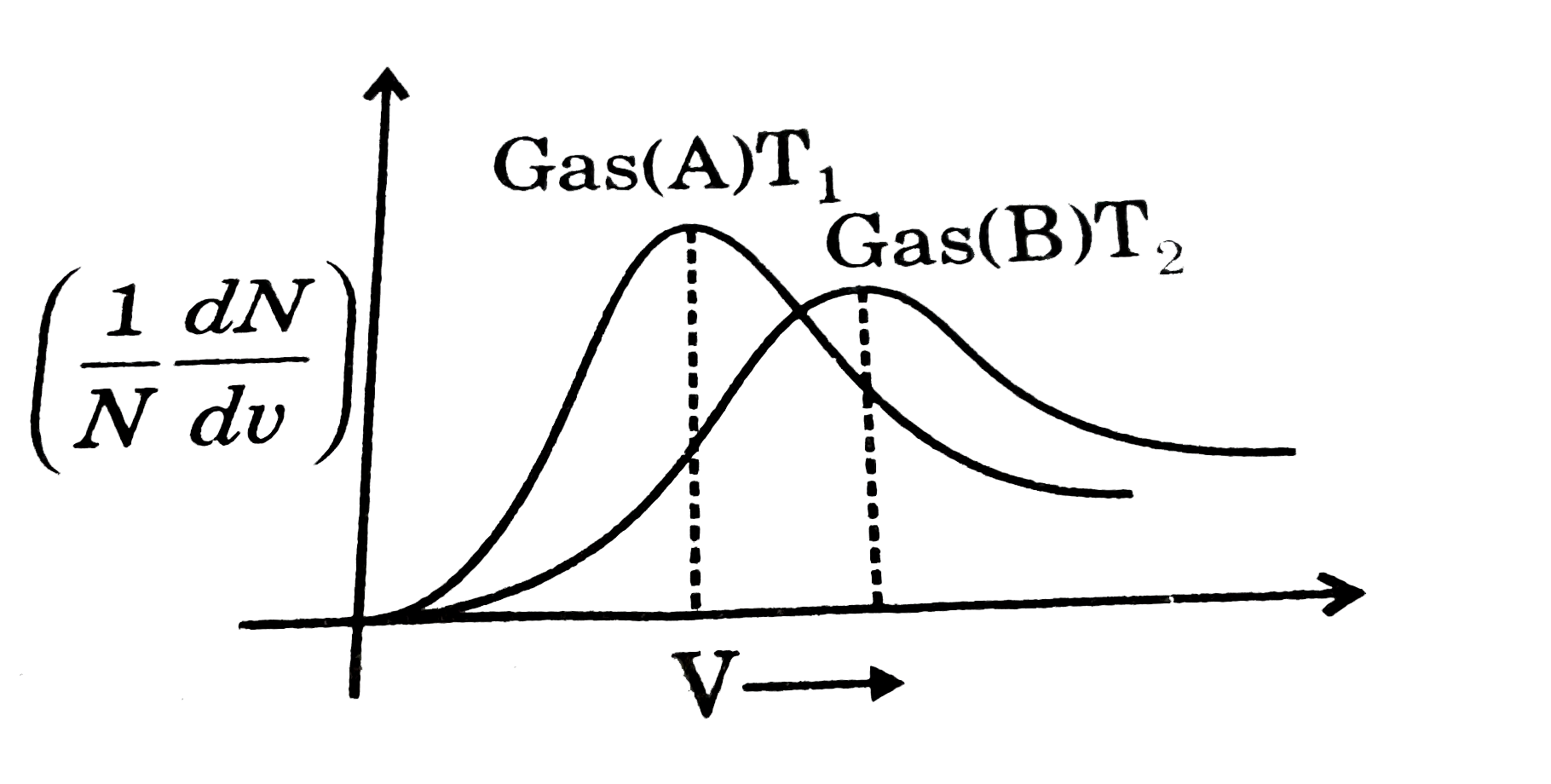
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same `"V"_("MPS")` will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.


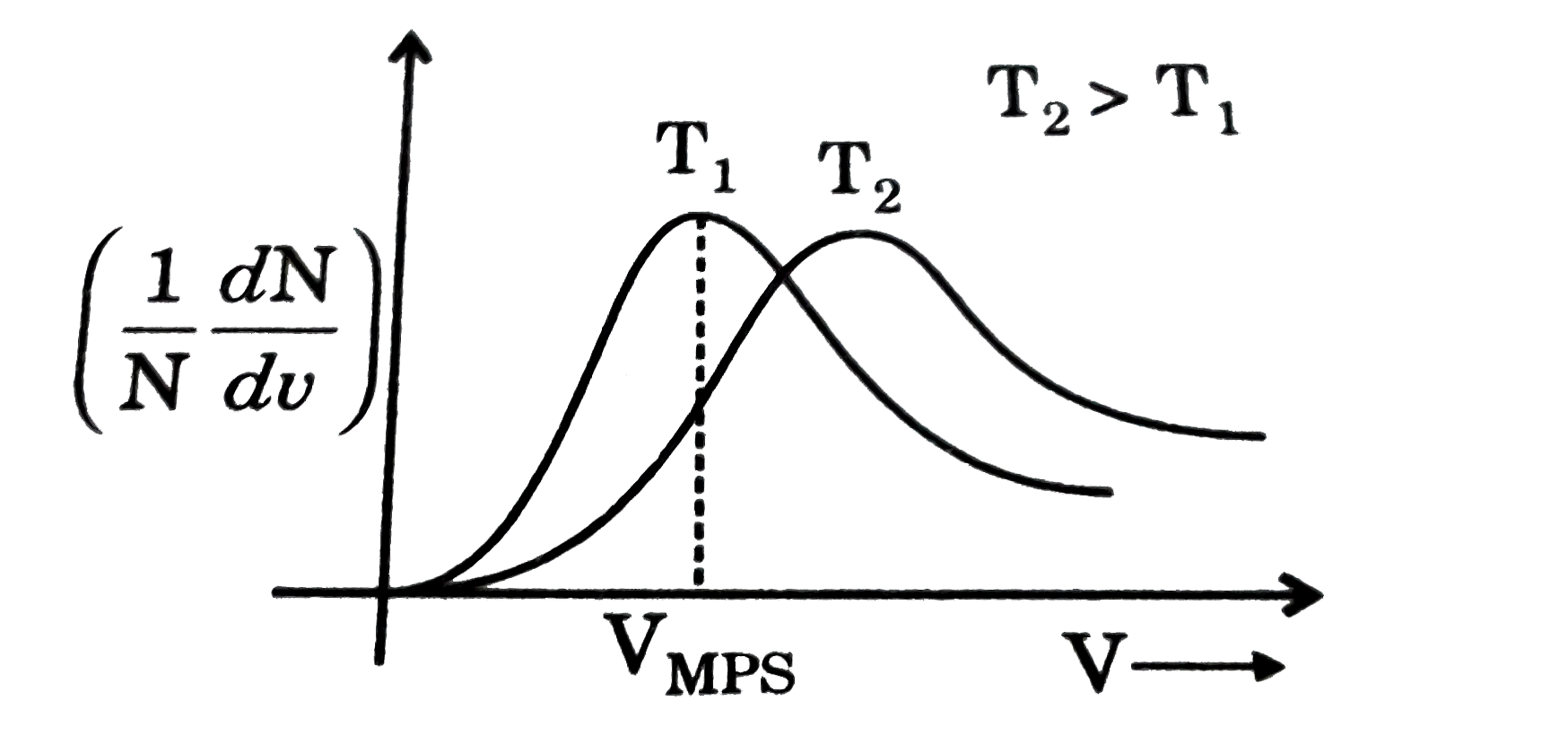
For the above graph, drawn for two different samples of gases at two different temperature `T_(1) "and" T_(2).` Which of the following statements is necessarily true?

The speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
`bar(KE) =1/N((1)/(2)m underset(i)SigmadN_(i)u_(1)^(2)) = 1/2 m(underset(i)Sigma(dN_(i))/(N).u_(1)^(2))`
where `(dN)/(N)` is the fraction of molecules having speeds between `u_(i)` and `u_(i) + du` and as proposed by maxwell `(dN)/(N) = 4pi ((m)/(2pi KT))^(3//2) exp (-("mu"^(2))/(2KT)).u^(2).du`
The plot of `((1)/(N) (dN)/(du))` is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around `"v"_("MPS")` in the middle of the range of v. There area under the curve between any two speeds `V_(1) "and" V_(2)` is the fraction of molecules having speeds between`V_(1) "and" V_(2).`
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same `"V"_("MPS")` will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.

If two gases A and B and at temperature `T_(A) "and"T_(B)` respectivley have identical Maxwellian plots then which of the following statement are true?

Concentrations measured as a function of time when gaseous `N_(2)O_(5)` at initial concentration of `0.0200 M` decomposes ot gaseous `NO_(2)"and"O_(2) "at" 50^(@)C.`The change in concentration with time is given by the following graph.

The rate of formation of `O_(2)` during the period 600-700 s is :

Concentrations measured as a function of time when gaseous `N_(2)O_(5)` at initial concentration of `0.0200 M` decomposes ot gaseous `NO_(2)"and"O_(2) "at" 50^(@)C.`The change in concentration with time is given by the following graph.

The rate of decomposition of `N_(2)O_(5)`during the period 300-400 s is :

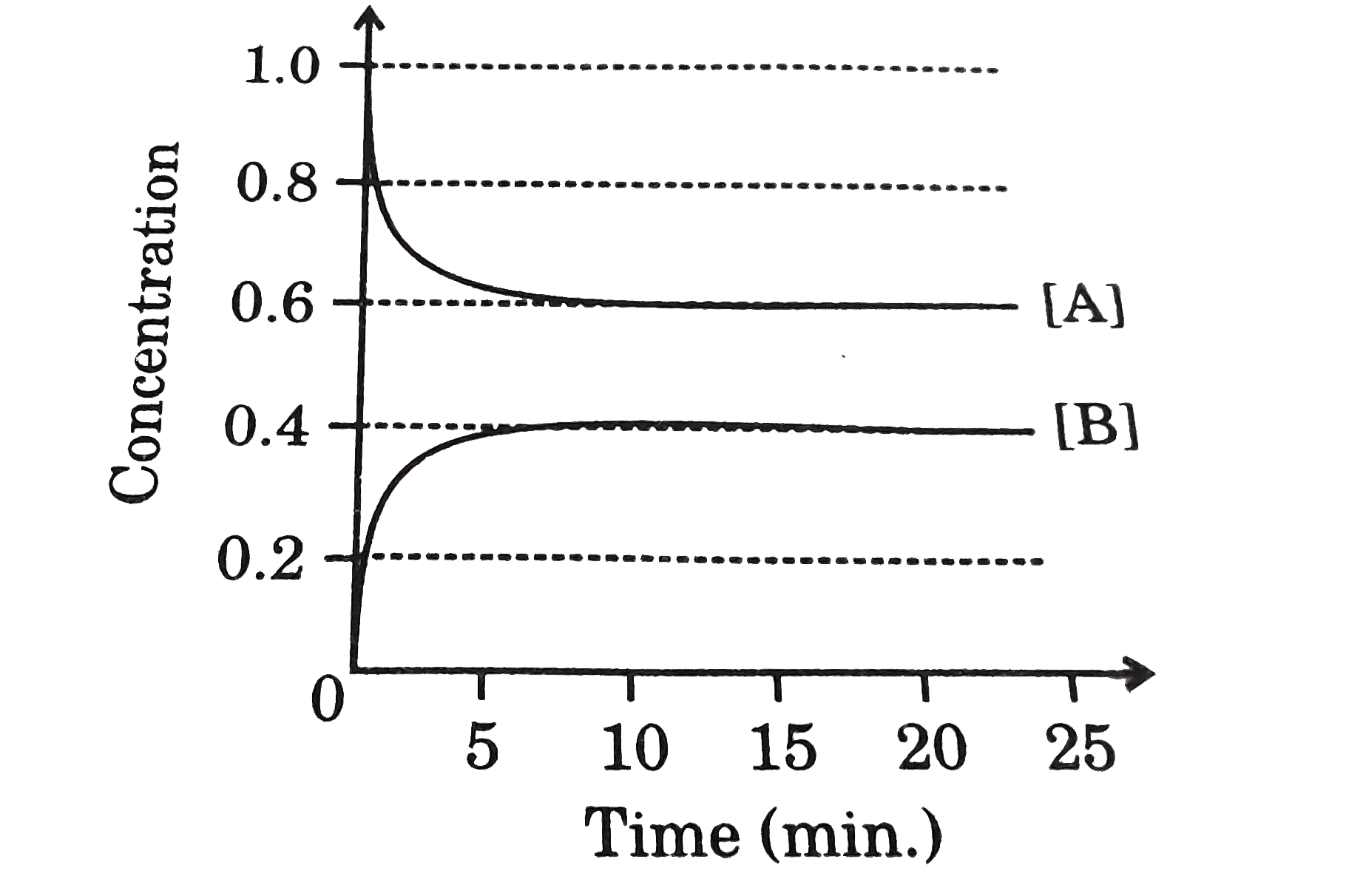
For the reversible reaction `A underset(k_(b))overset(k_(f))(hArr)B` (having Ist order in both direction) the concentration as a function of time are given for a certain experimantal run.
Calculate [B] at time `t=1/5`min.
`["Given" : k_(b) =3 "min"^(-1) "and"1/e=0.37]`

According to collision theory for determining the variation of rate of reaction with temperature the rate constant,`k= Ae^(-Ea//RT).` For most of the practical purposes A and `E_(a`[Arrhenius factor and Activation energy] are temperature independent. However they may vary slightly.
Assuming the conditions given above answer the following questions.
`"If"A=K,T"and"E_(a)=K_(2)T^(2)` and the given equation is still applicable where `K_(1)"and" K_(2)` are the constant and T represent temperature then which will be correct option?
(P) The maximum value of k will be equal to A
(Q) At lower temperature rate of reaction will increase with increase in temperature
(R) At higher temperature, rate of reaction will decrease with increase in temperature

The adsorption of a gas at a metal surface is called occlusion. The extent of gas adsorbed at metal surface at a certain temperature depends on pressure as
`(x)/(m)=K.P^(1//n)`
where K and n are constant for a particular combination of gas and metal at fixed temperature and `(x)/(m)`is the mass of gas adsorbed per unit mass of metal .For `H_(2)` gas adsorbing at Pt-surface, the following graph is obtained.

The mass of `H_(2)` gas adsorbed on the surface of 10 gm Pt at 16 atm is :

A,B and C react in the 1:1:1 stoichiometric ratio. The concentration of A,B and C where found to vary with time as shown in the figure below:

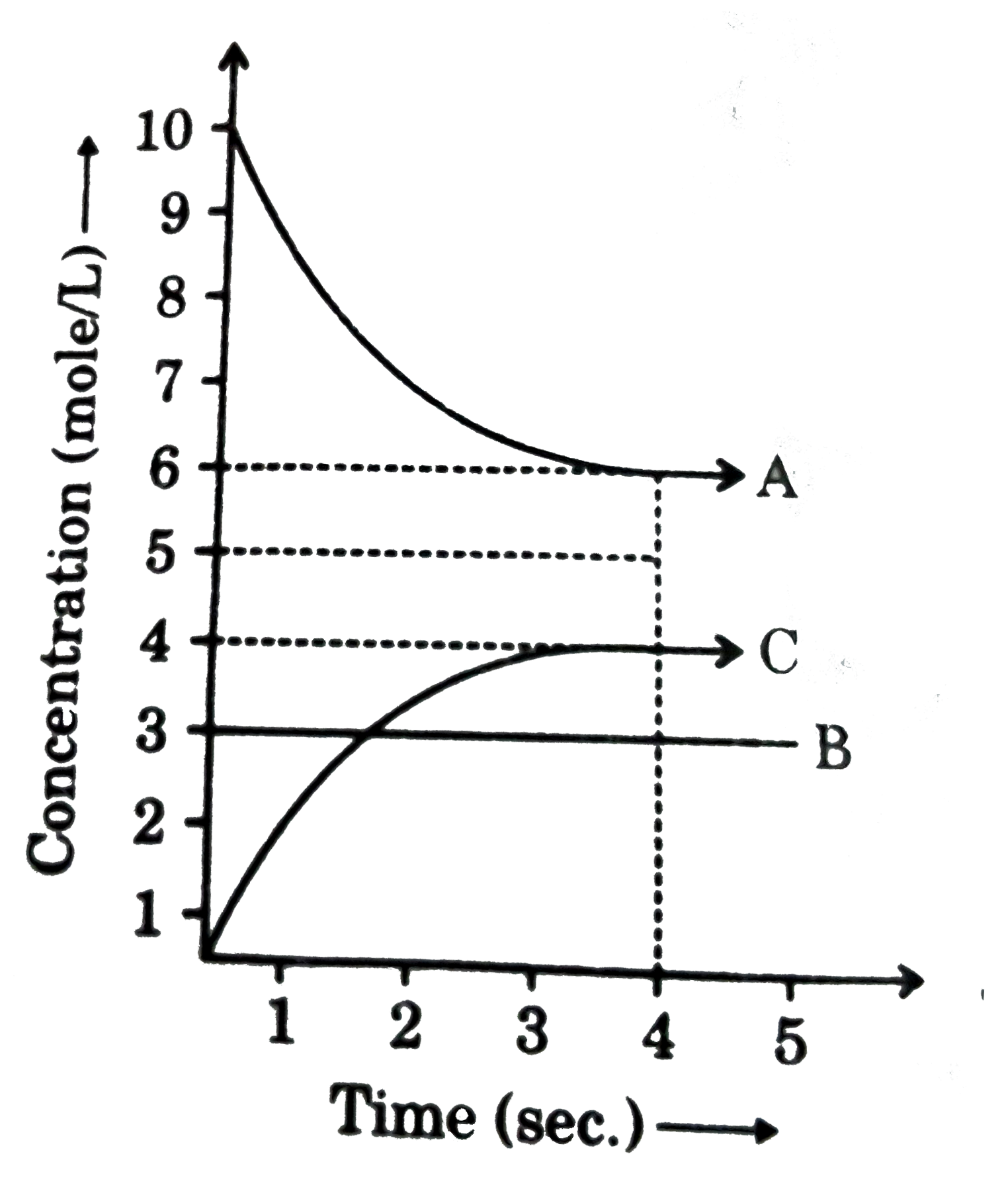
The value of equilibrium repreasented in above sketch will be :

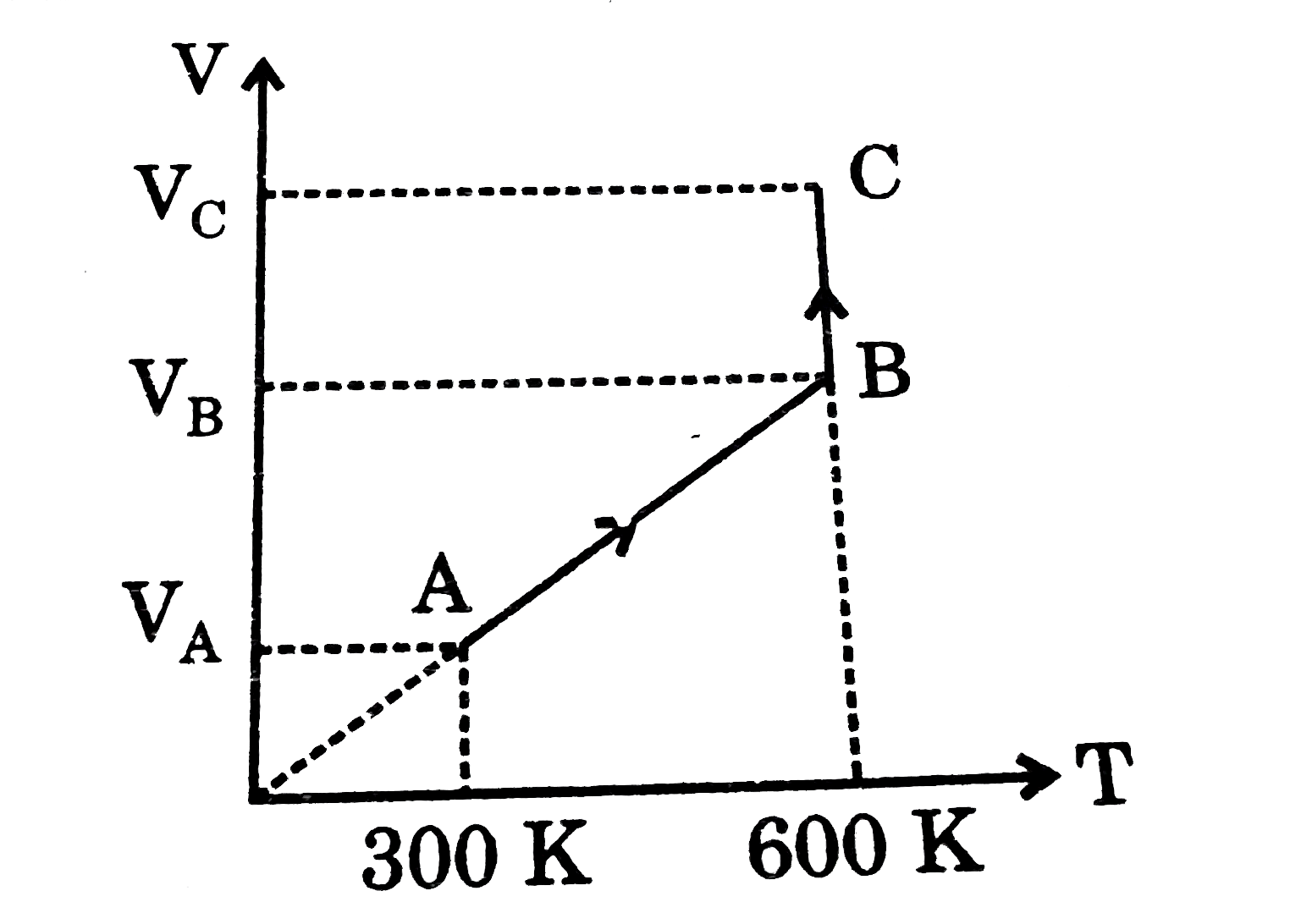
Above graph is plotted for 1 mole of ideal monoatomic gas.
Find net heat exchange for the process `BC,"if" (V_(C))/(V_(B))=4/1:`

The process by which a gas through a small hole into vacuum is called effusion. The rate of change of pressure (p) of a gas at constant temperature due to effusion of gas from a vessel of constant volume can be related to rate of change of number of molecules by the expression:
`(dp)/(dt)=(kT)/(V)((dN)/(dt))`
where Rate of change of number of molecules
`rArr" "-(dN)/(dt)=(pA_(0))/((2pimkR)^(1//2))`
where, k= Boltzmann constant
`N_(A) = `Avogadro's number
`T=` temperature (in K) `rArr" "-(dN)/(dt)=(pA_(0))/((2pimkR)^(1//2))`
`N_(A) = `Avogadro's number
`T=`temperature (in K)
`V=`volume of vessel
`N=1` no.of molecules
`A_(0)=` area of aperture
`m=`mass of single molecule
`gamma=(V)/(A_(0))sqrt((2pim)/(kT))`
If under any conditions `gamma=100 sec` then select the correct graph of pressure of gas at any time `(P_(t))` us Time (t). [Given : In 2=0.7]

Titration of diprotic acid `(H_(2)A)` by strong base has been summarised in following graph

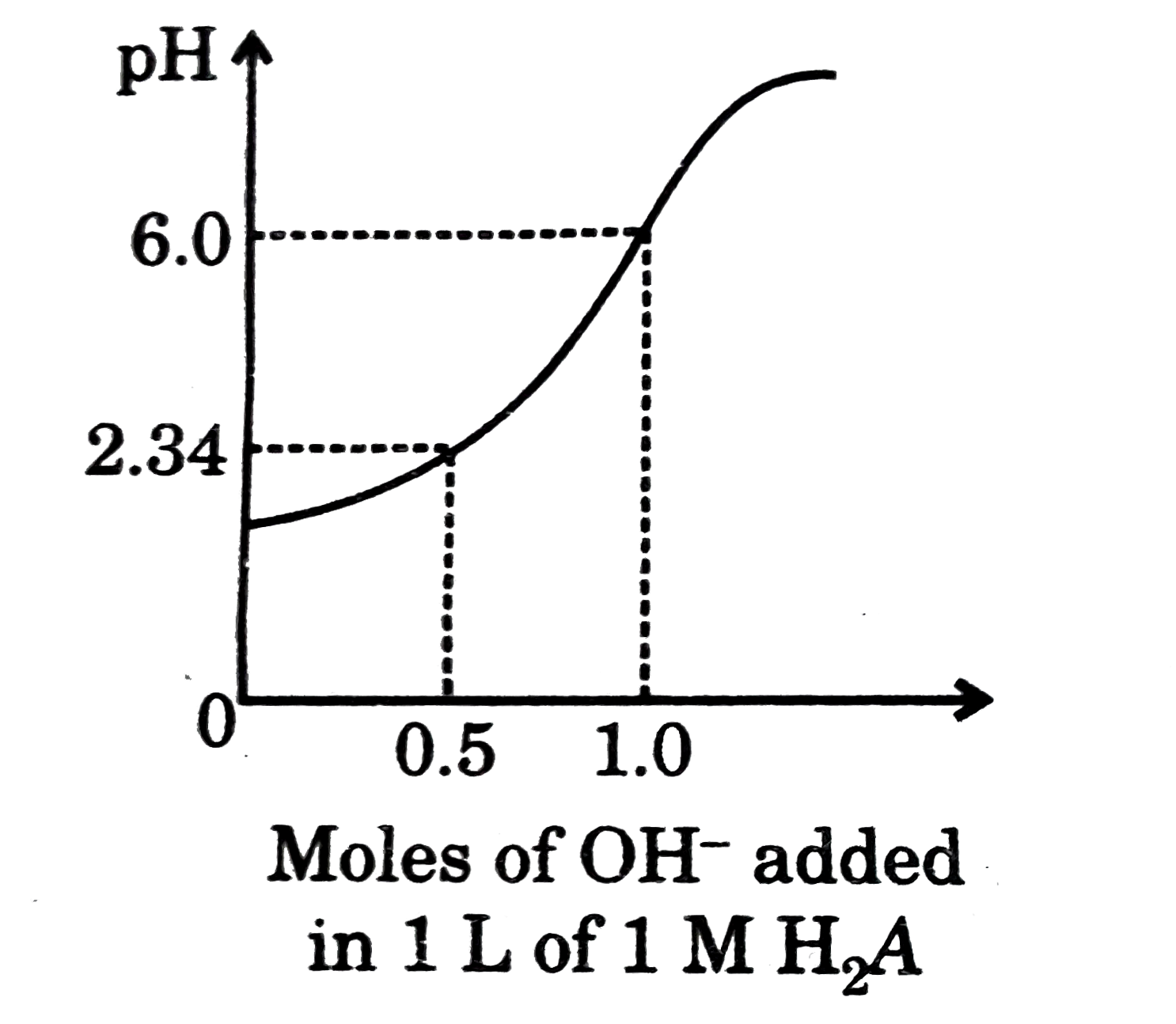
What is the pH at II equivalence point?

Titration of diprotic acid `(H_(2)A)` by strong base has been summarised in following graph

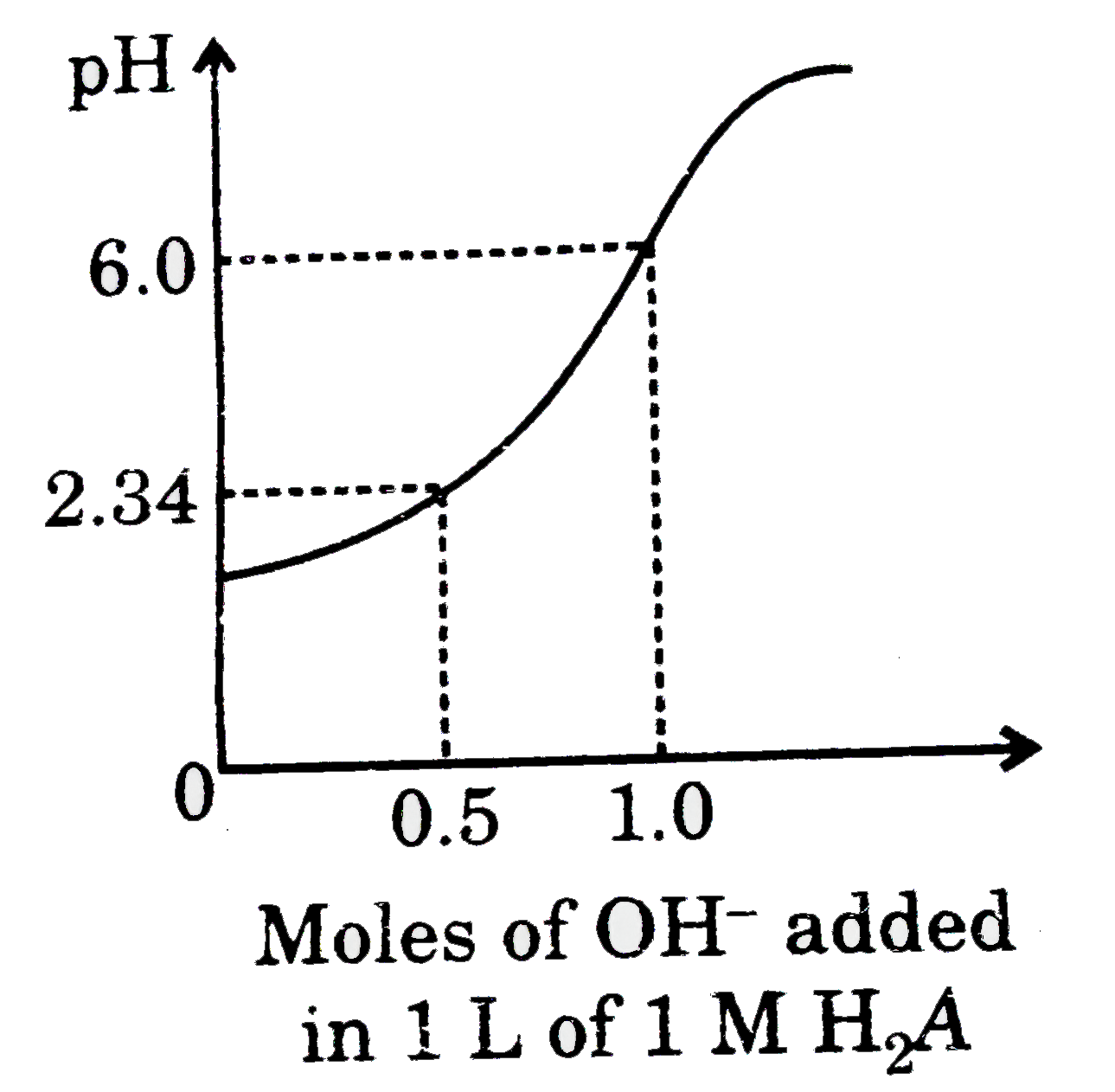
What is composition of mixture when pH of solution is `10.137?`

For an ideal gas if heat given in process AB is 10kJ then answer the following questions.
`(1"bar".l=0.1kJ)`

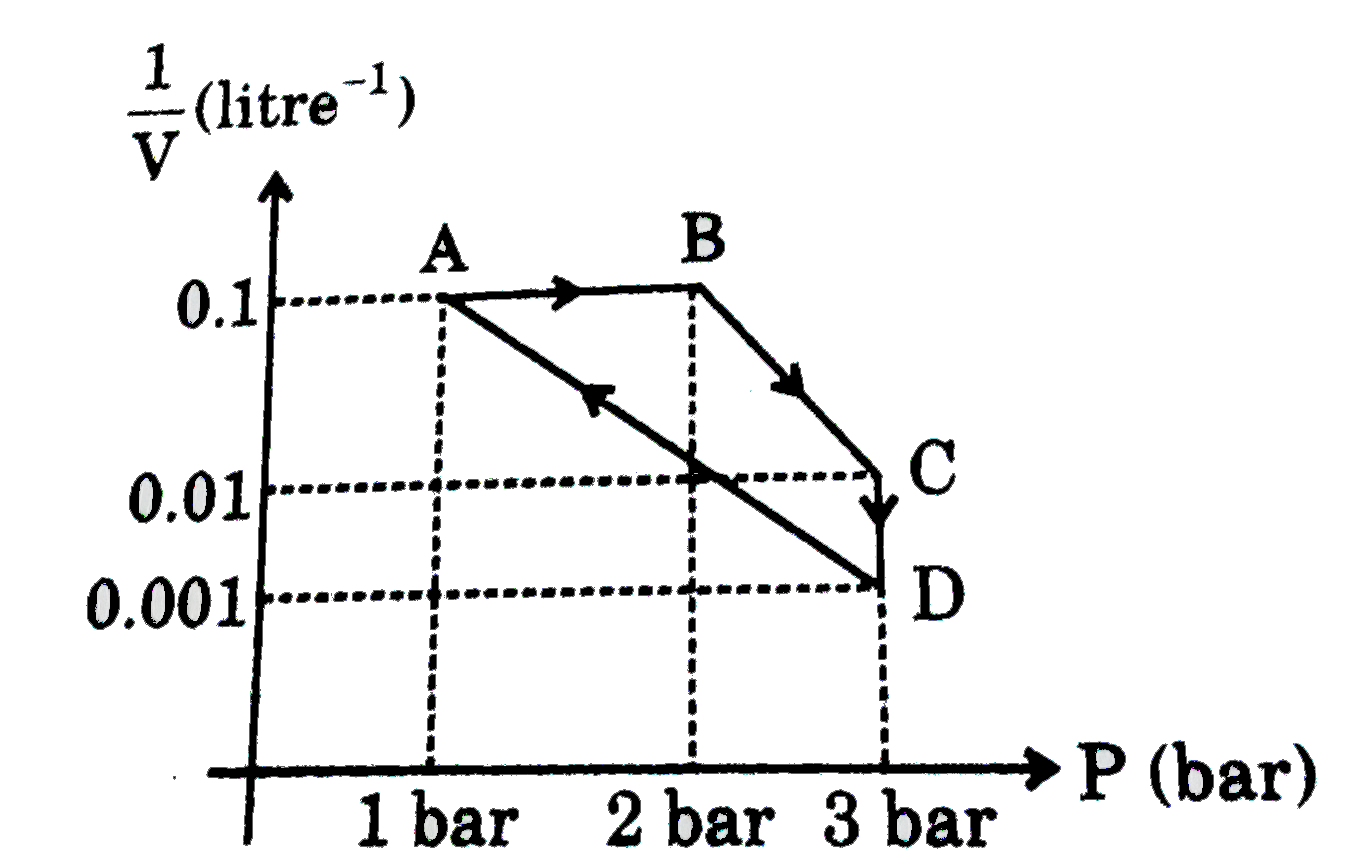
Enthalpy change in process BCD is :

Thermodynamics stability is often used in chemical reactions to predict extent of reaction or to predict the preferred product in some reaction. Thermodynamically a more stable substance will be the one which has lower Gibb's free energy.In various cases,it might be decided on the basis of enthalpy, however , that may not always be true. The thermodynamic data Therefore can be used for prdicting stability among isotopes and to decide the possible transformation.Based on this information and the data given below, answer the questions that follow.
Date: `{:(DeltaH_(f)^(@) "of" Sn_(("white")) =0,DeltaH_(f)^(@) "of" Sn_(("grey")) =- 2.1 kJ//"mole"),(S^(@) "of" Sn_(("white")) = 0,S^(@) "of" Sn_(("grey")) = 44 J//K-"mole"):}`
All above data at 300K.
Density of `Sn_((w)) = 7.36 g//ml`
Density of `Sn_((g)) = 5.769 gm//ml`
One such transformation is 'tin pest' which is an autocatalytic, allotropic transformation of the element tin causing deterioration of tin objects at low temperatures.
As temperature is reduced, what can be predicted for objects containing tin ?

This type of deviation is also expected in the following mixture :

Total vapour pressure of mixture of 1 mol of volatile component A(`p_(A)^(@)=100`mm Hg) and 3 mol of volatile component B(`p_(B)^(@)`=60 mm Hg) is 75 mm. For such case:

Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Elevation in b.p of an aqueous urea solution is `0.52^(@) (K_(b) = 0.52^(@) mol^(-1)kg)`. Hence, mole fraction of urea in this solution is:

Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Ratio of `DeltaT_(b)//K_(b)` of `6% AB_(2)` and `9% A_(2)B (AB_(2)` and `A_(2)B` both are non-electrolytes) is 1 mol/kg in both cases. Hence, atomic masses of A and B are respectively.

Answer the questions (given below) which are based on the following diagram. Vapour pressure plots of benzene-toluence mixture at `20^(@)C`. Solution of benzene and toluence are ideal. Raoult's law is valid for both components over the entrie range of concentration.

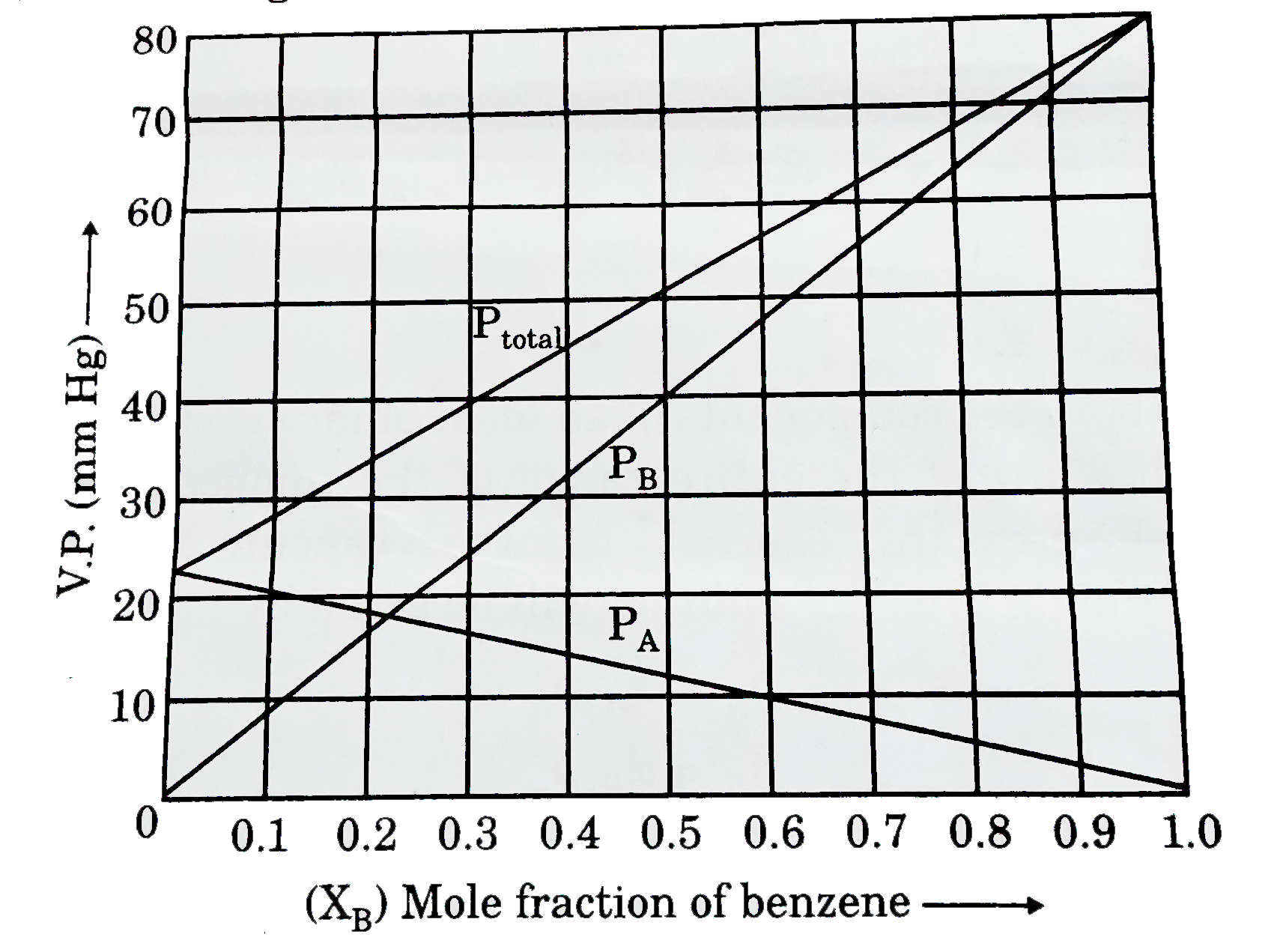
There is deviation from ideal behaviour if mixture contains:

When a liquid is completely miscible with another liquid, a homogeneous solution consisting of a single phase is formed. If such a solution is placed in a closed evacuated vessel, the total pressure exerted by the vapour, after the system attained equilibrium will be equal to the sum of partial pressures of the constituents. A solution is said to be ideal if its constituents follow Raoult's law under all conditions of concentrations, i.e., where `p_(i)` is the partial pressures of the constituent i, whose mole fraction in the solution is `x_(i)` and `p_(i)^(@)` is the corresponding vapour pressure of the pure constituent. The change in the thermodynamic functions when an ideal solution is formed by mixing pure components is given by the following expression.
`Delta_(mix) = G = n_("total") RT sum_(i) x_(i) In x_(i)` ...(i)
where, `n_("total")` is the total amount of all the constituents present in the solution.
`Delta_(mix)F =- n_("total") R sum_(i) x_(i) In x_(i)` ......(ii)
`Delta_(mix)H =- n_("total") RT sum_(i) x_(i) In x_(i) - n_("total") R sum_(i) x_(i) In x_(i) = 0` ........(iii)
`Delta_(mix) U = 0` .........(iv)
Since botli the components of an ideal binary system follow Raoult's law of the entire range of the compositions, the partial pressure exerted by the vapours of these constituents over the solution will be given by
`p_(A) = x_(A) p_(A)^(@)` ..........(v)
`p_(B) = x_(B) p_(B)^(@)` .........(vi)
where, `x_(A)` and `x_(B)` are the mole fractions of the two constituents in the liquid phase and `p_(A)^(@)` and `p_(B)^(@)` are the respective vapour pressure of the pure constituents. The total pressure (p) over the solution will be the sum of the partial pressure. The composition of the vapour phase `(y_(A))` can be determined with the help of Dalton's law of partial pressures.
A plot of reciprocal of total pressure `((1)/(p))` (y-axis) us `y_(A)` (x-axis) gives :

When a liquid is completely miscible with another liquid, a homogeneous solution consisting of a single phase is formed. If such a solution is placed in a closed evacuated vessel, the total pressure exerted by the vapour, after the system attained equilibrium will be equal to the sum of partial pressures of the constituents. A solution is said to be ideal if its constituents follow Raoult's law under all conditions of concentrations, i.e., where `p_(i)` is the partial pressures of the constituent i, whose mole fraction in the solution is `x_(i)` and `p_(i)^(@)` is the corresponding vapour pressure of the pure constituent. The change in the thermodynamic functions when an ideal solution is formed by mixing pure components is given by the following expression.
`Delta_(mix) = G = n_("total") RT sum_(i) x_(i) In x_(i)` ...(i)
where, `n_("total")` is the total amount of all the constituents present in the solution.
`Delta_(mix)F =- n_("total") R sum_(i) x_(i) In x_(i)` ......(ii)
`Delta_(mix)H =- n_("total") RT sum_(i) x_(i) In x_(i) - n_("total") R sum_(i) x_(i) In x_(i) = 0` ........(iii)
`Delta_(mix) U = 0` .........(iv)
Since botli the components of an ideal binary system follow Raoult's law of the entire range of the compositions, the partial pressure exerted by the vapours of these constituents over the solution will be given by
`p_(A) = x_(A) p_(A)^(@)` ..........(v)
`p_(B) = x_(B) p_(B)^(@)` .........(vi)
where, `x_(A)` and `x_(B)` are the mole fractions of the two constituents in the liquid phase and `p_(A)^(@)` and `p_(B)^(@)` are the respective vapour pressure of the pure constituents. The total pressure (p) over the solution will be the sum of the partial pressure. The composition of the vapour phase `(y_(A))` can be determined with the help of Dalton's law of partial pressures.
Two liquids A and B form an ideal solution at temperature T. when the total vapour pressure above the solution is 600 torr, the mole fraction of A in the vapour phase is 0.35 and in the liquid phase 0.70. The vapour pressure of pure B and A are:

Consider the following partially labelled figure (graph is upto scale) for an ideal binary solution of benzene and toluence and answer the following questions.

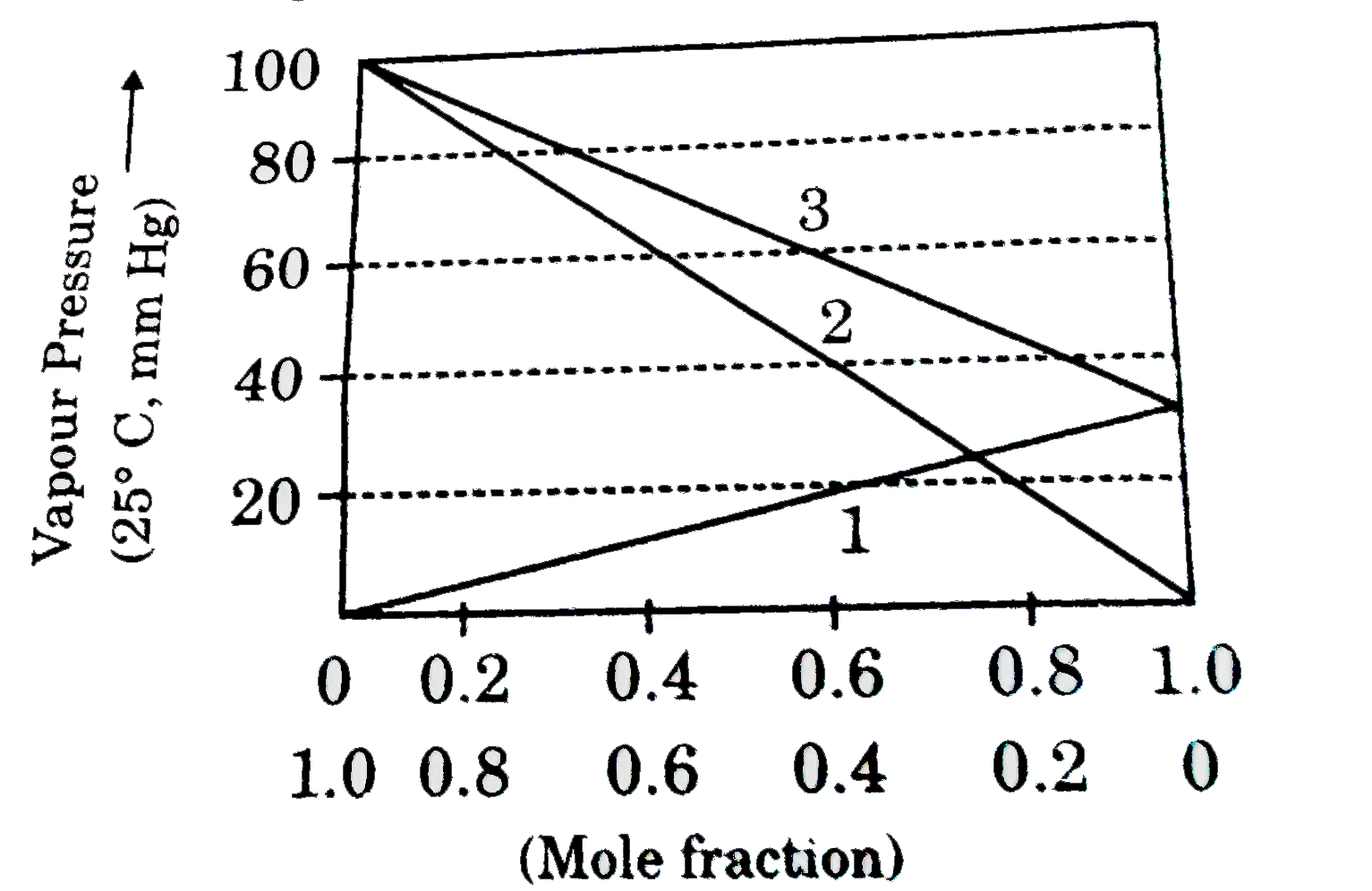
What is `p_("toluence")^(@) (25^(@)C)`?

Consider the following partially labelled figure (graph is upto scale) for an ideal binary solution of benzene and toluence and answer the following questions.

Consider the following partially labelled figure (graph is upto scale) for an ideal binary solution of benzene and toluence and answer the following questions.

The composition of liquid for which the vapour contains equal number of benzene and toluence molecules is about:

Consider the following partially labelled figure (graph is upto scale) for an ideal binary solution of benzene and toluence and answer the following questions.

`p_("total") = p_("benzene") +p_("toluene")` and `p_("total") = p_("benzene")^(@)` or `p_("toluene")^(@)`, are simultaneously valid for:

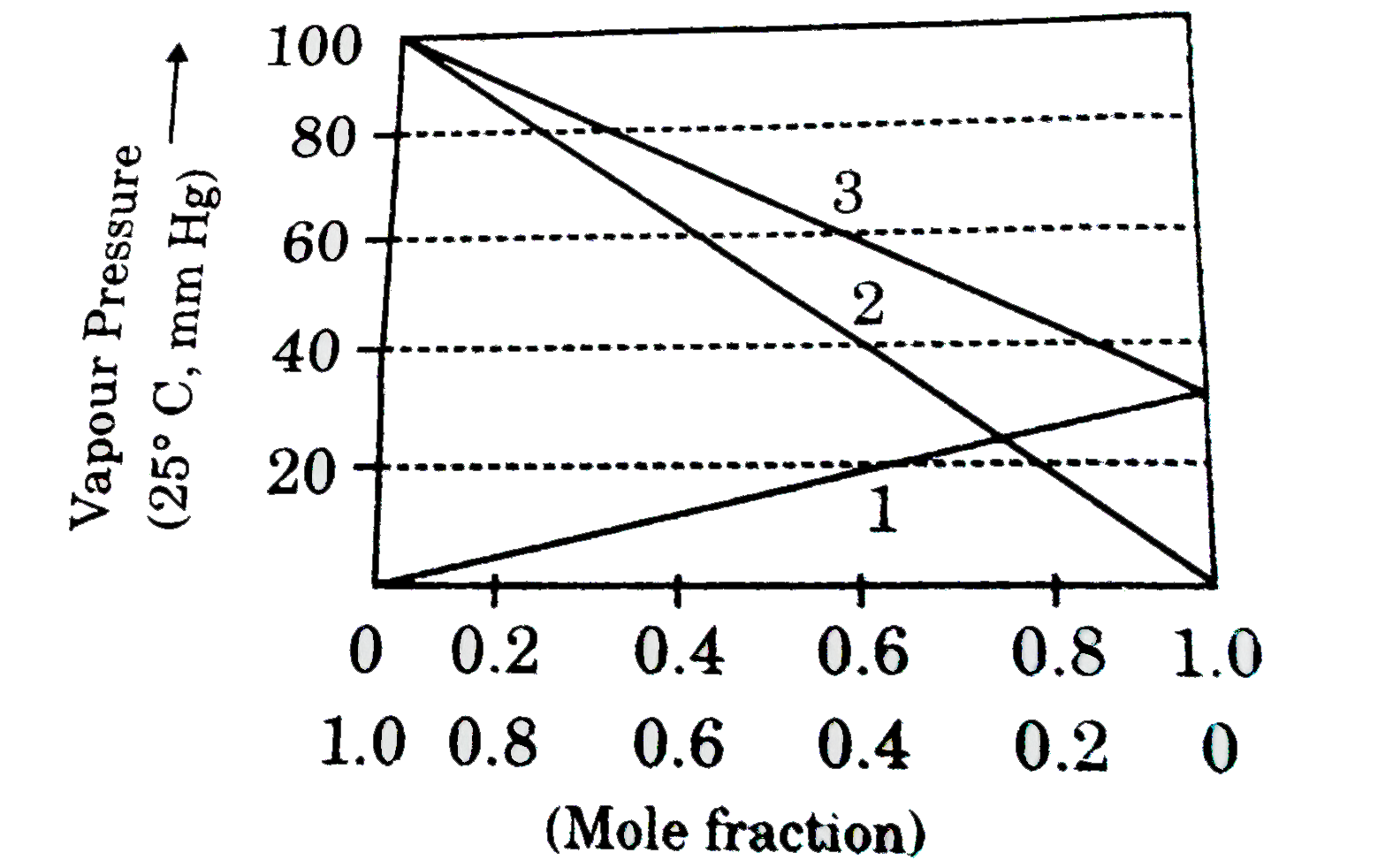
Consider the following partially labelled figure (graph is upto scale) for an ideal binary solution of benzene and toluence and answer the following questions.

Which laws are exemplified by the diagram ?

One moles of an ideal monoatomic gas undergo the state change as shown in following graph (ln 2 = 0.7)

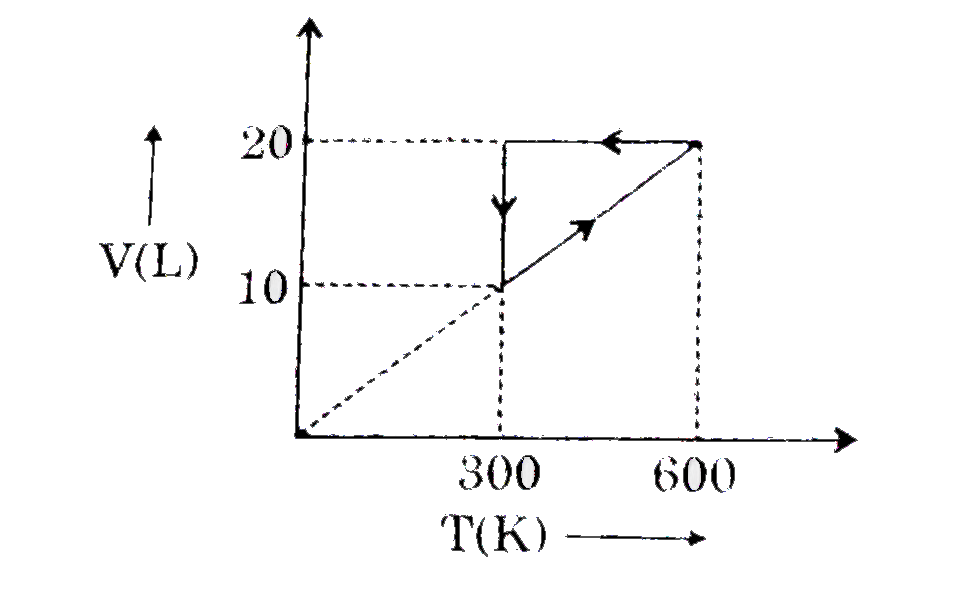
Efficiency of the cycle will be :