Complete Solutions to Solved Example of chapter ELECTRO MAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRO MAGNETIC INDUCTION |
| NARAYANA | Solved Example |
| Number Of Questions | 70 |
| Academic Year | 2023-24 |
A reactangular loop of area `0.06 m^(2)` is placed in a uniform magnetic field of `0.3T` with its plane (i) normal to the field (ii) inclined `30^(@)` to the field (iii) parallel to the field. Find the fliux linked with the coil in each case.
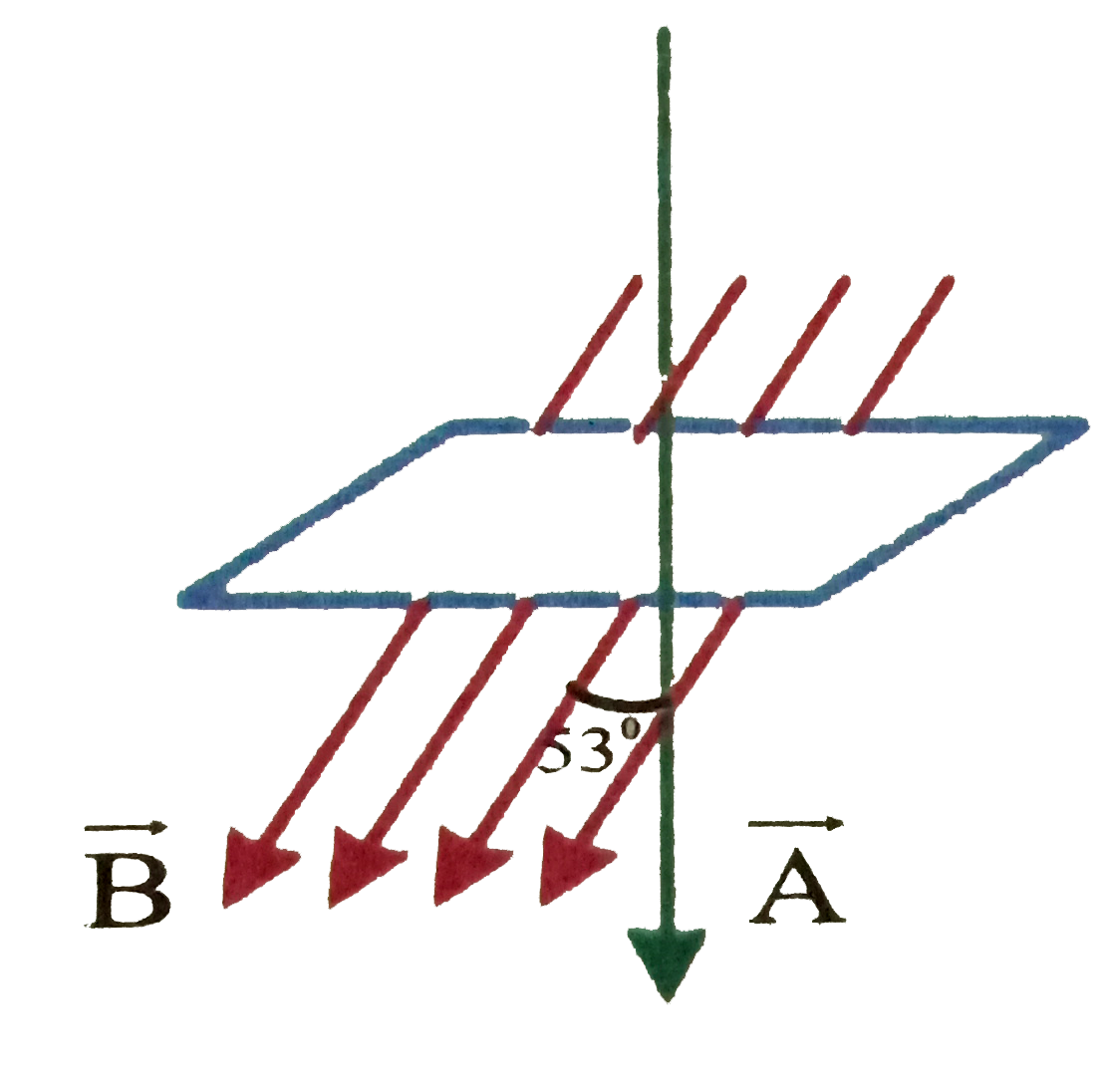
View SolutionAt a certain location in the northern hemisphere, the earth's magnetic field has magnitude of `42 mu T` and points downwards at `53^(@)` to the vertical. Calculate the flux through a horizontal surface of area `2.5 m^(2).[sin 53^(@) = 0.8]`
View SolutionThe magnetic flux through a coil is varying according to the relation `phi = (5 t^(3) + 4 t^(2) + 2t - 5)` Wb. Calculate the induced current through the coil at `t = 2` s if resistiance of coil is 5 ohm.
View SolutionA circular coil opf `500` turns of wire has an enclosed area of `0.1 m^(2)` per turn. It is kept perpendicular to a magnetic field of induction `0.2 T` and rotated by `180^(@)` about a diameter perpendicular to the field in `0.1` sec. how much charge will pass when the coil is connected to a gavanometer with a combined resistance of `50 ohms`
View SolutionSome magnetic flux is changed from a coil of resitance `10 Omega`. As a result, an induced current is developed it, which varies with time as shown in Fig. 3.213. Find the magnitude of the change in flux through ythe coil in weber.

View SolutionA long solenoid with `1.5` turns per `cm` has a small loop of area `2.0 cm^(2)` placed inside the solenoid normal to its axis. If the current in the solenoid changes steadily from `2.0 A` to `4.0 A` in `1.0 s`. The emf induced in the loop is
View SolutionA square loop of side `10 cm` and resistance `0.5 Omega` is placed vertically in the east-west plane. A uniform magnetic field of `0.10 T` is set up across the plane in the north-east direction. The magnetic field is decreased to zero in `0.70 s` at a steady rate. The magnetude of current in this time-interval is.
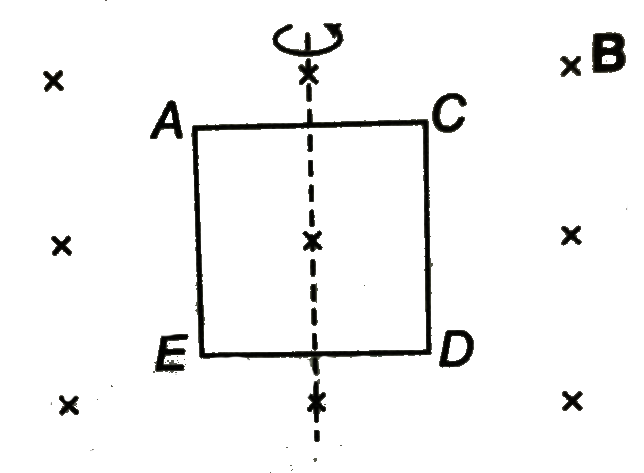
View SolutionA square loop `ACDE` of area `20 cm^2 ` resistance `5Omega` is rotate in as magnetic field `B=2T` through `180^@` (a) in `0.01S` and (b) in `0.02 s`
Find the magnitudes of averasge values of e i and `/_\q` in both the cases.
View SolutionA rectangular loop of length `'l'` and breadth `'b'` is placed at a distance of `x` from an infinitely long wire carrying current `'i'` such that the direction of current is parallel to breadth. If the loop moves away from the current wire in a direction perpendicular to it with a velocity `'v'`, the magnitude of the e.m.f. in the loop is: (`mu_(0)=` permeability of free space)
View SolutionA horizontal magnetic field `B` is produced across a narrow gap between the two square iron pole pieces. A closed square loop of side a, mass `m` and resistance `R` is allowed to fall with the tope the lopp in the field. The loop attians a terminal velocity equal to :

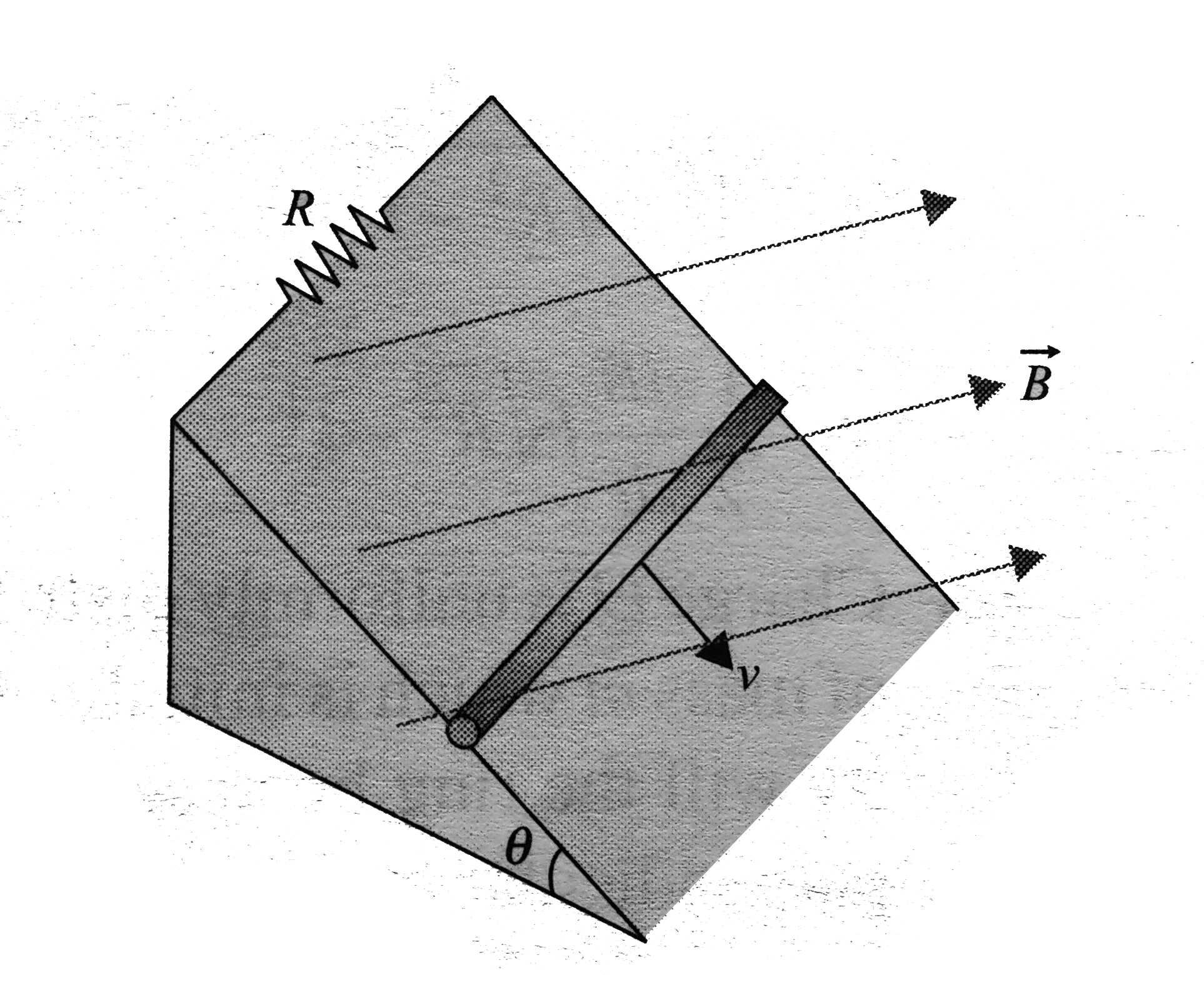
View Solutiona conducting wire os mass `m` slides down two smooth conducting bars, set at an angle `theta` to the horizontal as shown in . The separatin between the bars is `l`. The system is located in the magnetic field `B`, perpendicular to the plane of the sliding wire and bars. The constant velocity of the wire is
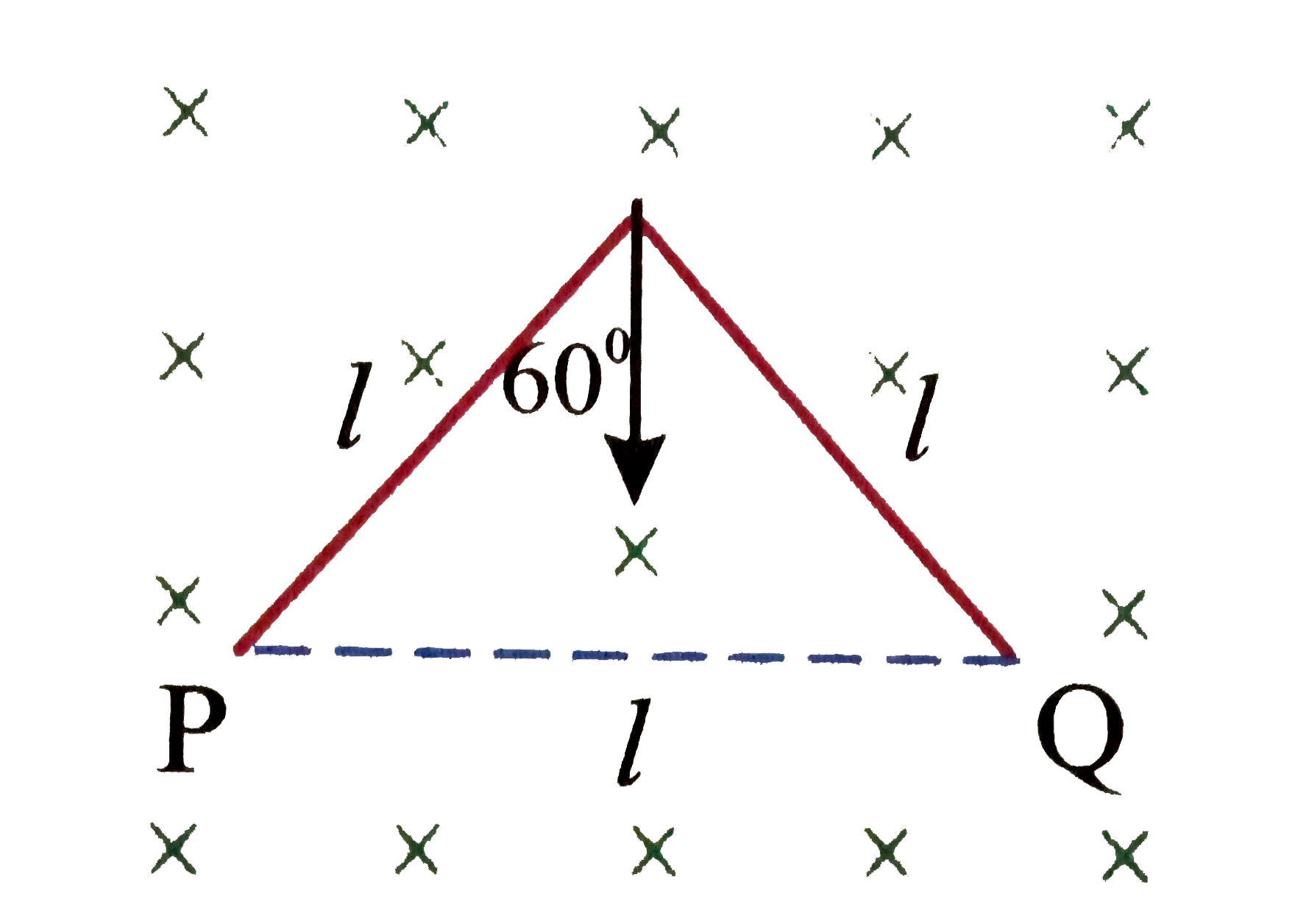
View SolutionA wire of length `2l` is bent at mid point so that the angle between two halves is `60^(@)`. If it moves as shown with a velocity `v` in a magnetic field `B` find the induced emf.
View SolutionA conductor or length `0.1m` is moving with a velocity of `4 m//s` in a uniform magnetic field of `2T` as shwon in the figure. Find the emf induced?
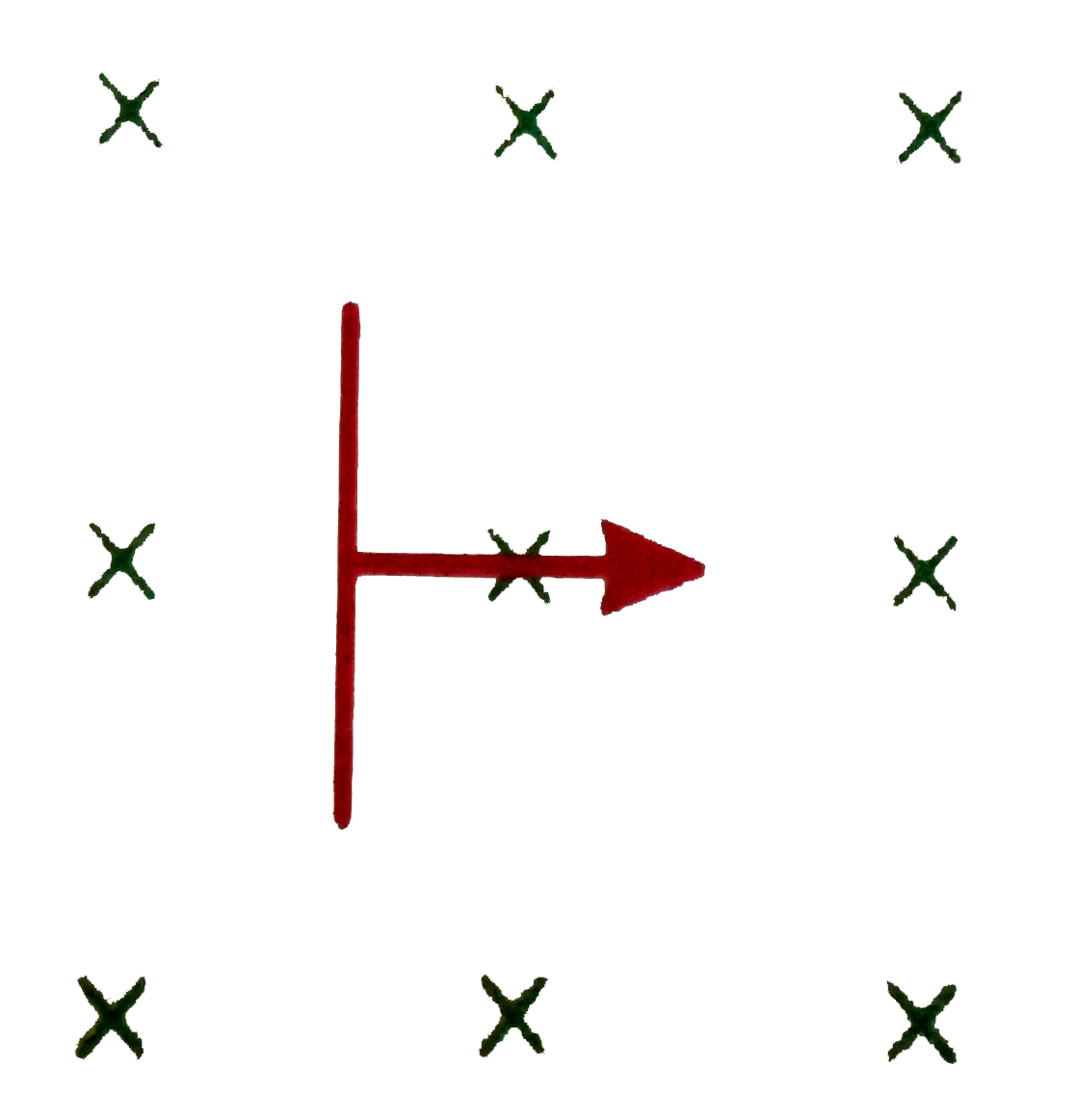
View SolutionFigure shows a conducting rod `PQ` in contact with metal rails `RP` and `SQ`, which are `0.25 m` apart in a uniform magnetic field of flux density `0.4T` acting perpendicular to the plane of the paper. Ends `R` and `S` are connected through a `5 Omega` resistance. What is the emf when the rod moves to the right with a velocity of `5ms^(-1)` ? What is the magnitude and direction of the current through the `5 Omega` resistance? If the rod `PQ` moves to the left with the same speed, what will be the new current and its direction?
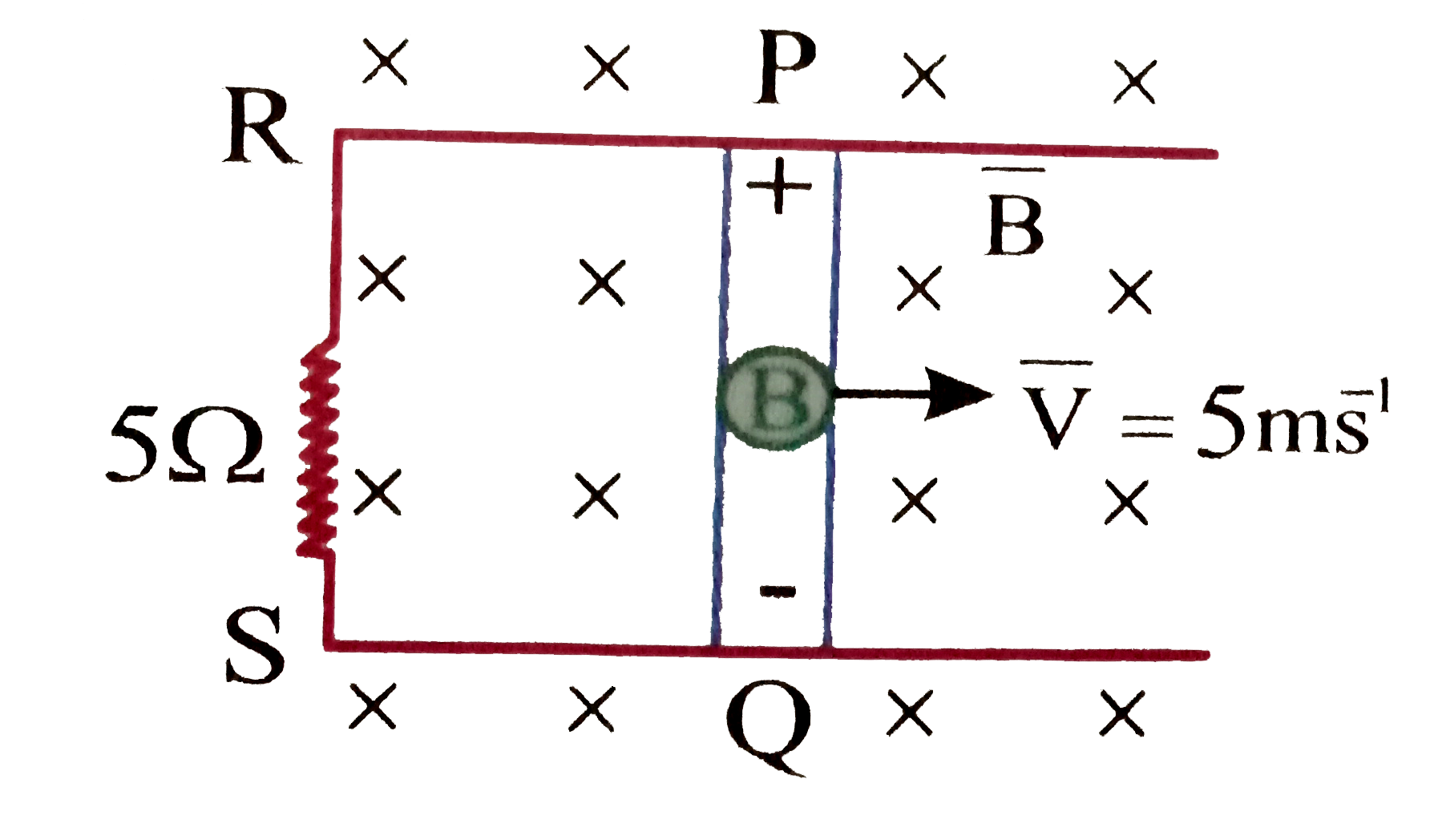
View SolutionA loop `ABCD` containing two resistors as shown in figure is placed in a uniform magnetic fielf `B` directed outwards to the plane of page. A sliding conductor `EF` of length `l` and of negligible resistance moves to th right with a uniform velocity `v` as shown in Fig. Determine the current in each branch.
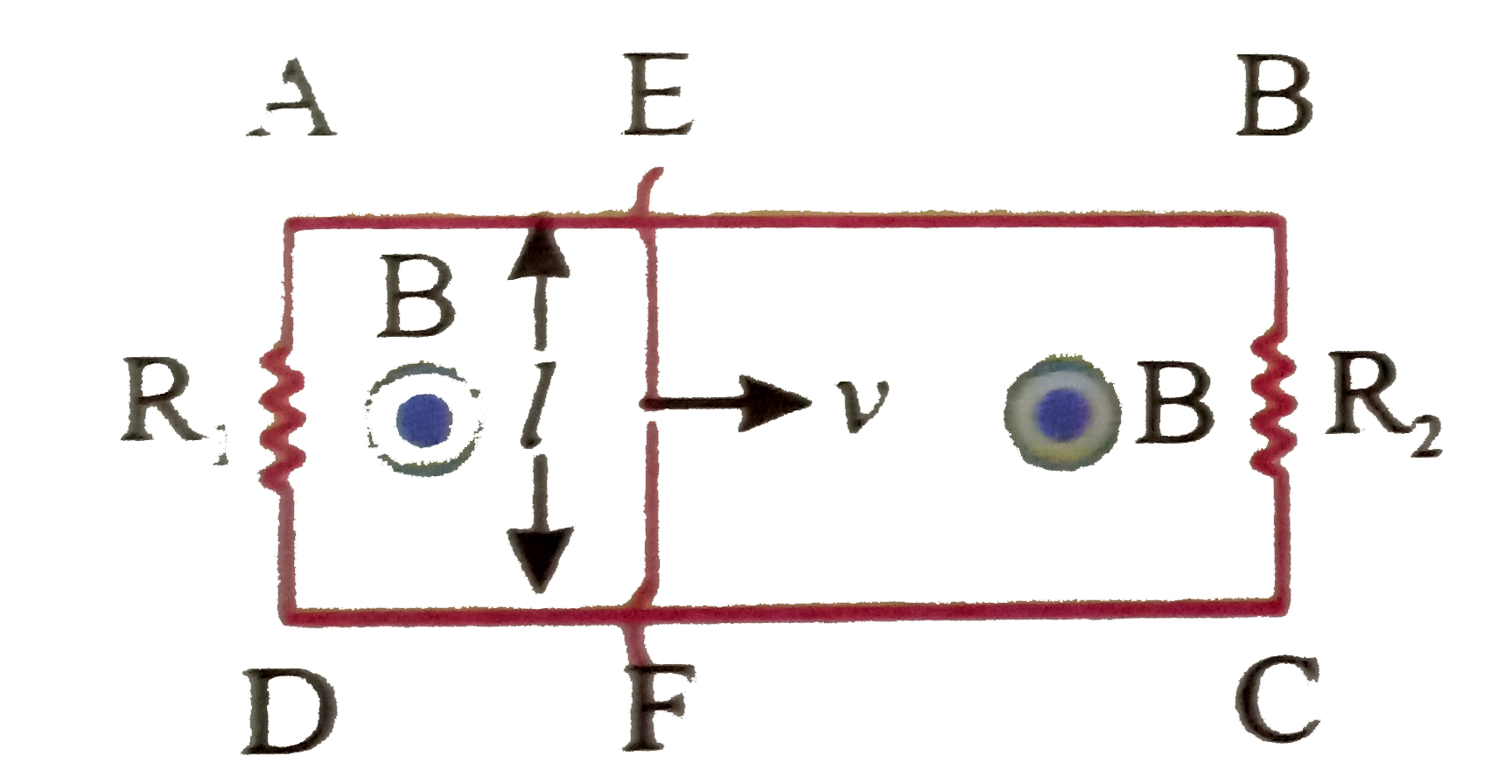
View SolutionA rectangular loop with a sliding connector of length `l` is located in a uniform magnetic field perpendicular to the loop plane. The magnetic induction is equal to B. The connector has an electric resistance `R`, the sides `ab` and `cd` have resistances `R_1` and `R_2`. Neglecting the self-inductance of the loop, find the current flowing in the connector during its motion with a constant velocity v.

View SolutionA conducting rod `PQ` of length `l=1.0m` is moving with a uniform speed `v2.0m//s` in a uniform magnetic field `B=4.0T` directed into the paper.
A capacitor of capacity `C=10muF` is connected as shown in figure. Then

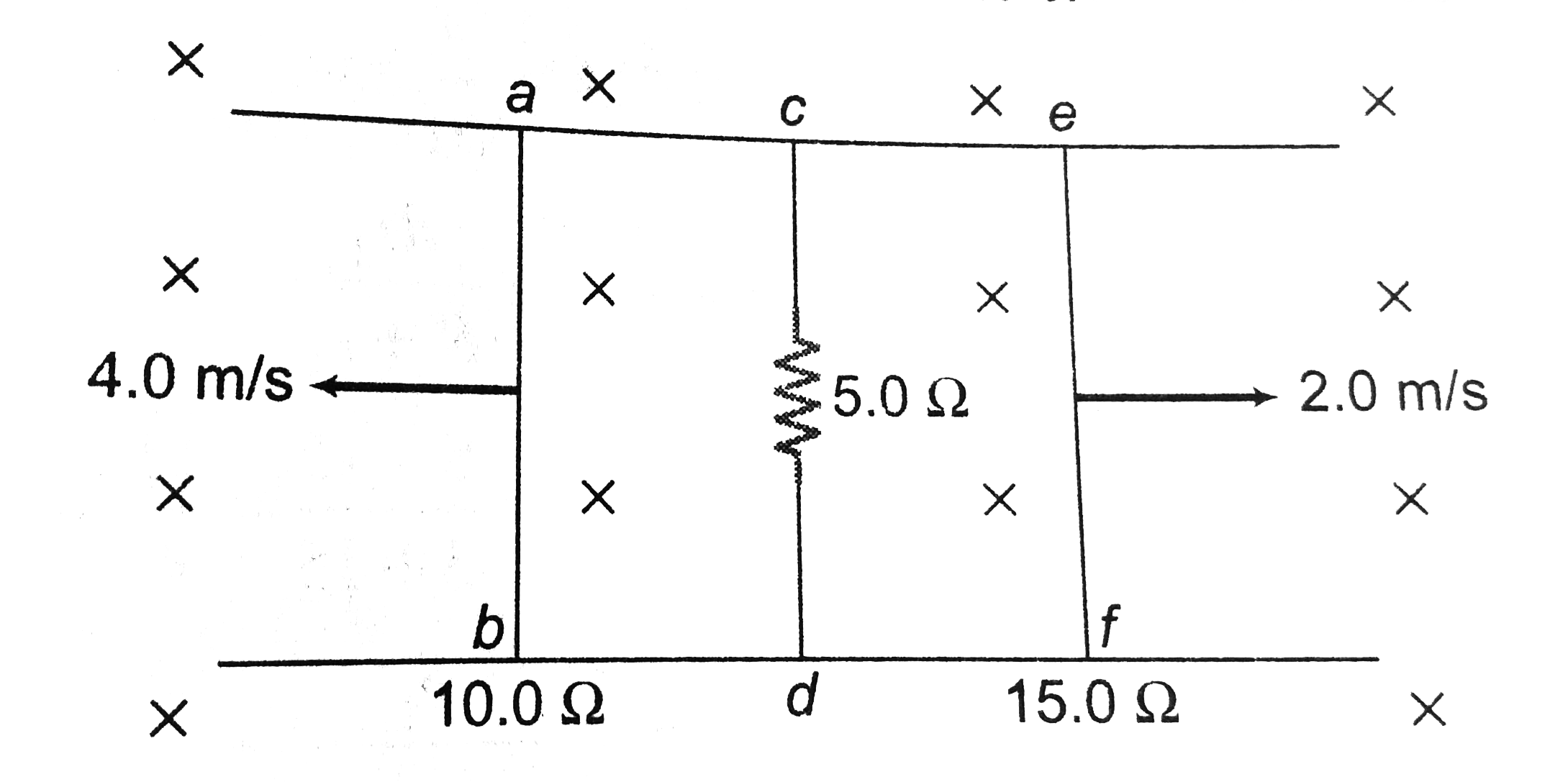
View SolutionTwo parallel rails with negligible resistance are `10.0 cm` apart. The are connected by a `5.0Omega` resistor. The circuit also contains two metal rods having resistances of `10.0Omega` and `15.0Omega` along the rails. The rods are pulled away from the resistor at constant speeds `4.00 m/\s` and `2.00 m//s` respectively. A uniform magnetic field of magnitude `0.01 T` is applied perpendicular to the, plane of the rails. Determine the current in the `5.0Omega` resistor.
View SolutionA conducting rod `MN` moves with a speed `v` parallel to a long straight wire which carries a constant current `i`, as shown in fig. The length of the rod is normal to the wire. Find the emf induced in the total length of the rod. State which end will be at a lower potential.
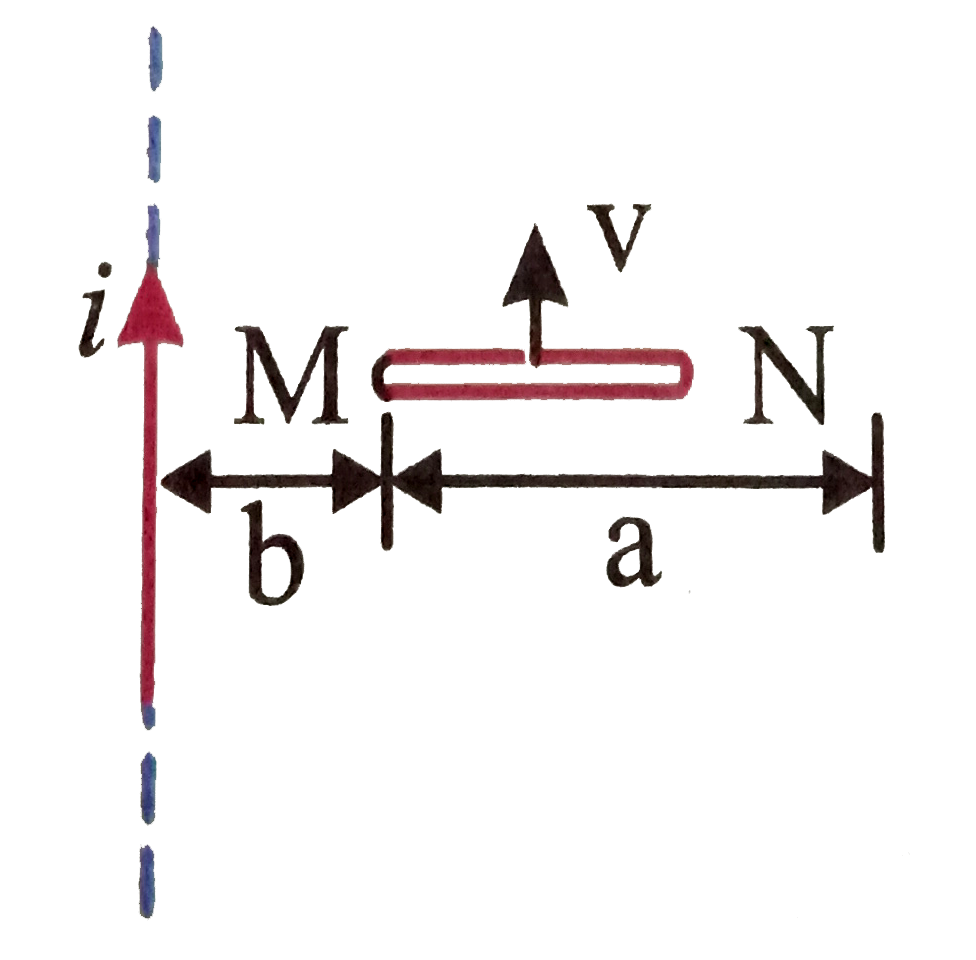
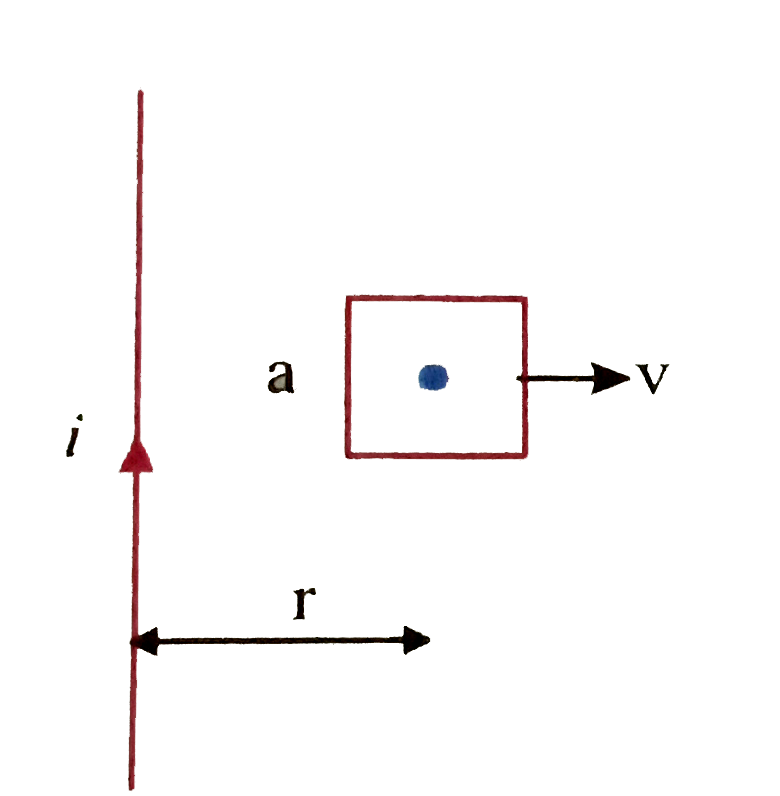
View SolutionA square loop of side `a` is placed in the same plane as a long straight wire carrying a current `i`. The centre of the loop is at a distance `r` from wire where `r gt gt a`. The loop is moved away from the wire with a constant velocity `v`. The induced `e.m.f` in the loop is
View SolutionTwo conducting rings of radii `r` and `2r` move in apposite directions with velocities `2 upsilon` and `upsilon` respectively on a conducting surface `S`. There is a uniform magnetic field of magnitude `B` perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
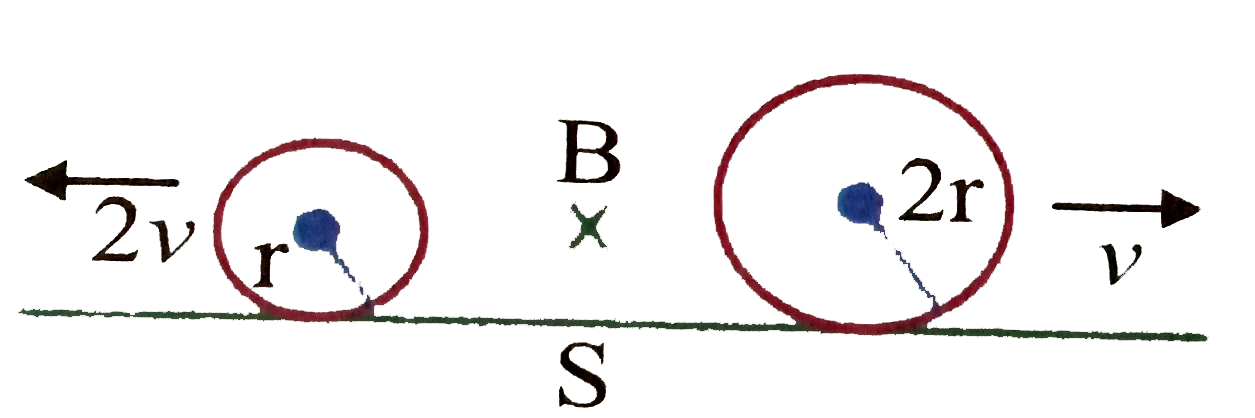
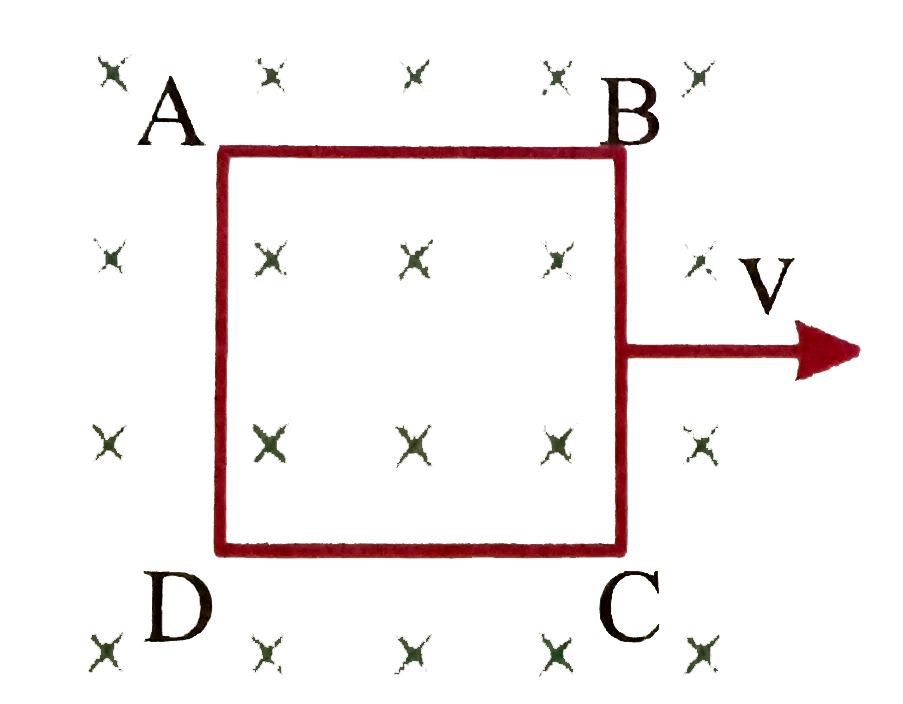
View SolutionA metallic square loop `ABCD` is moving in its own plane with velocity `v` in a uniform magnetic field perpendicular to its plane as shown in the figure. Find
`{:a)` In which sides of the loop electric field is induced.
`{:b)` Net emf induced in the loop
`{:c)` If one `'BC'` is outside the field with remaining loop in the field and is being pulled ot a constant velocity then induced current in the loop.
View SolutionA copper rod of length `2m` is rotated with a speed of `10 rps`, in a uniform magnetic field of `1` tesla about a pivot at one end. The magnetic field is perpendicular to the plane of rotation. Find the emf induced across its ends
View SolutionA wheel with 10 metallic spokes each 0.5 m long is rotated with a speed of 120 rpm, in a plane normal to earth's magnetic field at the place. If the megnitude of the field is 0.40 gauss, what is the induced e.m.f. between the axle and rim of the wheel.
View SolutionA metal rod of resistance `20 Omega` is fixed along a diameter of a conducting ring of radius `0.1 m` and lies on `x-y` plane. There is a magnetic field `vec(B) = (50 T)vec(k)`. The ring rotates with an angular velocity `omega = 20rad s^(-1)` about its axis. An external resistance of `10 Omega` is connected across the center of the ring and rim. The current external resistance is
View SolutionA copper disc of radius `1m` is rotated about its natural axis with an angular velocity `2 "rad"//"sec"` in a uniform magnetic field `5` telsa with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View SolutionA `0.1 m` long conductor carrying a current of `50 A` is perpendicular to a magentic field of `1.25 mT`. The mechanical power to move the conductor with a speed of `1ms^(-1)` is
View SolutionA short-circuited coil is placed in a time-varying magnetic field. Electrical power is dissipated due to the current induced in the coil. If the number of turns were to be quadrupled and the wire radius halved, the electrical power dissipated would be
View SolutionA pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table, A mass m, tied to the other end of the string hanges vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate.
(i) the terminal velocity achieved by the rod, and
the acceleration of the mass at the instant when the velocity of the rod is half the terminal velocity.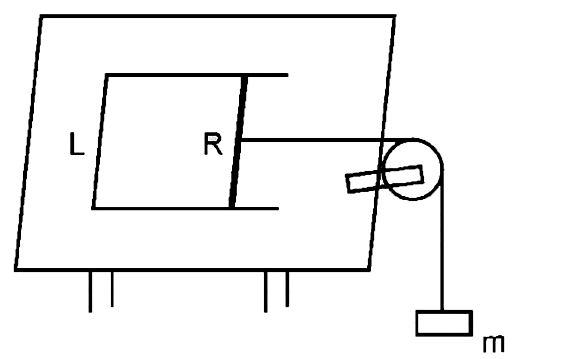
View SolutionTwo parallel vertical metallic bars `X X^(1)` and `Y Y^(1)`, of negligible resistance and separated by a length `'l'`, are as shown in Fig. The ends of the bars are joined by resistance `R_(1)` and `R_(2)`. A uniform magnetic field of induction `B` exsits in space normal to the plane of the bars. A horizontal metallic rod `PQ` of mass `m` starts falling vertically, making contact with the bars. It is oberved that in the steady state the powers dissipated in the resistance `R_(1)` and `R_(2)` and the terminal velocity attained by the rod `PQ`.
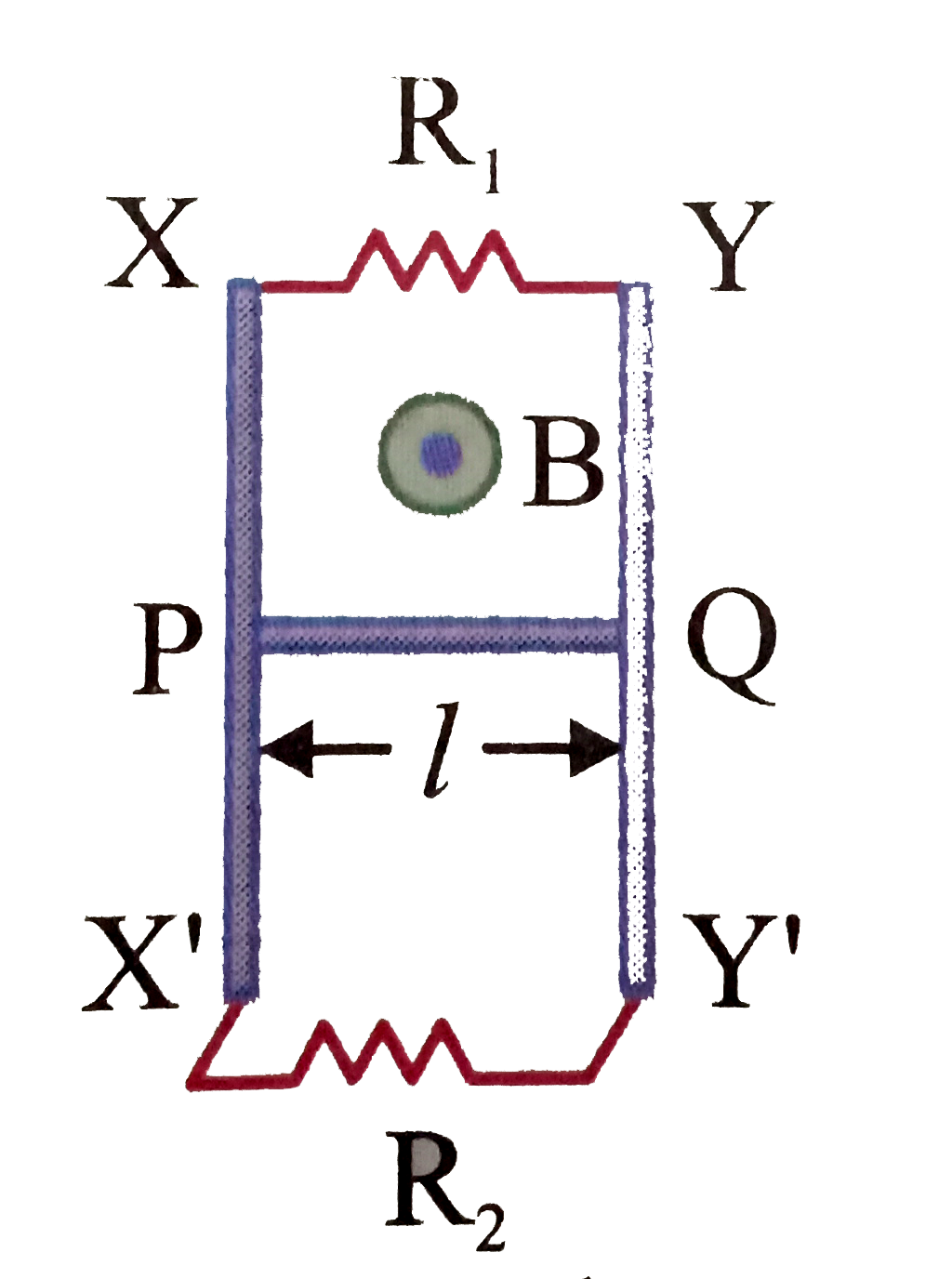
View SolutionThe loop `ABCD` is moving with velocity `'v'` towards right. The magnetic field is `4T`. The loop is connected to a resistance of `8 Omega`. If steady current of `2A` flows in the loop then value of `'v'` if loop has a resistance of `4 Omega`, is : (Given `AB = 30 cm, AD = 30 cm`)
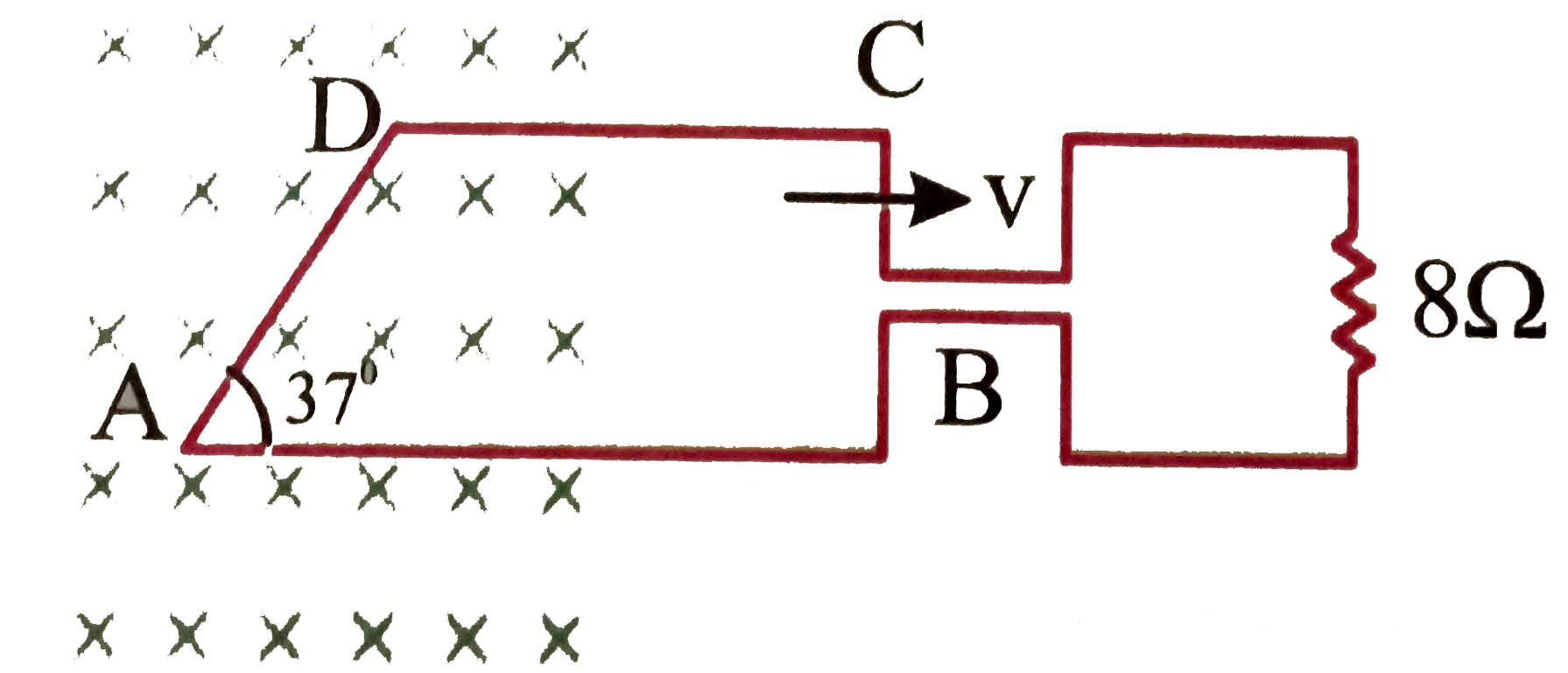
View SolutionA square loop of side `12 cm` with its sides parallel to `x` and `y`- axes is moved with a velocity `8 cm//s` along positive `x`-direction in an environment containing magnetic field along `+ve` z-direction. The field has a gradient of `10^(-3) "tesla"//"em"` along `-ve` x-direction (increasing along `-ve` x-axis) and also decreases with time at the rate of `10^(-3) "tesla"//s`. The emf induced in the loop is
View SolutionA bar of mass `m` and length `l` moves on two frictionless parallel rails in the presence of a uniform magnetic field directed into the plane of the paper. The bar is given and initial velocity `v_(i)` to the right and released. Find the velocity of bar, induced emf across the bar and the current in the circuit as a function of time
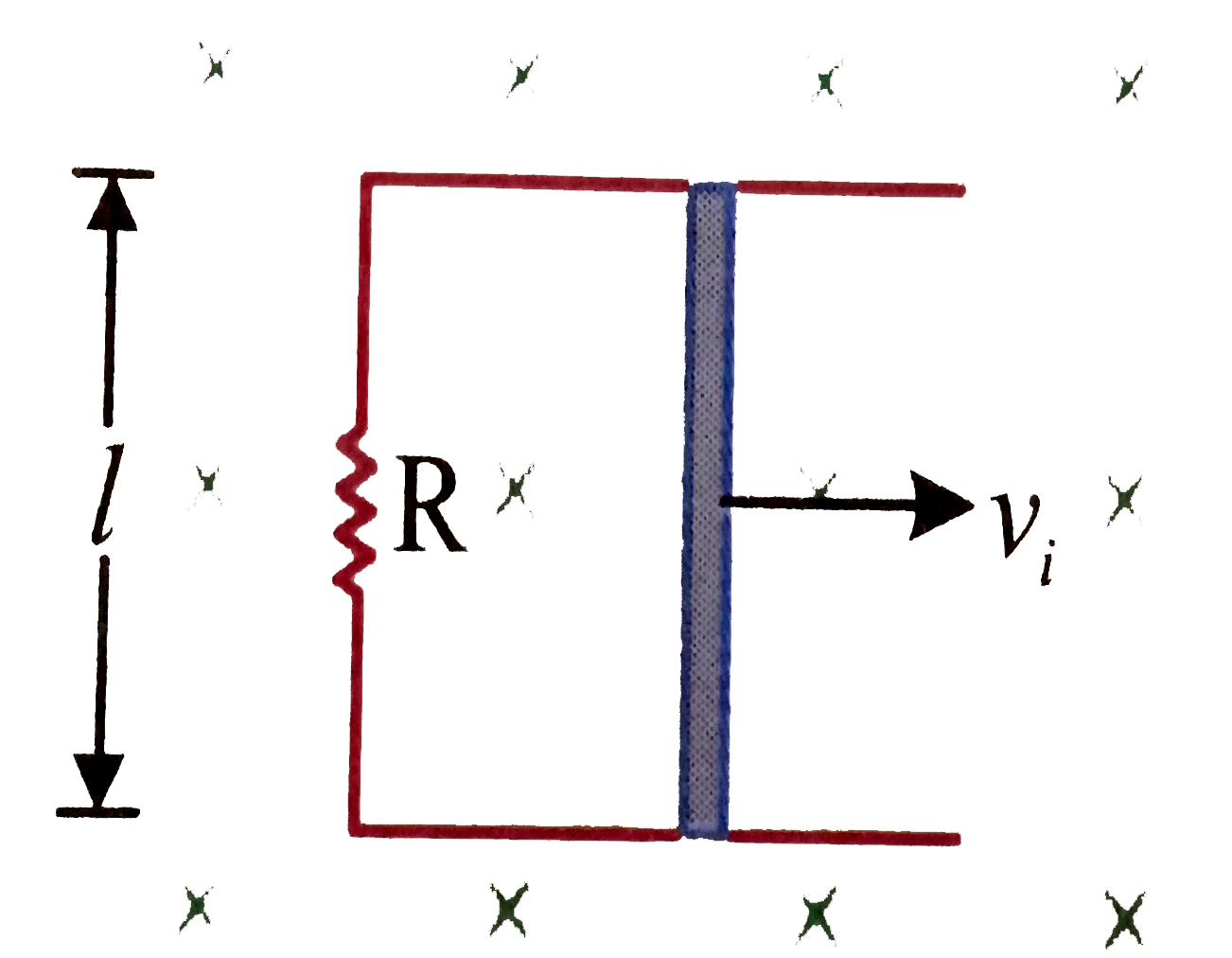
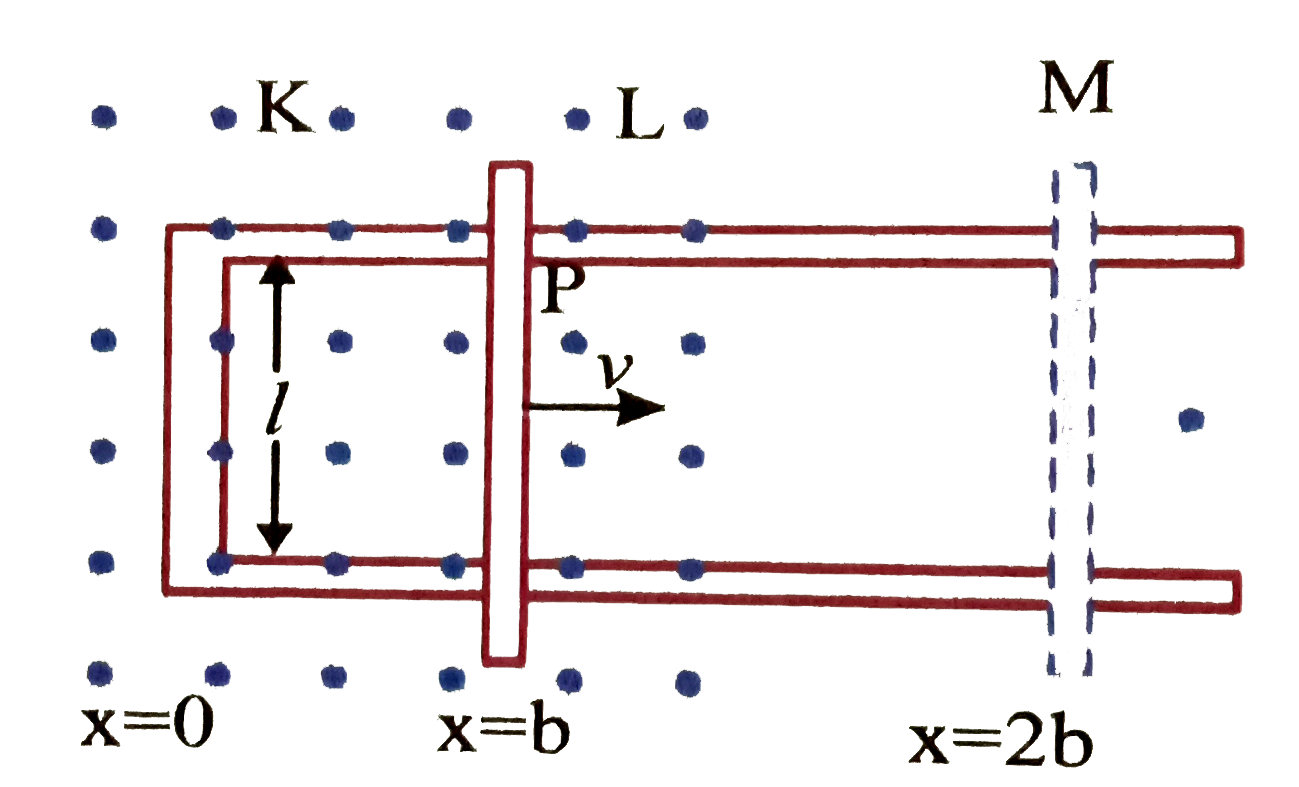
View SolutionThe arm `PQ` of the rectangular conductor is moved from `x=0`, outwards in the uniform magnetic field which extends from `x=0` to `x=b` and is zero for `x gt b` as shown. Only the arm `PQ` possess substantial ressitance `r`. Consider the situation when the arm `PQ` is pulled outwards from `x = 0` to `x = 2b`, and is then moved back to `x = 0` with constant speed `v`. Obtain expression for the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with distance.
View SolutionTwo different coils have self-inductances `L_(1) = 8 mH and L_(2) = 2 mH`. The current in one coil is increased at a constant rate. The current in the second coil is also increased at the same constant rate. At a certain instant of time, the power given to the two coil is the same. At that time, the current, the induced voltage and the energy stored in the first coil are `i_(1), V_(1) and W_(1)` respectively. Corresponding values for the second coil at the same instant are `i_(2), V_(2) and W_(2)` respectively. Then:
View SolutionTwo coaxial solenoids are made by winding thin insulated wire over a pipe of cross-sectional area `A=10 cm^(2)` and length =20cm. If one of the solenoid has 300 turns and the other 400 turns, their mutual indcutance is
View SolutionThe self inductance of a coil having 200 turns is 10 mH. Compute the total flux linked with the coil. Also, determine the magnetic flux through the cross section of the coil, corresponding to current of 4 mA.
View SolutionA coil of inductane `0.2` henry is connected to `600` volt battery. At what rate, will the current in the coil graw when circuit is completed ?
View SolutionAn inductor of 5 H inductance carries a steady current of 2 A. How can a 50 V self induced e.m.f. be made to appear in the inductor ?
View SolutionTwo different coils have self inductane `L_(1) = 16mH` and `L_(2) = 12mH`. At a certain instant, the current in the two coils is increasing at the same rate of power supplied to th two coils is the same. Find the ratio of `{:i)` induced voltage `{:ii)` current `{:iii)` energy stored in the two coils at that instant.
View SolutionThe newtwork shown is a part of the closed circuit in which the current is changing. At an instant, current in it is `5A`. Potential difference between the points `A` and `B` if the current is
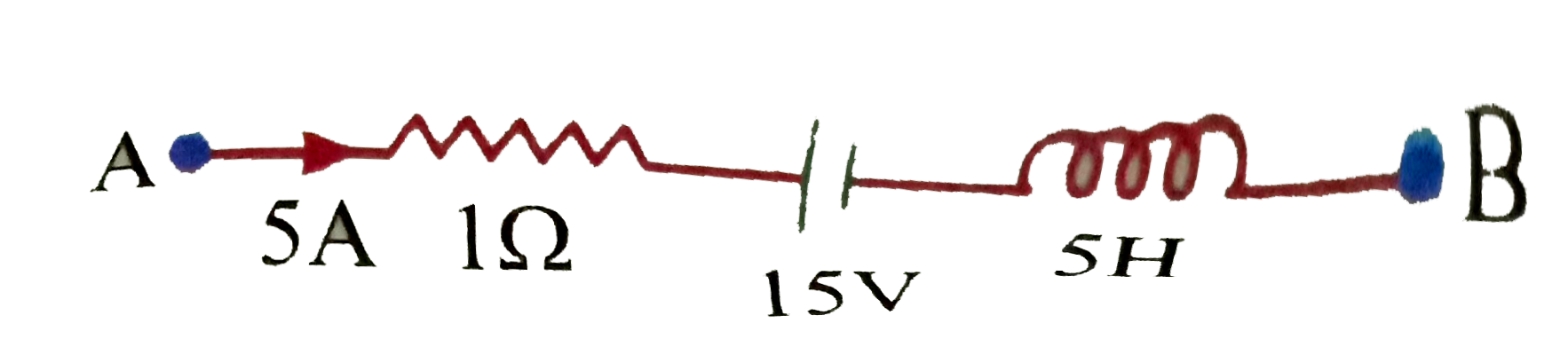
(1) Increasing at `1A//sec`
(2) Decreasing at `1A//sec`
View SolutionCalculate the mutual inducatnce between two coils when a current of `2A` changes to `6A` in `2` seconds and induces an emf of `20 mV` in the secondary coil
View SolutionIf the coefficient of mutual induction of the primary and secondary coils of an induction coil is `6H` and a current of `5A` is cut off in `1//5000` second, calculate the emf induced in the secondary coil.
View SolutionA solenoid is of length `50 cm` and has a radius of `2cm`. It has `500` turns. Around its central section a coil of `50` turns is wound. Calculate the mutual inductance of the system.
View SolutionA solenoidal coil has `50` turns per centimetre along its length and a cross-sectional area of `4 xx 10^(-4) m^(2)`. `200` turns of another wire is wound round the first solenoid co-axially. The two coils are electrically insulated from each other. Calculate the mutual inductance between the two coils.
View SolutionTwo circular coils, one of smaller radius `r_(1)` and the other of very large radius `r_(2)` are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionA small square loop of wire of side `l` is placed inside a large square loop of wire of side `L (L gt gt l)`. The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
View SolutionA torodal solenoid with an air core has an average radius of 15 cm, area of cross-section `12 cm^(2) and 1200 turns. Obtain the self inductance of the toroid. Ignore field variations across the cross-section of the toroid.
(b) A second coil of 300 turns is wound closely on the toroid above. If the current in the primary coil is increased from zero to 2.0 A in 0.05 s, obtain the induced e.m.f. in the second coil.
View SolutionA boy pedals a stationary bicycle at one revolution per second. The pedals are attached to `100` turns coil of are `0.1 m^(2)` and placed in a uniform magnetic field of `0.1 T`. What is the maximum voltage generated in the coil ?
View SolutionA coil of `800` turns `50 cm^(2)` area makes `10 rps` about an axis in its own plane in a magnetic field of `100` gauss perpendicular to the this axis. What is the instantaneous inducted emf in the coil ?
View SolutionA person peddles a stationary bicyle the pedals of the bicycle are attached to a `100` turn coil of area `0.10 m^(2)`. The coil rotated at half a revolution per second and it is placed in a uniform magnetic field of `0.01 T`
perpendicular to the axis of rotation of the coil, What is the maximum voltage generated in the coil ?
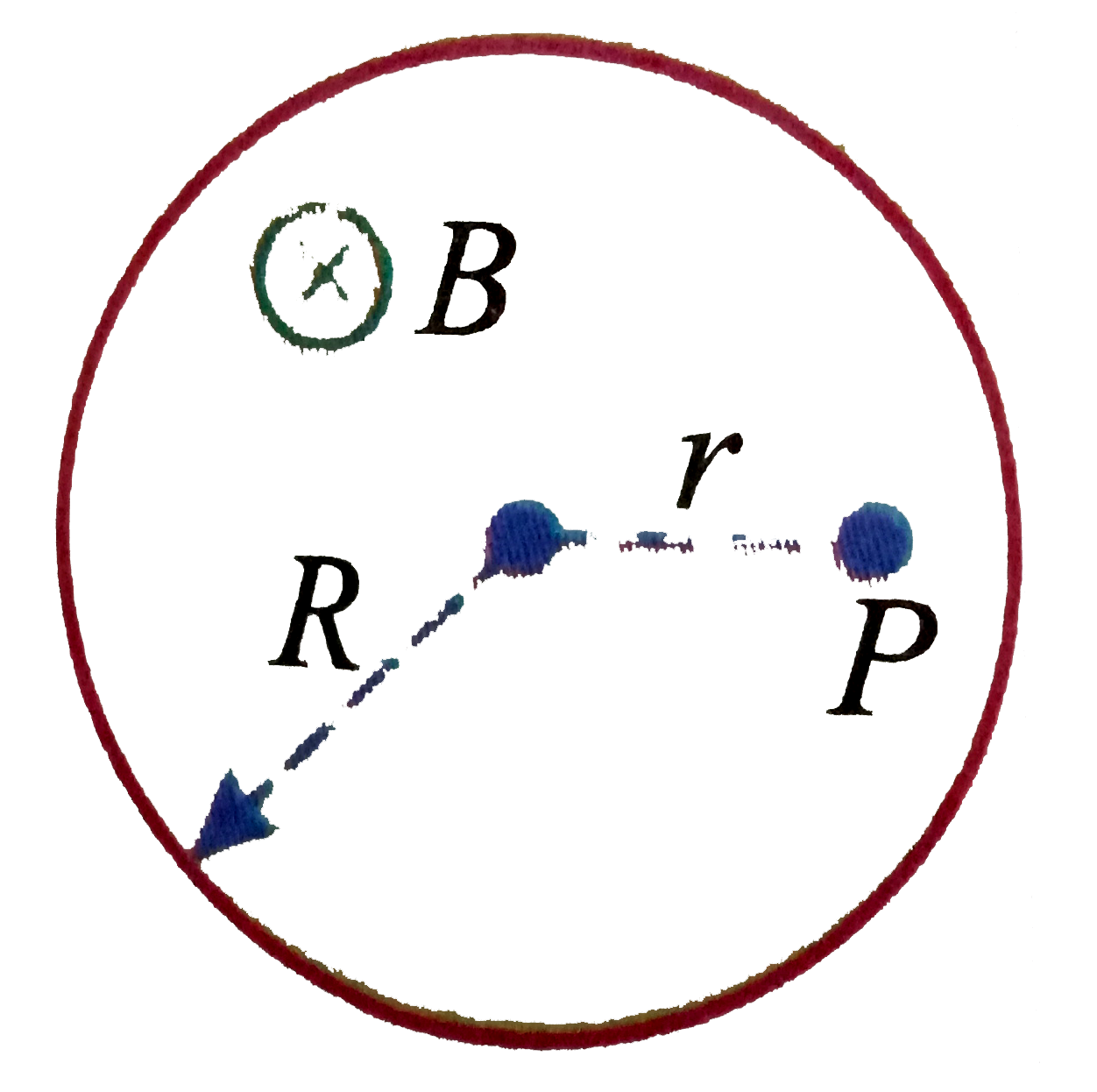
View SolutionA uniform magentic field of induction `B` is confined in a cyclinderical region of radius `R`. If the field is incresing at a constant rate of `(dB)/(dt)= alpha T//s`, then the intensity of the electric field induced at point `P`, distant `r` from the axis as shown in the figure is proportional to :
View SolutionA magnetic flux through a stationary loop with a resistance `R` varies during the time interval `tau` as `phi=at(tau-t)`. Find the amount of the generated in the loop during that time
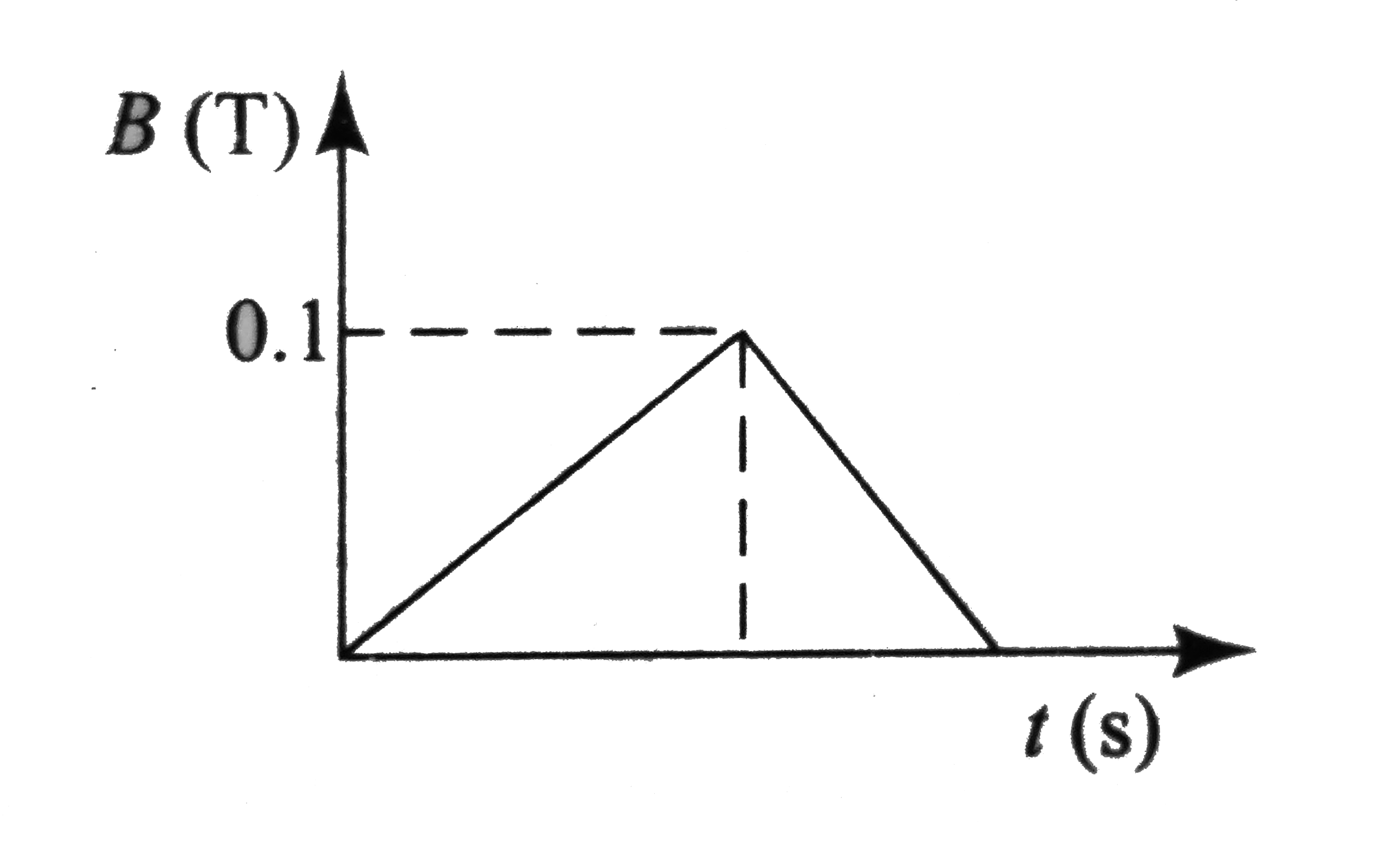
View SolutionA closed loop of cross-sectional area `10^(-2) m^(2)` which has inductance `L = 10 mH` and negligible resistance is placed in time- varying magnetic field. Figure shows the variation of `B` with time for the interval `4 s`. The field is perpendicular to the plane of the loop (given at `t = 0`, `B = 0`, `I = 0)`. The value of the maximum current induced in the loop is
View SolutionA magnetic field directed into the page changes with time according to `B = (0.0300t^(2) + 1440)T`, where `t` is in seconds. The field has a circular cross section of radius `R = 2.50 cm`. What are the magitude and direction of the electric field at point `P_(1)` when `t = 3.00 s` and `r_(1) = 0.0200 m`?

View SolutionThe magnetic field at all points within the cyllindrical region whose cross section is indicated in the accompanying Figure starts increasing at a constant rate `alpha`. `T//s`. find the magnitud of electric field as a function of `r`, the distance from the geometric centre of the region.

View SolutionA wire is bent in the form of a square of side `'a'` in a varying magnetic field `bar(B) = alpha B_(0) t hat(k)`. If the resistance per unit length is `lambda`, then find the following.
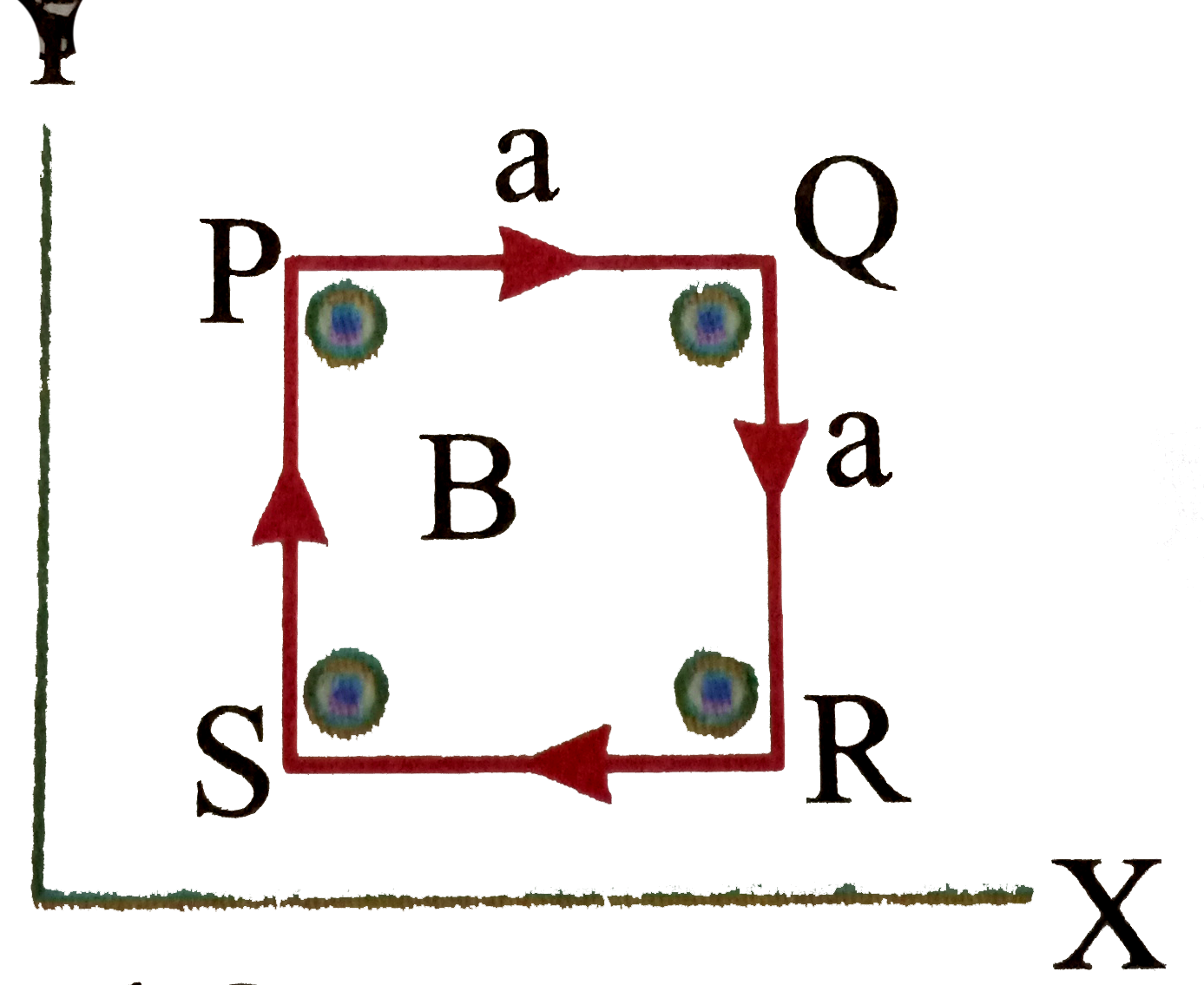
`{:i)` The direction of induction current
`{:ii)` The current in the loop
`{:iii)` Potential difference between `P` and `Q`
View SolutionShown in the figure is a circular loop of radius `r` and resistance `R`. A varible magnetic field of induction `B=B_(0)e^(-t)` is established inside the coil. If the key `(K)` is closed, the electrical power devloped right after closing the switch is equal to

View SolutionIn the given circuit, find the current through the `5 mH` inductor in steady state.
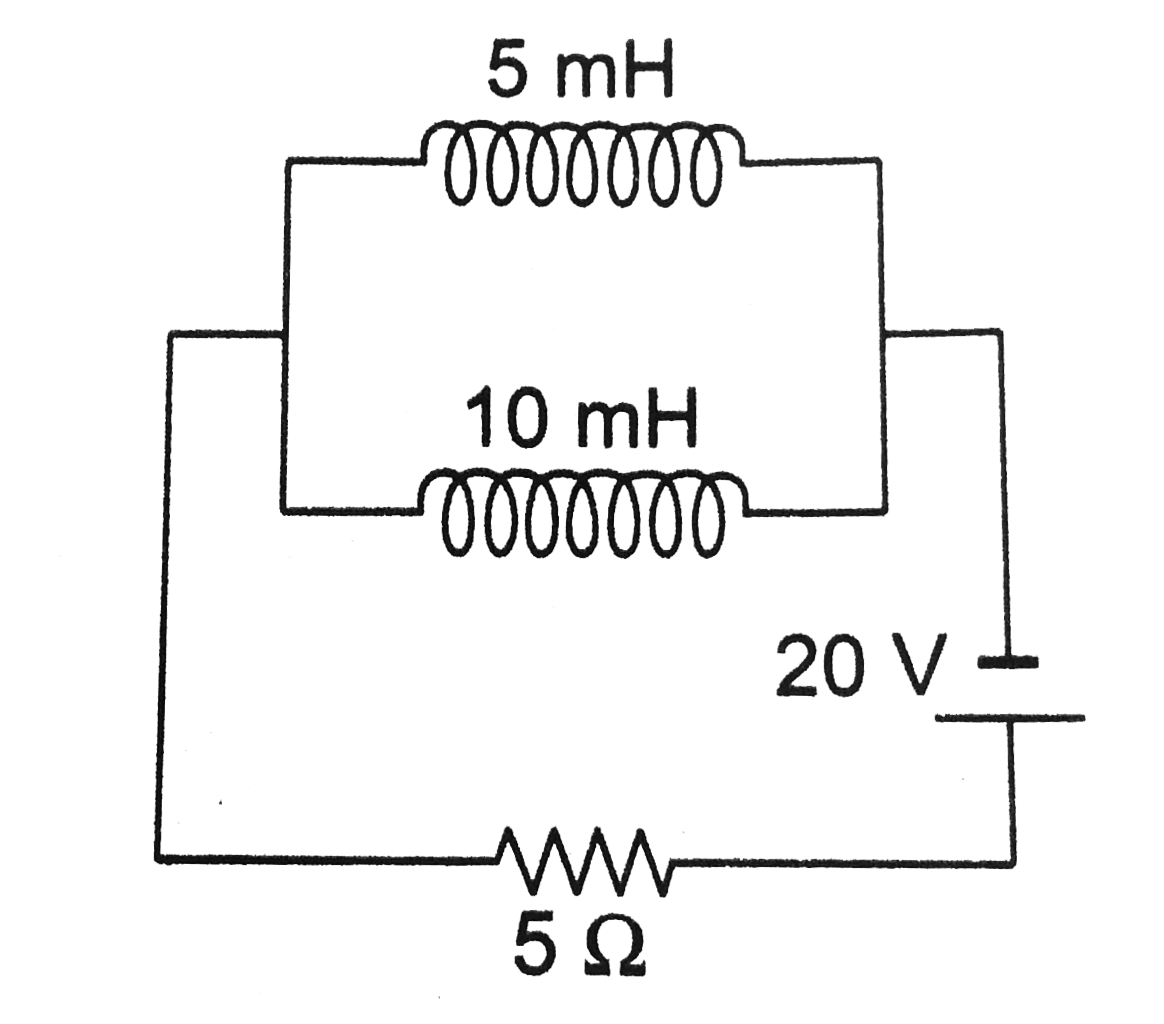
View SolutionIn the given circuit (Fig), key `K` is switched on the at `t = 0`. The ratio of current `i` through the cell at `t = 0` to that at `t = oo` will be

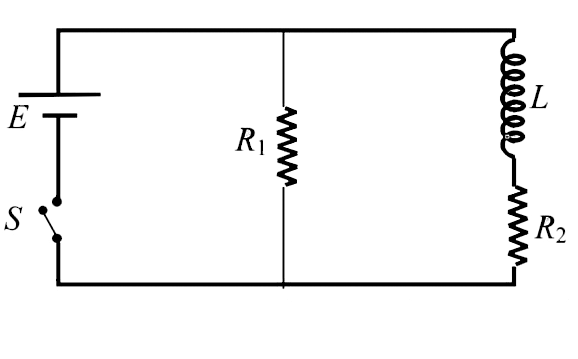
View SolutionAn inductor of inductance L=400 mH and resistor of resistance `R_(1) = 2(Omega) and R_(2) = 2 (Omega)` are connected to a battery of emf E = 12 Vas shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t =0. What is the potential drop across L as a function of time? After the steady state is reached, the switch is opened. What is the direction and the magnitude of current through `R_(1)` as a function of time?
View SolutionAn inductor of `3H` is connected to a battery of emf `6V` through a resistance of `100 Omega`. Calculate the time constant. What will be the maximum value of current in the circuit ?
View SolutionA cell of `1.5V` is connected across an inductor of `2mH` in series with a `2 Omega` resistor. What is the rate of growth of current immediately after the cell is switched on.
View SolutionA coil having resistance `15 Omega` and inductance `10H` is connected across a `90` Volt `dc` supply. Determine the value of current after `2sec`, What is the energy stored in the magnetic field at that instant.
View SolutionCalculate the back `e.m.f` of a `10H`, `200 Omega` coil `100 ms` after a `100V` d.c supply is connected to it.
View SolutionA coil of resistance `20Omega` and inductance `0.5H` is switched to `DC200V` supply. Calculate the rate of increase of current
a. at the instant of closing the switch and
b. after one time constant.
c. Find the steady state current in the circuit.
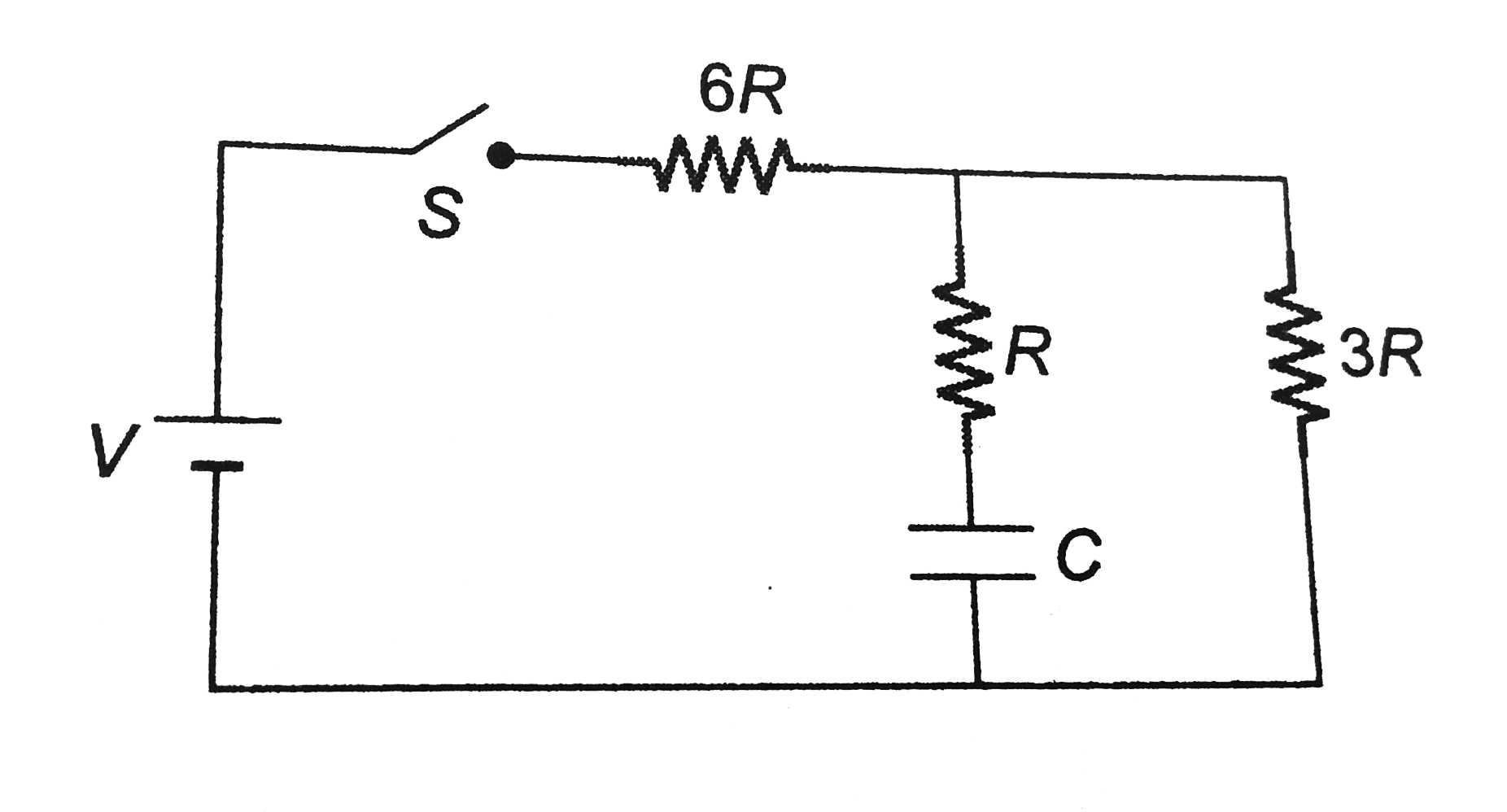
View SolutionIn the circuit shownin figure switch `S` is closed at time t=0. Find the current through different wire and charge stored on the capacitor at any time `t`.
View SolutionA parallel- plate capacitor, fileld with a dielectric of dielectric consatnt `k`, is charged to a potential `V_(0)`. It is now disconnected from the cell and the slab is removed. If it now discharges, with time constant `tau`, through a resistance then find time after which the potential difference across it will be `V_(0)` ?
View SolutionA `4 muF` capacitor, a resistance of `2.5 M Omega` is in series with `12V` battery. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [ Given In (2) = 0.693]
View SolutionIn a circuit inductance `L` and capacitance `C` are connected as shown in figure and `A_(1)` and `A_(2)` are ammeters. When key `k` is pressed to complete the circuit, then just after closing key `k`, the readig of `A_(1)` and `A_(2)` will be:
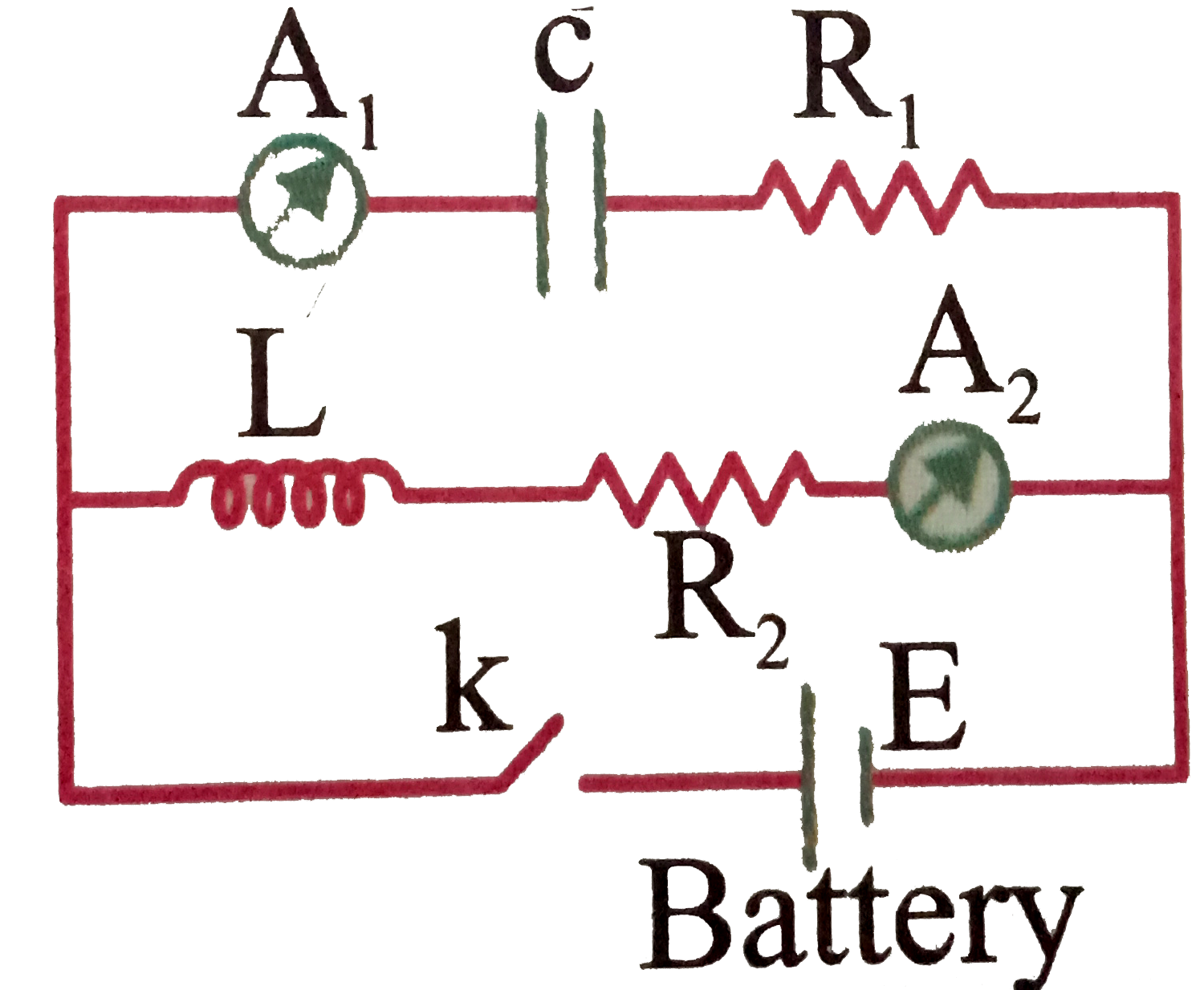
View Solution
Solved Example questions and complete solutions for chapter ELECTRO MAGNETIC INDUCTION of NARAYANA PHYSICS (HINGLISH) of Class 12