Complete Solutions to Solved Examples of chapter CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE |
| RS AGGARWAL | Solved Examples |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
In the given figure, Oa = OB and OC = OD. Which is the criteria to prove
`DeltaAOC ~=DeltaBOD`.

View Solution`A B` is a line segment and line `l` is its perpendicular bisector. If a point `P` lies on `l ,` show that `P` is equidistant from `A` and `Bdot`
View SolutionProve that each angle of an equilateral triangle is `60^0`
View SolutionIn an Isoceless triangle altitude from the vertex bisects the base.
View SolutionIf the altitude from one vertex of a triangle bisects the opposite side; then the triangle is isosceless.
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle;then the triangle is iscsceless.
View SolutionProve that the perpendiculars drawn from the vertices of equal angles of an isosceles triangle to the opposite sides are equal.
View SolutionIf the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
View SolutionProve that the medians of an equilateral triangle are equal.
View SolutionIf `D` is the mid-point of the hypotenuse `A C` of a right triangle `A B C ,` prove that `B D=1/2A C`
View SolutionIf two isosceles triangles have a common base, prove that the line segment joining their vertices bisects the common base at right angles.
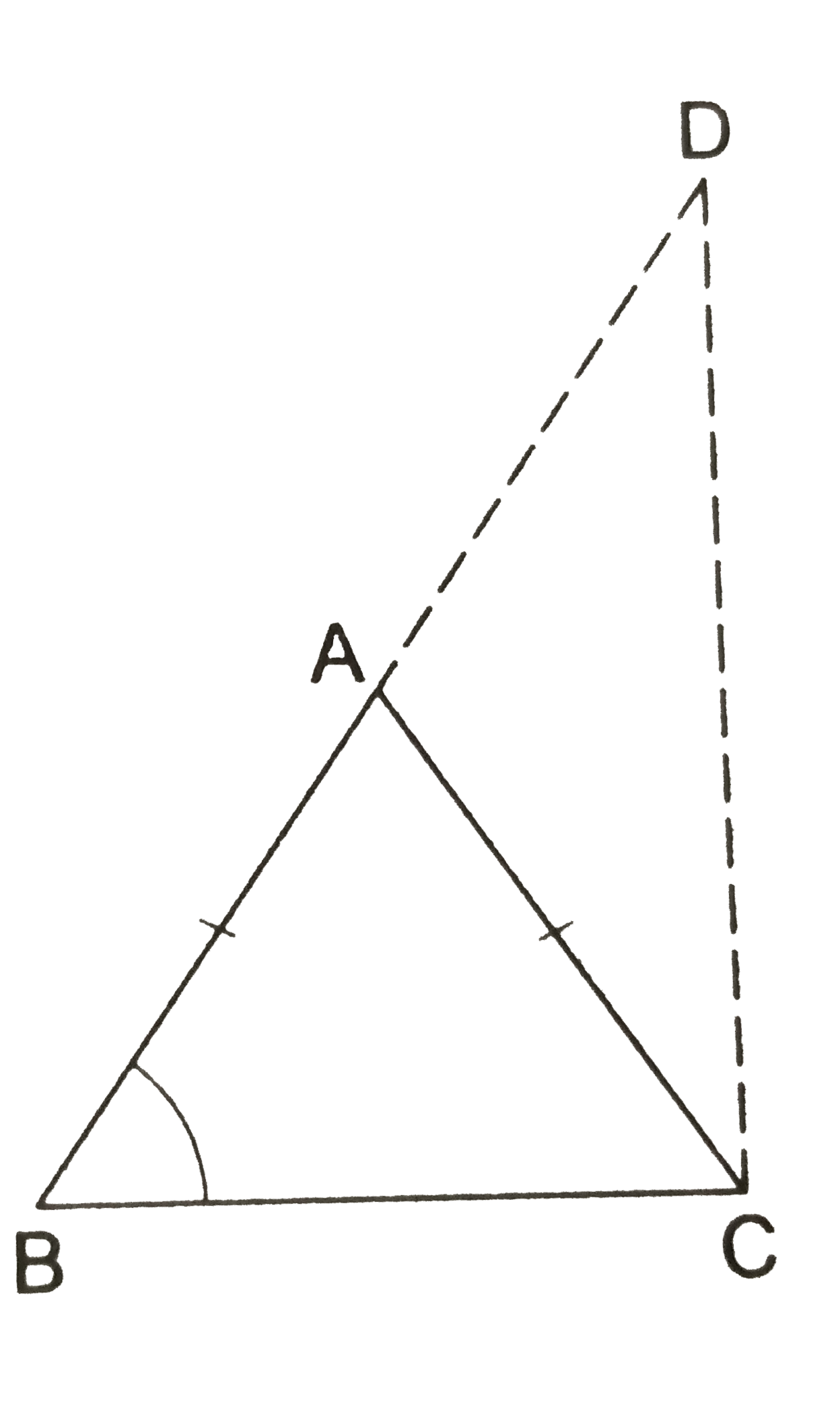
View Solution`DeltaABC` is an isosceles triangle with AB = AC.
Side BA is produced to D such that AB = AD.
Prove that `angleBCD` is a right angle.
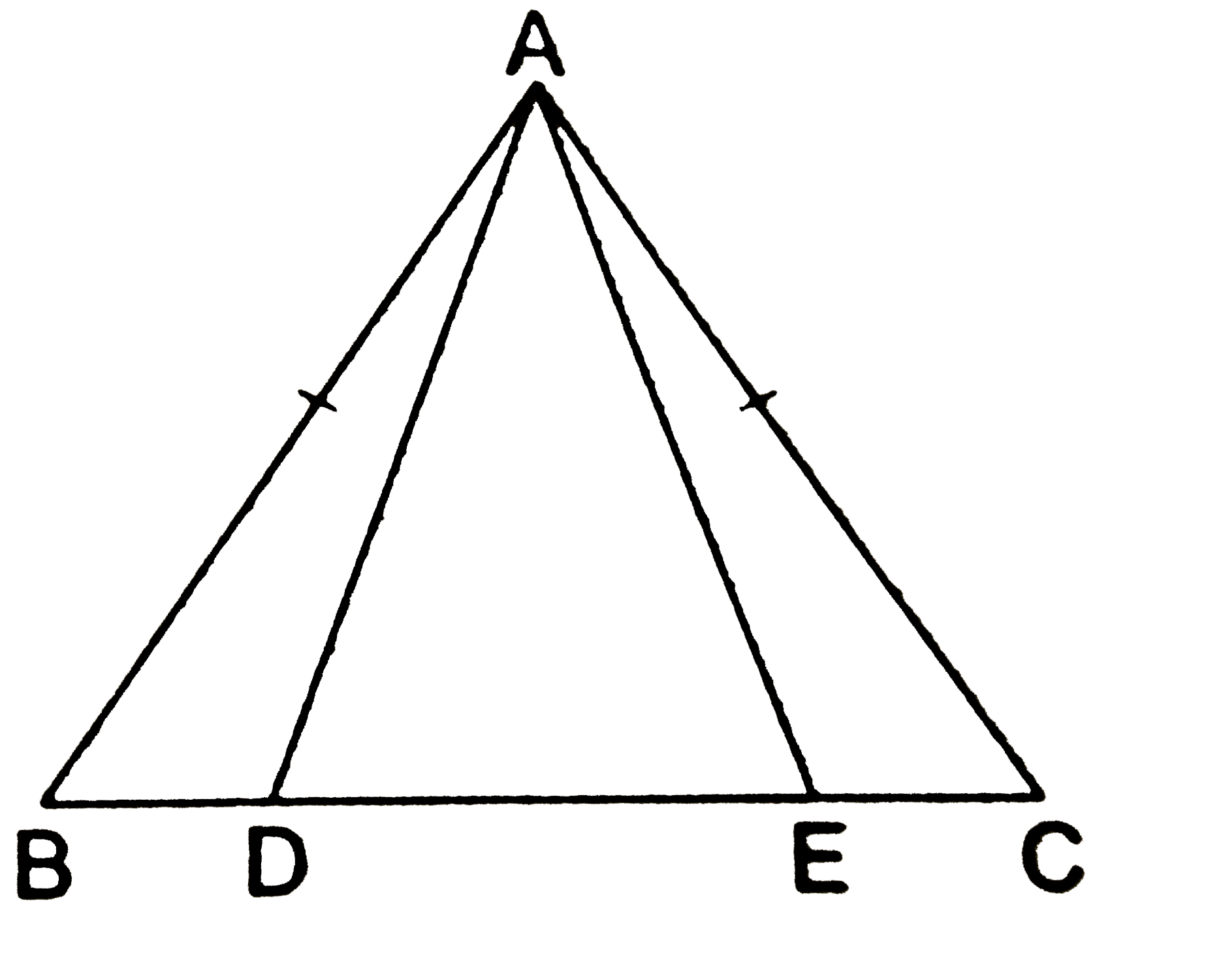
View SolutionIn an isosceles `DeltaABC` with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
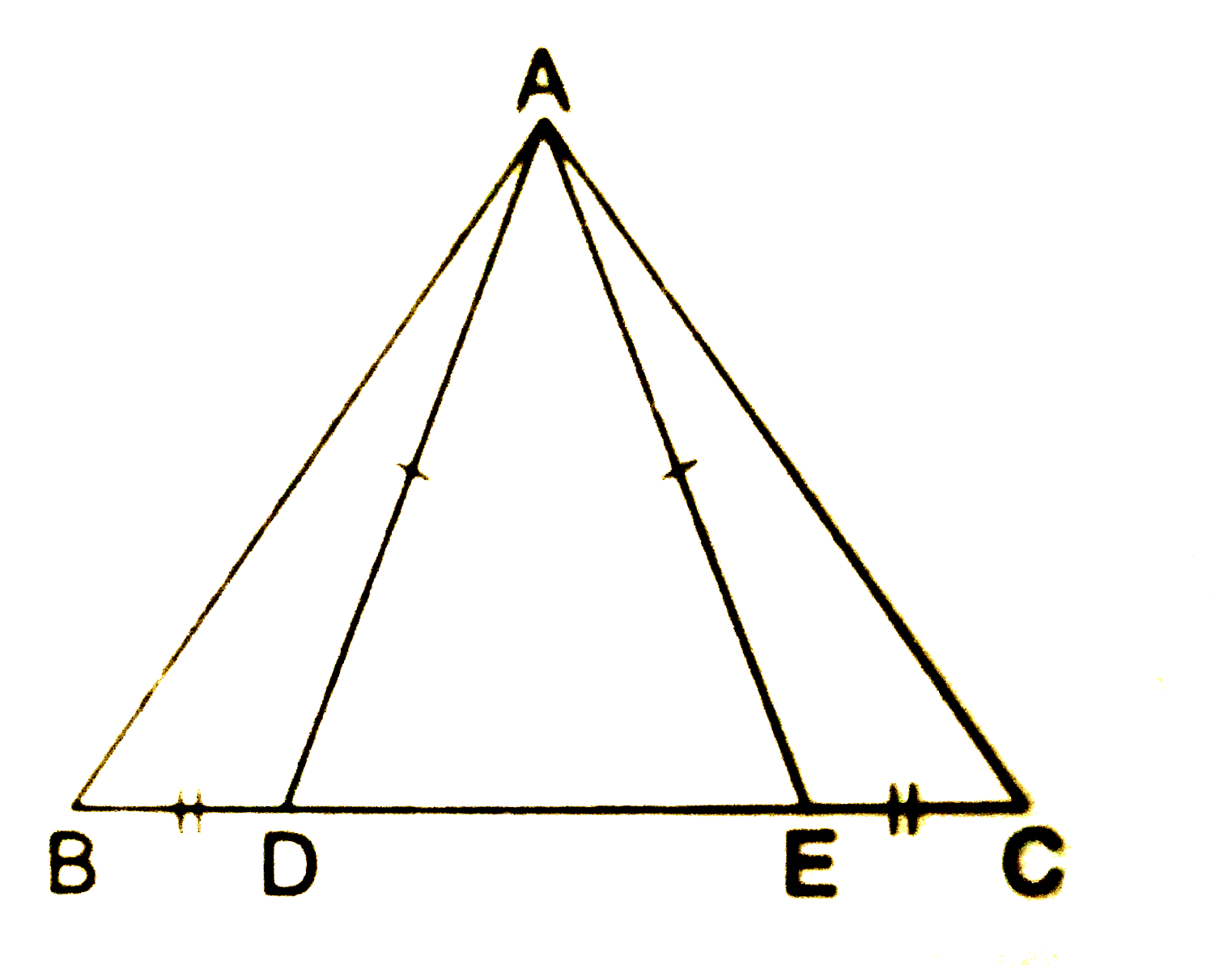
View SolutionIn the given figure, D and E are points on the side BC of a `DeltaABC` such that BD = CE and AD = AE. Show that `DeltaABD~=DeltaACE.`
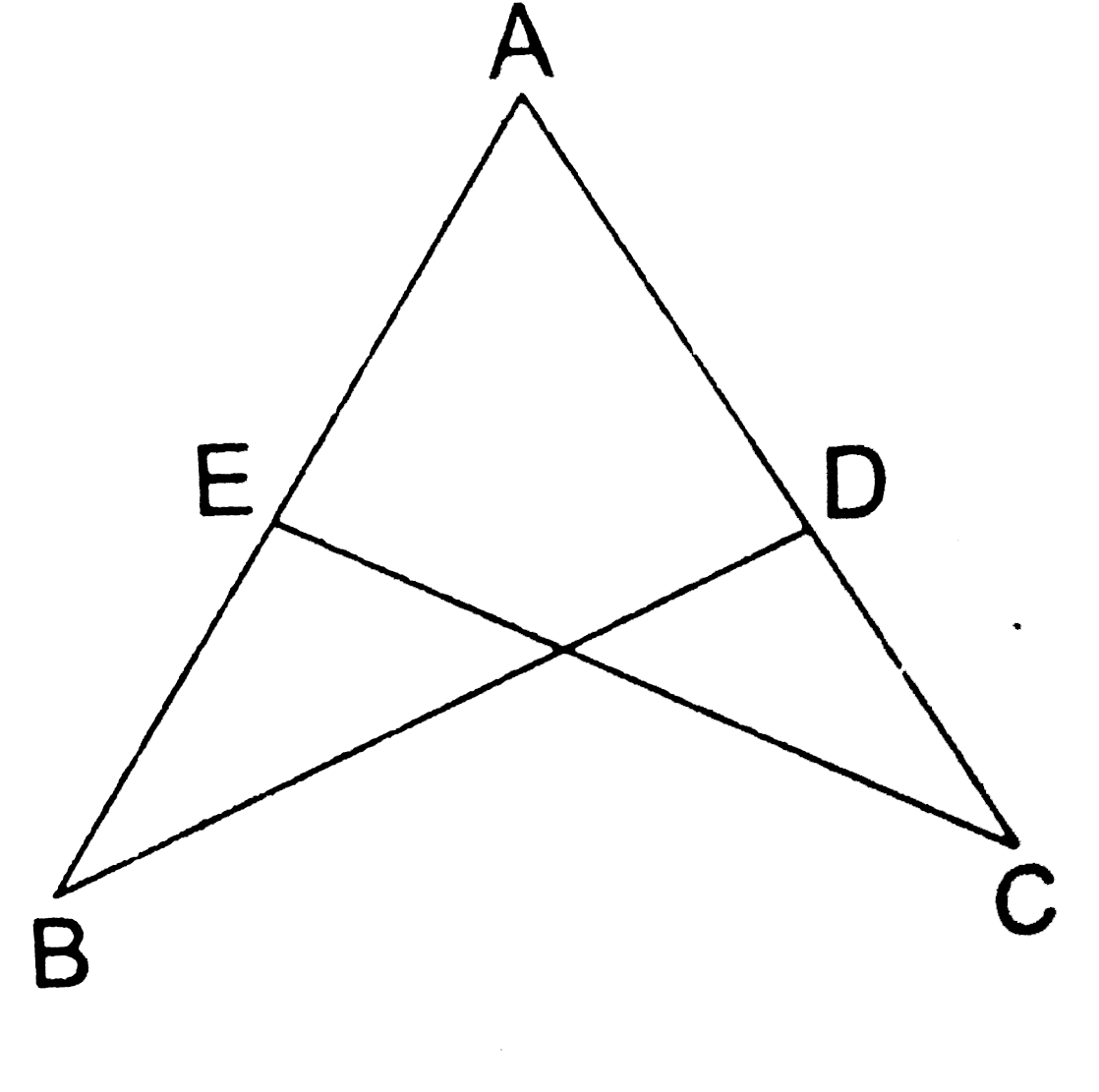
View SolutionIn the given figure, AB = AC and `angleB=angleC.`
Then `DeltaABD~=DeltaACE` by
View SolutionIn the given figure, `DeltaCDE` is an equilateral triangle on a side CD of a square ABCD. Show that `DeltaADE~=DeltaBCE.`
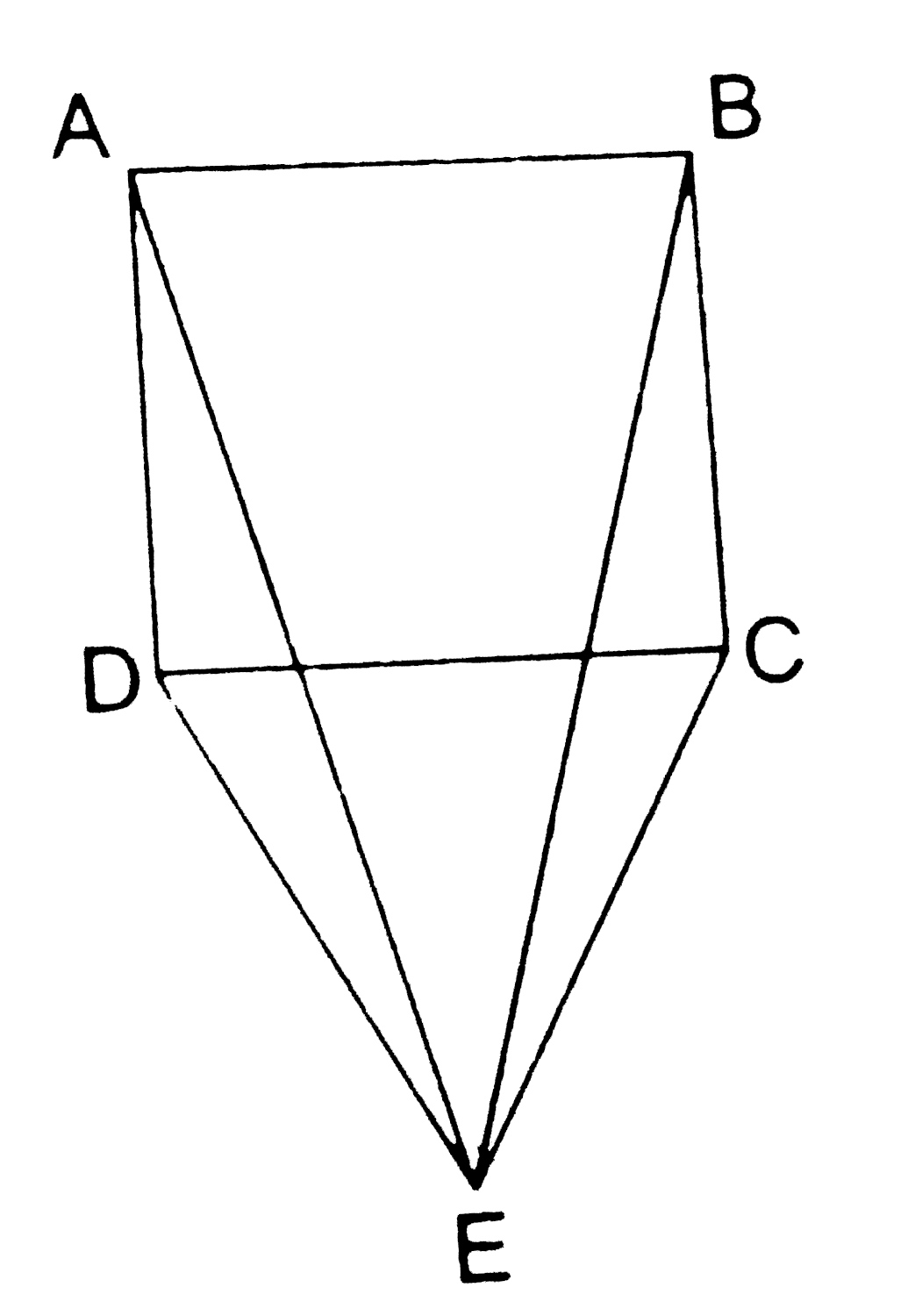
View SolutionIn the given figure, `BA_|_AC and DE_|_DF` such that AB = DE and BF = EC. Show that `DeltaABC~=DeltaDEF.`
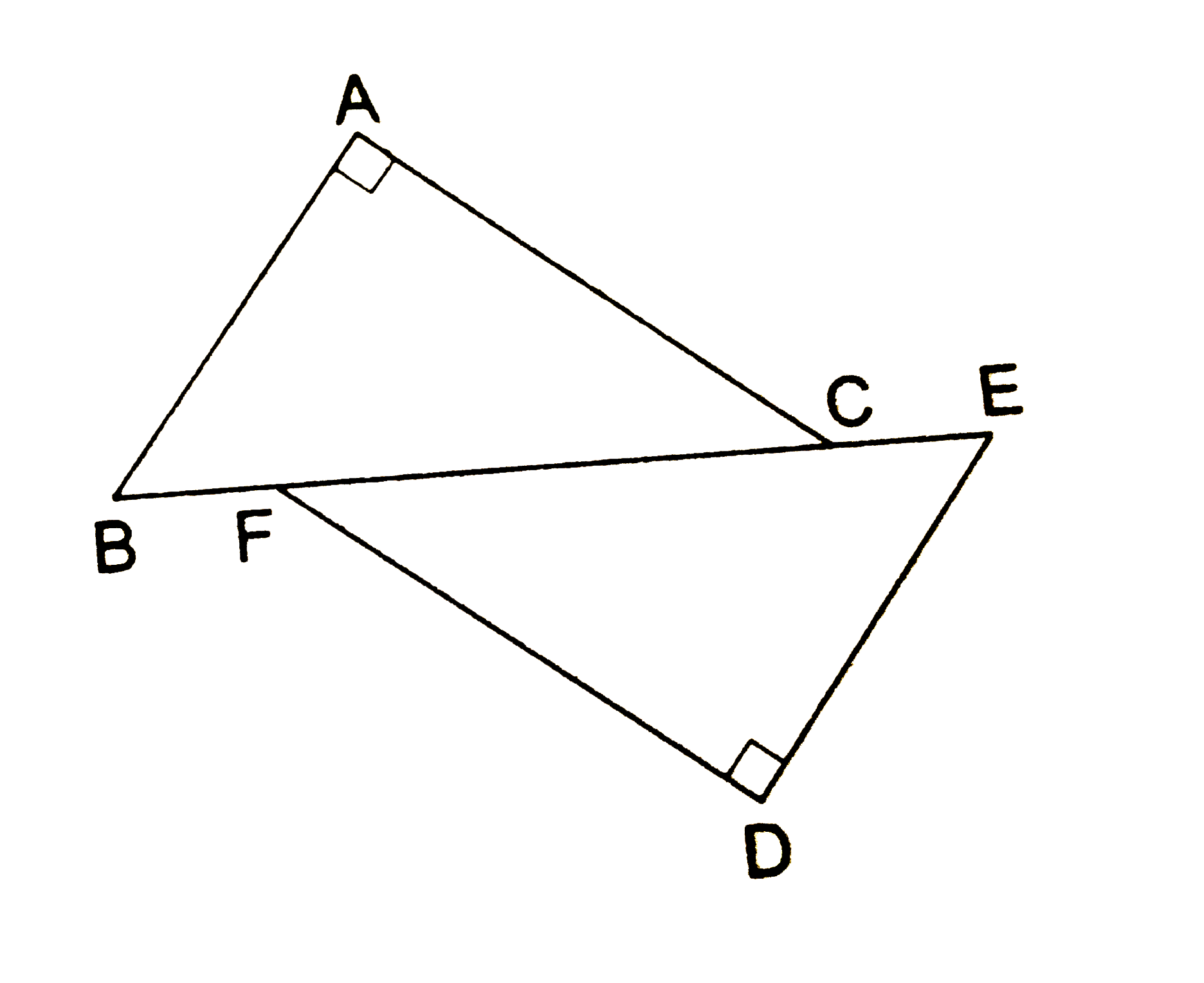
View SolutionIn the given figure, `AY_|_ZY and BY_|_XY` such that `AY=ZY and BY=XY.` Prove that `AB = ZX.`
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that `angleBAD=angleABE and angleEPA=angleDPB`.
Show that (i) `DeltaDAP~=DeltaEBP,`
`(ii) AD=BE.`
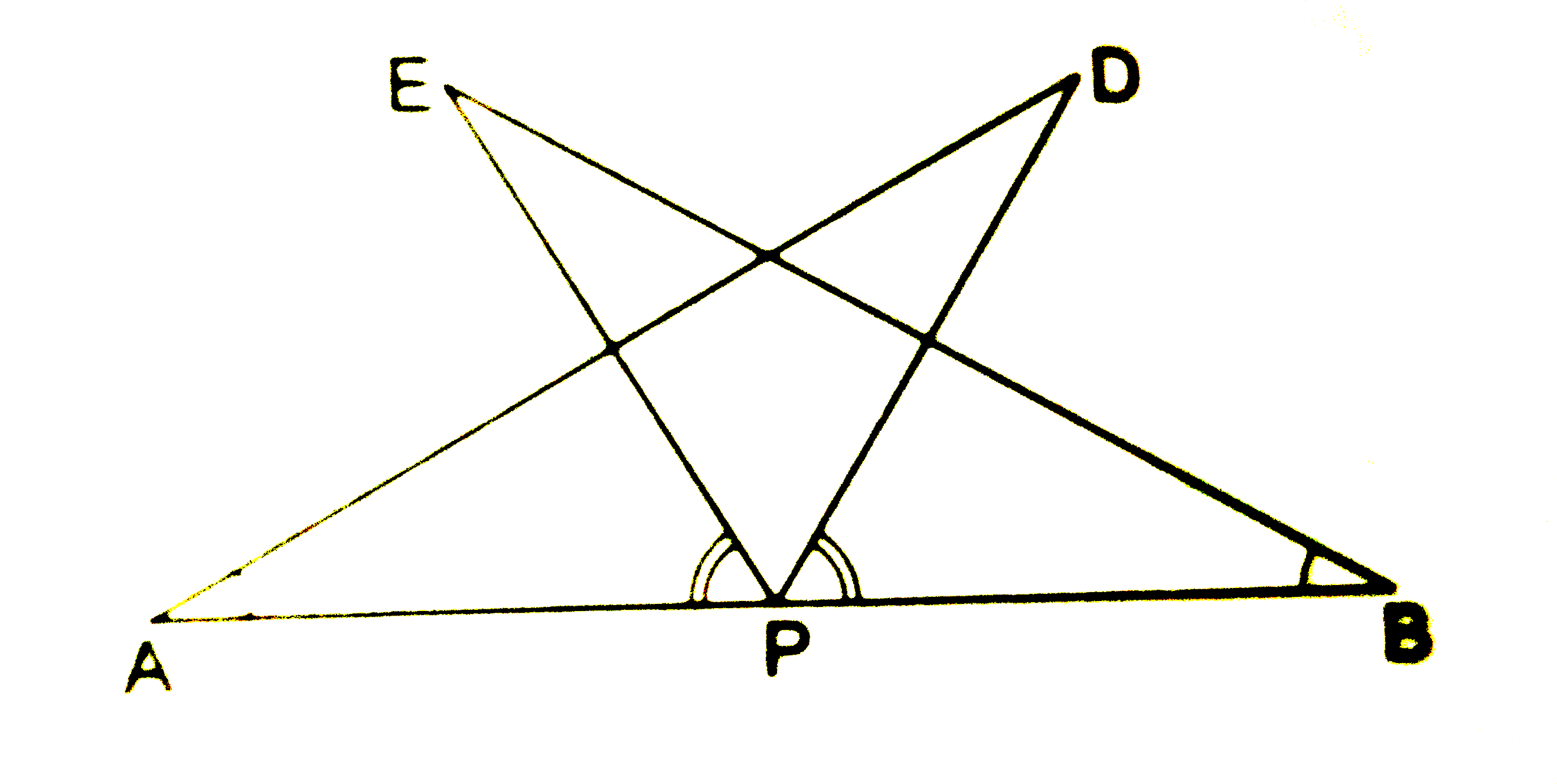
View SolutionP is a point equidistant from two lines l and m intersecting at a point A, as shown in the given figure. Show that the line AP bisects tha angle between them.
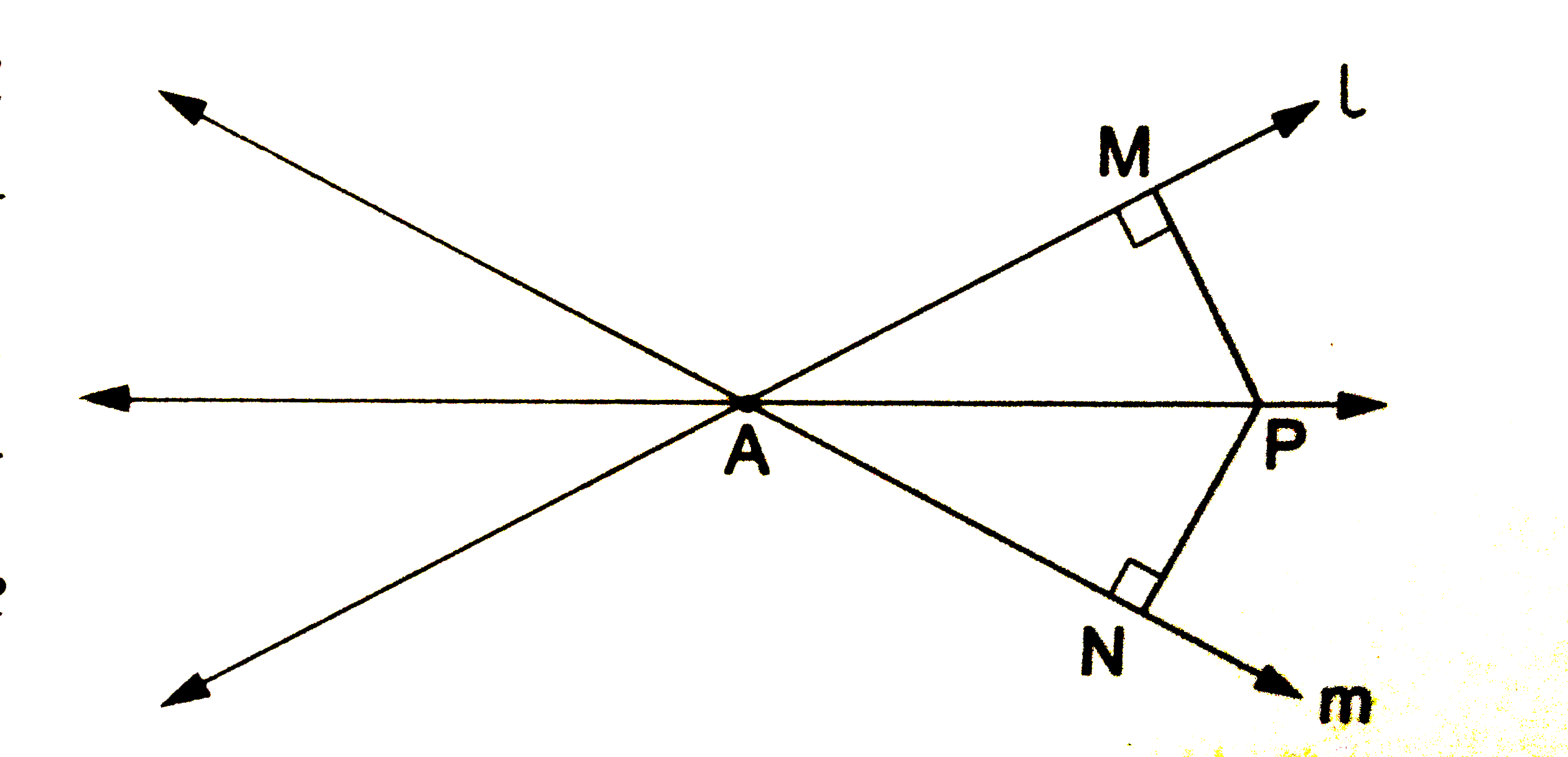
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
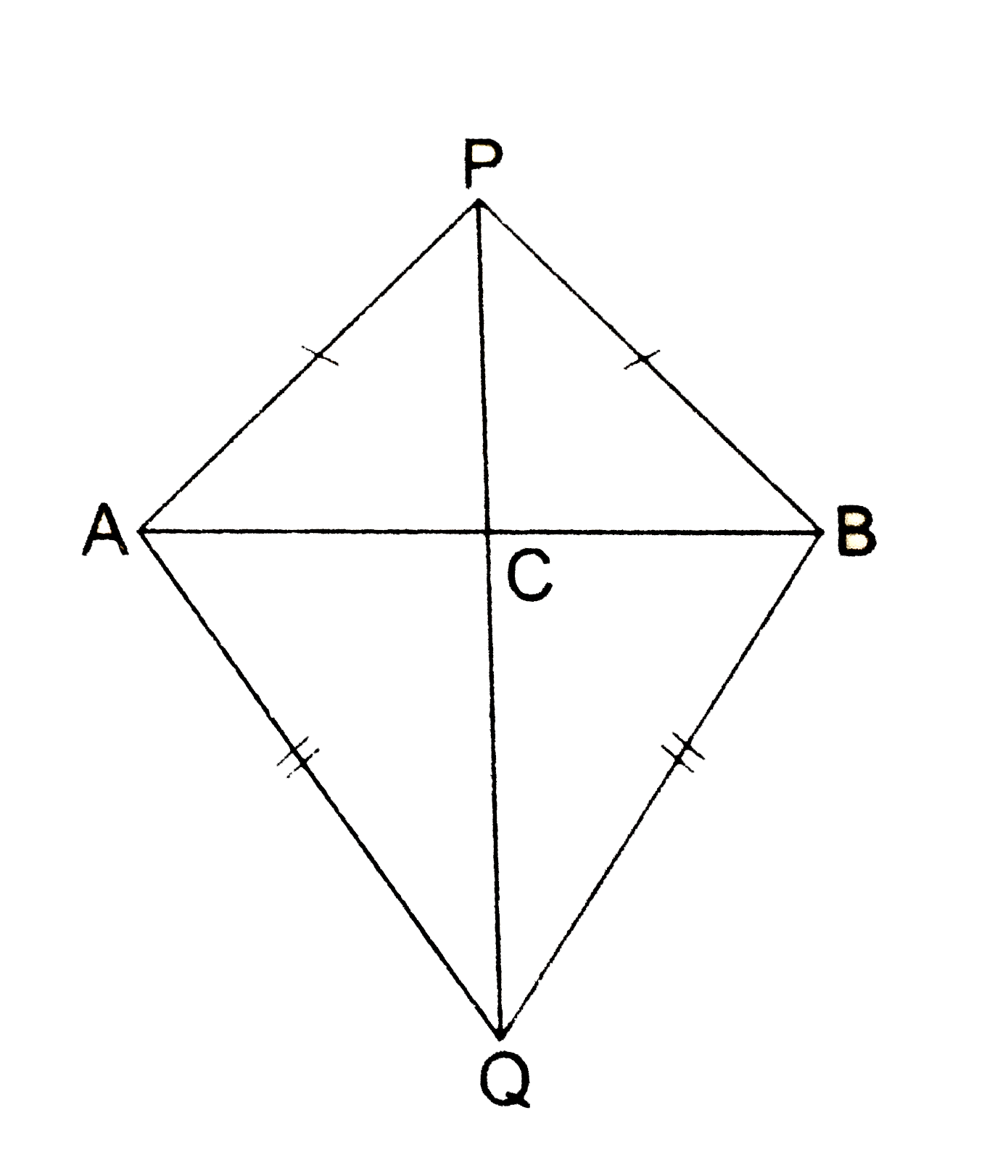
View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and `angleDAB=angleCBA.`
Prove that (i) `DeltaABD~=DeltaBAC,`
(ii) BD = AC,
(iii) `angleABD=angleBAC.`

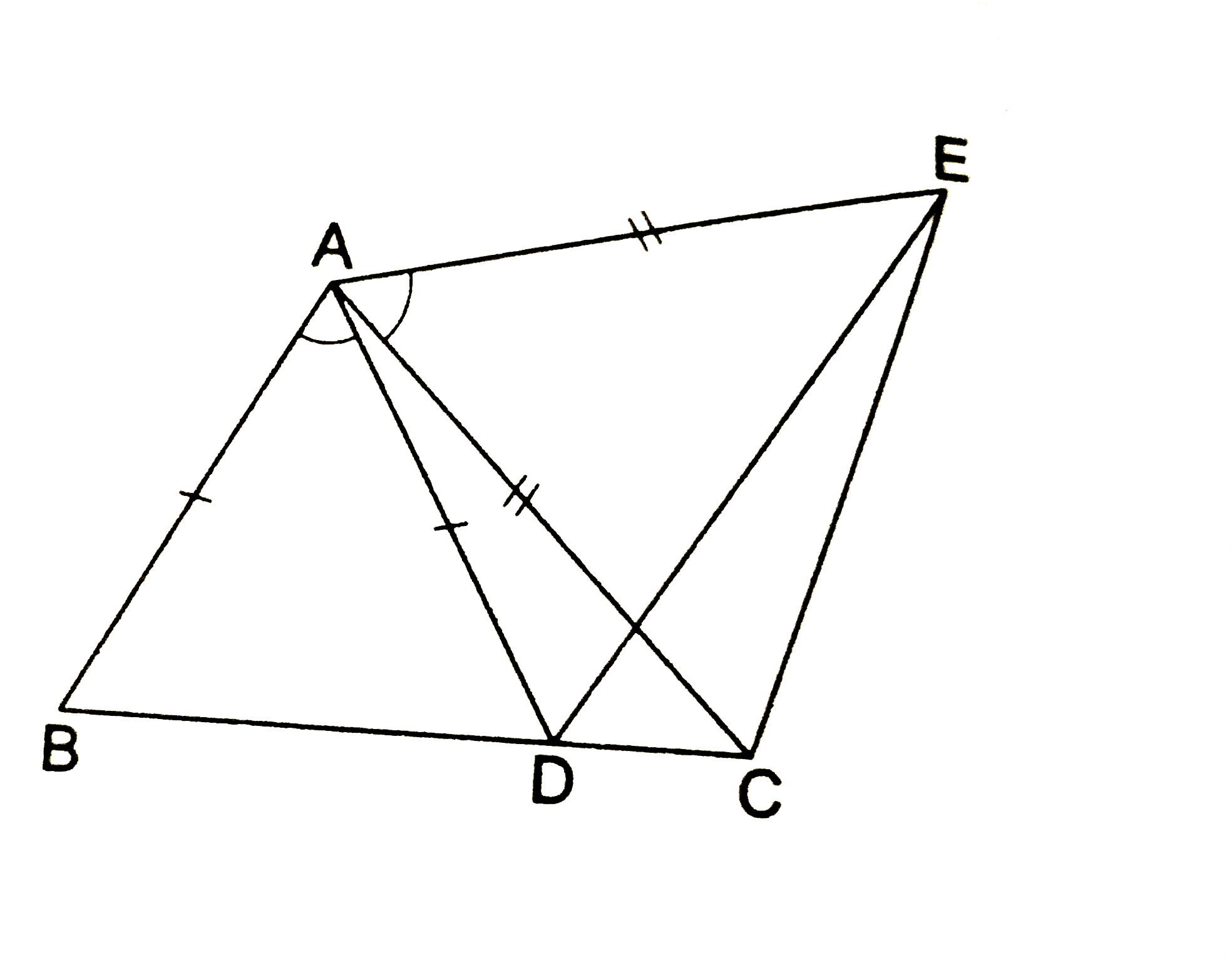
View SolutionIn the given figure, `AB=AD` in `DeltaABD and AC=AE` in `DeltaACE and angleBAD=angleEAC`. Show that `BC = DE`.
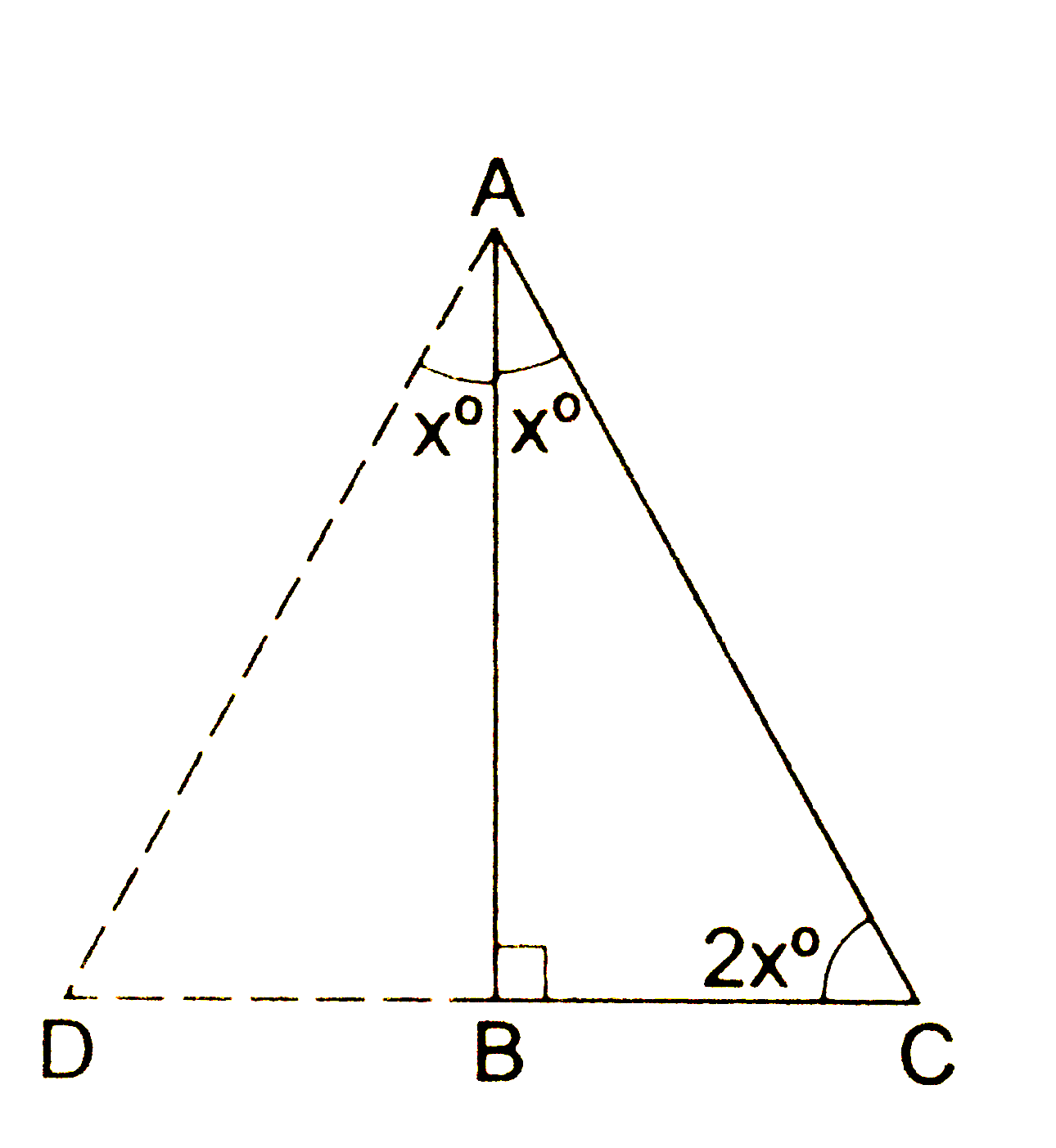
View SolutionIn the given figure, `DeltaABC` is right angled at B such that `angleBCA=2angleBAC.` Show that hypotenuse AC = 2BC.
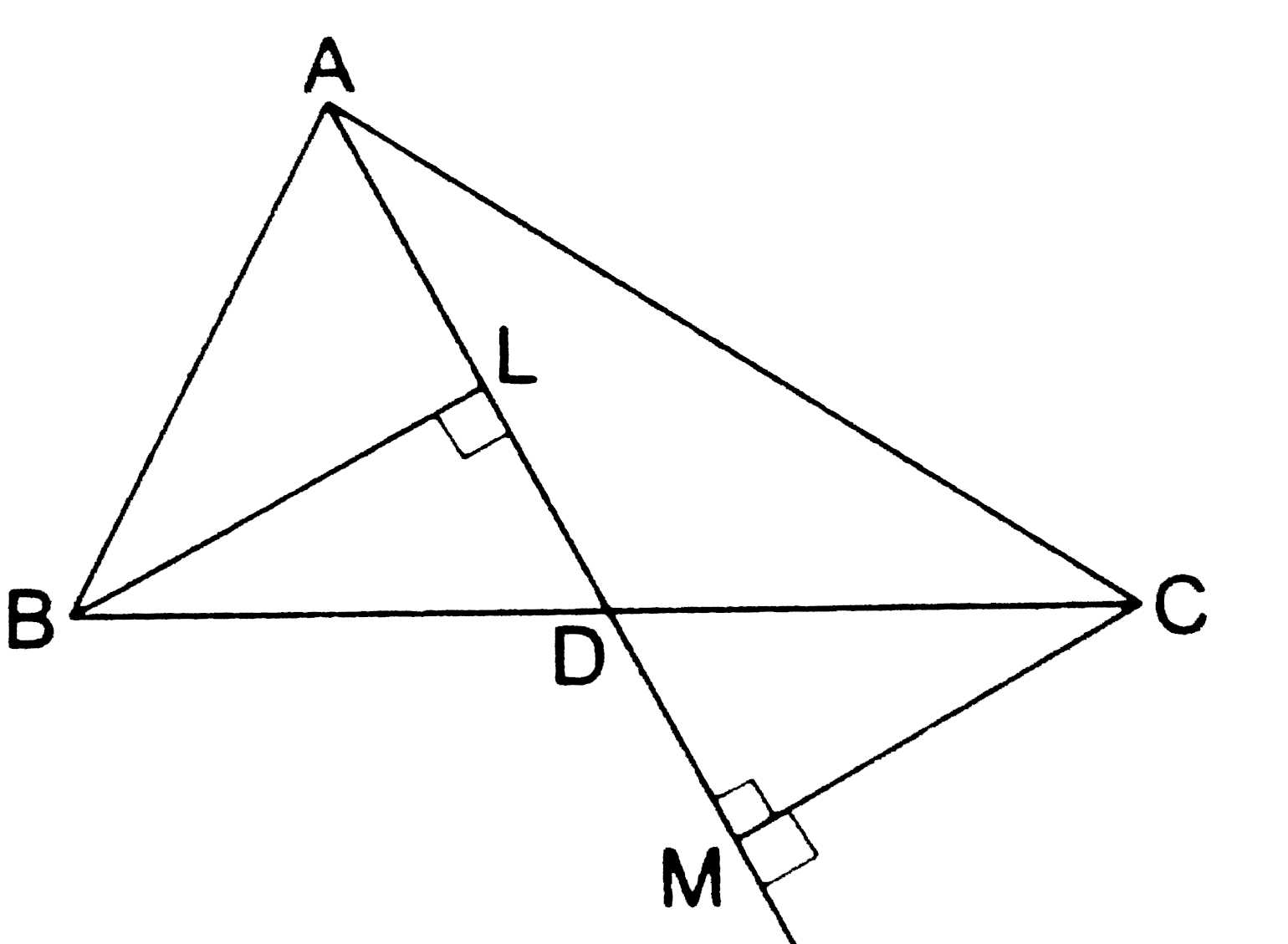
View SolutionIn the adjoining figure, AD is a median of `DeltaABC.` If BL and CM are drawn perpendiculars on AD and AD produced, prove that BL = CM.
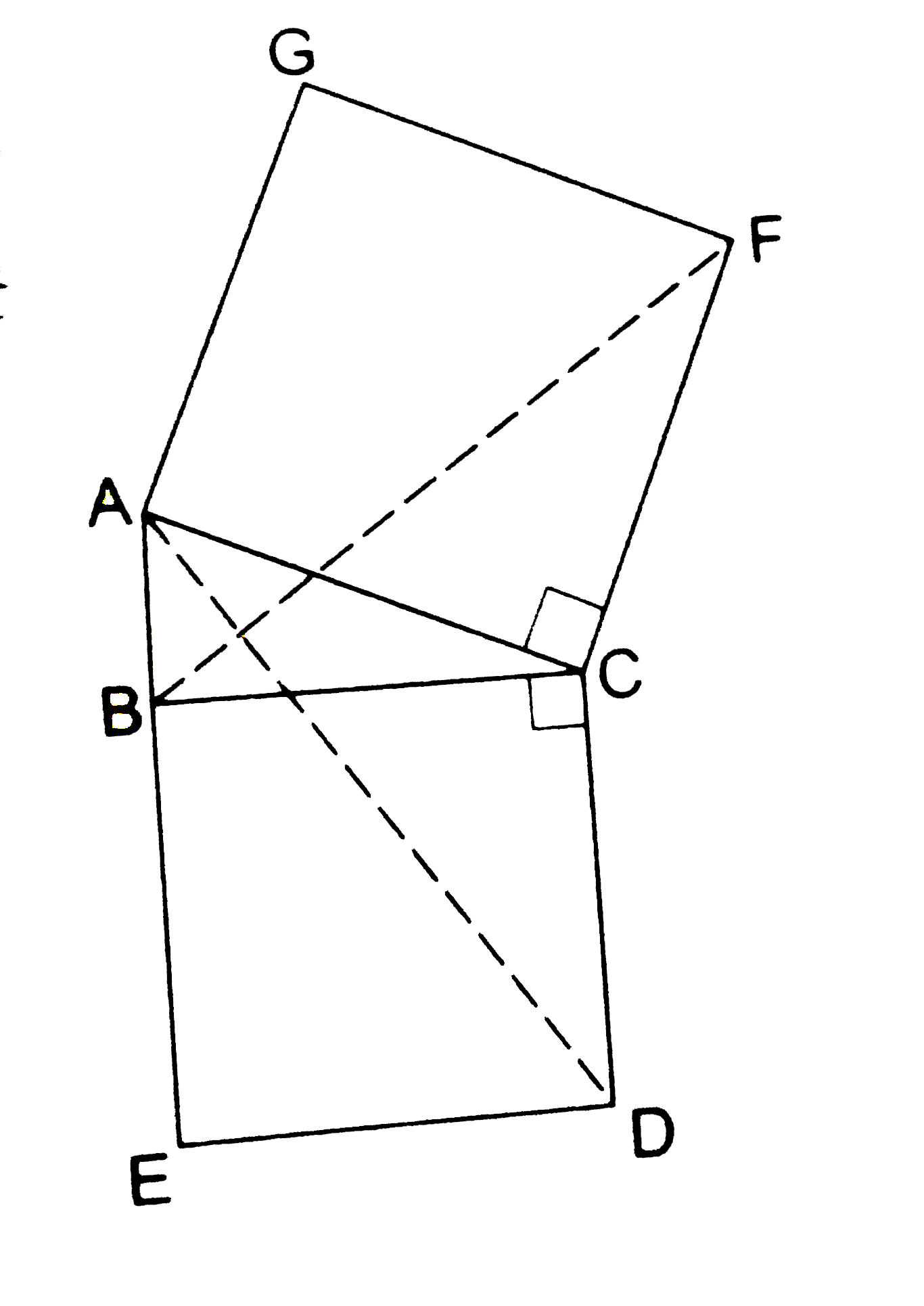
View SolutionIn the given figure, ABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = FB.
View SolutionIn the given figure, ABCD is a square, M is the midpoint of AB and `PQ_|_CM` meets AD at P and CB produced at Q. Prove that (i) PA = QB and (ii) `CP=AB+PA.`
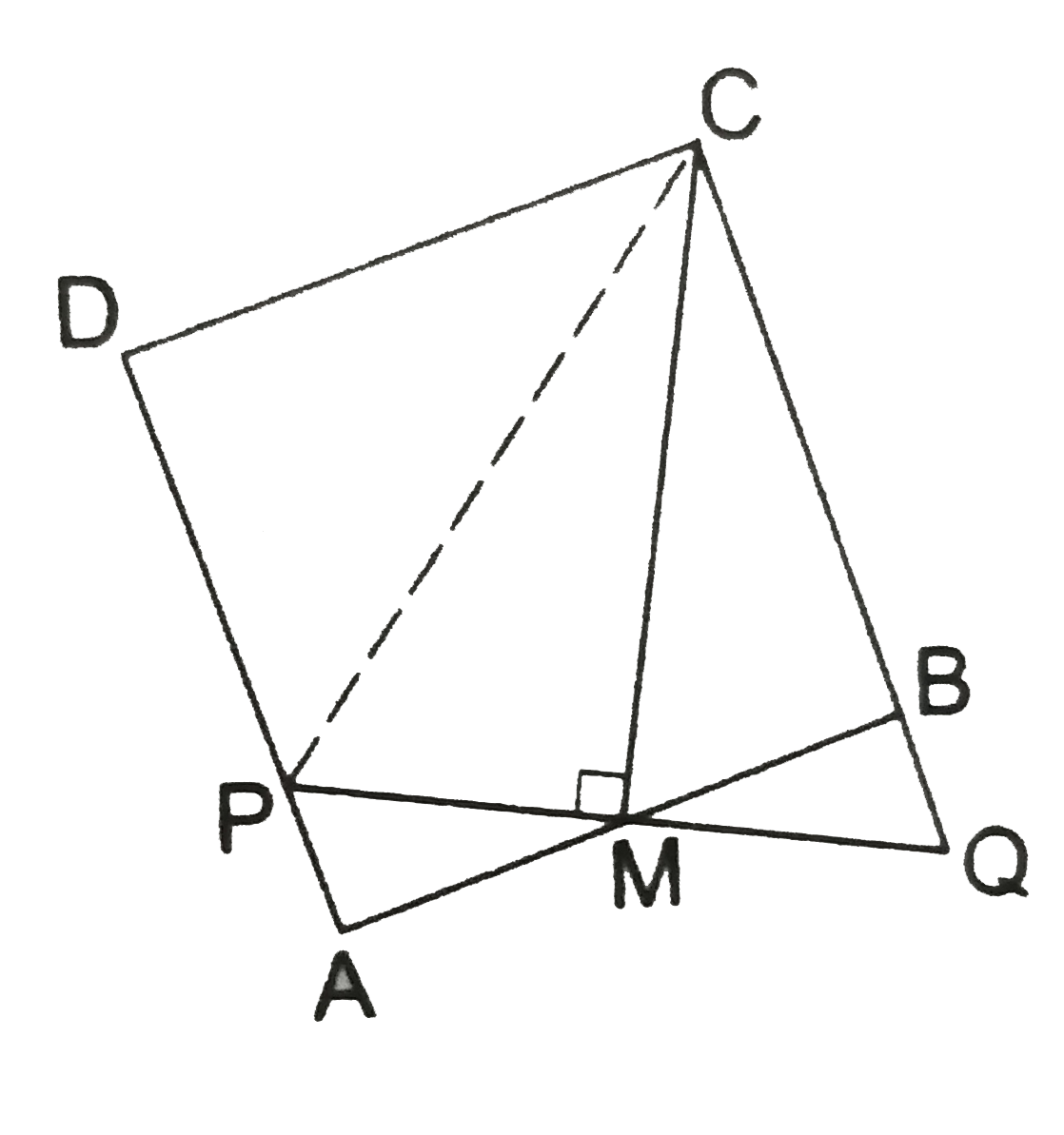
View SolutionIn the given figure, the two sides AB and BC, and the median AD of `DeltaABC` are correspondingly equal to the two sides PQ and QR, and the medium PM of `DeltaPQR`. Prove that `DeltaABC~=DeltaPQR.`
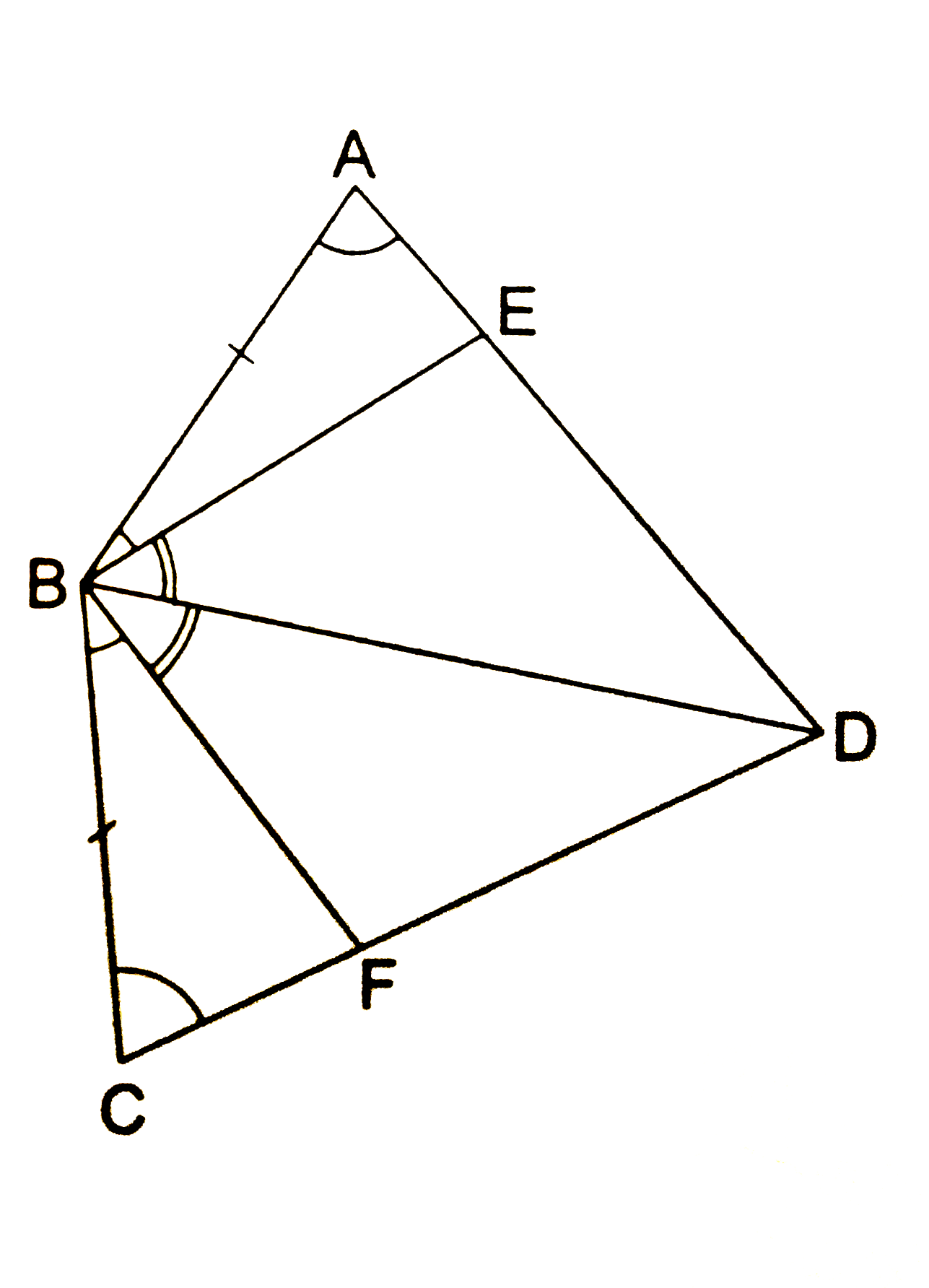
View SolutionIn the given figure, the bisectors of `angleB and angleC` of `DeltaABC` meet at `I`. If `IP _|_ BC,`` IQ _|_ CA` and `IR _|_ AB,` prove that (i) `IP = IQ = IR`, (ii) `IA` bisects `angleA`.
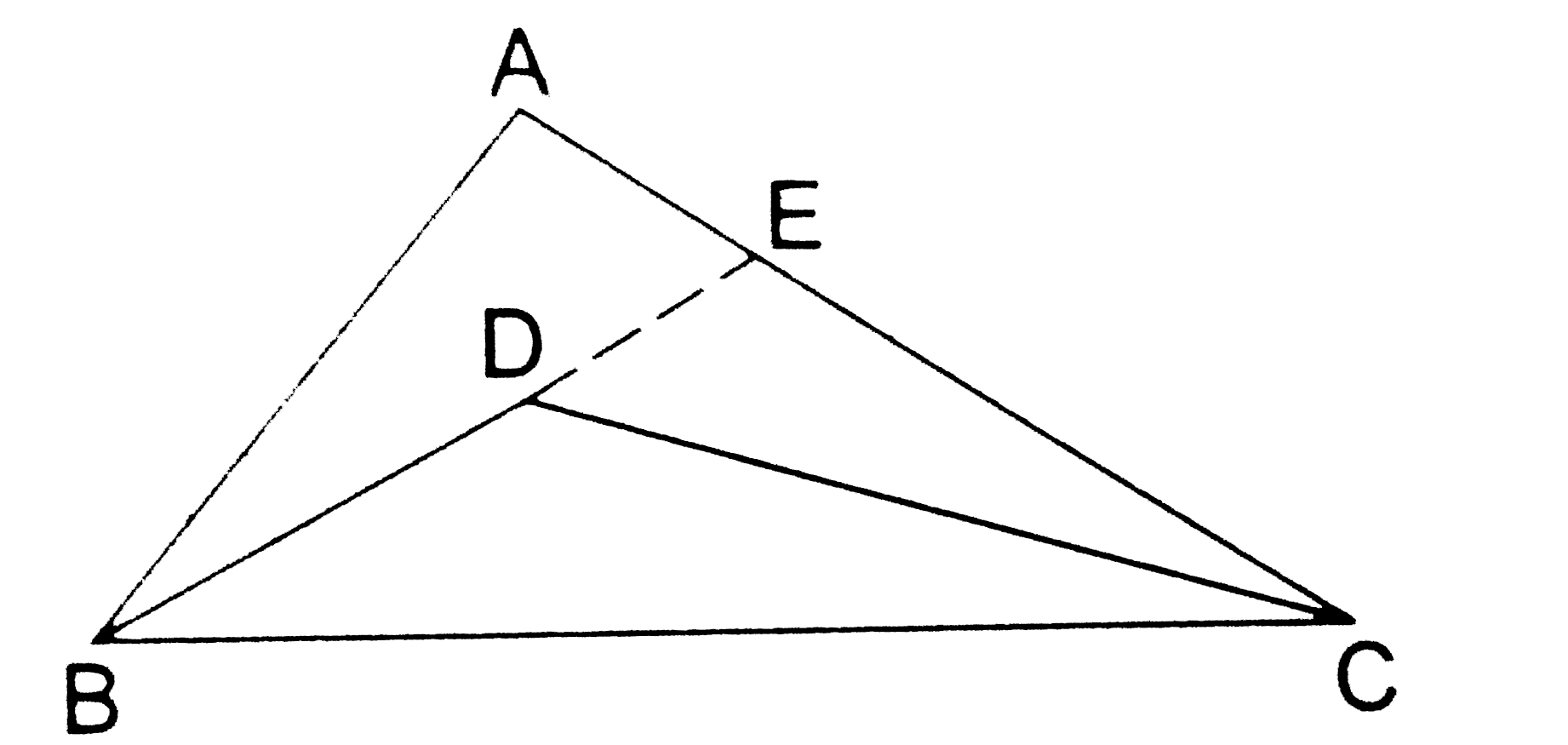
View SolutionIn the given figure, ABCD is a quadrilateral and E and F are points on AD and CD respectively such that AB = CB, `angleABE=angleCBF and angleEBD=angleFBD.` Prove that `BE=BF.`
View SolutionIn a `DeltaABC," if "angleA=40^(@) and angleB=60^(@)` then which side of the triangle is longest and which is shortest?
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionShow that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle.
View SolutionProve that the perimeter of a triangle is greater than the sum of its three medians.
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that `(BD+DC)lt(AB+AC).`
View SolutionIn the given figure, `AP_|_QR, PR gt PQ and PQ=PS`. Show that `ARgt AQ`.

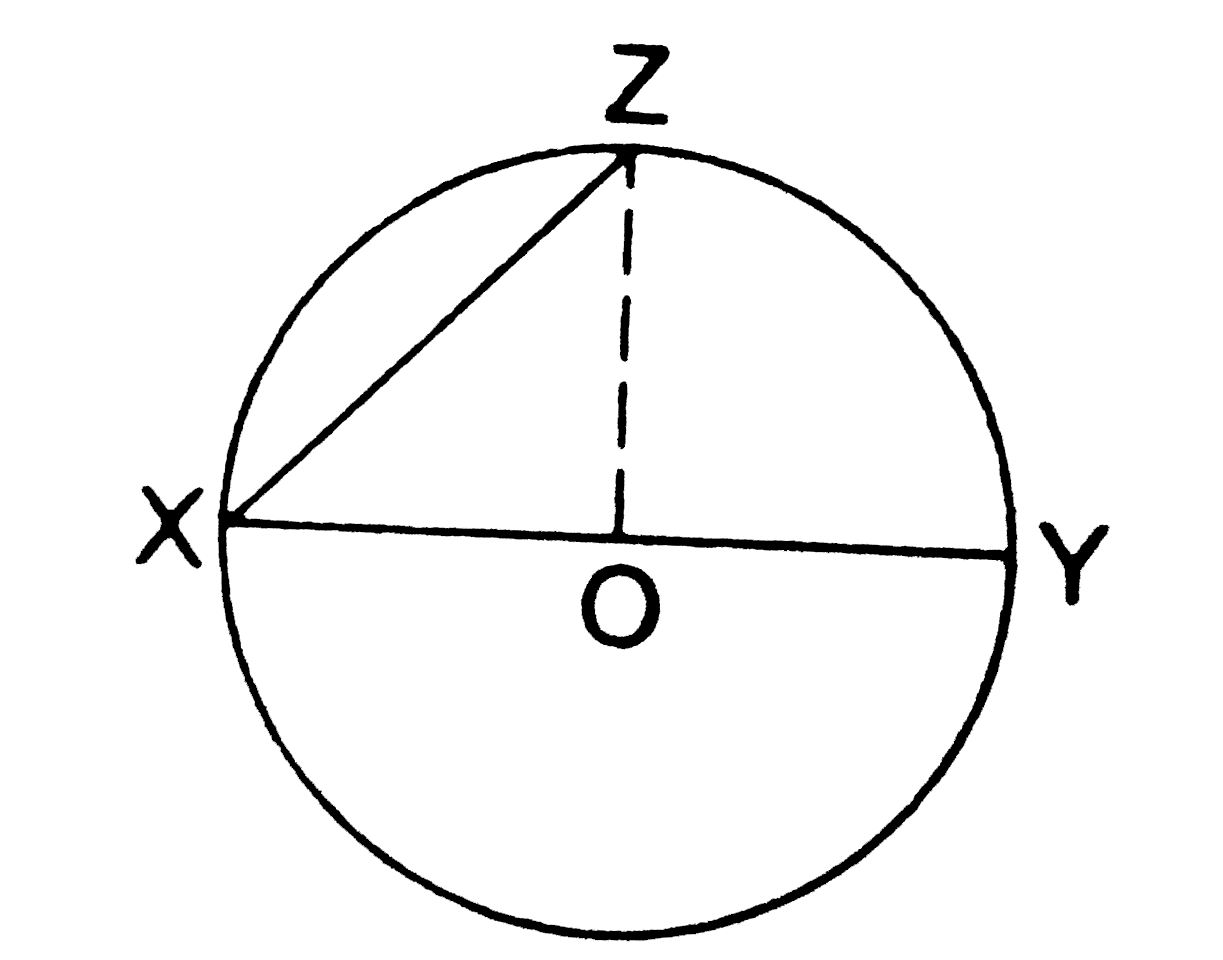
View SolutionIn the given figure, O is the centre of the circle and XOY is a diameter. If XZ is any other chord, show that XY gt XZ.
View SolutionIn `DeltaABC,` if D is any point on the side BC, show that `(AB+BC+AC)gt 2AD.`

View Solution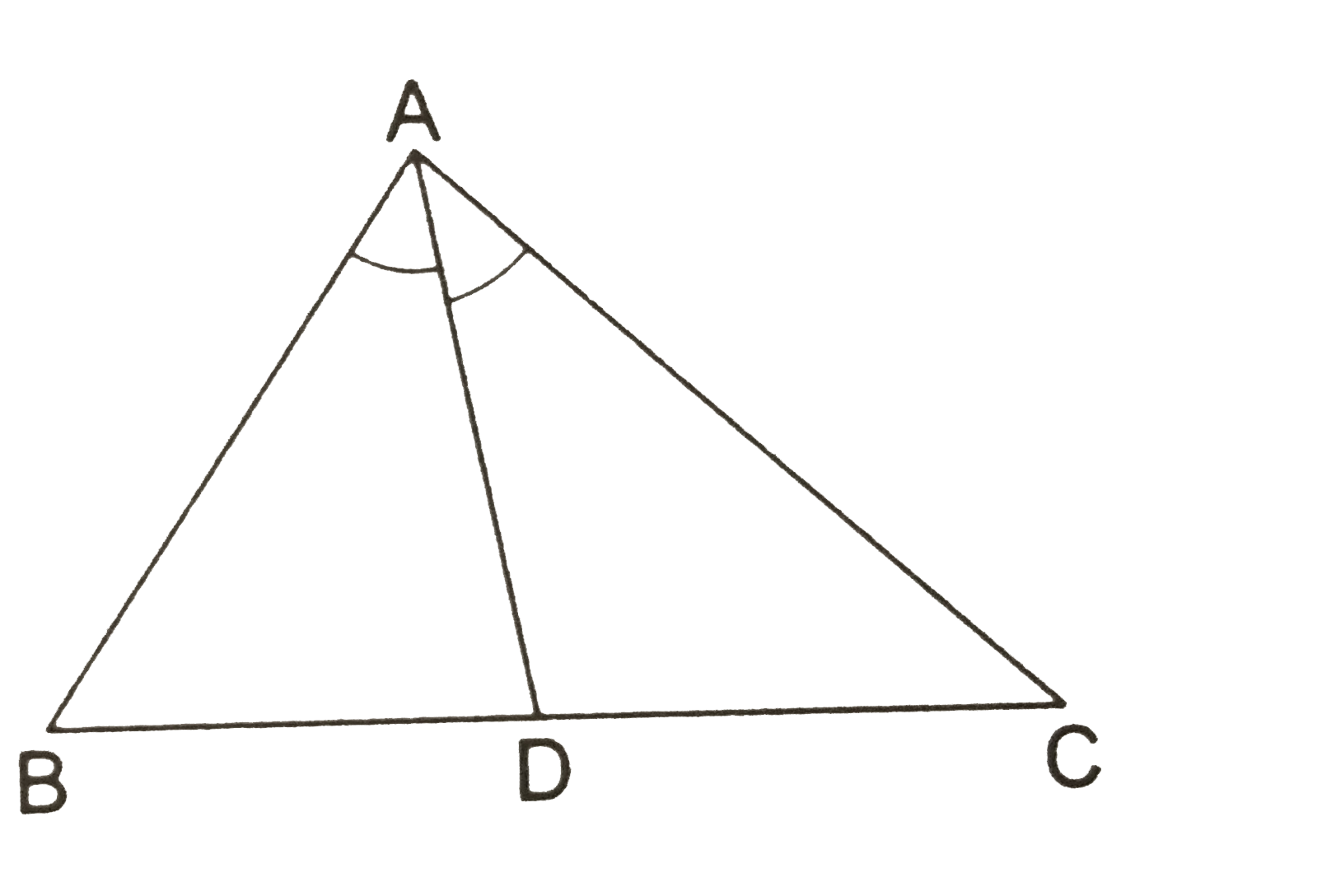
In `DeltaABC`, if AD is the bisector of `angleA,` show that `ABgtBD` and `ACgtDC`.
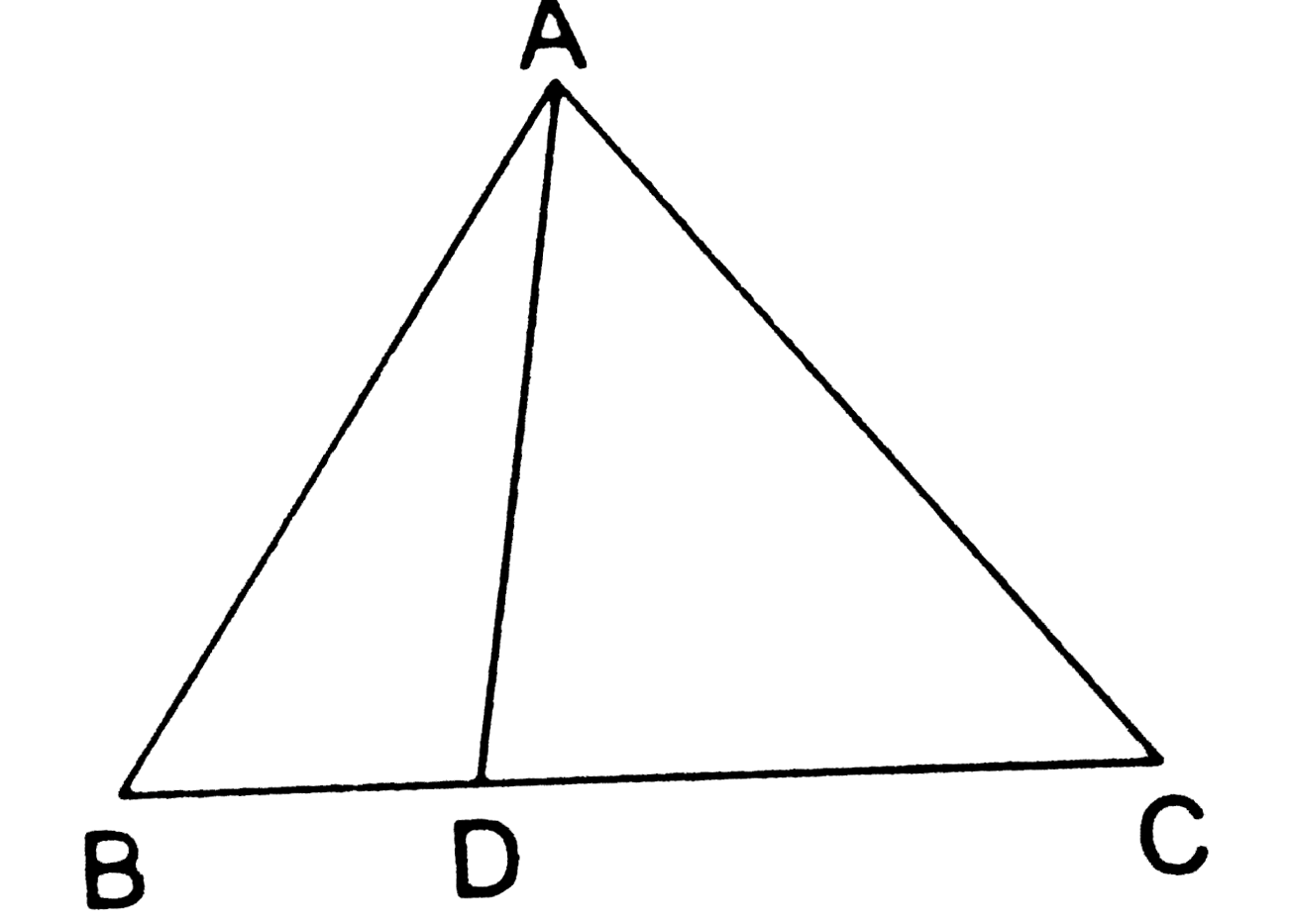
View SolutionIn the given figure, `ABgtAC.` If D is any point on BC, show that `ABgtAD`.
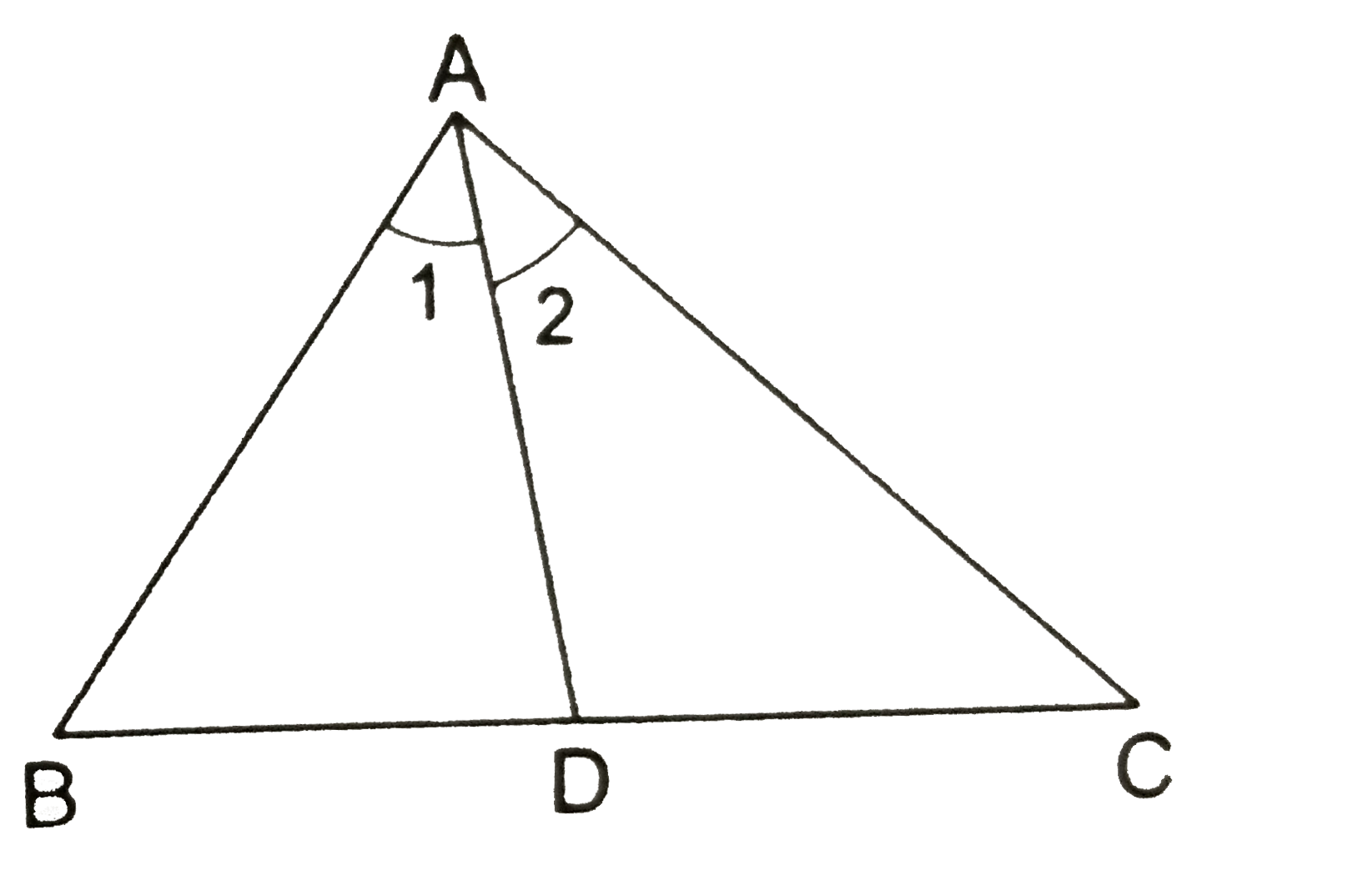
View SolutionIn the given figure, `ACgtAB` and AD is the bisector of `angleA.` show that `angleADC gt angleADB`.
View SolutionIn the given figure, the sides AB and AC of `DeltaABC` have been extended to D and E respectively. If `xgty`, show that `ABgtAC`.

View SolutionIn the given figure, Q is a point on the side SR of `DeltaPSR` such that PQ = PR. Prove that `PS gt PQ.`
View Solution
Solved Examples questions and complete solutions for chapter CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE of RS AGGARWAL MATHS (HINGLISH) of Class 9