Complete Solutions to साधित उदाहरण of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| KC SINHA HINDI | साधित उदाहरण |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
कोष्टक में दिए गए सही शब्द से रक्त स्थानों को भरें
सभी वृत्त .................... होते है । [सर्वांगसम , समरूप ]
View Solutionकोष्टक में दिए गए सही शब्द से रक्त स्थानों को भरें
त्रिज्या 1,2 और 3 cm के वृत ........... है ।
View Solutionकोष्टक में दिए गए सही शब्द से रक्त स्थानों को भरें
5cm और 1cm भुजा वाले दो वर्ग .............. है । [सर्वांगसम , समरूप ]
View Solutionसमरूप आकृतियों के लिए कोष्टक में दिए गए सही शब्द से रिक्त स्थानों को भरें
सभी ............ त्रिभुज समरूप होते है । [समबाहु , समद्विबाहु ]
View Solutionसमरूप आकृत्तियों के लिए कोष्टक में दिए गए सही शब्द से रिक्त स्थानों को भरें
उनके संगत कोण ............ है । [समान , समानुपाती]
View Solutionकोष्टक में दिए गए उपयुक्त शब्द से रिक्त स्थानों को भरें ।
उनकी संगत भुजाएँ ............. है । [समान , समानुपाती]
View Solutionकोष्टक में दिए गए उपयुक्त शब्द से रिक्त स्थानों को भरें ।
सभी .............. त्रिभुज समरूप होते है । [ समकोण , समद्विबाहु , समबाहु ]
View Solutionबतायें कि निम्नाकित आकृति समरूप है या नहीं ।
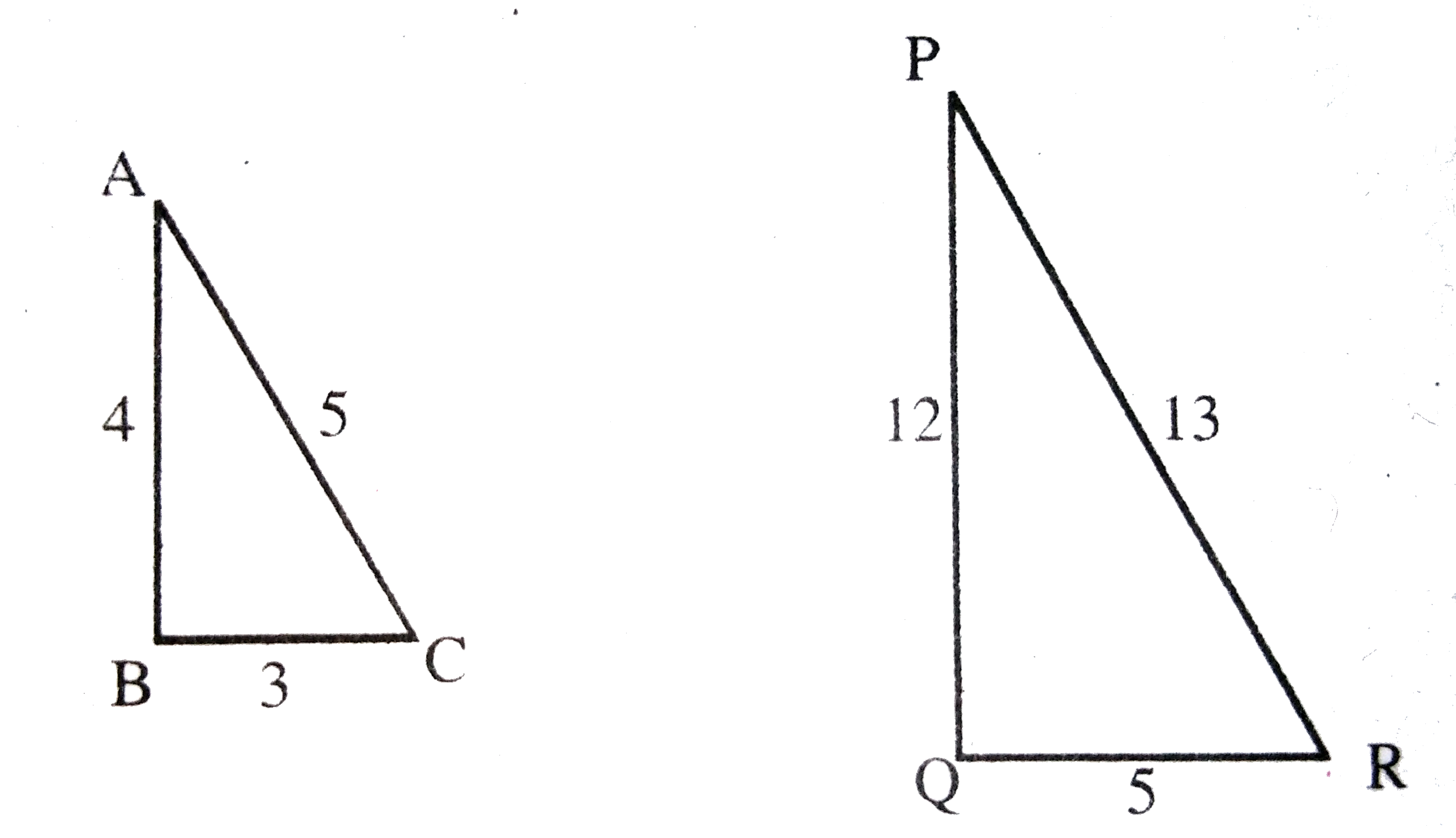
View Solutionबतायें कि निम्नाकित आकृति समरूप है या नहीं ।
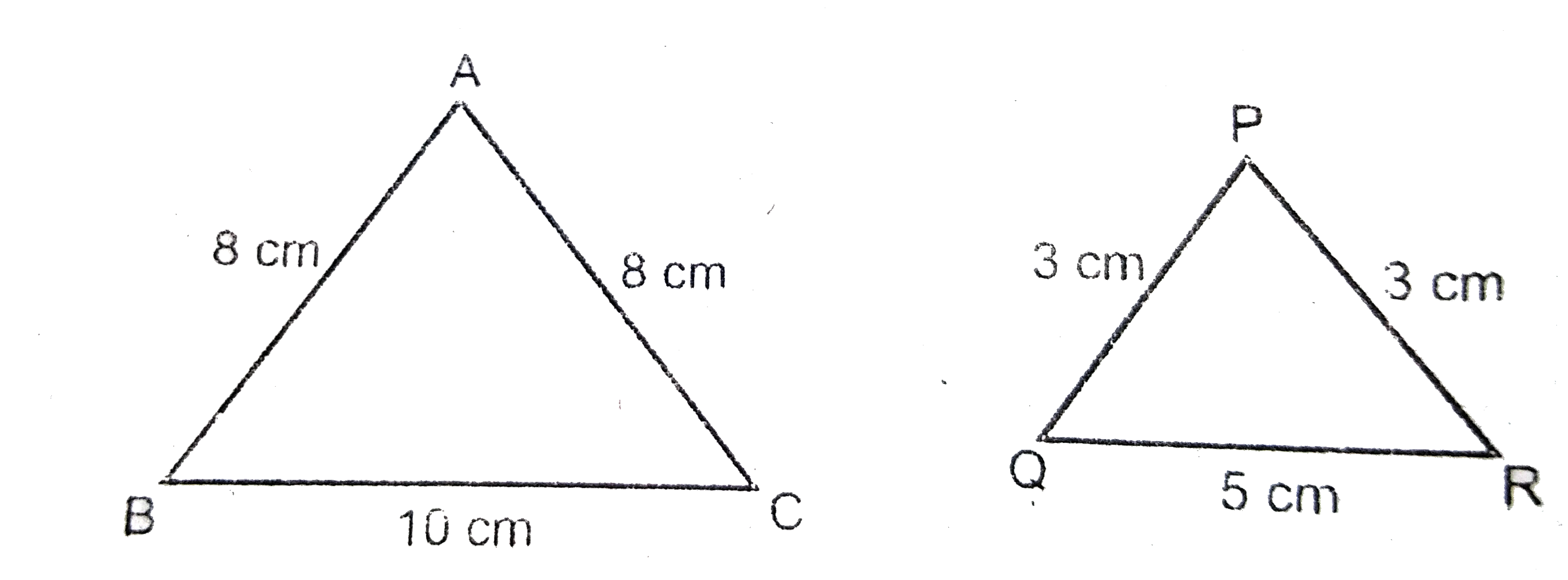
View Solutionबतायें कि निम्नाकित चतुर्भुज समरूप है या नहीं ।
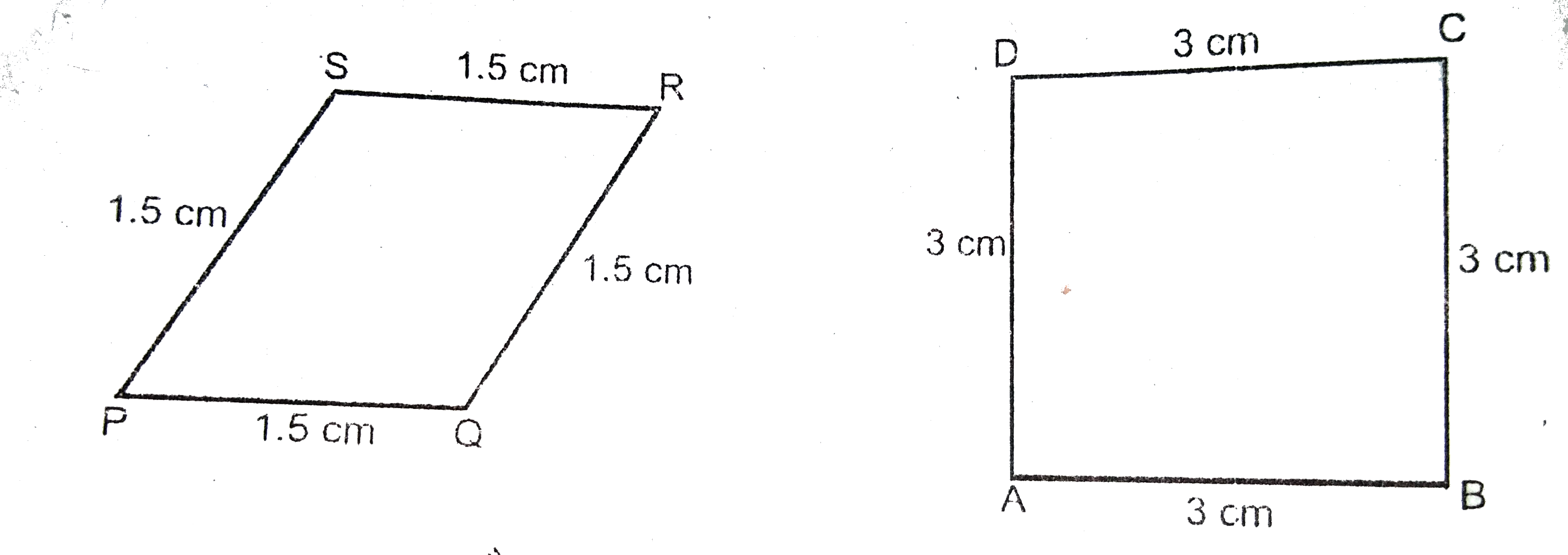
View Solutionदी गई आकृति में `DE` `||` `BC`, `AD=2cm`, `DB=2.5cm`, `AE=3.2cm`, तो `AC` ज्ञात करें।
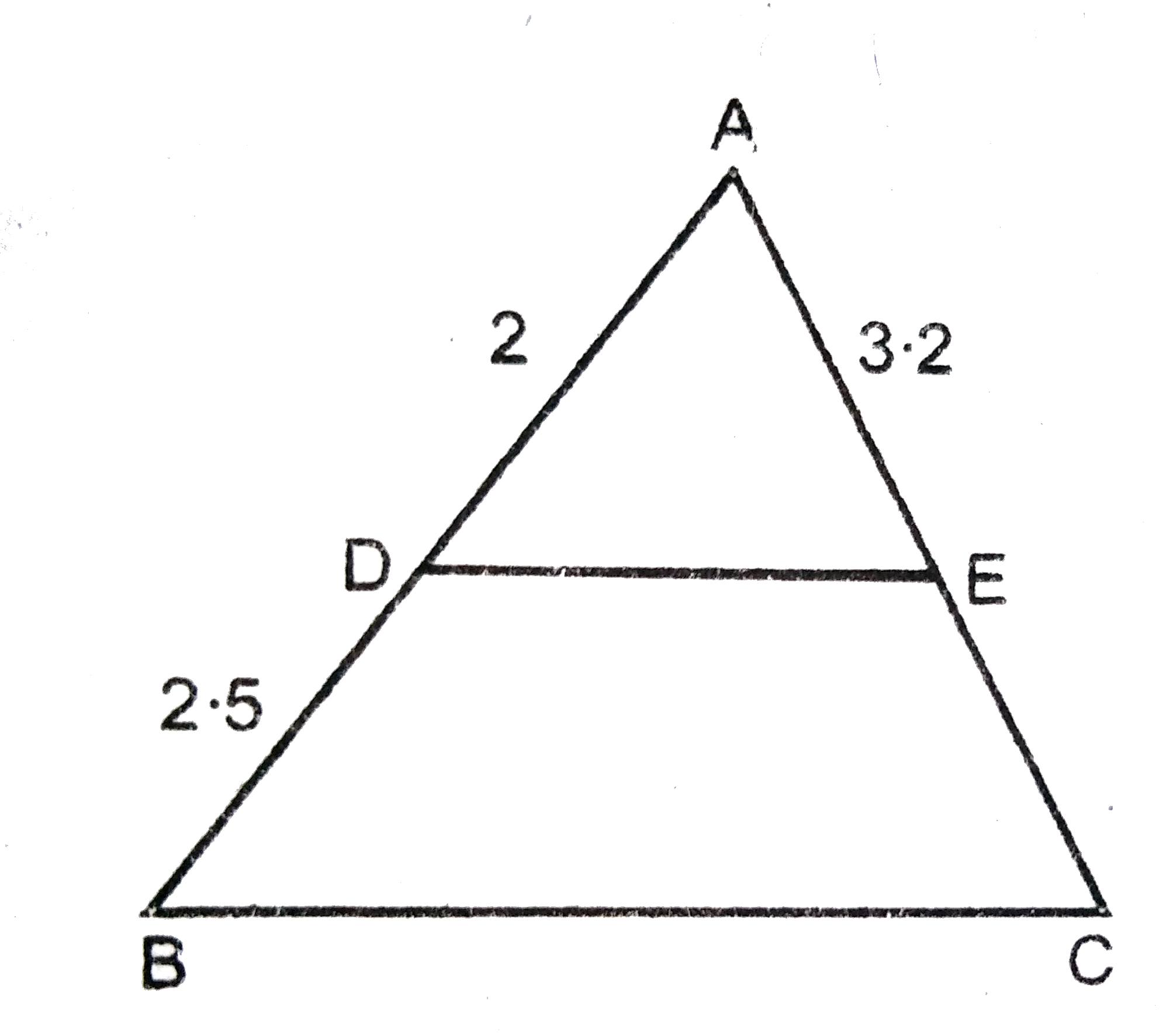
View Solutionदी गई आकृति में `DE||BC`, और `(AD)/(DB)=(3)/(5)`, यदि `AC=4.8cm`, तो AE ज्ञात करें ।
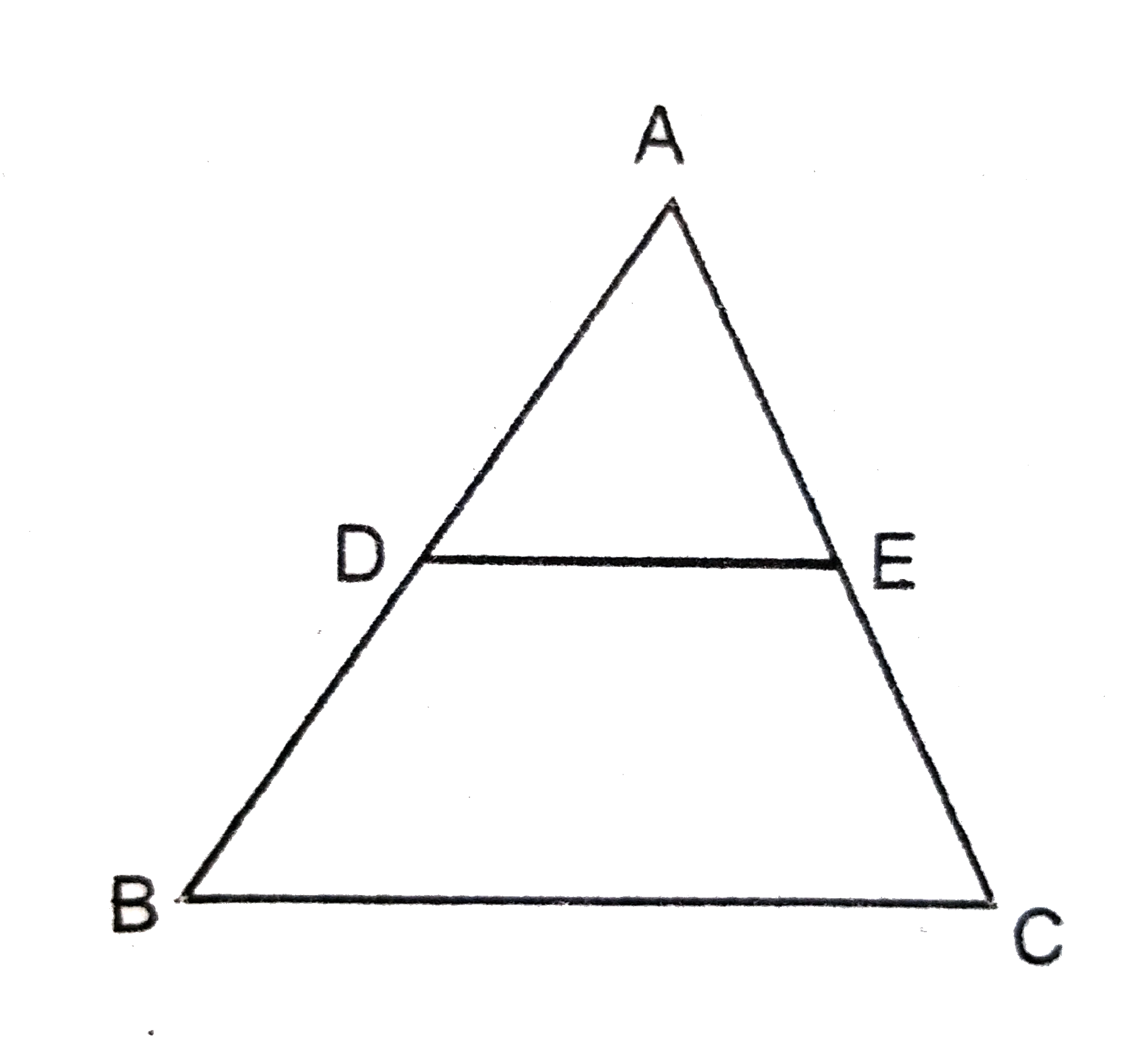
View Solutionदी गई आकृति में यदि `DE||BC` और `AD=4x-3,AE=8x-7,BD=3X-1` और `CE=5X-3` तो x का मान ज्ञात करें ।
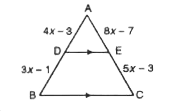
View Solutionसिद्ध करें कि किसी त्रिभुज की एक भुजा के मध्यबिन्दु से दूसरे भुजा के समान्तर खींची गई रेखा तीसरी भुजा को समद्विभाग करती है ।
View Solutionदी गई आकृति में यदि `LM||CB` और `LN||CD`, तो सिद्ध करें कि
`(AM)/(AB)=(AN)/(AD)`
View SolutionABCD एक समलम्ब चतुर्भुज है जिसमे `AB||DC` और इसके विकर्ण एक - दूसरे को O पर प्रतिच्छेद करते है । दिखायें कि `(AO)/(BO)=(CO)/(DO)`
View Solutionदिए गए चित्र में AB समानांतर है CD के । यदि `OA=3X-19,OB=x-4,OC=X-3` और `OD=4`, तो x ज्ञात करें ।
View SolutionABCD एक समलम्ब चतुर्भुज है जिसमे `AB||DC`. E और F क्रमशः असमान्तर भुजाओं AD और BC पर दो बिन्दु है । इस प्रकार `EF||AB`. दिखाये `(AE)/(ED)=(BF)/(FC)`.
View Solutionदिये गये चित्र में `DE||AC` और `DF||AE`. सिद्ध करें कि `(BF)/(FE)=(BE)/(EC)` .
View Solutionदिये गये चित्र में यदि `AB||DE` और `BD||EF`, तो सिद्ध करें कि `DC^2=CF.AC`.
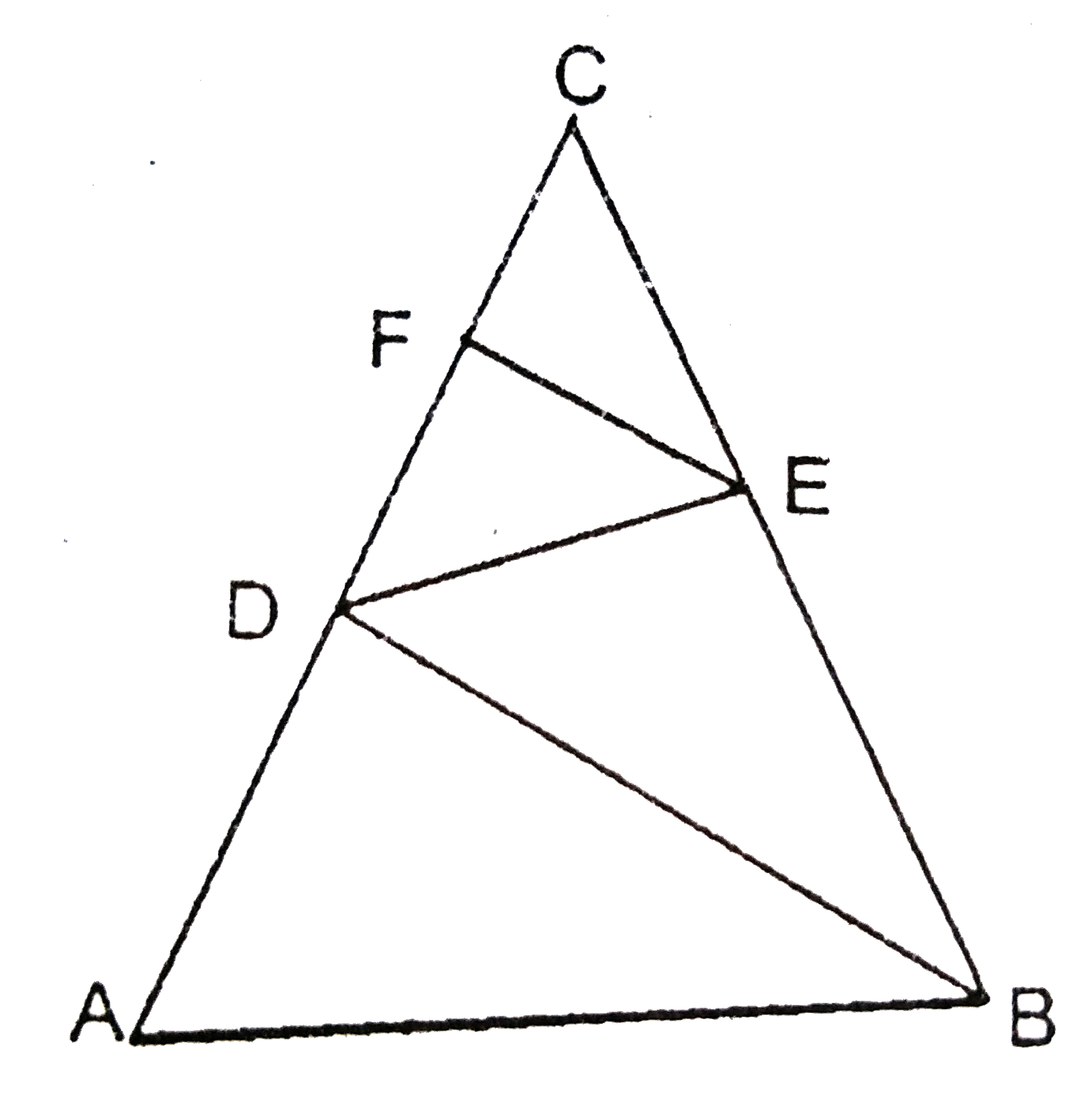
View Solution`Delta DEF` में कोई बिन्दु X है जिसे शीर्ष D,E तथा F से मिलाया गया है । DX पर कोई बिन्दु P लेकर , `PQ||DE` खींचा गया है , जो XE से Q पर मिलती है तथा Q से `QR||EF` जो XF से R पर मिलती है । सिद्ध करें कि `PR||DF`.
View Solutionयदि तीन या तीन से अधिक समांतर रेखाओं को तिर्यक रेखाएँ भिन्न - भिन्न बिन्दुओं पर प्रतिच्छेद करें तो इन रेखाओं द्वारा तिर्यक रेखाओं पर बने अतः खंड समानुपाती होते है ।
View Solution`Delta PQR` की भुजाओं PQ और PR पर क्रमशः E और F बिंदुएँ निम्नलिखित स्थितियों में है प्रत्येक के लिए बतायें कि `EF||QR` है या नहीं ।
(i) `PE=3.9cm, EQ=3cm, PF=3.6cm` और `FR=2.4cm`
(ii) `PE=4cm, QE=4.5cm,PF=8cm`, और `RF=9cm`
(iii) `PQ=1.28cm,PR=2.56cm,PE=0.18cm` और `PF=0.36cm`
View Solutionसिद्ध करें कि त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को मिलनेवाली रेखा , तीसरी भुजा के समान्तर होती है ।
View Solutionदिये गये चित्र में `DE||OQ` और `DF||OR`. दिखाये कि `EF||QR`.
View Solutionचतुर्भुज ABCD के विकर्ण एक - दूसरे को बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि `(AO)/(BO)=(CO)/(DO)`. दिखाएँ कि ABCD एक समलम्ब चतुर्भुज है ।
View Solutionदिये गये चित्र में `(PS)/(SQ)=(PT)/(TR)` और `angle PST=angle PRQ` प्रमाणित करें कि PQR एक समद्विबाहु त्रिभुज है ।
View Solution`Delta ABC` में, `AD angle BAC` का समद्विभाजक है । जो BC से D पर मिलती है, तो सिद्ध करें कि `(ar(Delta ABD))/(ar(Delta ACD))``=(AB)/(AC)`
View Solution`Delta ABC` में, AD एक माध्यिका है । `angleADB` और `angleADC` के समद्विभाजक क्रमशः AB एवं AC से E एवं F बिन्दु पर मिलते है । सिद्ध कीजिए कि `EF||BC` है ।
View Solutionबताएँ कि निम्नांकित त्रिभुजों में कौन - कौन समरूप है । प्रश्न के उत्तर के लिए आपके द्वारा प्रयुक्त समरूपता कसौटियों को भी लिखे । साथ ही साथ समरूप त्रिभुज युग्म को सांकेतिक रूप में लिखें ।
(i)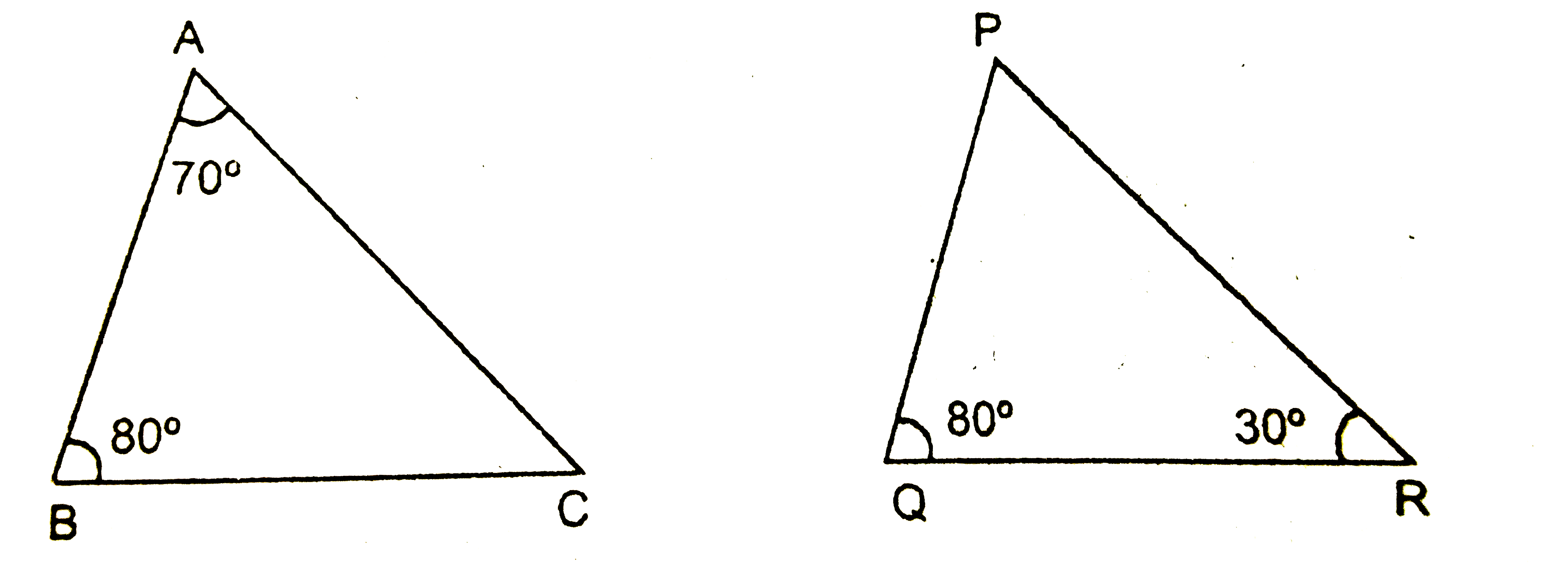
View Solutionबताएँ कि निम्नांकित त्रिभुजों में कौन - कौन समरूप है । प्रश्न के उत्तर के लिए आपके द्वारा प्रयुक्त समरूपता कसौटियों को भी लिखे । साथ ही साथ समरूप त्रिभुज युग्म को सांकेतिक रूप में लिखें ।
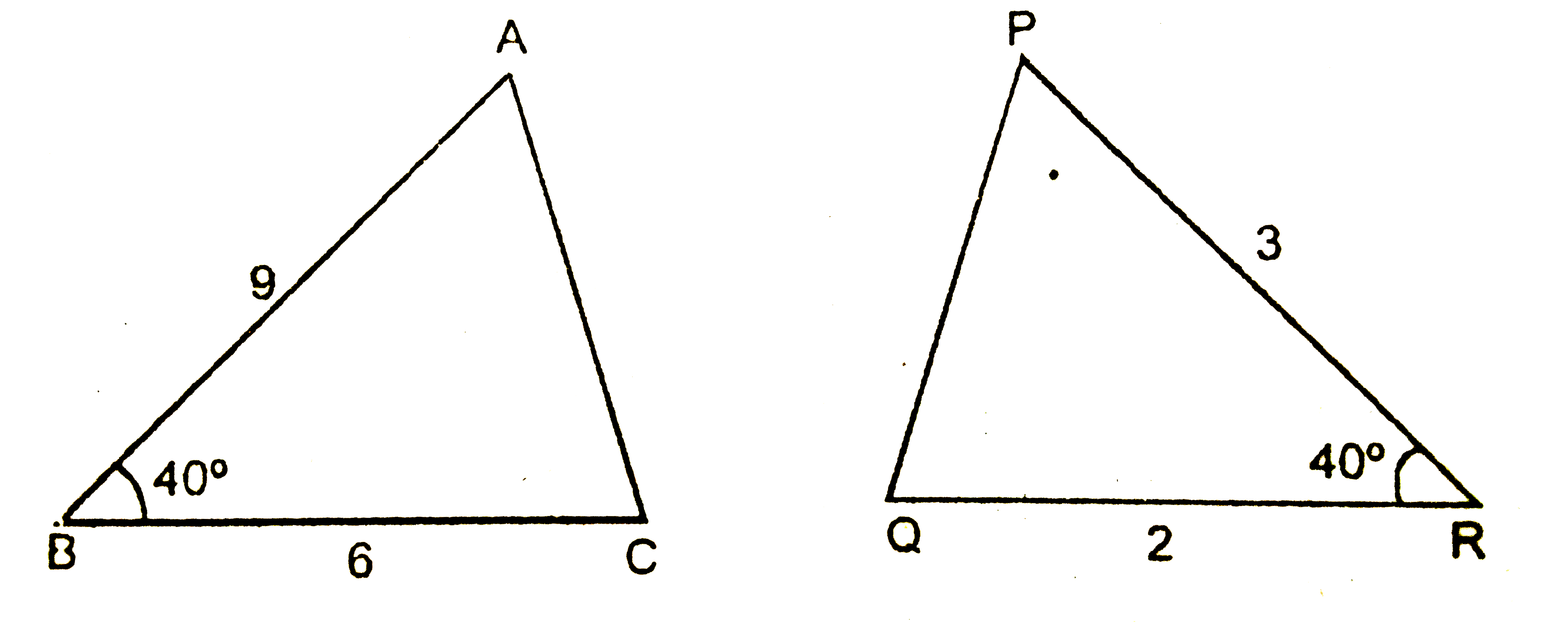
View Solutionबताएँ कि निम्नांकित त्रिभुजों में कौन - कौन समरूप है । प्रश्न के उत्तर के लिए आपके द्वारा प्रयुक्त समरूपता कसौटियों को भी लिखे । साथ ही साथ समरूप त्रिभुज युग्म को सांकेतिक रूप में लिखें ।

View Solutionबताएँ कि निम्नांकित त्रिभुजों में कौन - कौन समरूप है । प्रश्न के उत्तर के लिए आपके द्वारा प्रयुक्त समरूपता कसौटियों को भी लिखे । साथ ही साथ समरूप त्रिभुज युग्म को सांकेतिक रूप में लिखें ।
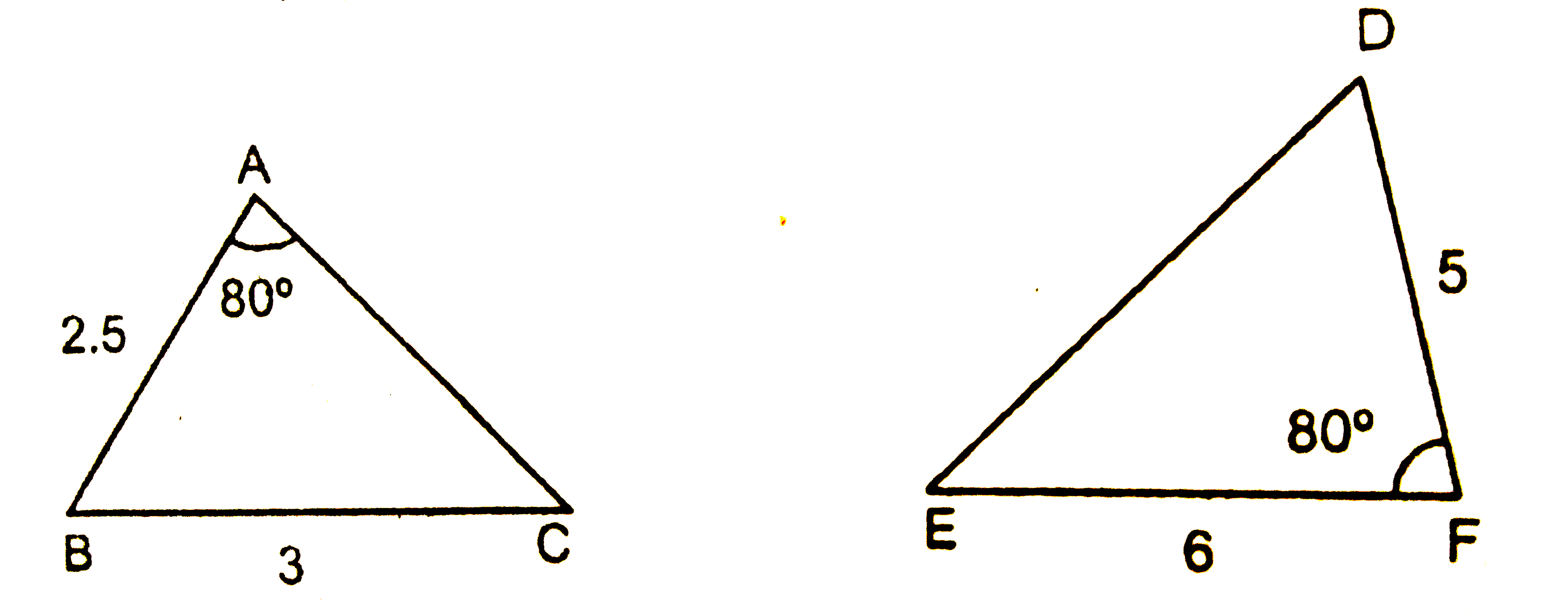
View Solutionबताएँ कि निम्नांकित त्रिभुजों में कौन - कौन समरूप है । प्रश्न के उत्तर के लिए आपके द्वारा प्रयुक्त समरूपता कसौटियों को भी लिखे । साथ ही साथ समरूप त्रिभुज युग्म को सांकेतिक रूप में लिखें ।
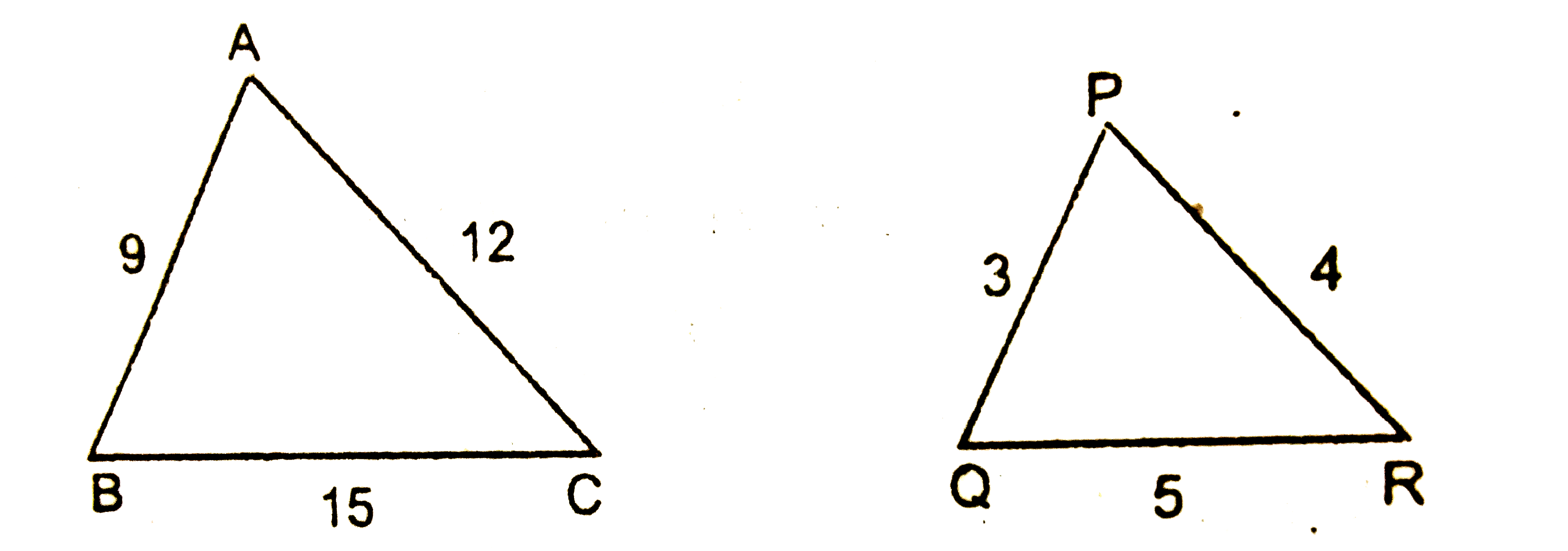
View Solutionदिए गए चित्र में `Delta ABC~Delta ADE,AD=5cm,AE=6cm,BC=12cm`तथा `AB=15cm`, तब EC और DE के मान ज्ञात करें ।
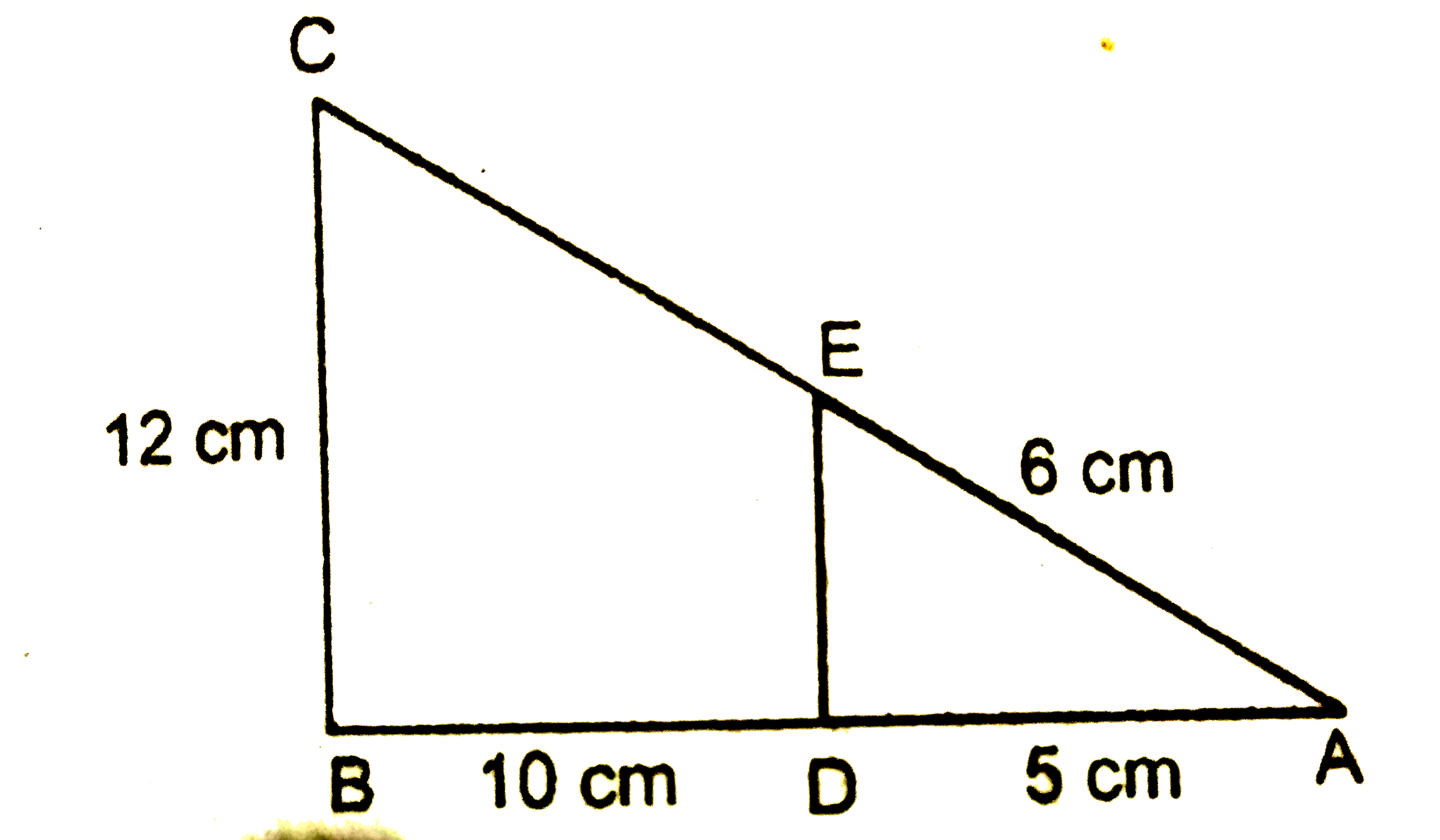
View Solutionदिए गए चित्र में `DeltaABO~DeltaDCO.CD=2cm,AB=3cm,OC=2.4cm` तथा `OD=3.2cm`, तो `OA` और `OB` की लम्बाई ज्ञात करें ।
View Solutionदिए गए चित्र में `DeltaODC~DeltaOBA,angle BOC=125^@` तथा `angleCDO=70^@.angle DOC ,angle DCO` और `angleOAB` को ज्ञात करें ।
View Solutionचित्र में `DeltaAOB~DeltaDOC` , सिद्ध करें कि `AB||CD`.
View Solutionसिद्ध करें कि दो समरूप त्रिभुजों की परिमाप उनकी भुजाओं के समानुपाती होती है ।
View Solutionदो समरूप त्रिभुजों के परिमाप क्रमशः 25cm और 15cm है । यदि पहले त्रिभुज की एक भुजा 9cm है । तो त्रिभुज की संगत भुजा ज्ञात करें ।
View Solutionयदि AD और PM `Delta ABC और Delta PQR` की क्रमशः मध्यिकाएँ है , और जहाँ `DeltaABC~DeltaPQR` सिद्ध करें कि
(i) `(AB)/(PQ) =(AD)/(PM)`
(ii) ` angle ADC = angle PMR `
View SolutionCD और GH क्रमशः `angle ACB` और `angleFGH` के अर्द्धक है इस प्रकार कि D और H क्रमशः `Delta ABC` और `DeltaFEH` की भुजाओं AB और EF पर स्थित है यदि `DeltaABC~DeltaFEG` तो दिखाएँ कि
(i)`(CD)/(GH)=(AC)/(FG)`
(ii) `DeltaDCB~DeltaHGE`
(iii) `Delta DCA~Delta HGF`
View Solution`Delta PQR` की भुजाएँ PR और QR पर S और T बिन्दुएँ इस प्रकार है , कि `angleP=angleRTS` दिखाये कि `Delta RPQ~Delta RTS`
View Solutionदिए गये चित्र में समद्विबाहु त्रिभुज ABC की भुजा CB के बढ़े भाग पर बिन्दु E इस प्रकार है कि `EFbotAC` है और `AB=AC` । यदि `AD bot BC` हो , तो सिद्ध कीजिए `Delta ABD~Delta ECF`.
View Solutionदिए गये चित्र में `(QR)/(QS)=(QT)/(PR)` और `angle1=angle2` दिखाएं कि `DeltaPQS~Delta TQR`.
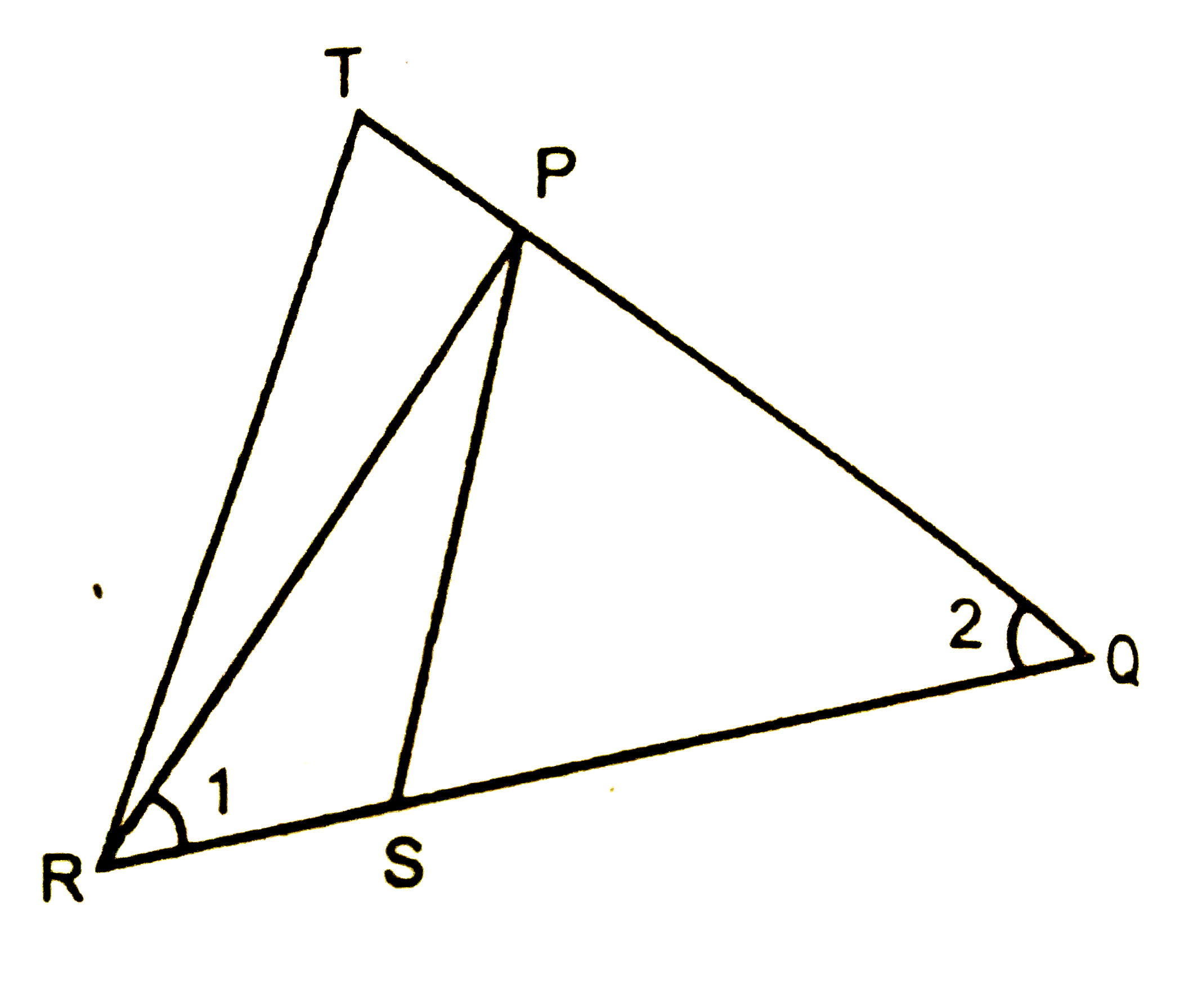
View Solutionएक समान्तर चतुर्भुज ABCD के भुजा AD के बढ़े हुए भाग पर E एक बिन्दु है और BE,CD को F पर काटती है । दिखाएँ कि `Delta ABE~Delta CFB`.
View Solution`DeltaABC` की भुजाएँ AB और BC तथा माध्यिका क्रमशः `DeltaPQR` की भुजा PQ और QR तथा माध्यिका PM के समानुपाती है । दिखायें कि `Delta ABC~Delta PQR`.
View Solutionदिए गये चित्र में यदि `DeltaABEcongDeltaACD` तो दिखाएँ कि `Delta ADE~Delta ABC`.
View Solutionदिए गये चित्र में यदि `Delta ABEcongDeltaACD`. दिखायें कि `Delta ADE~Delta ABC`.
View Solutionदिए गये चित्र में `DeltaABC` के शीर्ष लम्ब AD और CE परस्पर बिन्दु P पर प्रतिच्छेद करते है । दिखाए कि :
View SolutionABCD एक समलम्ब चतुर्भुज है जिसमें `AB||DC` है । विकर्ण AC और BD एक -दूसरे को O बिन्दु पर प्रतिच्छेद करते है । दो त्रिभुजों के लिए समरूपता का प्रयोग करते हुए दर्शाइए कि `(OA)/(OC)=(OB)/(OD)`
View Solutionसिद्ध करें कि समलम्ब चतुर्भुज के दोनों विकर्ण एक -दूसरे को समानुपाती खण्डों में विभाजित करते है ।
View Solutionयदि किसी चतुर्भुज के विकर्ण एक -दूसरे को समानुपाती खण्डों में प्रतिच्छेद करते है , तो सिद्ध करें कि वह चतुर्भुज एक समलम्ब चतुर्भुज है ।
View Solutionदिये गये चित्र में यदि `angleADE=angleB`, तो सिद्ध करें कि `DeltaADE~DeltaABC`. यदि ,`AD=6.8cm,AE=8.6cm,BE=2.4cm` और `BC=5.5cm,DE` का मान ज्ञात करें ।
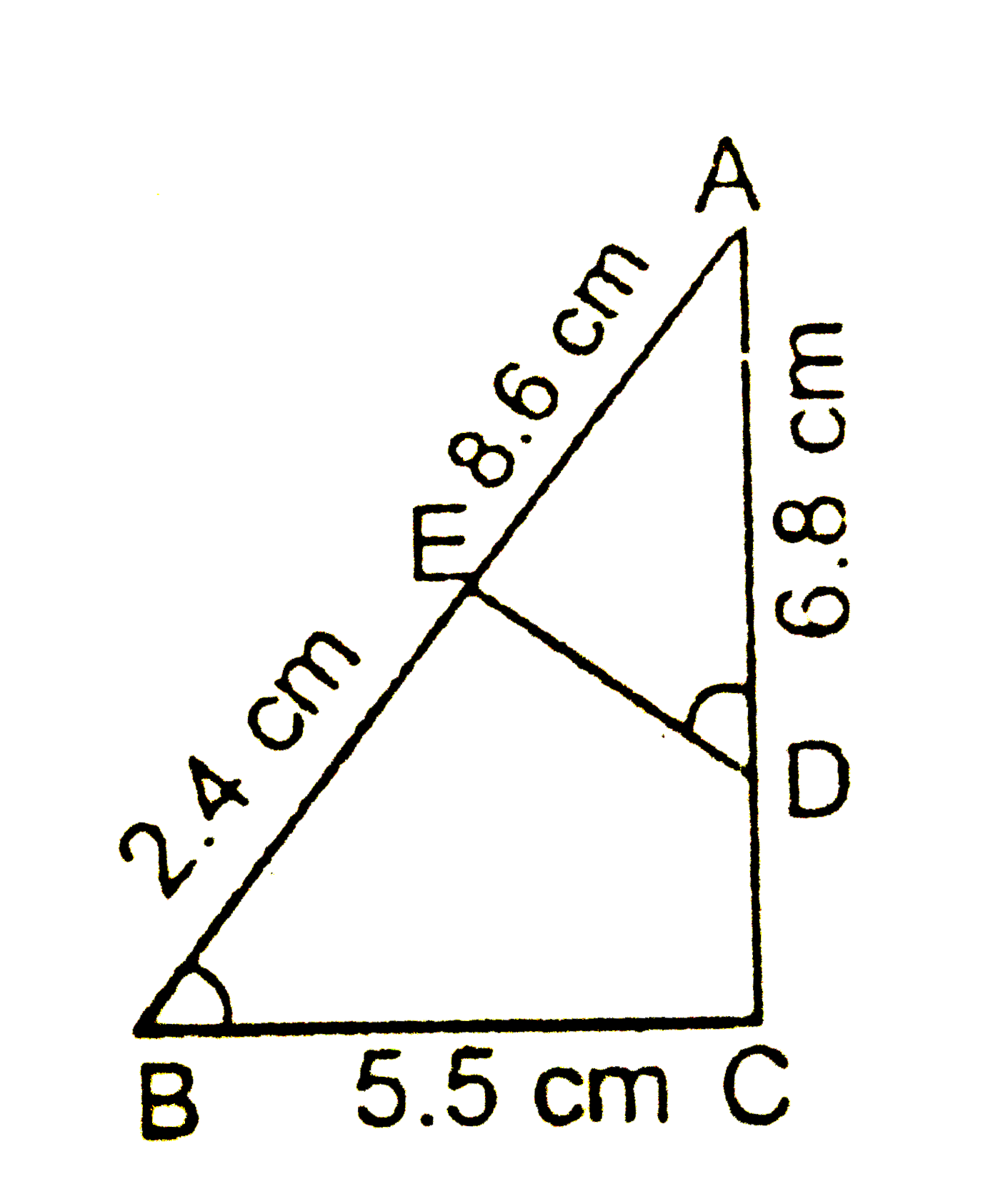
View Solutionदिये गये चित्र में `DE||BC,AD=2cm,BD=2.5cm,AE=3.2cm` और `DE=4cm` तब AC और BC ज्ञात करें ।
View Solution6cm ऊँचा एक उर्ध्वाधर स्तम्भ जमीन पर 4m लम्बी छाया बनाता है और ठीक उसी समय एक मीनार 28m लम्बी बनाता है । मीनार की ऊँचाई ज्ञात कीजिए ।
View Solution160 cm ऊँचाई वाला एक लड़का अंकित एक प्रकाश - स्तम्भ से दूर `2m//sec` की चाल से जा रहा है । यदि प्रकाश - स्तम्भ जमीन से `3.2m` ऊपर हो , तो अंकित की छाया की लम्बाई 5 सेकण्ड के बाद ज्ञात करें ।
View Solutionदिए गये चित्र में , `DeltaABC` की भुजा BC पर D इस प्रकार है कि `angleADC=angleBAC`. सिद्ध करें कि `CA^(2)=CBxxCD`.
View Solutionएक ही कर्ण BC पर एक ही तरफ दो समकोण त्रिभुज ABC और DBC खींचे गये है । यदि AC और BD , एक -दूसरे को P पर प्रतिच्छेद करते है , तो सिद्ध करें कि `APxxPO=BPxxPD`
View Solutionदिए गये चित्र में `DeltaABC` और `DeltaAMP` क्रमशः बिन्दु B और M पर समकोण है । सिद्ध करें कि
(i) `Delta ABC~DeltaAMP`
(ii) `(CA)/(PA)=(BC)/(MP)`
View Solutionदिए गये चित्र में DEFG एक वर्ग है और `angleBAC=90^@`. सिद्ध कीजिए कि :
(i) `Delta AGF~Delta DBG`
(ii) `DeltaAFG~DeltaEFC`
(iii) `Delta DBG~DeltaEFC`
(iv) `DE^2=DBxxEC`
View Solutionसिद्ध करें कि किसी त्रिभुज की तीनों भुजाओं के मध्य बिन्दुओं के मिलाने वाले रेखाखण्डों से बने चारों त्रिभुजों में प्रत्येक मूल त्रिभुज के समरूप होता है ।
View Solutionएक समान्तर चतुर्भुज ABCD की भुजा CD के मध्य बिन्दु M से गुजरने वाली रेखा BM खींची गई जोAC को L पर तथा AD को बढ़ाने पर E पर काटती है । सिद्ध कीजिए कि `EL=2BL`.
View Solutionदिए गये चित्र में , PA,QB तथा RC प्रत्येक , AC पर लम्ब है और `AP=x,QB=z,RC=y` है । सिद्ध करें कि `(1)/(x)+(1)/(y)=(1)/(z)`.
View Solution`Delta ABC` में , `AD botBC` और `AD^2=BD`.CD तो सिद्ध करें कि `angle BAC=90^@`
View Solutionदिए गये चित्र में `angleACB=90^@` तथा `CDbotAB` , तो सिद्ध करें कि `CD^2=BD.AD`
View Solutionदो समरूप त्रिभुजों ABC और PQR के क्षेत्रफल क्रमशः `25cm^2` और `49cm^2` है । यदि `QR=9.8cm` तो BC का मान ज्ञात करें ।
View Solutionदो समरूप त्रिभुजों ABC और PQR के क्षेत्रफलों का अनुपात `9:16` है । यदि `BC=4.5cm` तो QR की लम्बाई ज्ञात करें ।
View Solution`Delta ABC~Delta DEF` और उनके क्षेत्रफल क्रमशः `64cm^2` और `121cm^2` है यदि `EF=15.4cm` तो BC का मान ज्ञात करें ।
View SolutionABC और DEF दो समरूप त्रिभुज है इस प्रकार कि `BC=4cm,EF=5cm` और `DeltaABC` का क्षेत्रफल `=64cm^2` तब `DeltaDEF` का क्षेत्रफल ज्ञात करें ।
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल क्रमशः `81cm^2` और `49cm^2` है । यदि बड़े त्रिभुज की ऊँचाई `4.5cm` है , तो छोटे त्रिभुज की संगत ऊँचाई की संगत ऊँचाई ज्ञात कीजिए ।
View Solutionदिये गये चित्र में `DeltaABC~DeltaDEF,AB=5cm`, क्षे० `(DeltaABC)=20cm^2` और क्षेत्रफल `(DeltaDEF)=45cm^2` है , तो DE का मान ज्ञात करें ।
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल क्रमशः `121cm^2` और `4cm^2` है । यदि पहले त्रिभुज की माध्यिका `12.1cm` है तो दूसरे त्रिभुज की संगत माध्यिका ज्ञात करें ।
View Solutionनीचे दिए गए चित्र में `DeltaABC~DeltaDEF` जिसमे (AXऔर DY क्रमशः `angleA` और `angleD` के अर्द्धक है । यदि `AX=6.5cm` और `DY=5.2cm` तो `DeltaDEF` के क्षेत्रफलों के अनुपात ज्ञात करें ।
View SolutionABCD एक समलम्ब चतुर्भुज है जिसमे `AB||DC` इसके विकर्ण एक -दूसरे को O पर प्रतिच्छेद करते है । करते है यदि `AB=2CD`, तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि एक वर्ग की भुजा पर बने समबाहु त्रिभुज का क्षेत्रफल उस वर्ग के विकर्ण पर बने वर्ग के क्षेत्रफल से आधा होता है ।
View Solutionदिए गए चित्र में ABC और DBC दो त्रिभुज एक ही आधार BC पर स्थित है । यदि AD,BC को O पर प्रतिच्छेद करती है , तो दिखाएँ कि `("ar"(DeltaABC))/("ar"(DeltaBCD))=(AO)/(DO)`
View Solutionसमलम्ब चतुर्भुज ABCD में AC और BD का प्रतिच्छेद बिन्दु O है तथा `AB||CD` एवं `AB=2CD` यदि `DeltaAOB` का क्षेत्रफल `=84cm^2`, तो `DeltaCOD` का क्षेत्रफल ज्ञात करें
View Solutionदिए गये चित्र में `DE||BC` और `AD:BD=2:3`. दिखाएये कि क्षे० `(DeltaADE)`: क्षे० `(DeltaABC)4:25`.
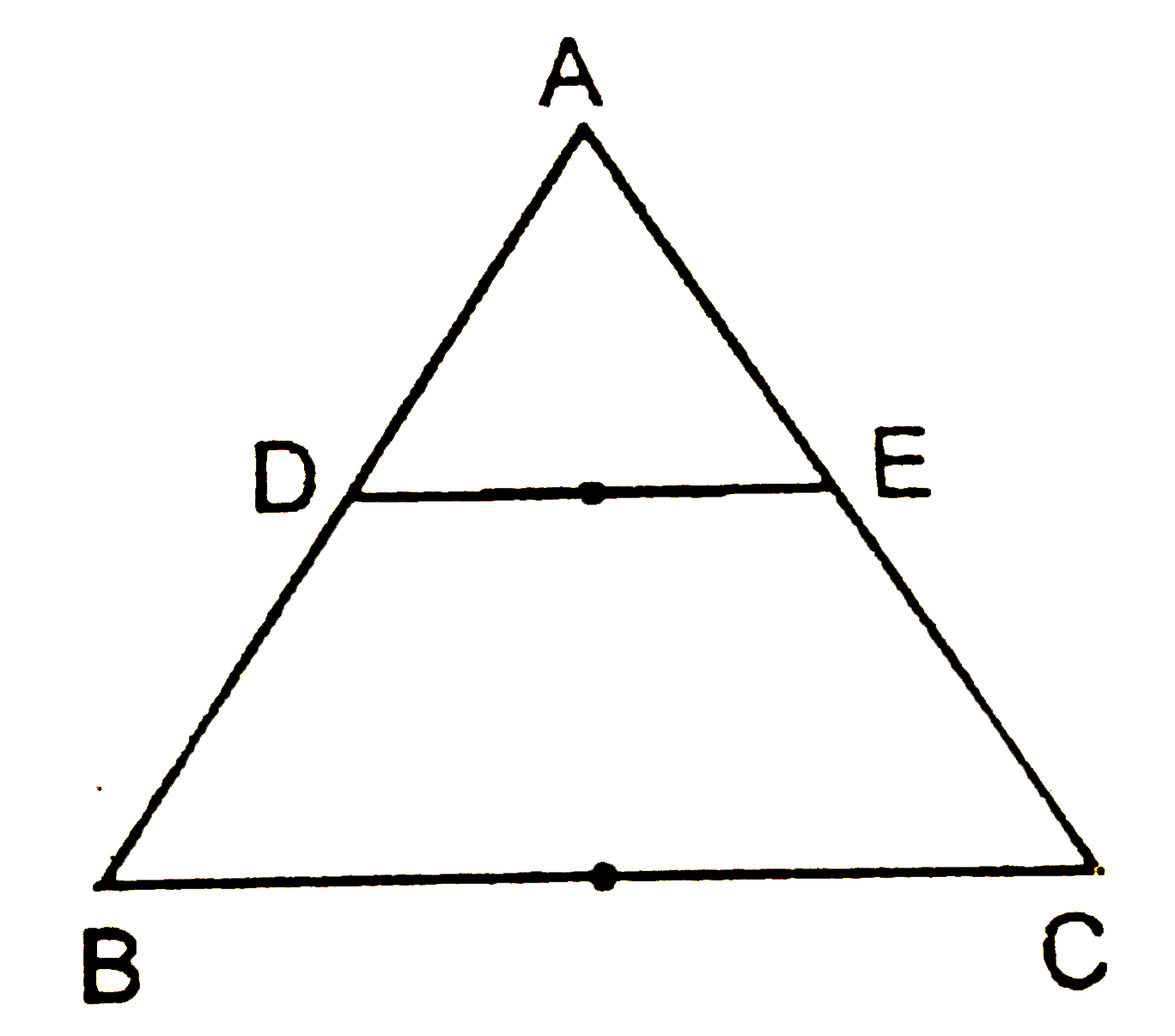
View Solutionदिए गये चित्र में `DeltaABC` और `DeltaDBC` एक ही आधार पर स्थित है । यदि AD,BC को O पर प्रतिच्छेद करती है । तो सिद्ध करें कि `("क्षे०" (DeltaABC))/("क्षे०"(DeltaBCD))=(AO)/(DO)`
View SolutionD,E और F क्रमशः `DeltaABC` की भुजाएँ AB,BC और CA के मध्य बिन्दु है , तो `DeltaDEF` एवं `DeltaABC` के क्षेत्रफलों का अनुपात ज्ञात करें ।
View Solution`Delta ABC` में रेखाखण्ड `XY||AC` है तथा यह AB को X तथा AC को Y पर प्रतिच्छेद करती है और `DeltaABC` को दो समान क्षेत्रफल वाले भाग में विभाजित करती है तो सिद्ध करें कि `(AX)/(AB)=(2-sqrt(2))/(2)`
View Solutionसिद्ध कीजिए कि समकोण समद्विबाहु त्रिभुज की एक युग्म पर बने समबाहु त्रिभुज का क्षेत्रफल उसके विकर्ण पर बनी समबाहु त्रिभुज के क्षेत्रफल का आधा होता है ।
View Solutionदिए गये चित्र में `DeltaABC` और `DeltaPQR` समद्विबाहु त्रिभुज है , जिसमे `angleA=angleP` यदि `("क्षे०"(DeltaABC))/("क्षे०"(DeltaPQR))=(9)/(16)` तो `(AD)/(PS)` का मान ज्ञात करें।
View Solutionनीचे कुछ त्रिभुजों की भुजाएँ दी गई है उनमे से कौन समकोण त्रिभुज है , निर्धारित करें । समकोण त्रिभुज के कर्ण ज्ञात करें ।
(i) `7cm,24cm,25cm`
(ii) `3cm,8cm,6cm`
(iii) `50cm,80cm,100cm`
(iv) `13cm,12cm,5cm`
View Solution`Delta ABC` की भुजाएँ `AB=9cm,BC=40cm` तथा `AC=41cm` है दीखाये कि त्रिभुज ABC एक समकोण त्रिभुज है । समकोण का नाम लिखें ।
View Solutionदो खम्भों 6cm और 11m ऊँची है और समतल जमीन पर उर्ध्वाधर खड़े है । यदि उनके पादों के बीच की दूरी 12m है तो उनके शिरों के बीच की दूरी ज्ञात करें ।
View Solutionप्रवीण 8m सीध पूरब जाता है तब वह 15m सीधे उत्तर जाता है । उसकी प्रारभिक बिन्दु से दूरी ज्ञात करें ।
View Solution15m लम्बी सीढ़ी मकान के एक तरफ 9m ऊँची खिड़की तक पहुँचती है सीढ़ी के पाद को उसी बिन्दु पर नियत रखते हुए सीढ़ी के सीरे को गली के दूसरे तरफ झुकाकर लगाने पर वह 12m ऊँची खिड़की तक पहुँचती है । गली की चौड़ाई ज्ञात करें ।
View Solution`DeltaABC` में , `ADbotBC` और `BD=3CD` तो सिद्ध करें कि `2AB^2=2AC^2+BC^2`.
View Solutionदिए गये चित्र में `DeltaPQR` समकोण त्रिभुज है PR और PQ ज्ञात करें जबकि `QR=26cm,PO=6cm` और `OR=8cm है ।
View Solution`DeltaABC`, में `ADbotBC` इस प्रकार कि `AD^2=BD.CD` सिद्ध करें कि `DeltaABC` का कोण A समकोण
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमे `AB=AC=13cm`. A से BC पर लम्ब की लम्बाई 5cm है तो BC का मान बताएँ ।
View Solutionदिए हुए `DeltaABC` में `angleA=90^@` और `AD botBC` , सिद्ध करें कि `AD^2=BD.CD`
View Solution`Delta ABC`में , AD लम्ब है BC पर सिद्ध करें कि `AB^2+CD^2=AC^2+BD^2`.
View Solution10 सेमी भुजा वाले समचतुर्भुज का एक विकर्ण 12cm लम्बा है तो इसके दूसरे विकर्ण की लम्बाई ज्ञात करें ।
View Solutionसिद्ध करें कि किसी समचतुर्भुज की भुजाओं पर के वर्गों का योग उसके विकर्णों पर के वर्णो के योग के बराबर होता है ।
View Solutionआयत ABCD के अन्दर O एक बिन्दु है । सिद्ध करें कि `OB^2+OD^2=OA^2+OC^2`
View Solutionकिसी समबाहु त्रिभुज में सिद्ध करें कि एक भुजा के वर्ग का तीन गुना , इसके किसी एक ऊँचाई के वर्ग के चार गुने के बराबर है ।
View Solutiona भुजा वाले समबाहु त्रिभुज में सिद्ध करें कि (i) ऊँचाई `=a(sqrt(3))/(2)`
(ii) क्षेत्रफल `=(sqrt(3))/(4)a^2`
View Solution
साधित उदाहरण questions and complete solutions for chapter त्रिभुज of KC SINHA MATHS (HINDI) of Class 10
All Exercises from KC SINHA HINDI Class 10 MATHS त्रिभुज
- EXCERCISE 6.1
- EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
- EXCERCISE 6.2 (लघु उत्तरीय प्रश्न )
- EXCERCISE 6.3 (दीर्घ उत्तरीय प्रश्न ) ( Long Answer Type Questions)
- EXCERCISE 6.3 (लघु उत्तरीय प्रश्न) ( Short Answer Type Questions)
- EXCERCISE 6.4 ( अतिलघु उत्तरीय प्रश्न ) ( Very Short Answer Type Questions)
- EXCERCISE 6.4 ( दीर्घ उत्तरीय प्रश्न ) ( Long Answer Type Questions)
- EXCERCISE 6.4 ( लघु उत्तरीय प्रश्न ) ( Short Answer Type Questions)
- EXCERCISE 6.5 Type I. (पाइथागोरस प्रमेय तथा उसके विलोम के सीधे प्रयोग पर आधारित प्रश्न :) ( अतिलघु उत्तरीय प्रश्न ) ( Very Short Answer Type Questions)
- EXCERCISE 6.5 Type I. (पाइथागोरस प्रमेय तथा उसके विलोम के सीधे प्रयोग पर आधारित प्रश्न :) ( दीर्घ उत्तरीय प्रश्न ) ( Long Answer Type Questions)
- EXCERCISE 6.5 Type I. (पाइथागोरस प्रमेय तथा उसके विलोम के सीधे प्रयोग पर आधारित प्रश्न :) ( लघु उत्तरीय प्रश्न ) ( Short Answer Type Questions)
- EXCERCISE 6.5 Type II. (पाइथागोरस प्रमेय , इसके उप -प्रमेयों और अन्य परिणामों पर आधारित प्रश्न : ( अतिलघु उत्तरीय प्रश्न ) ( Very Short Answer Type Questions)
- EXCERCISE 6.5 Type II. (पाइथागोरस प्रमेय , इसके उप -प्रमेयों और अन्य परिणामों पर आधारित प्रश्न : ( दीर्घ उत्तरीय प्रश्न ) ( Long Answer Type Questions)
- EXCERCISE 6.5 Type II. (पाइथागोरस प्रमेय , इसके उप -प्रमेयों और अन्य परिणामों पर आधारित प्रश्न : ( दीर्घउत्तरीय प्रश्न ) ( Long Answer Type Questions)
- वस्तुनिष्ठ प्रश्न
- साधित उदाहरण