Complete Solutions to JEE Advanced of chapter PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF MATTER |
| DC PANDEY MASTER PROBLEM PACKAGE | JEE Advanced |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
An ice cube of size `a = 10 cm` is floating in a tank (base area `A = 50 cm xx 50 cm`) partially filled with water. The change in gravitational potential energy, when ice melts completely is (density of ice is `900 kg//m^(2)`)
View SolutionA ball floats on the surface of water in a container exposed to the atmosphere. Volume `V_(1)` of its volume is inside the water. The container is now covered and the air is pumped out. Now let `V_(2)` be the volume immersed in water. Then
View SolutionTwo cylinders of same cross-section and length L but made of two different materials of densities `d_(1)` and `d_(2)` are cemented together to from a cylinder of length 2L. The combination floats in a liquid of density `d " " d_(1) lt d_(2)` then
View SolutionA cylinder of mass M and density `d_(1)` hanging from a string, is lowered into a vessel of cross-sectional area A, containing a liquid of density `d_(2) (d_(2) lt d_(1))` until it is fully immersed. The increase in pressure at the bottom of the vessel is
View SolutionA ball of mass m and density `rho` is immersed in a liquid of density `3 rho` at a depth `h` and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA balloon with mass `m` is descending down with an acceleration a `(where altg)` . How much mass should be removed from it so that it starts moving up with an acceleration a?
View SolutionA solid ball of density `rho_(1)` and radius r falls vertically through a liquid of density `rho_(2)`. Assume that the viscous force acting on the ball is `F = krv`, where `k` is a constant and v its velocity. What is the terminal velocity of the ball ?
View SolutionA small steel ball falls through a syrup at a constant speed of `10cms^-1`. If the steel ball is pulled upwards with a force equal to twice its effective weight, how fast will it move upwards?
View SolutionThere is a horizontal film of soap solution. On it a thread is placed in the form of a loop. The film is pierced inside the loop and the thread becomes a circular loop of radius `R`. If the surface tension of the loop be `T`, then what will be the tension in the thread?
View SolutionA drop of water of mass `m` and density `rho` is placed between two weill cleaned glass plates, the distance between which is `d`. What is the force of attraction between the plates?
`(T=` surface tension)
View SolutionWhat is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is `rho`)
View SolutionA small block of wood of specific gravity 0.5 is subnerged at a depth of 1.2 m in a vessel filled with water. The vessel is accelerated upwards with an acceleration `a_(0) = (g)/(2)`. Time taken by the block to reach the surface, if it is released with zero initial velocity is `(g = 10 m//s^(2))`
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case `theta =- 0^(@)` the force exerted by the hings on the rod is `(g = 10 m//s^(2))`
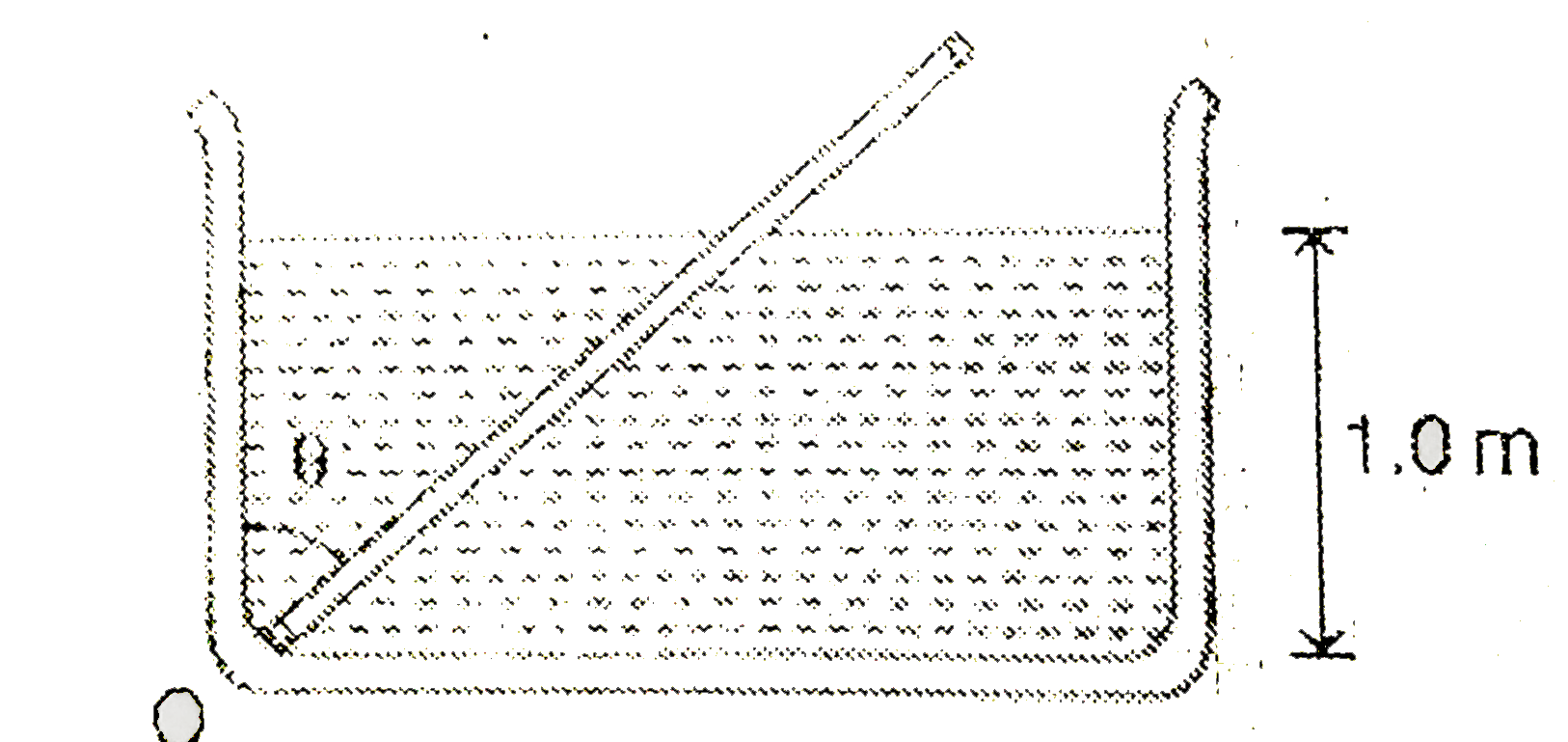
View SolutionA cubical block of wood of edge a and density `rho` floats in water of density `2rho`. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionThe opening near the bottom of the vessel shown in the figure has an area `A`. A disc is held against the opening keep the liquid from running out. Let `F_(1)` be the net forces on the disc applied by liquid and air in this case. Now the disc is moved away from the opening a short distance. The liquid comes out and strikes the disc in elastically. Let `F_(2)` be the force exerted by the liquid in this condition. The `F_(1)//F_(2)` is

View SolutionWhen at rest, a liquid stands at the same level in the tubes shown in figure. But as indicated a height difference h occurs when the system is given an acceleration a towards the right. Here, h is equal to
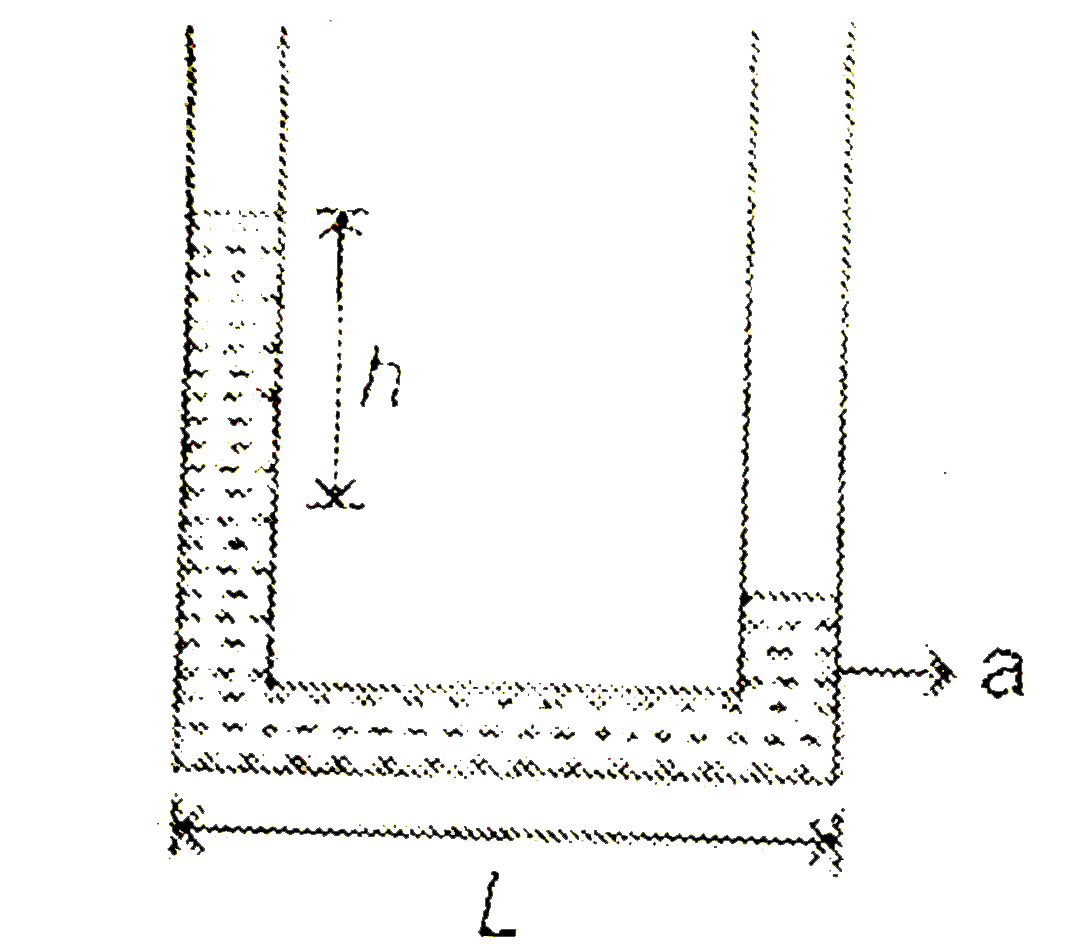
View SolutionA glass tube `80 cm` long and open ends is half immersed in mercury. Then the top of the tube is closed and it is taken out of the mercury. A column of murcury `20 cm` long then remains in the tube. The atmospheric (in cm of Hg) is
(assume temperature to be constant )
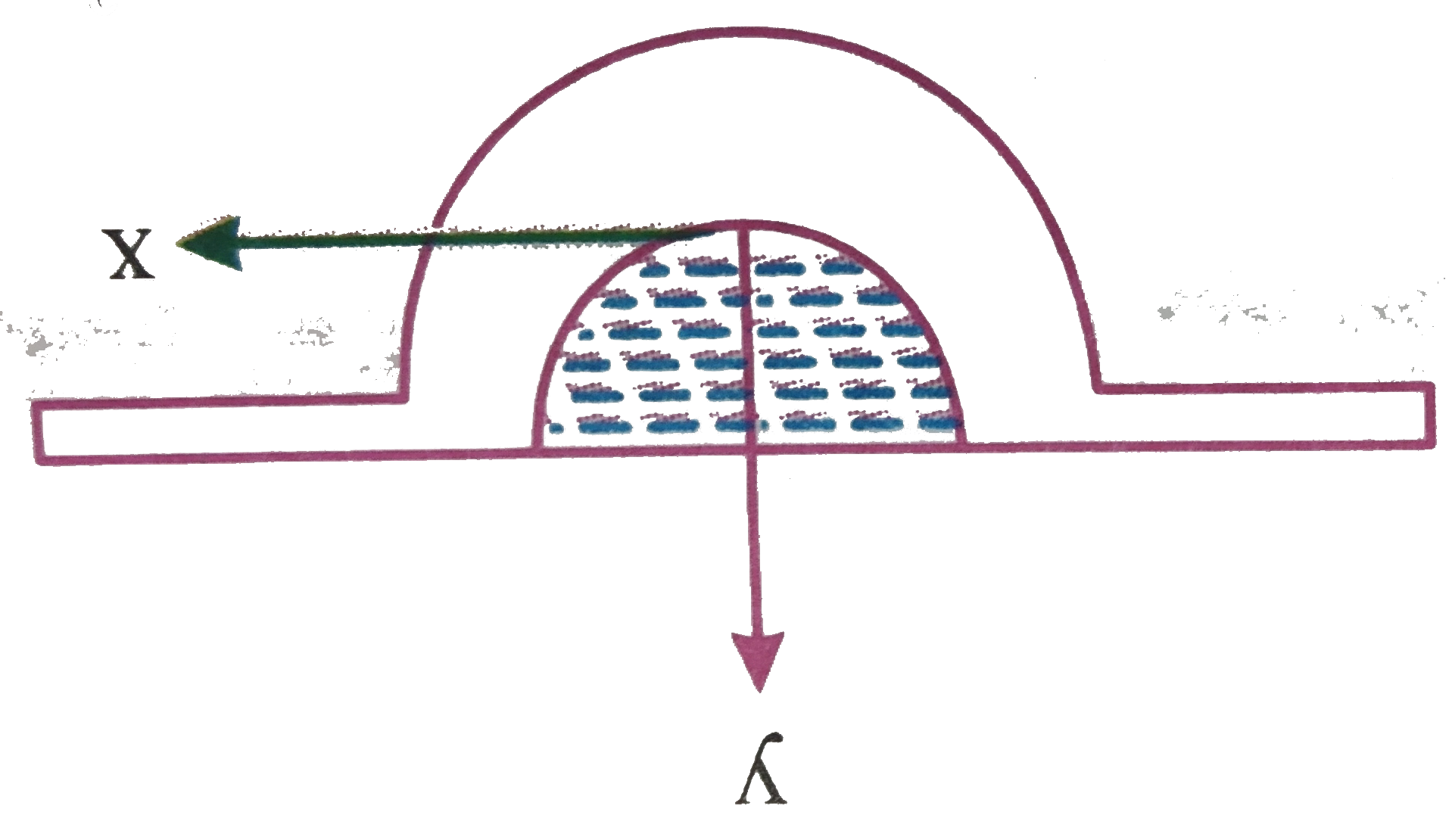
View SolutionA small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled in to the jar up to a certain height. The rate of dissension of liquid is independent of level of the liquid in the jar. Then the surface of jar is a surface of revolution of curve
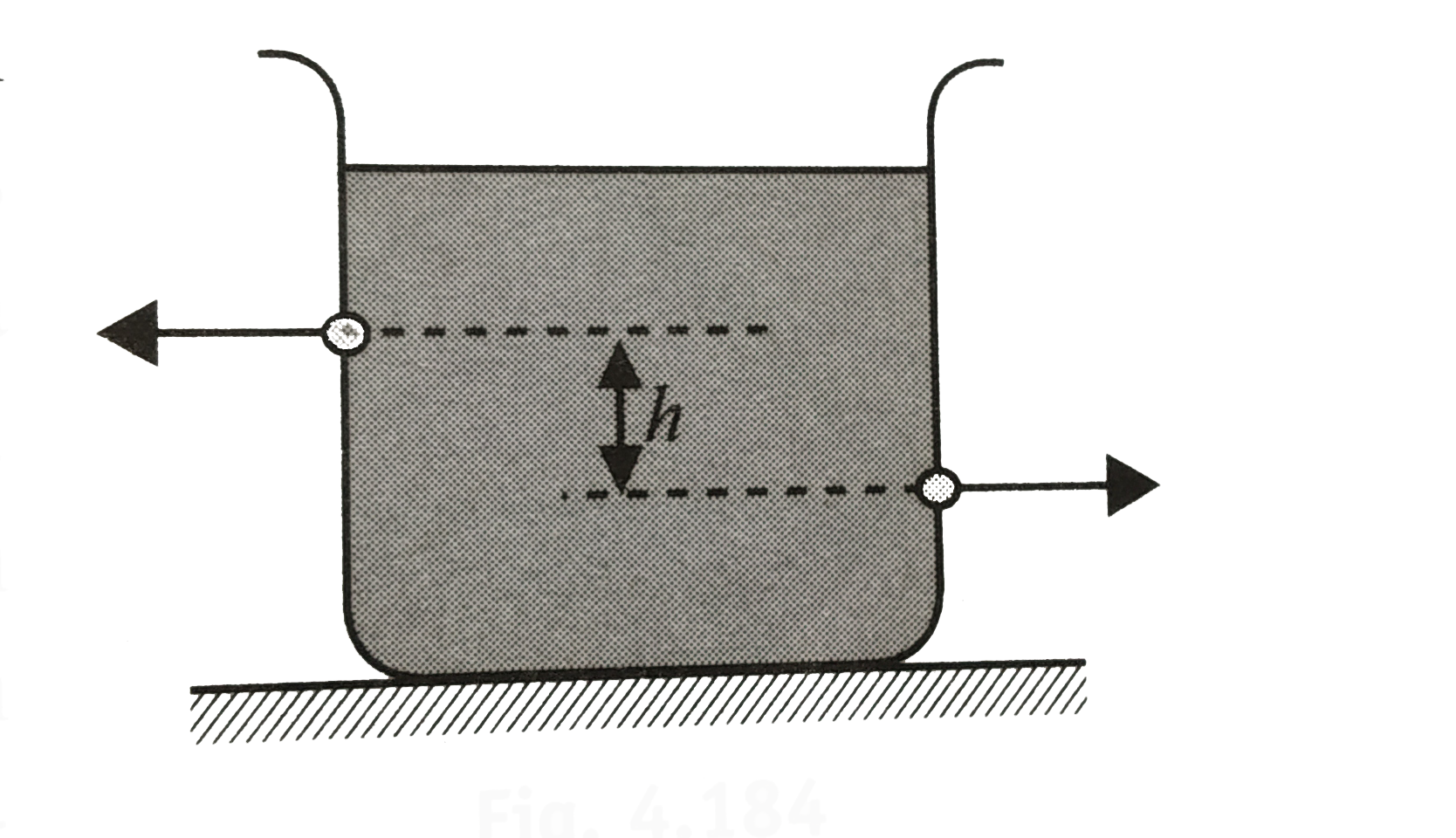
View SolutionThere are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density `rho`. The differences in height between the holes is `h`. The tank is resting on a smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it in equilibrium is
View SolutionEqual volume of two immiscible liquids of densities `rho` and `2rho` are filled in a vessel as shown in the figure. Two small holes are punched at depths `h//2` and `3h//2` from the surface of lighter liquid. If `v_(1)` and `v_(2)` are the velocities of efflux at these two holes, then `v_(1)//v_(2)` is
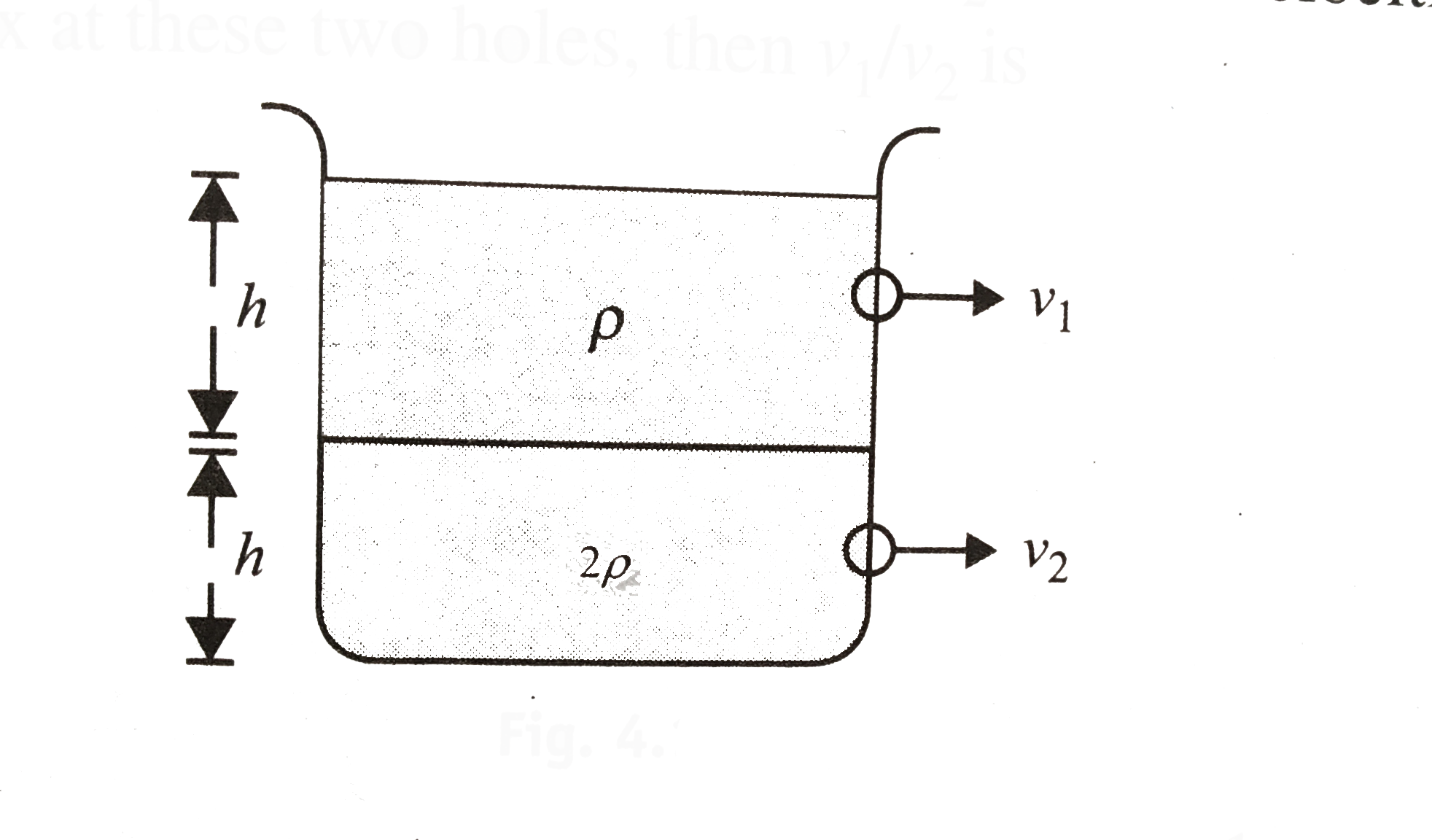
View SolutionTwo spheres of volume 250 cc each but of relative densities 0.8 and 1.2 are connected by a string and the combination is immersed in a liquid. Find the tension T in the string. `(g=10m//s^(2))`
View SolutionA tube `1 cm^(2)` in cross section is attached to the top of a vessel `1 cm` high and of cross section `100 cm^(2)`. Water is poured into the system filling it to a depth of `100 cm` above the bottom of the vessel as shown in the figure. Take `g = 10 ms^(-2)`. Find the correct statement.
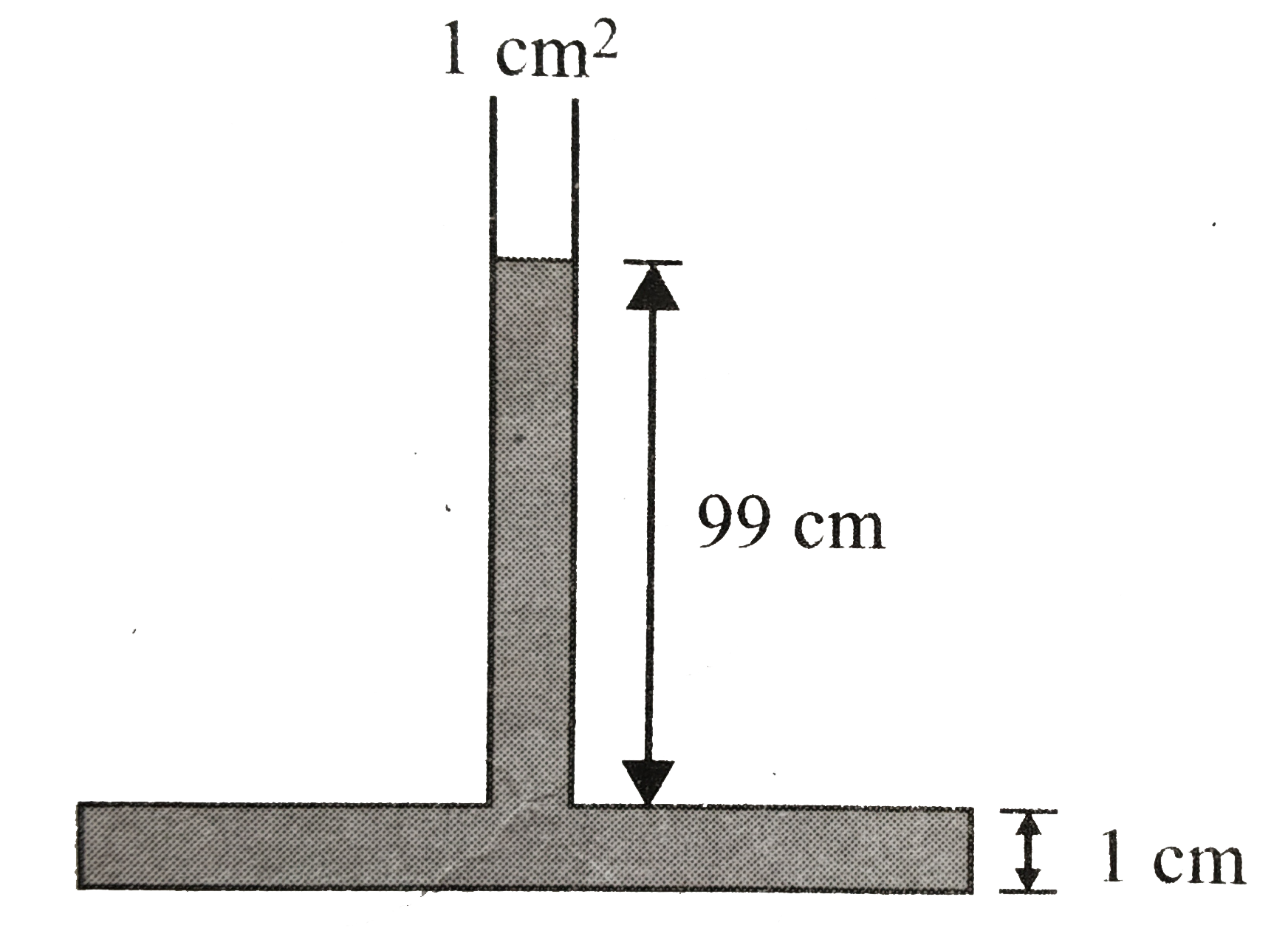
View Solution
In the arrangement shown in the figure `(m_(A))/(m_(B))=(2)/(3)` and the ratio of density of block B and the liquid is `2:1` The system is released from rest. Then
View SolutionA uniform elastic plank moves due to a constant force `F_(0)` applied at one end whose area is `S`. The Young's modulus of the plank is `Y`. The strain produced in the direction of force is
View Solutionif `rho` is the density of the meterial of a wire and `sigma` is the breaking stress. The greatest length of the wire that can hang freely without breaking is
View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are `a, b` and `c` respectively then the corresponding ratio of increase in their lengths is
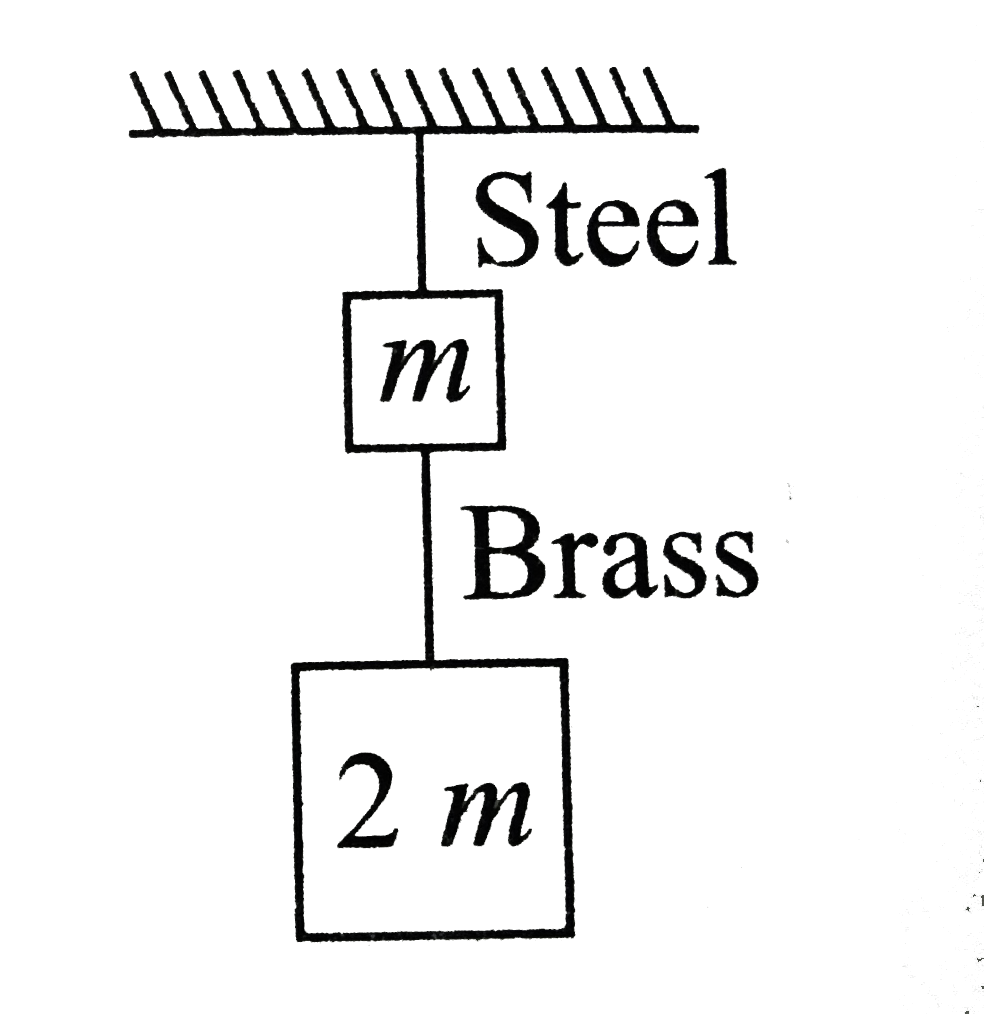
View SolutionA uniform rod of length `L`, has a mass per unit length `lambda` and area of cross section `A`. The elongation in the rod is `l` due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
View SolutionA vertical capillary is brought in contact with the water surface (surface tension = T). The radius of the capillary is r and the contact angle `theta = 0^(@)`. The increase in potential energy of the water (density `=rho`) is
View SolutionAn empty container has a circular hole of radius r at its bottom. The container is pused into water very slowly as shown. To what depth the lower surface of container (from surface of water) can be pushed into water such that water does not flow into the container?

View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opened again. The length of the water column remaining in the tube will be
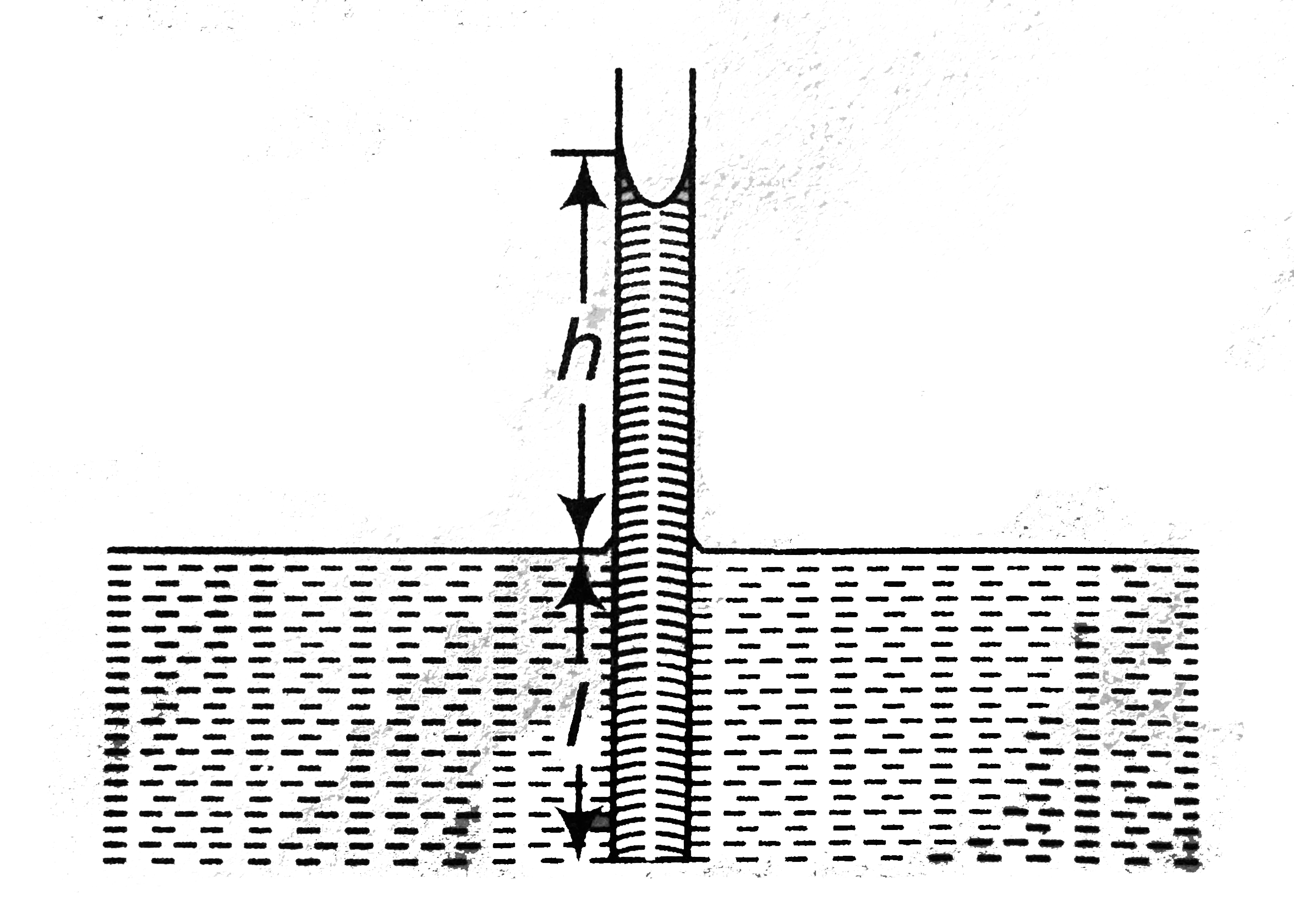 .
.
View SolutionA cylindrical vessel of area of cross-section A is filled with water to a height H. It has capillary tube of length l and radius r fitted horizontally at its bottom. If the coeffiecient of viscosity of water is `eta`, then time required in which level will fall to a height `(H)/(2)` is (density of water is `rho`)
View SolutionOne end of a glass capillary tube with a radius `r=0.05cm` is immersed into water to a depth of `h=2cm`.Excess pressure required to blow an air bubble out of the lower end of the tube will be `(S.T` of water `=70"dyne"//cm`).Take `g=980cm//s^(2)`.
View SolutionThe range of water flowing out of a small hole made at a depth `10 m` below water surface in a large tank is `R`. Find the extra pressure (in atm) applied on the water surface so that range becomes `2R`. Take `1atm=10^(5)Pa`.

View SolutionWhat force must be applied to detach two wetted photographic plates `(9 cm xx 12 cm)` in size from each other without shifting them. The thickness of water between the plates is 0.05 mm. Surface tension of water is 0.073 N/m.
View SolutionA cylinder with a movable piston contains air under a pressure `p_(1)` and a soap bubble of radius 'r' . The pressure `p_(2)` to which the air should be compressed by slowly pushing the piston into the cylinder for the soap bubble to reduce its size by half will be (The surface tension is `sigma` and the temperature T is maintained constant).
View SolutionA vertically jet of water coming out of a nozzle with velocity `20 m//s` supports a plate of mass M stationary at a height `h = 15 m`, as shown in the figure. If the rate of water flow is 1 litre per second, the mass of the plate is (Assume the collision to be perfectly inelastic).
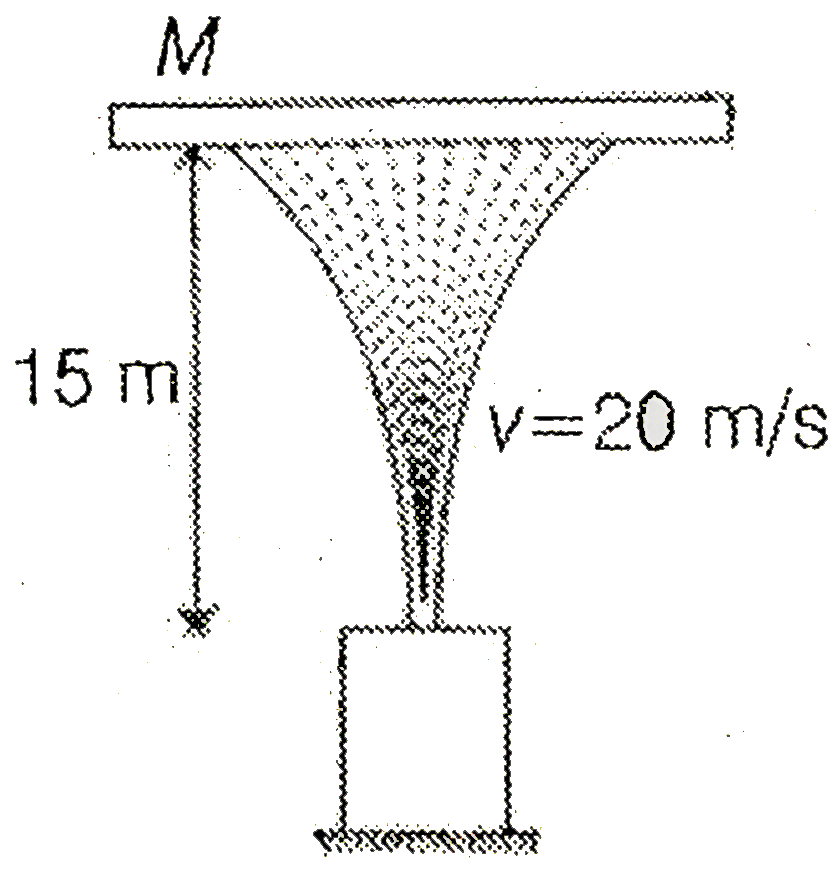
View SolutionA uniform rod `OB` of length `1m`, cross-sectional areal `0.012 m^(2)` and relative density `2.0` is free to rotate about smooth hinge `O` in vertical plane. The rod is held with a horizontal string `AB` which can withstand a maximum tension of `45N`. The rod and string system is kept in water as shown in figure. The maximum value of angle `alpha` which the rod can make with vertical without breaking the string is
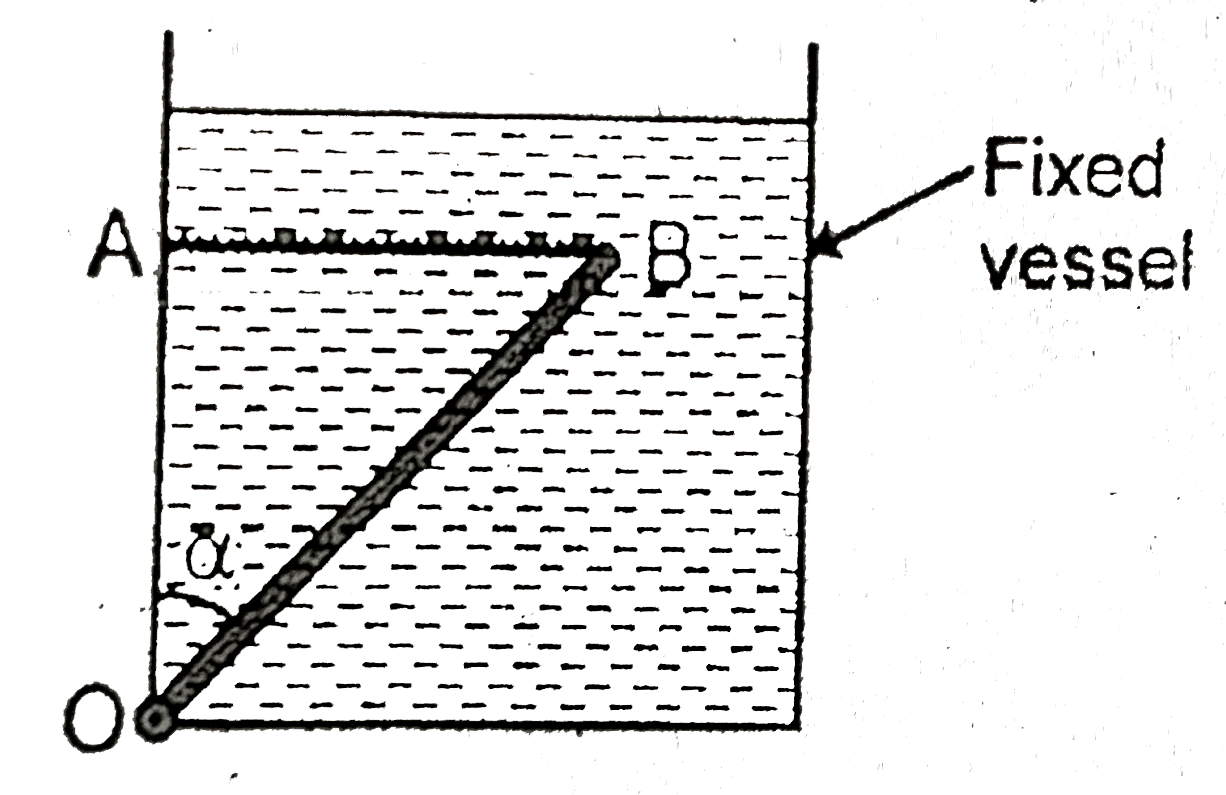
View Solution_S01_083_Q01.png)
Water (density `rho`) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
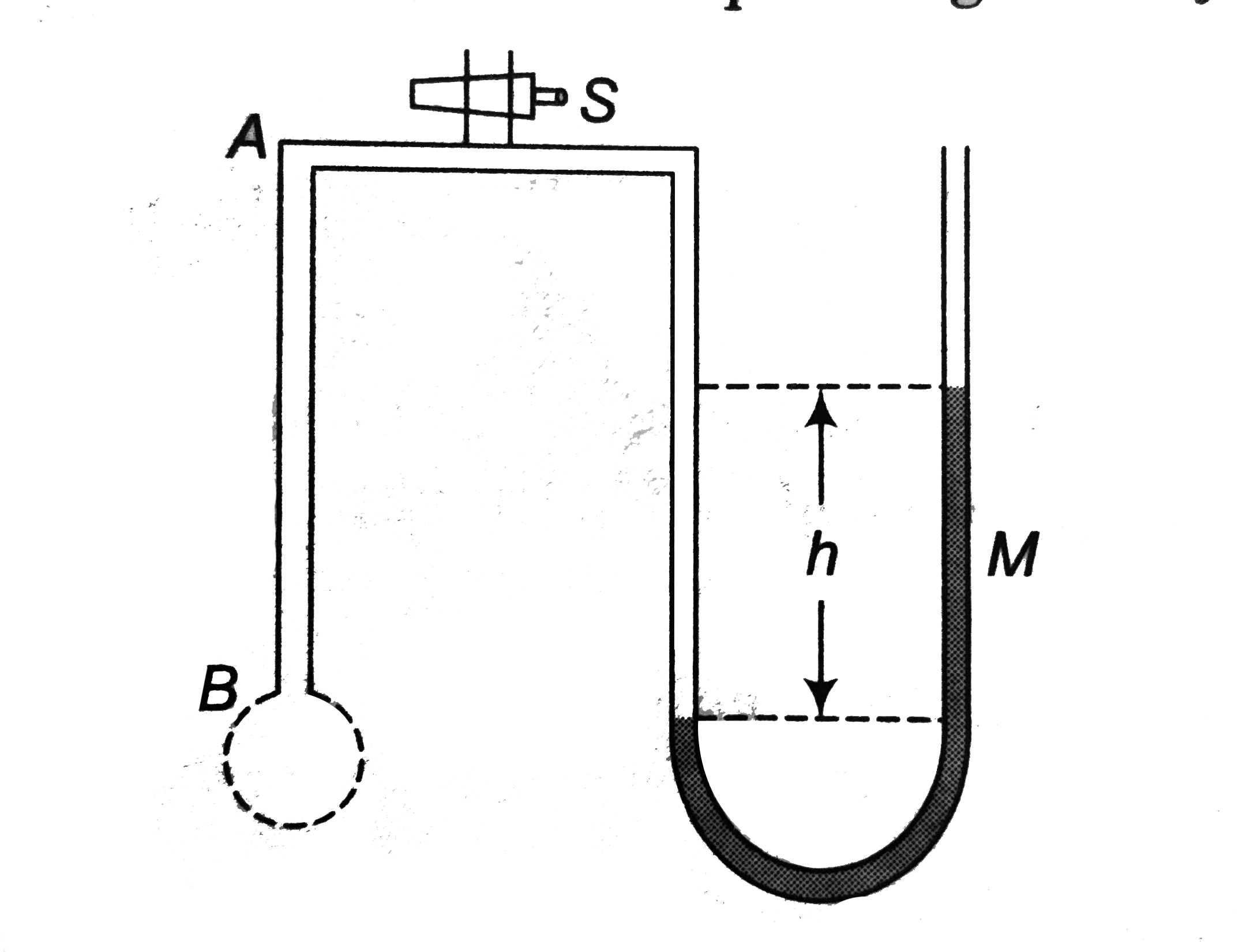
View SolutionA tube of fine bore `AB` is connected to a manometer `M` as shown. The stop cock `S` controls the flow of air. `AB` is dipped into a liquid whose surface tension is T. On opening the stop cock for a while, a bubble is formed at `B` and the mamometer liquid and r the radius of curvature of the bubble, then the surface tension `T` of the liquid is given by
View SolutionA bucket water filled upto a height = 15 cm. The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above atmospheric pressure at the bottom is
View SolutionAn open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one thrid of volume of water was spilled out. The acceleration was
View SolutionSome liquid is filled in a cylindrical vessel of radius R. Let `F_(1)` be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let `F_(2)` be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
View SolutionA glass capillary of length l and inside radius `r(r lt lt l)` is submerged vertically into water. The upper end of the capillary is scaled. The atmospheric pressure is `p_(0)`. To what length h has the capillary to be submerged to make the water levels inside and outside the capillary coincide. Assume that temperature of air in the capillary remains constant. (given, surface tension of water = T, angle of contact between glass water interface `= 0^(@)`)
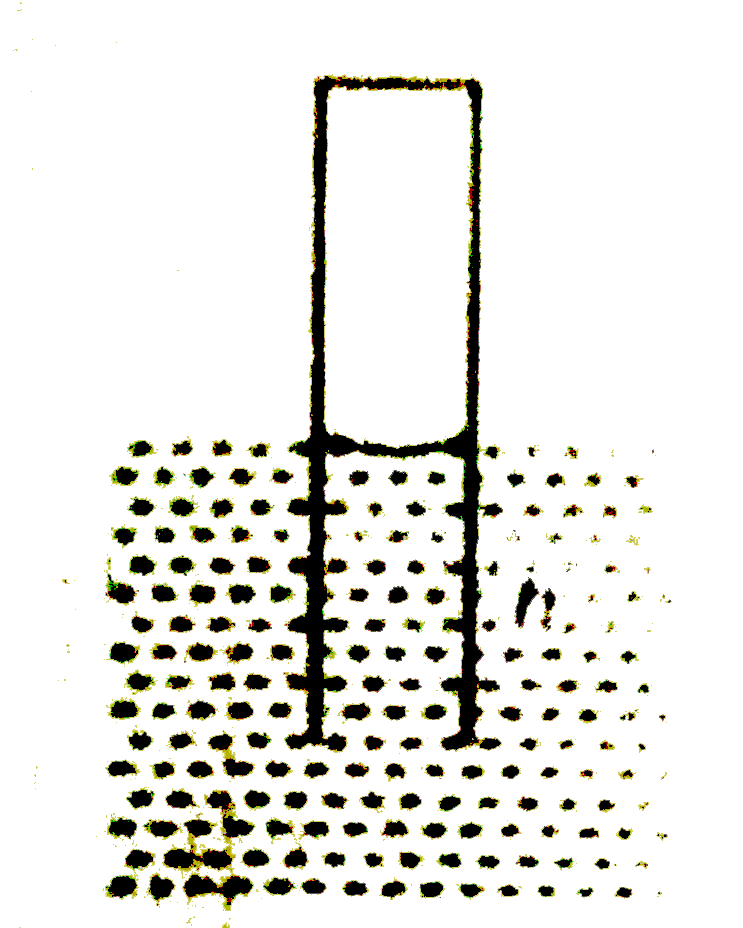
View SolutionThe pressure at the bottom of an open tank of water is 3p where p is the atmospheric pressure. If the water is drawn out till the level of water remains one fifth, the pressure at the bottom of the tank will now be
View SolutionFigure shows a siphon. Choose the wrong statement.

(`p_(0)` = atmospheric pressure)
View SolutionA U-tube of cross section A and 2A contains liquid of density `rho`. Initially, the liquid in the two arms are held with a level difference h as shown in figure. After being released the levels equalize after some time. The work done by gravity forces on the liquid in the process is :
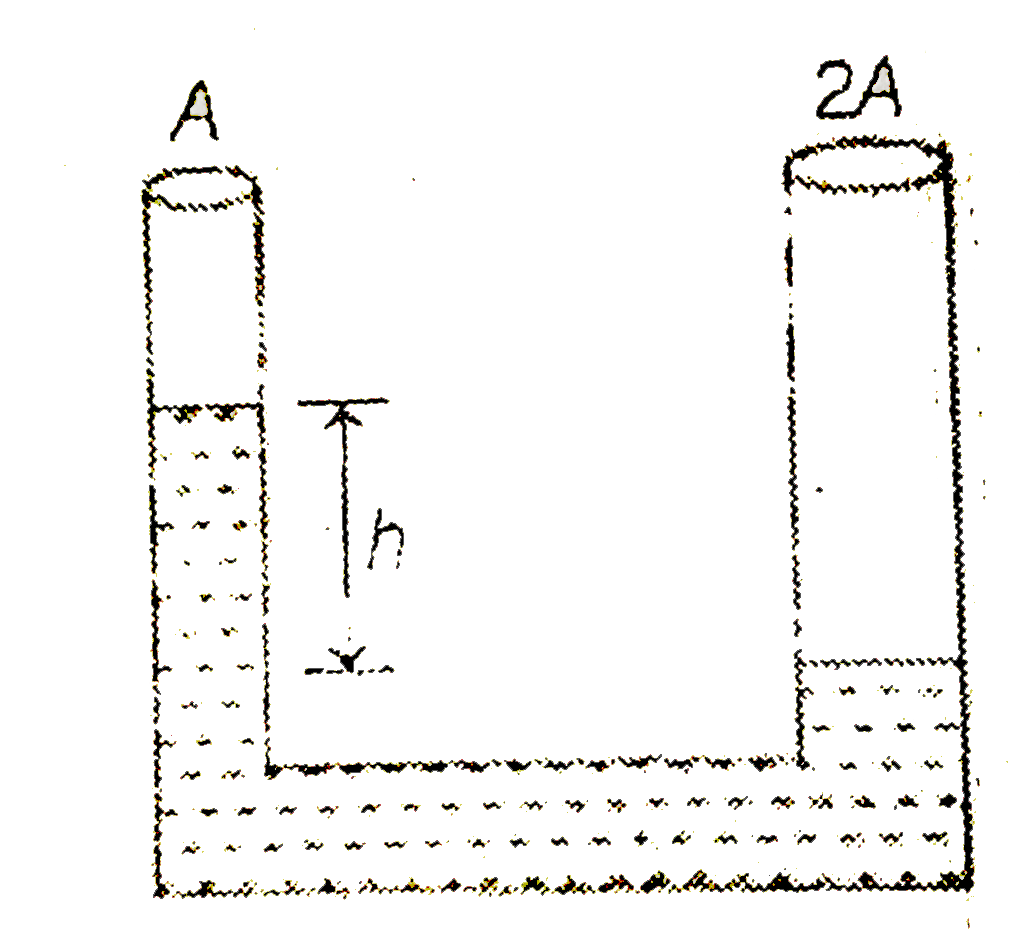
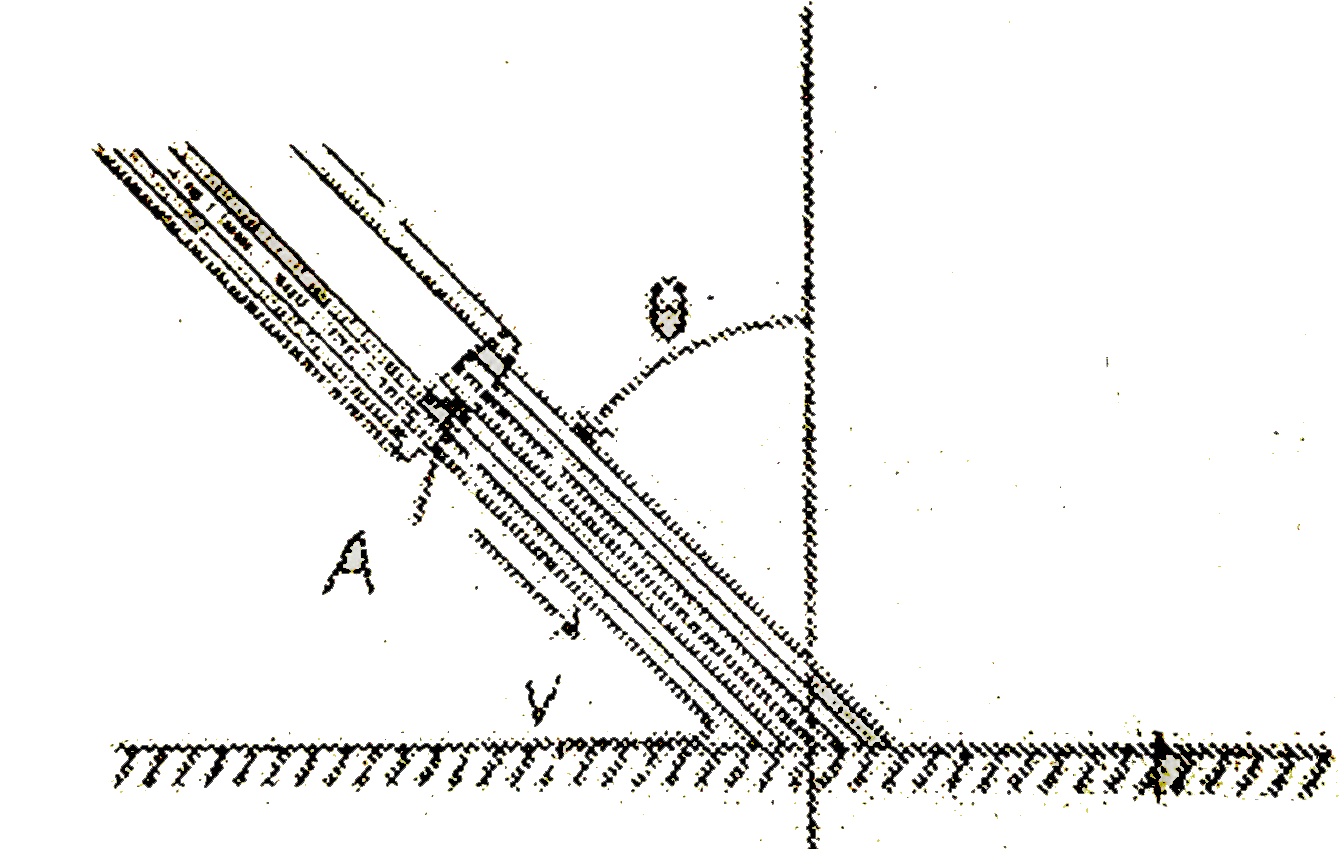
View SolutionA stream of liquid, set at an angle `theta`, is directed against a plane surface (figure). The liquid, after hitting the surface, spreads over it. Find the pressure on the surface. The density of the liquid is `rho` and its velocity is v.
View SolutionA tube of small uniform cross section is used to siphon the water from the vessel. Then choose the correct alternative (s) :
`(rho_("water") = 10^(3) kg//m^(3), g = 10 m//s^(2), P_(atm) = 10^(5) Pa)`

View Solution_E01_053_Q01.png)
There are three different liquids, with densities `rho_(1),rho_(2)` and `rho_(3)` in a U-shaped container as shown in the picture the lengths shown are `H_(1)=15cm` and `H_(2)=10cm` which of the following equations gives the correct relation between the densities of the fluids in the container?
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities `rho_(1)` and `rho_(2)(rho_(2) gt rho_(1))`, half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure `= p_(0)` and acceleration due to gravity is g):
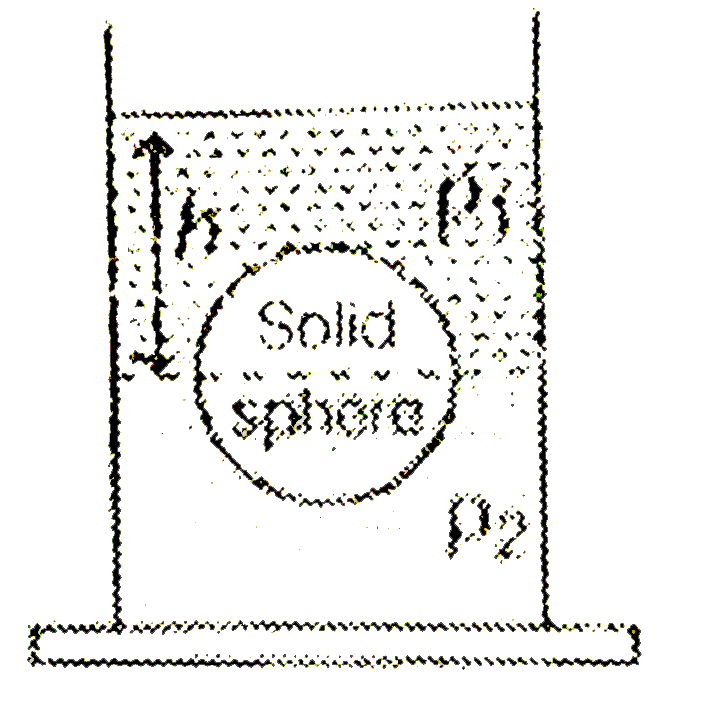
View SolutionA hollow sphere of volume V is floating on water surface with half immersed in it. What should be the minimum volume of water poured inside the sphere so that the sphere now sinks into the water ?
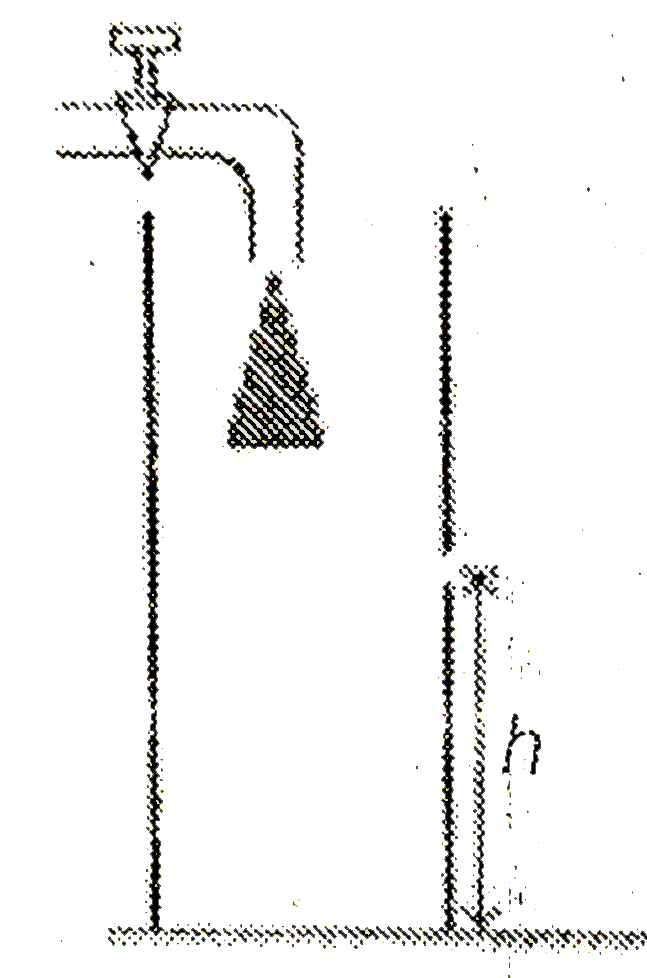
View SolutionThe diagram shows a tall cylindrical container kept on a horizontal surface. From a tap, water come with constant rate `q m^(3)//s`. Initially the container was empty. An orifice of area of cross section A is made at some height h in the side wall of the container. If the horizontal range of the water jet in steady is found to be 2h, then the relation between h and q is
View SolutionAir is blown through a pipe AB at a rate of 15 litres per minute. The cross sectional area of the broad portion of the pipe AB is `2 cm^(2)` and that of the narrow portion is `0.5 cm^(2)`. The difference in water level h is `(rho_("air") = 1.32 kg//m^(3))`

View SolutionA tube of radius r and sufficient height is dipped in a liquid of surface tension S and density `rho`. Heat developed upto steady state will be
Note: `theta` is the contact angle
View SolutionA hollow object of volume V is immersed in a tank. The object is tied to the bottom of the tank by two wires which make an angle `30^(@)` with the horizontal as shown in figure. The object would float if it was set free and one forth volume is immersed in liquid of density `rho_(0)`. The tension in the wires is
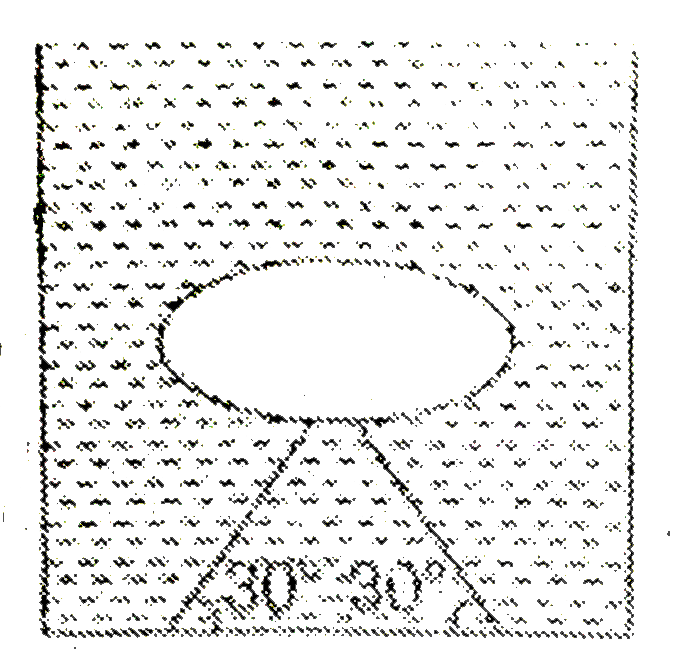
View SolutionA bent tube of uniform cross section is mounted on a cart which is accelerating towards right with constant acceleration 'a'. The total length of the liquid is `2sqrt(2)l`. Find the level difference between two limbs in equilibrium `(a=2 m//s^(2), l=10 m)`

View Solution
JEE Advanced questions and complete solutions for chapter PROPERTIES OF MATTER of DC PANDEY ENGLISH of Class 11