Complete Solutions to Passage of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | Passage |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by `A/2` and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
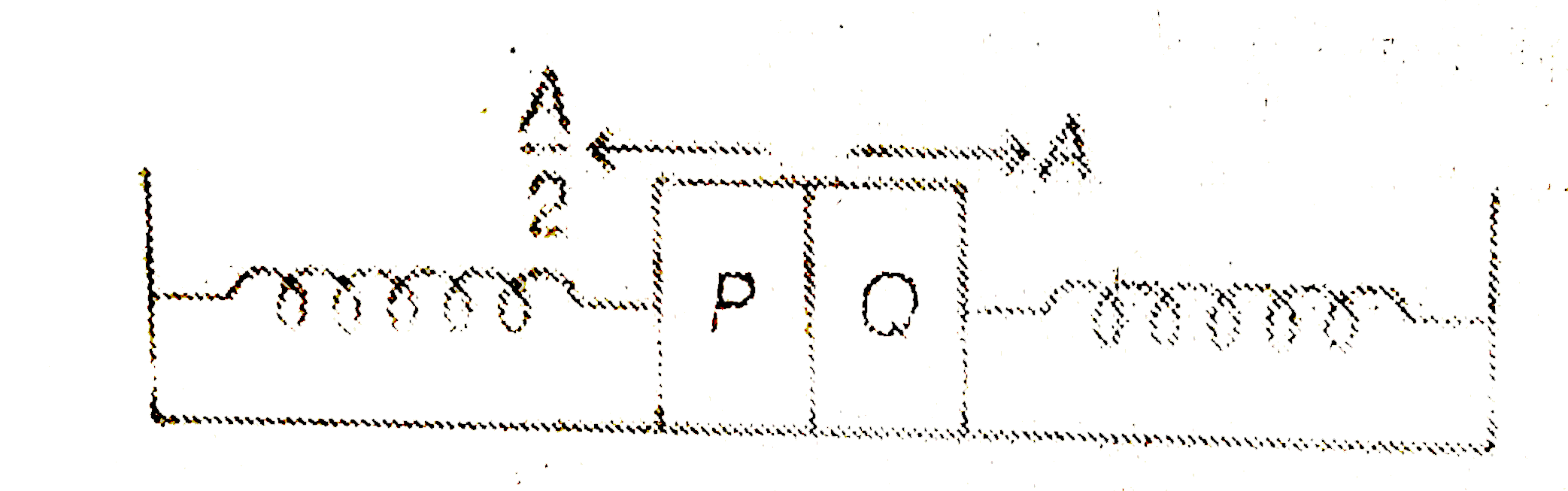
The amplitude of combined mass is
View SolutionTwo identical blocks `P` and `Q` have mass `m` each. They are attached to two identical springs initially unstretched. Now the left spring (along with `P)` is compressed by `A//2` and the right spring (along with `Q`) is compressed by `A`. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both the blocks was `T`.
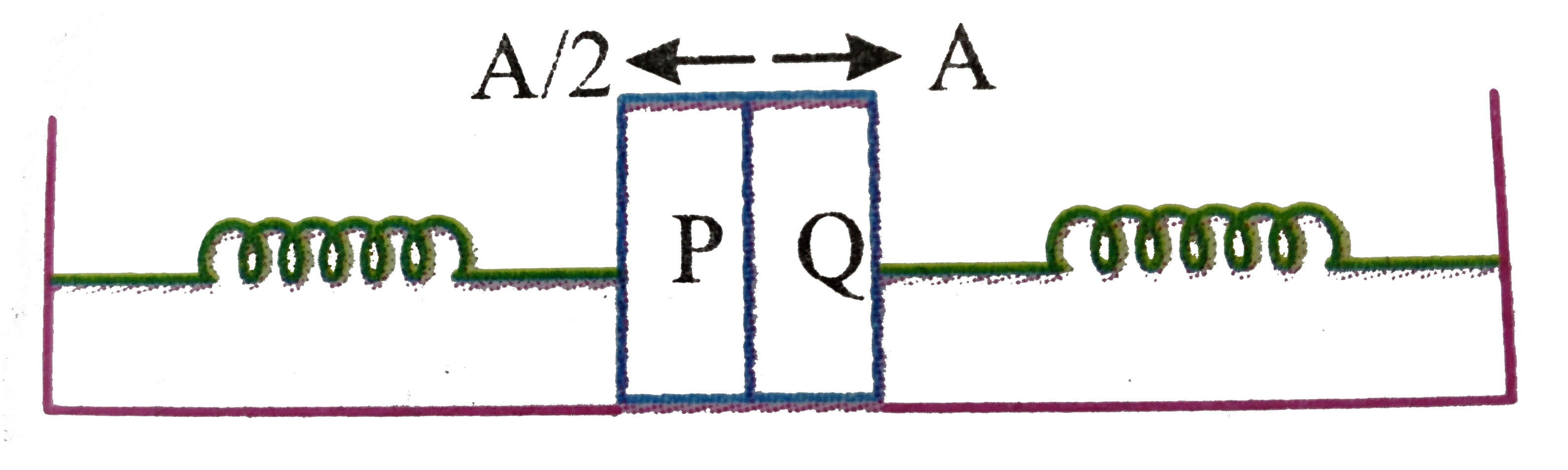
The energy of oscillation of the combined mass is
View SolutionFor `SHM` to take place force acting on the body should be proportional to `-x` or `F =- kx`. If `A` be the amplitude then enegry of oscillation is `1//2KA^(2)`.
If enegry of oscillation is `18J`, between what points does the block will oscillate?
View SolutionFor `SHM` to take place force acting on the body should be proportional to `-x` or `F =- kx`. If `A` be the amplitude then energy of oscillation is `1//2KA^(2)`.
The amplitude of oscillation is
View SolutionA circular tube of uniform cross section is filled with two liquids densities `rho_(1)` and `rho_(2)` such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle `theta` with horizontal find the value of `theta.`

View SolutionTwo identical balls `A and B` each of mass `0.1 kg` are attached to two identical mass less is springs. The spring-mass system is constrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horizontal plane. The center of the balls can move in a circle of radius `0.06 m`. Each spring has a natural length of `0.06 pi m` and force constant `0.1 N//m`. Initially, both the balls are displaced by an angle `theta = pi//6` radians with respect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the ball A when A and B are at the two ends of the diameter PQ.

View SolutionTwo identical balls (A) and (B) each of mass (0.1 kg), are attached to two identical massless springs. The spring - mass system is constrained to move inside a riged smooth pipe bant in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius (0.06 pi) meter. Each spring has a natural length `zof0.06 pi` meter and spring spring constant5 `0.1 N//m`. Initially, both the balls are displaced by an angle `theta = pi// 6` radian with respect to the diameter (pQ) of the circle (as shown in Fig.) and released from, rest.
 .
.
(i) Calculate the frequency of oscillation of ball (B).
(ii) Find the speed of ball (A) when (A) and (B) are at the two ends of the diameter (PQ).
(iii) What is the total energy of the system.
View SolutionYou are riding an automobile of mass 3000kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by` 50%` during one complete oscillation. Estimate the values of (a) the spring constant k and (b) damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports `750kg.g=10m//s^(2)`.
View SolutionIn the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between `m_(2)` and `m_(1)` is `mu`. There is no friction between `m_(1)` and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock `m_(2)` is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?
View SolutionIn the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between `m_(2)` and `m_(1)` is `mu`. There is no friction between `m_(1)` and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock `m_(2)` is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?
View Solution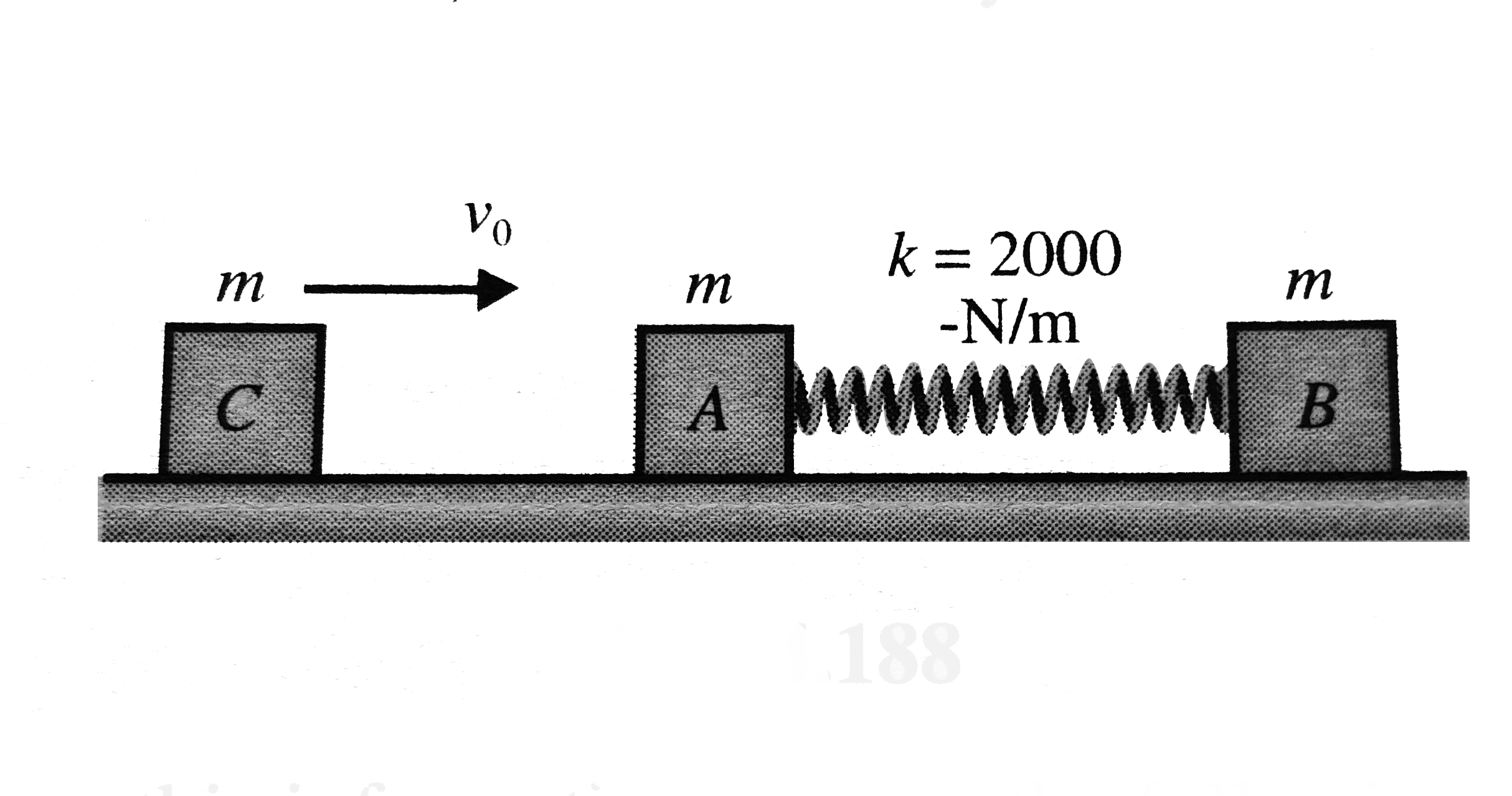
Two identical blocks A and B, each of mass `m=3kg`, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity `v_0=0.6(m)/(s)` collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. Oscillation energy of the system i.e., part of the energy which is oscillation (changing) between potention and kinetic forms is
View Solution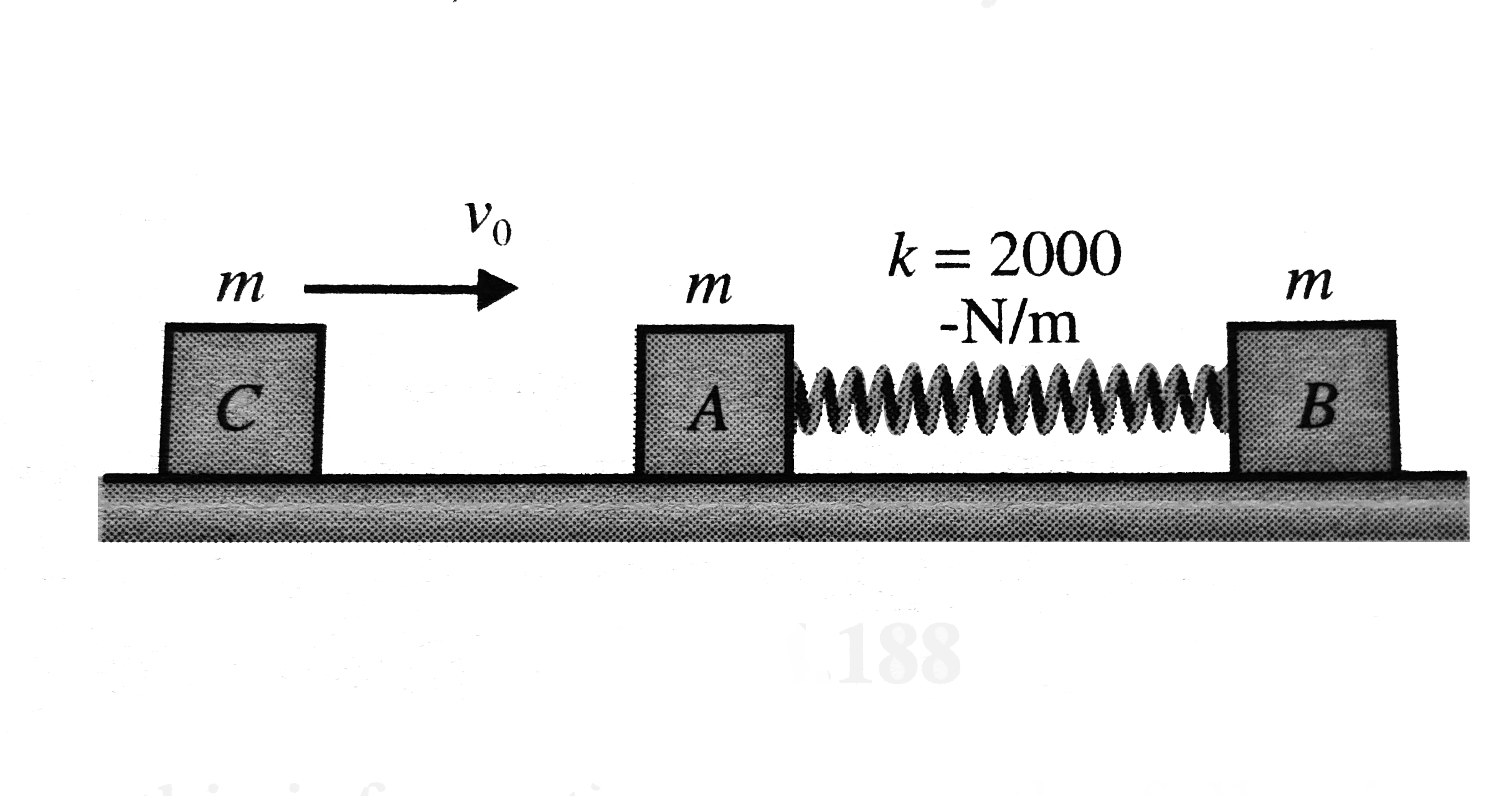
Two identical blocks A and B, each of mass `m=3kg`, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity `v_0=0.6(m)/(s)` collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. The maximum compression of the spring is
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant `k=(2mg)/(L)` and natural length `10L` The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. As the block is coming down, the maximum speed attained by the block is
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant `k=(2mg)/(L)` and natural length `10L` The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed is
View Solution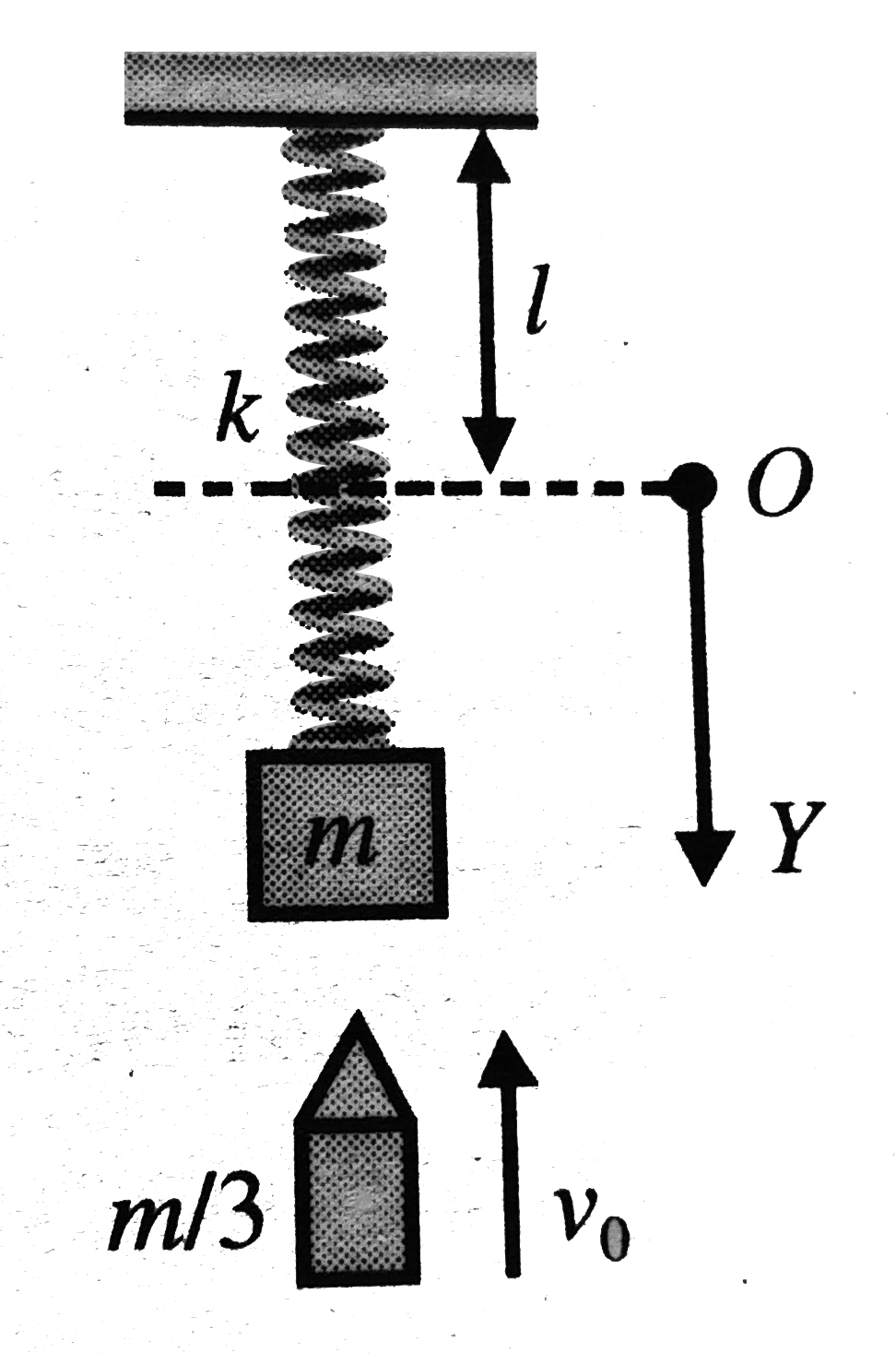
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass `(m)/(3)` moving in vertical up wards direction with velocity `v_0` strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The amplitude of oscillation would be
View Solution
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass `(m)/(3)` moving in vertical up wards direction with velocity `v_0` strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from `y=(mg)/(k)` (initial equilibrium position) to `y=0` (natural length of spring) is (A represents the amplitude of motion)
View Solution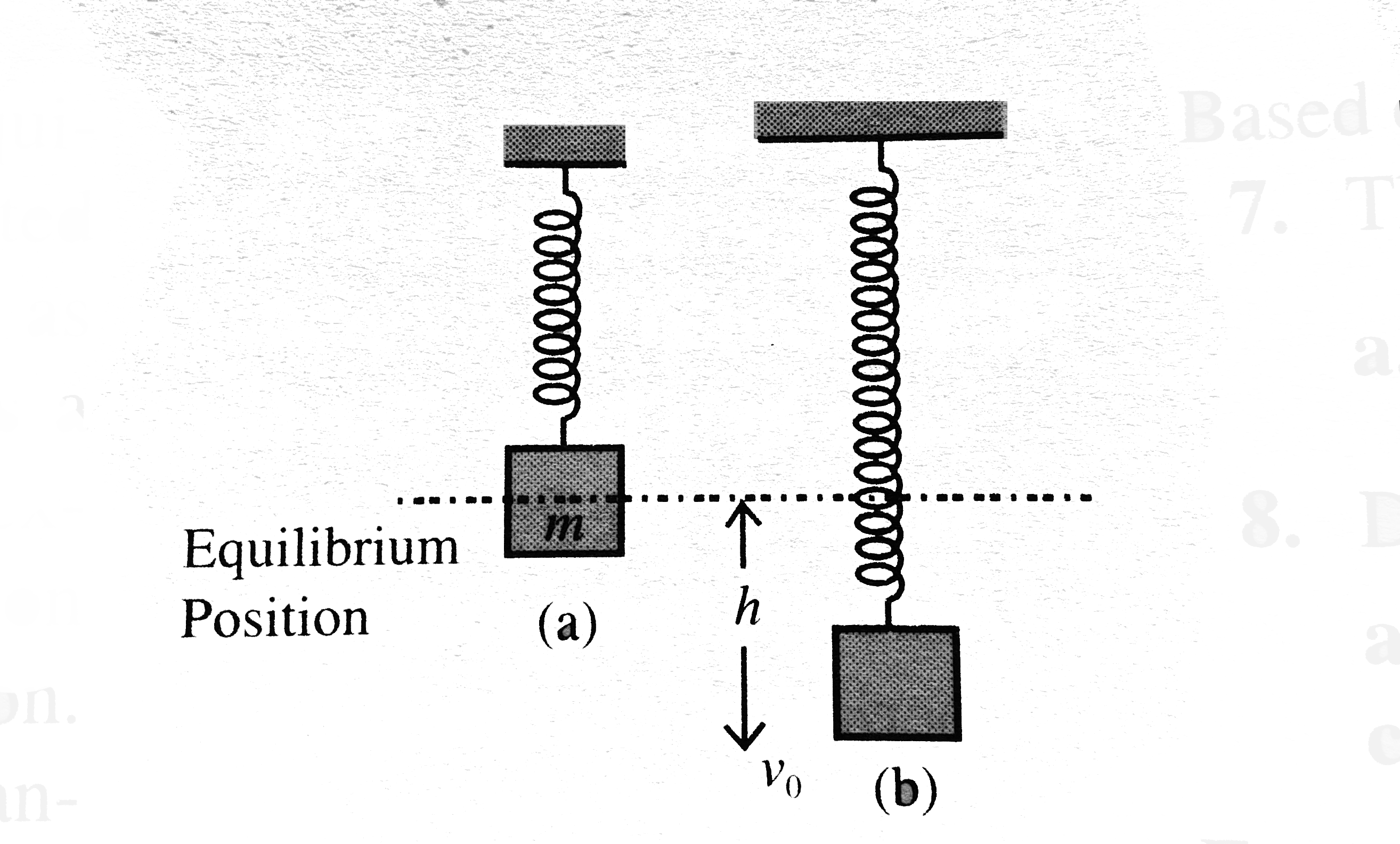
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed `v_0` towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The equation for the simple harmonic motion is
View Solution
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed `v_0` towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. Find the time taken by the block to cross the mean position for the first time.
View SolutionA plank of mass `M` is placed on a smooth hroizonal surface. Two light identical springs each of stiffness `k` are rigidly connected to structs at the ends of the plank as shown. When the spring are in their unextended position the distance between their free ends is `3l`. a block of mass `m` is placed on the plank and pressed aganist one of the springs so that it is compressed by `l`. To keep the blocks at rest it is connected to the strut by means of a light string, initially the syetem is at rest. Now the string is burnt.
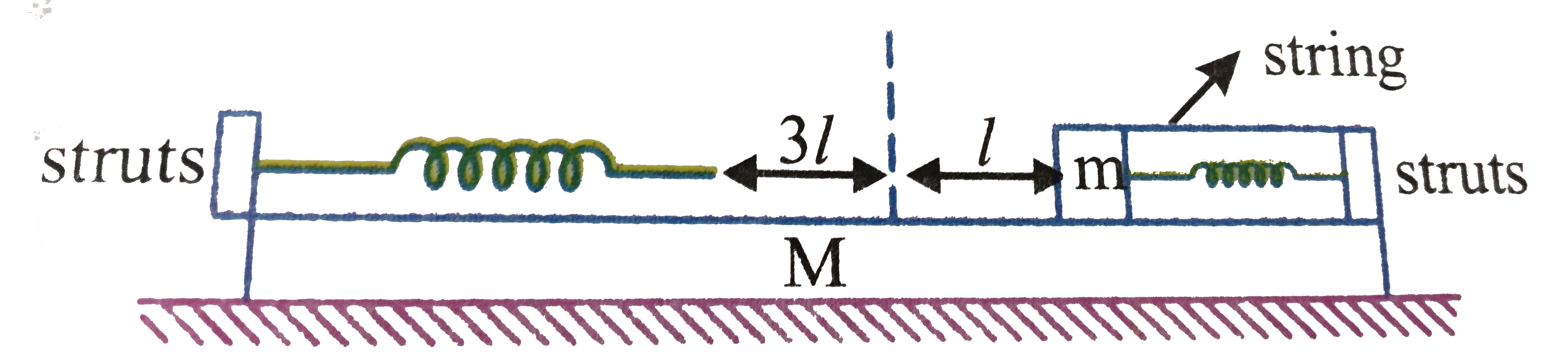
Time period of oscillation of block:
View SolutionTwo blocks of masses `3kg` block is attached to a spring with a force constant, `k k = 900N//ma` which is compressed `2m` initially from its equilibrium position. When `3kg` mass is released, it strikes the `6kg` mass and the two stick togther in an inelastic collision.
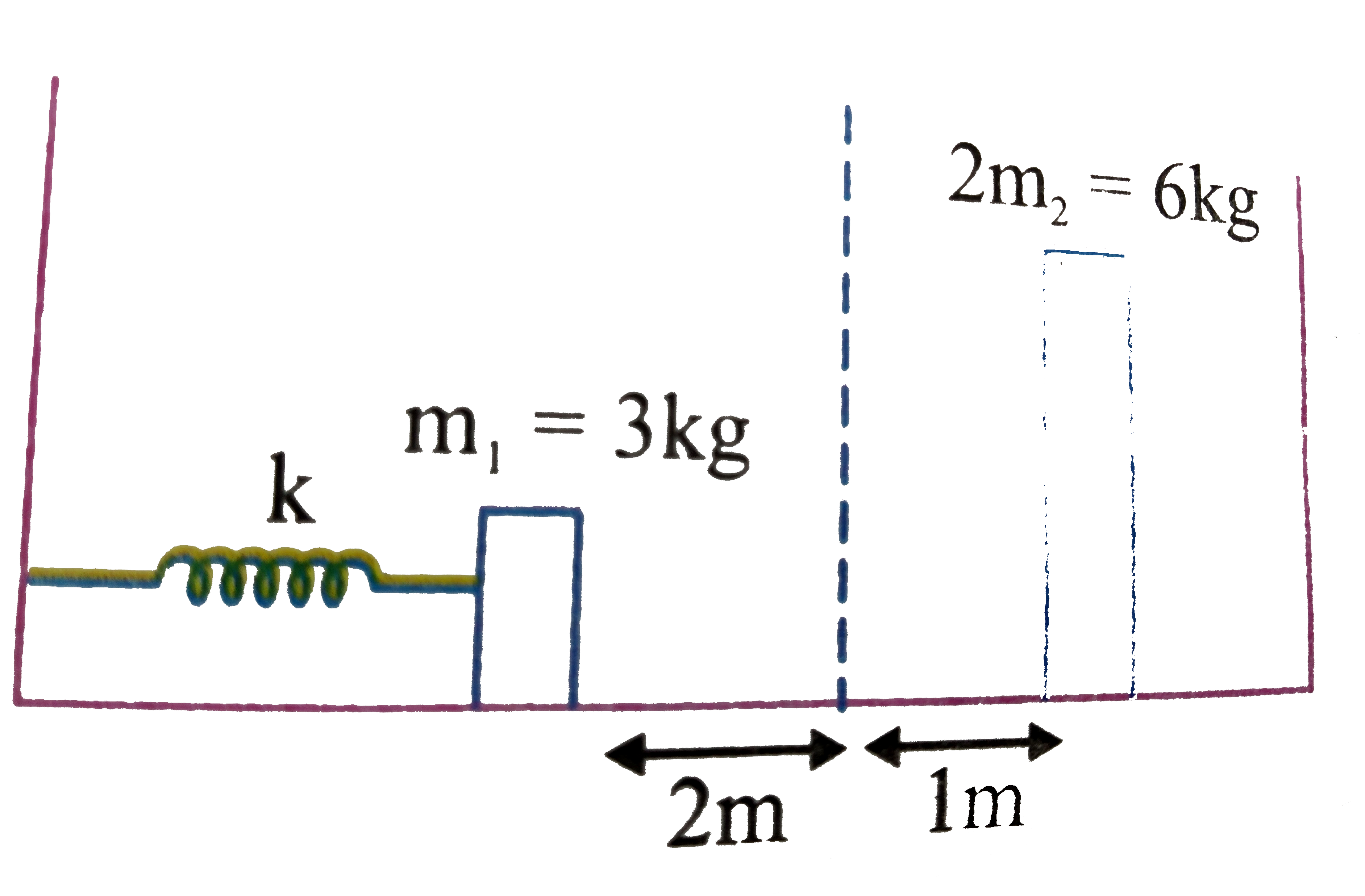
The amplitude of resulting oscillation after the collision is:
View SolutionTwo blocks of masses `3kg` block is attached to a spring with a force constant, `k k = 900N//ma` which is compressed `2m` initially from its equilibrium position. When `3kg` mass is released, it strikes the `6kg` mass and the two stick togther in an inelastic collision.
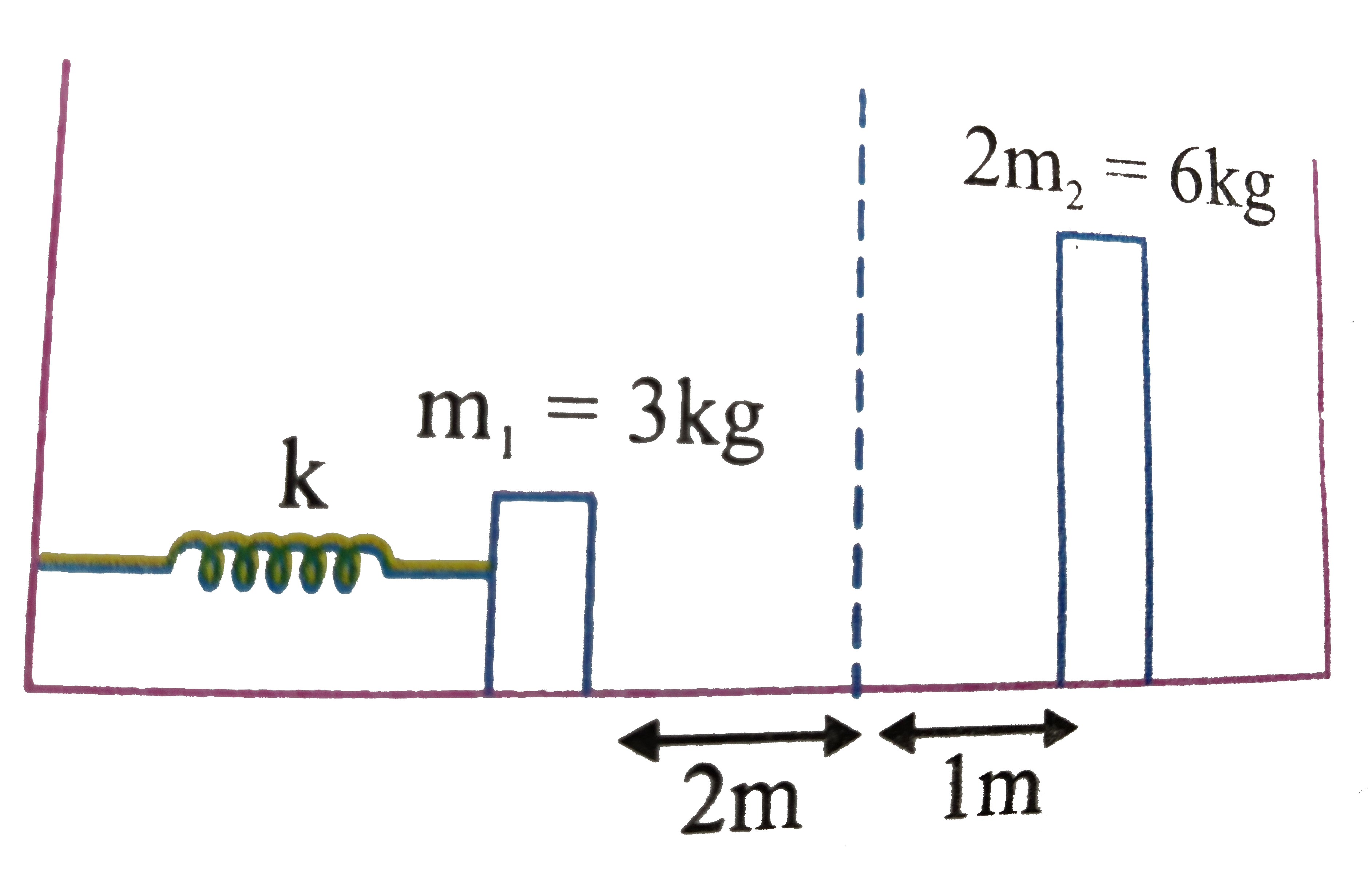
The velocities of a particle executing `S.H.M.` are `30cm//s` and `16 cm//s` when its displacements are `8cm` and `15cm` from the equilibrium position. then its amplitude of oscillation in cm is:
View SolutionA cube made of wood having specific gravity `0.4` and side length `a` is floated in a large tanck full of water.
If the cube is depressed slighly, it executes `SHM` from it's position. What is it's time period?
View SolutionA cube made of wood having specific gravity `0.4` and side length `a` is floated in a large tanck full of water.
What can be maximum amplitude of it's vertical simple harmonic motion?
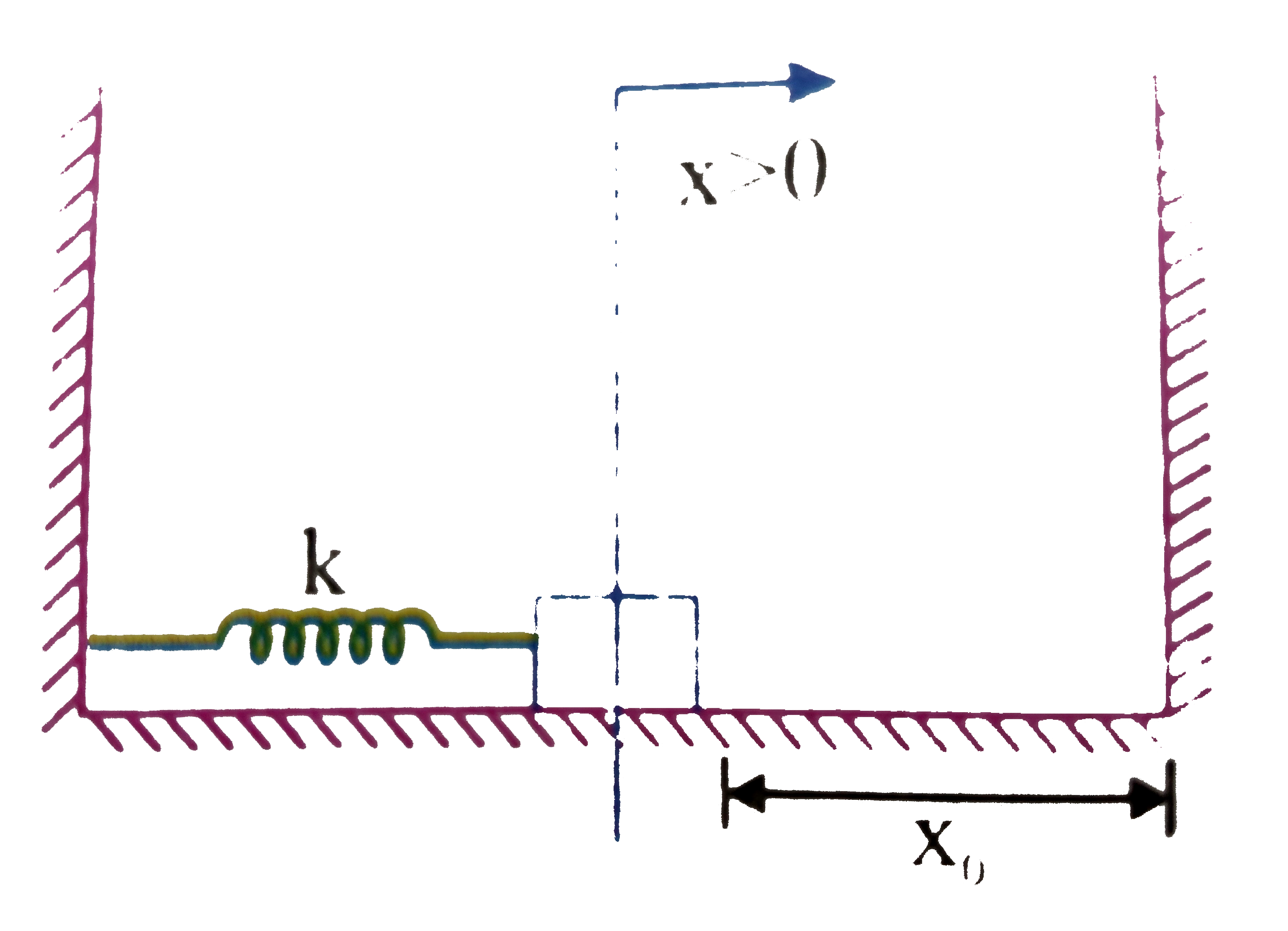
View SolutionA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression `2x_(0)` an block is released from rest. Collision with the wall `PQ` are elastic.
Write its equation of motion indicating position as a function of time:
View SolutionA block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression `2x_(0)` an block is released from rest. Collision with the wall `PQ` are elastic.
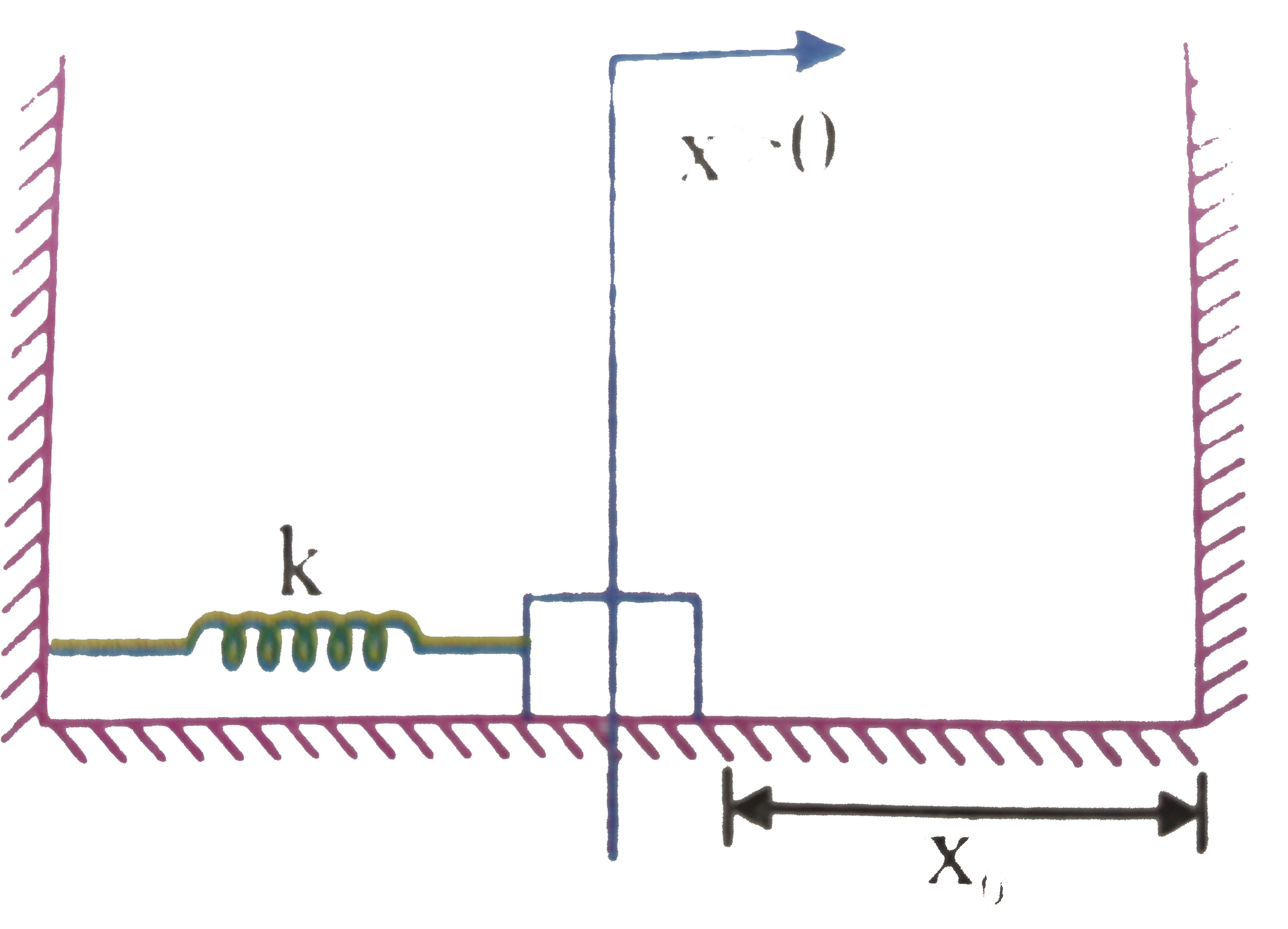
Draw `x-t` (position-time) graph for one period. Treating position of block in unstretched position of spring as origin
View SolutionA block is tied within two spring, each having spring constant equal to `k`. Initially the springs are in their natural length and horizontal as shown. The block is released from rest. The springs are ideal, acceleration due to gravity is `g` downwards. Air resistance is to be neglect. The natural length of spring is `l_(0)`.
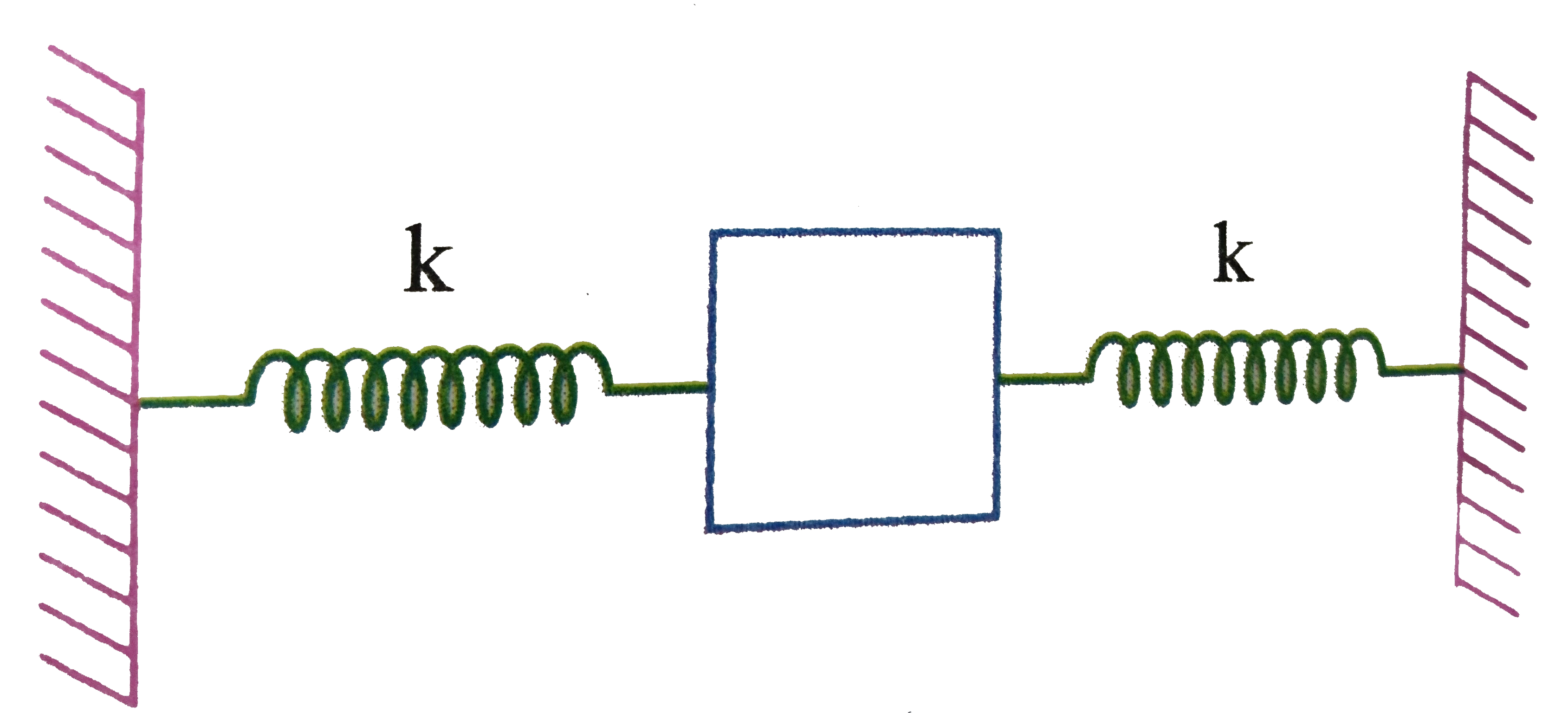
If the block is under equilibrium and the angle made by the spring with horizontal is `60^(@)` then the mass of the block is:
View SolutionA block is tied within two spring, each having spring constant equal to `k`. Initially the springs are in their natural length and horizontal as shown. The block is released from rest. The springs are ideal, acceleration due to gravity is `g` downwards. Air resistance is to be neglect. The natural length of spring is `l_(0)`.
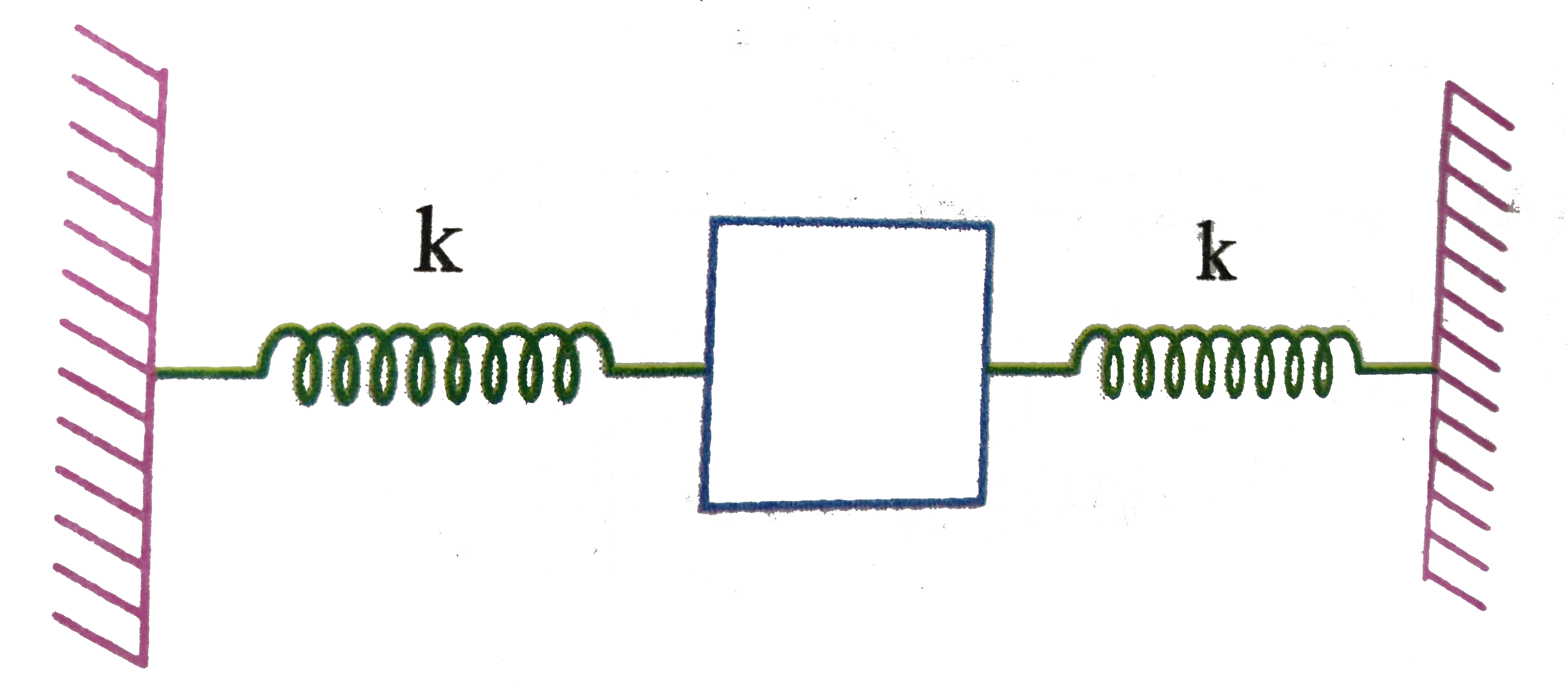
If the decrease in height of the block till its speed becomes zero is `sqrt(8l_(0))` then the mass of the block is:
View SolutionFor a particle oscillating along x-axis according to equation `x =A sin omegat`
The mean value of its velocity averaged over first `3//8` of the period is
View SolutionFor a particle oscillating along x-axis according to equation `x =A sin omegat`
The mean value of its velocity averaged over first `3//8` of the period is
View SolutionThe distabce travelled in a time, t by a particle moving along `x`-axis according to an equation `x = A cos omegat` is given by `S = nA +S_(0)`, when time `t` can be written as `t =n((T)/(4)) +t_(0)` such that `t_(0) lt T//4` and distance travelled in that `t_(0)` is `S_(0)`.
The distance `S` is, when 'n' is odd number.
View SolutionUsing graphical means find an amplitude `a` of oscillations resulting from the superposition of the following oscillations of the same direction `:`
`(a)``x_(1)=3.0 cos (omegat+pi//3), x_(2)=8.0 sin (omega t+ pi//6),`
`(b)` `x_(1)=3.0 cos omegat, x_(2)=5.0 cos (omegat+pi//4), x_(3)=6.0 sin omegat.`
View SolutionA point moves in the plane `y` according to the law `x = A sin omegat, y = B cos omegat`, where`A,B & omega` are positive constant.
The velocity of particle is given by
View SolutionA point moves in the plane `y` according to the law `x = A sin omegat, y = B cos omegat`, where`A,B & omega` are positive constant.
The acceleration of particle is given by [`:' barr` is position vector]
View Solution
Passage questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION