Complete Solutions to EXERCISE - IV of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | EXERCISE - IV |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
Two particles are executing SHM in a straight line. Amplitude A and the time period T of both the particles are equal. At time t=0, one particle is at displacement `x_(1)=+A` and the other `x_(2)=(-A/2)` and they are approaching towards each other. After what time they across each other? `T/4`
View SolutionA particle is executing SHM on a straight line. A and B are two points at which its velocity is zero. It passes through a certain point `P(APltBP)` at successive intervals of 0.5s and 1.5 s with a speed of 3m/s.
View SolutionA and B are two points on the path of a particle executing SHM in a straight line, at which its velocity is zero. Starting from a certain point X `(AXltBX)` the particle crosses this pint again at successive intervals of 2 seconds and 4 seconds with a speed of `5m//s`
Q. The ratio `(AX)/(BX)` is
View SolutionVertical displacement of a plank with a body of mass `'m'` on it is varying according to law `y=sin omegat +sqrt(3) cos omegat`. The minimum value of `omega` for which the mass just breaks off the plank and the moment it occurs first after `t=0` are given by: `(y "is positive vertically upwards")`
View SolutionA particle performing simple harmonic motion having time period 3 s is in phase with another particle which also undergoes simple harmonic motion at `t=0`. The time period of second particle is T (less that 3s). If they are again in the same phase for the third time after 45 s, then the value of T will be
View SolutionThe displacement `x` of a particle in motion is given in terms of time by `x(x-4) =1 -5 cos omegat`
View SolutionThe potential energy of a particle oscillating on x-axis is given as `U =20 +(x-2)^(2)`. The mean position is at
View SolutionA block A of mass m is placed on a frictionless horizontal surface. Another block B of the same mass is kept on A and connected to the wall with the helpf of a spring of force constant K as shown in the figure. The coefficient of friction between the blocks A and B is `mu`. The blocks move together execting simple harmonic motion of amplitude 'a'. What is the maximum value of the fricitional force between A and B ?
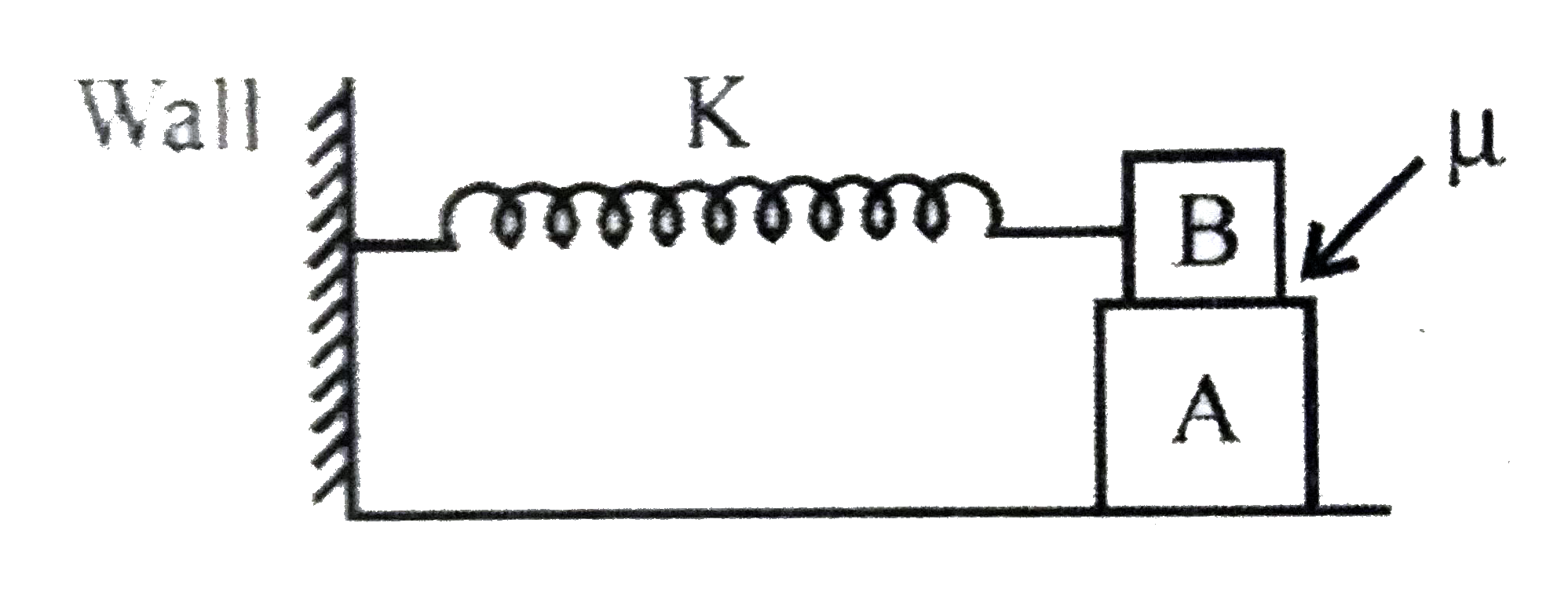
View SolutionTwo blocks lie on each other and connected to a spring as shown in figure. What should be the mass of blocks A placed on block B of mass 6 kg, so that the system's period is 0.75 s ? Assume no slipping, what should be the minimum value of coefficient of static friction `mu_(s)` for which block A will not slip relative to block B, if block B is displaced 50 mm from equilibrium position and released ?

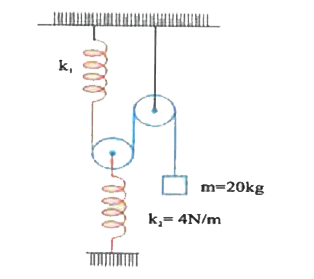
View SolutionIn the device shown in the figure, the block of mass 20 kg is displaced down slighty and released, it starts oscillating. Pulleys are smooth and massless, strings and springs are also massless. Find the time period of oscillation `(K_(1) = 4 N//m, K_(2) = 4N//m)`
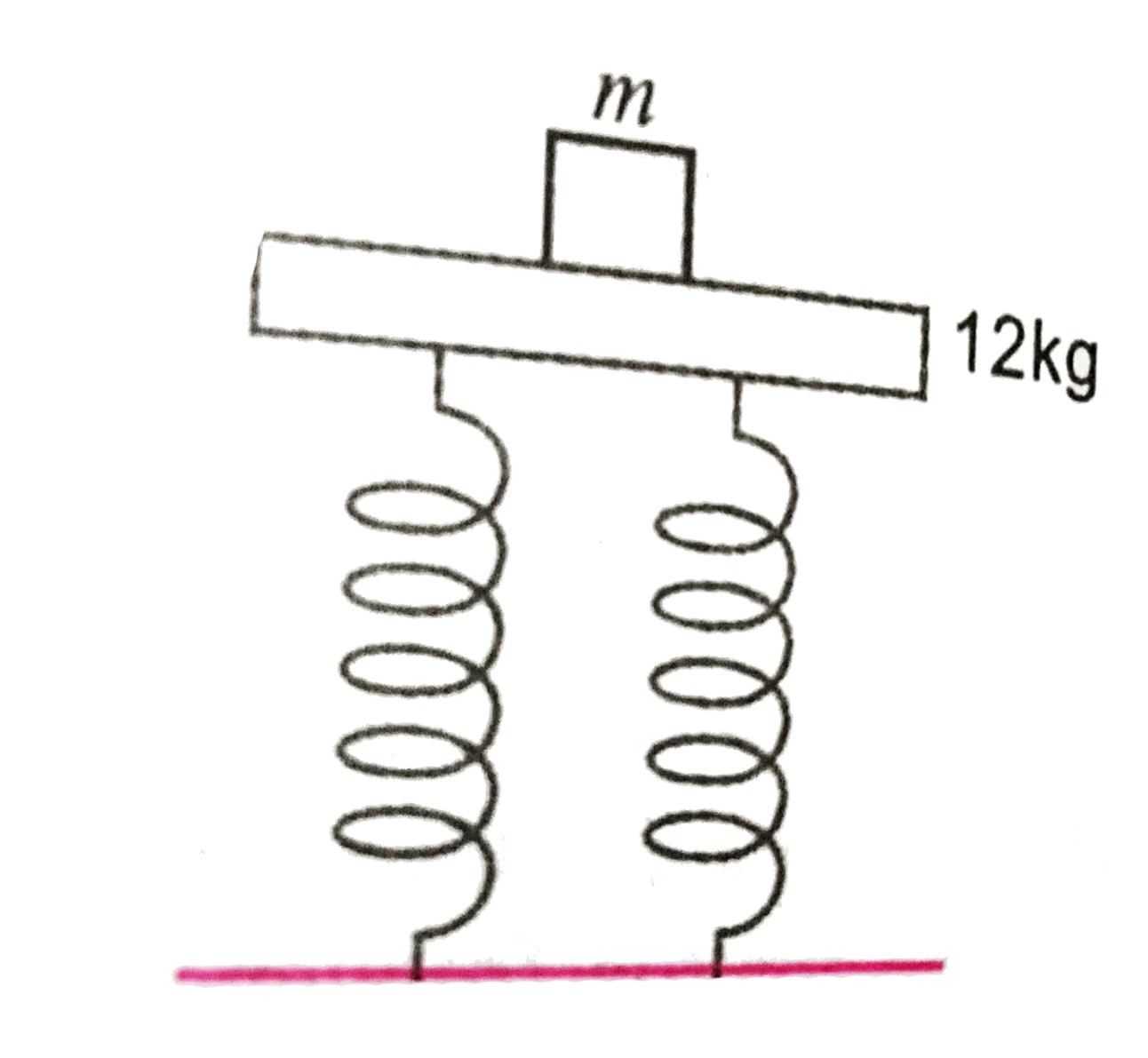
View SolutionA tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
View SolutionA particle of mass 'm' is attached to three identical springs `A,B` and `C` each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance `x_(0)` from the block. The spring is then compressed by `2x_(0)` and released. The time taken to strike the wall is

View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be `2.0s`, the tension in the string when the bob passes through 'O' is
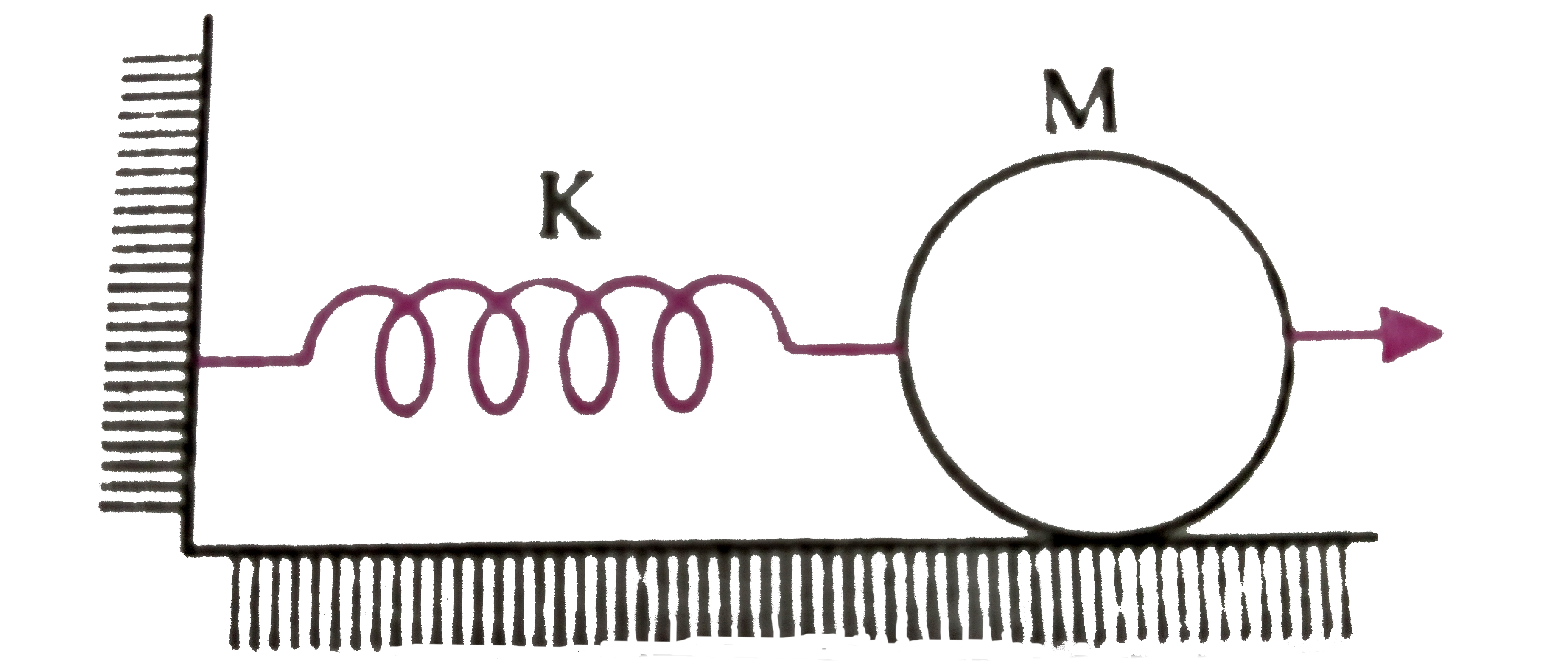
View SolutionA disc of mass `M` is attached to a horizontal massless spring of force constant `K` so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes `SHM` with a period of
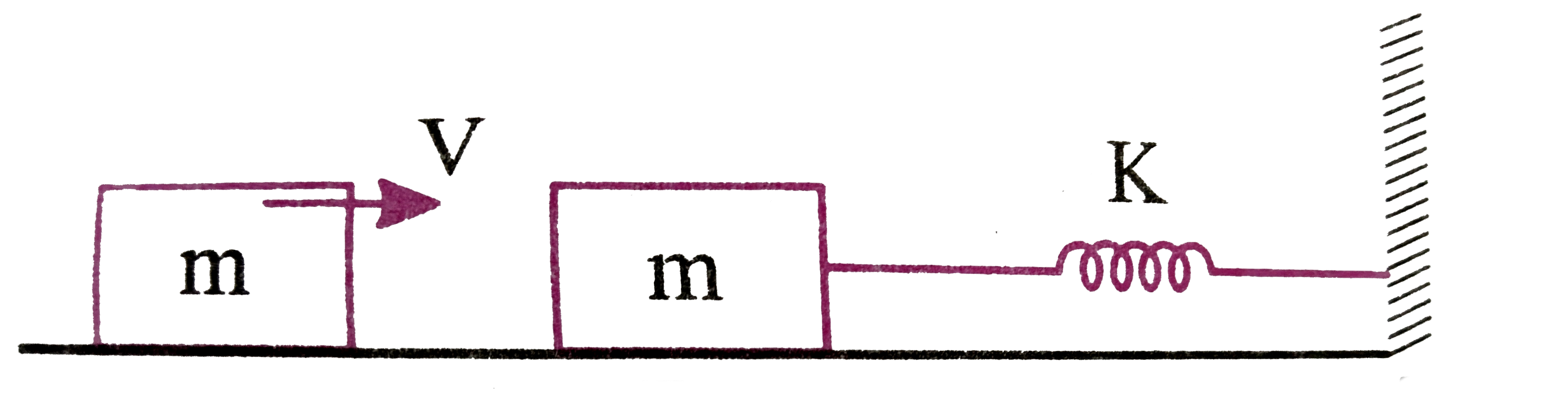
View SolutionA block of mass 'm' collides perfectly inelastically with another identical block connected to a spring of of force constant 'K'. The amplitude of resulting `SHM` will be
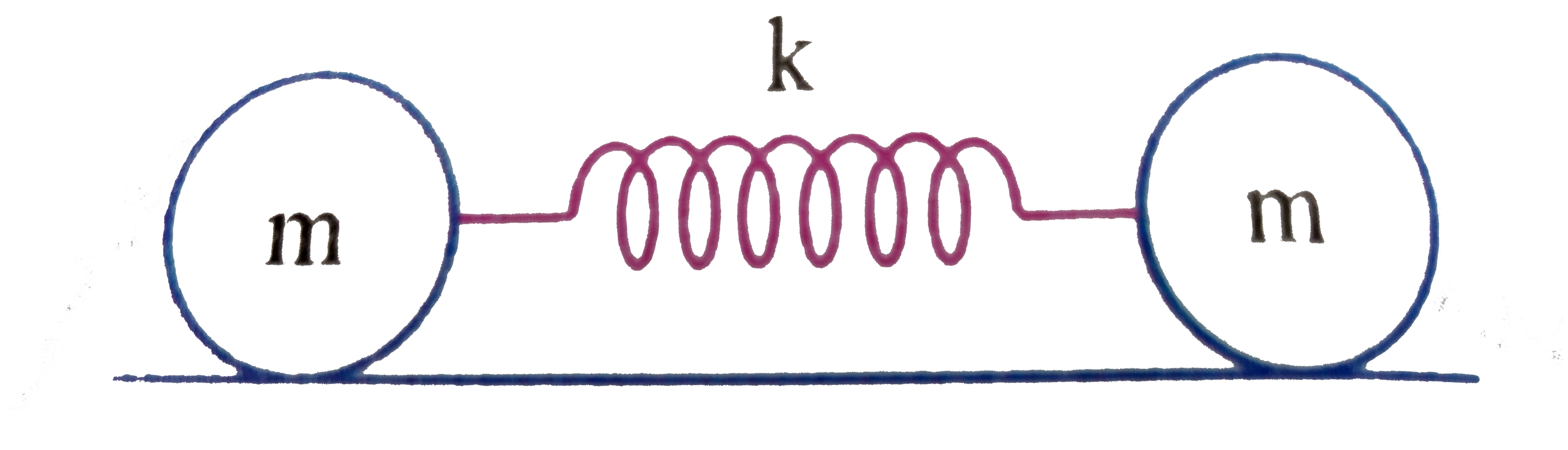
View SolutionTwo identical particles each of mass `0.5kg` are interconnected by a light springs of stiffness `100N//m`, time period of small oscillation is ….
View SolutionThe kinetic energy of SHM is 1/n time its potential energy. If the amplitude of the SHM be A, then what is the displacement of the particle ?
View SolutionThe potential energy of a particle oscillating along x-axis is given as
`U=20+(x-2)^(2)`
Here, `U` is in joules and `x` in meters. Total mechanical energy of the particle is `36J`.
(a) State whether the motion of the particle is simple harmonic or not.
(b) Find the mean position.
(c) Find the maximum kinetic energy of the particle.
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionTime period of a simple pendulum of length L is `T_(1)` and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is `T_(2)`. Amplitude of osciallations in both the cases is small. Then `T_(1)/T_(2)` is
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionIn an experiment with bar pendulum having four holes, the same time period is recorded when it is suspended at distances `12cm, 24cm, 40cm` and `52cm` respectively form one end. The length of bar pendulum is
View SolutionA sphere of radius r is kept on a concave mirror of radius of curation `R`. The arrangement is kept on a horizontal surface (the surface of concave mirror is friction less and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes `S.h.M.` The period of oscillation will be
View SolutionA disc of radius `R` and mass `M` is pivoted at the rim and it set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
View SolutionThe maximum tension in the string of an oscillating simple pendulum is 3% more than the minimum tension in the string. The angular amplitude of oscillations of the pendulum is
View SolutionThe equation of a damped simple harmonic motion is `m(d^2x)/(dt^2)+b(dx)/(dt)+kx=0`. Then the angular frequency of oscillation is
View SolutionA simple pendulum is set up in a trolley which moves to the right with an acceleration a on a horizontal plane. Then the thread of the pendulum in the mean position makes an angle `theta` with the vertical
View SolutionA particle is executing SHM along a straight line. Its velocities at distances `x_(1)` and `x_(2)` from the mean position are `v_(1)` and `v_(2)`, respectively. Its time period is
View SolutionA small mass m attached to one end of a spring with a negligible mass and an unstretched length L, executes vertical oscillations with angular frequency `omega_(0)`. When the mass is rotated with an angular speed `omega` by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during this rotation is
View SolutionA circular disc fixed at its centre to a metal wire and the other end of the wire is clamped. The disc is rotated about the wire as axis and is released. The disc about this axis makes simple harmonic oscillations with a frequency of `(1)/(2)`Hz. If moment of inertia of the disc about this axis is 0.1 kg `-m^(2)`, the torsional constant of the wire is
View SolutionA vertical spring has a time period of oscillations of `T_(1)` with a load `m_(1)` at its end. Its time period is `T_(2)` when the load is replaced by another of mass `m_(2)`. The force constant of the spring is
View SolutionA simple pendulum is oscillating with a maximum angular displacement of `theta` radian. If `theta` is very small, the ratio of maximum tension to the minimum tension in the string during oscillations is
View SolutionThe time period of a simple pendulum is T. When the length is increased by 10 cm, its period is `T_(1)`. When the length is decreased by 10 cm, its period is `T_(2)`. Then, the relation between T, `T_(1)` and `T_(2)` is
View SolutionThe seconds hand of pendulum clock (P) and that of a clock working based on spring oscilations (S) tick 60 divisions in one minute on earth. If the two clocks are taken to the moon, where the acceleration due to gravity is (1/5. 76)th that on the earth, the number of divisions ticked by P and S respectively in an actual time of 1 minute will be
View SolutionA piece of wood has dimensions 'a', 'b' and 'c'. Its relative density is d. It is floating in water such that the side 'a' is vertical. It is now pushed down gently and relesed. The time-period of S.H.M. is
View SolutionTwo light springs of same length and same area of cross section are made of materials whose young's modulii of elasticity are in the ratio 1 : 2. When loads of same mass are attached to the two springs, the ratio of their respectively time periods of oscillations is
View SolutionA pendulumd made of a uniform wire of cross sectional area (A) has time T.When an additionl mass (M) is added to its bob, the time period changes to `T_(M). If the Young's modulus of the material of the wire is (Y) then `1/Y` is equal to:
View SolutionAn ideal gas enclosed in a vertical cylindrical container supports a freely moving pistion of mass M. The pistion and the cylinder have equal cross sectional area A. When the pistion is in equilibrium, the volume of the gas is `V_(0)` and its pressure is `P_(0)`. The pistion is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the pistion executes a simple harmonic motion with frequency
View SolutionOne end of a long mettalic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass M hangs freely from the free end of the spring. The area of cross-section and Young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to
View SolutionA body of mass m is situated in a potential field `U(x)=U_(0)(1-cosalphax)` when `U_(0)` and `alpha` are constant. Find the time period of small oscialltions.
View Solution
EXERCISE - IV questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION