Complete Solutions to LEVEL -II (C.W) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | LEVEL -II (C.W) |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
Displacement time equation of a particle executing `SHM` is, `x = 10 sin ((pi)/(3)t+(pi)/(6))cm`. The distance covered by particle in `3s` is
View SolutionThe period of a particle in SHM is `8s`. At `t=0` it is at the mean position. The ratio of the distances travled by it in the first and the second second is
View SolutionThe equation of motion of a particle started at `t=0` is given by `x=5sin(20t+pi//3)` where x is in centimeter and t in second. When does particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
View SolutionA particle executes simple harmonic motion with a period of `16s`. At time `t=2s`, the particle crosses the mean position while at `t=4s`, its velocity is `4ms^-1` amplitude of motion in metre is
View SolutionTwo simple harmonic are represented by the equation `y_(1)=0.1 sin (100pi+(pi)/3) and y_(2)=0.1 cos pit`.
The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is.
View SolutionA particle is moving in a circel of radius `R = 1m` with constant speed `v =4 m//s`. The ratio of the displacement to acceleration of the foot of the perpendicular drawn from the particle onto the diameter of the circel is
View SolutionA body dropped from a height `h` onto the floow makes elastic collision with the floow. The frequency of oscillation of its periodic motion is
View SolutionA particle executes `SHM` on a straight line. At two positions, its velocities are `u` and `v` whle accelerations are `alpha` and `beta` respectively `[beta gt alpha gt ]`.The distance between these two positions is
View SolutionA particle performing `SHM` having amplitude 'a' possesses velocity `((3)^(1//2))/(2)` times the velocity at the mean position. The displacement of the particle shall be
View SolutionA particle moves such that its acceleration is given by `a =- beta (x-2)` Here `beta` is positive constant and `x` is the position form origin. Time period of oscillation is
View SolutionA body executes `SHM` has its velocity `10cm//s` and `7cm//s` when its displacements from mean positions are `3cm` and `4cm` respectively. The length of path is nearly
View SolutionA large horizontal surface moves up and down in SHM with an amplitude of 1 cm . If a mass of 10 kg (which is placed on the surface) is to remain continually in contact with it, the maximum frequency of S.H.M. will be
View SolutionThe time period of oscillation of a `SHO` is `(pi)/(2)s`. Its acceleration at a phase angle `(pi)/(3) rad` from exterme position is `2ms^(-1)`. What is its velocity at a displacement equal to half of its amplitude form mean position? (in `ms^(-1)`
View SolutionA particle under the action of a force has a period of `3s` and under the action of another force it has a period `4sec` in `SHM`. What will be its period under the combined action of both forces in the same direction?
View SolutionA particle executes `SHM` with an amplitude of `10cm` and frequency `2 Hz`. At `t = 0`, the particle is at a point where potential energy and kinetic energy are same. The equation for its displacement is
View SolutionFor a particle executing `SHM`, the kinetic energy `(K)` is given by `K = K_(0)cos^(2) omegat`. The equation for its displacement is
View SolutionA body is executing simple harmonic motion. At a displacement `x` its potential energy is `E_(1)` and at a displacement `y` its potential energy is `E_(2)` The potential energy `E` at displacement `(x+y)` is
View SolutionA body is executing `SHM` under action of the a force of whose maximum is `50 N`. magnitude of force acting on the particle at the time when its energy is half kineic energy and half potential is (Assume potential energy to be zero at mean position).
View SolutionA body of mass `0.5kg` is performing `SHM` with a time period `.^(pi)//_(2)` seconds. If its velocity at mean position is `1ms^(-1)`, then restoring force acting on the body at a phase angle `60^(@)` from exterme position is
View SolutionA body of mass 'm' is suspended to an ideal spring of force constant 'k'. The expected change in the position of the body due to an additional force 'F' acting vertically downwards is
View SolutionA spring balance has a scale that reads `0` to `20kg`. The length of the scale is `10cm`. A body suspended from this balance, when displaced and released, oscillates with period of `(pi)/(10)s`. The mass of the body is
View SolutionWhen a body of mass `1.0 kg` is suspended from a certain light spring hanging vertically, its length increases by `5cm`. By suspending `2.0kg` block to the spring and if the block is pulled through `10cm` and released, the maximum velocity of it in `m//s is (g = 10 m//s^(2))`
View SolutionA spring of force constant `k` is cut into two parts whose lengths are in the ratio `1:2`. The two parts are now connected in parallel and a block of mass `m` is suspended at the end of the combined spring. The period of oscillation of block is
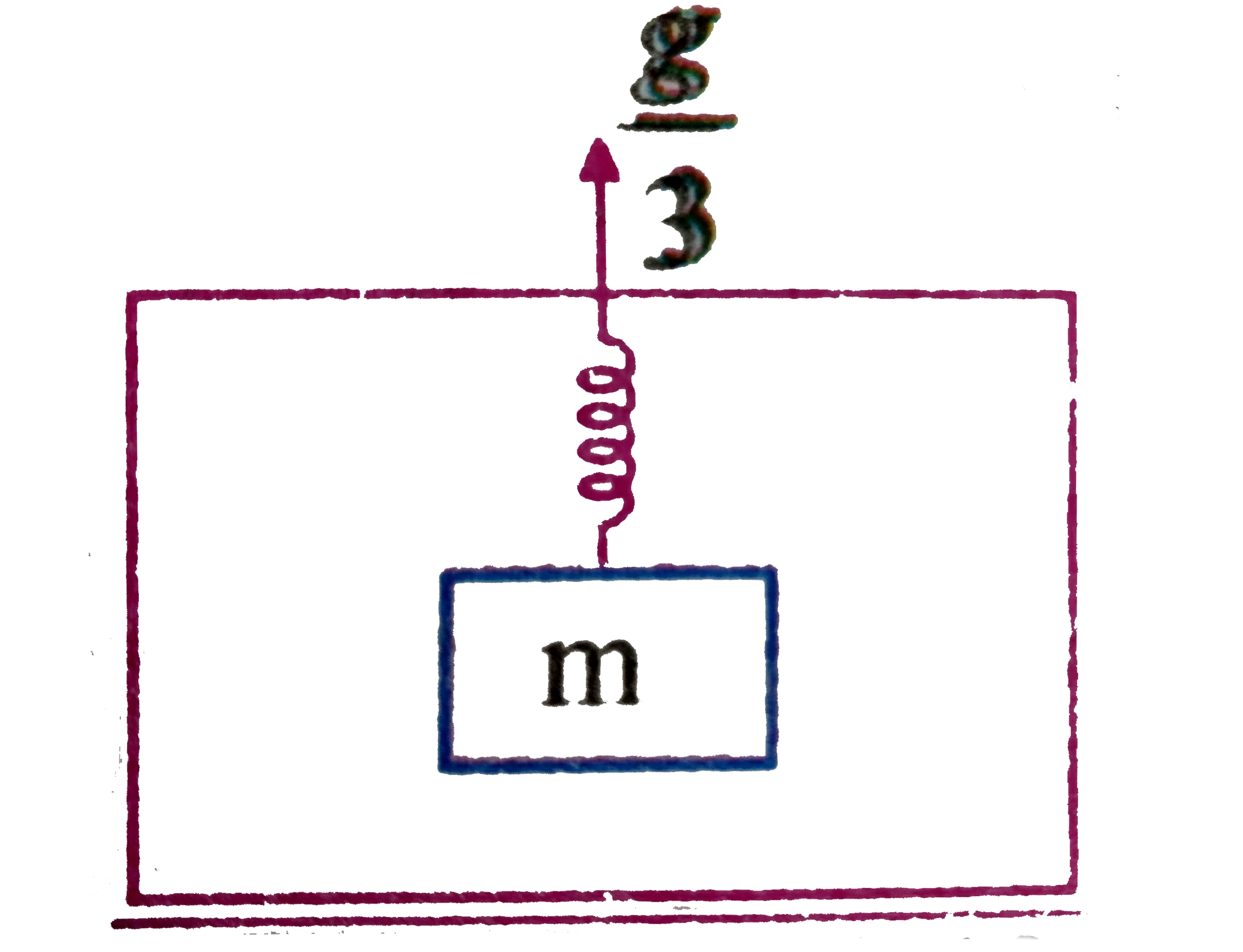
View SolutionA spring of spring constant `200N//m` has a block of mass `1kg` hanging at its one end and other end of spring is attached to ceiling of an elevator. The elevator is rising upwards with an acceleration `g//3`. What should be the angular frequency and elongation during the time when the elevator is accelerating?
View SolutionA block of mass `1kg` is connected with a massless spring of force constant `100 N//m`. At `t = 0`, a constant force `F = 10N` is applied on the block. The spring is in its netural length at `t = 0`. The speed of particel at `x = 6cm` form mean position is
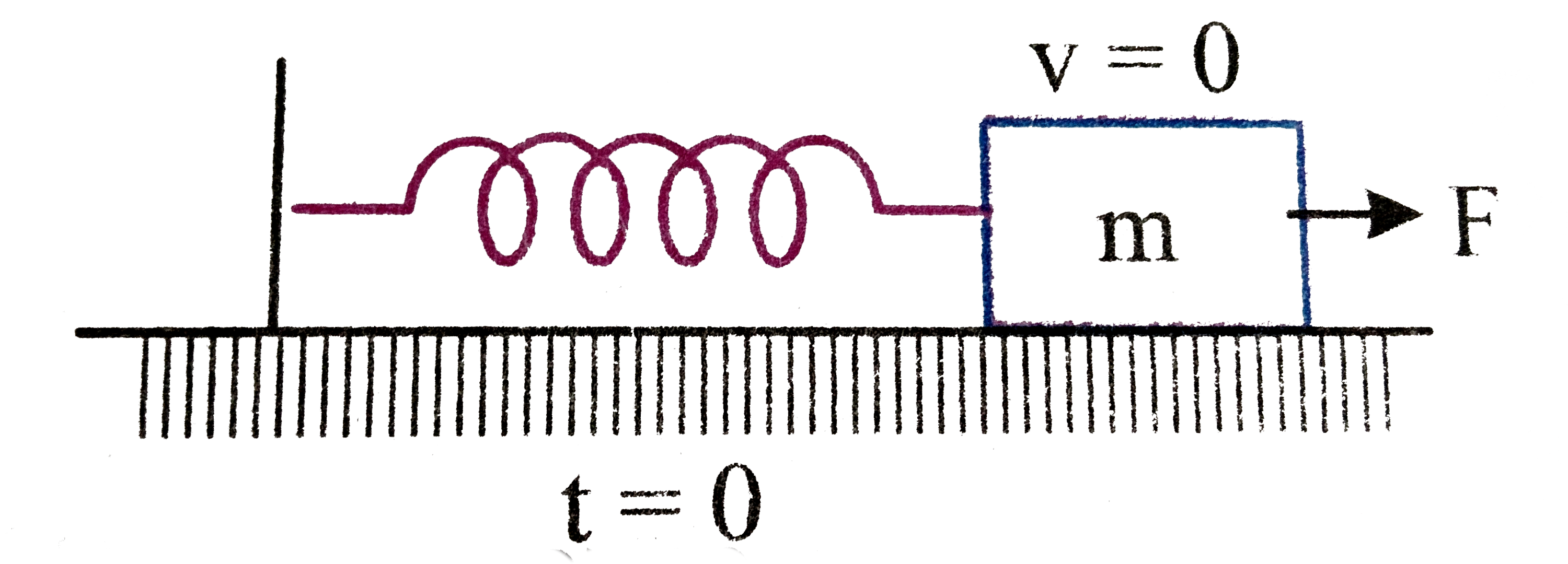
View Solution`A` mass `M` is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period `T`. If the mass is increased by `m`, the time period becomes `(5T)/(3)`. Find the ratio of `m//M`.
View SolutionTwo masses `m_(1)`and `m_(2)` are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, `m_(1)` is gently removed. The angular frequency and amplitude of oscillation of `m_(2)` will be respectively
View SolutionA block of mass `M` suspended from a spring oscillates with time period `T`. If spring is cut in to two equal parts and same mass `M` is suspended from one part, new period os oscillation is
View SolutionThe matallic bob of a simple pendulum has the relative density `rho`. The time period of this pendulum is `T` it the metallic bob is immersed in water the new time period is given by
View SolutionA simple pendulum with a brass bob has a period `T`. The bob is now immersed in a nonviscous liquid and oscillated. If the density of the liquid is `1//8th` of brass, the time period of the same pendulum will be
View SolutionA pendulum clock is taken `1km` inside the earth from mean sea level. Then the pendulum clock
View SolutionA simple pendulum of length `l` is connected to the ceiling of a vehicle that is moving down along a smooth inclined plane `4` in `5`. Then its period of oscillation is
View SolutionA pendulum suspended from the roof of an elevator at rest has a time period `T_(1)`, when the elevator moves up with an acceleration `a` its time period becomes `T_(2)`, when the elevator moves down with an acceleration `a`, its time period becomes `T_(3)`, then
View SolutionTime period of a simple pendulum inside a lift that is accelerating up at `2ms^(-2)` is `T_(1)`. If left is retarding down at `6ms^(-2)` then time period of same pendulum is `T_(1)`. Then `T_(1)//T_(2)` is
View SolutionA pendulum has a period `T` for small osillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.

View SolutionA particle of mass (m) is attached to a spring (of spring constant k) and has a narural angular frequency omega_(0). An external force `R(t)` proportional to cos omegat(omega!=omega)(0) is applied to the oscillator. The time displacement of the oscillator will be proprtional to.
View Solution
LEVEL -II (C.W) questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION