Complete Solutions to LEVEL -III of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | LEVEL -III |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
Two particles are in `SHM` in a straight line about same equilibrium position. Amplitude `A` and time period `T` of both the particles are equal. At time `t=0`, one particle is at displacement `y_(1)=+A` and the other at `y_(2)=-A//2`, and they are approaching towards each other. after what time they cross each other?
View SolutionTwo particles undergo `SHM` along the same line with the same time period `(T)` and equal amplitude `(A)`. At a particular instant one is at `x =- A` and the other is at `x =0`. If they start moving in the same direction then they will cross each other at

(i) `t = (4T)/(3)` (ii) `t = (3T)/(8)` (iii) `x = (A)/(2)` (iv) `x = (A)/(sqrt(2))`
View SolutionA particle starts SHM from mean position O executing SHM A and B are the two point at which its velocity is zero . It passes through a certain point P at time `t_(1) = 0.5 and t_(2) = 1.5 s` with a speed of `3 m//s`.

i. The maximum speed .......
ii. ratio `AP//PB` .....
View SolutionA particle starts SHM from mean position O executing SHM A and B are the two point at which its velocity is zero . It passes through a certain point P at time `t_(1) = 0.5 and t_(2) = 1.5 s` with a speed of `3 m//s`.

i. The maximum speed .......
ii. ratio `AP//PB` .....
View SolutionVertical displacement of a plank with a body of mass `'m'` on it is varying according to law `y=sin omegat +sqrt(3) cos omegat`. The minimum value of `omega` for which the mass just breaks off the plank and the moment it occurs first after `t=0` are given by: `(y "is positive vertically upwards")`
View SolutionA particle performing simple harmonic motion having time period 3 s is in phase with another particle which also undergoes simple harmonic motion at `t=0`. The time period of second particle is T (less that 3s). If they are again in the same phase for the third time after 45 s, then the value of T will be
View SolutionA partical slides back and forth between two inclined friction lessplanes.

a. If h is the initial height of the partical, the period of oscillation……
b. Is the motion oscillatory? Is it SHM?
View SolutionA simple pendulum executing `SHM` in a straight line has zero velocity at 'A' and 'B' whose distances form 'O' in the same line `OAB` are 'a' and 'b'. If the velocity half wat between them is 'v' then its time period is
View SolutionThe `x-t` graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at `t = 4//3 s` is
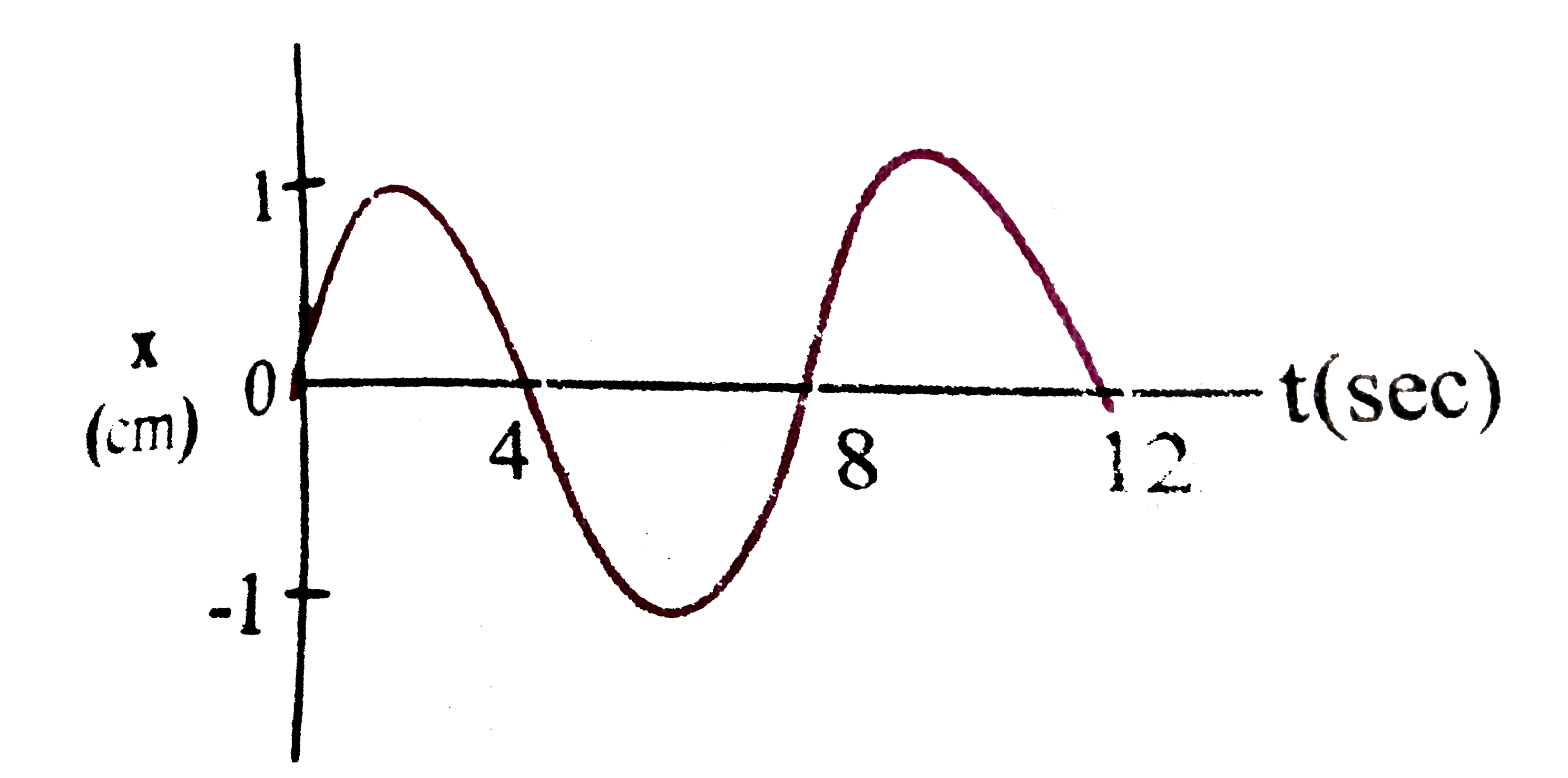
View SolutionThe displacement `x` of a particle in motion is given in terms of time by `x(x-4) =1 -5 cos omegat`
View SolutionThree `SHO's` of equal amplitude `A` and equal time period combine in the same direction. The difference in phase between successive `SHO's` os `60^(@)`ahead of the other. The amplitude of the resultant oscillation is
View SolutionThe potential energy of a particle oscillating on x-axis is given as `U +20 +(x-2)^(2)`. The mean position is at
View SolutionA particle of mass `4g` is in a gravitational potential `V =(800x^(2) +150) erg//g`. Its frequency of oscillation is
View SolutionA particle free to move along the (x - axis) hsd potential energy given by `U(x)= k[1 - exp(-x^2)] for -o o le x le + o o`, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionThe variation of potential energy `(U)` of a simple harmonic oscillator is as shown. Then force constant of the system is `(PE` is in joules, displacement 'x' is in mm)
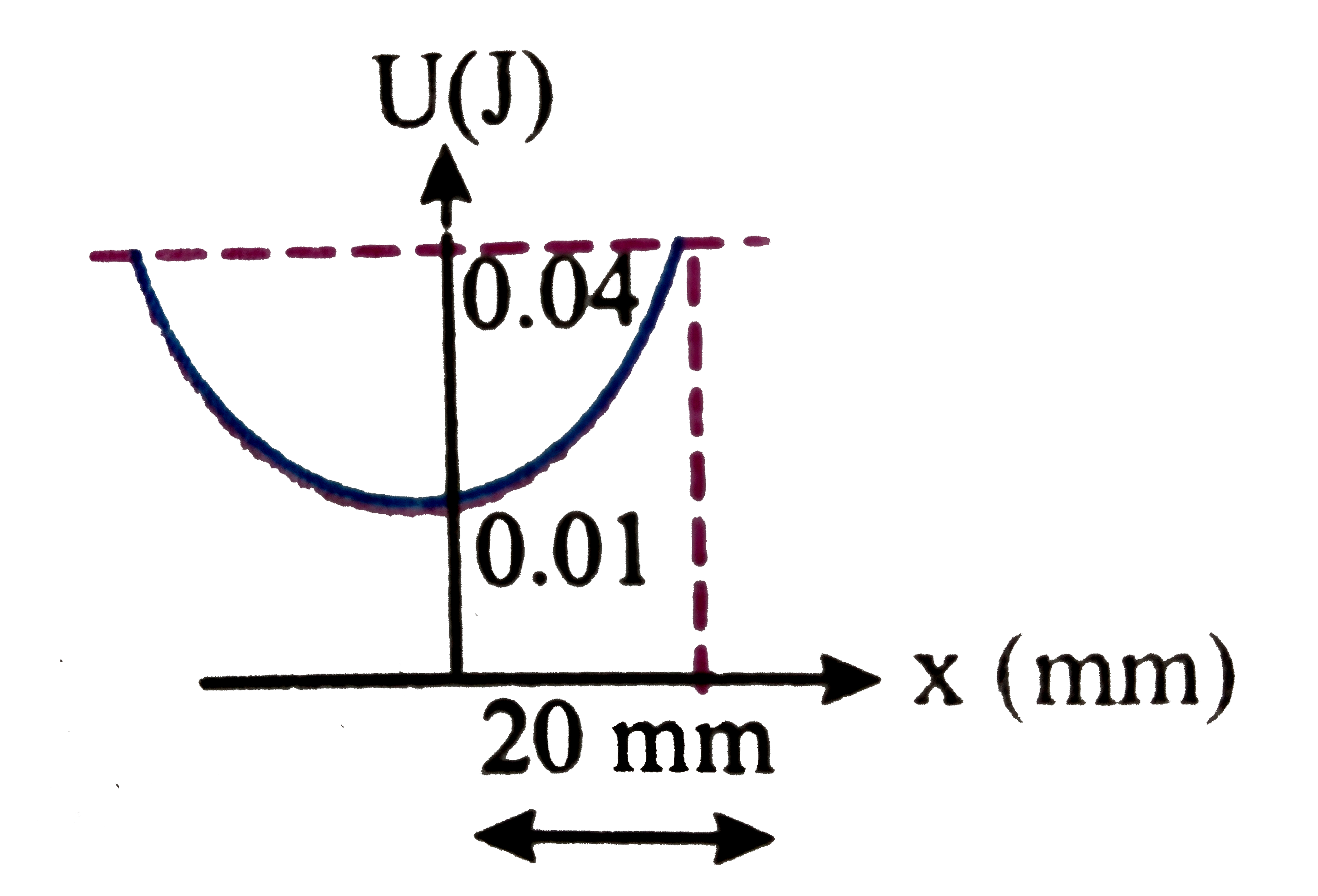
View SolutionA mass of `0.98 kg` suspended using a spring of constant `K = 300 Nm^(-1)` is hit by a bullet of `20g` moving with a velocity `3m//s` vertically. The bullet gets embeded and oscillates with the mass. The amplitude of oscillation is (neglect gravity)
View SolutionA small block is connected to one end of a massless spring of un - stretched length `4.9 m`. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by `0.2 m` and released from rest at `t = 0`. It then executes simple harmonic motion with angular frequency `(omega) = (pi//3) rad//s`. Simultaneously at `t = 0`, a small pebble is projected with speed (v) from point (P) at an angle of `45^@` as shown in the figure. Point (P) is at a horizontal distance of `10 m from O`. If the pebble hits the block at `t = 1 s`, the value of (v) is `(take g = 10 m//s^2)`.
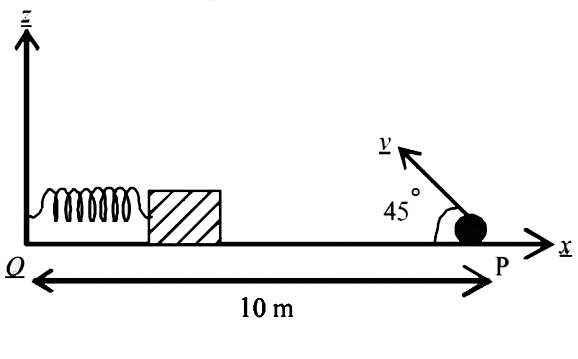 .
.
View SolutionThe mass (M) shown in the figure oscillates in simple harmonic motion with amplitude of the point (P) is.
 .
.
View SolutionA block `(B)` is attached to two unstriched sprig `S_(1)` and S_(2) with spring constant `K` and `4K` , respectively (see fig 1) The other ends are atteched in identical support `M_(1)` and `M_(2)` not attached in the walls . The springs and supports have negligible mass . There is no friction anywhere . The block `B` is displaced toword wall `1` by a small distance `z` (figure (ii)) and released . THe block return and moves a maximum displacements `x` and `y` are musured with reoact to the equalibrum of the block `B` and the ratio `y//x` is
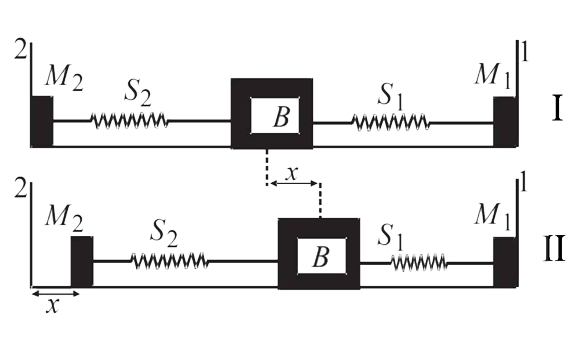
View SolutionA spring is loaded with two blocks `m_(1)` and `m_(2)` where `m_(1)` is rigidly fixed with the spring and `m_(2)` is just kept on the block `m_(1)`. The maximum energy of oscillation is possible for the system having the block `m_(2)` in constant with `m_(1)` is
View SolutionA body of mass `m` is released from a height h to a scale pan hung from a spring. The spring constant of the spring is `k`, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA block P of mass m is placed on horizontal frictionless plane. A second block of same mass m is placed on it and is connected to a spring of spring constant k, the two blocks are pulled by distance A. Block Q oscillates without slipping. What is the maximum value of frictional force between the two blocks.

View SolutionWith the assumption of no slipping, determine the mass m of the block which must be placed on the top of a `6 kg` cart in order that the system period is `0.75s`. What is the minimum coefficient of static friction `mu_(s)` for which the block will not slip relative to the cart is displaced `50 mm` from the equilibrium position and released? Take `(g = 9.8 m//s^(2))`.

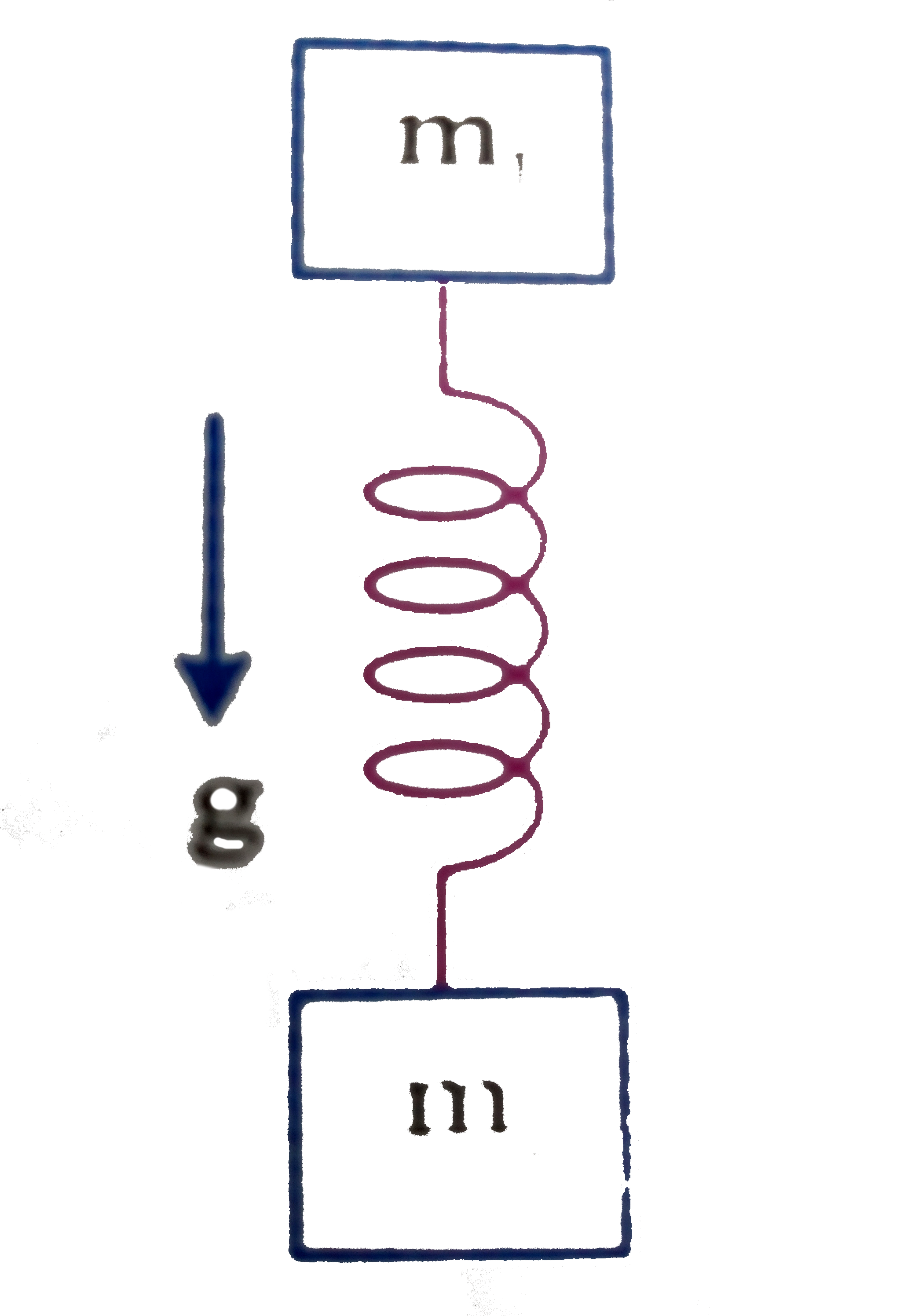
View SolutionThere is a spring with netural length `L_(0)`. Two masses `m_(1)` and `m_(2)` are connected to both of its ends as shown in figure. The whole system is held at rest. At any time `t =0, m_(2)` is released and system starts free fall. Initial stretched length of spring before fall is `L.` what is the displacement of centre of mass as function of time?
View SolutionA pendulum of mass `m` and length `L` is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
View SolutionA small block is connected to a massless rod, which in turns attached to a spring of force constnat `(K =2N//m)` as shown in the fig. The block is displaced down slightly and left free. Find its time period.
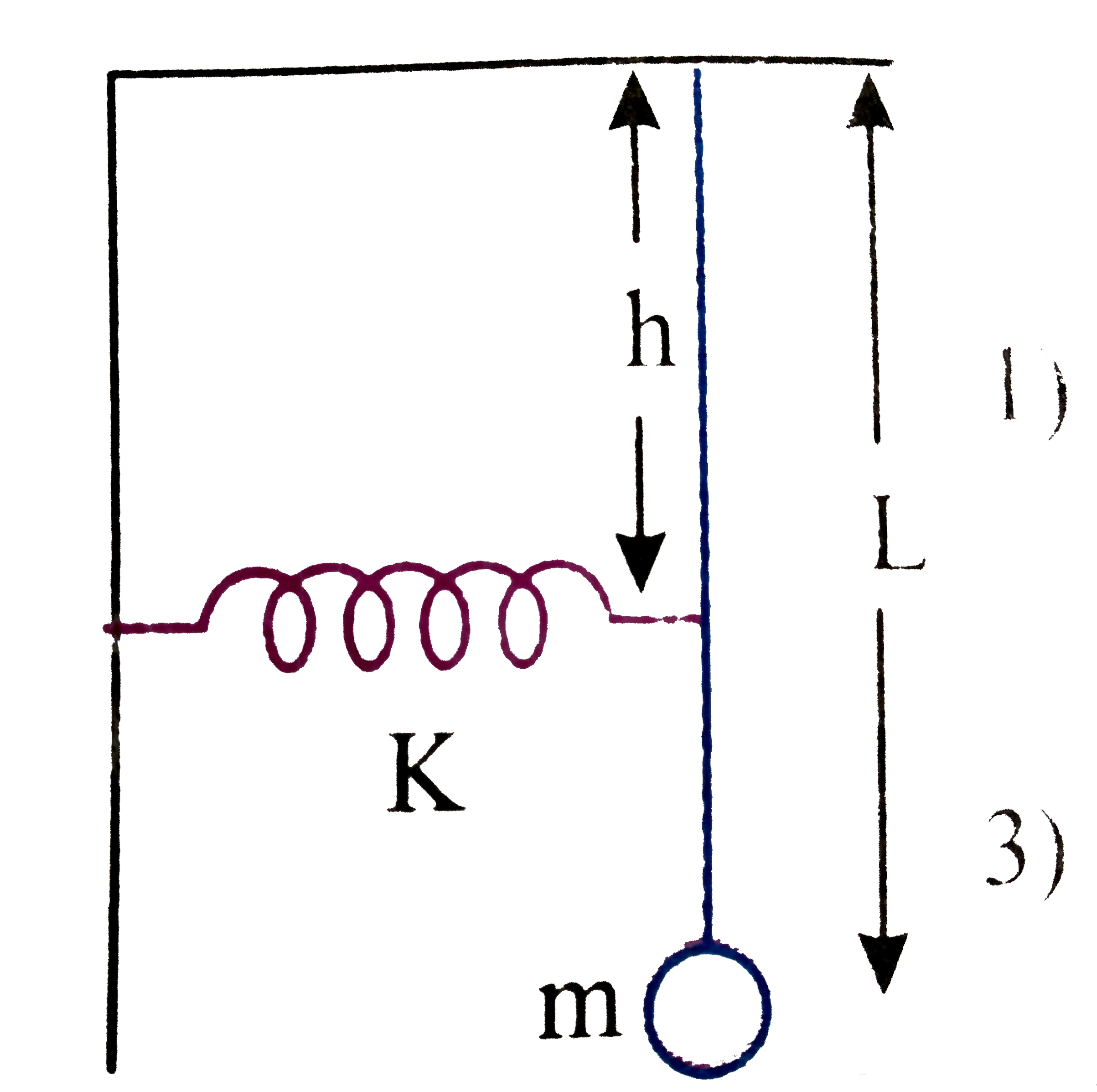
View SolutionIn the device shown in Fig, the block `m` is displaced down slightly and released. It starts oscillating. Pulleys are smooth and massless string and springs are also massless. Find time period of oscillations.

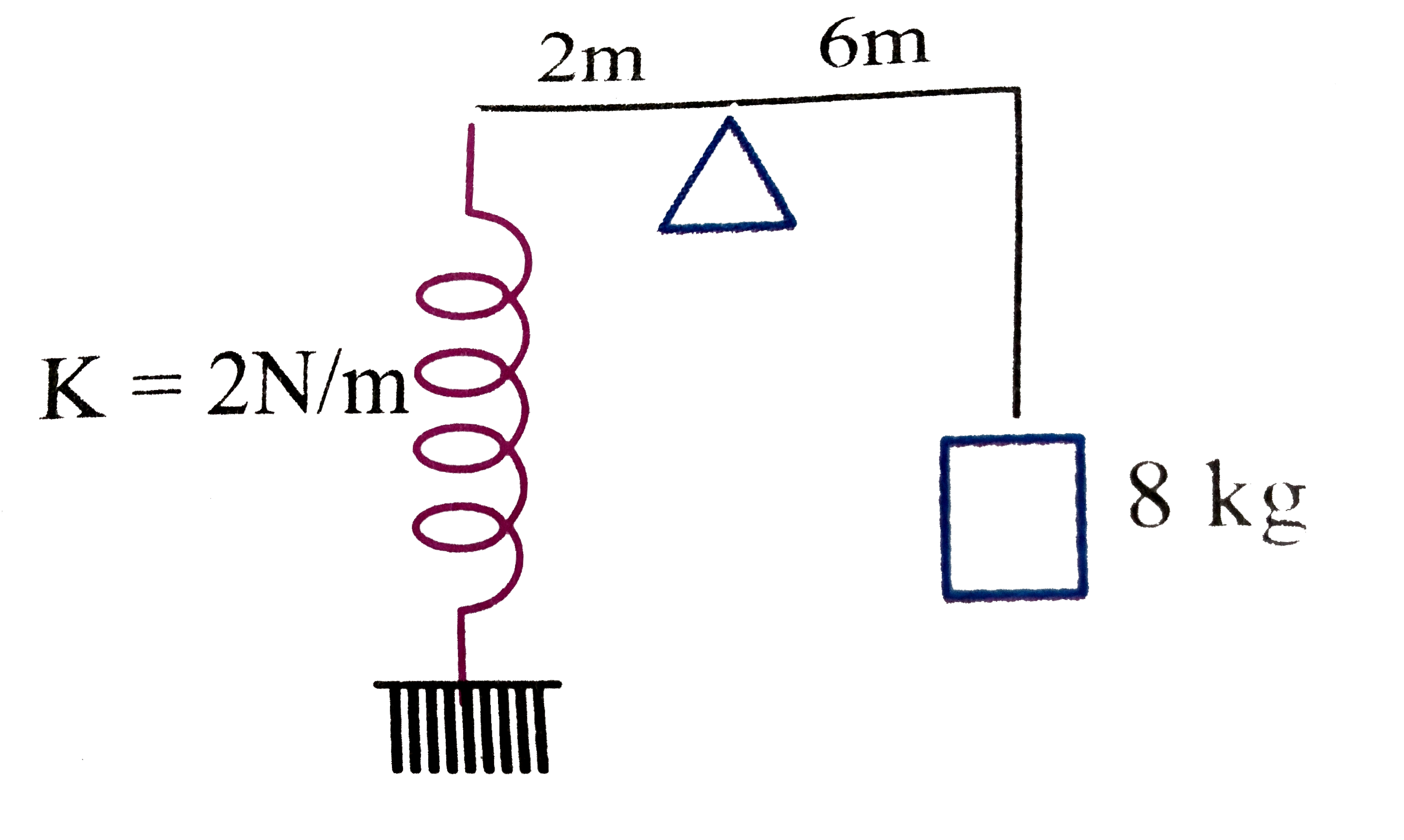
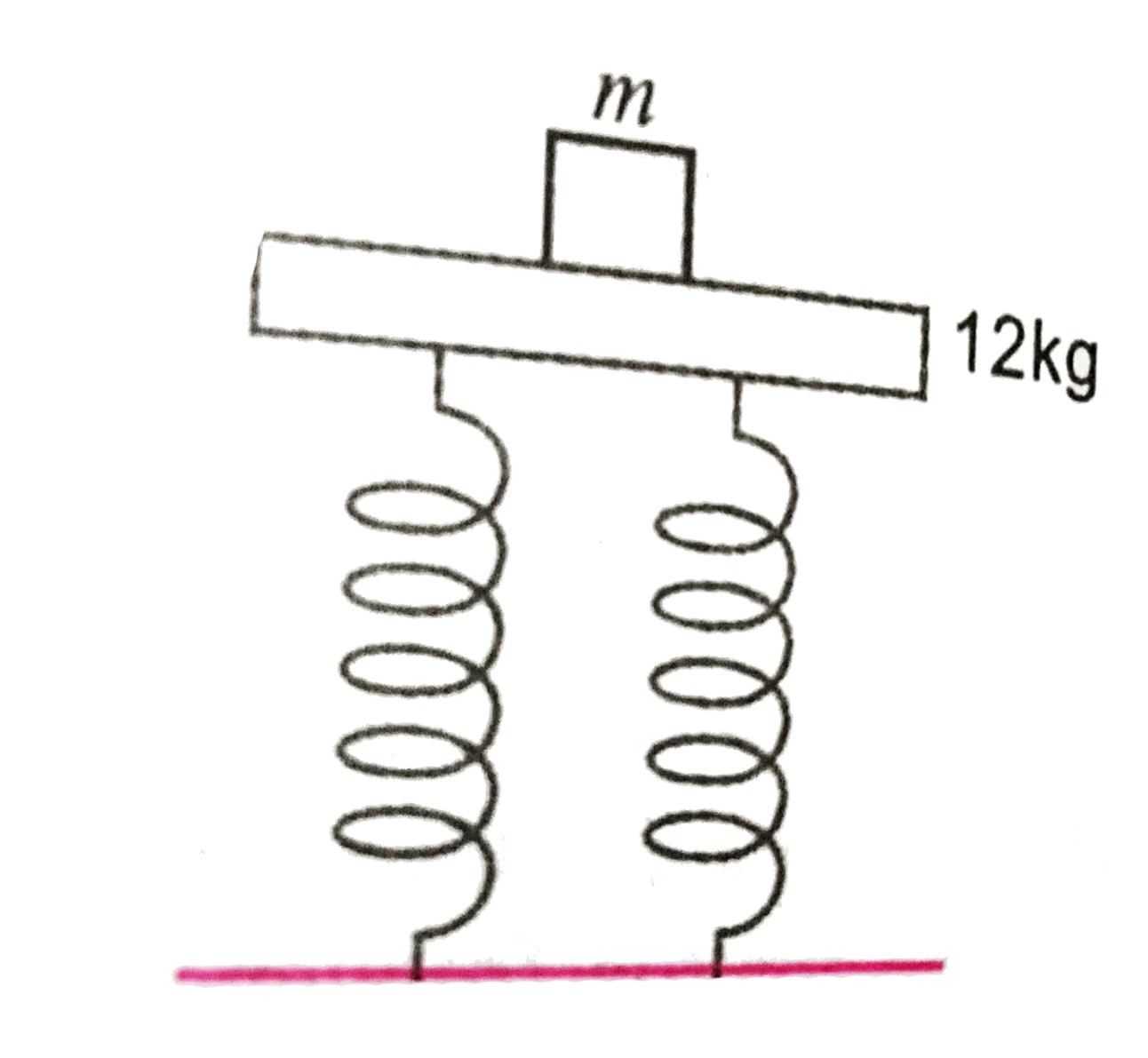
View SolutionA tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
View SolutionA particle of mass 'm' is attached to three identical springs `A,B` and `C` each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

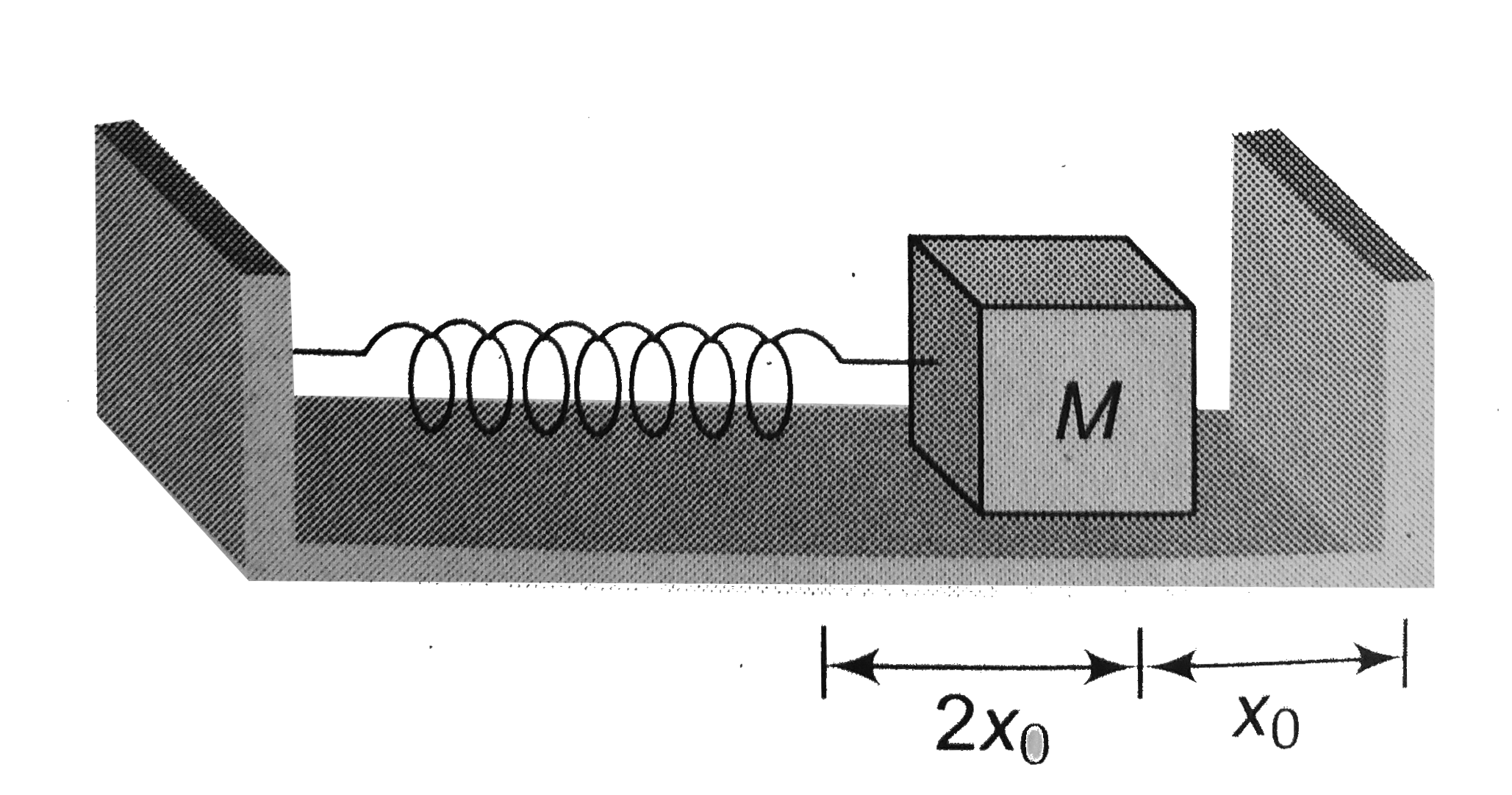
View SolutionOne end of a spring of force constant `k` is fixed to a vertical wall and the other to a block of mass `m` resting on a smooth horizontal surface There is another and wall at a distance `x_(0)` from the block The spring is then compressed by `2x_(0)` and released The time taken to strike the wall is
View SolutionA simple pendulum of length `4.9m` is immersed in a liquid of density `rho =0.4 kg//m^(3)`. Then the time period of pendulum is (density of bob `=0.8 kg//m^(3))`
View SolutionA simple pendulum is hanging from a peginserted in a vertical wall. Its bob is strteched to horizontal position form wall and left freee to move, the bob hits the wall. If coefficient of restitution is `(2)/(sqrt(5))`. After how many collisions the amplitude of vibration will becomes less then `60^(@)`.
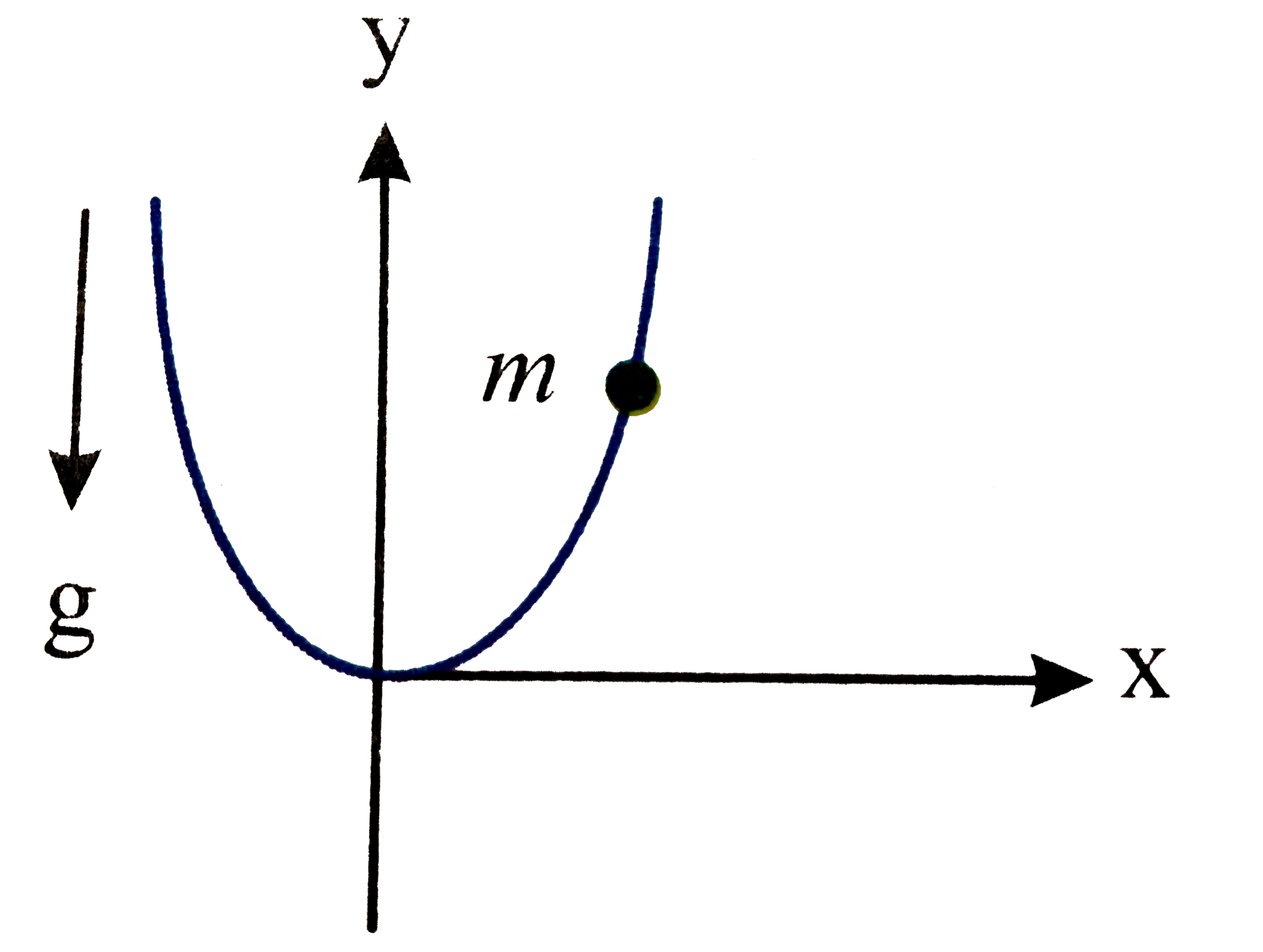
View SolutionA particle of mass `m` is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton `x^(2) =4ay`. The angular frequency of small oscillation is given by
View SolutionIn the previous problem, if tunnel is dug along a chord, find time period.

View SolutionA simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View SolutionThe angular amplitude of a simple pendulum is `theta_(0)`. The maximum tension in its string will be
View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be `2.0s`, the tension in the string when the bob passes through 'O' is
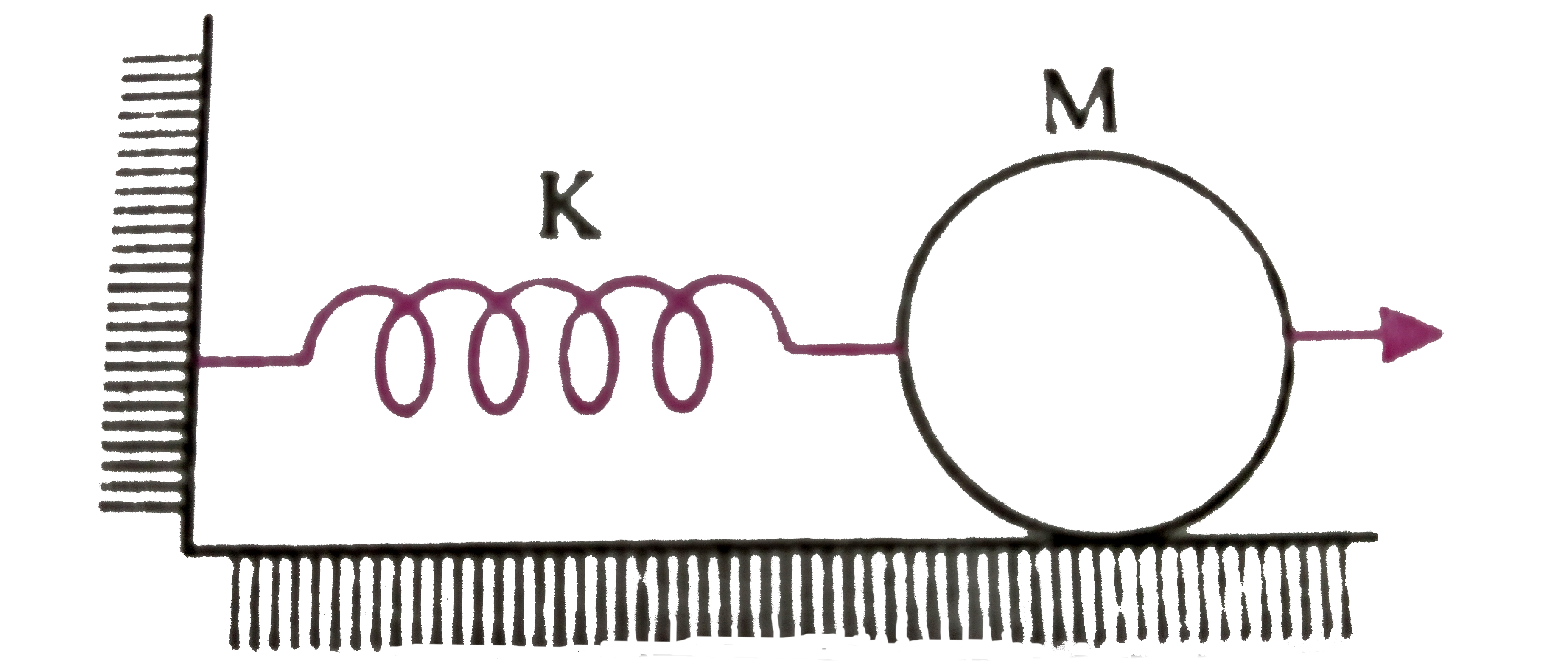
View SolutionA disc of mass `M` is attached to a horizontal massless spring of force constant `K` so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes `SHM` with a period of
View SolutionA block of mass 'm' collides perfectly inelastically with another identical block connected to a spring of of force constant 'K'. The amplitude of resulting `SHM` will be
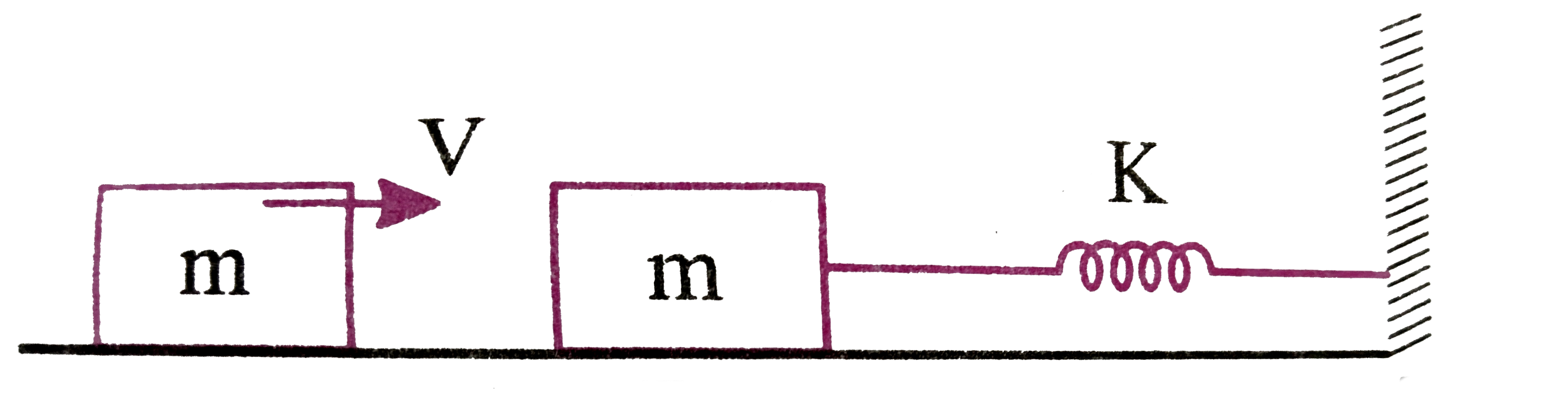
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant `k` and a block of mass `m`. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

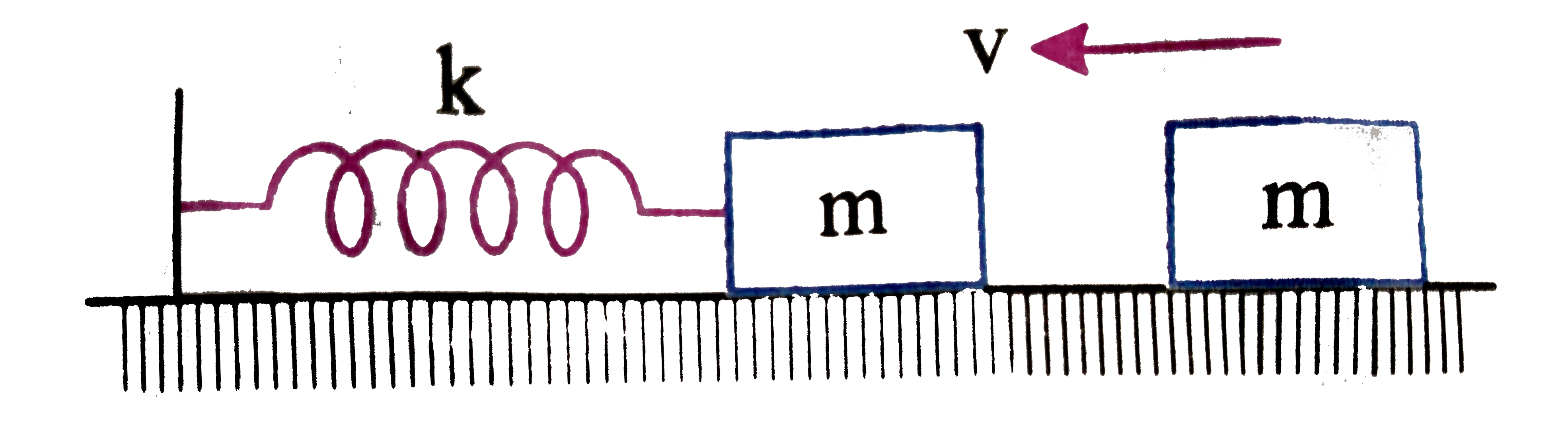
View SolutionThe collision between both blocks shown in figure is completely inelastic. The total energy of oscillation after collision is
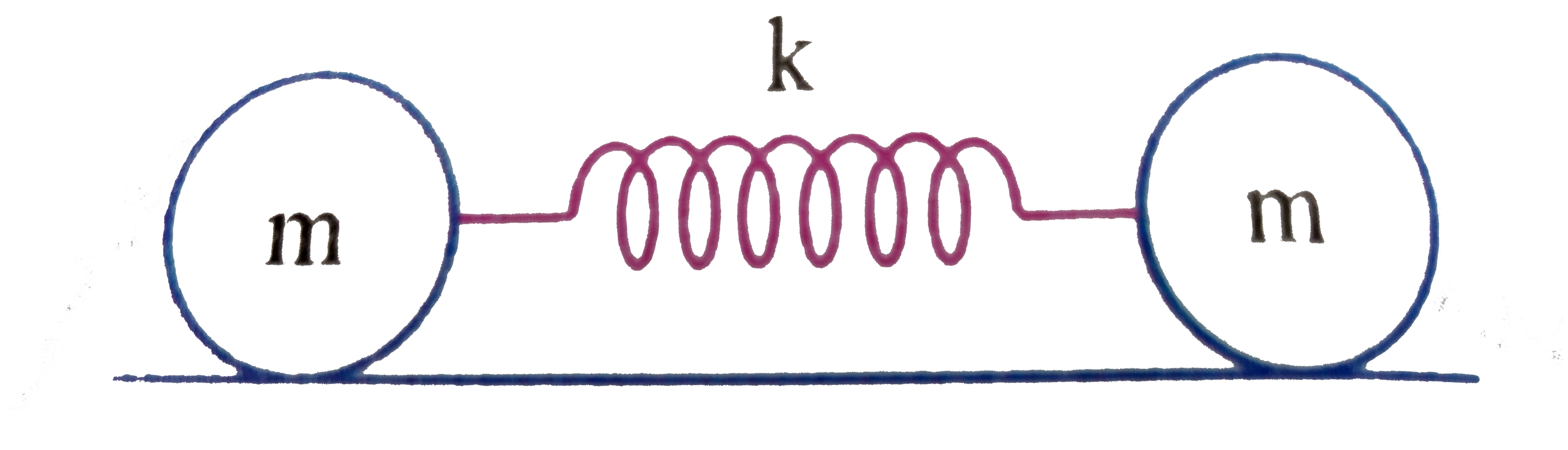
View SolutionTwo identical particles each of mass `0.5kg` are interconnected by a light springs of stiffness `100N//m`, time period of small oscillation is ….
View SolutionTime period of is simple pendulum of length `L` is `T_(1)` and the point time peirod of a uniform rod of the same length `L` pivotal about one end and oscillating in vertical plane is `T_(2)`. Amplitude of oscillation in both the cased is small. The `T_(1)//T_(2)` is:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionIn an experiment with bar pendulum having four holes, the same time period is recorded when it is suspended at distances `21cm, 24cm, 40cm` nad `52cm` respectively form one end. The length of bar pendulum is
View SolutionA sphere of radius r is kept on a concave mirror of radius of curation `R`. The arrangement is kept on a horizontal surface (the surface of concave mirror is friction less and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes `S.h.M.` The period of oscillation will be
View SolutionIf the distance between the cnetre of gravity and point of suspension of a compound pendulum is `l` and the radius of gyration about the axis passing through its centre of gravity is `k`, its time period will be infinite if
View SolutionA disc of radius `R` and mass `M` is pivoted at the rim and it set for small oscillations. If simple pendulum has to have the same period as that of the disc, the length of the simple pendulum should be
View SolutionA particle performs simple harmonic mition with amplitude A. Its speed is trebled at the instant that it is at a destance
`(2A)/3` from equilibrium position. The new amplitude of the motion is:
View SolutionFor a simple pendulum, a graph is plotted between itskinetic energy `(KE)` and potential energy `(PE)`against its displacement `d`. Which one of the following represents these correctly? (graph are schematic and not drawn to scale)
View SolutionA particle moves with simple harmonic motion in a straight line. In first `taus`, after starting form rest it travels a destance a, and in next `tau s` it travels 2a, in same direction, then:
View Solution
LEVEL -III questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION