Complete Solutions to EXERCISE - I (H.W) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | EXERCISE - I (H.W) |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
A particle oscillates as per the equation `x = (7 cos 0.5 pi t)m`, the time taken by the particle to move from the mean position to a point `3.5m` away is
View SolutionA particle executes `SHM` with an amplitude of `0.2 m`. Its displacement when its phase is `90^(@)` is
View SolutionA particle performing `SHM` with a frequency of `5Hz` and amplitude `2cm` is initially at position extreme position. The equation for its displacement (in meter) is
View SolutionThe period of oscillation of a particle in `SHM` is `4sec` and its amplitude of vibration is `4cm`. The distance of the particle `0.5s` after passing the mean position is
View SolutionA particle starts its `SHM` from mean position at `t = 0`. If its time period is `T` and amplitude `A` then the distance traveled by the particle in the time from `t = 0 to t = (5T)/(4)` is
View SolutionA `20g` particle is executing `SHM` between the limits `(5,0,0)cm` and `(15, 0, 0)cm`. The total distance convered during one oscillation is
View SolutionA particle is subjected to two `SHMs ` `x_(1) = A_(1) sin omegat` and `x_(2) = A_(2)sin (omegat +(pi)/(4))`. The resultant `SHM` will have an amplitude of
View SolutionThree `SHO's` of equal amplitude `A` and equal time period combine in the same direction. The difference in phase between successive `SHO's` os `60^(@)`ahead of the other. The amplitude of the resultant oscillation is
View SolutionThe displacement of an obuect attached to a spring and executing simple harmonic motion is given by `x=2xx100^(-2) cos pit` metre. The time at which the maximum speed first occurs is.
View SolutionIf the displacement `x` and velocity `v` of a particle executing `SHM` are related as `4v^(2) = 25 - x^(2)`. Then its maximum displacement in meter `(x, v` are in `SI`) is
View SolutionThe equation for the displacement of a particle executing `SHM` is `x = 5sin (2pit)cm` Then the velocity at `3cm` from the mean position is( in cm//s)
View SolutionThe ratio of velocities of particle in `SHM` at displacements `A//3` and `2A//3` is
View SolutionThe time period of oscillation of a particle that executes `SHM` is `1.2s`. The time starting from mean position at which its velocity will be half of its velocity at mean position is
View SolutionAn object is attched to the bottom of a light vertical spring and set vibrating. The maximum speed of the object is `15cm//s` and the period is `628` milli seconds. The amplitude of the motion in centimetres is
View SolutionA particle executes `SHM` along a straight line `4cm` long. When the displacement is `1cm` its velocity and acceleration are numerically equal. The time period of `SHM` is
View SolutionThe equation of motion of a particle in `SHM` is `a +16 pi^(2)x = 0`. Here 'a' is linear acceleration of the particle at displacement `x (a,x` are in `SI)`. Its time period is
View SolutionA body executing `SHM` has a maximum velocity of `1ms^(-1)` and a maximum acceleration of `4ms^(-1)`. Its time period of oscillation is
View SolutionThe acceleration of a particle in `SHM` is `0.8ms^(-2)`, when its displacement is `0.2m`. The frequency of its oscillation is
View SolutionA body of mass `0.5kg` is performing `SHM` with a time period `.^(pi)//_(2)` seconds. If its velocity at mean position is `1ms^(-1)`, then restoring force acting on the body at a phase angle `60^(@)` from exterme position is
View SolutionA body of mass `1//4 kg` is in `SHM` and its displacement is given by the relation `x = 0.05 Sin(20t +(pi)/(2))m`. If `t` is in seconds, the maximum force acting on the particle is
View SolutionFour simple harmonic vibrations
`x_(1) = 8s "in" (omegat), x_(2) = 6 sin (omegat +(pi)/(2))`,
`x_(3) = 4 sin (omegat +pi)` and `x_(4) =2 sin (omegat +(3pi)/(2))` are superimposed on each other. The resulting amplitude is……units.
View SolutionA sewing machine needle is oscillating simple harmonically in a vertical line of length `6cm` with a frequency `30` per minute. The displacement of the needle `1//6s` after crossing the mean position is
View SolutionA particle executing SHM is described by the displacement function `x(t)=Acos(omegat+phi)`, if the initial (t=0) position of the particle is 1 cm, its initial velocity is `pii" cm "s^(-1)` and its angular frequency is `pis^(-1)`, then the amplitude of its motion is
View SolutionThe velocities of a body executing `SHM` at displacement 'a' and 'b' are 'b' and 'a' respectively. The amplitude of `SHM` is
View SolutionA block of `0.5kg` is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of `0.5 Hz`. The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly
View SolutionDue to some force `F_(1)` a body oscillates with period `4//5s` and due to other force `F_(2)` it oscillates with period `3//5s`. If both the forces acts simultaneously in same direction then new period is
View SolutionA simple pendulum performs simple harmonic motion about `x=0` with an amplitude a ans time period T. The speed of the pendulum at `x = (a)/(2)` will be
View Solutionparticle is executing the motion `x=A cos (omegat-theta)` The maximum velocity of the particle is
View SolutionA particle executes simple harmonic motion with a period of `16s`. At time `t=2s`, the particle crosses the mean position while at `t=4s`, its velocity is `4ms^-1` amplitude of motion in metre is
View SolutionA particle executing simple harmonic motion with amplitude of 0.1 m. At a certain instant when its displacement is 0.02 m, its acceleration is 0.4 `m//s^(2)`. The maximum velocity of the particle is (in m/s)
View SolutionA body is executing `SHM`. If the force acting on the body is `6N` when the displacement is `2cm`, then the force acting on the body at a displacement of `3cm` is
View SolutionA particle executes `SHM` on a straight line. At two positions, its velocities are `u` and `v` whle accelerations are `alpha` and `beta` respectively `[beta gt alpha gt ]`.The distance between these two positions is
View SolutionA particle moves such that its acceleration is given by `a =- beta (x-2)` Here `beta` is positive constant and `x` is the position form origin. Time period of oscillation is
View SolutionThe displacement of a particle executing `S.H.M` from its mean position is given by `x = 0.5 sin (10 pit +phi) cos (10pit +phi)`. The ratio of the maximum velocity to the maximum acceleration of the body is given by
View SolutionA particle is executing SHM with an amplitude of 2 m. The difference in the magnitudes of its maximum acceleration and maximum velocity is 4. The time period of its oscillation is
View SolutionA simple pendulum having a bob of mass 100 g is oscillating with a maximum angular displacement of `3^(@)`. The maximum restoring force acting on the bob is (take `g = 10 ms^(-2)`)
View SolutionA simple pendulum of length `l` is connected to the ceiling of a vehicle that is moving down along a smooth inclined plane with `sinx=4/5`. Then its period of oscillation is
View SolutionA pendulum suspended from the roof of an elevator at rest has a time period `T_(1)`, when the elevator moves up with an acceleration `a` its time period becomes `T_(2)`, when the elevator moves down with an acceleration `a`, its time period becomes `T_(3)`, then
View SolutionA seconds pendulum is suspended from the roof of a lift. If the lift is moving up with an acceleration `9.8 m//s^(2)`, its time period is
View SolutionIf the length of a seconds pendulum is increased by `2%` then in a day the pendulum
View SolutionTwo simple pendulums have time periods `T` and `5T//4`. They start vibrating at the same instant from the mean position in the same phase. The phase difference between them when the pendulum with higher time period complets one oscillation is
View SolutionTwo simple pendulums of length `100m` and `121m` start swinging together. They will swing together again after
View SolutionA second pendulum is attached to roof of a car that is moving with acceleration `10m//s^(2)` on a straight road. Its frequency of oscillation is
View SolutionA second pendulum is attached to roof of a car that is sliding down along a smooth inclined plane of inclination `60^(@)`. Its perios of oscillation is
View SolutionA simple pendulum executing `SHM` in a straight line has zero velocity at 'A' and 'B' whose distances form 'O' in the same line `OAB` are 'a' and 'b'. If the velocity half wat between them is 'v' then its time period is
View SolutionA seconds pendulum at the equator `(g = 9.78 ms^(-2))` is taken to the poles `(g = 9.83 ms^(-2))`. If it is to act as second's pendulum its length should be
View SolutionThe time period of a simple pendulum of infinite length is (R=radius of earth).
View SolutionThe mass `M` shown in the figure oscillates in simple harmnonic motion and amplitude `A`. The amplitude of the point `P` is
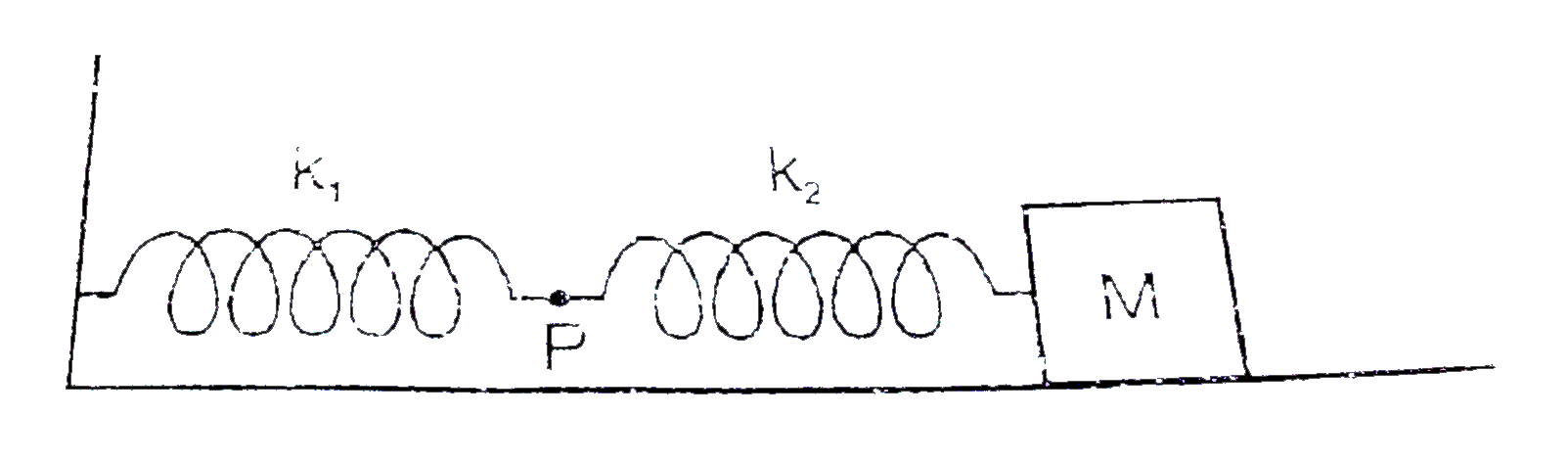
View SolutionA body of mass `m` is suspended from three springs as shown in figure. If mass `m` is displaced slightly then time period of oscillation is

View SolutionA load of mass `M` is attached to the bottom of a spring of mass `'M //3'` and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View SolutionAn oscillating mass spring system has mechanical energy `1` joule, when it has an amplitude `0.1m` and maximum speed of `1ms^(-1)`. The force constant of the spring is (in `Nm^(-1))`
View SolutionA light spiral spring supports `200g` weight at its lower end oscillates with a period of `1s`. The weight that must be removed from the lower end to reduce the period to `0.5s` is
View SolutionThe time period of a mass loaded spring is 'T'. If `20%` of its turns are cut and removed and same mass is attached to the remaining spring then it oscillates with a period of
View SolutionA particle executes `SHM` with an amplitude of `10cm` and frequency `2 Hz`. At `t = 0`, the particle is at a point where potential energy and kinetic energy are same. The equation for its displacement is
View SolutionA body performs simple harmonic oscillations along the straight line `ABCDE` with `C` as the midpoint of `AE`. Its kinetic energies at `B` and `D` are each one fourth of its maximum value. If `AE = 2R`, the distance between `B` and `D` is

View SolutionThe amplitude of oscillation of particles in `SHM` is `sqrt(3)cm`. The displacement from mean position at which its potential and kinetic energies are in the ratio `1:2` is
View SolutionFind the average kinetic energy of a simple harmonic oscillator if its total energy is `10` joule and minimum potential energy is `2` joule.
View SolutionThe total energy of a particle executing simple harmonic motion is `16J`. What will be total energy of particle if amplitude is halved and frequency is doubled?
View SolutionThe displacement of a particle of mass `3g` executing simple harmonic motion is given by `x =3sin (0.2t)` in `SI` units. The kinetic energy of the particle at a point which is at a displacement equal to `1//3` of its amplitude from its mean position is
View SolutionStarting from the origin a body osillates simple harmonicall with a period of 2 s. A fter what time will its kinetic energy be 75% of the total energy?
View SolutionThe total mechanical energy of a harmonic oscillator of amplitude `1m` and force constant `200N//m` is `150J`. Then
View SolutionRatio of kinetic energy to potential energy of an oscillator when it is at distance `1//N` times of amplitude from mean positions in
View SolutionThe potential energy of a simple harmonic oscillator of mass 2 kg in its mean position is 5 J. If its total energy is 9 J and its amplitude is 0.01 m, its time period would be
View SolutionA particle is executing SHM. At a displacement `y_(1)` its potential energy is `U_(1)` and at a displacement `y_(2)` its potential energy is `U_(2)`. The potential energy of the particle at displacement `(y_(1)+y_(2))` is
View SolutionThe amplitude of a damped oscillator becomes `(1)/(27)^(th)` of its initial value after `6` minutes. Its amplitude after `2` minutes is
View SolutionThe amplitude of vibration of a particle is given by `a_m=(a_0)//(aomega^2-bomega+c)`, where `a_0`, a, b and c are positive. The condition for a single resonant frequency is
View Solution
EXERCISE - I (H.W) questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION