Complete Solutions to ILLUSTRATION of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | ILLUSTRATION |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
Which one of the following is a periodic motion but not oscillatory ?
(i) Motion of pendulum of a wall clock.
(ii) Oscillation of a mass suspended from a spring.
(iii) Motion of a planet around the sun.
(iv) Vibrations of the wire of a guitar.
View SolutionFor a particle executing SHM along x-axis, force acting on it, is given by `(A, k gt 0)`
View SolutionWhich of the following expression does not repressent SHM?
View SolutionThe motion of a particle executing S.H.M. is given by `x= 0.01 sin 100 pi (t+.05)` , where x is in metres and time is in seconds. The time period is
View SolutionA particle executing SHM has velocities `v_(1), v_(2)` and accelerations `f_(1), f_(2)` at two of its positions A and B on the same side of the equilibrium position. Find the angular frequency of the SHM.
View SolutionIn an SHM of time period T
(i) What minimum time is taken by the oscillator to move between - A/2 to +A
(ii) What maximum time is taken by it to go from -A/2 to +A/2 without crossing any point not more than twice.
View SolutionFor a particle in SHM find phase difference between situations (a) 1 & 2 (b) 1 & 3
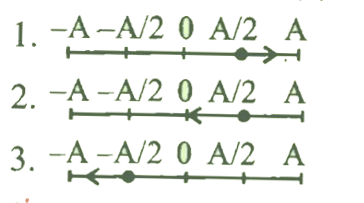
View SolutionA body oscillates with SHM, accroding to the equation, `x=(5.0m)cos[(2pirads^(-1))t+pi//4]`
At `t=1.5s`, calculate the `(a)` diplacement `(b)` speed and `(c)` acceleration of the body.
View SolutionA particle executes SHM with a time period of `4 s`. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
View SolutionThe motion of a particle in S.H.M. is described by the displacement function, `x=Acos(omegat+phi)`, If the initial `(t=0)` position of the particle is 1cm and its initial velocity is `omega cm s^(-1)`, what are its amplitude and initial phase angle ? The angular frequency of the particle is `pis^(-1)`. If instead of the cosine function, we choose the sine function to describe the SHM`: x=B sin(omegat+alpha)`, what are the amplitude and initial phase of the particle with the above initial conditions ?
View SolutionA stone is swinging in a horizontal circle of diameter `0.8m` at `30 rev//min`. A distant light causes a shadow of the stone on a nearly wall. The amplitude and period of the SHM for the shadow of the stone are
View SolutionA simple harmonic oscillation has an amplitude `A` and time period `T`. The time required to travel from `x = A` to ` x= (A)/(2)` is
View SolutionTwo simple harmonic motions are given by `y_(1) = a sin [((pi)/(2))t + phi]` and `y_(2) = b sin [((2pi)/( 3))t + phi]`. The phase difference between these after `1 s` is
View SolutionTwo bodies A and B of equal mass are suspended from two separate massless springs of spring constant `k_1 and k_2` respectively. If the bodies iscillte vertically such that their maxixum velocities are equal, the ratio of the amplitude of A to that of B is
View SolutionThe time period and the amplitude of a simple pendulum are 4 seconds and 0.20 meter respectively. If the displacement is 0.1 meter at time t=0, the equation on its displacement is represented by :-
View SolutionTwo simple harmonic motions are represented by the equations `y_(1) = 10 sin (3pit + (pi)/(4))`
and `y_(2) = 5 (3 sin 3 pi t+sqrt(3) cos 3 pi t)`. Their amplitudes are in the ratio of
View SolutionA simple pendulam with a solid metal bob has a period T. The metal bob is now immersed in a liquid having density one-teeth that of the metal of the bob. The liquid is non-viscuous. Now the period of the same pendulum with its bob remaining all the time in the liquid will be
View SolutionThe system of simple pendulum is immersed in liquid of a density `rho_(l)`. Prove that its new period of oscillation inside the liquid will be `T = 2pi sqrt((l)/(g(1-(rho_(l))/(rho_(s)))))` where `rho_(s)` is density of bob.
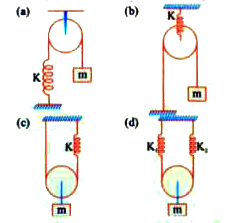
View SolutionFind the time period in each of the following cases, if the mass is pulled and left.
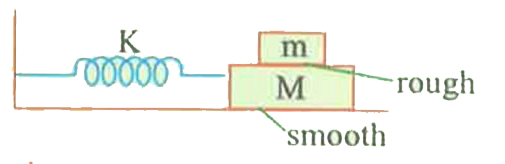
View SolutionThe system is pulled to an elongation A and Then released. Find the minimum value of coefficient of friction between m and M for which m doesn't slips over M.
View SolutionA 50 gm mass at the end of a spring vibrates in SHM. The amplitude of the motion is 12 c.m. and the period is 1.70 s. Find (a) the frequency (b) the spring constant (c) the maximum speed of the mass (d) the maximum acceleration of the mass (e) the speed when the displacement is 6 c.m. (f) the acceleration when x = 6 c.m.
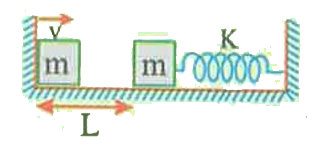
View SolutionThe left block in figure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.

View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance `x_(0)` from the block. The spring is then compressed by `2x_(0)` and released. The time taken to strike the wall is

View SolutionA horizontal platform vibrate up and down with a simple harmonic motion of amplitude 20 c.m. At what frequency will an object kept on the platform remain just in contact with the platform ? Take `g = 9.81 m//s^(2)`.
View SolutionFind time period of oscillation of the system.

View SolutionThe surface shown in the diagram are smooth and all collisions are elastic. Find the time period of the periodic motion.
View SolutionTotal mechanical energy of an oscillator is 160 J. Its force constant is 200 N/m and amplitude is 1m. Find its
`{:((1)" "KE_(max),(2)" "KE_(min)),((3)" "PE_(max),(4)" "PE_(min)):}`
View SolutionA point particle of mass `0.1kg` is executing SHM of amplitude `0.1m`. When the particle passes through the mean position, its kinetic energy is `8xx10^-3J`. Obtain the equation of motion of this particle if the initial phase of oscillation is `45^@`.
View SolutionThe average energy in one time period in simple harmonic motion is
View SolutionA particle moves on the `X-`axis according to the equation `x = x_(0) sin^(2)omegat`. The motion is simple harmonic
View SolutionA particle of mass m is dropped in a tunnel dug along the diameter of the earth, from the surface find. (1) Its energy of oscillation (2) Time taken to move from surface to a depth Re/2 (3) Velocities at a depth Re/2 and centre (4) graph between a Vs v (5) If it is released from a height h above the surface, will the motion be SHM ?
View SolutionA disc of mass 'm' is suspended at a point R/2 above its centre. Find its period of oscillation.
View SolutionA simple pendulum oscillates simple harmonically. The tension in the string at lowest point is T. What is the total acceleration of the bob at its lowest position ?
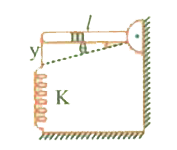
View SolutionThe end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
View SolutionIn a damped oscillation amplitude at (t = 0) is `A_(0)` and at (t = T) its value `A_(0)//2` if E (t = 0) `= E_(0)` find E (t = 2T)
View SolutionThe equation of a damped oscillator of mass 1kg is `(d^(2)y)/(dt^(2)) = - 25 y + 6 (dy)/(dt)`. Find its angular frequency.
View SolutionD is disturbed, and ultimately all the pendulums start oscillating. Match the following

`{:("1. Oscillations of A","(a) free oscillation"),("2. Oscillations of B","(b) forced oscillation"),("3. Oscillations of C","(c) Resosnant oscillation"),("4. Oscillations of D",):}`
View Solution
ILLUSTRATION questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION