Complete Solutions to C.U.Q of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | C.U.Q |
| Number Of Questions | 78 |
| Academic Year | 2023-24 |
Which of the following expressions represent simple harmonic motion?
View SolutionA particle moves in the `x-y` plane according to the equation `vec(r)=(vec(i)+vec(j)) (A sin omega t +B cos omega t)`. Motion of particle is
View SolutionAt two particular closest instants fo time `t_(1)` and `t_(2)`, the displacemets of a particle performing `SHM` are equal. At these instants
View SolutionThe displacement (x) of a particle as a function of time (t) is given by
`x=asin(bt+c)`
Where a,b and c are constant of motion. Choose the correct statemetns from the following.
View SolutionThe composition of two simple harmonic motions of equal periods at right angle to each other and with a phase difference of `pi` result in the displacement of the particle along
View SolutionThe displacement of a particle varies with time according to the relation `y=a sin omega t +b cos omega t `.
View SolutionTwo linear SHM of equal amplitudes `A` and frequencies `omega` and `2omega` are impressed on a particle along `x` and `y - axes` respectively. If the initial phase difference between them is `pi//2`. Find the resultant path followed by the particle.
View SolutionA particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.
View SolutionWhich of the following is not simple harmonic function ?
View SolutionA particle is moving in a circle with uniform speed its motion is
View SolutionThe function sin^(2) (omegat) represents.
View SolutionThe displacement equation of a spring block system is given by `y = A sin omegat` in air. It is completely immersed in water. If `A^(1)` and `omega^(1)` be new amplitude and angular freuency then
View SolutionIn given statements correct alternative is
View SolutionWhich of following is charecteristic of `SHM`?
View SolutionIn `SHM` there is always a constant ratio between displacement of the body and its
View SolutionA particle move along y-axis according to equation `y +3+4 cos omega t`. The motion of the particle is
View SolutionA particle moves on the X-axis according to the equation `x=x_0 sin^2omegat`. The motion simple harmonic
View SolutionIf a particle is executing `SHM`, with an amplitude `A`, the distance moved and the displacement of the body during its time period is
View SolutionThe equation of motion of particle is given by `(dp)/(dt) +m omega^(2) y =0` where `P` is momentum and `y` is its position. Then the particle
View SolutionPosition of a particle varies as `y = cos^(2) omegat - sin^(2) omegat`. It is
View SolutionThe motion of a particle in `SHM` of
View SolutionThe displacement (from intial position) of a particle executing `SHM` with amplitude `A` in half the time period is always
View SolutionA particle moves on y-axis according to the equation `y = A +B sin omegat`. Amplitude of motion is
View SolutionA system executing `SHM` must possesses
View SolutionThe angular velocities of three bodies in `SHM` are `omega_(1), omega_(2), omega_(3)` with their respective amplitudes as `A_(1),A_(2),A_(3)`. If all three bodies have same mass and maximum velocity then
View SolutionFor a particle in `SHM` the amplitude and maximum velocity are `A` and `V` respectively. Then its maximum acceleration is
View SolutionThe amplitude of a particle performing `SHM` is 'a'. The displacement at which its velocity will be half the maximum velocity is
View SolutionA `SHO` has amplitude `A` and time period `T`. The maximum velocity will be
View SolutionA particle performs SHM with a period `T` and amplitude a. The mean velocity of particle over the time interval during which it travels `a//2` from the extreme position is
View SolutionA particle perform `SHM` with period `T` and amplitude `A.` the mean velocity of the particle averaged over quarter oscillation, Starting from right exterme position is
View SolutionA particle is executing SHM. Then the graph of acceleration as a function of displacement is
View SolutionA particle is executing a simple harmonic motion its maximum acceleration is a and maximum velocity is `beta` .Then its time of vibration will be
View SolutionThe phase difference between the displacement and acceleration of a particle execuliting simple harmonic motion is
View SolutionA particle in `SHM` is located at different positions as shown below. The phase difference between the position marked by `A` and

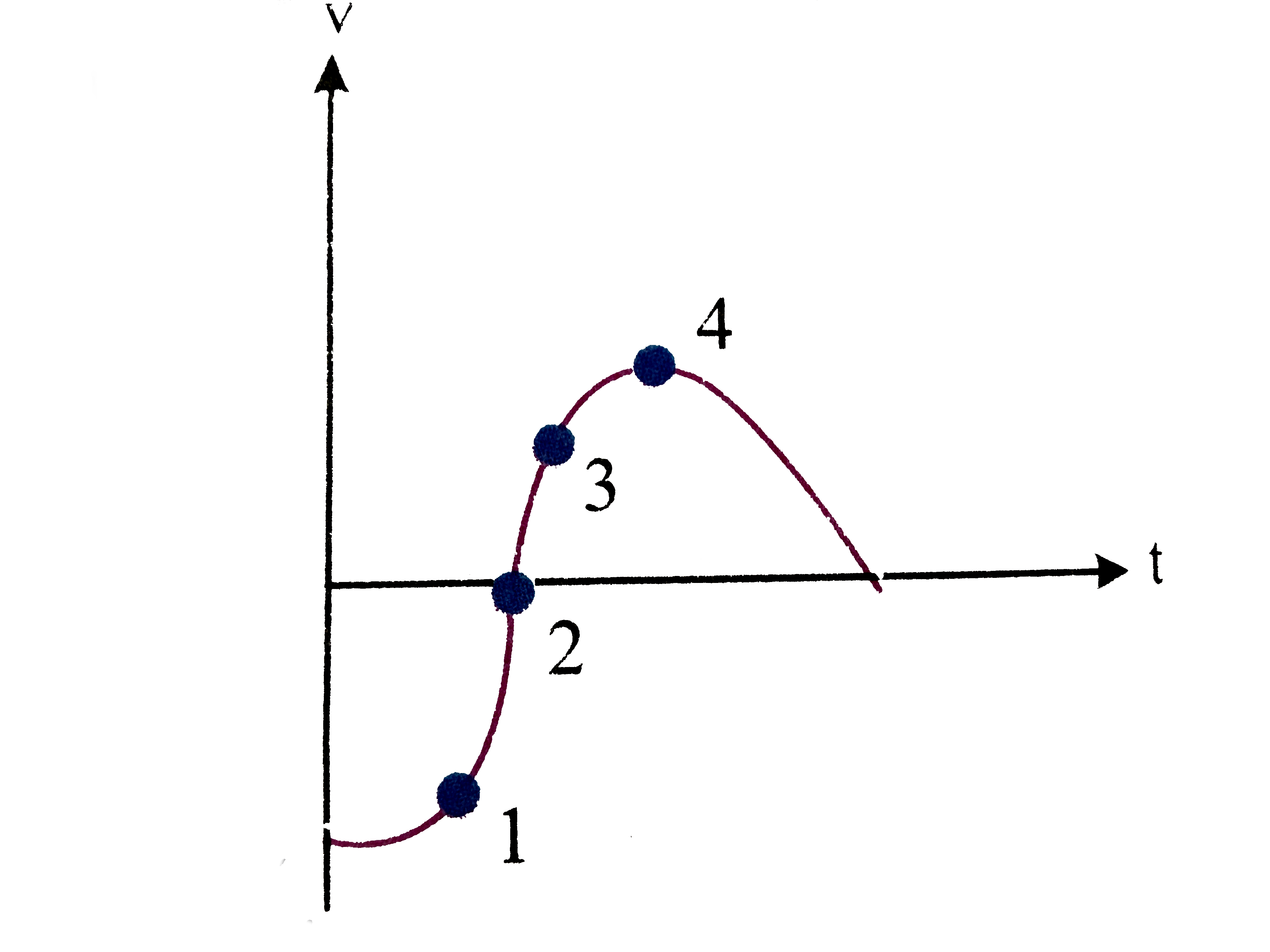
View SolutionVelocity -time graph of a particle executing `SHM` is as shown in fig. Select the ocrrect alternatives.
(i) at position 1, displacement of particle may be +ve or-ve
(ii) at position 2, displacement of particel is -ve
(iii) at position 3, acceleration of particel is+v
(iv) at position 4, acceleration of particle is +ve
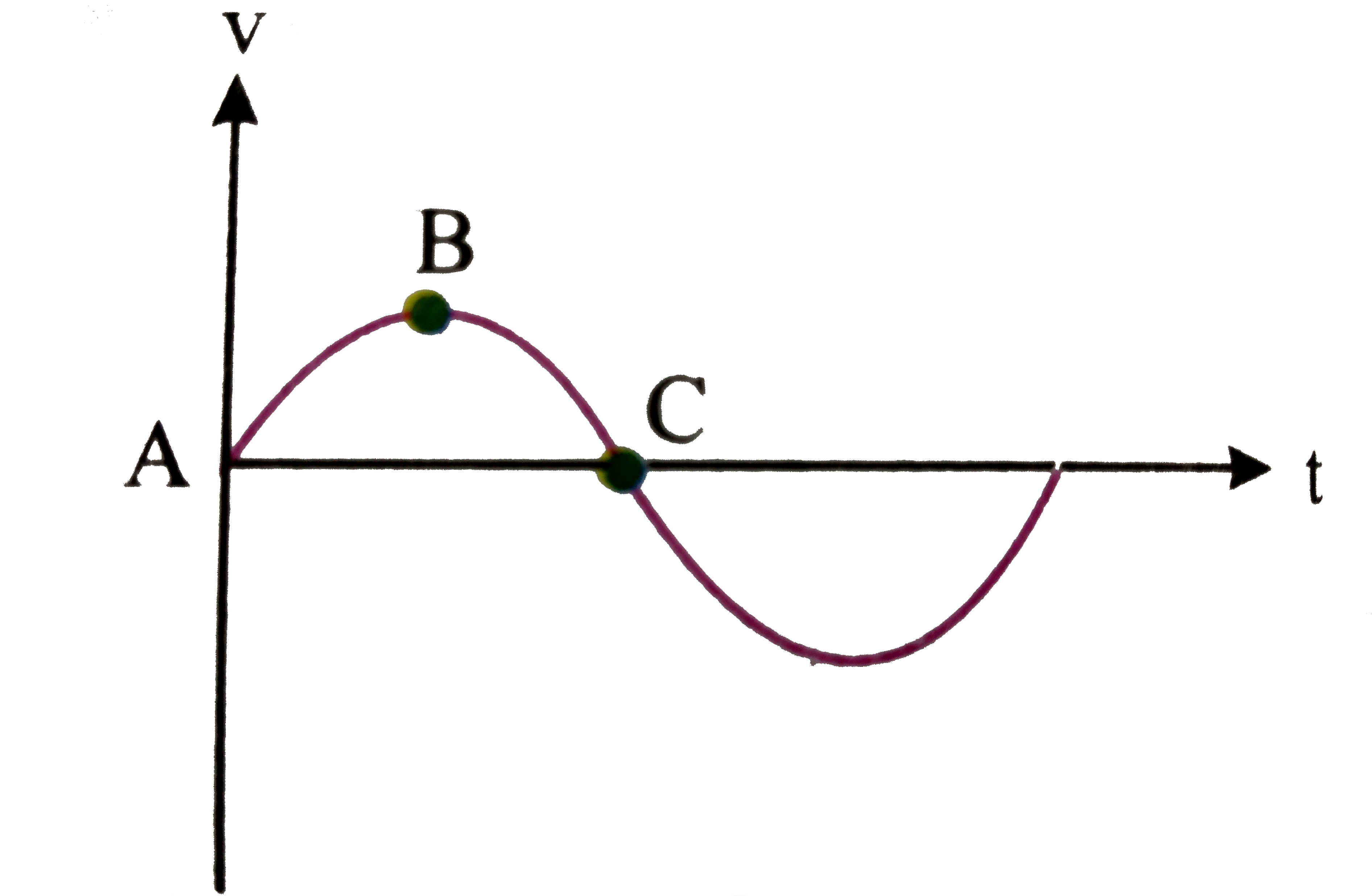
View SolutionAcceleration -time graph of a particel executing `SHM` is as shown in fig. Then
(i) displacement of particle at `1` is -ve
(ii) velocity of particel at `2` is +ve
(iii) potential enegry of particel at `3` is maximum
(iv) speed of particel at `4` is decreasing.

View Solution`v-t` graph of a particle in `SHM` is as shown is figure. Choose the wrong option.
View SolutionA particle executes simple harmonic motion with a frequency. (f). The frequency with which its kinetic energy oscillates is.
View SolutionA body executing `SHM` has a total energy `E`. When its kinetic energy is `3E//4`, the displacement of the particle is `(A` is amplitude)
View SolutionFor a particle executing `S.H.M.,` the kinetic energy `K` is given `K = K_(0) cos ^(2)omega t`. The maximum value of potential energy is:
View SolutionA particle executes `SHM` with a time period `T`. The time period with which its potential energy changes is
View SolutionIn `SHM` at the equilibrium position
(i) displacement is minimum
(ii) acceleration is zero
(iii) velocity is maximum
(iv) potential energy is maximum
View SolutionThe amplitude of a simple harmonic oscillation is doubled. How does this affect
(i) periodic time (ii) maximum velocity (iii) maximum acceleration and
(iv) maximum energy
View SolutionA body executes simple harmonic motion. The potential energy (P.E), the kinetic energy (K.E) and energy (T.E) are measured as a function of displacement `x`. Which of the following staements is true?
View SolutionThe total energy of a particle executing simple garmonic motion is `(x-`displacement)
View SolutionThe potential energy of a particle `(U_(x))` executing `SHM` is given by
View SolutionFor a particle executing SHM, the displacement `x` is given by `x = A cos omegat`. Identify the graph which represents the variation of potential energy `(PE)` as a function of time `t` and displacement `x`.

(a) `I, III`
(b) `II, IV` (c ) `II, III`
(d) `I, IV`
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If `U_((0))=0`, the graph of `U (x)` verses x will be (where U is the potential energy function.)
View SolutionIf the potential energy of an oscillator is `U =a +bx +cx^(2) +dx^(3)`, the term (quantity) which indicates the `SHM` of the oscillator is
View SolutionThe time period of a loaded spring on earth is `6s`. On the surface of moon, the time period of the same loaded spring will be
View Solution`T_(1),T_(2)` are time periods of oscillation of a block when individually suspended to springs of force constants `K_(1),K_(2)` respectively. If same block is suspended to series combination of same two springs, then it time period of oscillation.
View Solution`T_(1),T_(2)` are time periods of oscillation of a block when individually suspended to springs of force constants `K_(1),K_(2)` respectively. If same block is suspended to parallel combination fo same two springs. Its time period is
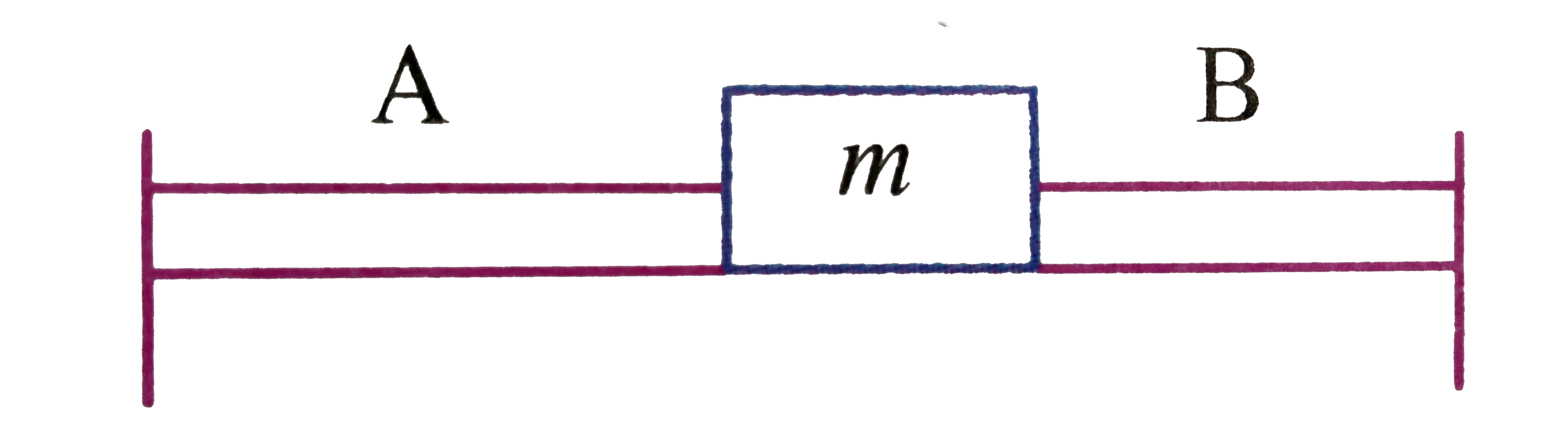
View Solution`A` and `B` are two thin rubber bands, each of force constant `k`. Assuming that they obey Hooke's law, the time period of horizontal `SHM` of the mass `m` is given by
View Solution`A` mass `M` is suspended from a light spring. An additional mass `m` added to it displaces the spring further by distance `x` then its time period is
View SolutionA clock `S` is based on oscillations of a spring and clock `P` is based on pendulum motion, both clocks run at the same rate on Earth. On a planet having the same mass, but twice the radius that of the earth
View Solution
Two blocks connected by a spring rest on a smooth horizontal plane as shown in Fig. A constant force `F` start acting on block `m_2` as shown in the figure. Which of the following statements are not correct?
View SolutionIn a simple pendulum if iron sphere is replaced by a wooden sphere of same mass its time period of oscillation will
View SolutionA simple pendulum has a hollow sphere containing mercury suspended by means of a wire. If a little mercury is drained off, the period of the pendulum will
View SolutionA pendulum clock thast keeps correct time on the earth is taken to the moon. It will run
View SolutionA girl is in standing position in an oscillating swing. If the girl sits in the swing, the frequency of oscillation
View SolutionThe frequency of oscillation of a simple pendulum suspended in a satellite that revolve around the earth is
View SolutionA hollow sphere of simple pendulum is first filled with mercury and then with water. The time periods are in the ratio of their densities are in the ratio `13.6 :1`
View SolutionThe work done by the tension in the strings of a simple pendulum in one complete oscillation is equal to
View SolutionThe period of a simple pendulum suspended from the ceiling of a car is `T` when the car is at rest. If the car moves with a constant acceleration the period of the pendulum
View SolutionA pendulum clock is taken to the bottom of a deep mine. Will it gain or lose time? How should its length be altered to correct the time?
View SolutionIf `T_(1),T_(2)`and `T_(3)` are the time periods of a given simple pendulum on the surface of the earth, at a depth 'h' in a mine and at an altitude 'h' above the earth's surface respectively, then
View SolutionA simple pendulum is vibrating in an evacuated chamber. It will
View SolutionThe percentage change in the time period of a second pendulum when its amplitude is reduced by `30%` is (assume `theta` is very small)
View SolutionA simple pendulum of length `L` has been set up inside a railway wagon sliding down a frictionless inclined plane of inclination `theta` with the horizontal. Its period of oscullation as recorded by an observer inside wagon is
View SolutionA metallic sphere is filled with water and hung by a long thread. It is made to oscillate. If there is a small hole in the bottom through which water slowly flows out, the time period will
View SolutionIf a simple pendulum is arranged in an artificial satellite its
(i) time period becomes infinity
(ii) frequecny becomes infinity
(iii) both time period and frequency becomes infinity.
(iv) it does not oscillate
View SolutionA girl is swinging on a swing in the sitting position. How will the period of swing be affected if she stands up?
View SolutionIf different types of pendulums are taken to the moon, the time period will change for
View SolutionIn a simple pendulum the period of oscillation `(T)` is related to the length of the pendulum `(L)` as
View SolutionWhich of the following figure represents damped harmonic motion
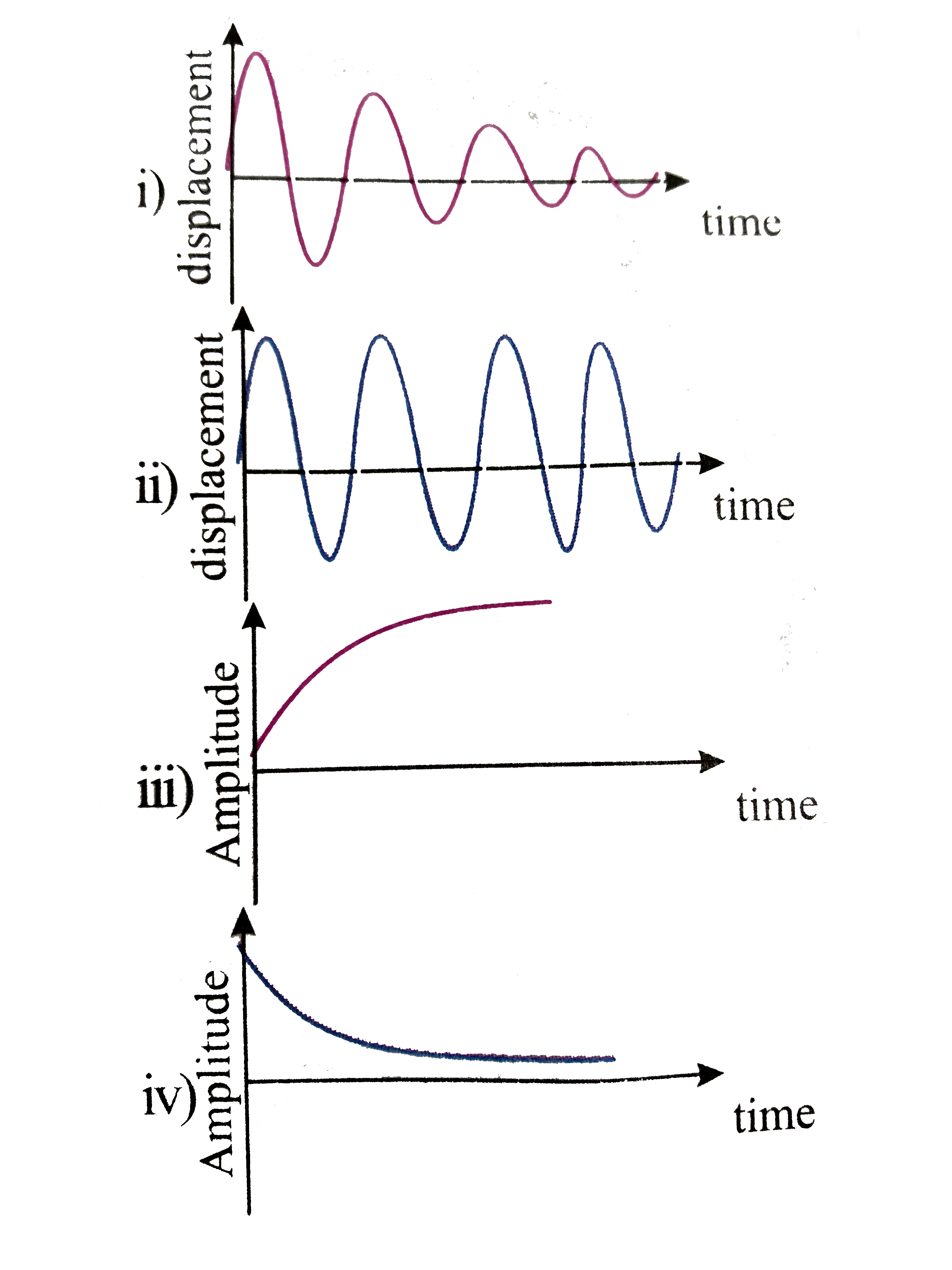
View SolutionA body having netural frequency `v_(o)` is executing forced oscillations under driving force of frequency `v`. The system will vibrate
View SolutionA body executing forced oscillations under driving force is in sharp resonance. If damping increases then sharpness of resonance
View SolutionFor a bar pendulum the distance between two points of minimum time period is
View Solution
C.U.Q questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION