Complete Solutions to INTEGER ANSWER QUESTIONS of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | INTEGER ANSWER QUESTIONS |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
In the given spring block system if `k = 25 pi^(2) Nm^(-1)`, find time period of oscillation.

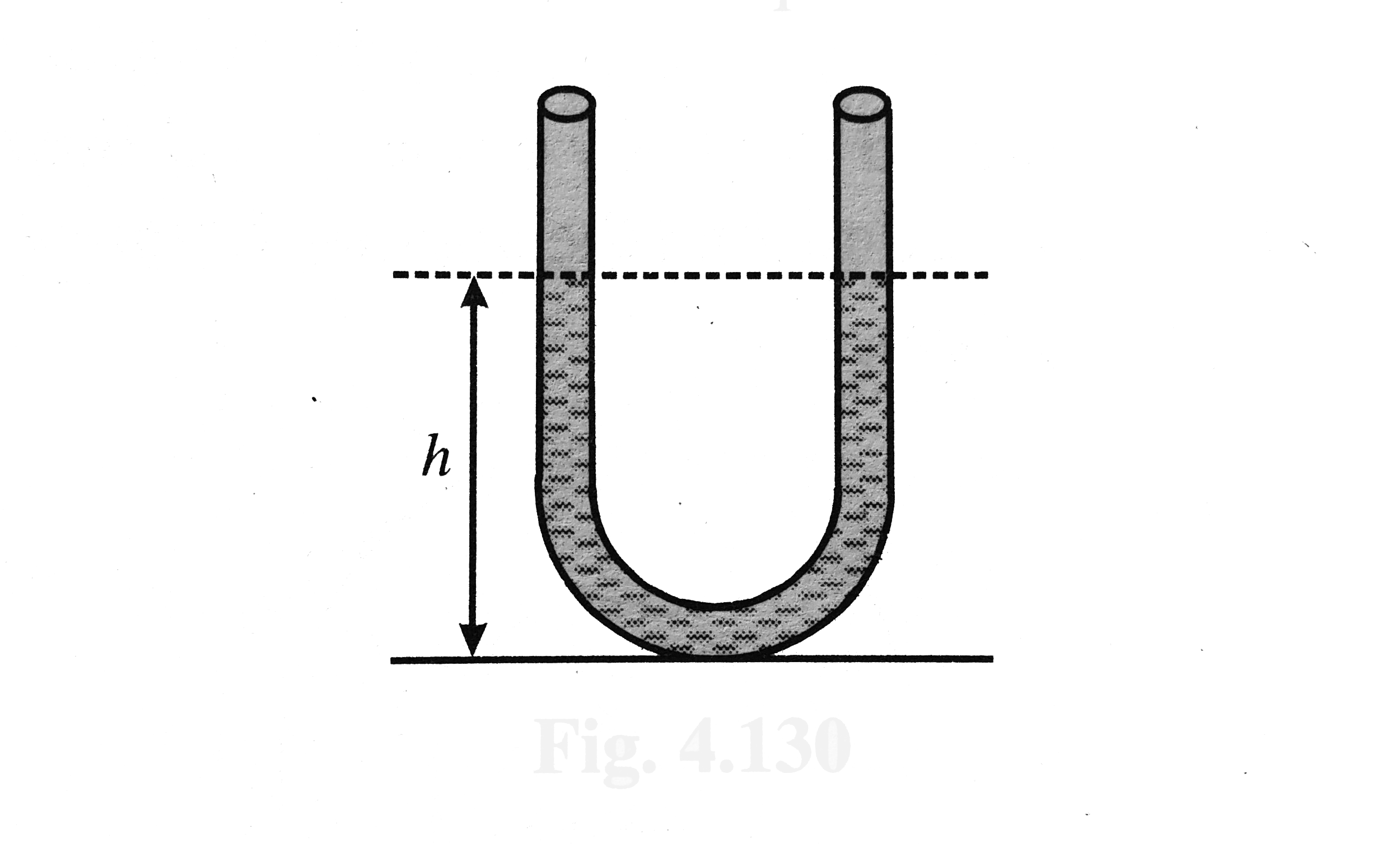
View SolutionConsider a liquid which fills a uniform `U` - tube uniform `U`- tube, as shown in figure , up to a height `h`. Find angular the frequency of small oscillation of th eliquid in the `U` - tube.
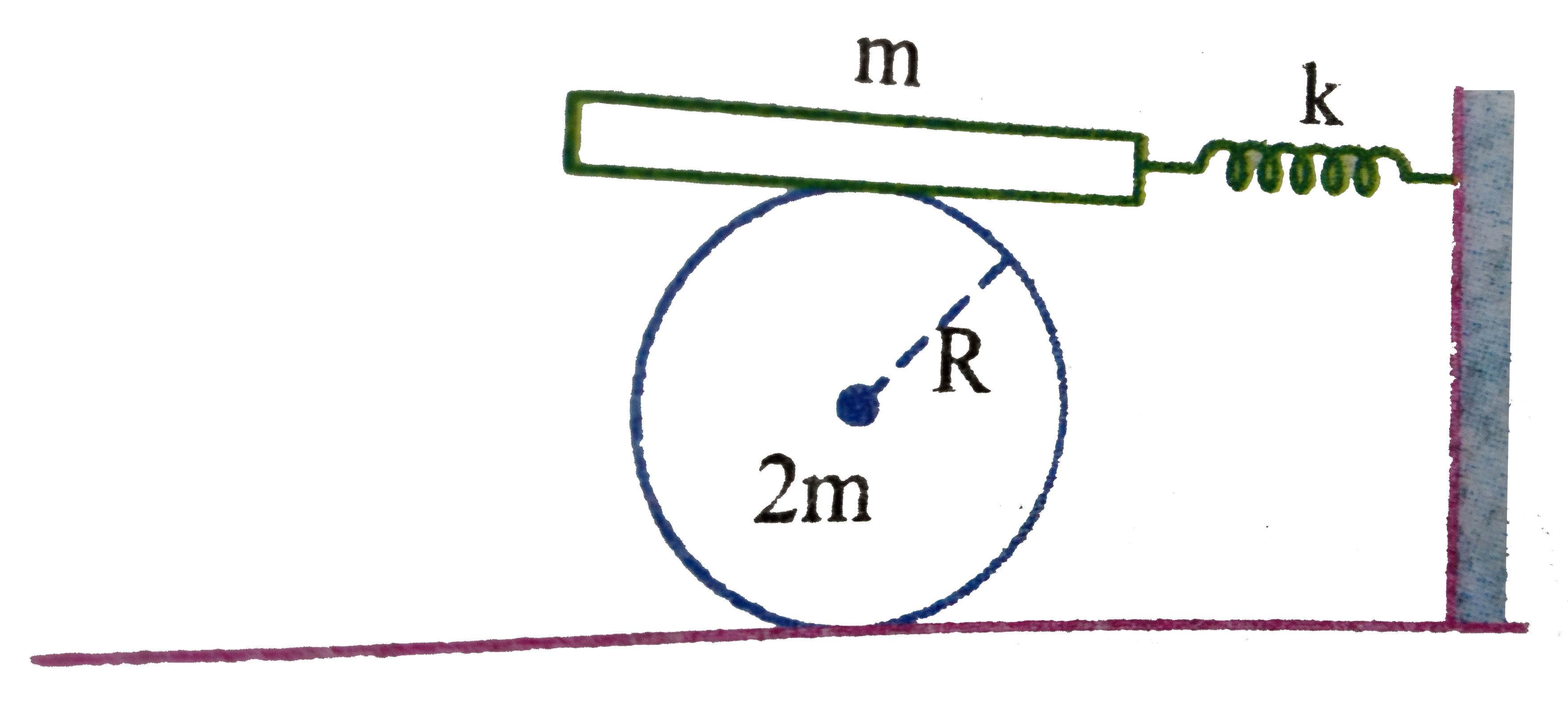
View SolutionA uniform plank of mass `m = 1kg`, free to move in the horizontal direction only, is placed at the top of a solid cylinder of mass `2m` and radius `R`. The plank is attched to a fixed wall by means of light spring of spring constant `k = 7N//m^(2)`. There is no slipping between the cylinder and the plank, and between the cylinder and the ground. the angular frequency of small oscillations of the system is
View Solution
Two simple pendulums `A` and `B` having lengths `l` and `(l)/(4)` respectively are released from the position as shown in Fig. Calculate the time (in seconds) after which the two strings become parallel for the first time. (Take `l=(90)/(pi^2)`m and `g=10(m)/(s^2)`.
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. `K_(1)`, `k_(2)`, `k_(3)`and `k_(4)` are force constant of the spring. Calculate period of small vertical oscillations of block of mass `m`.

View SolutionTwo very small particles are executing `SHM` along very near parallel lines about the same mean position, same amplitude and the same frequency. At `t = 0` both the particle are moving with speed of `1m//sec` but on the opposite side of the mean position and having same direction of velocity at a distance of `5cm` from the mean position. At `t = 4sec` they are at the same position moving with speed of `1m//sec` but in opposite direction. Assuming that this is the minimum time form `t = 0` where they are meeting for the `1st` time. If the maximum speed of either particle is `(xpi)/(4sqrt(2))cm//sec` Find `x`
View SolutionA string secured at its ends is stretched with a force of tension `F`. The mass of the string and the force of gravity can be neglected. A point weight with a mass m is attached to the middle of the string. The time period of small oscillations of the weight is `2pi sqrt((ml)/(xF))`. the value of `x` is ________
(Neglect any change in the magnitude of tension of the string during oscillations)

View SolutionThe system shown is lying on a smooth horizontal surface. Mass `m` is constrained to move along the line `3`. Springs `1` and `2` at right angles with respect to one another are symmetrically arranges with respect to `3` which is an elastic cord. The force constants of `1,2` and `3`are `k` each and they are all just taut in the condition shown. For small oscillations of `m` along `3`, time period is `pisqrt((m)/(yk)) (1+sqrt(x))`. The valye of `xy` is___________

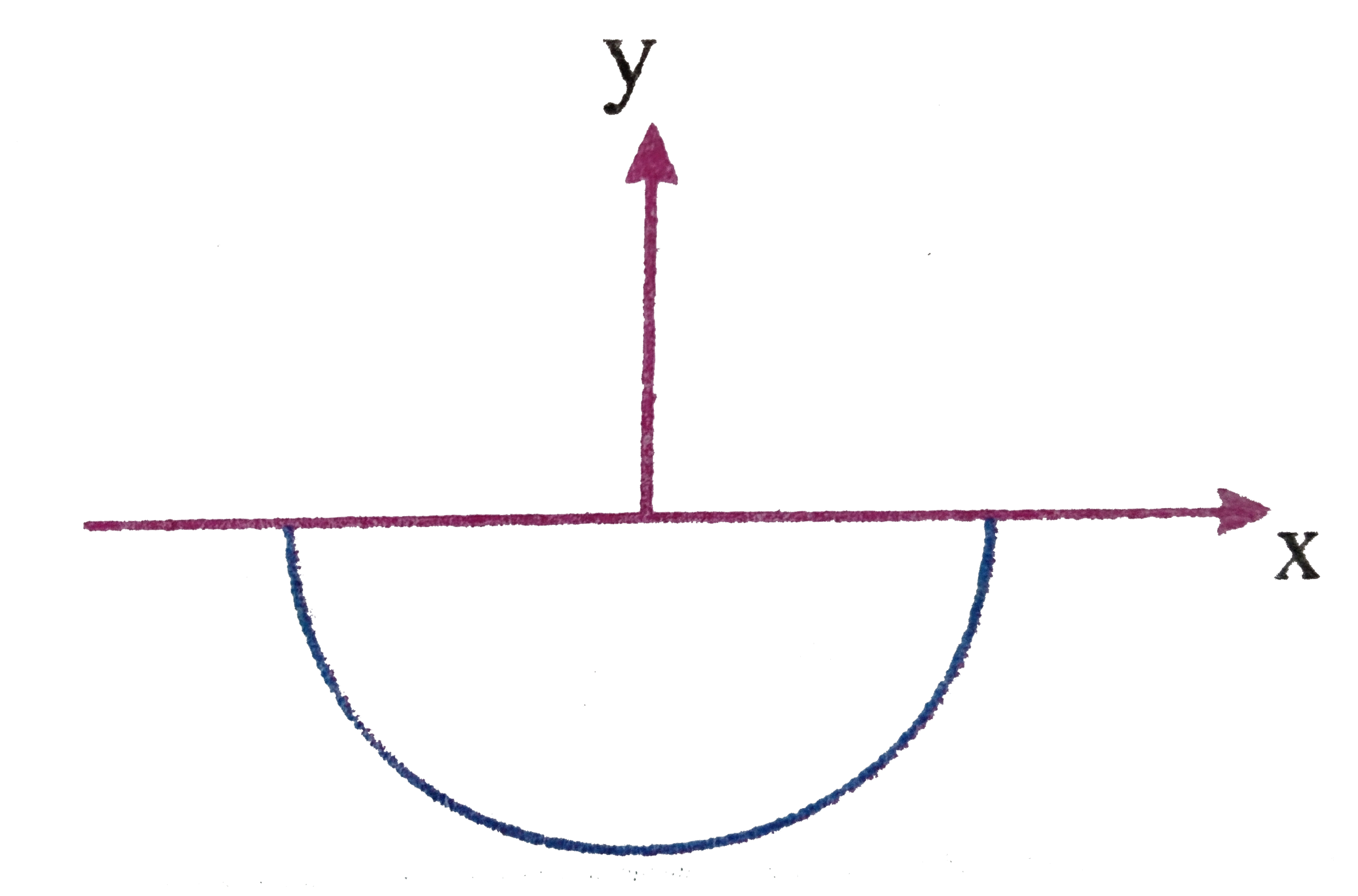
View SolutionA seimicircular uniform wore of radius `R = pi` can rotate frelly about x-axis. The cnetre of curvature is at origin as shown. The acceleration due to gravity is given by `vec(g)=-x^(2)hatj` units. For small oscillations of the wire its time period is given by `pisqrt(x)`. the value of `x` is ________
View Solution
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length `20cm`, fixed at its midpoint. The bob is displaced slightly perpenducular to the plane of the rod and string. Find period of small oscillations of the system in the form `(piX)/(10)s` and fill the value of X.
View Solution
A rod of mass `m` and length `l` hinged at one end is connected by two springs of spring constant `k_1` and `k_2` so that it is horizontal at equilibrium What is the angular frequency of the system? (in `(rad)/(s)`) (Take mass =3kg `l=1m`,`b=(1)/(4)m`,`K_1=16(N)/(m)`,`K_2=63(N)/(m)`.
View Solution
A uniform dics of mass m and radius `R=(80)/(23pi^2)`m is pivoted smoothly at `P`. If a uniform ring of mass `m` and radius `R` is welded at the lowest point of the disc, find the period of `SHM` of the system (disc `+` ring). (in seconds)
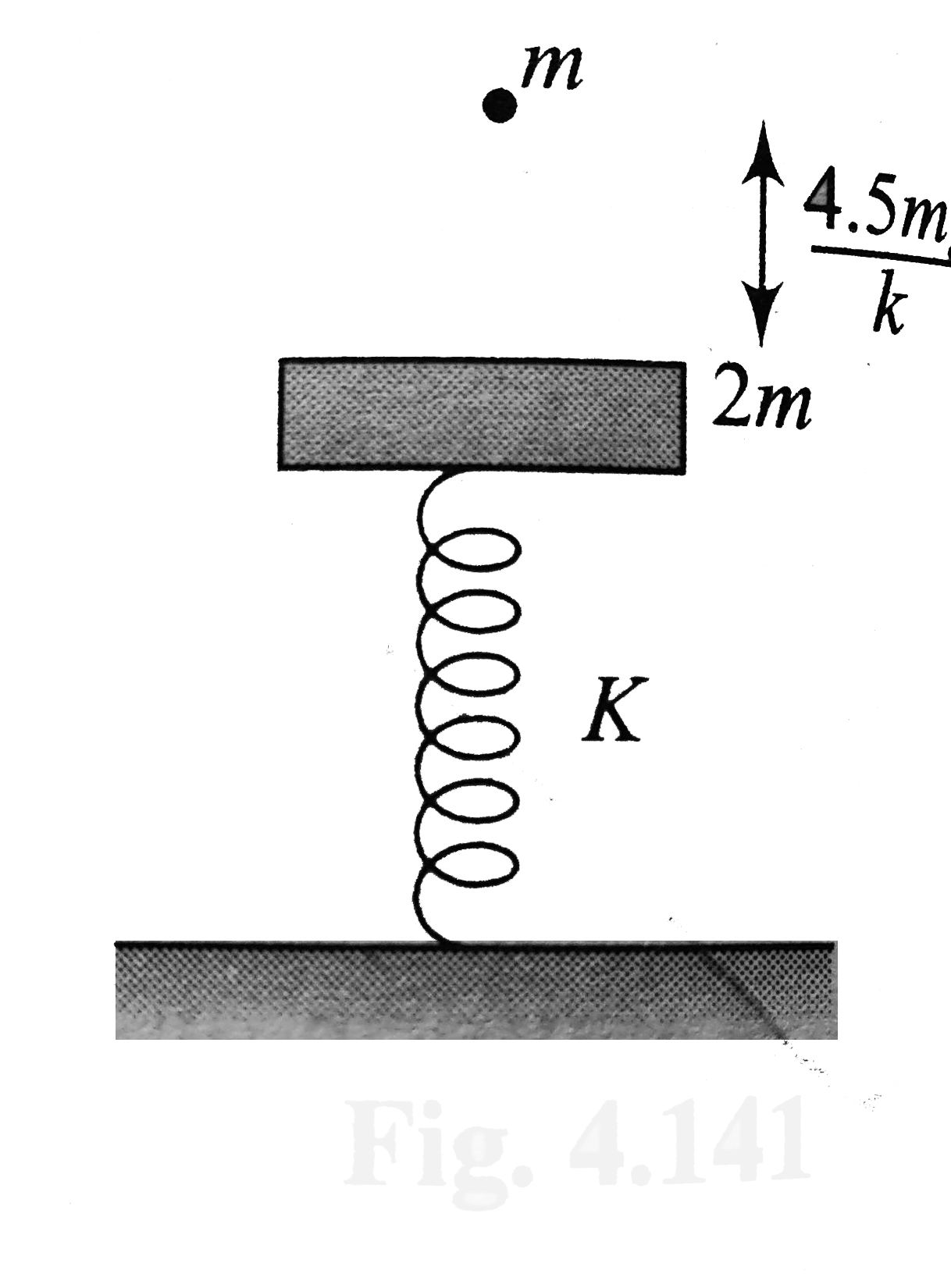
View SolutionIn the figure shown, mass `2m` connected with a spring of force constant `k` is at rest and in equilibrium. A particle of mass `m` is released from height `4.5 mg//k` from `2m` . The particle stick to the block. Neglecting the duration of collision find time from the release of `m` to the moment when the spring has maximum compression.
View Solution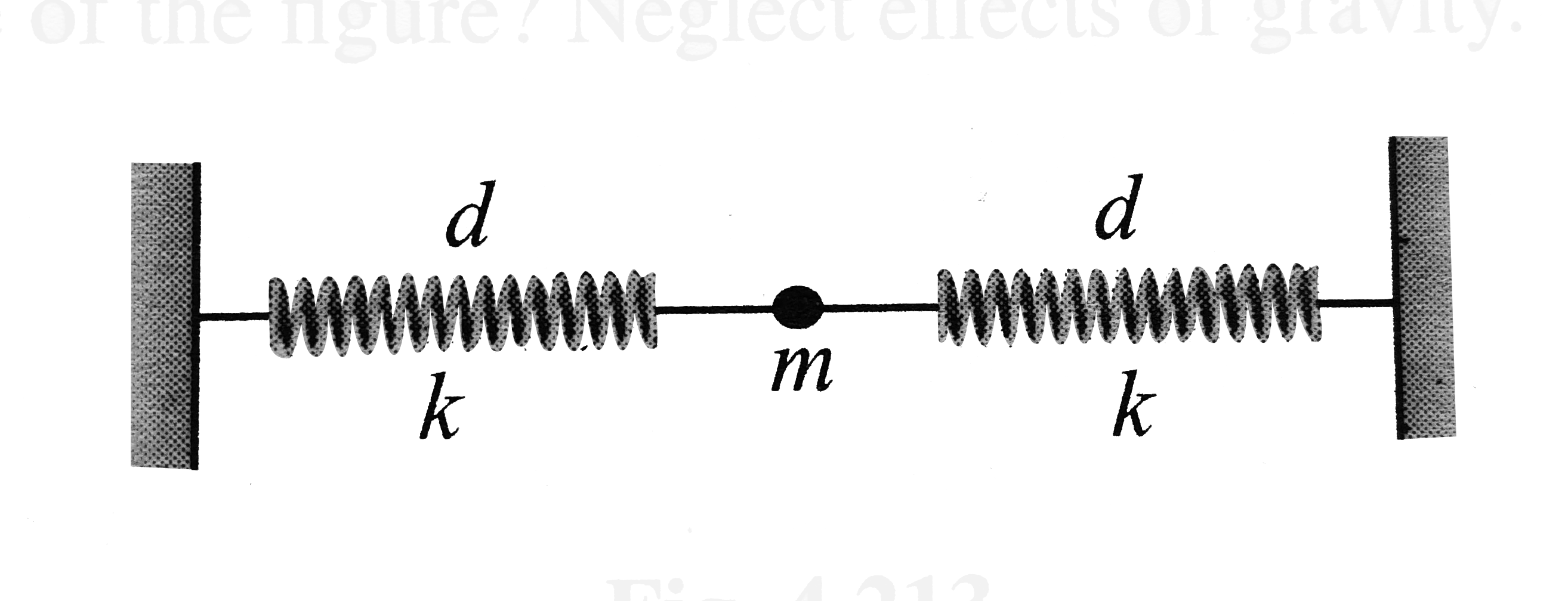
A small body of mass `m` is connected to two horizontal spring of elastic constant `k`, natural length `(3d)/(4)`. In the equilibrium position botgh springs are stretched to length `d`, as shown in Fig. What will be the ratio of perod of the motion `((T_b)/(T_a))` If the body is displaced horizontally by a small distance where `T_a` is the time period when the particle owscillates along the line of spring `T_b` is time plane of the figure? Neglect effect of gravity.
View SolutionA particle of mass `1kg` constrained to move along x axis under the action of the only conservation force for which the potential energy is given by `u = x^(3) - 4x^(2)` and was initially at rest at stabel equilibrium position and was very slightly displaced along x axis and then it oscillates with a period of `(pi)/(sqrt(x))`sec, the value of x is__________
View SolutionA small particle is tied by the help of two strings to vertical walls with the parameters as shown in the figure `(g = pi^(2))`. The time period of the small oscillations of the particle if it is displaced perpendicular to the plane of the paper slightly is x sec, the value of x is ____________

View SolutionIn the system shown in figure `A_(0)` and `4A_(0)` are the area of the pistons of masses `m` and `2m` respectively and the system is in a gravity free space. If one of the piston is displaced slightly by an amount `Deltax` then the time period of the resulting oscillations is `2pi sqrt((xm)/(yk))`. (spring constant are `k `and `2k`) and consider the mass of liquid to be negligible as compared to the masses of the pistons and the piston can slide smoothly without the liquid spilling out.The value of `y-x` is _________
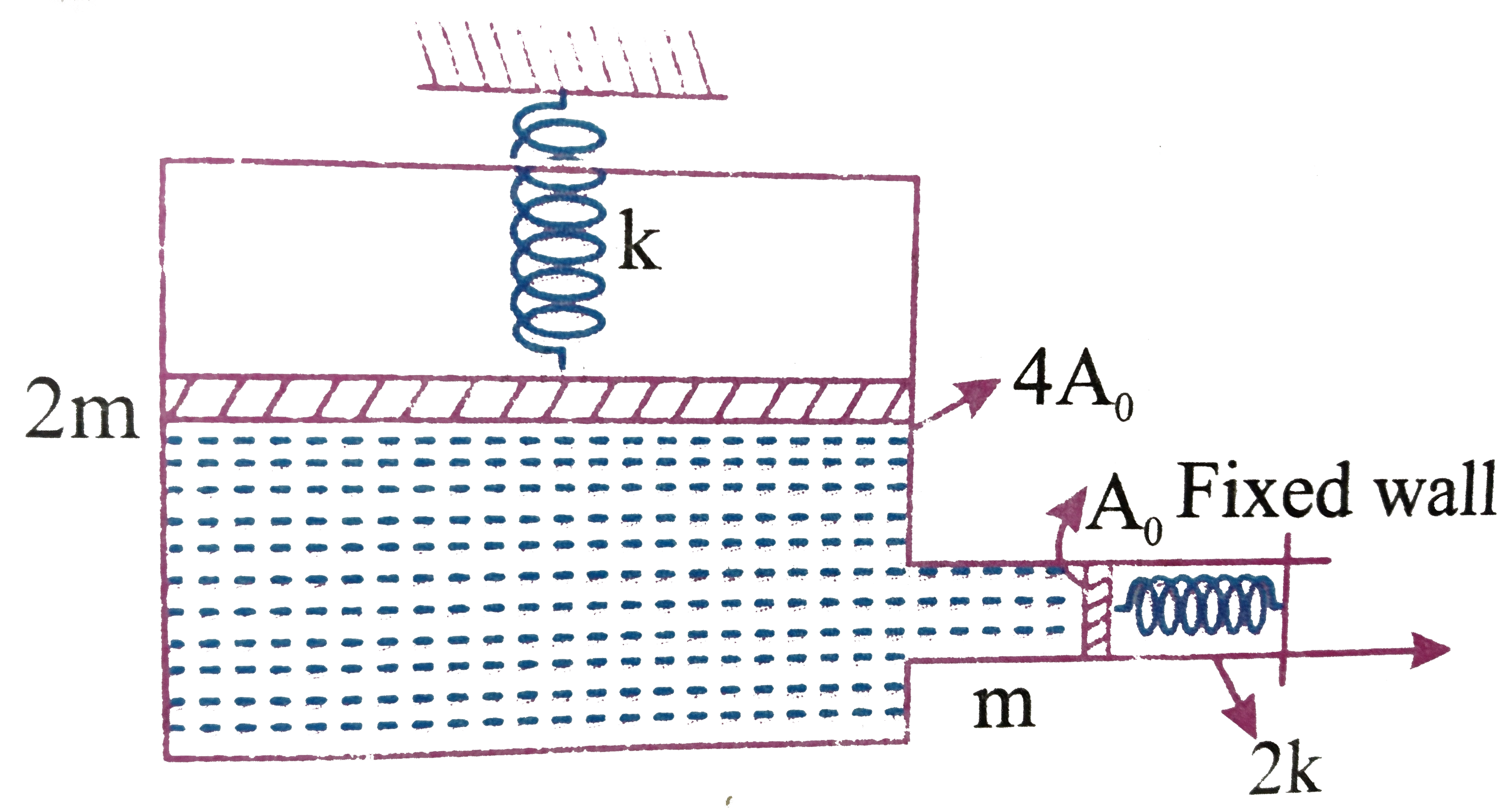
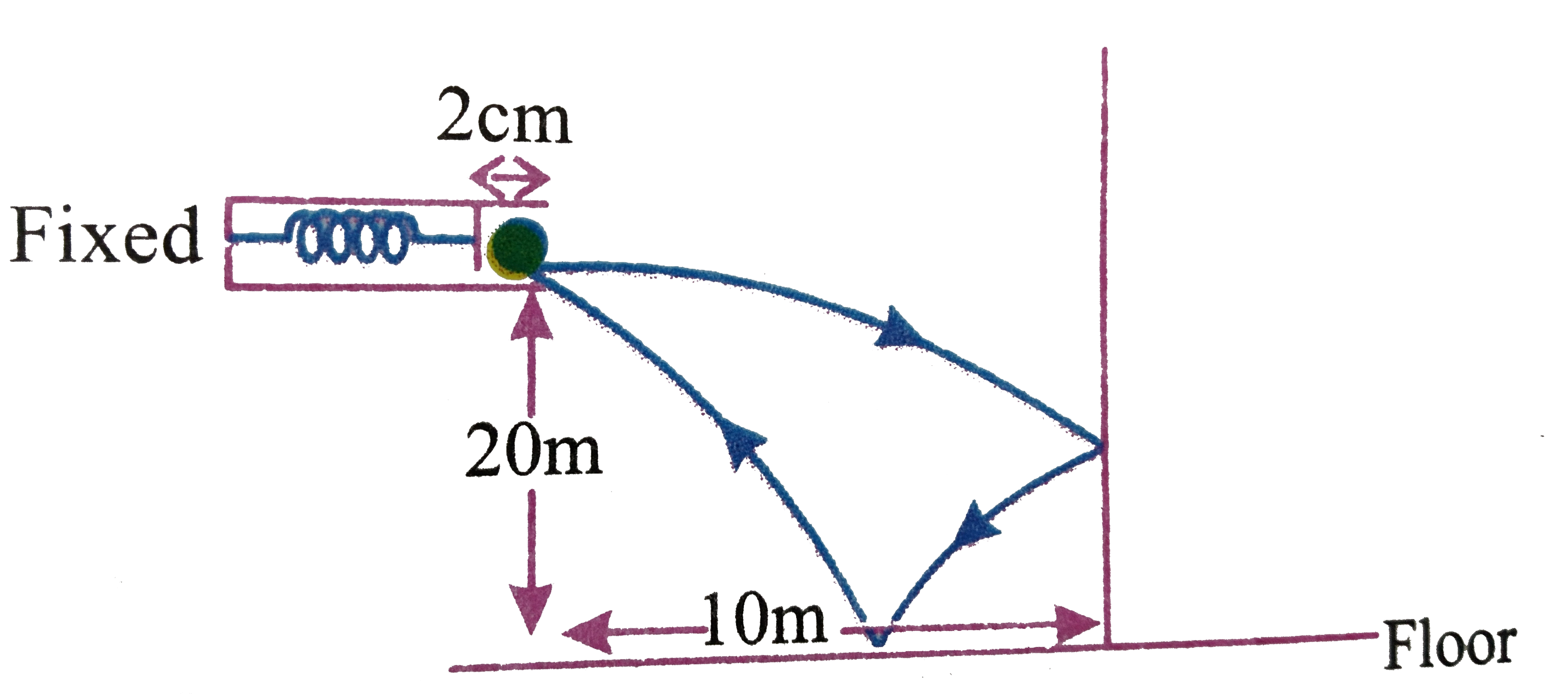
View SolutionA small ball of mass `1kg` is released from a smooth horizontal pipe containing a spring fixed at a height of `20m` and `10m` away from a vertical wall as shown in the figure. The initial compression of a spring is `2cm` and it strikes a smooth vertical wall and smooth horizontal floor repeatedly and elastically as shown. The time period of one complete oscillation `(g = 10m//s^(2))`. (The ball do not collide with walls of the pipe ) is `P +(pi)/(50Q)`, the value of `Q -P` is__________
View SolutionTwo point masses `m` and `2m` initially at rest are at separation `R` apart and due to the mutual gravitational force they come togther and collide elastically and then separates and the process continues. The time period of the resulting oscillations is `pisqrt((R)/(xg))`, the value of `x` is__________(Take `g = (Gm)/(R^(2)))`
View Solution
INTEGER ANSWER QUESTIONS questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION