Complete Solutions to EXERCISE - II (H.W) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | EXERCISE - II (H.W) |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
A particle of mass `m` is released from rest and follow a particle part as shown Assuming that the displacement of the mass from the origin is small which graph correctly depicts the position of the particle as a function of time?
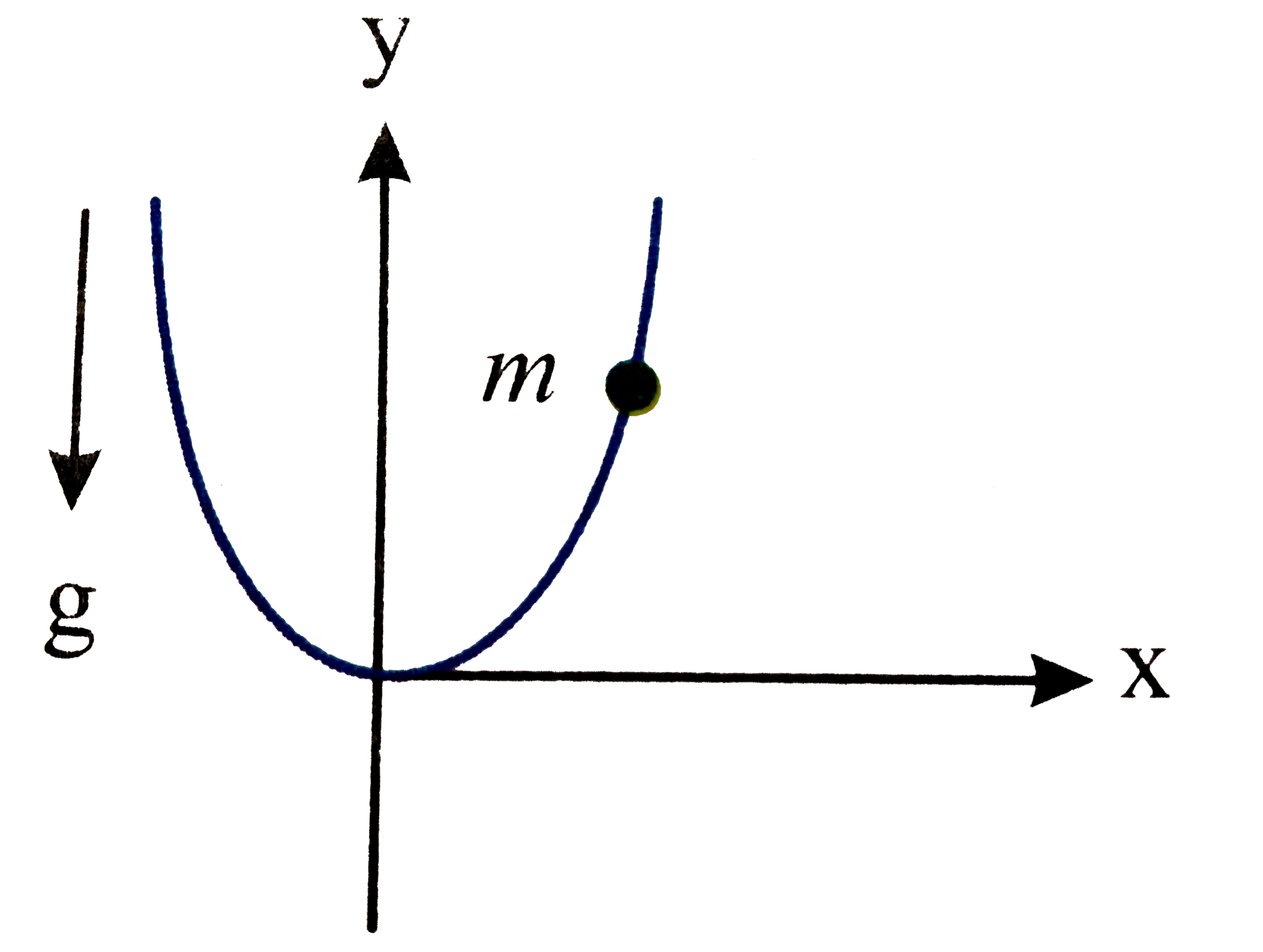
View SolutionA particle of mass `m` is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton `x^(2) =4ay`. The angular frequency of small oscillation is given by
View Solution`{:("List - I","List - II"),("(a) Planets revolving around the sun","(e) SHM"),("(b) Vibrations of a tuning fork","(f) linear motion"),("(c) Motion of projectile","(g) periodic motion"),("(d) Motion of a freely falling body","(h) translatory motion"):}`
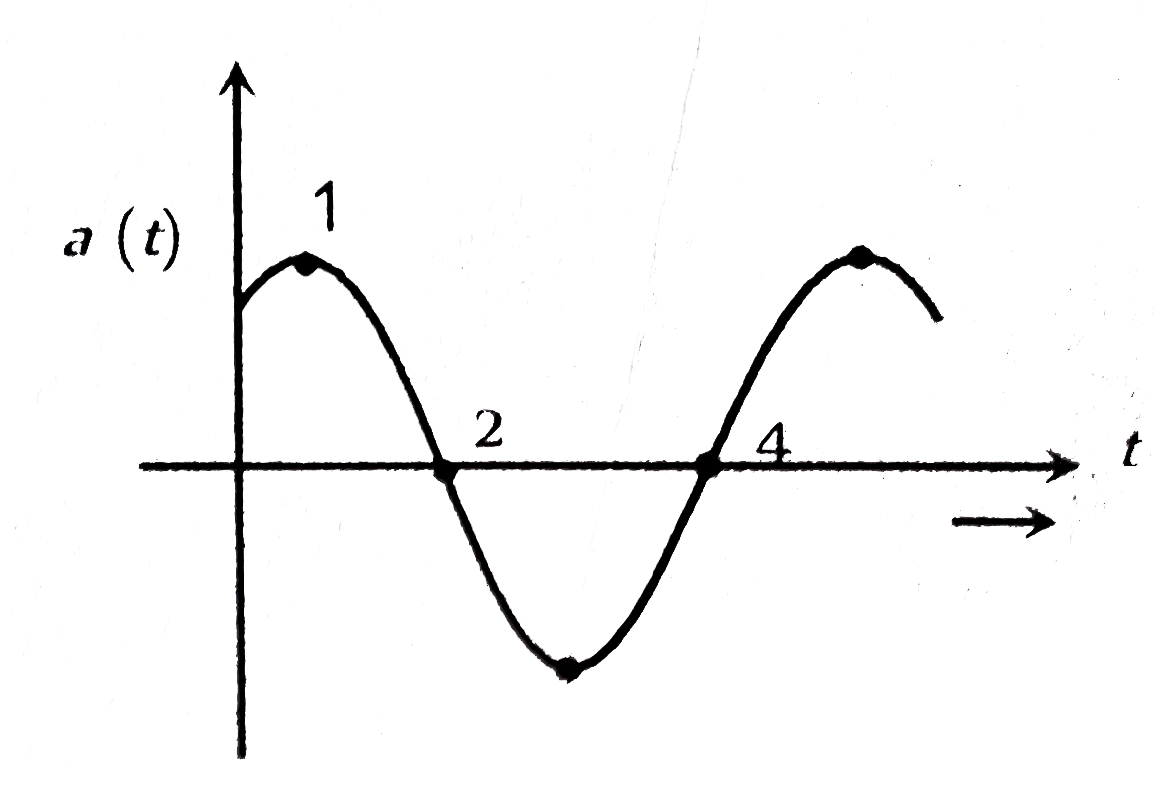
View SolutionThe acceleration a of a particle undergoing S.H.M. is shown in the figure. Which of the labelled points corresponds to the particle being at -x
View SolutionGraph between velocity and displacement of a particle, executing S.H.M. is
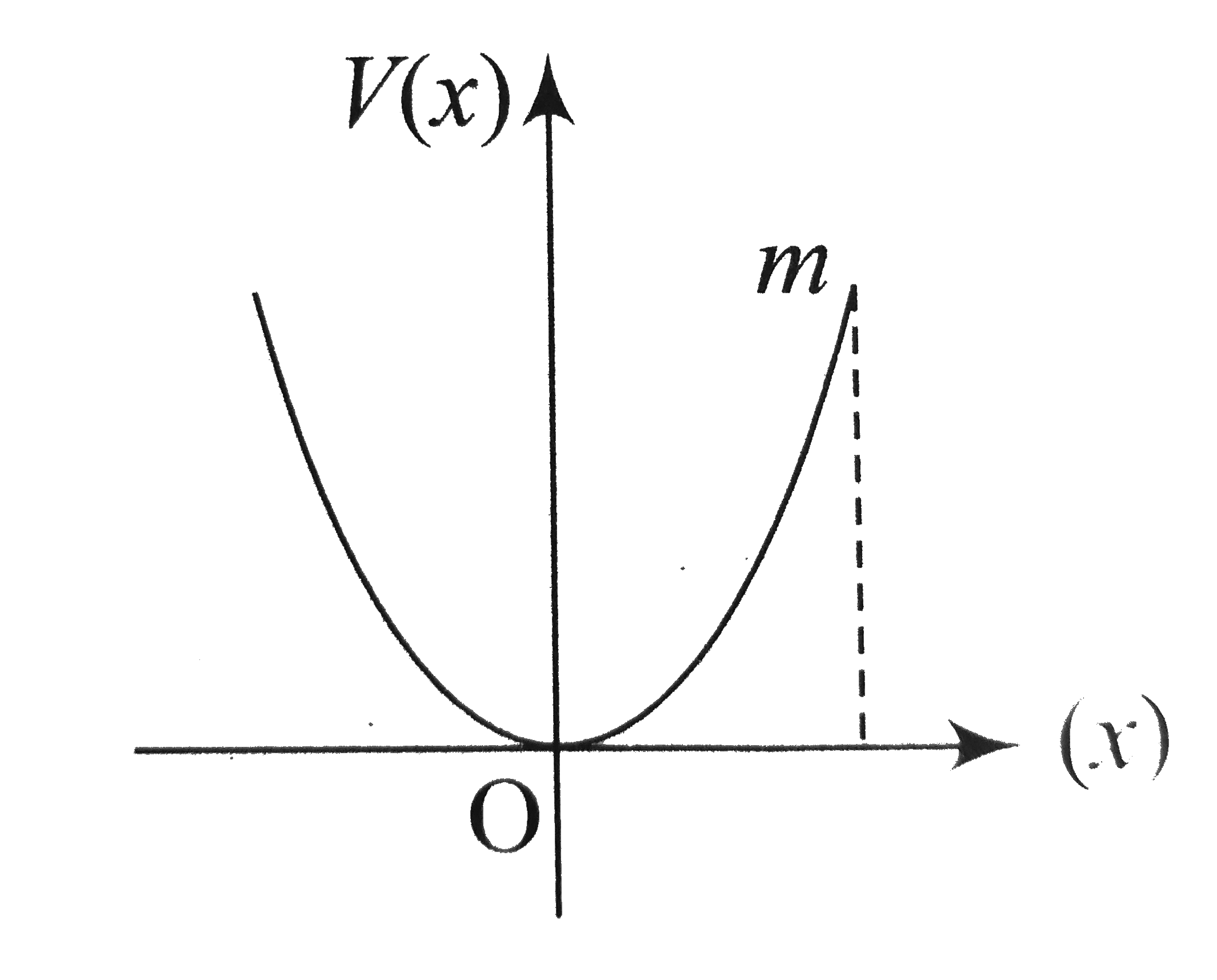
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If `U_((0))=0`, the graph of `U (x)` verses x will be (where U is the potential energy function.)
View SolutionThe velocity-time graph of a particle executing SHM is as shown in the figure. The amplitude and maximum acceleration of the particle respectively are
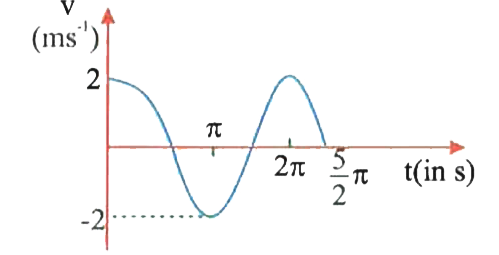
View SolutionThe smallest time interval between maximum and minimum velocities of the particle in the figure given in the above problem is
View SolutionThe acceleration-displacement graph of a particle executing SHM is as shown in the figure. The velocity of the particle at y = 0 is (take `tan 14^(@)` = 0.25)
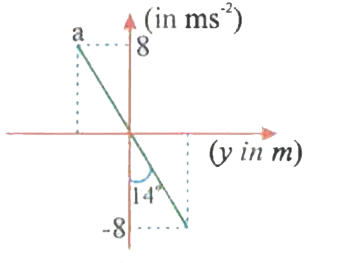
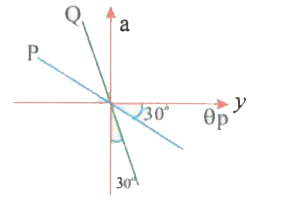
View SolutionThe acceleration-displacement graph of two particles P and Q exeucting SHM are represented as shown in the figure. The ratio of time periods of P, q respectively is
View SolutionA simple harmonic oscillator starts from mean position at time, t = 0, moves along +x-direction are reaches the extreme point in 1s covering a distance of 20 cm
(a) The equation of its motion is `x = 0.2 "cos" (pi)/(2) t`
(b) Its maximum speed is 0.314 `ms^(-1)`
(c) Its angular frequency is `(pi)/(2) rad s^(-1)`
(d) Its maximum acceleration is `(pi^(2))/(100) ms^(-2)`
View SolutionFor a particle executing SHM, if x, v, a and F represent dispacement, velocity, acceleration and restoring force, then
(A) `vec(F).vec(x)` is always negative
(B) `vec(v).vec(x)` is always negative
(C) `vec(v) xx vec(a)` is always zero
(D) `vec(a) xx vec(v)` is always positive
View SolutionA second pendulum is shifted from a plane where `g = 9.8 m//s^(2)` to another place where `g = 9.82 m//s^(2)`. To keep period of oscillation constant its length should be
View SolutionA simple pendulum with a brass bob has a period `T`. The bob is now immersed in a nonviscous liquid and oscillated. If the density of the liquid is `1//8th` of brass, the time period of the same pendulum will be
View SolutionCalculate the time period of a simple pendulum whose length is equal to radius of earth.
Hint `: L =R_(e) = 6.4 xx 10^(6) m , g = 9.8 ms^(-2)`
`T ' = 2pi sqrt(( R_(e))/(2g))`
View SolutionThe `l - T^(2)` graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
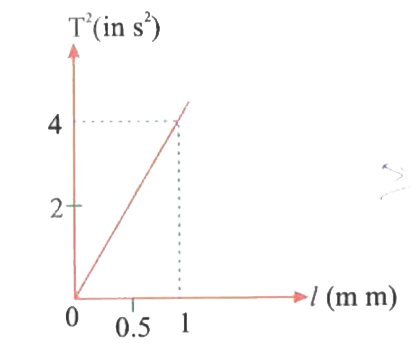
View Solutionl - T and `l-T^(2)` graphs of a simple pendulum on earth are as shown in the figure. The x-coordiante (OA) of point of intersection of the graphs is nearly equal to (on the earth `g = 9.8ms^(-2)`)
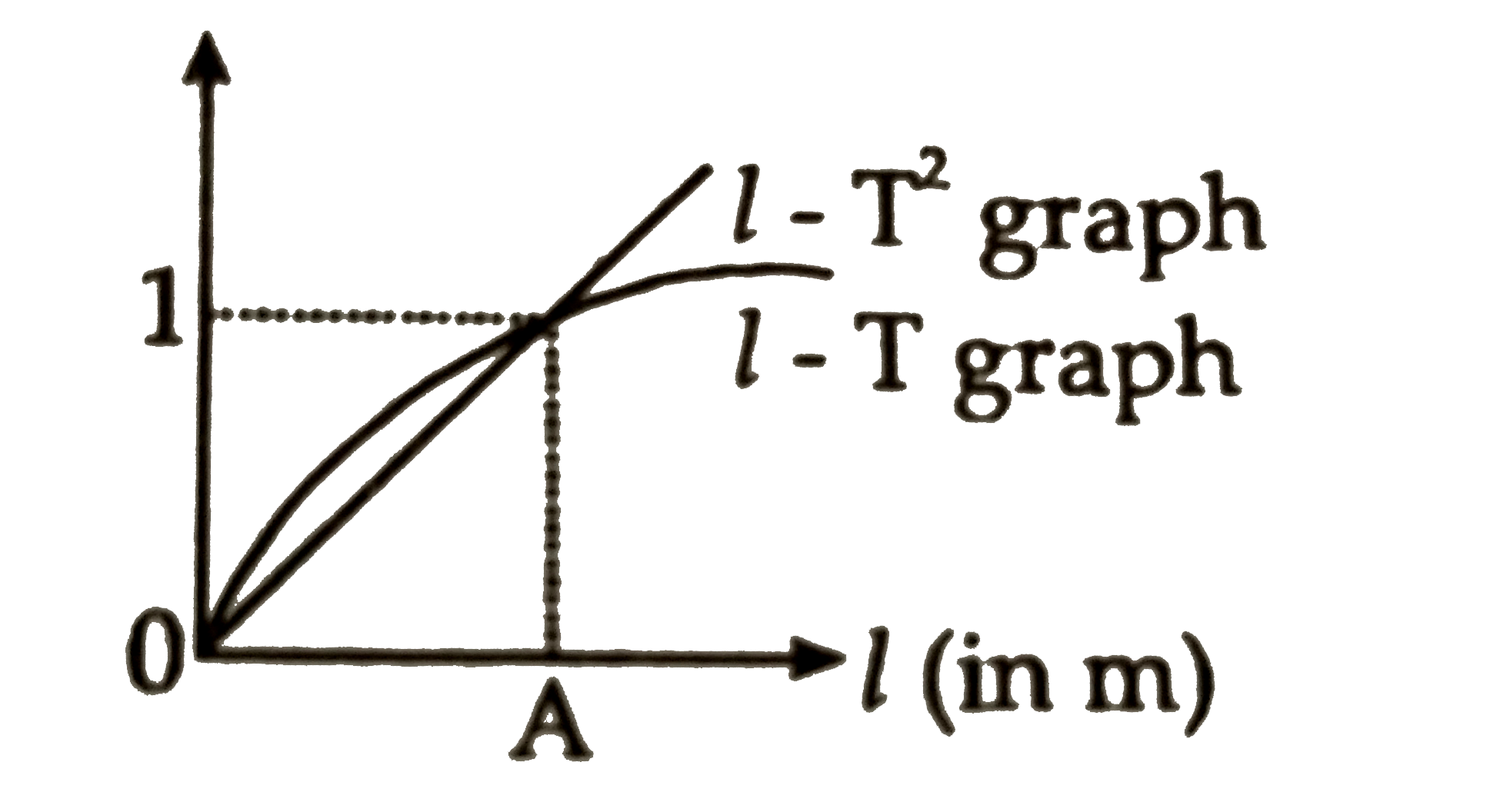
View SolutionFor a particle executing S.H.M. the displacement x is given by ` x= A cos omegat` . Identify the graph which represents the variation of potential energy (P.E.) as a function of time
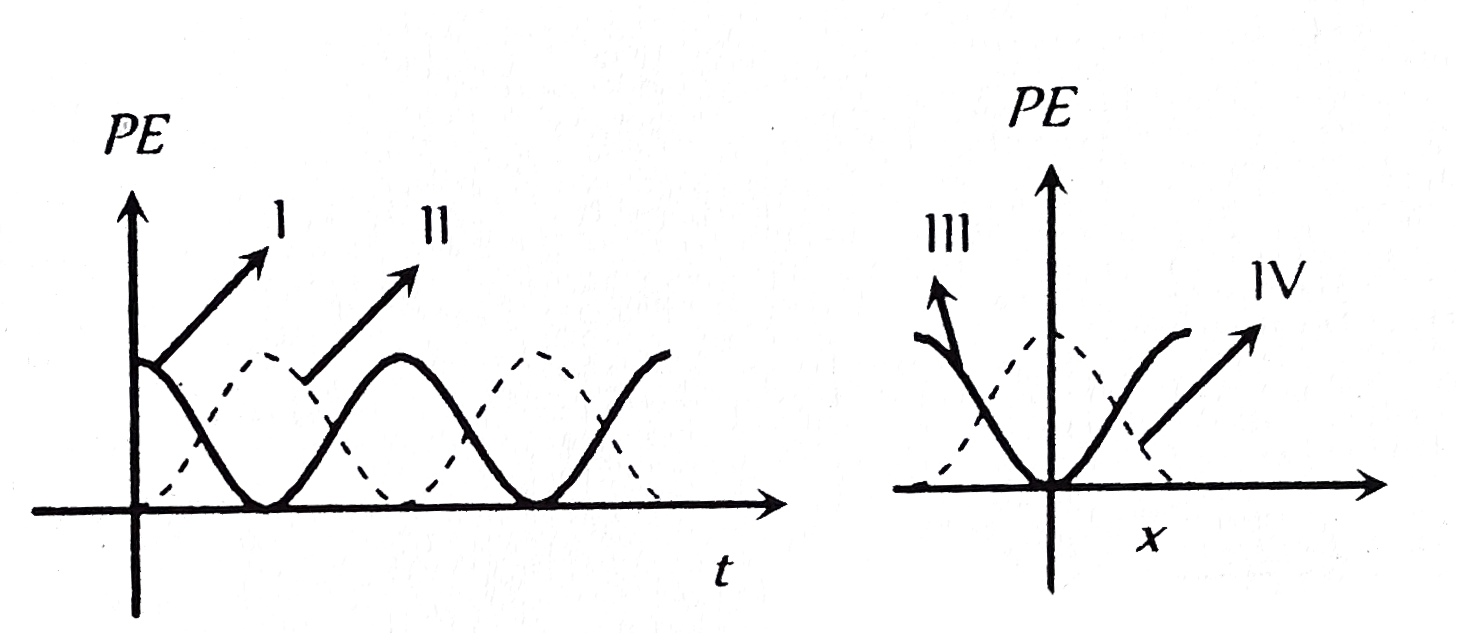
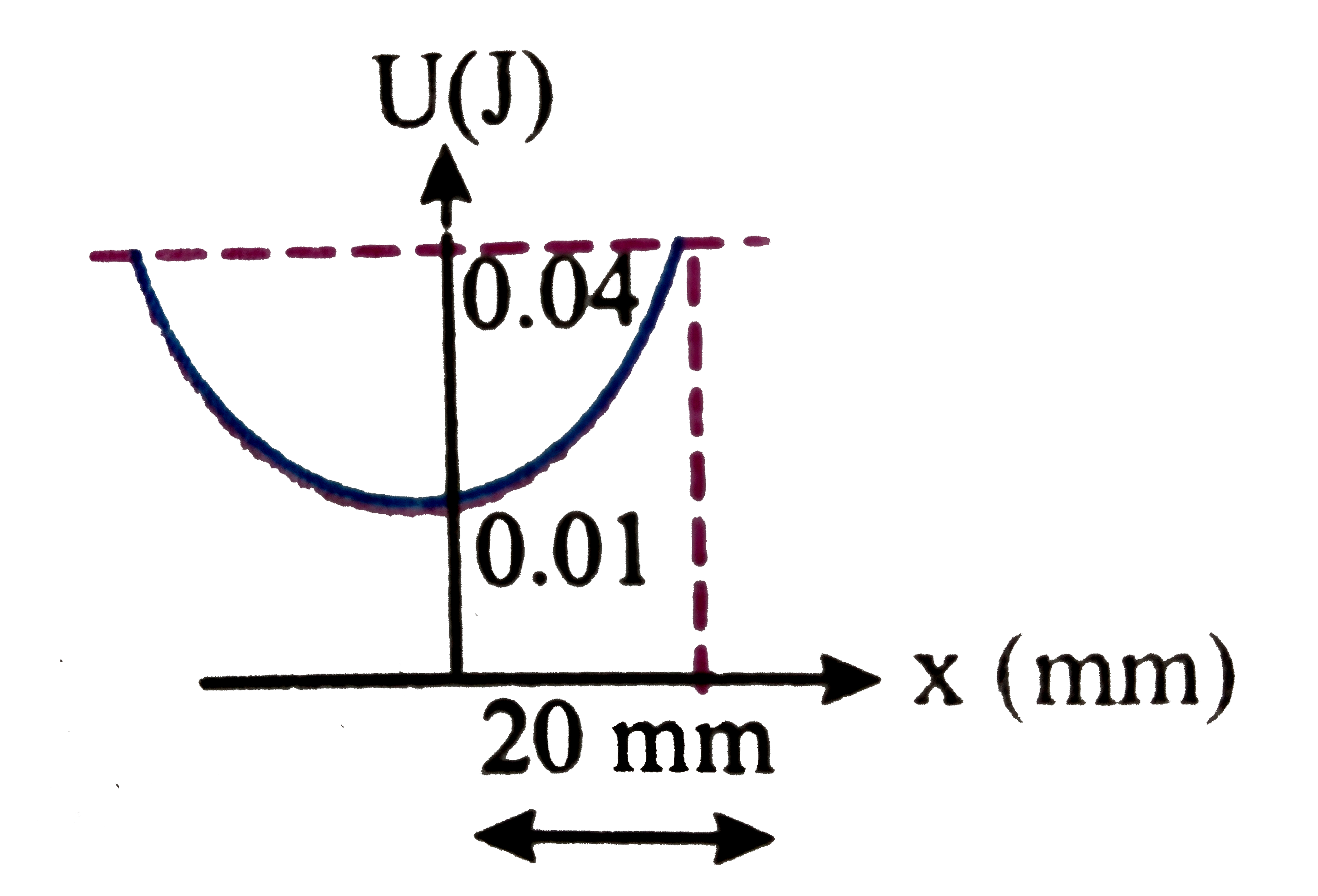
View SolutionThe variation of potential energy `(U)` of a simple harmonic oscillator is as shown. Then force constant of the system is `(PE` is in joules, displacement 'x' is in mm)
View Solution
EXERCISE - II (H.W) questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION