Complete Solutions to Solved Example of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | Solved Example |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
Which of the following functions of time represents (a) simple harmonic motion and (b) periodic motion? Given the period for each case.
i. `Sin omega t - cos omegat` ii. `Sin^(2)omegat`
View SolutionWhich of the following functions of time represent (a) simple harmonic (b) periodic but not simple harmonic and (c ) non periodic motion? Give period for each case of periodic motion `(omega` is nay positive constant)
(1) `Sin^(3) omegat` (2) `3cos (pi//4 -2 omegat)`
(3) `cos omegat +cos 3 omegat + cos 5 omegat`
(4) `e^(-omega^(2)t^(2))` (5) `1 + omegat +omega^(2) t^(2)`
View SolutionThe displacement of a particle executing SHM is given by `y=cos^(2)(t//2)sin(1000t).` Finid the independent constituent SHM's.
View SolutionTwo particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is one third their amplitude. What is the phase difference between them?
View SolutionA particle executing `SHM` from exterme position towards centre is observed to be at distances `x_(1),x_(2)` and `x_(3)` from the centre at the end of three successive seconds. The period of `SHM` is.
View SolutionA particle executes `SHM` in a straight line. In the first second starting from rest it travels distance a and in the next second it travels distance `a` and in the next second it travels distance `d` in the same direction. The amplitude of `SHM` is :
View SolutionA particle moves simple harmonically in a straight line starting from rest. In first 't' sec it travels a distance 'a' and in next 't'sec it travels '2a' in same direction. Then its time period is ?
View SolutionThe displacement of an obuect attached to a spring and executing simple harmonic motion is given by `x=2xx100^(-2) cos pit` metre. The time at which the maximum speed first occurs is.
View SolutionA particle is performing harmonic motion if its velocity are `v_(1)` and `v_(2)` at the displecement from the mean position are `y_(1)` and `y_(2)` respectively then its time period is
View SolutionA particle is executing `SHM`. It passes through mean position at the instant `t = 0`. At what instants the speed of it is `50%` of its maximum speed?
View SolutionFigure shows the graph of velocity versus displacement of a partciel executing simple harmonic motion. Find the period of oscillation of the particle.

View Solution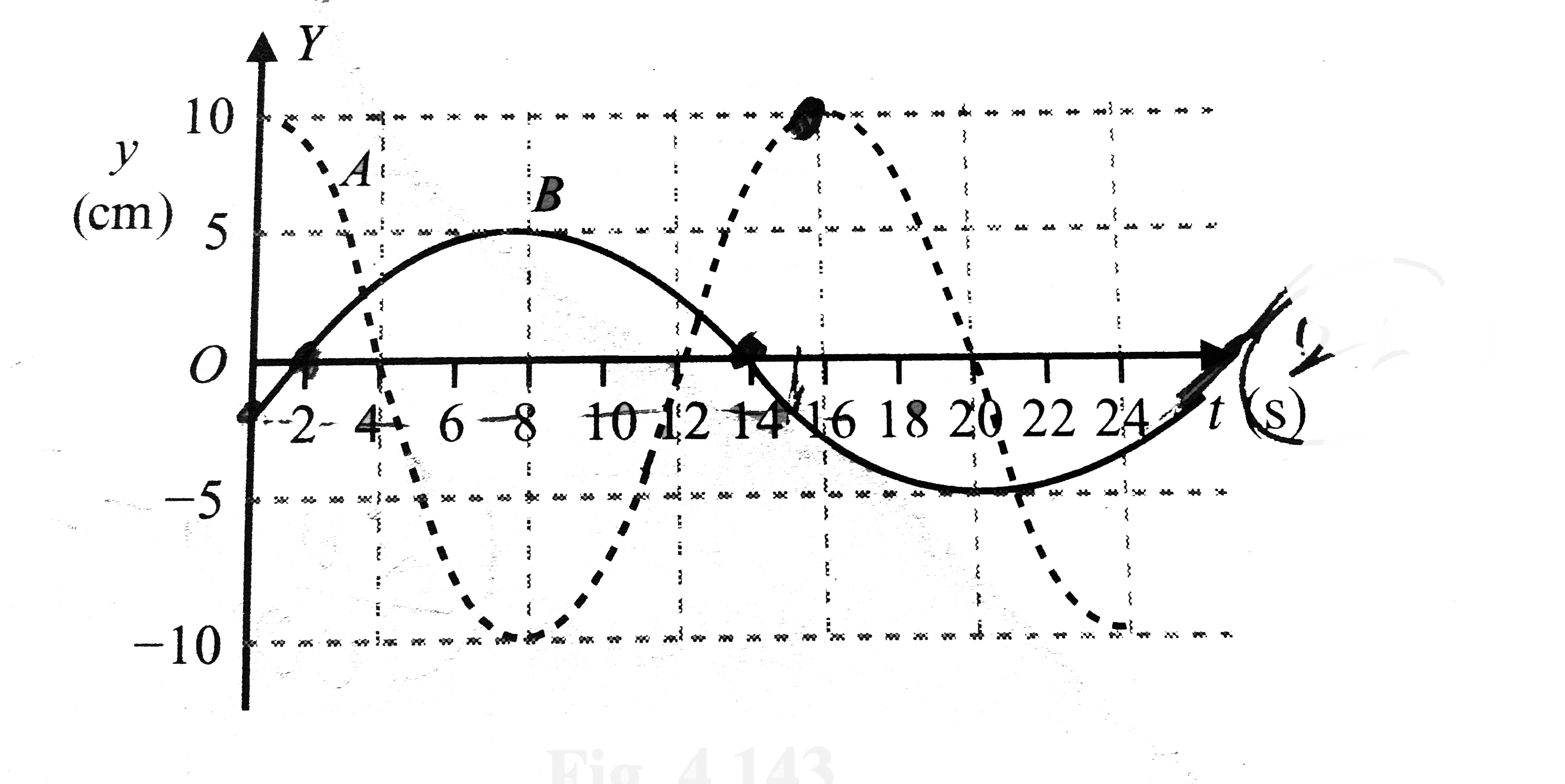
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities is
View SolutionThe particle is moving such that its displacement along x-axis as a function of time is given by `x(x -6) = 1 - 10 cos omegat`. Find amplitude, time period and mean position.
View SolutionA particle performs linear `SHM` of period `(2pi)/(omega)` about a point 'O' and is observed to have a velocity `b omega sqrt(3)` when at a distance `b` from 'O'. If the particle is moving towards the positive extermity at that instant, show that it will travel a further distance `b` in a time `(pi)/(3 omega)` before coming momentarily to rest.
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency `omega` along the x-axis . Their mean position is separated by distance `X_(0)(X_(0)gtA). If the maximum separation between them is (X_(0)+A), the phase difference between their motion is:
View SolutionA particle executes `SHM` represented by the equation, `y = 0.02 sin (3.14t+(pi)/(2))m`. Find (i) amplitude (ii) time period (iii) frequecy (iv) epoch (v) maximum velocity and (vi) maximum acceleration.
View SolutionA body executes `SHM`, such that its velocity at the mean position is `1ms^(-1)` and acceleration at exterme position is `1.57 ms^(-2)`. Calculate the amplitude and the time period of oscillation.
View SolutionA point mass oscillates along the x-axis according to the law `x=x_(0) cos(moegat-pi//4). If the acceleration of the particle is written as `a=A cos(omegat+delta), the .
View SolutionIf `x, v` and a denote the displacement, velocity and acceleration of a particle exceuting simple harmonic motion of time period `T`, then, which of the following does not change with time.
(1) `a^(2)T^(2) +4pi^(2)v^(2)` (2) `(aT)/(x)`
(3) `aT = 2piv` (4) `(aT)/(v)`
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View SolutionWhen a particle is performing `SHM` of time period `T_(1)` the force acting on it is `F_(1)` for a certain displacement. When the same particle is performing `SHM` of time period `T_(2)` the force acting is `F_(2)` for the same displacement. What will be the time period of the particle when a combined force of `F_(1)` and `F_(2)` produce the same displacement in `SHM` is different cases?
View SolutionA linear harmonic oscillator of force constant `2 xx 10^6 N//m` and amplitude (0.01 m) has a total mechanical energy of (160 J). Its.
View SolutionA particle of mass `1 kg` is executing `SHM` with an amplitude of `1m` and time pariod. `pis`. Calculate kinetic enegry of the particle at the moment when the displacement is `0.8 m`.
View SolutionA particle of mass `10g` executes a linear `SHM` of amplitude `5 cm` with a pariod of `2s`. Find the `PE` and `KE,(1)/(6) s` after crossing the mean position.
View SolutionA particle of mass `0.1kg` executes `SHM` under a force `F =- 10x (N)`. Speed of particle at mean position is `6 m//s`. Find its amplitude of oscillation.
View SolutionWhen a particle is performing linear `SHM` its `KE` is two times its `pE` at a position `A` and its `PE` is two times its `KE` at another position `B`. Find ratio of `KE_(A)` to `KE_(B)`
View SolutionThe potential energy of a simple harmonic oscillator of mass 2 kg in its mean position is 5 J. If its total energy is 9 J and its amplitude is 0.01 m, its time period would be
View SolutionAn object of mass `0.2 kg` executes simple harmonic oscillation along the `x - axis`with a frequency of `(25//pi) Hz`. At the position `x = 0.04`, the object has Kinetic energy of `0.5 J` and potential energy `0.4 J. The amplitude of oscillations is……m.
View SolutionThe displacement of two identical particles executing `SHM` are represented by equations `x_(1) = 4 sin (10t+(pi)/(6)) & x_(2) = 5 cos (omegat)` For what value of `omega`, energy of both the particles is same.
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is `V(x) = k|x|^3` where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThe potential energy of a particle of mass `1kg` in motion along the x- axis is given by: `U = 4(1 - cos 2x)`, where `x` in meters. The period of small oscillation (in sec) is
View SolutionThe displacement of `SHO` is, `y = 6 sin(pit +pi//3)` find (1) Instants at which `PE` is minimum (or) `KE` is maximum. (2) Instants at which `PE` is maximum (or) `KE` is minimum.
View SolutionA particle of mass `m` executes `SHM` with amplitude 'a' and frequency 'v'. The average kinetic energy during motion from the position of equilibrium to the end is:
(1) `2pi^(2) ma^(2) v^(2)` (2) `pi^(2)ma^(2) v^(2)`
(3) `(1)/(2) ma^(2) v^(2)` (4) `4pi^(2) ma^(2) v^(2)`
View SolutionA block of mass 'm' is attached to the light spring of force constant `K` and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA spring of force constant `1200Nm^(-1)` is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA light vertical spring is stretched by `0.2 cm` when a weight of `10g` is attached to its free end. The weight is further pulled down by `1cm` and released. Compute the frequency and maximum velocity of load.
View SolutionA mass `m = 8 kg` is attached to a spring passing over a pulled whose other end is fixed to ground and held in position so that the spring remains unstretched. The spring constant is `200 N//m`. The mass `m` is then released and begins to undergo small oscillations. Find maximum velocity of mass
View SolutionFrequency of a particle executing `SHM` is `10Hz`. The particle is suspended form a vertical spring. At the highest point of its oscillation the spring is unstretched. Find the maximum speed of the particle: `(g = 10 m//s^(2))`
View SolutionA `15 gm` ball is shot from a spring whose spring has a force constant of `600 N//m`. The spring is compressed by `5 cm`. The greater possible horizontal range of the ball for this compression is
View SolutionA block with mass `M` attached to a horizontal spring with force constant `k` is moving with simple harmonic motion having amplitude `A_(1)`. At the instant when the block passes through its equilibrium position a lump of putty with mass `m` is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.
View SolutionTwo particles `A` and `B` of masses 'm' and '2m' are suspended form massless springs of force constants `K_(1)` and `K_(2)`. During their oscillation if maximum speeds are equal then ratio of their amplitudes is
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between block and plank is `1//2`. Plank is undergoing `SHM` is angular frequency `10 rad//s`. Find the maximum amplitude of plank in which the block does slip over plank `(g = 10 m//s^(2))`.
View SolutionA mass `M` attached to a horizontal spring executes `SHM` with an amplitude `A_(1)`. When mass `M` passes through its mean position a smaller mass `m` is placed over it and both of them move togther with amplitude `A_(2)`. Ratio of `((A_(1))/(A_(2)))` is:
View SolutionFind the period of the oscillations of the devices shown in figure if `m` is displaced slightly.
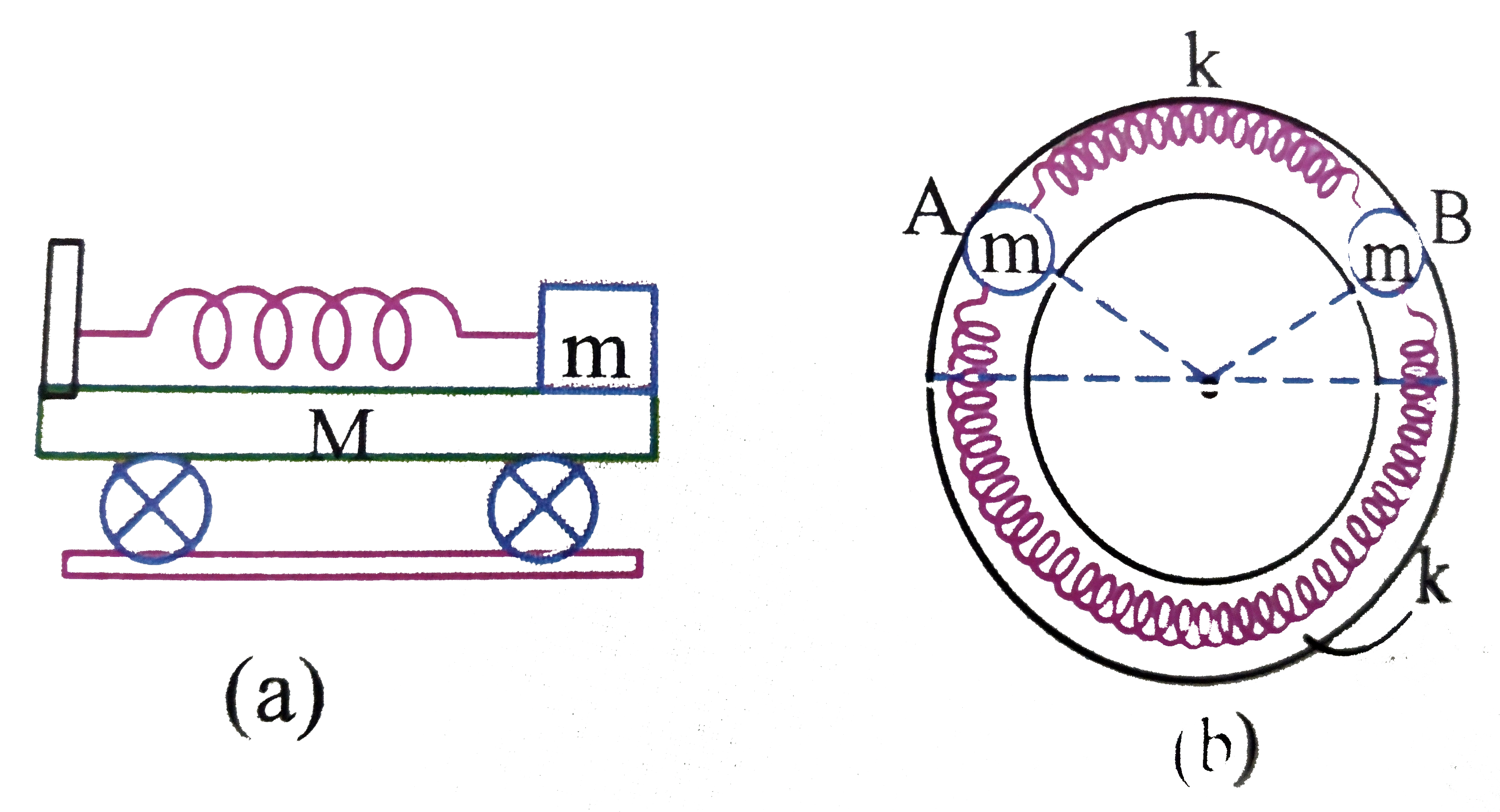
View SolutionA block of mass `m` is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionTwo pendulums of lengths `1.69m` and `1.44m` start swinging togther. After how many vibrations will they again start swinging togther?
View SolutionIn the diagram shown find the time period of pendulum for small oscillations
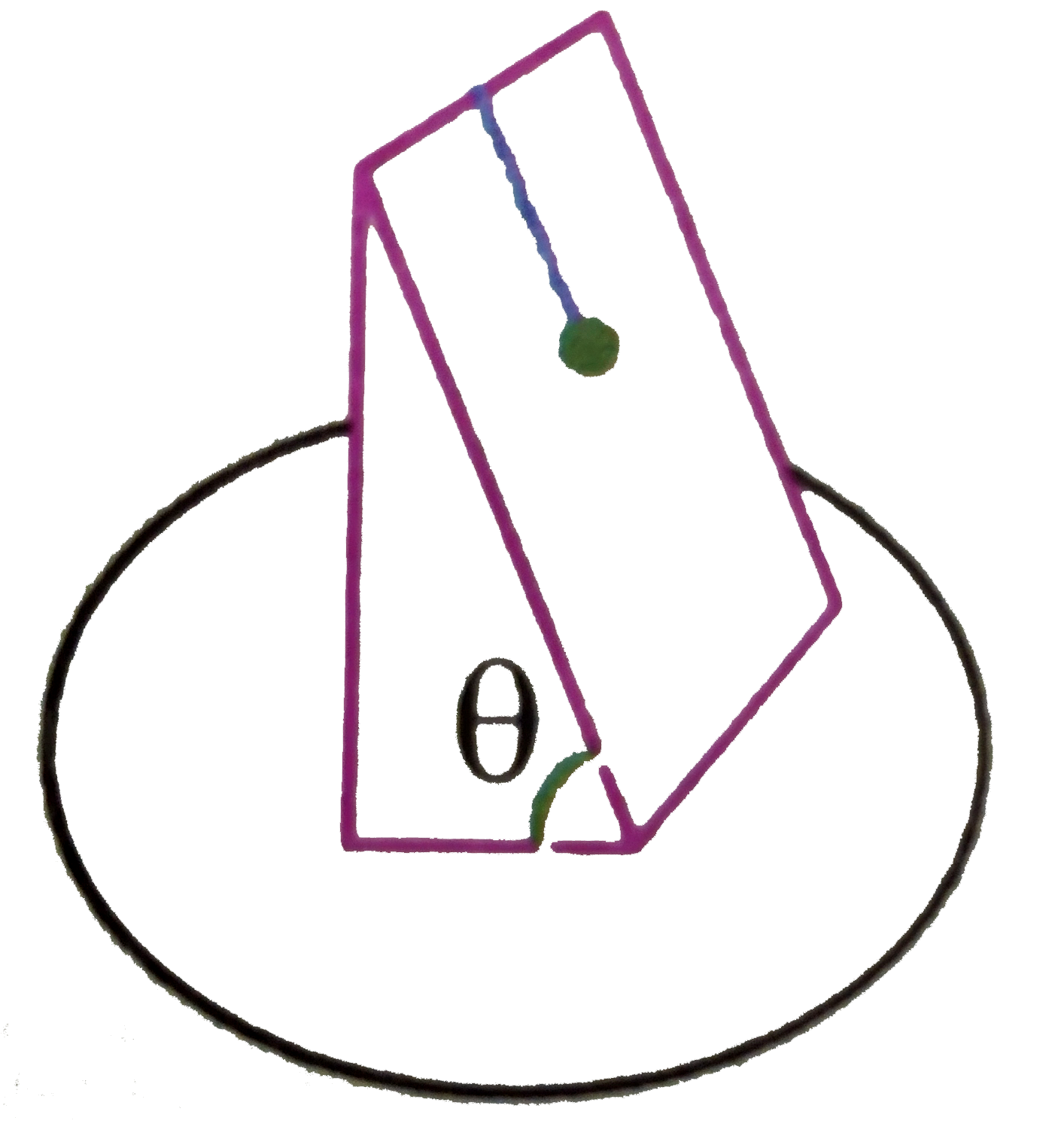
View SolutionThe trollet car having simple pendulum decelerated by friction. In consequence, the pendulum has time period `T`. If `T_(o)` is time period of the simple pendulum in the absence of any acceleration of the trolley car, the value of `(T)/(T_(o))` is---
View SolutionA simple pendulum has time period `T_(1)`. When the point of suspension moves vertically up according to the equation `y=kt^(2)` where `k=1m//s^(2)` and `'t'` is time then the time period of the pendulum is `T_(2)` then `(T_(1)//T_(2))^(2)` is
View SolutionA simple pendulum `4m` long swing with an amplitude of `0.2m`. What is its acceleration at the ends of its path?
View SolutionA uniform rod of mass 'm' and length 'l' is hinged at one end 'A'. It can rotate freely about a horizontal axis passing through 'A'. If it is given a sloght angular displacement and left to itself then it oscillate. Find the time period of small oscillations.

View SolutionA uniform ring of radius 'R' is suspended from a horizontal nail 'A' as shown. Find time period of its small oscillations.

View SolutionThe amplitude of a damped oscillator decreases to `0/9` times ist oringinal magnitude in `5s`, In anothet `10s` it will decrease to a times its original magnitude, wherea eqcrease .
View SolutionA mass of `2kg` oscillates on a spring with force constant `50 N//m`. By what factor does the frequency of oscillation decrease when `a` damping force with constant `b = 12` is introduced ?
View SolutionIn damped oscillatory motion a block of mass `20kg` is suspended to a spring of force constant `90N//m` in a medium and damping constant is `40g//s`. Find (a) time period of oscillation (b) time taken for amplitude of oscillation to drop to half of its intial value (c) time taken for its mechanical energy to drop to half of its initial value.
View SolutionIf a simple pendulum has significant amplitude (up to a factor of1//e of original) only in the period between `t-0s to t=tau s`, then `tau` may be called the average life of the pendulum. When the sphetical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity with b as the constant of propotional to average life time of the pendulum is (assuming damping is small) in seconds:
View SolutionTwo simple harmonic motion `y_(2) A sin omegat` and `y_(2)=A cos omegat` are superimposed on a particle of mass `m`. The total mechanical energy of the particle is:
View SolutionThe speed `v` of particle moving along x-axis is given by `v^(2) = 8bx - x^(2) - 12 b^(2)`, where 'b' is a constant. Find amplitude, maximum velocity and time period of oscillation.
View SolutionA small block is connected to a mass less rod, which is turn is attached to a spring of force constant `k` as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
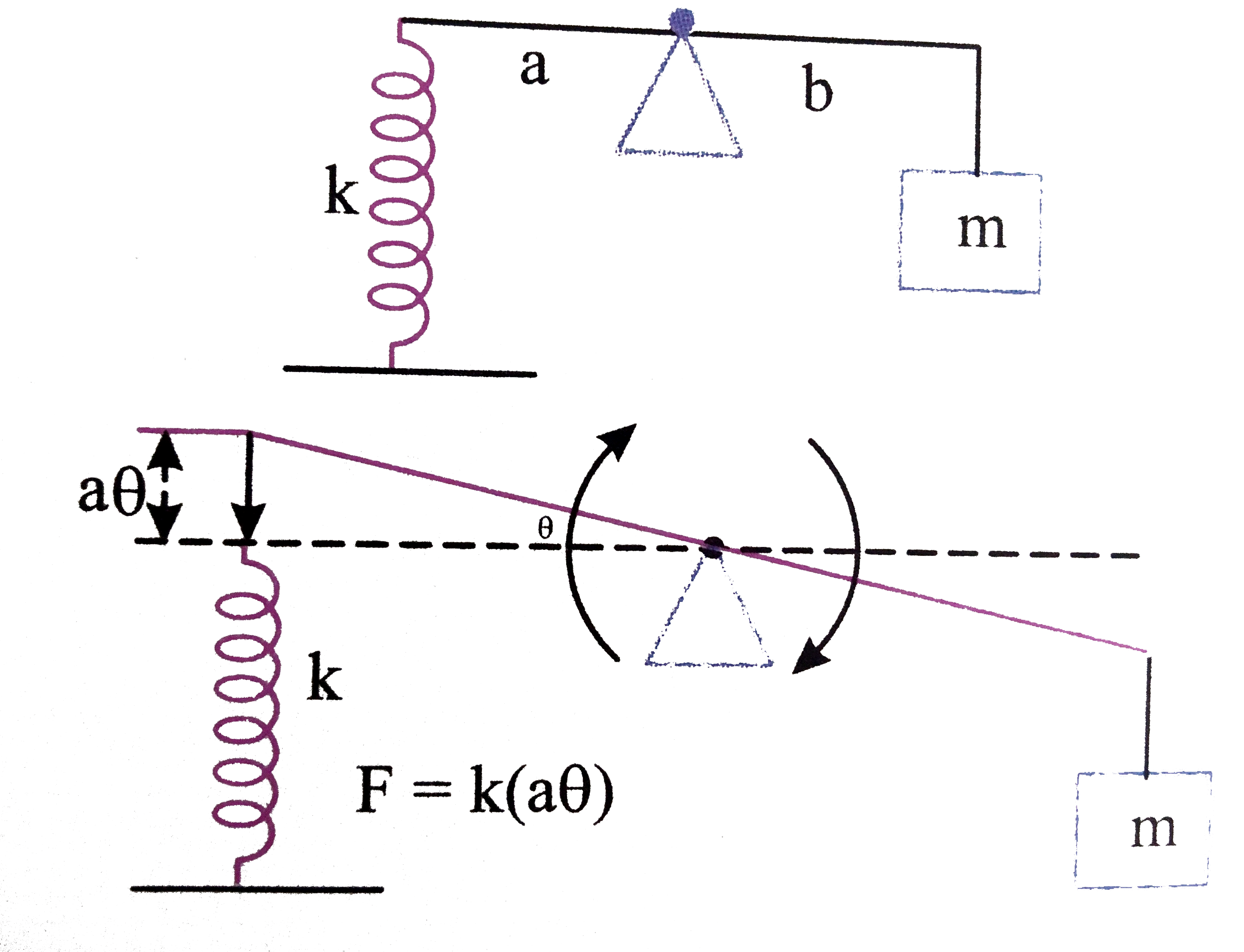
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant `k` and a block of mass `m`. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionA block of mass `m` is attached to one end of a light intextensible string passing over a smooth light pulled `A` and under another smooth light pulled `B` as shown in Fig. The other end of a springs is fixed to a ceiling. `A` and `B` are held by spring of force constant `k_(1)` and `k_(2)`. Find the period of small oscillations of system.
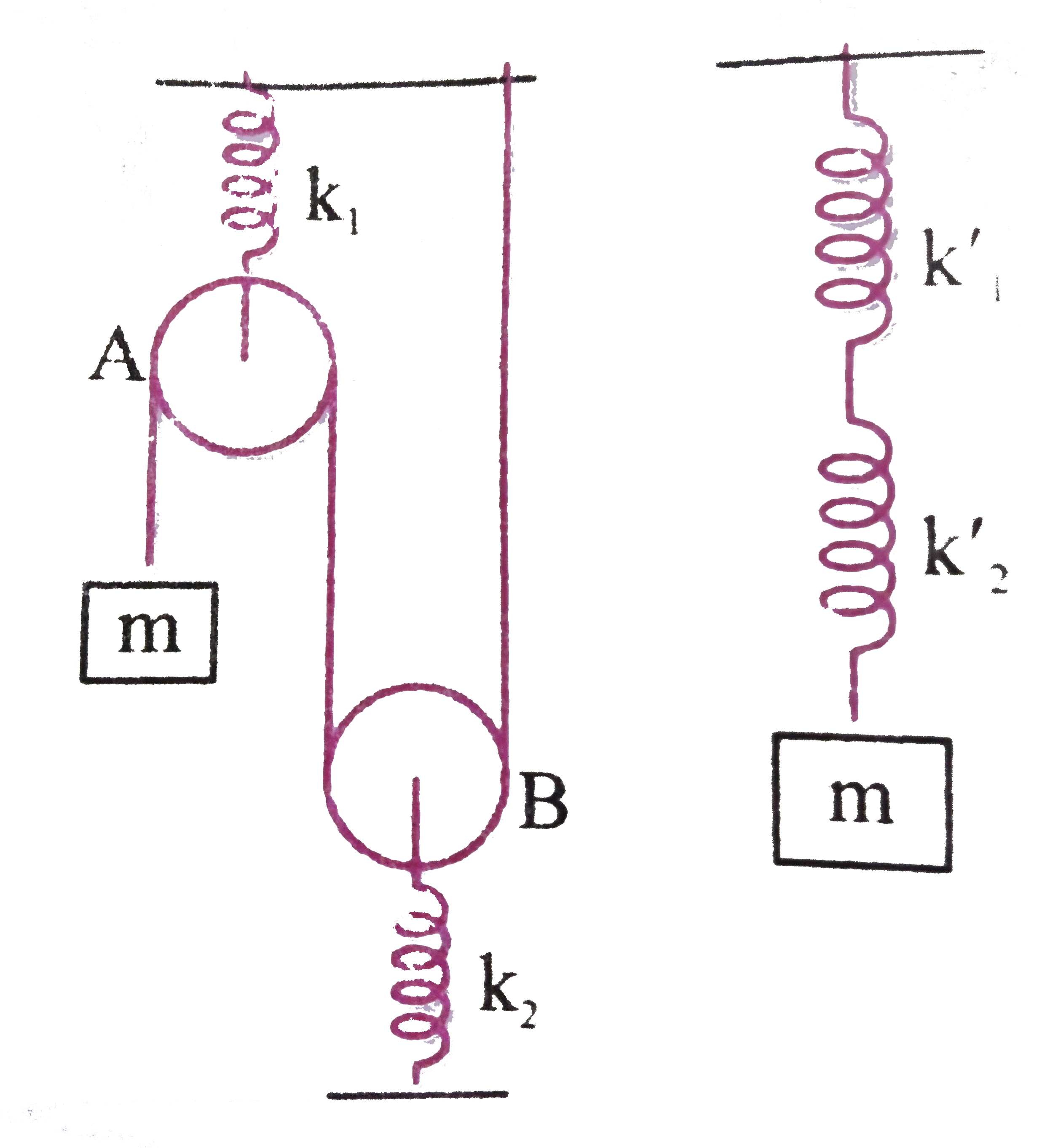
View SolutionIn the device shown in Fig, the block `m` is displaced down slightly and released. It starts oscillating. Pulleys are smooth and massless string and springs are also massless. Find time period of oscillations.

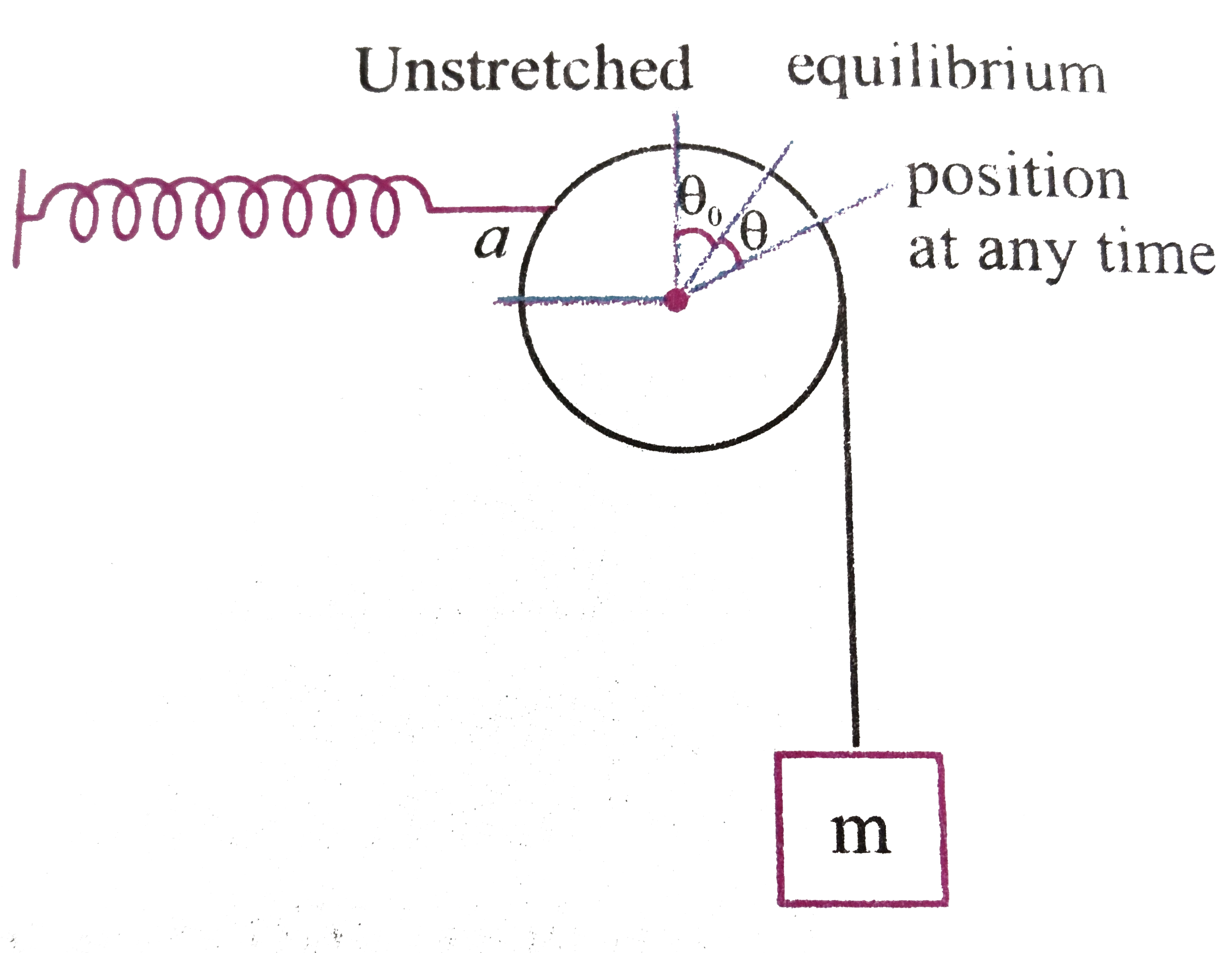
View SolutionIn the system shown in Fig, a disc pivoted at its centre has a spring attached at a distance 'a' form centre and `a` mass 'm' that cen rotate the disc. For small angular displacement calculate the frequency of oscillation
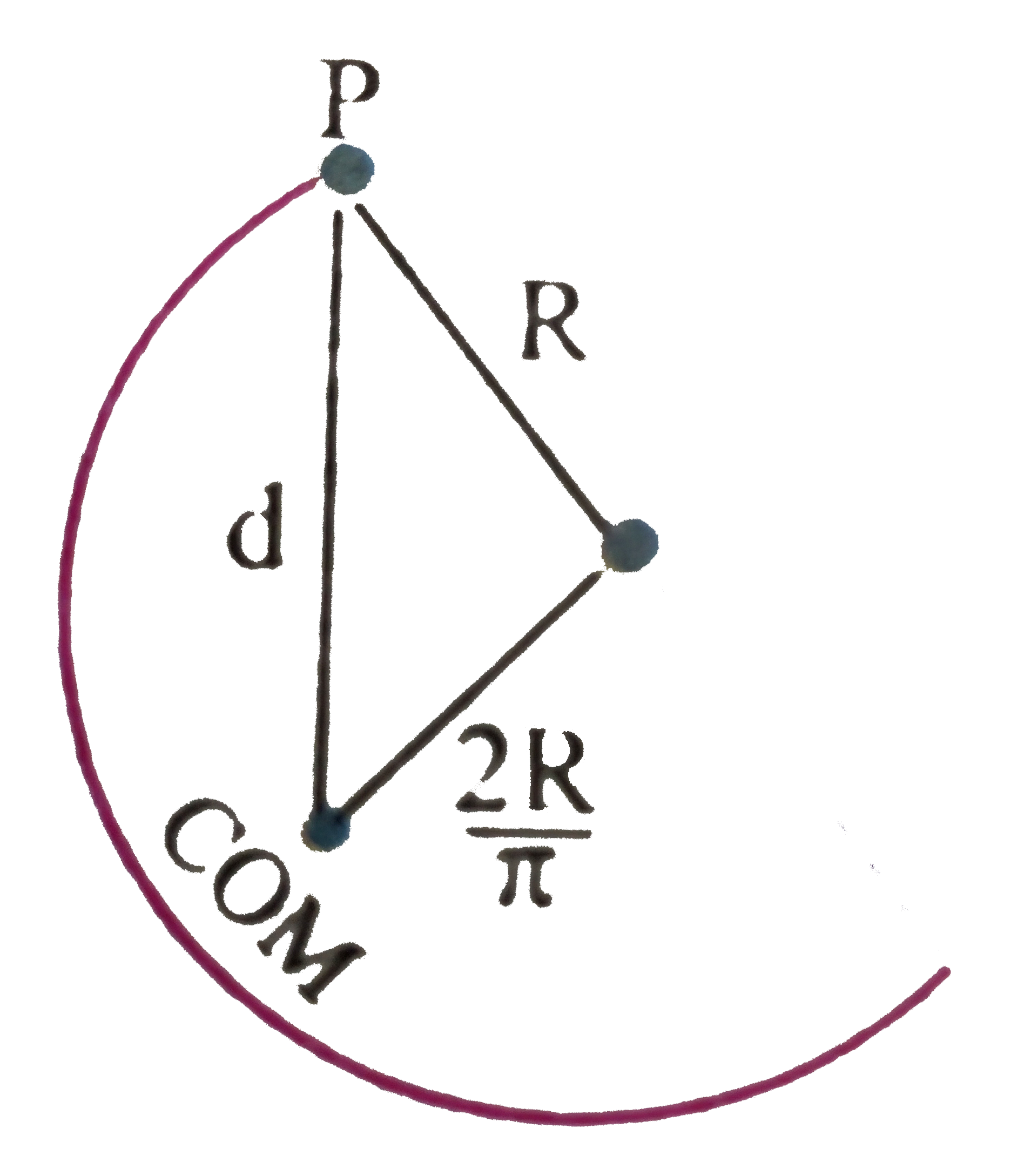
View SolutionA semicircular rigid wore of radius of curvature 'R' is smothly pivoted at 'P'. Find the frequency of small oscillations of the wire under gavity
View SolutionConsider a semicircular shell of mass 'm' and radius 'r' which rolls without slipping as shown in Fig. Use the fact that maximum kinetic energy at mean position is equal to maximum potential at exterme position and find out the frequency of oscillation.

View Solution
Solved Example questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION