Complete Solutions to EXERCISE - II (C.W) of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | EXERCISE - II (C.W) |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
The displacement time graph of a particle executing SHM is as shown in the figure
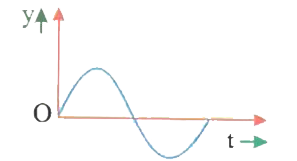
The corresponding force-time graph of the particle is
View SolutionTwo particles undergo SHM along the same line with the same time period (T) and equal amplitude (A). At a particular instant one is at x = -A and the other is at x = 0. If they start moving in the same direction then they will cross each other at
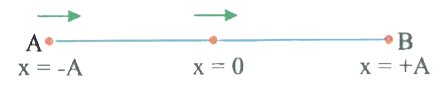
(i) `t = (4T)/(3)`
(ii) `t = (3T)/(8)`
(iii) `x = (A)/(2)`
(iv) `x = (A)/(sqrt(2))`
View Solution(A) : Projection of a uniform circular motion on the diameter of the circle is simple harmonic.
(B) : The energy of a body executing SHM is directly proportional to square of its amplitude.
View SolutionA particle is executing SHM. Then the graph of acceleration as a function of displacement is
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
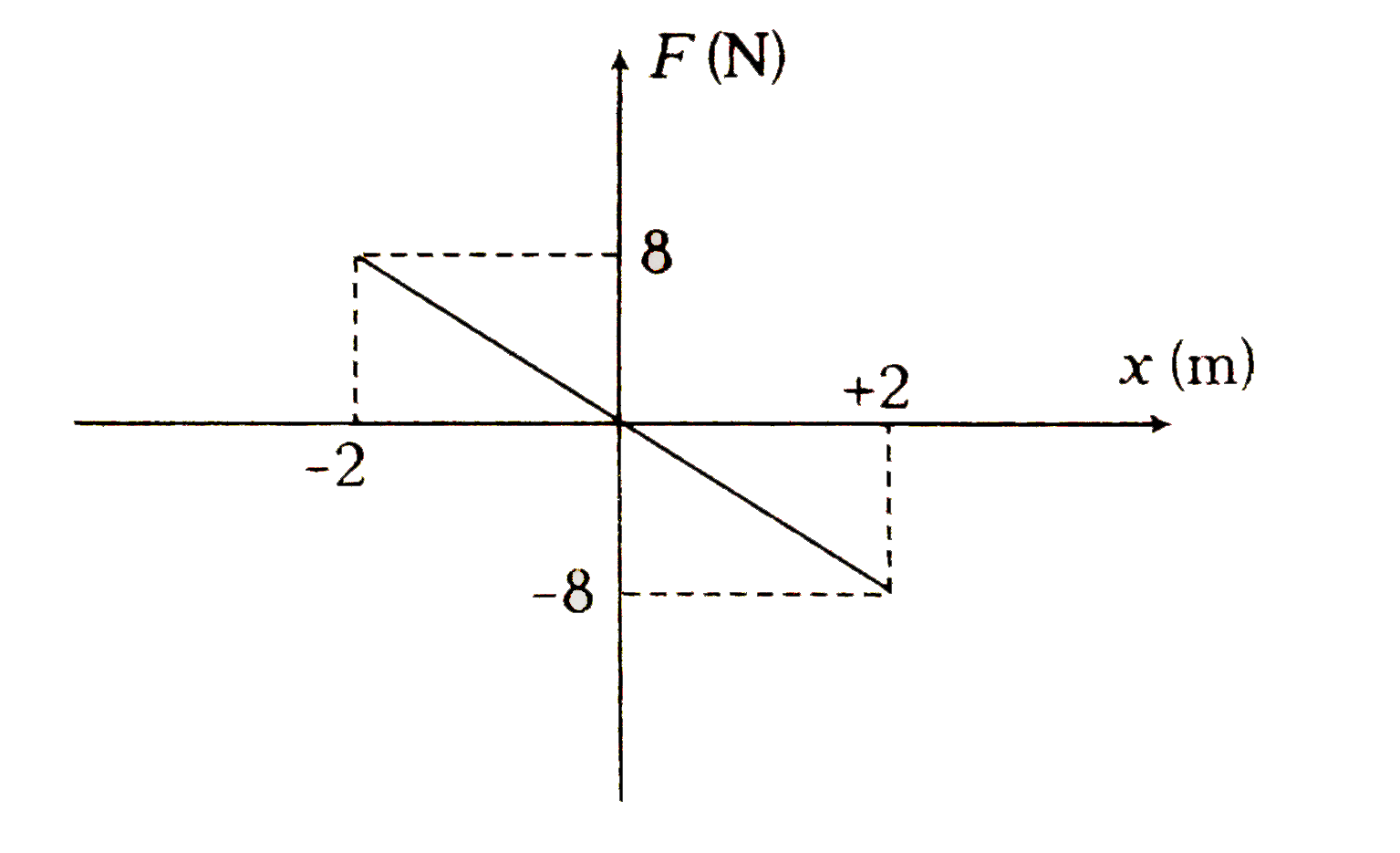
View SolutionThe oscillation of a body on a smooth horizontal surface is represented by the equation,
`X = A cos (omega t)`
where, X = displacement at time t
`omega =` frequency of oscillation
Which one of the following graphs shows correctly the variation a with t?
Here, a = acceleration at time t
T = time period
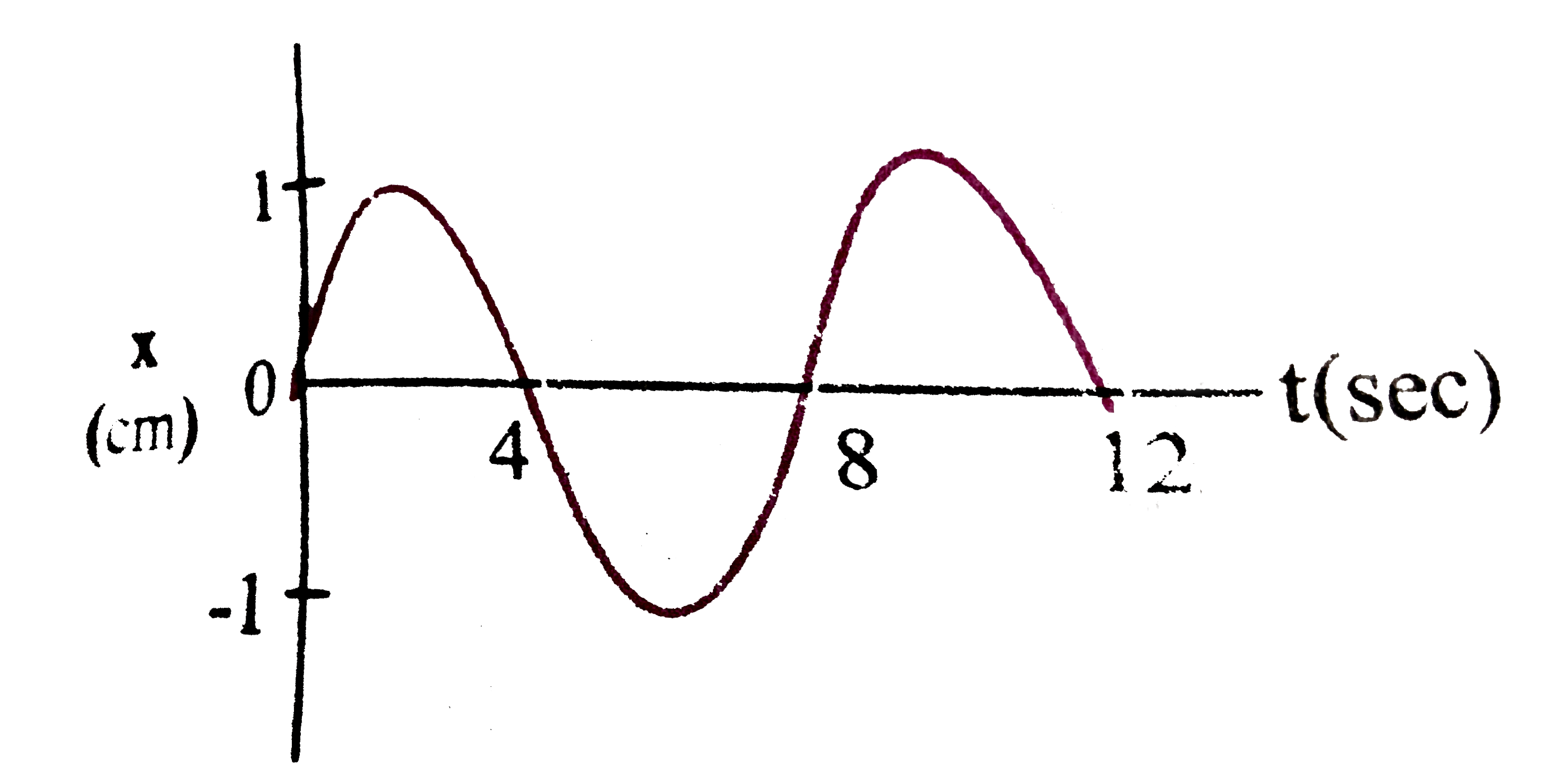
View SolutionThe `x-t` graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at `t = 4//3 s` is
View SolutionThe displacement - time graph of a particle executing SHM is as shown in the figure. The maximum velocity of the particle is

View SolutionThe acceleration of the particle at t = 3 s in the above figure is
View SolutionThe minimum time the particle takes to travel from `y = + "1 m to y" = - 1m` in the figure given in problem (61)is
View SolutionMatch the following
`{:("List - I","List - II"),("(a) acceleration","(e) A"sin omega t),("(b) time period","(f) A"^(2) omega cos omega t),("(c) displacement","(g) A" omega cos omega t),("(d) velocity","(h) -A" omega^(2) sin omega t),(,"(i) 2"pi sqrt((l)/(g))):}`
View SolutionFor a particle executing SHM along a straight line (displacement is measured from mean position).
`{:("Column - I","Column - II"),("(a) velocity-time graph will be","(p) straight line"),("(b) acceleration-velocity graph may be","(q) circle"),("(c) acceleration-displacement graph will be","(r) ellipse"),("(d) acceleration-time graph will be","(s) sinusoidal curve"):}`
View Solution`{:("List - I","List - II"),("(A) x-t graph of simple harmonic oscillator","(E) Straight line with +ve slope"),("(B) a-x graph of SHO","(F) Straight line with -ve slope"),("(C) l-T graph of a simple pendulum","(G) Sine curve"),("(D) l-"T^(2) "graph of a simple pendulum","(H) Parabola"):}`
View SolutionThe mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this plenet. If it is a 2 second's pendulum on earth?
View SolutionThe length of a second's pendulum on the surface of the moon, where g is `1//6^(th)` if the value of g on the surface of the
View SolutionThe matallic bob of a simple pendulum has the relative density `rho`. The time period of this pendulum is `T` it the metallic bob is immersed in water the new time period is given by
View SolutionA pendulum clock is taken `1km` inside the earth from mean sea level. Then the pendulum clock
View SolutionA seconds pendulum is suspended from rof of a vehicle that is moving along a circular track of radius `(10)/(sqrt(3))m` with speed `10m//s`. Its period of oscillation will be `(g = 10m//s^(2))`
View SolutionFor a simple pendulum, the graph between `T^(2) and L` (where T is the time period & Lis the length) is
View SolutionIn case of a simple pendulum, time period versus length is depicted by
View SolutionAssuming the earth as an spherical body, for seconds pendulum
`{:("Column - I","Column - II"),("(a) at pole","(p) T"gt 2s),("(b) on a satellite","(q) T" lt 2s),("(c) at mountain","(r) T = 2s"),("(d) at centre of earth","(s) T = 0"),(,"(t) T"gt oo):}`
View Solution`{:("List - I","List - II"),("(A) Frequency of seconds pendulum","(E)"A omega),("(B) Angular frequency of oscillating spring","(F)" (1)/(2)),("(C) Maximum velocity of simple harmonic oscillator","(G)"A omega^(2)),("(D) Maximum acceleration of simple harmonic oscillator","(H)"sqrt((k)/(m))):}`
View SolutionFor a simple pendulum, a graph is plotted between itskinetic energy `(KE)` and potential energy `(PE)`against its displacement `d`. Which one of the following represents these correctly? (graph are schematic and not drawn to scale)
View SolutionAs a body performs SHM its potential energy U. varies with time as indicated in
View SolutionA particle of mass m oscillates with simple harmonic motion between points `x_(1)` and `x_(2)`, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph
View SolutionA simple harmonic oscillator
(A) Always has maximum KE at the equilibrium position
(B) Always has zero KE at the extreme position
(C) Always has maximum PE at extreme position
(D) always has zero PE at the equilibrium position
View SolutionWhich of the following figure represents damped harmonic motion
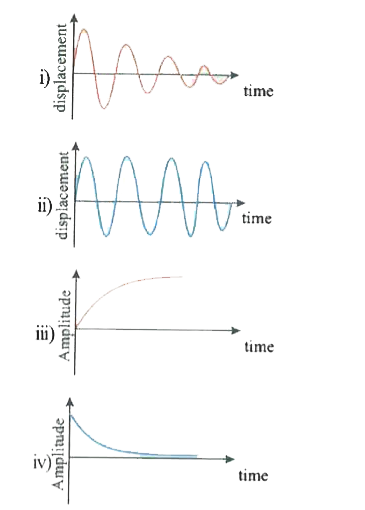
View Solution
EXERCISE - II (C.W) questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION