Complete Solutions to SINGLE ANSWER QUESTIONS of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NARAYANA | SINGLE ANSWER QUESTIONS |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
The displacement of a particle is represented by the equation `y=sin^(3)omegat.` The motion is
View SolutionThe relation between acceleration and displacement of four particles are given below. The particle undergoing SHM is:
View SolutionMotion of an oscillating liquid column in a U-tube is
View SolutionA particle is acted simultaneously by mutually perpendicular simple harmonic motion `x = a cos omega t` and `y= a sin omega t`. The frequency of motion of the particle will be
View SolutionThe displacement of a particle varies with time according to the relation `y=a sin omega t +b cos omega t `.
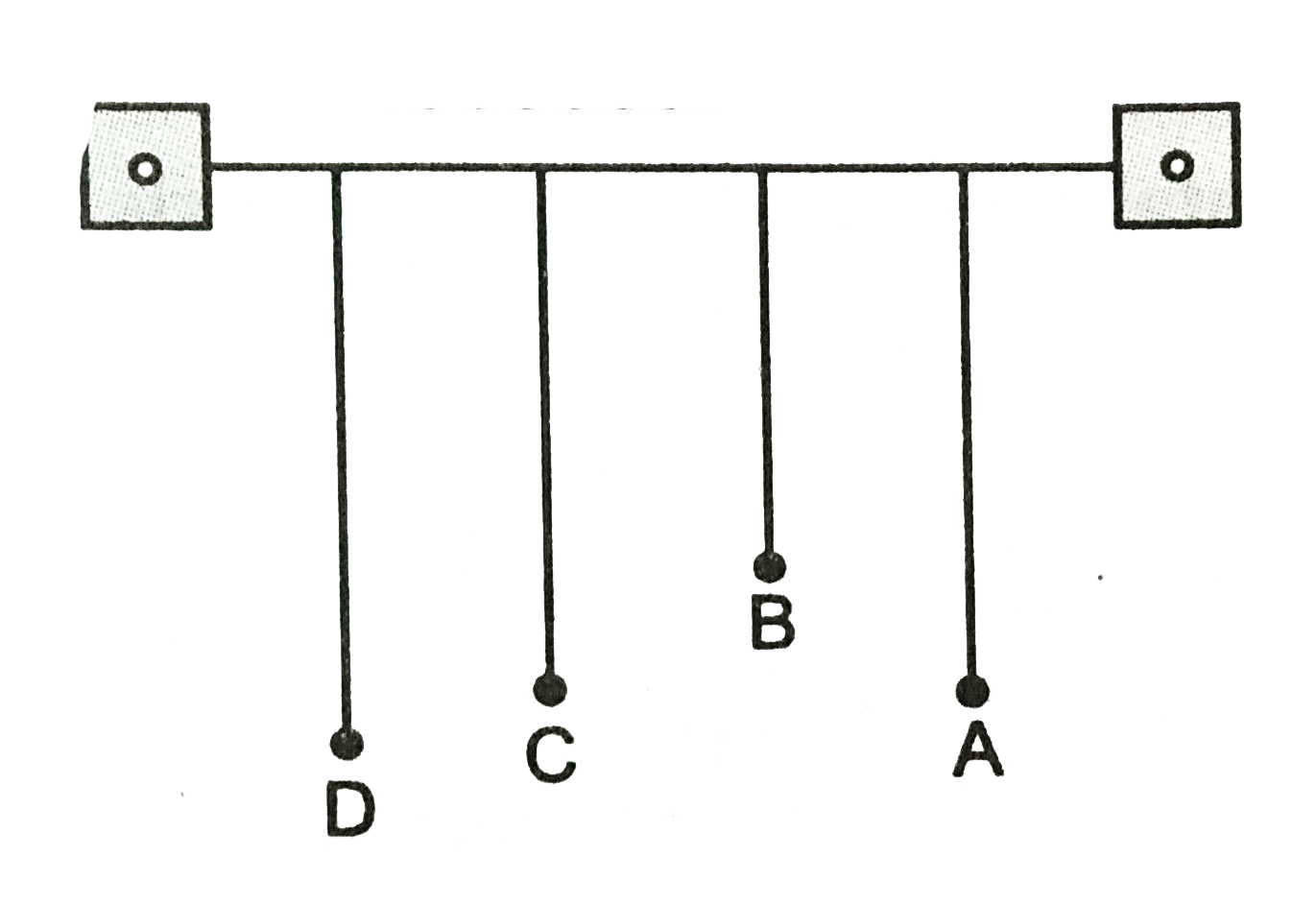
View SolutionFour pendulums A,B,C and D are suspended from the same elastic support as shown in figure. A and C are of the same length , while B is smaller thatn A and D is larger than A. If A is given a transverse displacement,
View Solutionthe circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
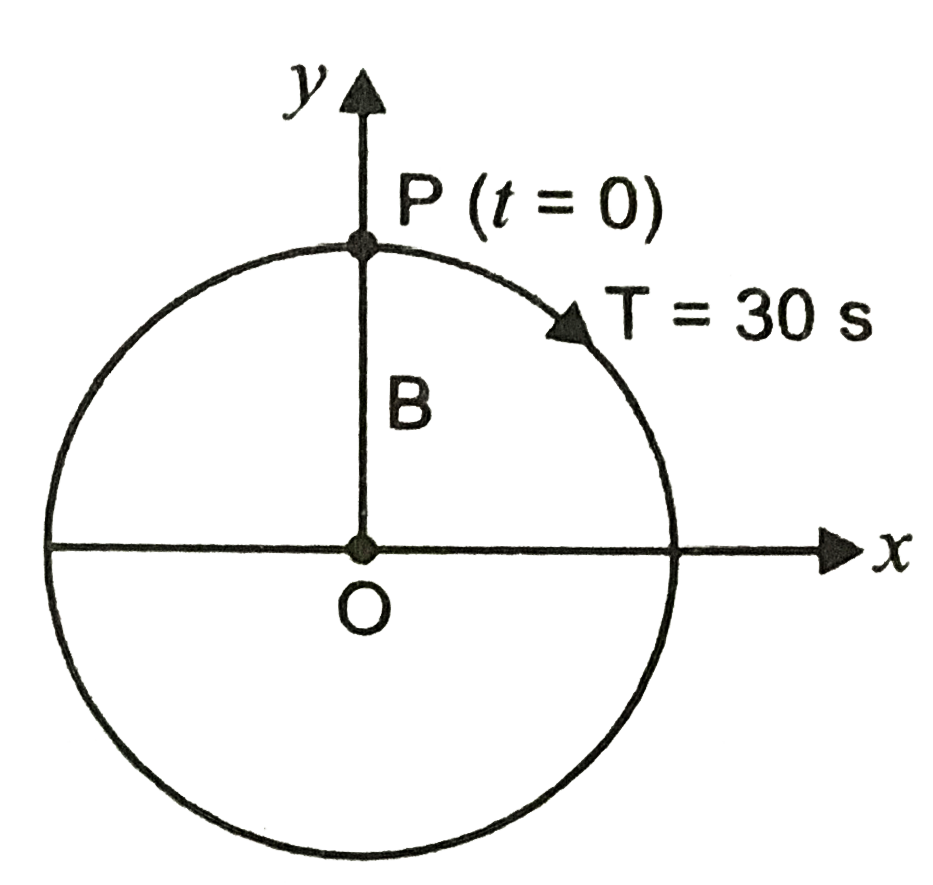
View SolutionThe equation of motion of a particle is
`x=acos(alphat)^(2).` The motion is
View SolutionA particle executing S.H.M. has a maximum speed of 30`cm//s` and a maximum acceleration of `60cm//s^(2)`. The period of oscillation is
View SolutionWhen a mass m is connected individually to two spring `S_(1)` and `S_(2)` , the oscillation frequencies are `v_(1) and v_(2)`. If the same mass is attached to the two springs as shwon in figure., the oscillation frequecy would be

View SolutionThe driver of a car record a period of `(pi)/(3)` seconds for a pendulum of `1m` hung form the roof. The acceleration of the car is `(g = 10 ms^(-2))`
View SolutionA bob of mass `M` is hung using a string of length `l`. A mass `m` moving with a velocity `u` pierces thorugh the bob and emerges out with velocity `(u)/(3)` horizontally. The frequency of small oscillations of the bib, considering `A` as amplitude is,
View SolutionA block of mass `m` moves with a speed `v` towards the right block which is in equilibrium with a spring attached to rigid wall. If the surface is frictionless and collisions are elastic, the frequency of collisions between the masses will be:
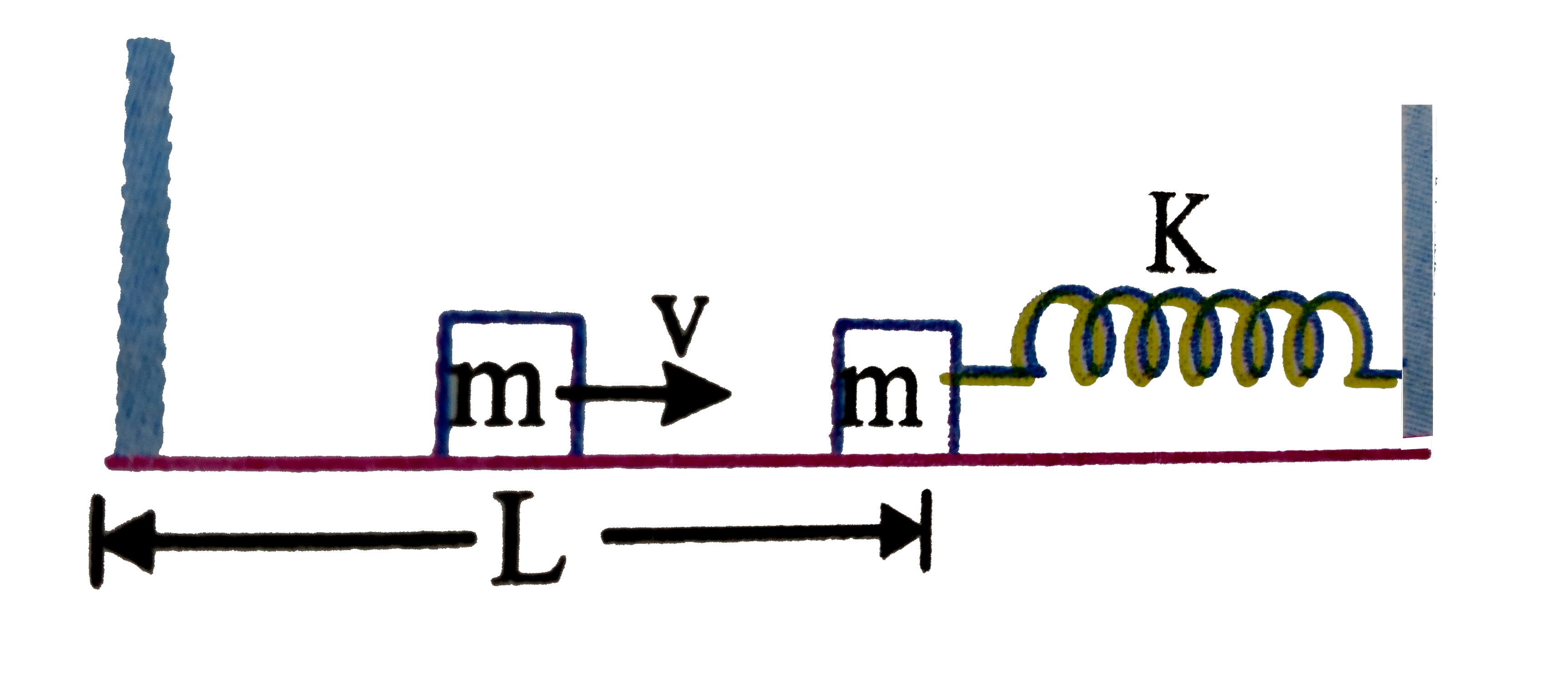
View SolutionA block of mass `M` is connected to a spring of force constant `k` and is placed on a smopth horizontal surface. The block is displaced and compressed the spring by ''A''. The block is left free to move form this position, when the block is at distance `A//2` form mean position to collides elastically with the identical block. tme to be taken by block to move from exterme position to mean position is....

View SolutionA uniform stick of length `l` is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance `d` from the centre of mass. The time period of small oscillation has a minimum value when `d//l` is
View SolutionAparticle of mass `m` oscillating as given by `U(y) =K|y|^(3)` with force constant `K` has an amplitude `A`. The maximum velocity during the oscillation is proportional to
View SolutionA particle at the end of a spring executes S.H,M with a period `t_(2)` If the period of oscillation with two spring in .
View SolutionA body of mass `m`, is attached to a vertical rod of mass `M` nad length `L`, hung from a pivoted supprot. A springs of constant `K` fixed to a support on the left as shown and is attached to the rod at a distance form the pivot. The frequency of the oscillation is:
View SolutionA smooth semicircular wire track of radius `R` if fixed in a vertical plane. One end of massless spring of netural length `(3R)/(4)` is attached to the lowest point `O` of the wire track. A small ring of mass `m` which can slide on the track is attched to the other end of the spring. the ring is held stationary at point `P` such that the spring makes an angle of `60^(@)` with the vertical. The spring constant is `K = (mg)/(R )`. considering the instance when the ring is released, the free body diagram of the ring, when `a_(T)` is tengential acceleration, `F` is restoring force and `N` is normal reaction is
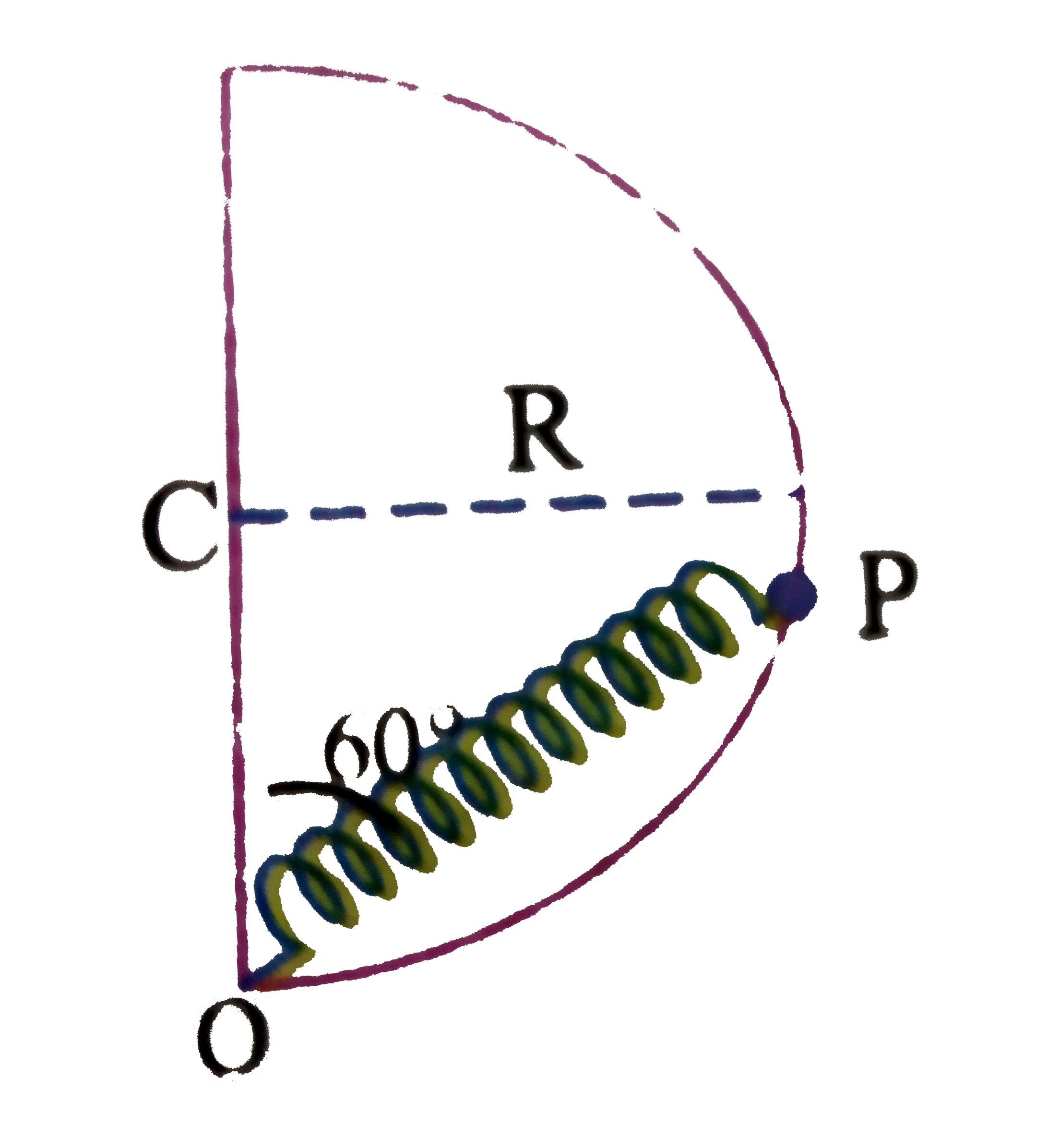
View SolutionA block of mass `m` is attached to one end of a light inextensible string passing over a smooth light pulley `B` and under another smooth light pulley `A` as shown in the figure. The other end of the string is fixed to a ceiling. `A` and `B` are held by spring of spring constants `k_(1)` and `k_(2)`. Find angular frequency of small oscillations of small oscillations of the system.

View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum.
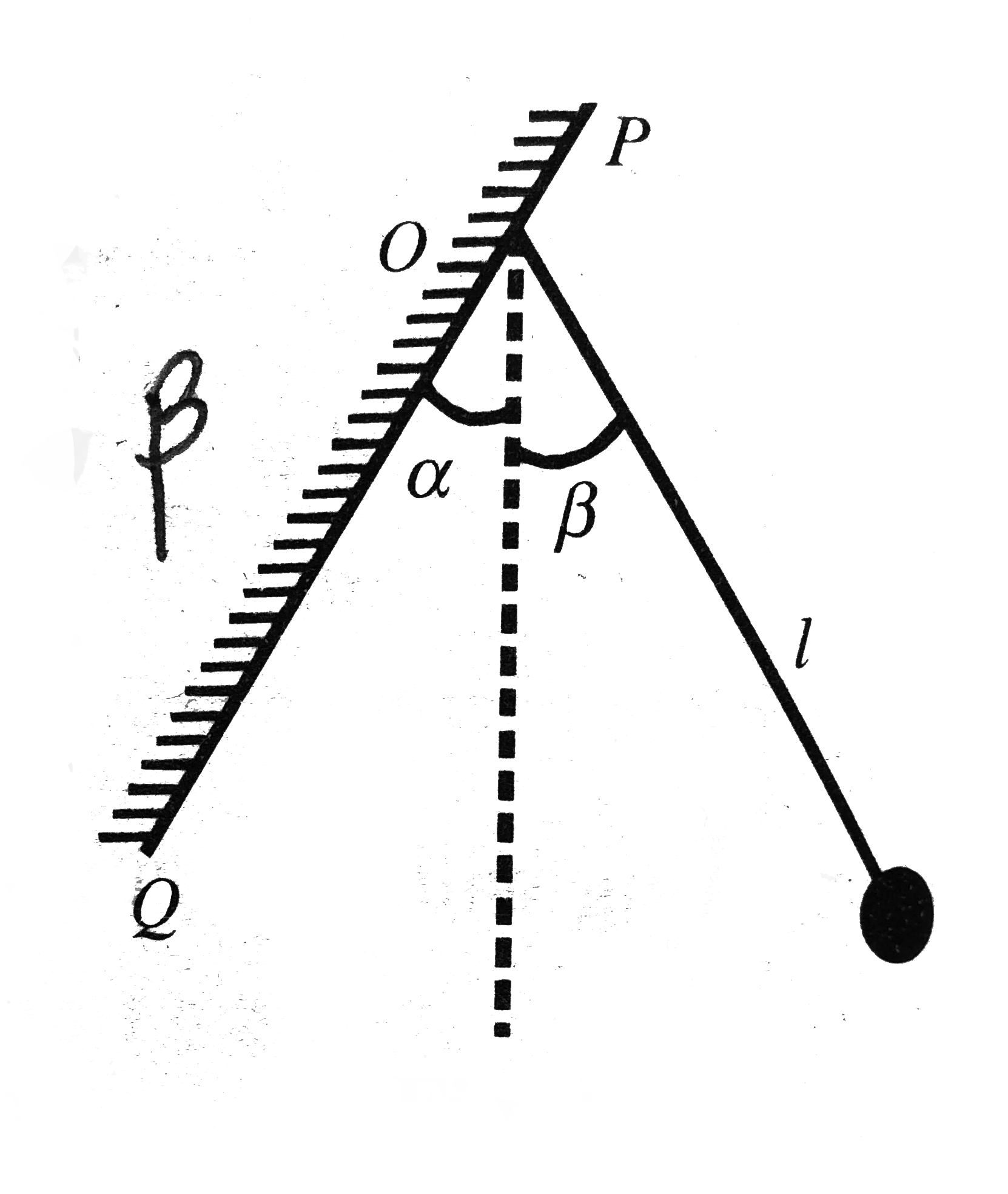
Consider both cases
a. `alpha gt beta`
b. `alpha lt beta`
Assuming that any impact between the wall and the ball is elastic.
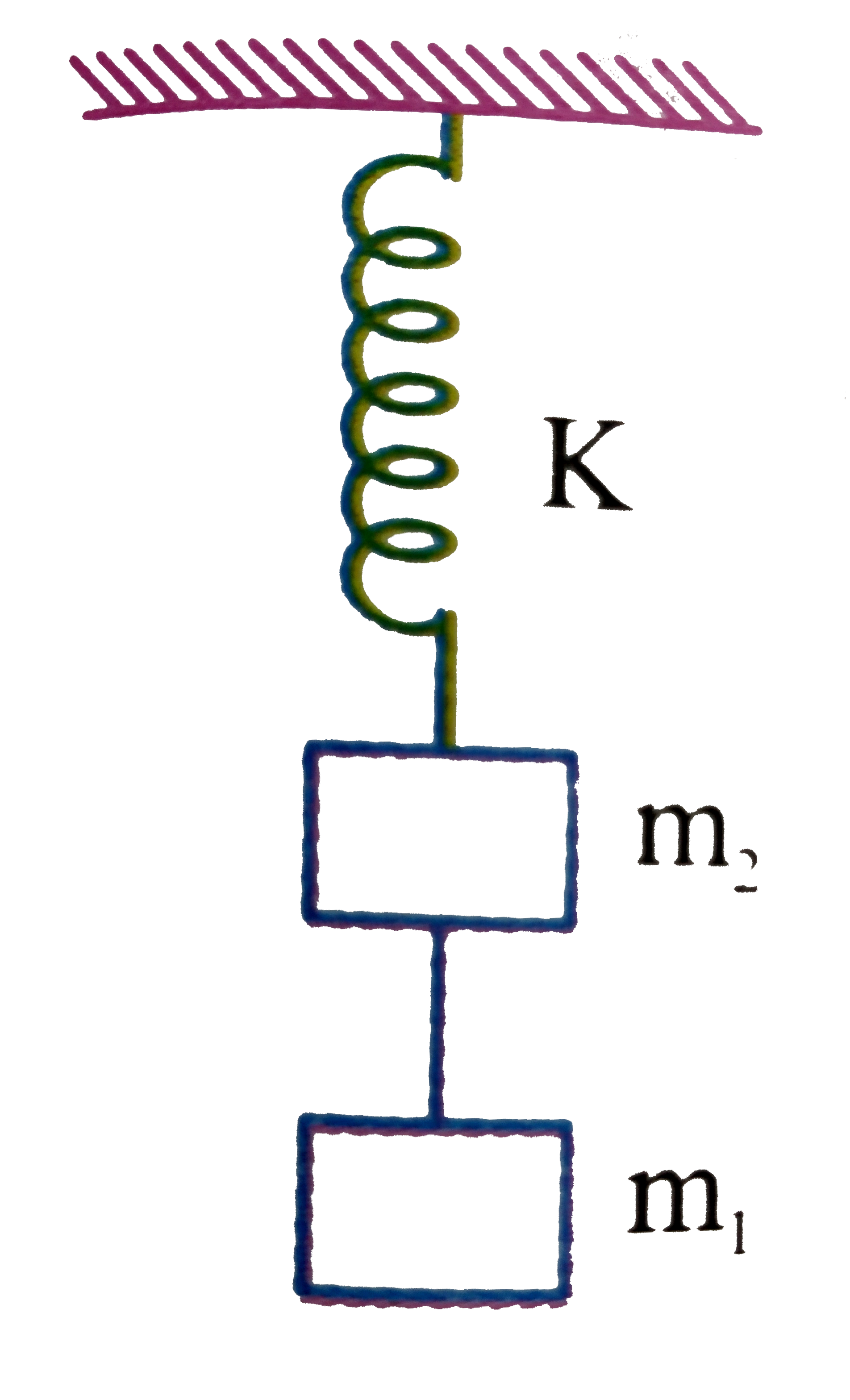
View SolutionTwo masses `m_(1)` and `m_(2)` are suspeded togther by a massless spring of spring constnat `k` (Fig). When the masses are in equilibrium, `m_(1)` is removed. Frequency and amplitude of oscillation of `m_(2)` are
View SolutionTwo light spring of force constants `k_(1)` and `k_(2)` and a block of mass m are in one line `AB` on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance `CD` between the spring is `60cm`. If the block moves along `AB` with a velocity `120 cm//s` in between the springs, calculate the period of oscillation of the block. (take `k_(1) = 1.8 N//m`, `k_(2) = 3.2 N//m`, `m = 200 g`)

View SolutionA solid sphere of radius `R` is floating in a liquid of density `sigma` with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View SolutionA small body attached to one end of a vertically hanging spring is performing (SHM) about is mean position with angular frequency (omega) and amplitude (a). If at a height (y*) from the mean position, the body gets detached from the spring, calculate the value of (y*) so that the height (H) attained by the mass is maximum. The body does noy interact with the spring during its subsquent motion after detachment. `(a omega^2 gt g)`.
 .
.
View SolutionThe block of mass `m_1` shown in figure is fastened to the spring and the block of mass `m_2` is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance `(2/k)(m_1+m_2)gsintheta` against the spring and released. Find the position where the two blocks separate. c. What is the common speed of blocks at the time of separation?

View SolutionIn figure, `k = 100 N//m, M = 1kg` and `F = 10 N`

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of `2 m//s` to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
View SolutionA rectangular plate of sides a and b is suspended fropm a ceilling by two parallel strings of length L each figure. The separation between the strings is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute harmonic motion. Find the time period.

View SolutionA small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation.

View SolutionAssume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of `sqrt((gR)` (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of `sqrt(gR).`
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
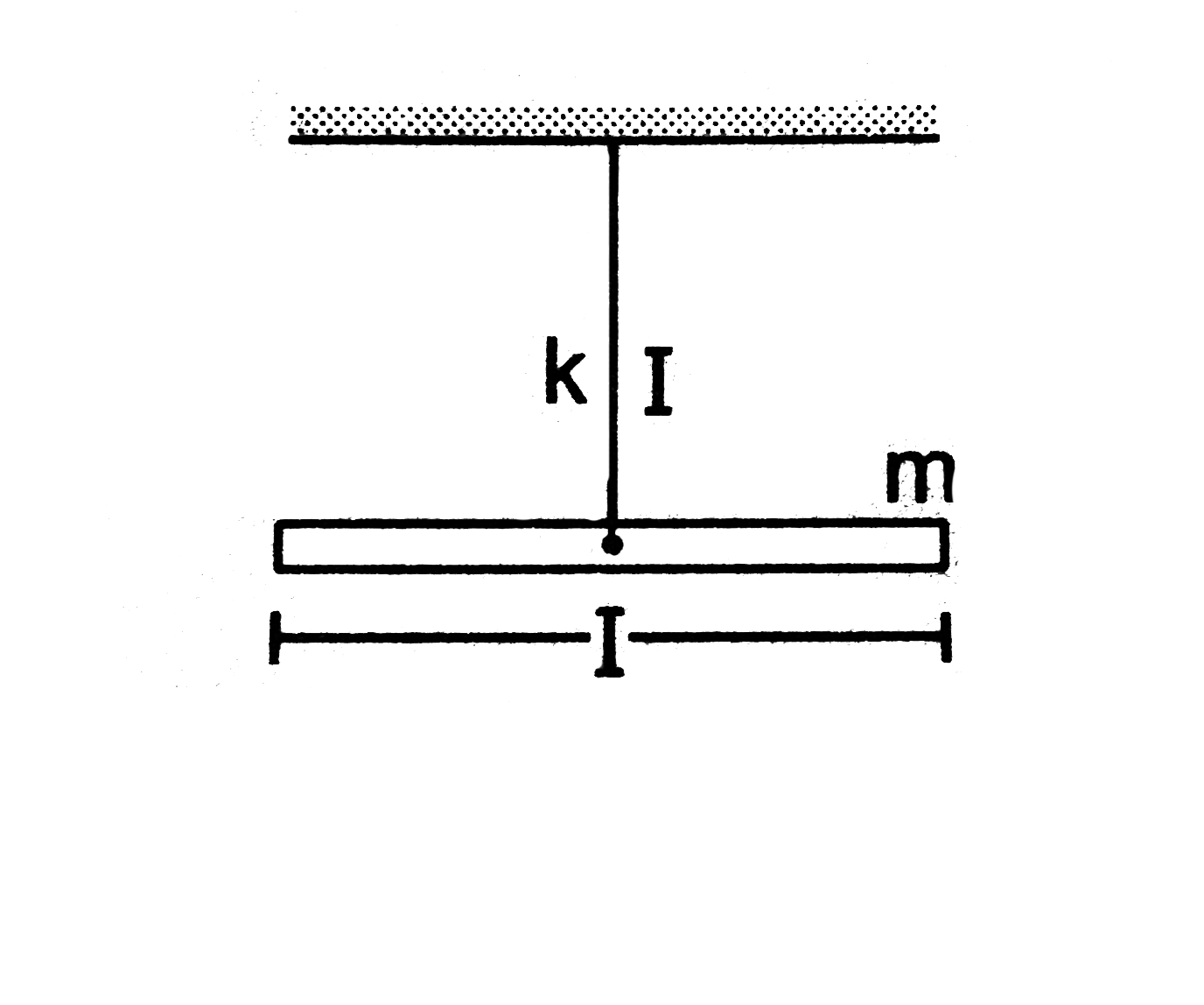
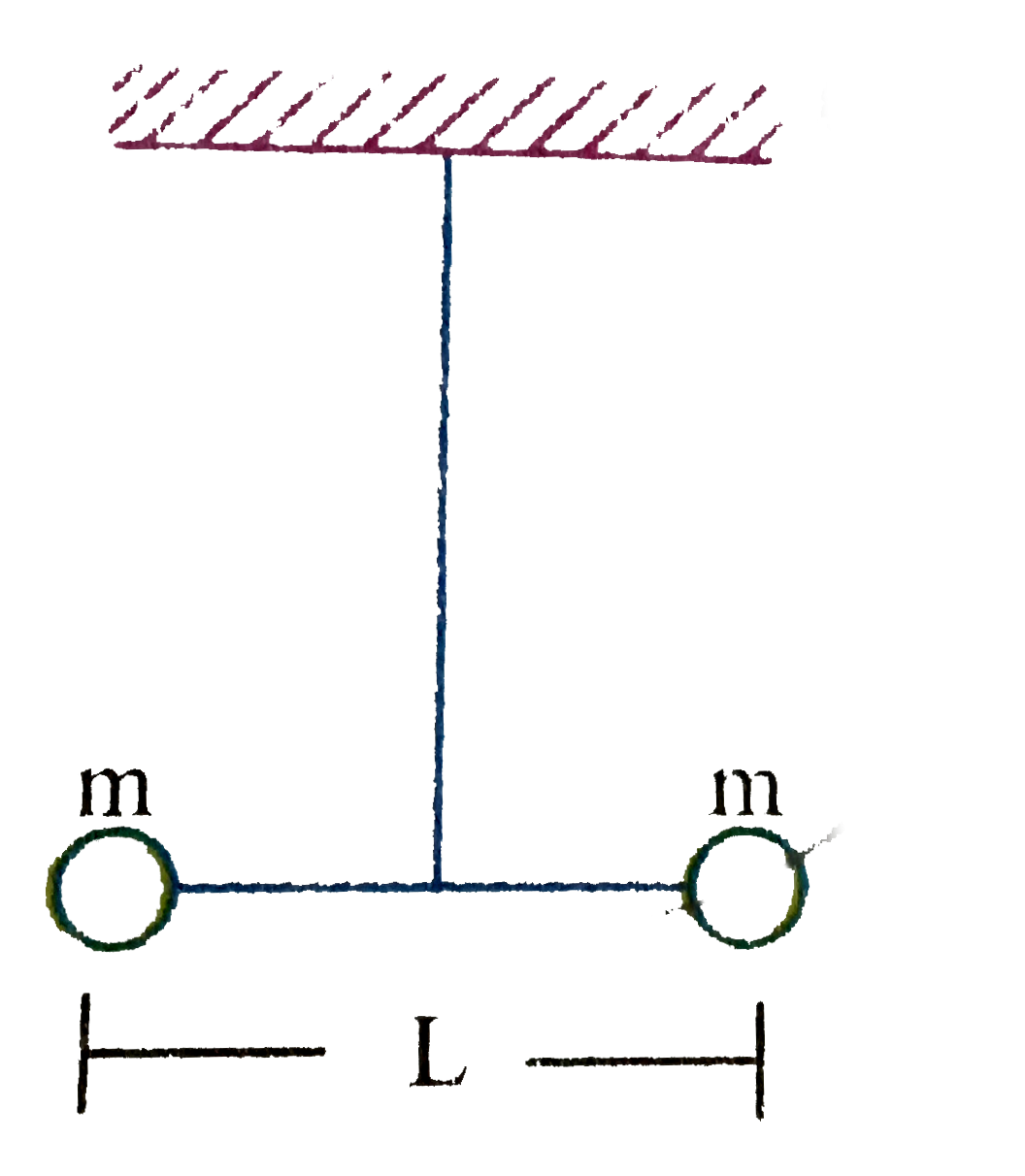
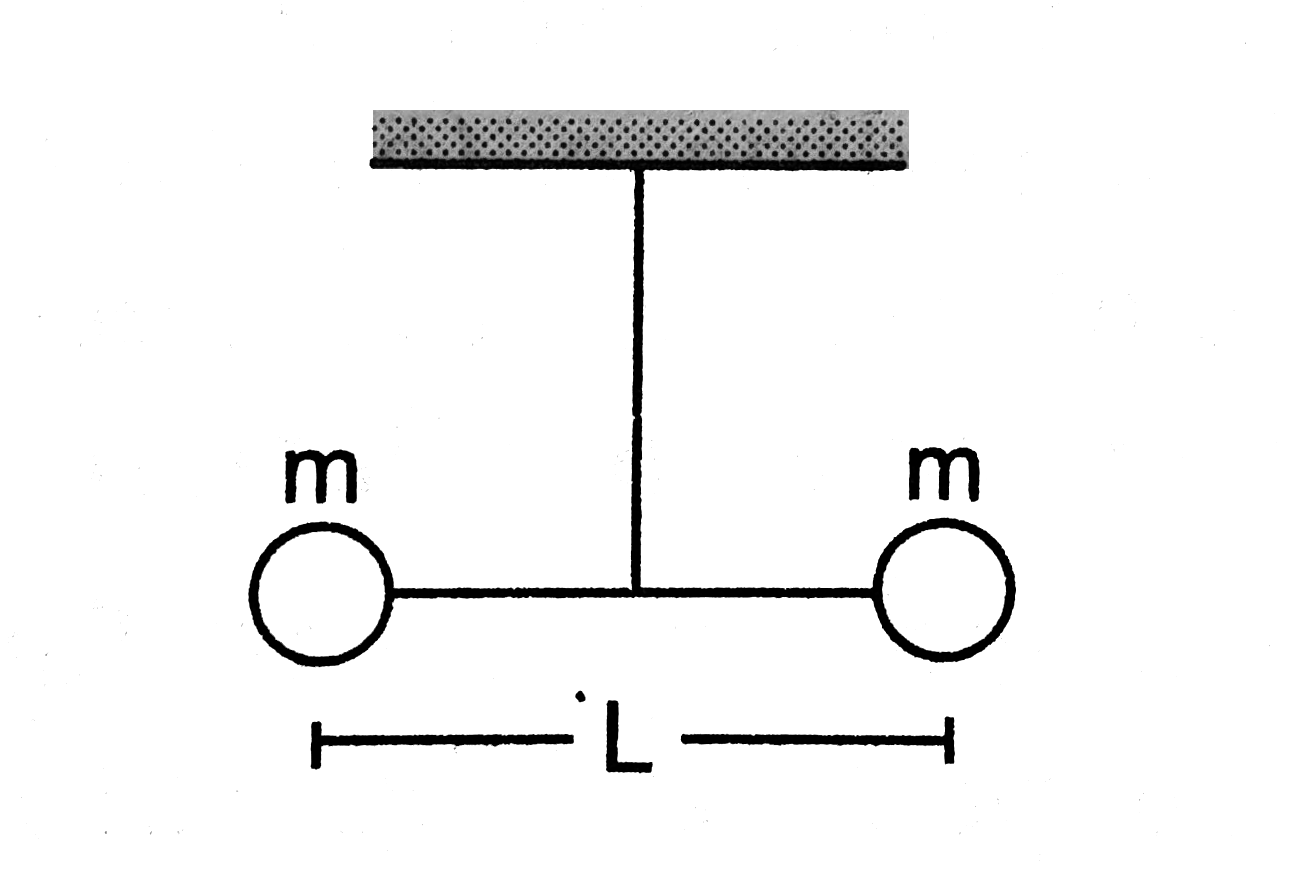
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle `theta_0` and released. Find the tension in the rod as the system passes through the mean position.
View SolutionIn the fig the pulled has a mass `M`, radius `r` and the string does not slip over it. The time period of oscillation is
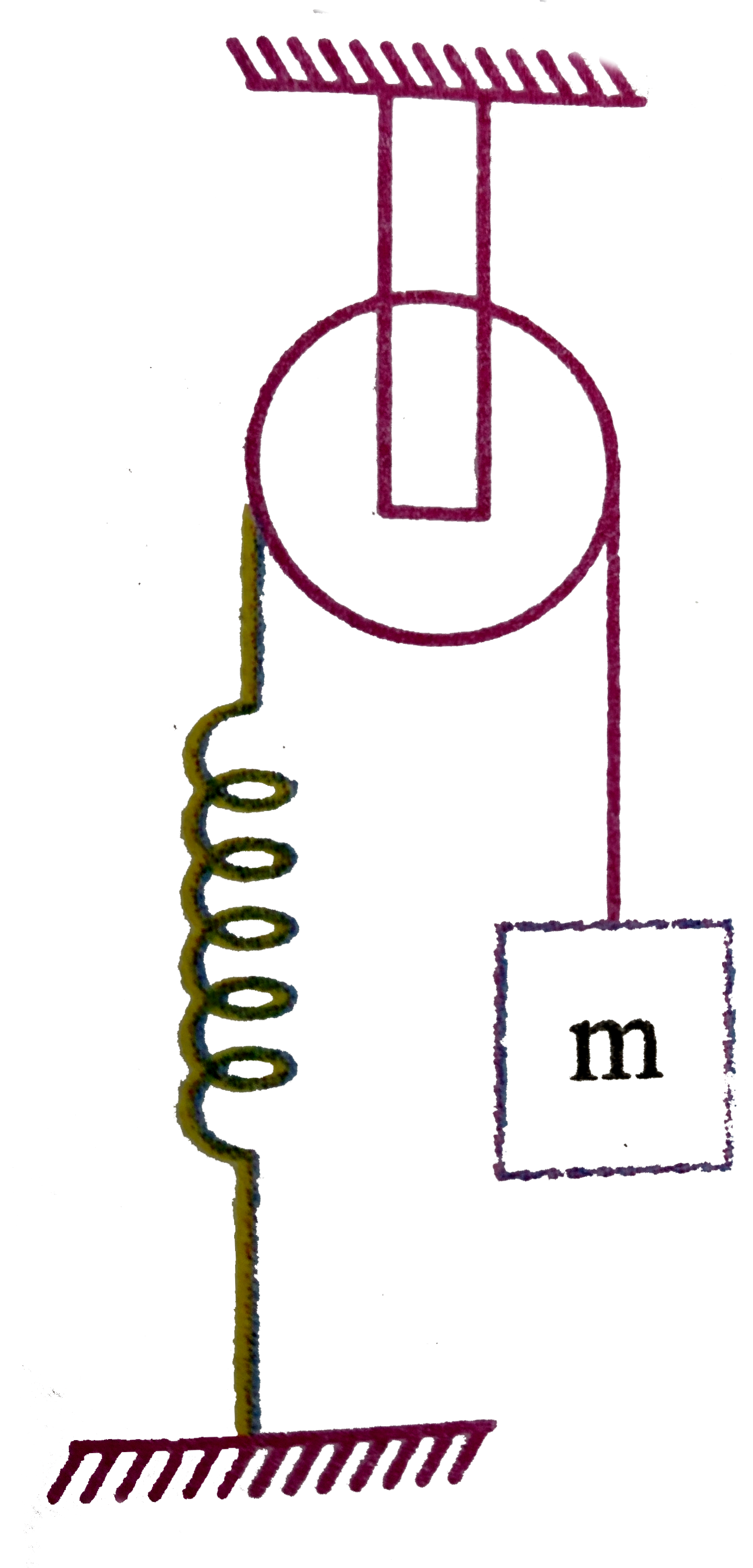
View SolutionThe avergae kinetic energy of particle of mass `m` undergoing `S.H.M.` with angular frequency `omega` and amplitude `A,` over half of one time period is
View SolutionThe time periods of system depicted below under identical conditions are respectively.
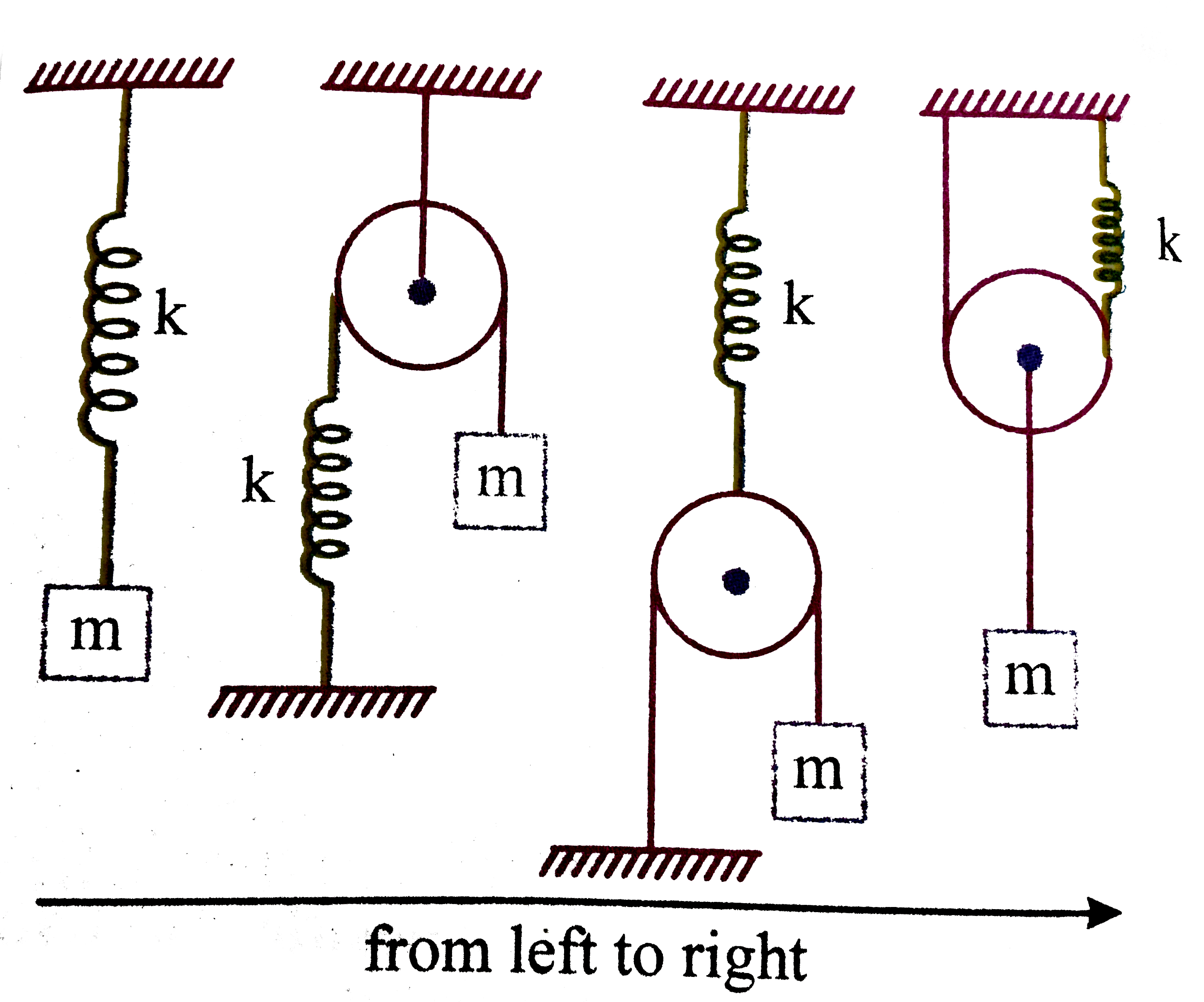
(i) `2pi sqrt((m)/(k))`, (ii) `2pi sqrt((4m)/(k))`, (iii) `2pi sqrt((m)/(4k))`
View SolutionTwo identical simple pendulums each of length 'l' are connected by a weightless spring as shown. In equilibrium, the pendulums are vertical and the spring is horizontal and undformed. The time period of small oscillations of the linked pendulums, when they are deflected form their equilibrium positive through equal displacements in the same vertical plane in the opposite directions and released, is

View SolutionA mass of `0.98 kg` suspended using a spring of constant `K = 300 Nm^(-1)` is hit by a bullet of `20g` moving with a velocity `3m//s` vertically. The bullet gets embeded and oscillates with the mass. The amplitude of oscillation is (neglect gravity)
View SolutionThe following figure shows a particle of mass, `m`, attached with four identical springs, each of length `l`. Initial tension in each spring is `F_(0)`. The period of small oscillations of the particle along a line perpendicular to the plane of the figure is (neglect gravity)

View SolutionA V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrium the level of liquid in both limbs of tube are equal. Find the angular frequency of small oscillation of liquid.

View SolutionA `L`-shaped bar of mass `M` is pivoted at one of its end so that it can freely rotate in a vertical plane as shwon. If it is slightly displaced from its equilibrium position then the frequency of oscillation is…….
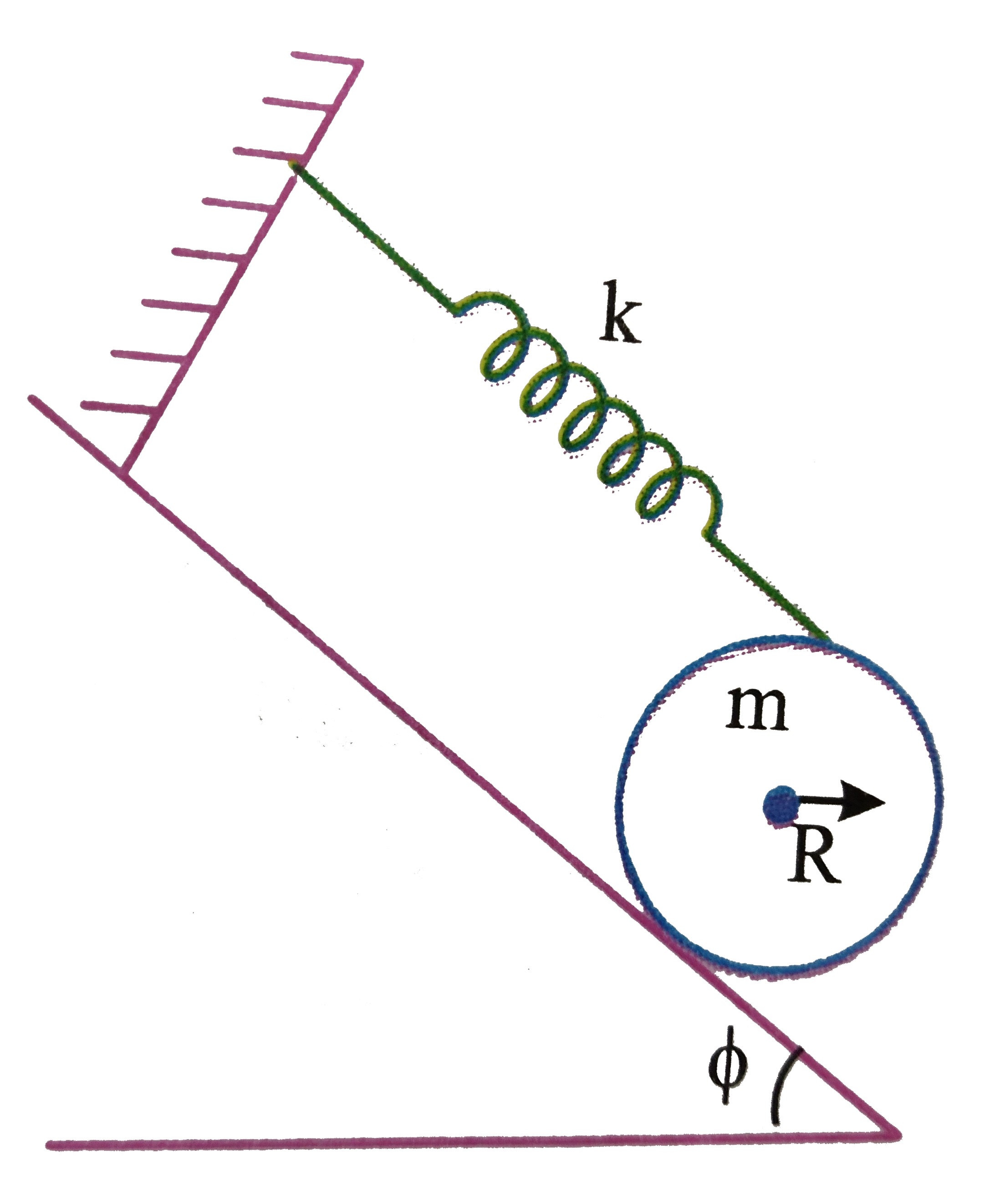
View SolutionA uniform cylinder of mass `m` and radius `R` is in equilibrium on an inclined plane by the action of a light spring of stiffness `k`, gravity and reaction force acting on it. If the angle of inclination of the plane is `phi`, then angular frequency of small oscillations of the cylinder is...........
View SolutionA body `A` of mass `m_(1)` and body `B` of mass `m_(2)` are interconnected by a massless spring as shown. The body `A` performs free vertical harmonic oscillations with the amplitude `A` and frequency `f`. The maximum value of `f` such that body `B` does not leave the surface is

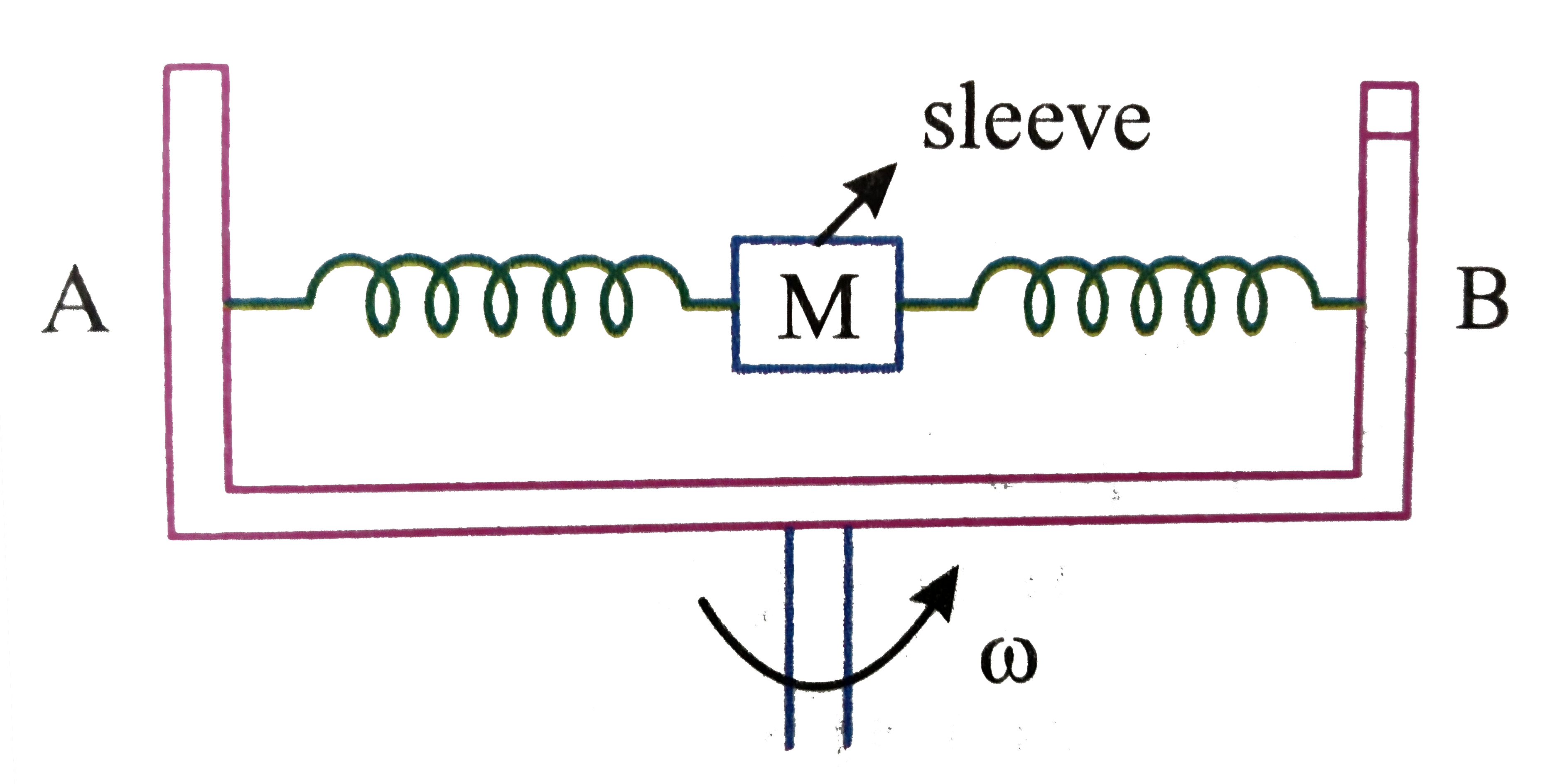
View SolutionIn the arrangement shown, the sleeve of mass `M` is fixed between two identical springs whose combined force constant is `k`. The sleeve can slide without friction over a horizontal bar `AB`. The arragement rotates with a constant angular velocity `omega` about a vertical axis passing through the middle of the bar. the period of small oscillations of teh sleeve is.........
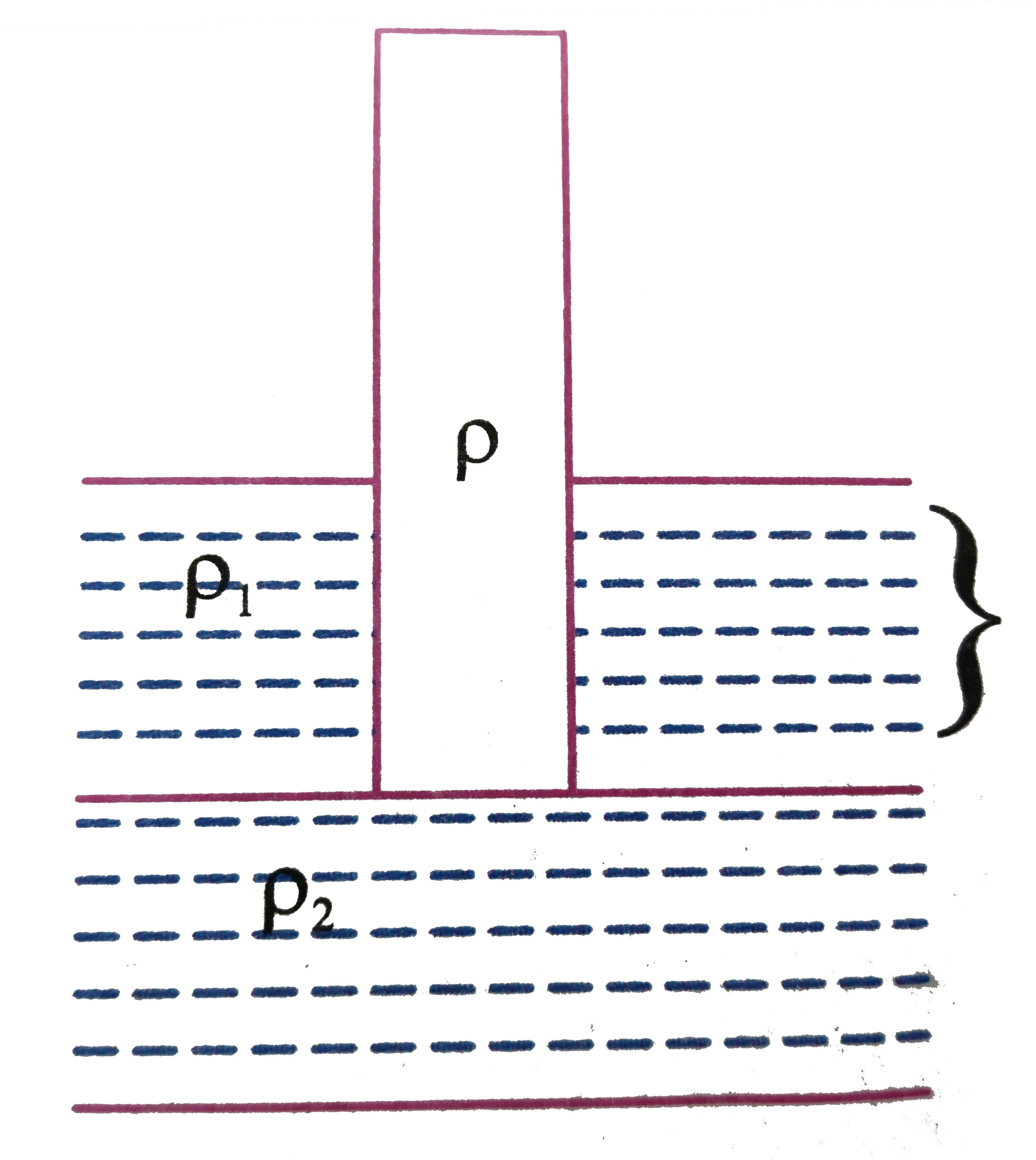
View SolutionA vertical pole of length `l`, density `rho`, area of cross section `A`, floats in two immiscible liquids of densities `rho_(1)` and `rho_(2)`. In equilibrium position the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, the time period of oscillation is..........
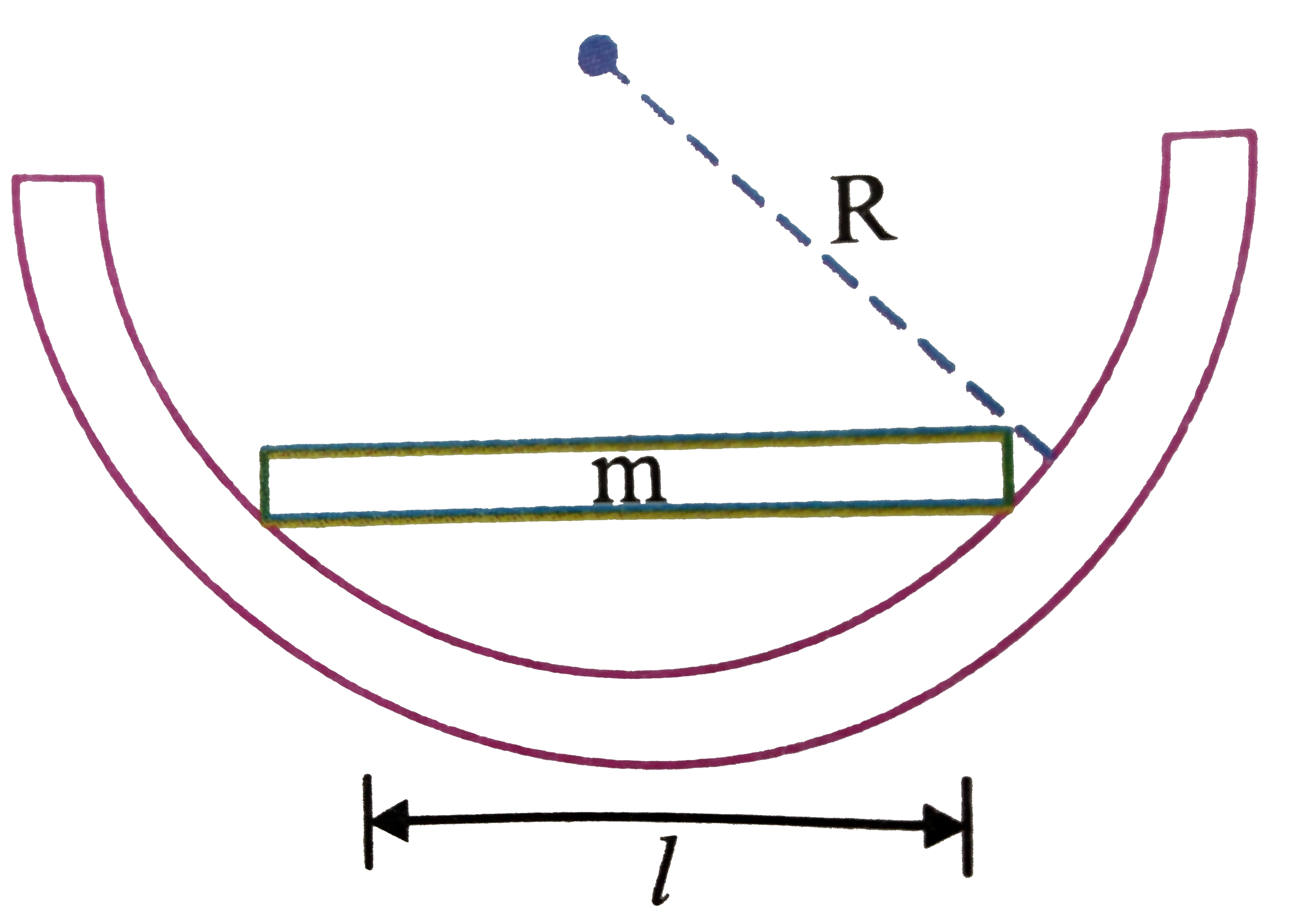
View SolutionA uniform rod of mass, `m`, and length `l` remains in equilibrium inside a smooth hemisphere of radius `R` as shown. The period of small oscillations of the rod is….. [`:' r^(2) =R^(2) -l^(2)//4]`
View SolutionA thin uniform vertical rod of mass `m` and length `l` pivoted at point `O` is shown in Fig. The combined stiffness of the springs is equal to `k`. The mass of the springs is negligible. The angular frequency of small oscillation is
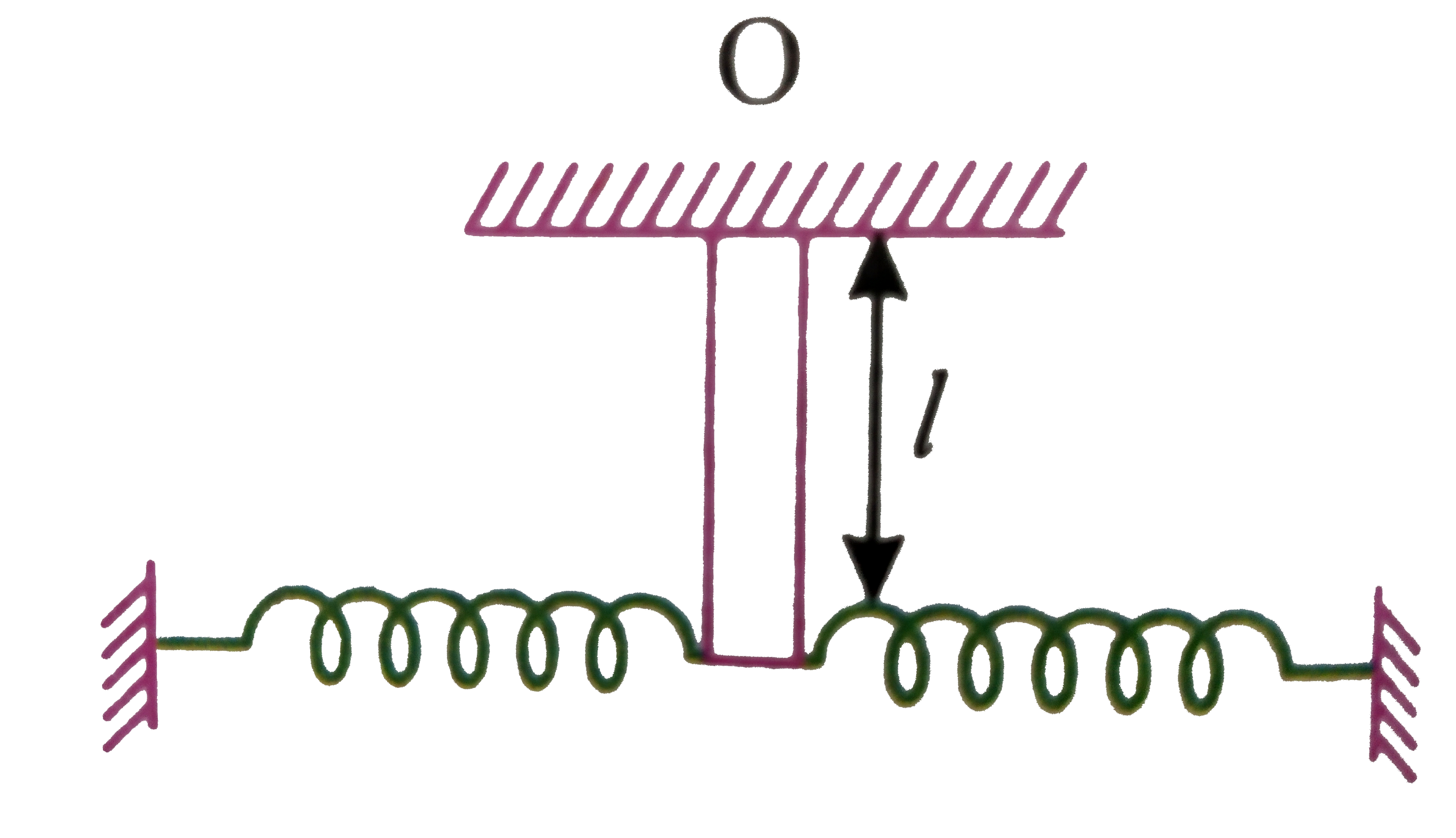
View Solution
A thin-walled tube of mass m and radius R has a rod of mass m and vry small cross section soldered on its inner surface. The side-view of the arrangement is as shown in the following figure. The entire arrangement is placed on a rough horizontal surface. The system is given a small angular displacement from its equilibrium position, as a result, the system performs oscillations. The time period of resulting oscillations if the tube rolls without slipping is
View SolutionAn elastic string of constant `k` is attached to a block of mass `m` as shown. The block is given an extension of `(2mg)/(k)` from the equilibrium position and released. The time period of oscillations of the block is

View SolutionA ring of mass `m` can freely slide on a smooth vertical rod. The ring is symmetrically attached with two springs, as shown, each of stiffness `k`. Ring is displaced such that each spring makes an angle `theta` with the horizontal. If the ring is slightly displaced vertically, then time period is.......
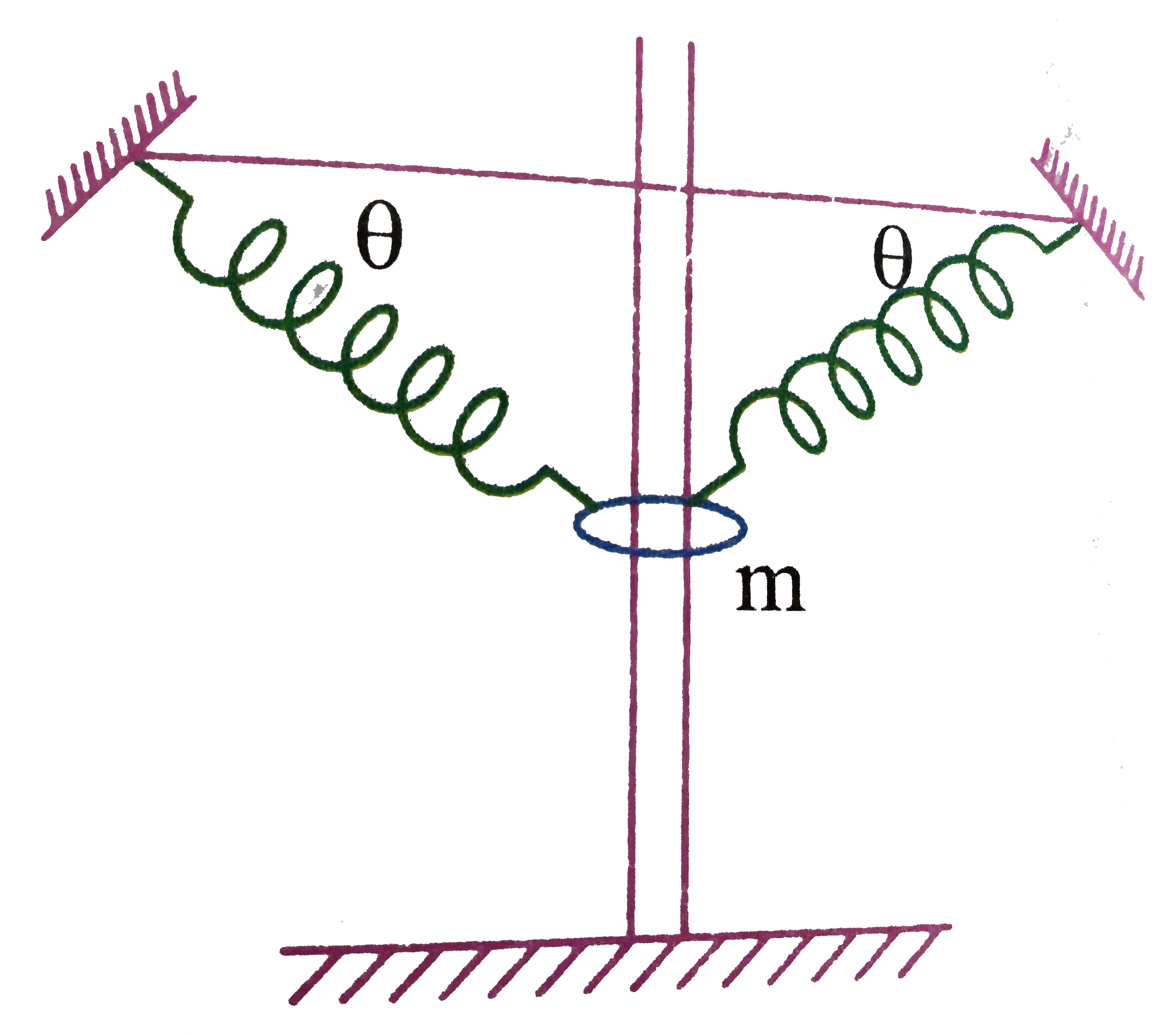
View SolutionA light inextensible string carrying a springs is passed over two smooth fixed pulles as shown. If the rod is slightly displaced about the hinge form is equilibrium position, then time period is.
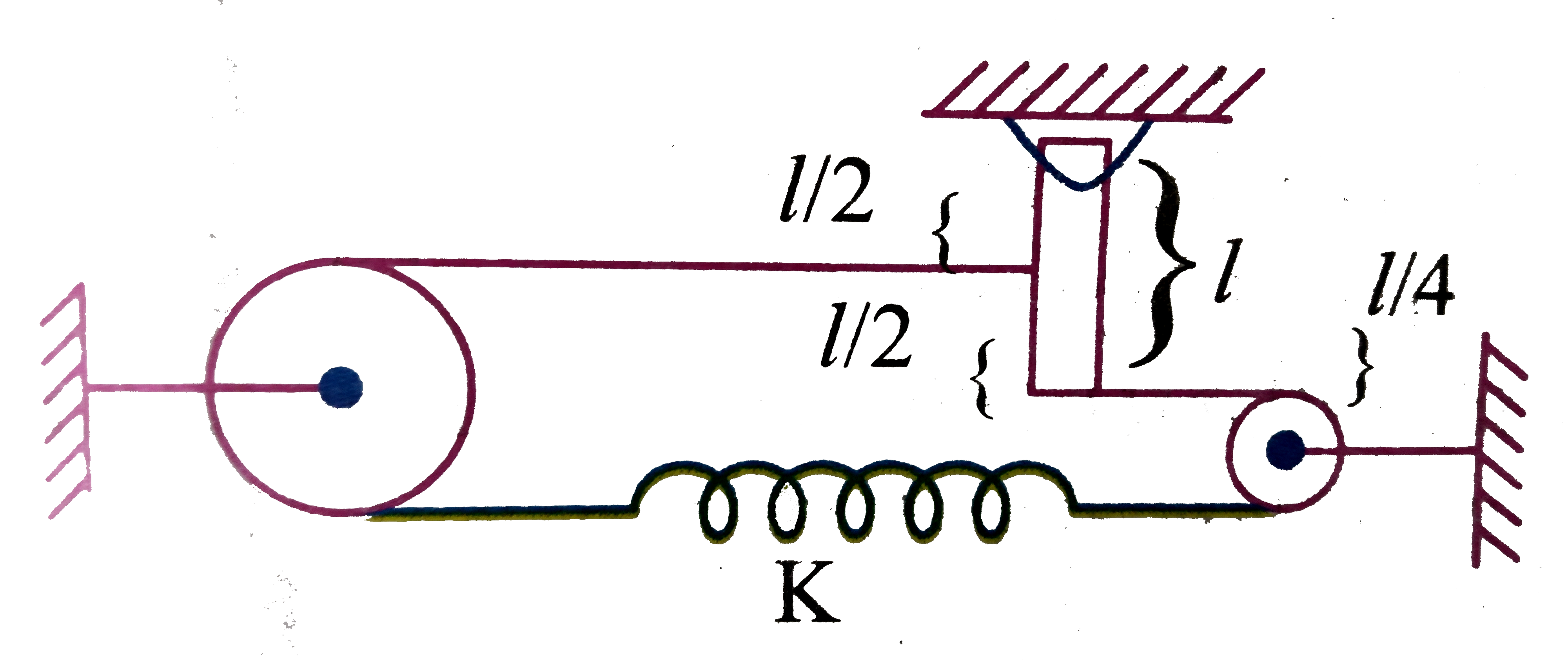
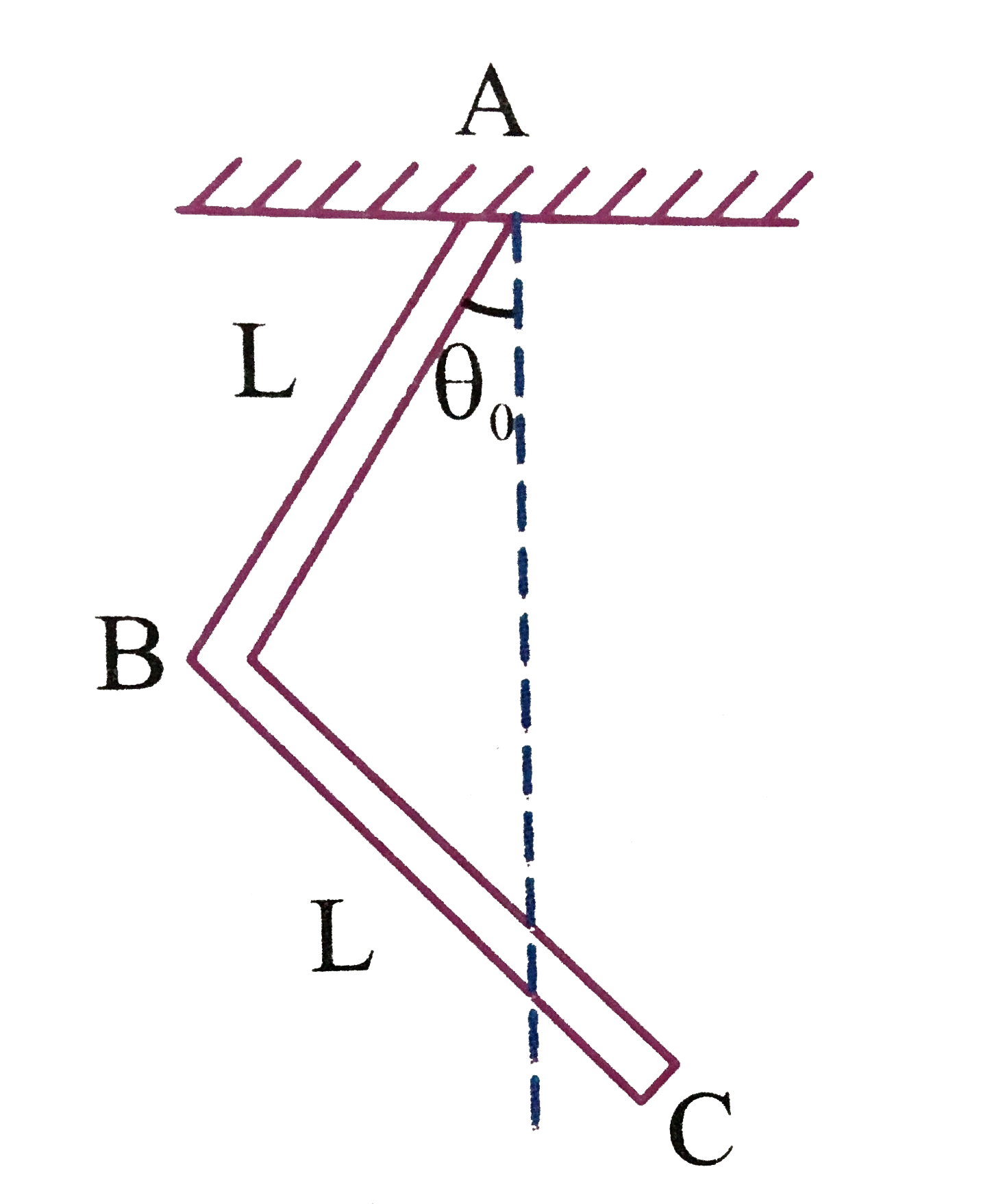
View SolutionConsider a swing whose one end is fixed above the other rope by ''b'. The distance between the poles of swing is `a`. The lengths `l_(1)` and `l_(2)` are such that `l_(1)^(2) +l_(2)^(2) =a^(2) +b^(2)` as shown. The period of the smaller oscillations of the swing, by neglecting the height of the swinging person, is.....
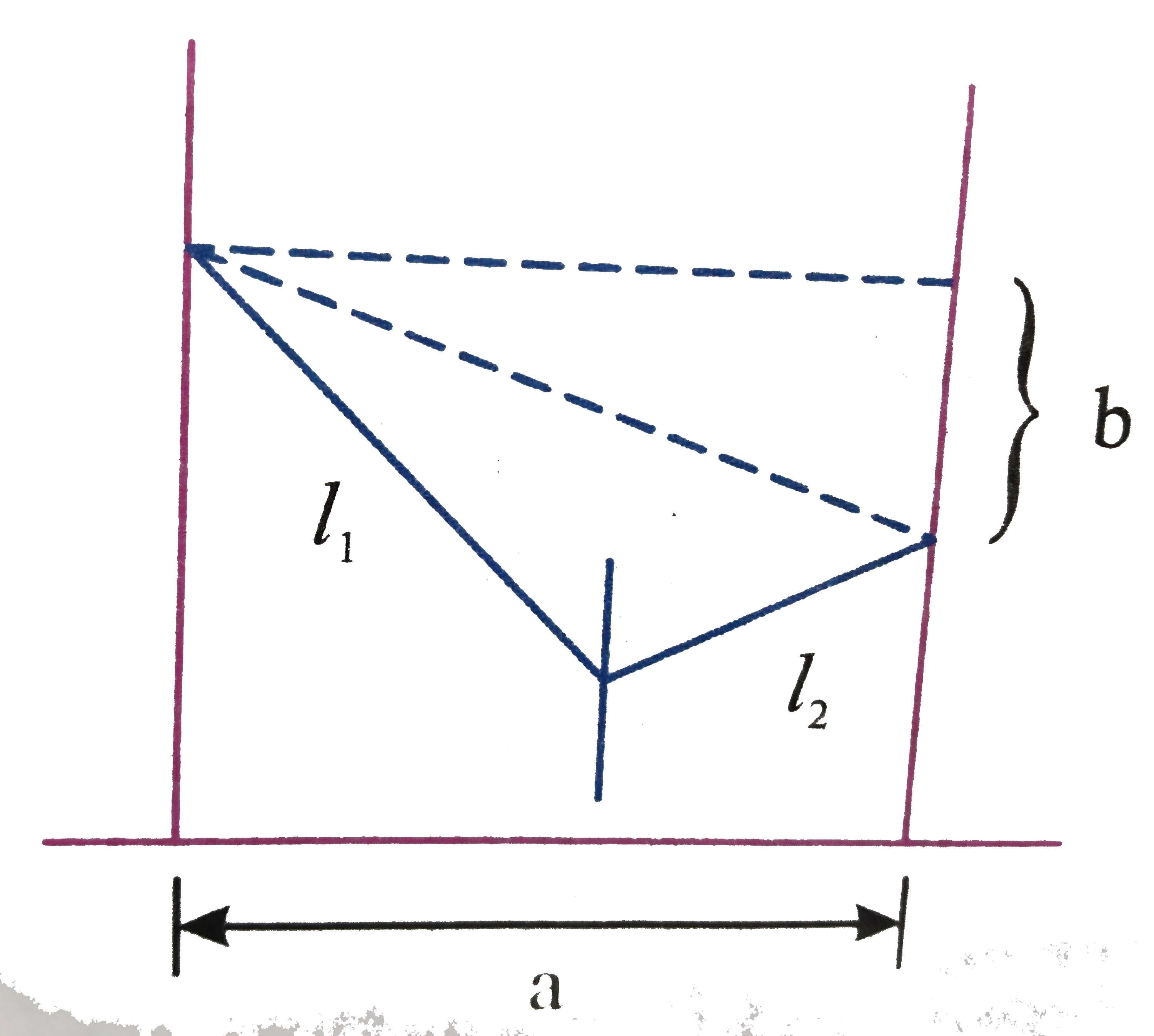
View Solution
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle `theta` from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View SolutionFour identical bars of mass `m`, length `l` are connected by pins at `A,B,C` and `D`. The bars are attached to four springs of same stiffness as shown. The entire sysetm can move in horizontal plane. In the equilibrium position shown, `theta = 45^(@)`. if the corners `A` and `C` are given small displacements towards each other and released, then time period of vibration is

View SolutionA rod of mass `m` and length `l` is pivoted at a point `O` in a car whose acceleration towards left is `a_(0)`. The rod is free to oscillate in a vertical plane. In the equilibrium state the rod remains horizontal then other end is suspended by a spring of stiffness `k`. The time period of oscillations is..........
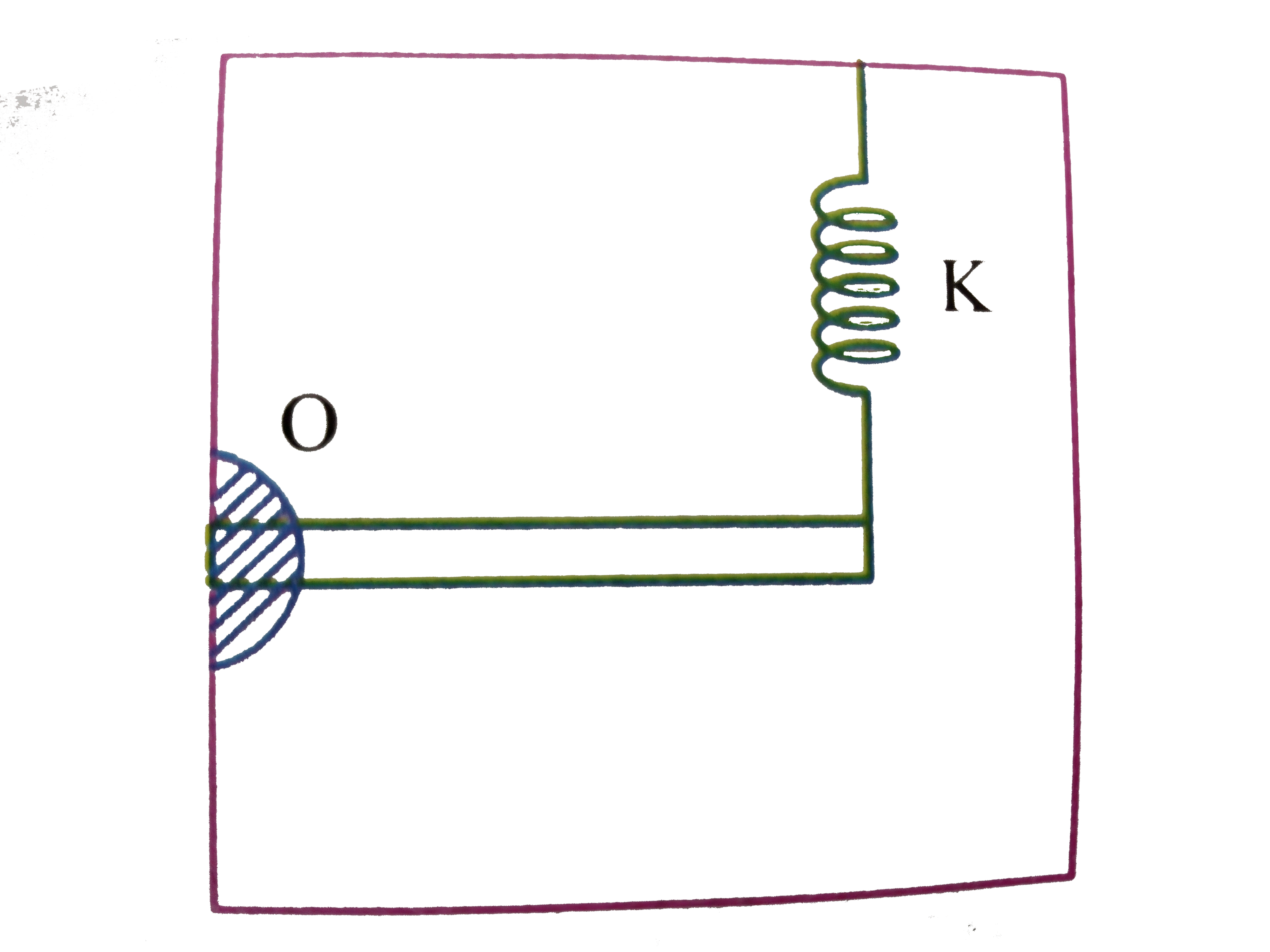
View SolutionA body `A` of mass moving with velocity `v` while passing through its mean position collides in perfect inelastically with a body `B` of same mass which is connected to a vertical wall through a spring whose spring constant is `k`. After collision it sticks to `B` and executes `S.H.M.` Find the amplitude of reulting motion:
View SolutionTwo particles move parallel to `x-`axis about the origin with same amplitude 'a' and frequency `omega`. At a certain instant they are found at a distance `a//3` from the origin on opposite sides but their velocities are in the same direction. What is the phase difference between the two?
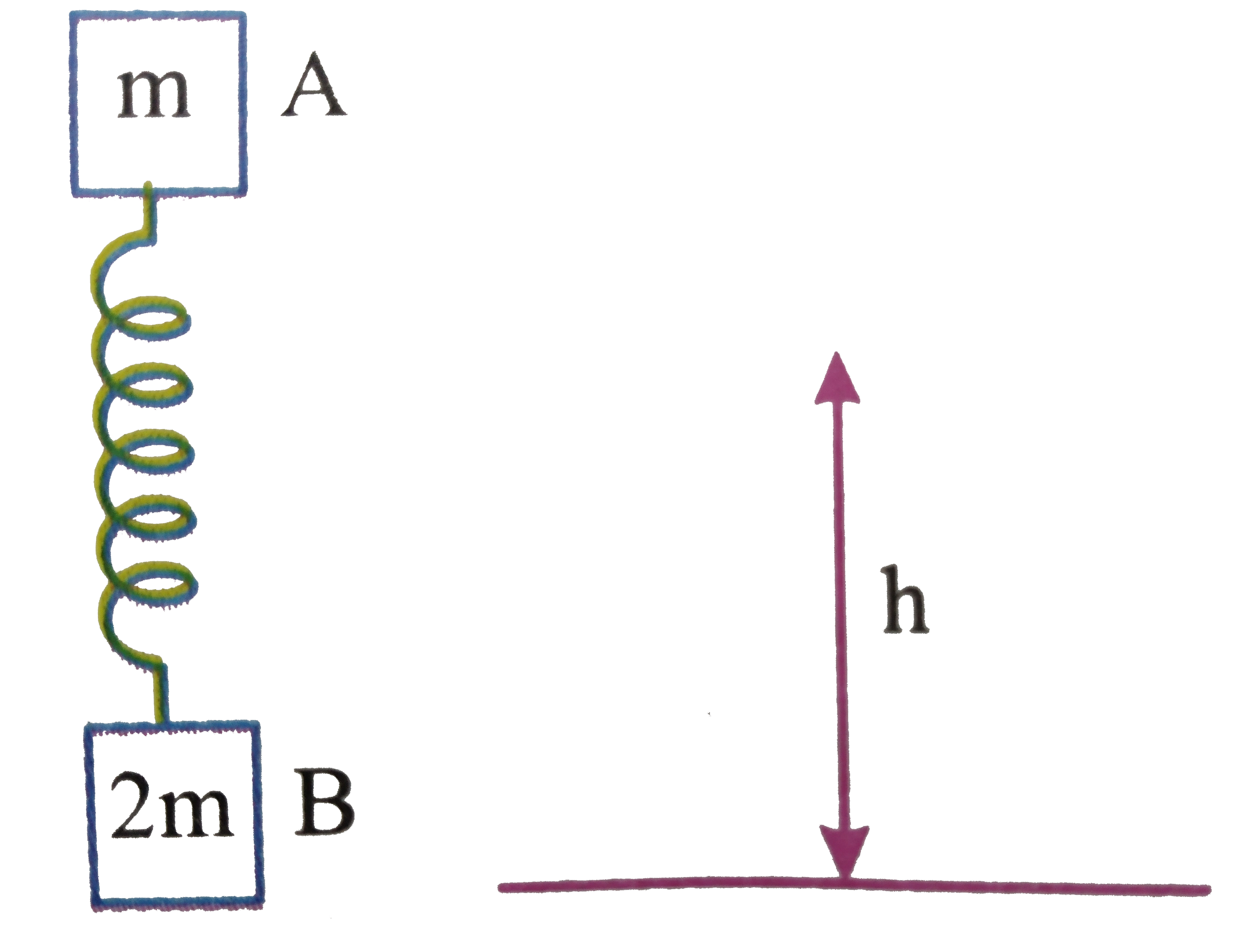
View SolutionFrom what minimum height `h`must the system be released when spring is unstretches so that after perfectly inelastic collision `(e =0)` with ground, `B` may be lifted off the gound: (Spring constant `=k)`
View SolutionThe mean velocity of a particle performing `S.H.M.` with time epriod of `0.6s` and amplitude of `10cm` averaged over a time interval during which it travels a distance fo `5cm`, starting from exterme position is
View SolutionFind the period of small oscillations in a vertical plane performed by a ball of mass `m=40g` fixed at the middle of a horizontallly stretched string `l=1.0m` in length. The tension of the string is assumed to be constant and equal to `F=10N`.
View SolutionThe maximum velocity of a point undergoing simultaneous two oscillations given by `x_(1) =a cos wt` and `x_(2) = a cos 2 wt`is:
View SolutionA particle pendulum is positioned such that is centre of gravity is vertically above suspension point. From that position the pendulum started moving tward the stable equilibroum and passed it with an angular velocity `omega`. By neglecting the friction at point of suspension, the period of small oscillations of the pendulum is
View SolutionA fly wheel of mass `35kg` swings as pendulum about a knife-edge as shown. The period of oscillations is `1.22s`, the motion of inertia of the fly wheel about its centre is
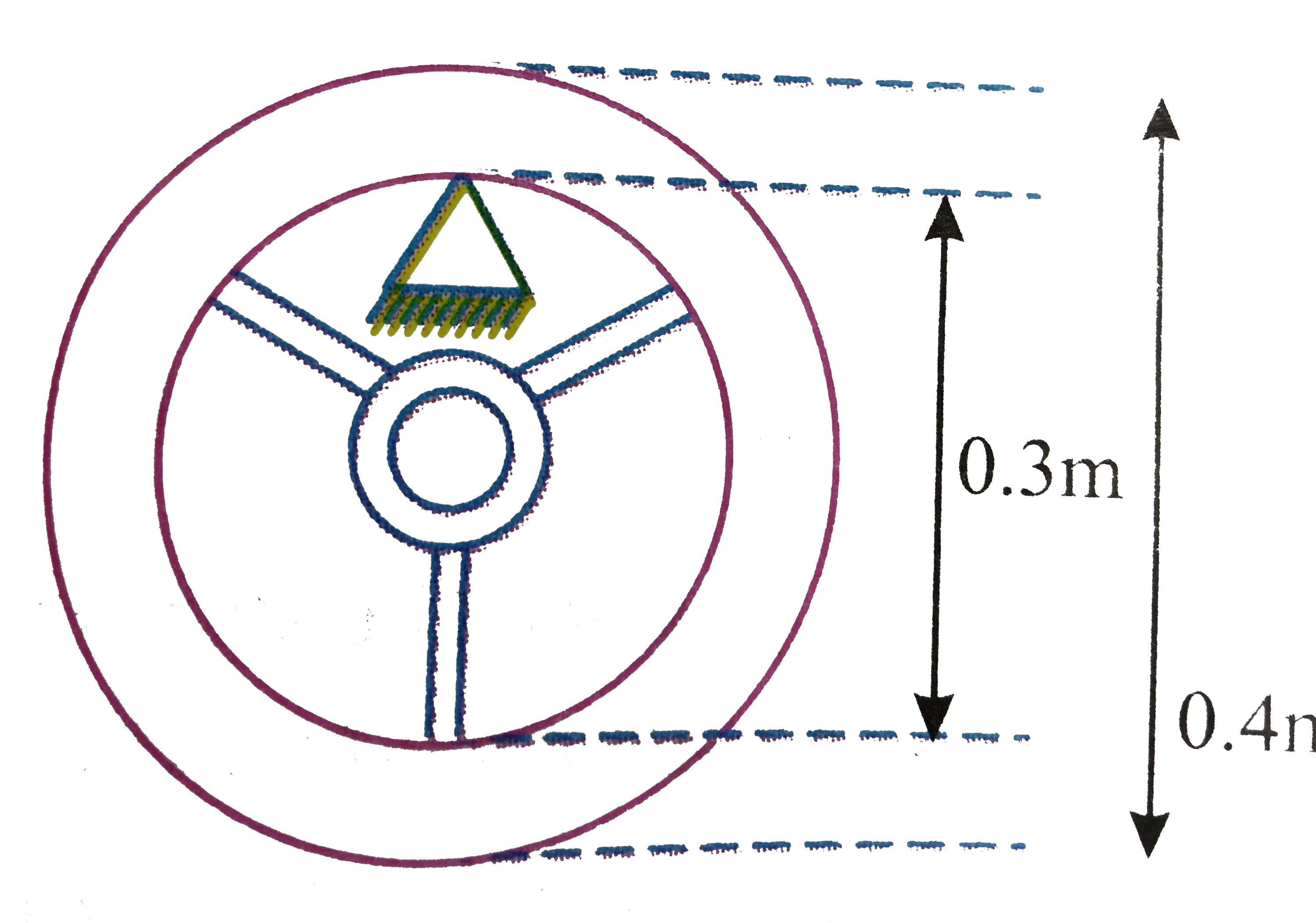
View SolutionA thin uniform plate shaped as an equilateral triangle with a height 'h' performs small oscillations about the horizontal axis coinciding with one of its sides. The time period of oscillation is…..
View SolutionA smooth horizontal disc rotates about the vertical axis `O` (figure) with a constant angular velocity `omega`. A thin uniform rod `AB` of length `l` performs small oscillation about the vertical axis `A` fixed to the disc at a distance `a` from the axis of the disc. Find the frequency `omega_(0)` of these oscillations.

View SolutionTwo balls with masses `m_(1) =1kg` and `m_(2) = 2kg` are slipped on a thin smooth horizontal rod as shown. The balls are interconnected by a light spring of stiffess `K = 24N//m`. The left hand ball `(m_(1))` is imparted the initial velocity `12cm//s` towards second ball. the amplitude of oscillations made by the arrangement is............
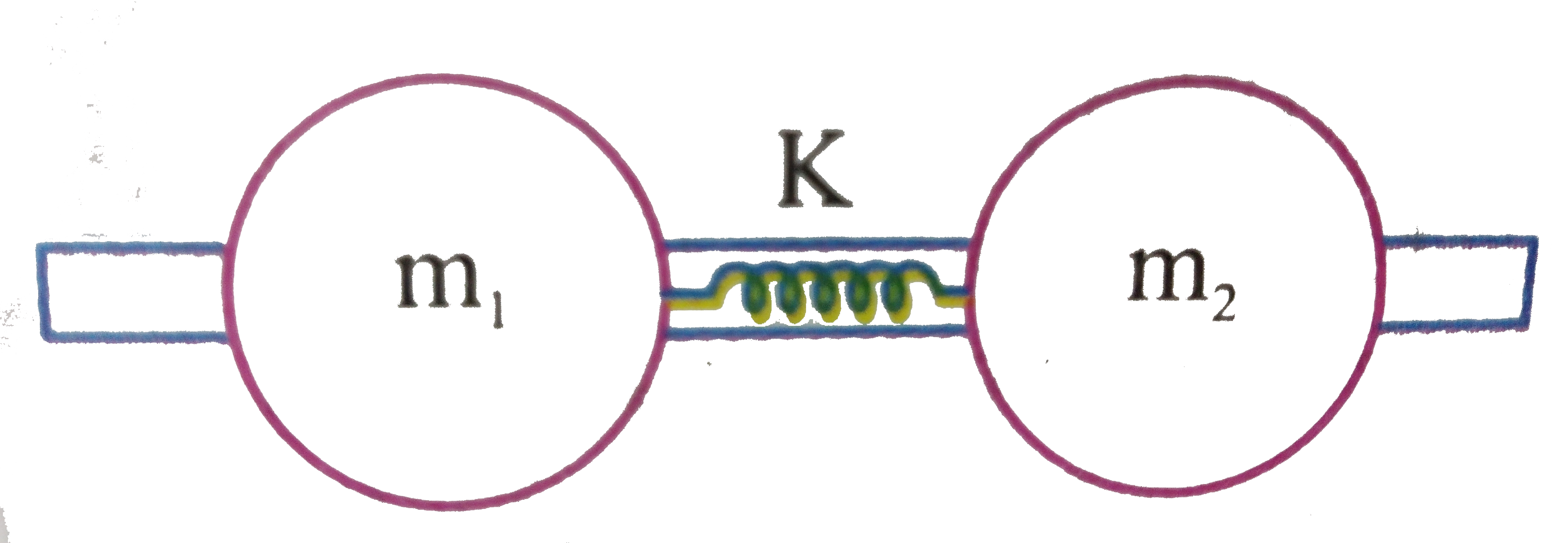
View Solution
SINGLE ANSWER QUESTIONS questions and complete solutions for chapter OSCILLATIONS of NARAYANA PHYSICS (HINGLISH) of Class 11
All Exercises from NARAYANA Class 11 PHYSICS OSCILLATIONS
- ASSERTION & REASON QUESTIONS
- C. U . Q
- C.U.Q
- DAMPED AND FORCED OSCILLATIONS
- DAMPED OSCILLATIONS
- DISPLACEMENT
- DISPLACEMENT, VELOCITY AND ACCELERATION
- ENERGY OF A PARTICLE EXECUTING SHM
- EVALUATE YOURSELF - 1
- EVALUATE YOURSELF - 2
- EVALUATE YOURSELF - 3
- EVALUATE YOURSELF - 4
- EXERCISE - I (C.W)
- EXERCISE - I (H.W)
- EXERCISE - II (C.W)
- EXERCISE - II (H.W)
- EXERCISE - III
- EXERCISE - IV
- ILLUSTRATION
- INTEGER ANSWER QUESTIONS
- LEVEL -I (C.W)
- LEVEL -II (C.W)
- LEVEL -III
- LEVEL-I (H.W)
- LEVEL-II (H.W)
- LEVEL-V
- LEVEL-VI
- MULTIPLE ANSWER QUESTIONS
- NCERT BASED QUESTIONS
- OSCILLATIONS DUE TO A SPRING
- Passage
- Passage-I
- Passage-II
- Passage-III
- Passage-IV
- Passage-IX
- Passage-V
- Passage-VI
- Passage-VII
- Passage-VIII
- Passage-X
- Passage-XI
- Passage-XII
- Passage-XIII
- SIMPLE PENDULUM
- SINGLE ANSWER QUESTIONS
- Solved Example
- VELOCITY AND ACCELERATION