Level 3 from ARIHANT PHYSICS (HINGLISH) SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| ARIHANT PHYSICS (HINGLISH) | Level 3 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
(i) The acceleration (a) of a particle moving along a straight line is related to time (t) as per the differential equation d2adt2=−ba. b is a positive constant. Is the particle performing SHM? If yes, what is the time period?
(ii) A particle is executing SHM on a straight line. A and B are two points at which its velocity is zero. It passes through a certain point P (AP>PB) with a speed of 3m/s at times recorded as t = 0, 0.5 s, 2.0 s, 2.5 s, 4.0 s, 4.5 s......Determine the maximum speed of the particle and also the ratio AP/PB. View SolutionQuestion 3
A particle moves along X axis such that its acceleration is given by a=−β(x−2),where β is a positive constant and x is the position co-ordinate.
(a) Is the motion simple harmonic?
(b) Calculate the time period of oscillations.
(c) How far is the origin of co-ordinate system from the equilibrium position? View SolutionQuestion 4
A particle is performing simple harmonic motion along the x axis about the origin. The amplitude of oscillation is a. A large number of photographs of the particle are shot at regular intervals of time with a high speed camera. It was found that photographs having the particle at x1+Δx were maximum in number and photographs having the particle at x2+Δx were least in number. What are values of x1 and x2? View SolutionQuestion 5
Position vector of a particle as a function of time is given by
→R=(asinωtˆi+(acosωt)ˆj+(bsinω0t)ˆk
The particle appears to be performing simple harmonic motion along z direction, to an observer moving in xy plane.
(a) Describe the path of the observer.
(b) Write the distance travelled by the observer himself in the time interval he sees the particle completing one oscillation. View SolutionQuestion 6
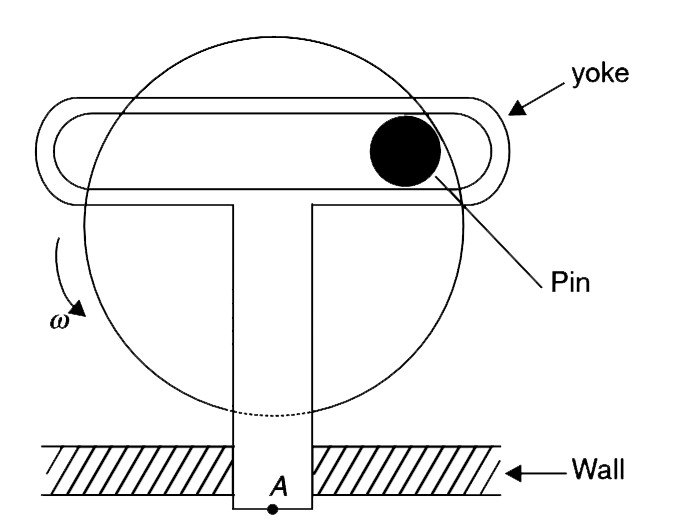
A wheel is revolving at an angular speed of ω. A pin welded at the circumference of the wheel forces a T shaped body to move up and down. The pin slides freely inside the slot of the yoke as the wheel rotates. The T shaped body is constrained to move vertically by a set of walls
(a) Find the time period of oscillatory motion of point A at the base of the T shaped body
(b) Is the motion of A simple harmonic?
 View Solution
View SolutionQuestion 7
(i) A particle is performing simple harmonic motion with time period T. At an instant its speed is 60% of its maximum value and is increasing. After an interval Δt its speed becomes 80% of its maximum value and is decreasing. Find the smallest value of Δt in terms of T.
(ii) A particle is doing SHM of amplitude 0.5 m and period π seconds. When in a position of instantaneous rest, it is given an impulse which imparts a velocity of 1m/s towards the equilibrium position. Find the new amplitude of oscillation and find how much less time will it take to arrive at the next position of instantaneous rest as compared to the case if the impulse had not been applied. View SolutionQuestion 8
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
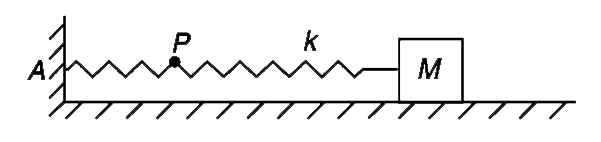 View Solution
View SolutionQuestion 9
A particle of mass m is suspended with the help of a spring and an inextensible string as shown in the figure. Force constant of the spring is k. The particle is pulled down from its equilibrium position by a distance x and released.
(a) Find maximum value of x for which the motion of the particle will remain simple harmonic.
(b) Find maximum tension in the string if
x=mg2k
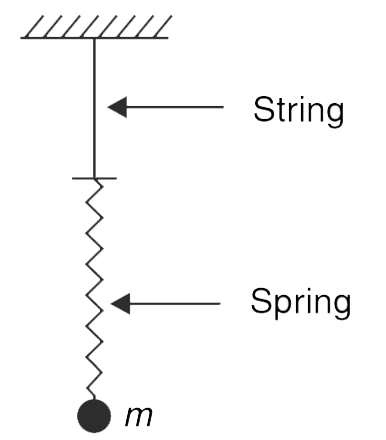 View Solution
View SolutionQuestion 10
A block of mass M is placed on top of a hole in a horizontal table. A spring of force constant k is connected to the block through the hole. The other end of the massless spring has a particle of mass m connected to it. With what maximum amplitude can the particle oscillate up and down such that the block does not lose contact with the table?
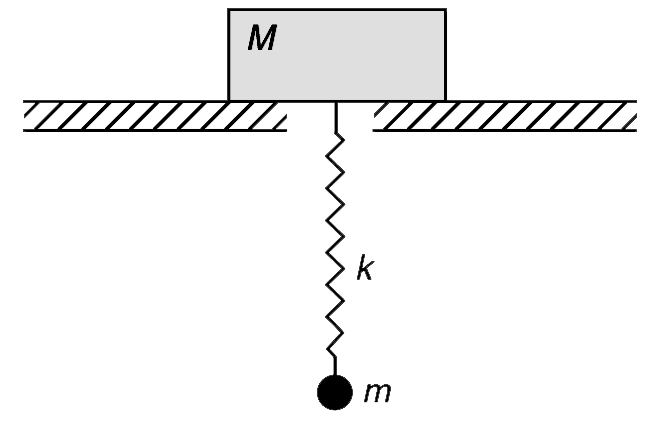 View Solution
View SolutionQuestion 11
A block of mass m is moving along positive x direction on a smooth horizontal surface with velocity u. It enters a rough horizontal region at x = 0. The coefficient of friction in this rough region varies according to μ=ax, where a is a positive constant and x is displacement of the block in the rough region. Find the time for which the block will slide in this rough regionView SolutionQuestion 12
(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.

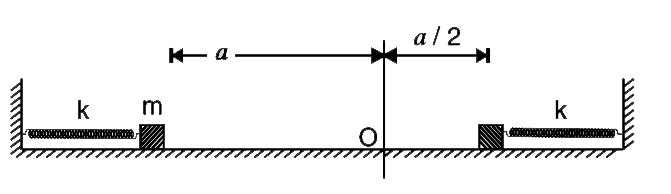 View Solution
View SolutionQuestion 13
Two blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant K=800N/m and the system is placed on a horizontal surface as shown.
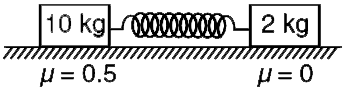
The coefficient of friction between 10 kg block and surface is 0.5 but friction is absent between 2 kg and the surface. Initially blocks are at rest and spring is relaxed. The 2 kg block is displaced to elongate the spring by 1 cm and is then released. (a) Will 10 kg block move subsequently? (b) Draw a graph representing variation of magnitude of frictional force on 10 kg block with time. Time t is measured from that instant when 2 kg block is released to move. View SolutionQuestion 14
A particle of mass m is tied at the end of a light string of length L, whose other end is fixed at point C (fig), and is revolving in a horizontal circle of radius r to form a conical pendulum. A parallel horizontal beam of light forms shadow of the particle on a vertical wall.
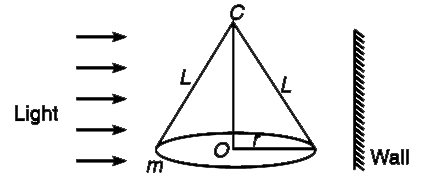
If the tension in the string is F find -
(a) The maximum acceleration of the shadow moving on the wall.
(b) The time period of the shadow moving on the wall. View SolutionQuestion 15
A small ball of mass m is attached to the middle of a tightly stretched perfectly flexible wire AB of length 2 l (figure ). The ball is given a small lateral displacement in horizontal direction and released. The initial tension (T) in the wire is high and change in it due to small lateral displacement of the ball can be neglected. Prove that the ball will perform simple harmonic motion, and calculate the period. If there is a device which can change the tension in the wire at will , how will the time period change if tension in the wire is increased
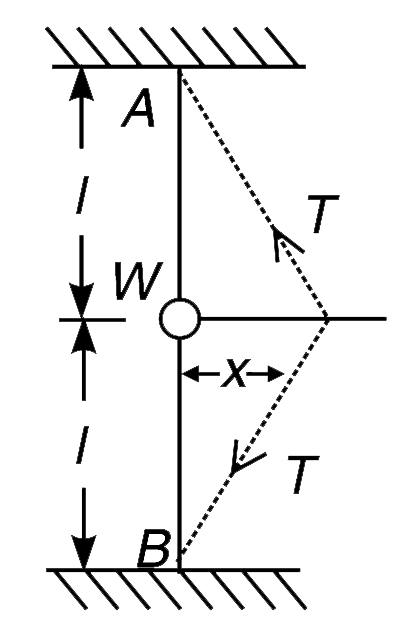 View Solution
View SolutionQuestion 16
A simple pendulum oscillating with a small amplitude has a time period of T=1.0s . A horizontal thin rod is now placed beneath the point of suspension at a distance equal to half the length of the pendulum. The string collides with the rod once in each oscillation and there is no loss of energy in such collisions. Find the new time period T of the pendulumView SolutionQuestion 17
(i) A small steel ball (B) is at rest on the edge of a table of height h. Another identical steel ball (A) is tied to a light string of length L =1.0 m and is released from the position shown so that it swings like a pendulum. At the lowest position of its path it hits the ball B which is at rest. Ball B flies off the table and hits the ground in time t. After collision the ball A keeps moving for a time t before coming to rest for the first time. Find the value of h if t = t. Collision between the balls is head on and coefficient of restitution is e = 0.995.
(ii) A pendulum has a particle of mass m attached to a massless rod of length L. The rod is released from a position where it makes an angle θ0(>π2) with the vertical. The time period of oscillation is observed to be T0. Another similar pendulum has a rod of length 2L. Time period of this pendulum when released from position θ0 is T. Which is larger T or T0 ?
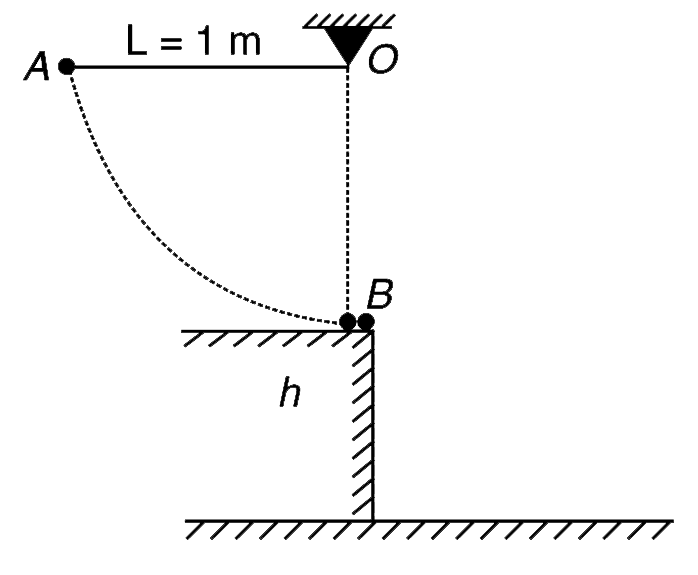 View Solution
View SolutionQuestion 18
A disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.
 View Solution
View SolutionQuestion 19
A rigid body is to be suspended like a physical pendulum so as to have a time period of T=0.2π second for small amplitude oscillations. The minimum distance of the point of suspension from the centre of mass of the body is l1=0.4m to get this time period. Find the maximum distance (l2) of a point of suspension from the centre of mass of the body so as to get the same time period. [g=10m/s2]View SolutionQuestion 20
A square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.
 View Solution
View SolutionQuestion 21
Two particles A and B are describing SHM of same amplitude (a) and same frequency (f) along a common straight line. The mean positions of the two SHMs are also same but the particles have a constant phase difference between them. It is observed that during the course of motion the separation between A and B is always less than or equal to a.
(a) Find the phase difference between the particles.
(b) If distance between the two particles is plotted with time, with what frequency will the graph oscillate? View SolutionQuestion 22
(i) A particle of mass m executes SHM in xy- plane along a straight line AB. The points A (a, a) and B (- a, - a) are the two extreme positions of the particle. The particle takes time T to move from one extreme A to the other extreme B. Find the x component of the force acting on the particle as a function of time if at t = 0 the particle is at A. (ii) Two particle A and B are performing SHM along X-axis and Y-axis respectively with equal amplitude and frequency of 2 cm and 1 Hz respectively. Equilibrium positions for the particles A and B are at the coordinate (3, 0) and (0, 4) respectively. At t = 0, B is at its equilibrium position and moving toward the origin, while A is nearest to the origin. Find the maximum and minimum distances between A and B during their course of motionView SolutionQuestion 23
A particle is performing SHM along x - axis and equation for its motion is x=acos(πt)
Let the time t be expressed as t2=n+m
Where n = 0,1,2,3,4.... and m is a positive fraction.
Calculate the distance travelled by the particle during the interval from t=0 to t=t if
(a) m>0.5 (b) m>0.5View SolutionQuestion 24
Two blocks A and B having mass m = 1 kg and M = 4 kg respectively are attached to a spring and placed vertically on a weighing machine as shown in the figure. Block A is held so that the spring is relaxed. A is released from this position and it performs simple harmonic motion with angular frequency w=25rads−1. The spring remains vertical
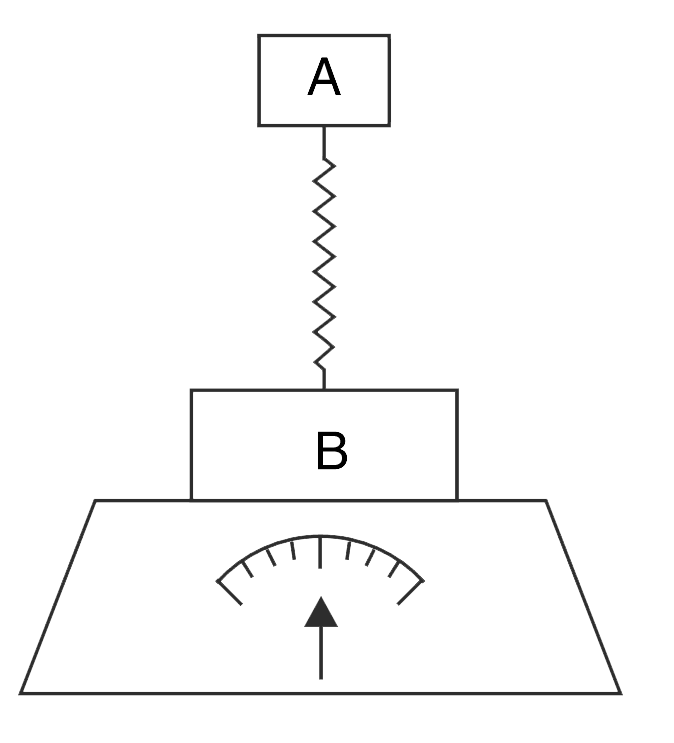
(a) Find the reading of the weighing machine as a function of time. Take t = 0 when A is released.
(b) What is the maximum reading of the weighing machine ? View SolutionQuestion 25
A block of mass M rests on a smooth horizontal table. There is a small gap in the table under the block through which a pendulum has been attached to the block. The bob of the simple pendulum has mass m and length of the pendulum is L. The pendulum is set into small oscillations in the vertical plane of the figure. Calculate its time period. The table does not interfere with the motion of the string.
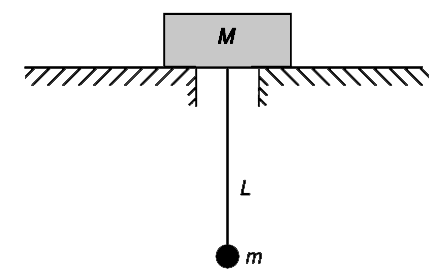 View Solution
View SolutionQuestion 26
A circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle θ with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
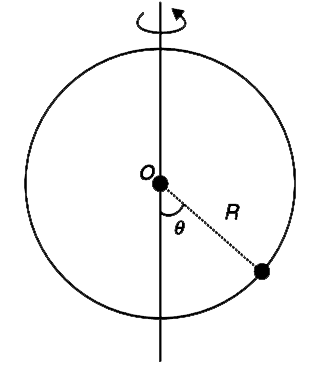 View Solution
View SolutionQuestion 27
In the system shown in the figure the string, springs and pulley are light. The force constant of the two springs are k1=k and k2=2k. Block of mass M is pulled vertically down from its equilibrium position and released. Calculate the angular frequency of oscillation. The top surface of the block (represented by line AB) always remains horizontal.
 View Solution
View SolutionQuestion 28
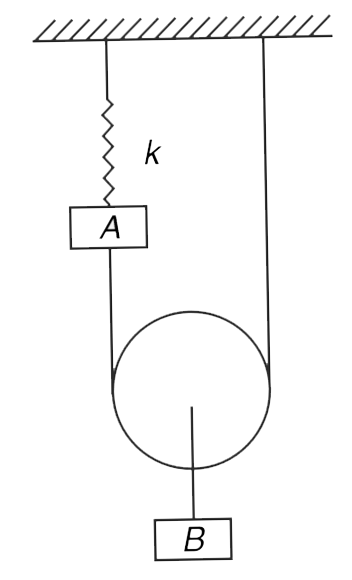
(i) In the system shown in figure, find the time period of vertical oscillations of the block A. Both the blocks A and B have equal mass of m and the force constant of the ideal spring is k. Pulley and threads are massless
(ii) In the arrangement shown in the figure the spring, string and the pulley are mass less. The force constant of the spring is k. A rope of mass per unit length equal to λ(kgm−1) hangs from the string as shown. In equilibrium a length L of the rope is in air and its bottom part lies in a heap on the floor. The rope is very thin and size of the heap is negligible though the heap contains a fairly long length of the rope. The rope is raised by a very small distance and released. Show that motion will be simple harmonic and calculate the time period. Assume that the hanging part of the rope does not experience any force from the heap or the floor (For example there is no impact force while the rope hits the floor while moving downward and there is no impulsive pull when the vertical part jerks a small element of heap into motion).
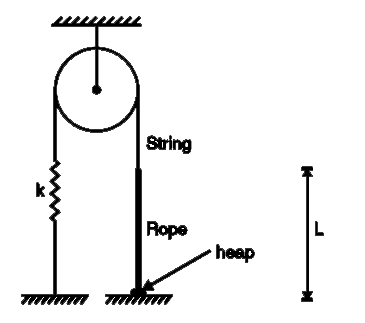 View Solution
View SolutionQuestion 29
A box B of mass M hangs from an ideal spring of force constant k. A small particle, also of mass M, is stuck to the ceiling of the box and the system is in equilibrium. The particle gets detached from the ceiling and falls to strike the floor of the box. It takes time t for the particle to hit the floor after it gets detached from the ceiling. The particle, on hitting the floor, sticks to it and the system thereafter oscillates with a time period T. Find the height H of the box if it is given that t=T6√2. Assume that the floor and ceiling of the box always remian horizontal.
 View Solution
View SolutionQuestion 30
A block has a L shaped stand fixed to it. Mass of the block with the stand is M. At the free end of the stand there is a spring which carries a ball of mass m. With the spring in its natural length, the ball is released. It begins to oscillate and the stand is tall enough so that the ball does not hit the block.
(a) Find maximum value of mass (m) of the ball for which the block will not lose contact with the ground?
(b) If the stand is not tall enough and the ball makes elastic impact with the block, will your answer to part (a) change?
 View Solution
View SolutionQuestion 31
Two ideal springs of same make (the springs differ in their lengths only) have been suspended from points A and B such that their free ends C and D are at same horizontal level. A massless rod PQ is attached to the ends of the springs. A block of mass m is attached to the rod at point R. The rod remains horizontal in equilibrium. Now the block is pulled down and released. It performs vertical oscillations with time period T=2π√m3k where k is the force constant of the longer spring.
(a) Find the ratio of length RC and RD.
(b) Find the difference in heights of point A and B if it is given that natural length of spring BD is L.
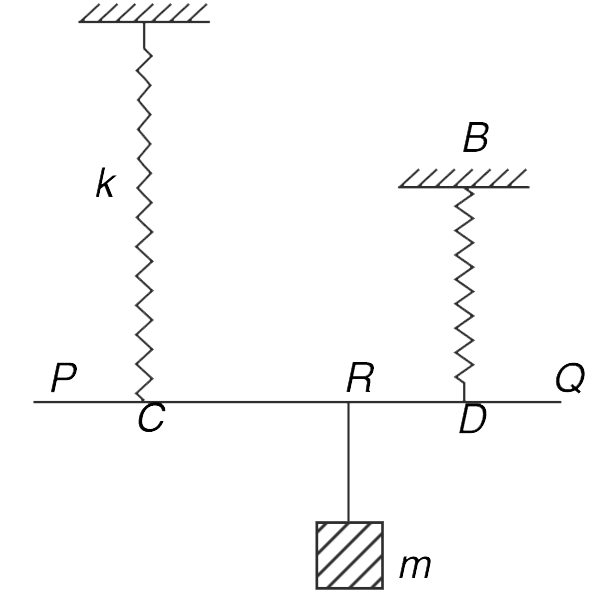 View Solution
View SolutionQuestion 32
A block of mass M connected to an ideal spring of force constant k lies in equilibrium on the smooth floor of a room. The other end of the spring is fixed to the left wall of the room. The room begins to move to the right with a constant acceleration a0. In the reference frame of the room the block begins to perform simple harmonic motion.
At a certain instant (say t=t0) when the block was at its left extreme, the acceleration of the room vanishes. Plot the x - t graph for the block taking time t = 0 when the room started accelerating.
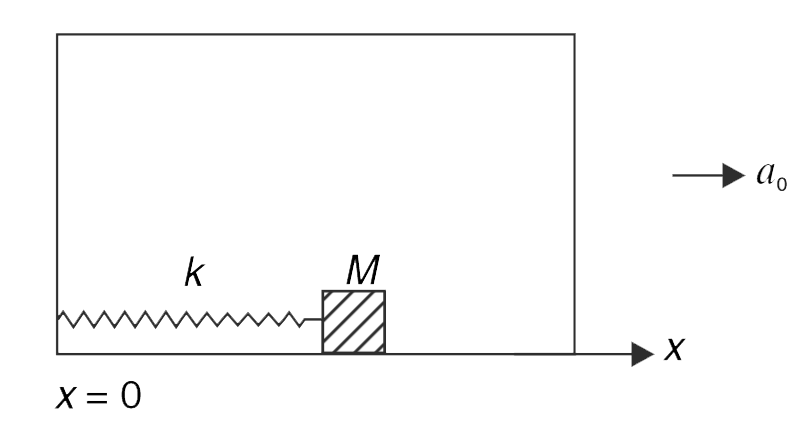
Show the graph till time t0 and beyond that. Take origin to be at the left wall and positive x direction towards right (as shown in figure). Assume no collision of the block with walls.View SolutionQuestion 33
A block of mass M connected to an ideal spring of force constant k, is placed on a smooth surface. The block is pushed to the left so as to compress the spring by a length A and then it is released. The block hits an elastic wall at a distance 3A2 from its point of release. Assume the collision to be instantaneous.
(a) Calculate the time required by the block to complete one oscillation
(b) Draw the velocity - time graph for one oscillation of the block.
(c) Find the value of k for which average force experienced by the wall due to repeated hitting of the block is F0.
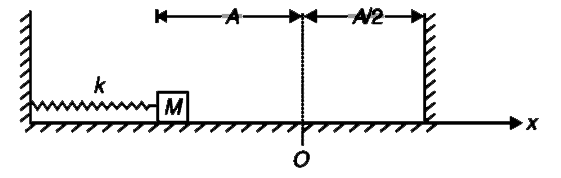 View Solution
View SolutionQuestion 34
A particle of mass m is constrained to move along a straight line. A and B are two fixed points on the line at a separation of L. When the particle is at some point P, between A and B, it is acted upon by two forces
→F1=(6mgL)→PA and →F2=(3mgL)→PB
At time t=0, the particle is projected from A toward B with a speed of √gL.
At what time 't' will the particle reach at B for the first time ?
 View Solution
View SolutionQuestion 35
An equilateral prism of mass m is kept on a smooth table between two identical springs each having a force constant of k. The two springs have their lengths perpendicular to the inclined faces of the prism and are constrained to remain straight. The ends of the springs have light pads aligned parallel to the faces of the prism, and distance between pads and the incline faces is d. The prism is imparted a velocity v to the right. Find time period of its oscillation.
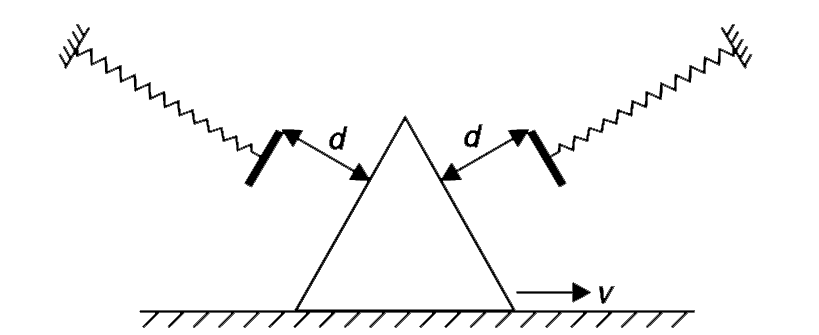 View Solution
View SolutionQuestion 38
A spring has force constant k=200N/m and its one end is fixed. There is a block of mass 2 kg attached to its other end and the system lies on a smooth horizontal table. The block is pulled so that the extension in the spring becomes 0.05 m. At this position the block is projected with a speed of 1m/s in the direction of increasing extension of the spring. Consider time t = 0 at the moment the block is projected and find
(a) the extension (or compression) in the spring as a function of time.
(b) the maximum extension in the spring and the time at which it occurs for the first time.
(c) the time after which the speed of the block becomes maximum for the first time. Given: sin−1(0.446)=0.46 radian View SolutionQuestion 39
Two identical simple pendulums A and B are fixed at same point. They are displaced by very small angles α and β(=2α) respectively and are simultaneously released from rest at time t = 0. Collisions between the pendulum bobs are elastic and length of each pendulum is l.
(a) What is the minimum number of collisions between the bobs after which the pendulum B will again reach its original position from where it was released ?
(b) Find the time (t) at which B reaches its initial position for the first time after the release.
(c) Write the kinetic energy of pendulum B just after nth collision? Take mass of each bob to be m.
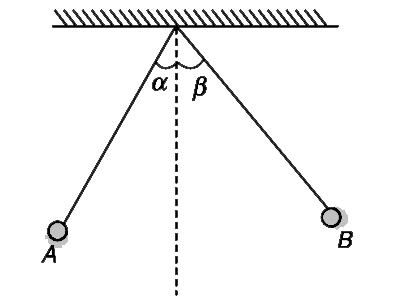 View Solution
View SolutionQuestion 40
Two spheres A and B of the same mass m and the same radius are placed on a rough horizontal surface. A is a uniform hollow sphere and B is uniform solid sphere. They are tied centrally to a light spring of spring constant k as shown in figure. A and B are released when the extension in the spring is x0. Friction is sufficient and the spheres do not slip on the surface. Find the frequency and amplitude of SHM of the sphere A.
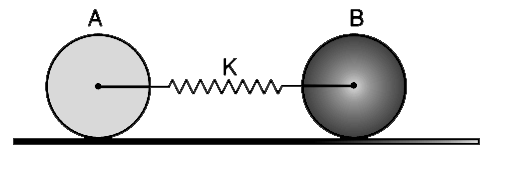 View Solution
View SolutionQuestion 41
Two small blocks of mass m and 4m are connected to two springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that both the springs get compressed by a distance a. First the block of mass m is released and after it travels through a distance(1−√32)
the second block is also released.
(a) At what distance from point O will the two blocks collide?
(b) How much time the two blocks need to collide after the block of mass 4m is released?
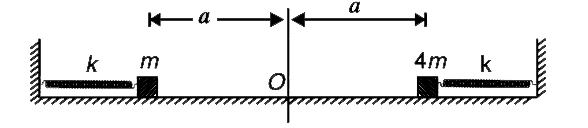 View Solution
View SolutionQuestion 42
A block of mass M = 40 kg is released on a smooth incline from point A. After travelling through a length of 30 cm it strikes an ideal spring of force constant K=1000N/m . It compresses the spring and then gets pushed back. How much time after its release, the block will be back to point A?
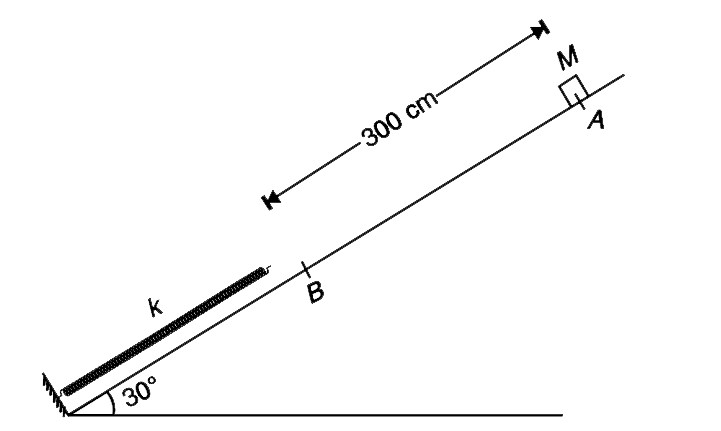 View Solution
View SolutionQuestion 43
Two tunnels - T1 and T2 are dug across the earth as shown in figure. One end of the two tunnels have a common meeting point on the surface of the earth. Two particles P1 and P2 are oscillating from one end to the other end of the tunnels. At some instant particles are at mid point of their tunnels as shown in figure. Then -

(a) Write phase difference between the particle P1 and P2. Can the two particles ever meet?
(b) Write the ratio of maximum velocity of particle P1 and P2. View SolutionQuestion 45
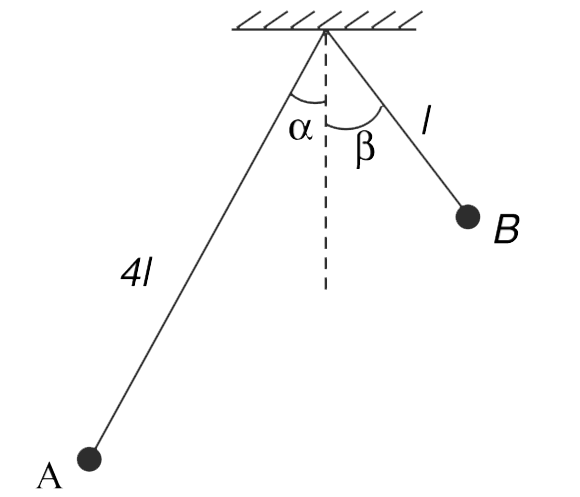
Two identical small elastic balls have been suspended using two strings of different length (see fig (a)). Pendulum A is pulled to left by a small angle θ0 and released. It hits ball B head on which swings to angle 2θ0 from the vertical. Calculate the time period of oscillation of A if its length is known to be L.
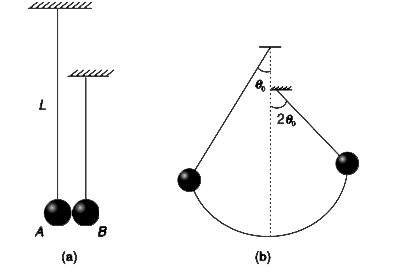 View Solution
View SolutionQuestion 46
A simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
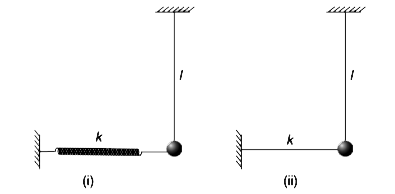 View Solution
View SolutionQuestion 47
A uniform rod AB of mass m and length L is tied, at its end B, to a thread which is attached to point P on the ceiling. Length of the thread PB is 0.75 L. The other end A of the rod is hinged at a point on the ceiling. Distance AP = 1.25 L. End B of the rod is pushed gently perpendicular to the plane of the figure and it starts oscillating
(a) Find the moment of inertia of the rod about line AP.
(b) Assuming that the triangle APB makes a small angle θ with the vertical plane, write the restoring torque acting on the rod.
(c ) Calculate the time period of small oscillations.
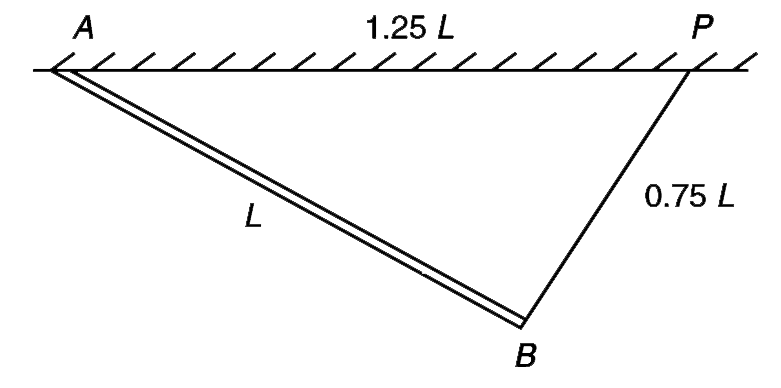 View Solution
View SolutionQuestion 48
A railway tank wagon with its 2m diameter and 6m long horizontal cylindrical body, half full of petrol is driven around a curve of radius 100m, at a speed of 8.33m/s. The curve runs smoothly into a straight track and the train maintains a constant speed. Find the angular amplitude and frequency of subsequent oscillation of the petrol due to this change of motion. Neglect viscosity and consider petrol as a solid semi cylinder sliding inside the tank. Given: tan−1(0.07)=4∘ View SolutionQuestion 49
A pendulum consists of an inextensible thread connected to a solid spherical ball of radius r. The distance between the point of suspension and the centre of the ball is L(>>r) . Calculate the percentage difference in the time period of this pendulum to the time period of a simple pendulum of length L. How large is this difference for r = 5 cm and L = 100 cm. View SolutionQuestion 50
A disc of radius r is connected to a string of length L. The string is tied to a point on the circumference of the disc. This system is made to oscillate in vertical plane of the disc with a small angular amplitude θ0. Find the speed of the lowest point of the disc at the moment the string become vertical.
 View Solution
View SolutionQuestion 51
(i) A cylindrical container has area of cross section equal to 4A and it contains a non viscous liquid of density 2ρ. A wooden cylinder of cross sectional area A and length L has density ρ. It is held vertically with its lower surface touching the liquid. It is released from this position. Assume that the depth of the container is sufficient and the cylinder does not touch the bottom.
(a) Find amplitude of oscillation of the wooden cylinder.
(b) Find time period of its oscillation.
Two cubical blocks of side length a and 2a are stuck symmetrically as shown in the figure. The combined block is floating in water with the bigger block just submerged completely. The block is pushed down a little and released. Find the time period of its oscillation. Neglect viscostiy.

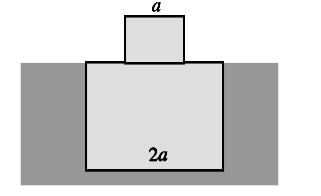 View Solution
View SolutionQuestion 52
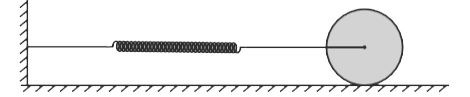
A hollow cylindrical shell of radius R has mass M. It is completely filled with ice having mass m. It is placed on a horizontal floor connected to a spring (force constant k) as shown. When it is disturbed it performs oscillations without slipping on the floor.
(a) Find time period of oscillation assuming that the ice is tightly pressed against the inner surface of the cylinder.
(b) If the ice melts into non viscous water, find the time period of oscillations. (Neglect any volume change due to melting of ice)
 View Solution
View SolutionQuestion 54
Two particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time
 View Solution
View SolutionQuestion 57
Assume a smooth hole drilled along the diameter of the earth. If a stone is dropped at one end it reaches the other end of the hole after a Time T0. Now instead of dropping the stone, you throw it into the hole with an initial velocity u. How big should u be, so that the stone appears at the other end of the hole after a time T02. Express your answer in terms of acceleration due to gravity on the surface of the earth (g) and the radius of the earth (R ).View SolutionQuestion 58
A large horizontal turntable is rotating with constant angular speed ω in counterclockwise sense. A person standing at the centre, begins to walk eastward with a constant speed V relative to the table. Taking origin at the centre and X direction to be eastward calculate the maximum X co-ordinate of the person.View SolutionQuestion 59
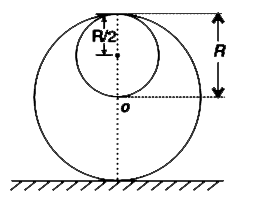
A spherical cavity of radiusR2 is removed from a solid sphere of radius R as shown in fig. The sphere is placed on a rough horizontal surface as shown. The sphere is given a gentle push. Friction is large enough to prevent slippage. Prove that the sphere perform SHM and find the time period.
 View Solution
View SolutionQuestion 60
Two blocks 1 and 2, each having mass m, are placed on a smooth table connected to three identical springs as shown in the figure. Each spring has a force constant K. Initially, all springs are relaxed. The system is disturbed and starts moving. Let x1 and x2 represent the displacements of the two blocks from their respective mean positions.
(a) Prove that the quantity A=x1+x2 varies sinusoidally and calculate its angular frequency wa.
(b) Prove that the quantity B=x1−x2 varies sinusoidally and calculate its angular frequency wb.
(c) Prove that motion of block 1 is superposition of two SHMs. Write frequency of the component SHMs.
 View Solution
View SolutionQuestion 61
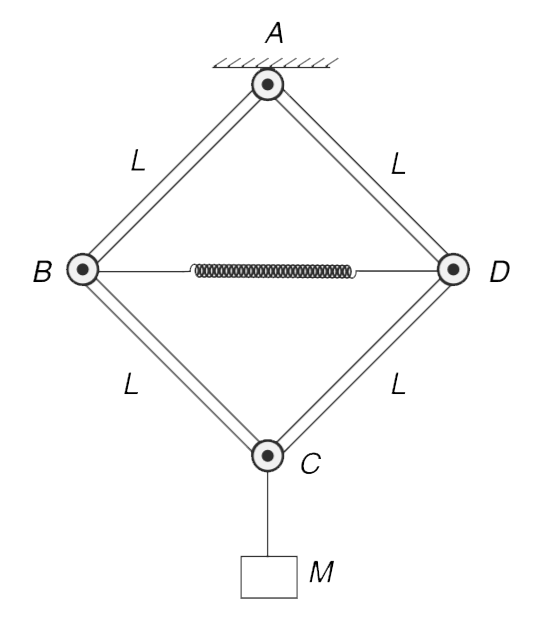
Four identical mass less rods are connected by hinged joints to form a rhombus of side length L. Rods can rotate freely about the joints. The joints B and D are connected by a mass less spring of relaxed length 1.5 L. The system is suspended vertically with a load of mass M attached at C (see fig). In equilibrium the rods form an angle of 30∘ with the vertical. Find time period of small oscillations of the load.
 View Solution
View SolutionQuestion 62
Two identical blocks 1 and 2, each of mass m, are kept on a smooth horizontal surface, connected to three springs as shown in the figure. Each spring has a force constant k. Under suitable initial conditions, the two blocks oscillate in phase and their respective displacement from the mean position is given by
x1=Asinωt and x2=Asinωt
(i) Suggest one such initial condition that will result in such oscillation.
(ii) Find ω
 View Solution
View Solution