Illustration from CENGAGE PHYSICS Chapter 20 RIGID BODY DYNAMICS 2 for Class 11
| Class 11 | PHYSICS |
| Chapter | RIGID BODY DYNAMICS 2 |
| CENGAGE PHYSICS | Illustration |
| Medium | English |
| Academic Year | 2023-2024 |
Question 6
A thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment, the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. The angular velocity of the rod as a function of its rotation angle θ measured relative to the initial position should be.View SolutionQuestion 8
The top is figure has moment of inertia equal to 4.00×104kgm2 and is initially at rest. It is free to rotate about the stationary axis AA'. A string wrapped around a ped alonng the axis of the top is pulled in such a manners as to maintain a constant tension of 5.57N.If the string does not slip while it is unwound from the peg, what is the angular speed of the top after 80.0CM of string has been pulled of the peg?
 View Solution
View SolutionQuestion 10
A solid cyinder of mass m=4kg and radius R=10cm has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.
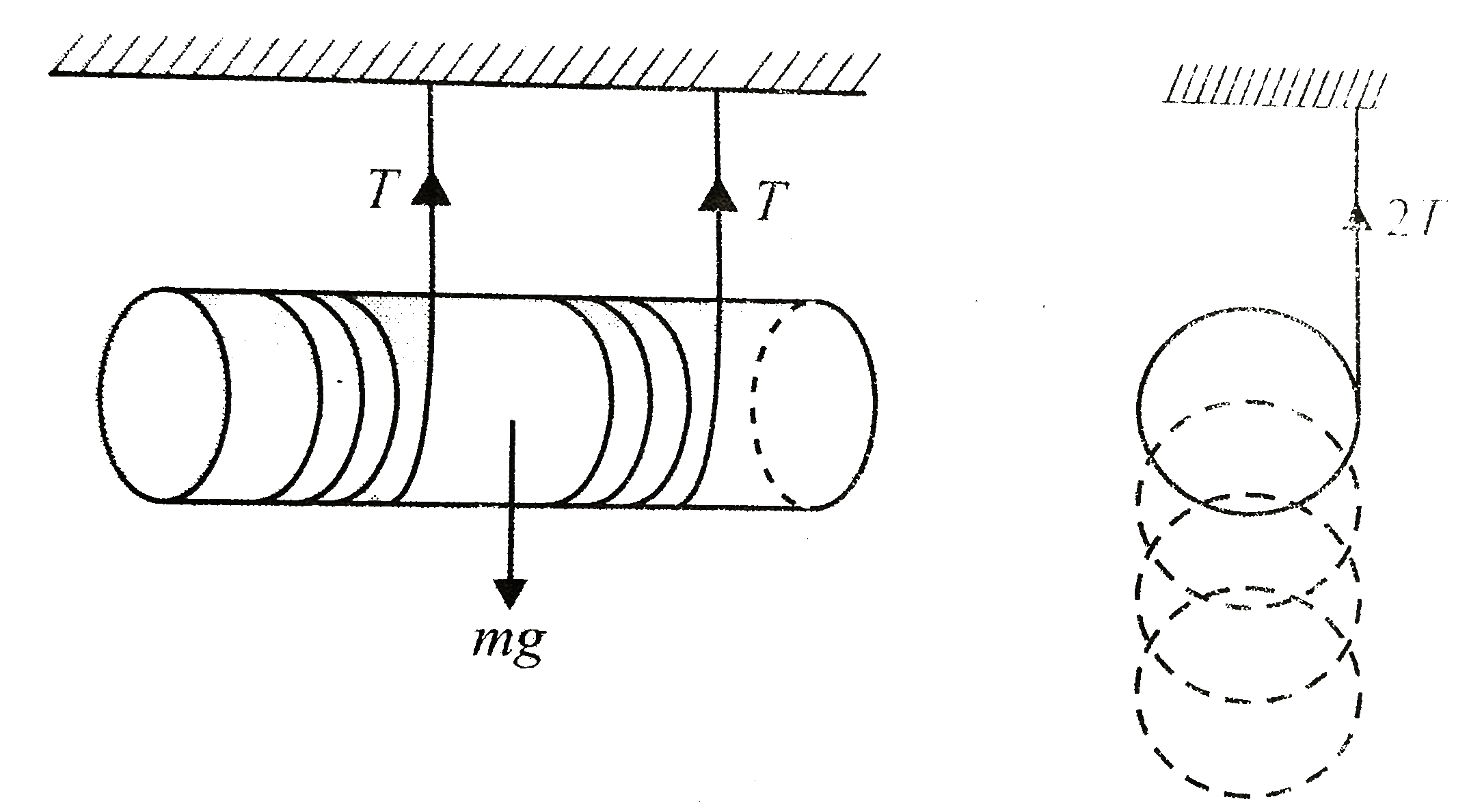 View Solution
View SolutionQuestion 11
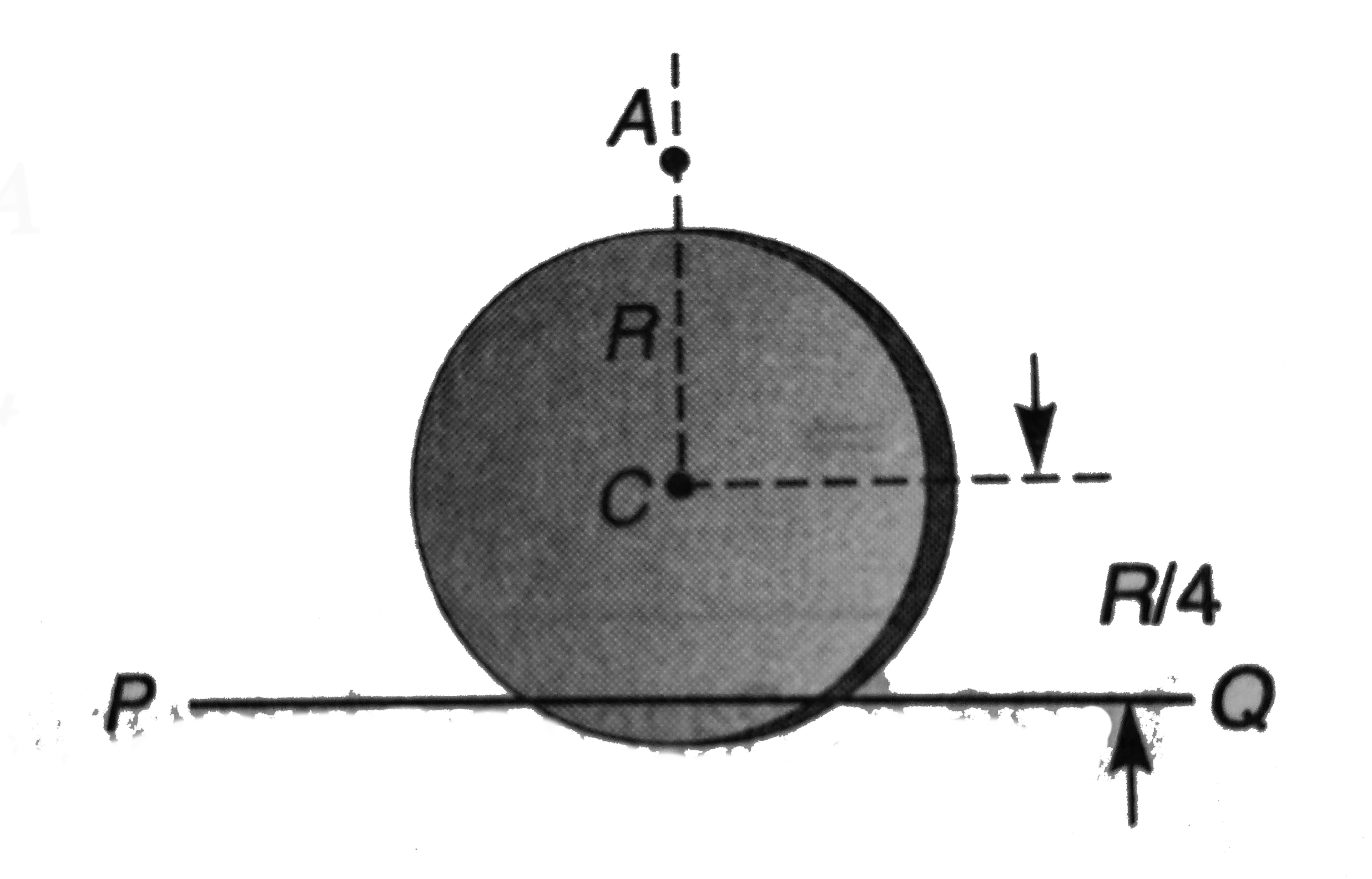
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position. View SolutionQuestion 14
A uniform disc of mas M and radius R is smoothly pivoted at O. A light inextensible string wrapped over the disc hangs a particle of mass m. If the system is released from rest, assuming that the string does not slide on the disc, find the angular speed of the disc as the function of time using impulse momentum equation.
 View Solution
View SolutionQuestion 16
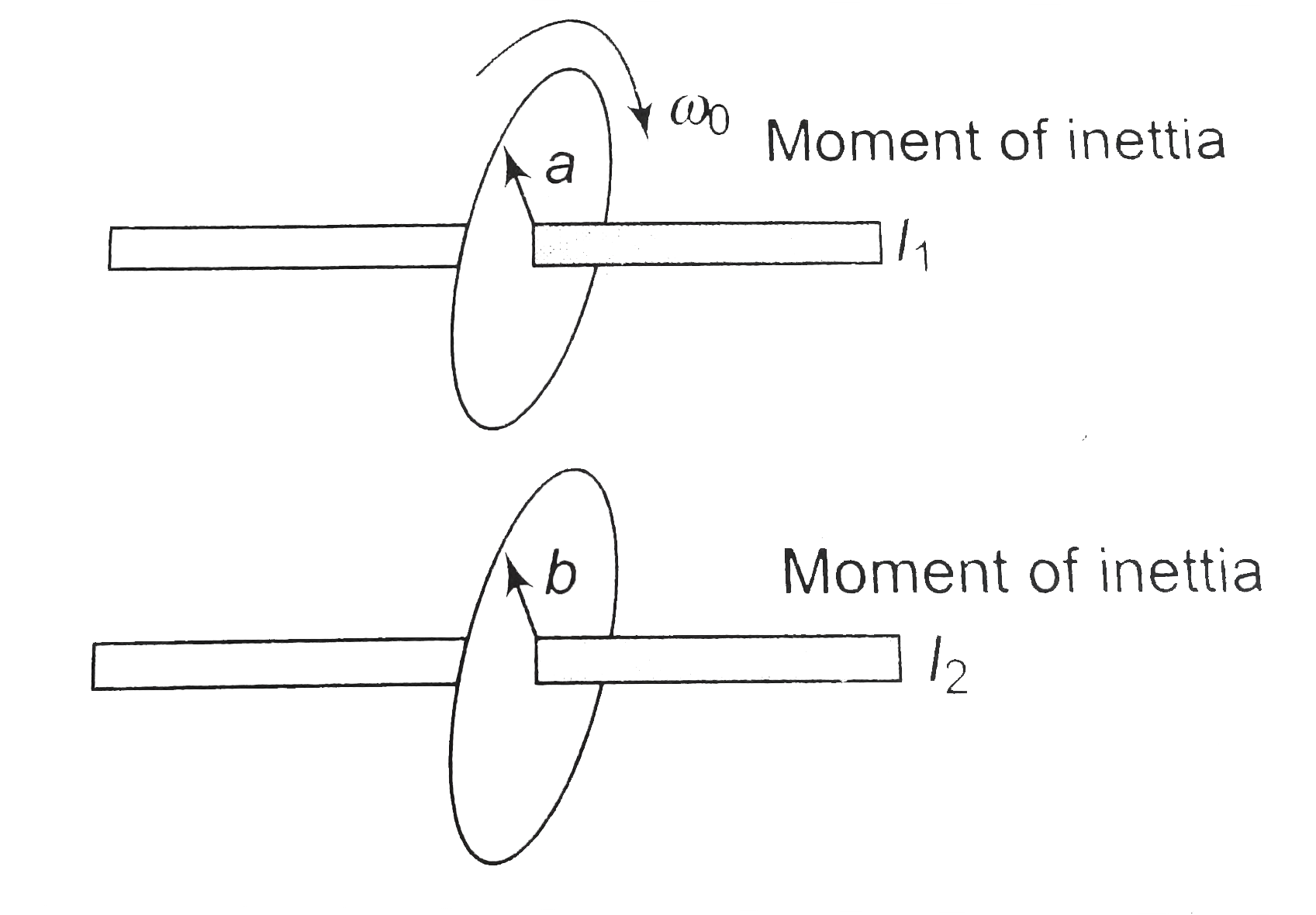
The two uniform discs rotate separately on parallel axles. The upper disc (radius a and momentum of inertia I1) is given an angular velocity ω0 and the lower disc of (radius b and momentum of inertia I2) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
 .View Solution
.View SolutionQuestion 17
A turntable turns about a fixed vertical axis, making one revolution in 10s. The moment of inertia of the turntable about the axis is 1200kgm2. A man of 80kg, initially standing at centre of the turnable, runs out along the radius. What is the angular velocity of the turnable when the man is 2m from the centre?View SolutionQuestion 18
A man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.
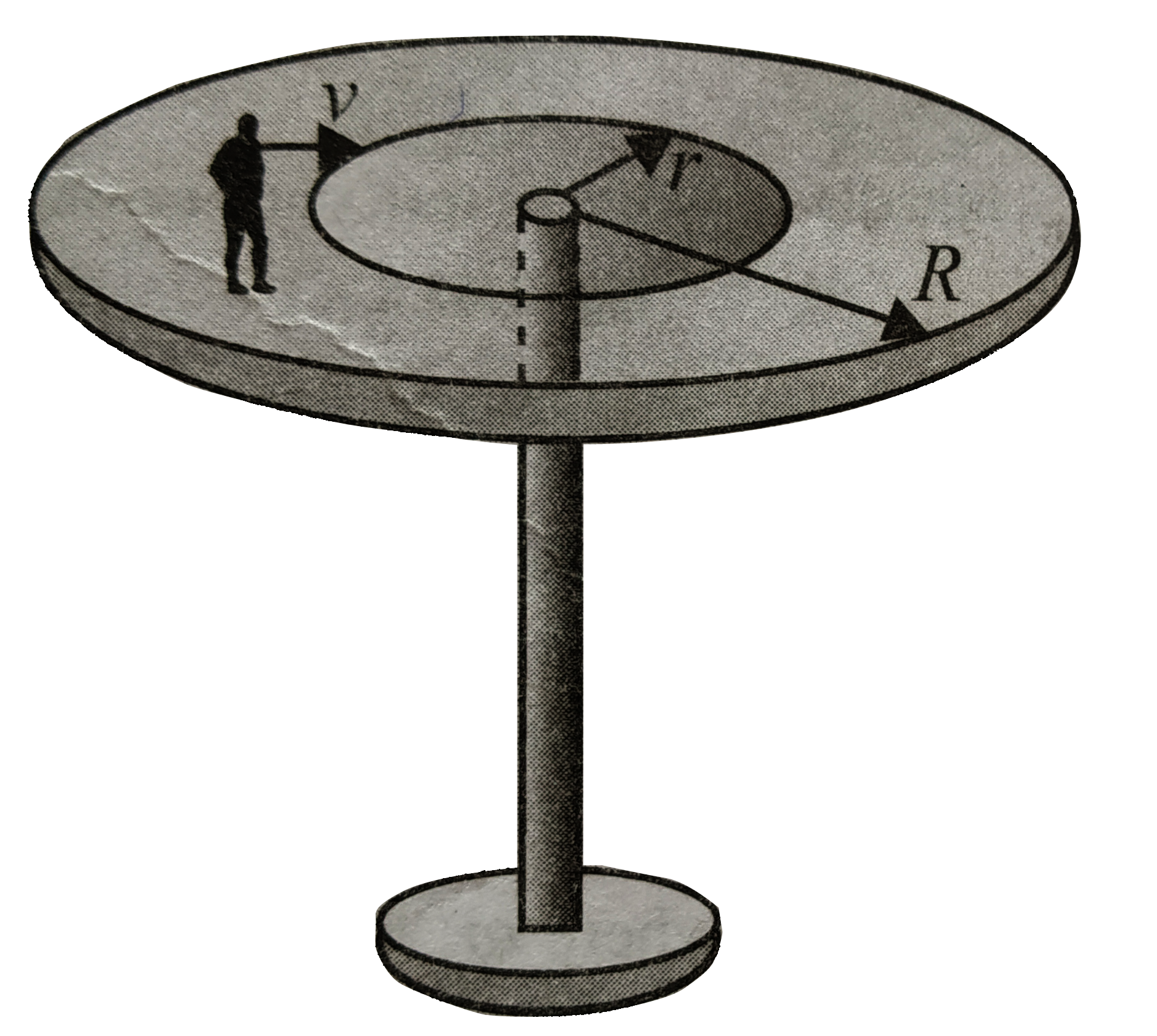 View Solution
View SolutionQuestion 19
A man of mass 100kg stands at the rim of a turtable of radius 2m and moment of inertia 4000kgm2 mounted on a vertical frictionless shaft at its centre. The whole system is initially at rest. The man now walks along the outer edge of the turntable with a velocity of 1m/s relative to the earth
a. With what angular velocity and in what direction does the turntable rotate?
b. Through what angle will it have rotated when the man reaches his initial position on the turntable?
c. Through what angle will it have rotated when the man reaches his initial position relative to the earth?View SolutionQuestion 20
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius 0.5m about the hole with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shorting the radius of the circle in which the block revolves. The breaking strength of the cord is 600N. What will be radius of the circle when the cord breaks?
 View Solution
View SolutionQuestion 21
Two skaters each of mass 50kg, approach each other along parallel paths separated by 3m. They have equal ad opposite velocities of 10m/s. The first skater carries a long light pole, 3m long, and the second skater grabs the end of it as he passes (assume frictionless ice).
a. Described quantitatively the motion of the skaters after they are connected by the pole.
b. By pulling on the skaters reduce their distance to 1m. What is their motion then?
c. Compare the KEs of the system in parts a. and b. where does the change come from?View SolutionQuestion 22
A string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
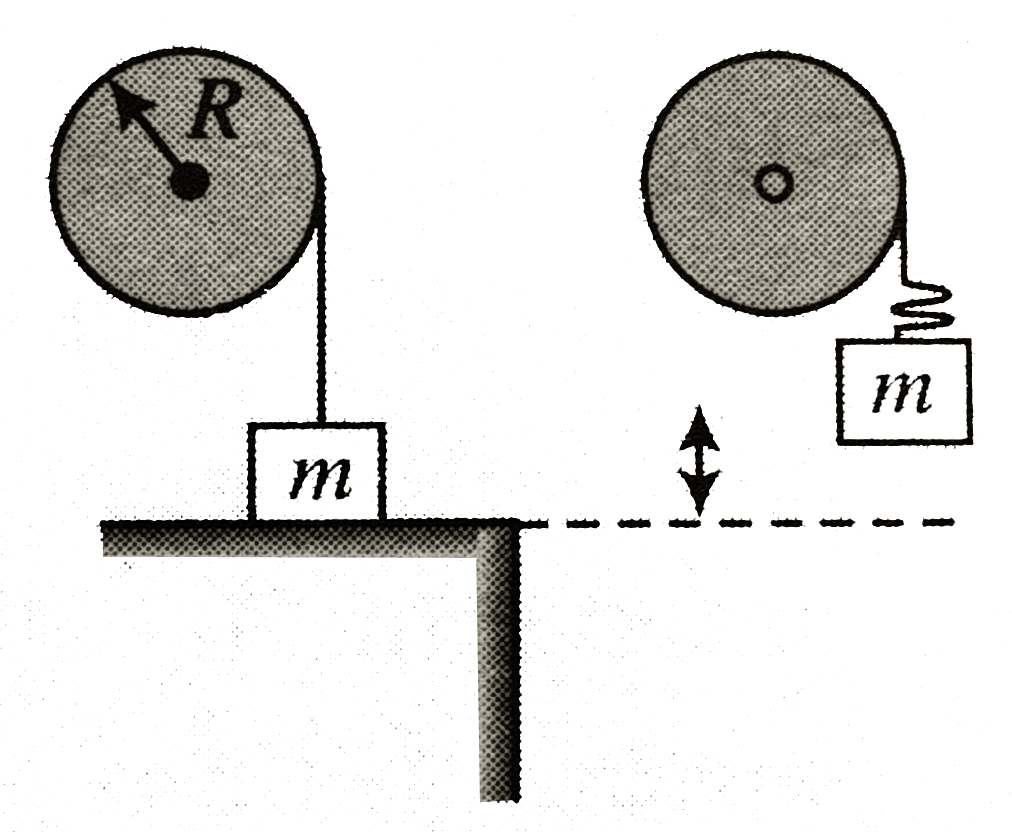 View Solution
View SolutionQuestion 23
AB is a horizontal diameter of a ball of mass m=0.4kg and radius R=0.10m. At time t=0, a sharp impulse is applied at B at angle of 45∘ with the horizontal as shown in figure so that the ball immediately starts to move with velocity v0=10ms−1

a. Calculate the impulse and angular velcity of ball just after impulse provided.
If coefficient of kinetic friction between the floor and th ball is μ=0.1. Calculate. The
b. velocity of ball when it stops sliding,
c. time t at that instant
d. horizontal distance travelled by the ball up to that instant.
e. angular displacement of the ball about horizontal diameter perpendicular to AB, up to that instant, and
f. energy lost due to friction (g=10ms−2)View SolutionQuestion 24
A pulley of radius b=20cm is fixed with a shaft of radus a=10cm. Moment of inertia of shaft puley system is I=(33−800)kgm2 and the system is free to rotate about axis O of the shaft without friction.
A block B of mass m2=8kg is resting over ann ideal spring of force costant. K=2048Nm−1
Lower end of the spring is fixed to the floor and the spring is vertical. Thread connected betwen shaft and block B is just taut.

Another thead is connected between pulley and block A of mass m1=4kg. Initially this thread is loose. When block A is released first it falls freely through a height h=4051024m then the thread becomes taut and block B is jerked into motion.
calculate:
a. Initial compressiion of the spring
b. Velocity of block B when it is jerked into motion,
c. Loss of energy during that jerk (g=10ms−2)View SolutionQuestion 35
A ball (solid sphere) is thrown down the valley in such a way that it slides with a speed v0 initially without rolling. Prove that it will roll without any sliding when its speed falls to (57)v0. The transition from pure sliding to pure rolling is gradual, so that both sliding and rolling take place during this interval.View SolutionQuestion 36
A uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at t0.
Assuming that the coefficient of friction to be μ, calculate t0.
 View Solution
View SolutionQuestion 37
A plank of mass M, whose top surface is rough with coefficient of friction μ is placed on a smooth ground. Now a disc of mass m=M/2 and radius r is placed on the plank. The disc is now given a velocity v0 in the horizontal direction at t=0

a. Find the time when the disc starts rolling
b. Find the velocity of the plank and the disc up to that time.
c. Find the distance travelled by the plank up to this instant.
Find the work done by the friction force up to this instant.View SolutionQuestion 38
A uniform cylinder (mass M) of radius R is kept on an accelerating platform (mass M) as shown in figure. If the cylinder rolls withut slipping on the platform, determine the magnitude of acceleration of the centre of mass of the cylinder. Assuming th coefficient of friction μ=0.40, determinete maximum acceleration the platform may have without slip between the clyinder and the platform.
 View Solution
View SolutionQuestion 43
A cotton reel has a inner radius r and outer radius R. Mass of the reel is M and moment of inertia about longitudinal rotational axis is I. A force P is applied at the free end of thread wraped of the reel as shown in fig. If the reel moves without sliding.

a. Determine the frictional force exerted by the table on the reel and the direction in which it acts.
b. In what direction does the reel begin to move? View SolutionQuestion 44
A wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
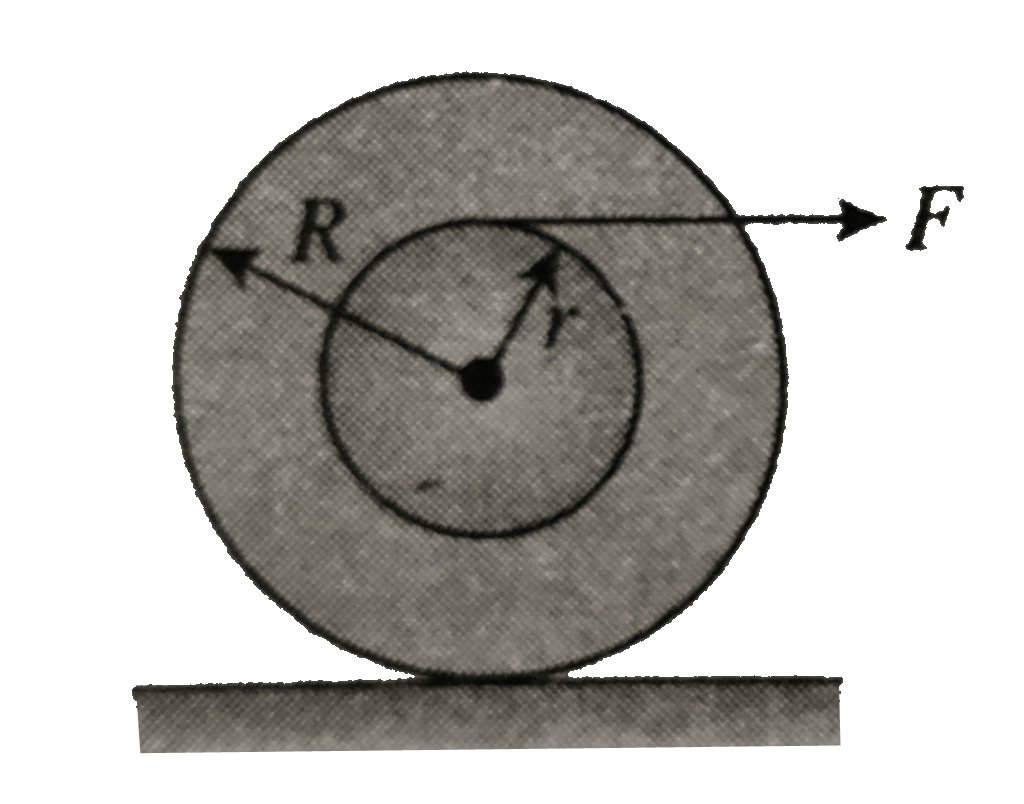
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.View SolutionQuestion 46

A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its backward slipping eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.View SolutionQuestion 52
A solid cube of wood of side 2a and mass M is resting on a horizontal surface. The cube is constrained to rotate about an axis passing through D and perpendicular to face ABCD. A bullet of mass m and speed v is shot at a height of 4a/3 as shown in the figure. The bullet becomes embedded in the cube. Find the minimum value of v required to topple the cube. Assume m>>M.
 View Solution
View SolutionQuestion 53
A particle of mass m=1kg collides with the end with velocity v0=6ms−1 of a spinning rod of mass2m and length l=1m at the end of he rod. If the coefficient of restitution of collision e=(2/3), find the
a. velocity of the particle
b. angular velocity of the rod just after the impact.
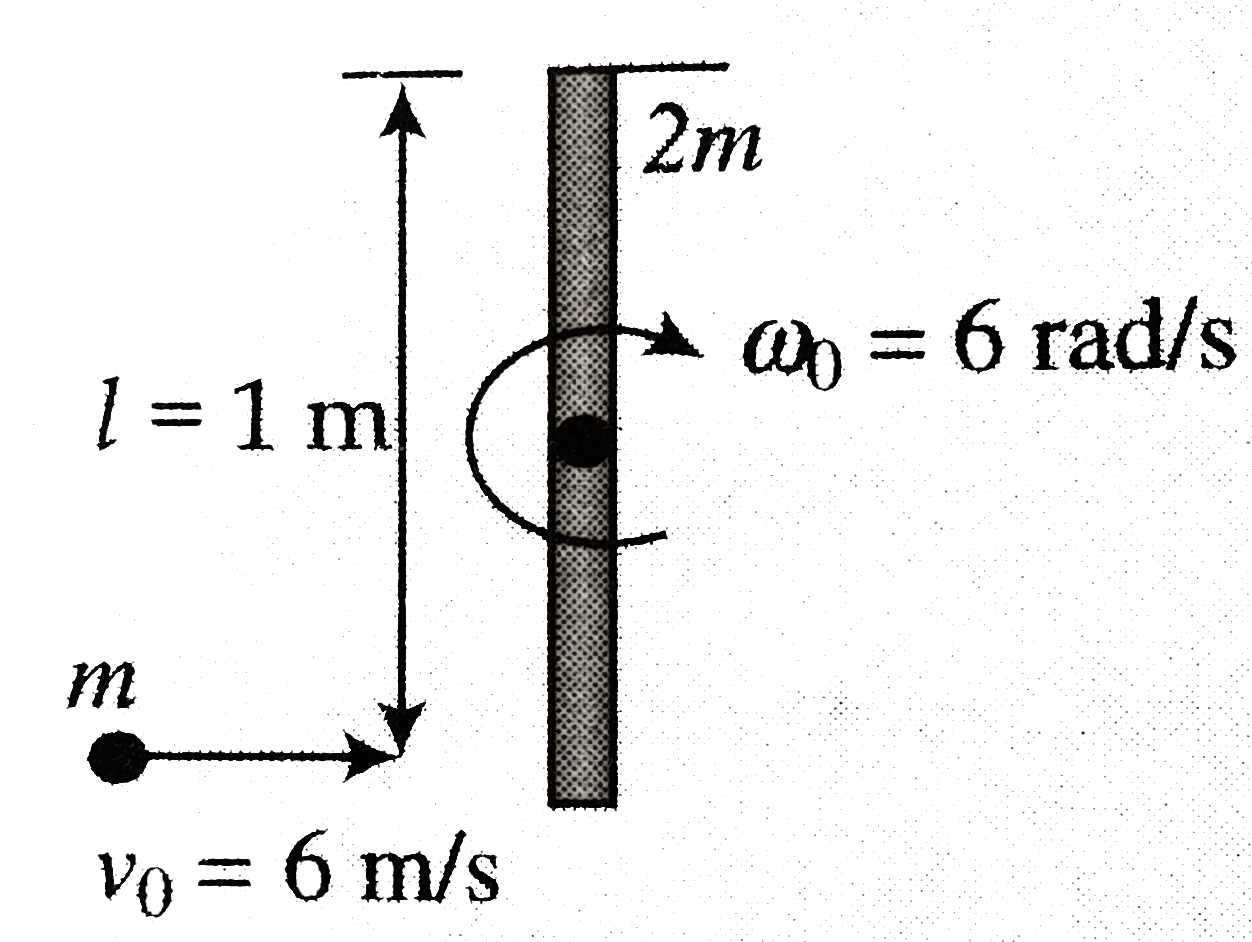 View Solution
View SolutionQuestion 55
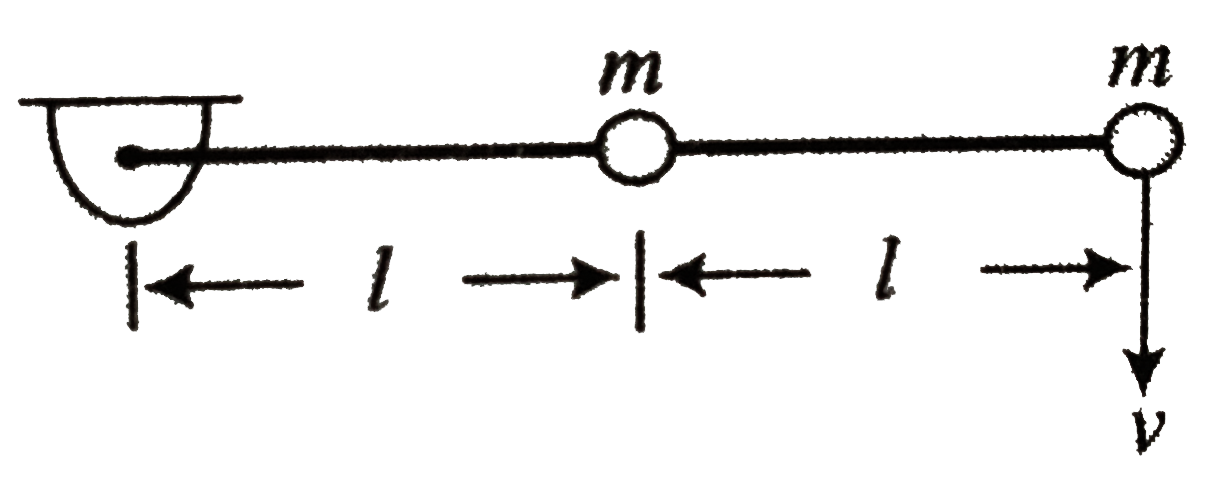
Two particles A and B of mass m each hit the ends of a rigid bar of mass M and length l in-elastically from opposite sides the speeds v and perpendicular to the rod. The bar is kept on a smooth horizontal plane (as shown). Find the linear and angular speed of the system (bar+particle).
 View Solution
View SolutionQuestion 56
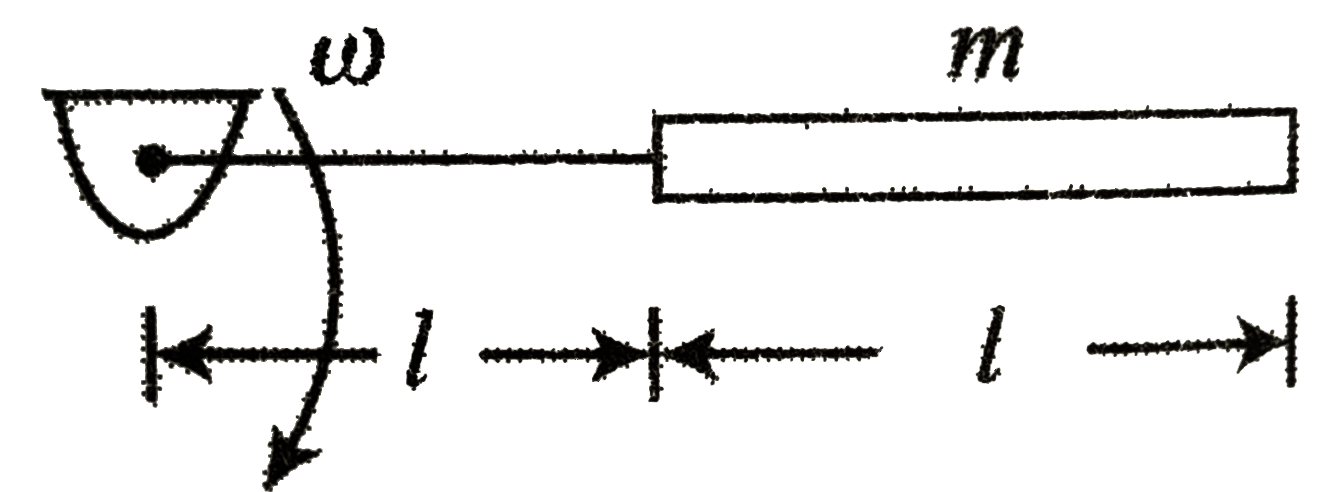
A vertically oriented uniform rod of mass M and length l can rotate about its upper end. A horizontally flying bullet of mass m strikes the lower end of the rod and gets stuck in it as a result the rod swings through an angle α. Assuming that m<<M. find
a. the velocity of the flying bullet:
b. the moment change in the system bullet rod during the impact: what causes that change of momentum.
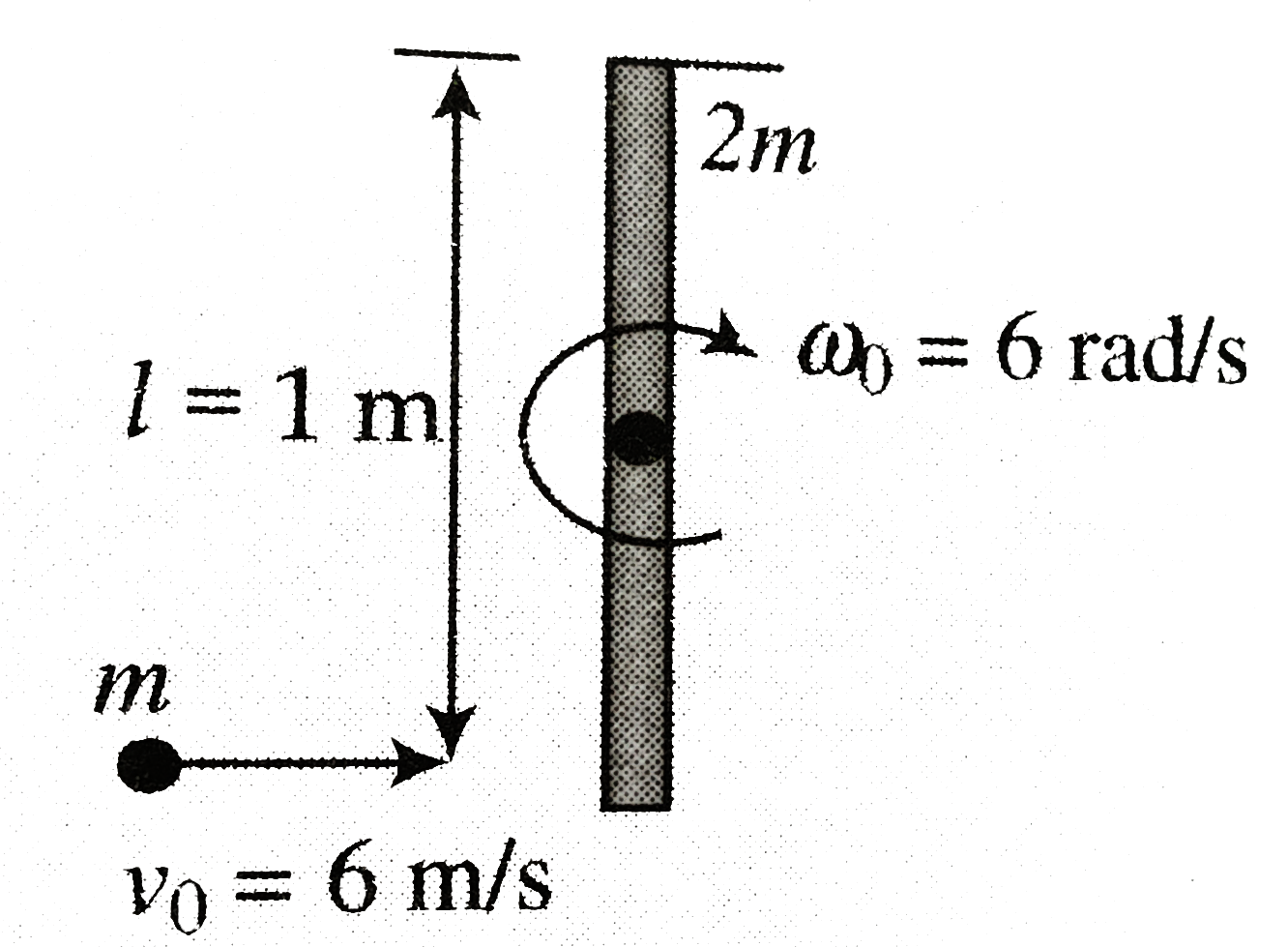 View Solution
View SolutionQuestion 57
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision. View Solution

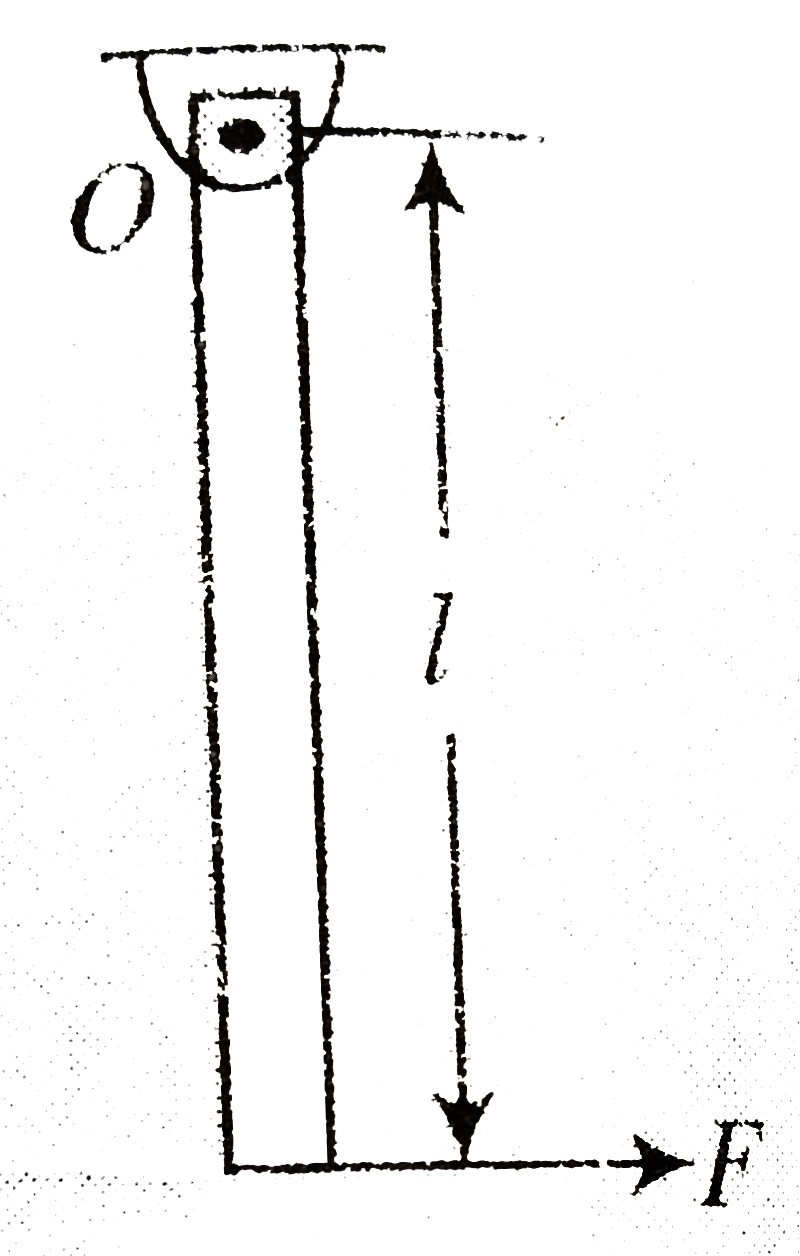

 .
.



 .
.