Three machines, A, B and C can be used to produce a product. Machine A will take 60 hours to produce a million units. Machine B is twice as fast as Machine A. Machine C will take the same amount of time to produce a million units as A and B running together. How much time will be required to produce a million units if all the three machines are used simultaneously?
12 hours
10 hours
8 hours
6 hours
The correct Answer is:B
To solve the problem step by step, let's break down the information given and calculate the required time when all three machines are used simultaneously.
Step 1: Determine the time taken by Machine A
Machine A takes 60 hours to produce a million units.
Step 2: Determine the time taken by Machine B
Machine B is twice as fast as Machine A. Therefore, the time taken by Machine B can be calculated as:
Time taken by Machine B=60 hours2=30 hours
Step 3: Determine the combined efficiency of Machines A and B
To find out how long it takes for Machines A and B to produce a million units together, we first calculate their combined work rate:
- Machine A's work rate: 160 (million units per hour)
- Machine B's work rate: 130 (million units per hour)
Now, we add their work rates:
Combined work rate of A and B=160+130
To add these fractions, we need a common denominator:
160+130=160+260=360=120
This means that A and B together can produce a million units in 20 hours.
Step 4: Determine the time taken by Machine C
Machine C takes the same amount of time to produce a million units as Machines A and B running together, which we calculated to be 20 hours.
Step 5: Calculate the combined efficiency of Machines A, B, and C
Now we need to find the time taken when all three machines are working together. The work rates of the three machines are:
- Machine A: 160
- Machine B: 130
- Machine C: 120
Now, we add these work rates:
Combined work rate of A, B, and C=160+130+120
To add these fractions, we need a common denominator. The least common multiple of 60, 30, and 20 is 60:
160+260+360=1+2+360=660=110
Step 6: Calculate the total time taken when all machines are used together
If the combined work rate of all three machines is 110, then the time taken X to produce a million units is:
1X=110⟹X=10 hours
Final Answer
The time required to produce a million units if all three machines are used simultaneously is 10 hours.
---
Machine A takes 60 hours to produce a million units.
Machine B is twice as fast as Machine A. Therefore, the time taken by Machine B can be calculated as:
Time taken by Machine B=60 hours2=30 hours
To find out how long it takes for Machines A and B to produce a million units together, we first calculate their combined work rate:
- Machine A's work rate: 160 (million units per hour)
- Machine B's work rate: 130 (million units per hour)
Combined work rate of A and B=160+130
To add these fractions, we need a common denominator:
160+130=160+260=360=120
This means that A and B together can produce a million units in 20 hours.
Machine C takes the same amount of time to produce a million units as Machines A and B running together, which we calculated to be 20 hours.
Now we need to find the time taken when all three machines are working together. The work rates of the three machines are:
- Machine A: 160
- Machine B: 130
- Machine C: 120
Combined work rate of A, B, and C=160+130+120
To add these fractions, we need a common denominator. The least common multiple of 60, 30, and 20 is 60:
160+260+360=1+2+360=660=110
If the combined work rate of all three machines is 110, then the time taken X to produce a million units is:
1X=110⟹X=10 hours
The time required to produce a million units if all three machines are used simultaneously is 10 hours.
Topper's Solved these Questions
Similar Questions
A manufacturer has three machines A,B and C installed in his factory. Machines A and B are capable of being operated for atmost 12 hours whereas machine C must be operated for atleast 5 hours a day. He produces only two items X and Y each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of X and Y on three machines are given in the following table:
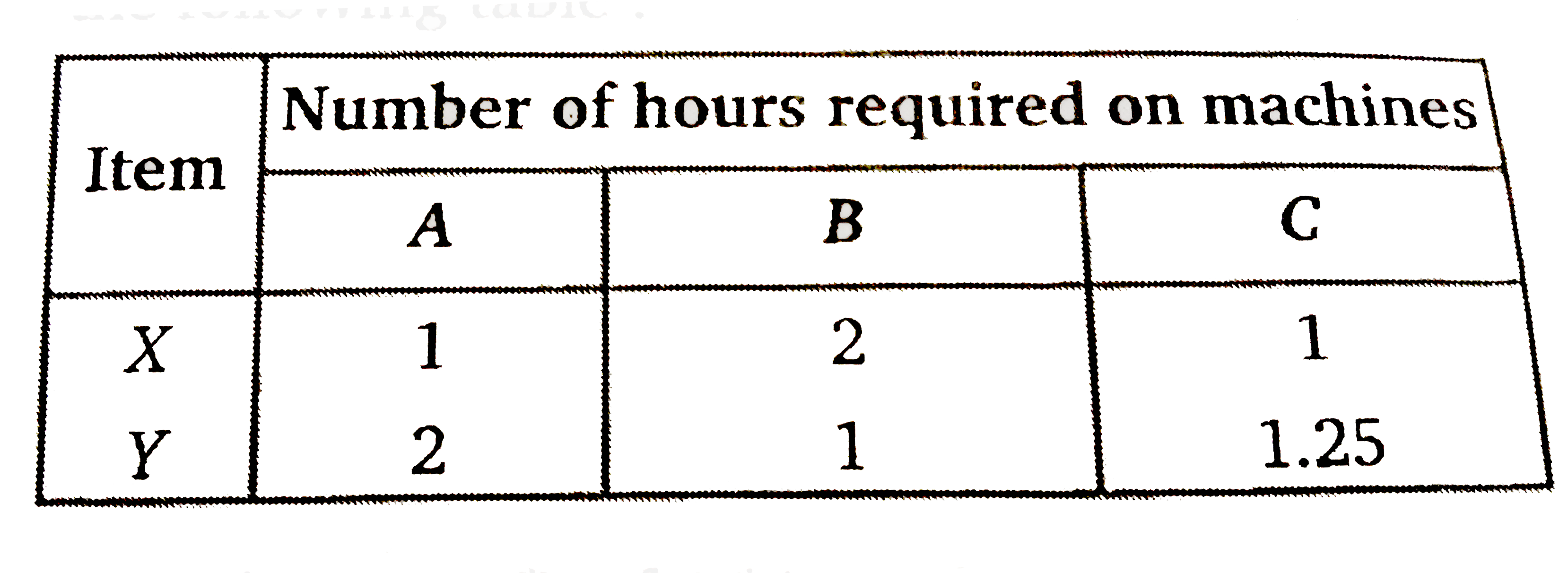
He makes a profit of Rs. 600 and Rs. 400 on each item of X and Y respectively. How many of each item should he produce so as to maximize his profit assuming that he can sell all the items that he produced?
View SolutionA factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
View Solution
Knowledge Check
A machine can increase
Adistance by decreasing forceBforce by decreasing distanceCneither distance nor forceDeither (A) or (B)Graphite powder is used in machines to
Aenhance frictionBenchance profitCreduce frictionDreduce efficiencyIf there are 3 machines A, B and C, conditions for reducing a 3machine problem to a 2 machine problem with respect to minimum processing time is…
AMinAi≥MaxBiORM∈Ci≥MaxBi,i=1,2,3…n.BMinAi≤MaxBiORMinC≤MaxBi,i=1,2,3,...n.CMaxAi≥MinBiORMaxB≥MinAi,i=1,2,3,…n.DMax Ai ≤ Min Bi OR Max B ≤ Min Ai, i=1,2,3,…n.
A factory requires 42 machines to produce a given number of articles in 56 days. How many machines would be required to produce the same number of articles in 48 days?
View Solution(Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine HI must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given m the following table:She makes a profit of Rs 600 and Rs 400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
View SolutionIn a certain factory, machines A, B and C produce bolts. Of their production. machines A. B. and c produce 2% 1 % and 3% defective bolts respectively. Machine A produces 35 % of the total output of bolts. machine B produces 25% and machine C produces 40% A bolts is chosen at random from the factory's production and is found to be defective. The probability it was produced on machine C is
View SolutionA company has a job to prepare certain number cans and there are three machines A, B and C for this job. A can complete the job in 3 days, B can complete the job in 4 days, and C can complete the job in 6 days. How many days will the company take to complete the job if all the machines are used simultaneously?
View Solution
What is the least number of machine hours required to produce 30 pieces of P and 25 pieces of Q?
View Solution
