Complete Solutions to PHYSICS of chapter ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| ARIHANT MASTER PROBLEM | PHYSICS |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass `m`. When the block is at a height `h` above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance `2h`. Find the angle by which the pulley must have rotated by this time.
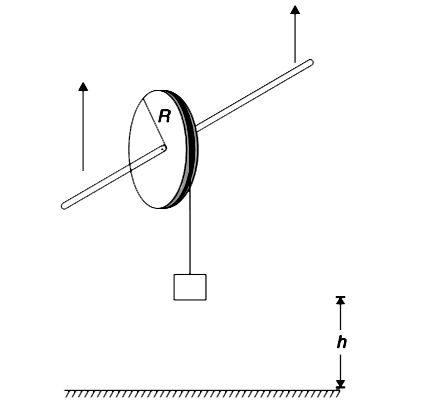 02:27View Solution
02:27View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is `V`. Then the maximum relative sped of any point on the circumference of the disc with respect to point `P` is.
 03:33View Solution
03:33View SolutionA ring is rolling, without slipping on a horizontal surface with constant velocity. Speed of point A (at the top) is `v_(A)`. After an interval `T`, the speed of point A again becomes `v_(A)`. During what fraction of the interval T speed of point A was greater than `(sqrt3)/(2) v_(A)`
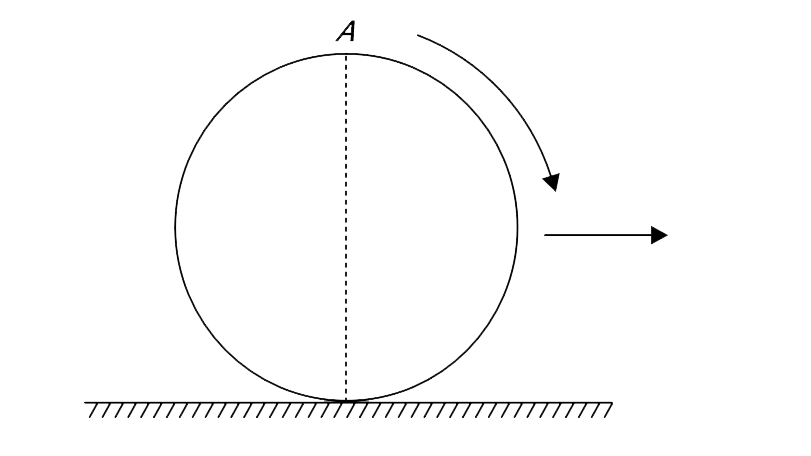 06:27View Solution
06:27View SolutionCalculate the ratio of moment of inertia of a thin uniform disc about axis 1 and 2 marked in the figure. `O` is the centre of the disc.
 05:02View Solution
05:02View SolutionA uniform circular disc has a sector of angle `90^(@)` removed from it. Mass of the remaining disc is M. Write the moment of inertia of the remaining disc about the axis `x x` shown in figure (Radius is R)
 05:12View Solution
05:12View SolutionAn Indian bread ‘‘Roti’’ is a uniform disc of mass M and radius R. Before eating a person usually folds it about its diameter (say about x axis). After folding it a sector of angle `60^(@)` is removed from it. Find the moment of inertia of the remaining ‘‘Roti’’ about Z-axis
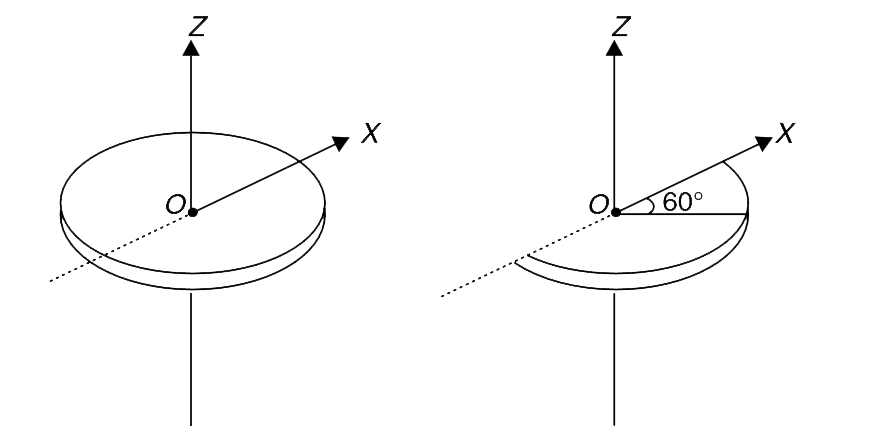 02:25View Solution
02:25View SolutionA uniform rectangular plate has side length `l` and `2 l`. The plate is in `x - y` plane with its centre at origin and sides parallel to x and y axes. The moment of inertia of the plate about an axis passing through a vertex (say A) perpendicular to the plane of the figure is `I_(0)`. Now the axis is shifted parallel to itself so that moment of inertia about it still remains `I_(0)`. Write the locus of point of intersection of the axis with `xy` plane
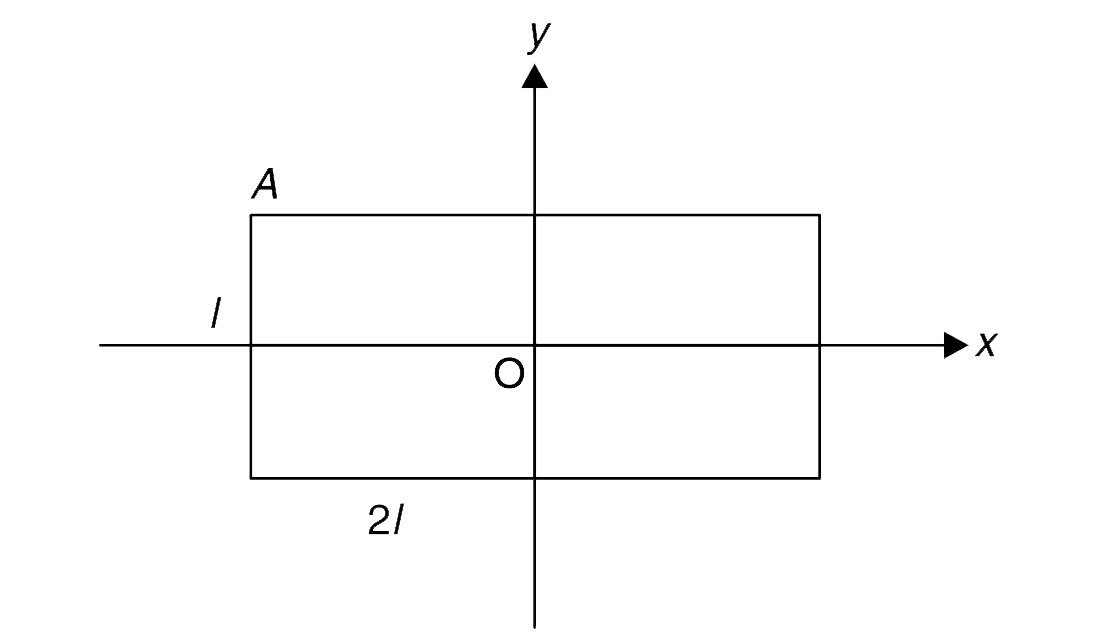 05:45View Solution
05:45View SolutionA thin semi circular cylindrical shell has mass M and radius R. Find its moment of inertia about a line passing through its centre of mass parallel to the axis (shown in figure) of the cylinder.
 02:04View Solution
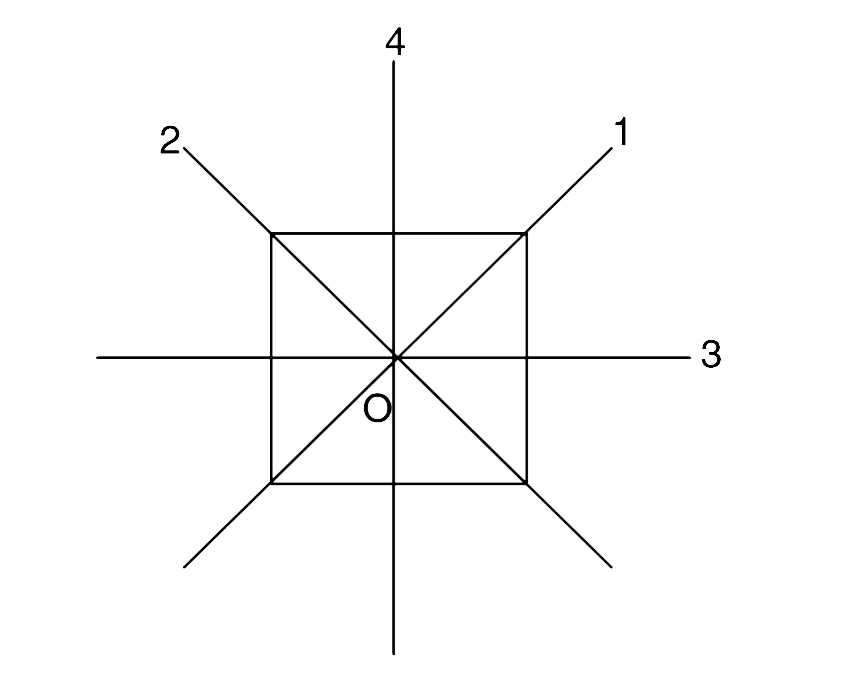
02:04View SolutionConsider a uniform square plate shown in the figure. `I_(1), I_(2), I_(3)` and `I_(4)` are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) `I_(3) + I_(4)`
(b) `I_(1) + I_(3)`
(c) `I_(2) + I_(3)`
(d) `(1)/(2) (I_(1) + I_(2) + I_(3) + I_(4))`
 03:10View Solution
03:10View SolutionAn asteroid in the shape of a uniform sphere encounters cosmic dust. A thin uniform layer of dust gets deposited on it and its mass increases by `2%`. Find percentage change in its moment of inertia about diameter
02:19View Solution(i) Consider an infinitesimally thin triangular strip having mass M and length L. Find the moment of inertia of the strip about on axis passing through its tip and perpendicular to the plane. Compare the result with moment of inertia of a uniform disc of mass M and radius L about an axis passing through its centre and perpendicular to the plane the disc. Why the two expressions are same?

(ii) A circular fan made of paper is in shape of a disc of radius R. The fan can be folded (various stages shown in figure `(a)` through `(f))` to the shape of a thin stick. The moment of inertia of the circular fan about an axis passing through centre O and perpendicular to the plane of the figure is `I_(0) = (1)/(2) MR^(2)` where `M =` mass of the fan.

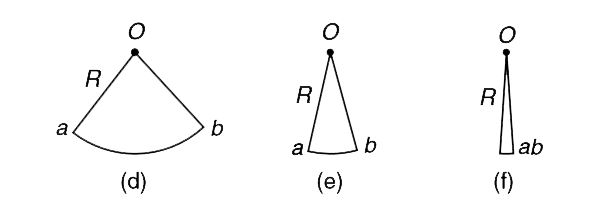
(a) How does the moment of inertia (I), about an axis perpendicular to the plane of the figure passing through O, change as the fan is folded through stage a to b to c to d to e?
(b) When the fan is completely folded in the shape of a stick (fig. `(f))`, write its moment of inertia about the above mentioned axis.
Note : Moment of inertia of a uniform rod about an axis through its end and perpendicular to it is `(ML^(2))/(3)`View SolutionA uniform rectangular plate has moment of inertia about its longer side, equal to I. The moment of inertia of the plate about an axis in its plane, passing through the centre and parallel to the shorter sides is also equal to I. Find its moment of inertia about an axis passing through its centre and perpendicular to its plane.
04:32View SolutionA uniform rectangular plate has been bent as shown in the figure. The two angled parts of the plate are of identical size. The moment of inertia of the bent plate about axis xx is I. Find its moment of inertia about an axis parallel to `x x` and passing through the centre of mass of the plate.
 10:30View Solution
10:30View SolutionThree identical rings each of mass M and radius R are welded together with their planes mutually perpendicular to each other. Ring A is vertical and B is also vertical in a plane perpendicular to A. Ring C is in horizontal plane. Find moment of Inertia of this system about a horizontal axis perpendicular to the plane of the figure passing through point P (top point of ring A)
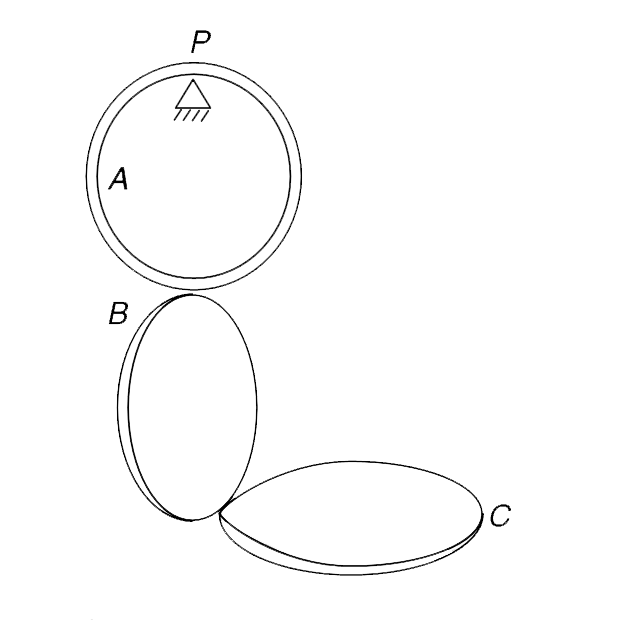 04:08View Solution
04:08View SolutionDetermine the moment of inertia of the shaded area about `y` axis. The mass of the shaded area is `M`.
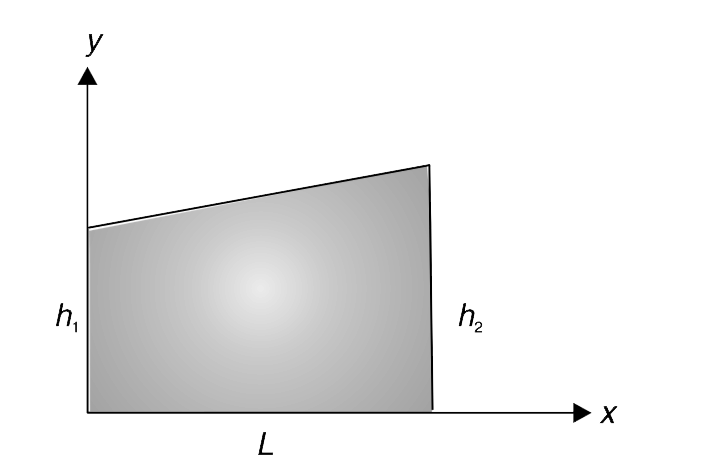 05:52View Solution
05:52View SolutionTwo uniform semicircular discs, each of radius `R`, are stuck together to form a disc. Masses of the two semicircular parts are `M` and `3M`. Find the moment of inertia of the circular disc about an axis perpendicular to its plane and passing through its centre of mass.
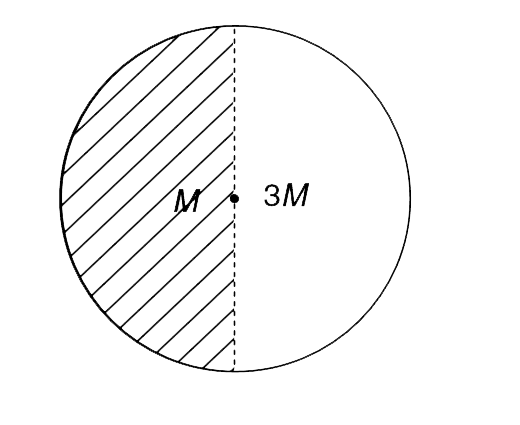 06:11View Solution
06:11View SolutionA stick AB of mass M is tied at one end to a light string OA. A horizontal force `F = Mg` is applied at end B of the stick and its remains in equilibrium in position shown. Calculate angles `alpha` and `beta`.
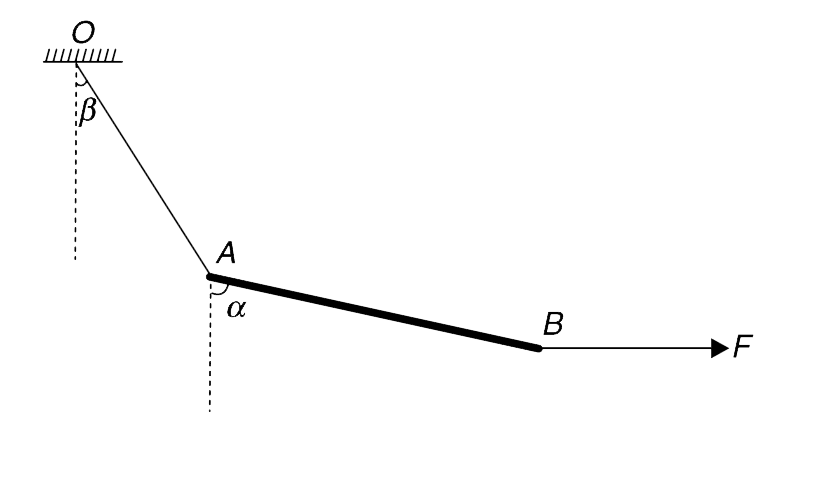 06:32View Solution
06:32View SolutionWhen brakes are applied on a moving car, the car dips to the front. Why ? [That is try to show that front wheels are more pressed as compared to rear ones when the brakes are applied]. Assume that centre of mass of the car is equidistant from the front and rear wheels.
03:59View SolutionA uniform wire has been bent in shape of a semi circle. The semicircle is suspended about a horizontal axis passing through one of its ends, so that the semicircular wire can swing in vertical plane. Find the angle `alpha` that the diameter of the semicircle makes with vertical in equilibrium.
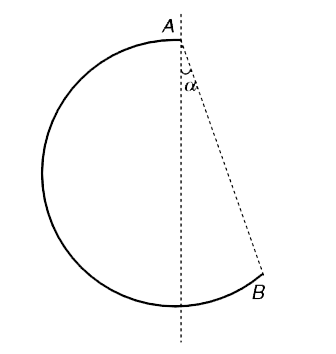 05:57View Solution
05:57View SolutionA uniform cylindrical body of radius r has a conical nose. The length of the cylindrical and conical parts are `4r` and `3r` respectively. Mass of the conical part is M. The body rests on a horizontal surface as shown. A ring of radius `(r)/(2)` is to be tightly fitted on the nose of the body. What is maximum permissible mass of the ring so that the body does not topple?
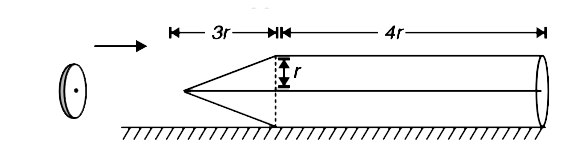 05:51View Solution
05:51View SolutionThere is a step of height `h` on an incline plane. The step prevents a ball of radius R from rolling down.
(a) If the inclination `(theta)` of the incline is increased gradually, at what value of `theta` the ball will just manage to climb the step?

(b) Does the gravitational potential energy of the ball increases or decreases as it climbs the step ?04:44View SolutionThe centre of mass of an inhomogeneous sphere is at a distance of 0.3 R from its geometrical centre. R is the radius of the sphere. Find the maximum inclination `(theta)` of an incline plane on which this sphere can be placed in equilibrium. Assume that friction is large enough to prevent slipping.
03:25View SolutionRectangular block B, having height `h` and width `d` has been placed on another block A as shown in the figure. Both blocks have equal mass and there is no friction between A and the horizontal surface. A horizontal time dependent force `F = kt` is applied on the block A. At what time will block B topple? Assume that friction between the two blocks is large enough to prevent B from slipping.
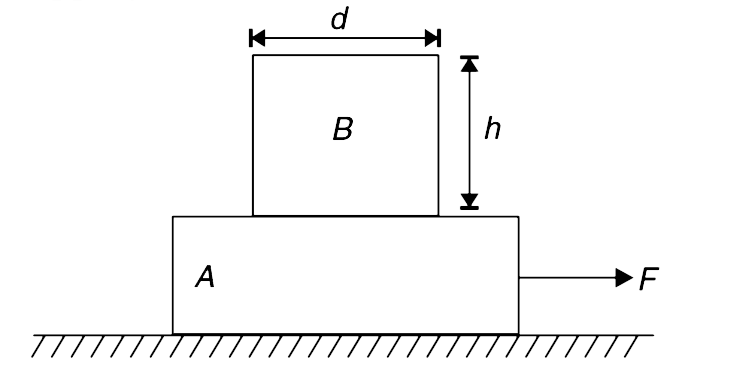 03:06View Solution
03:06View SolutionA cylinder C rests on a horizontal surface. A small particle of mass m is held in equilibrium connected to an overhanging string as shown. The other end of the mass less string is being pulled horizontally by a force F as shown. Find F.
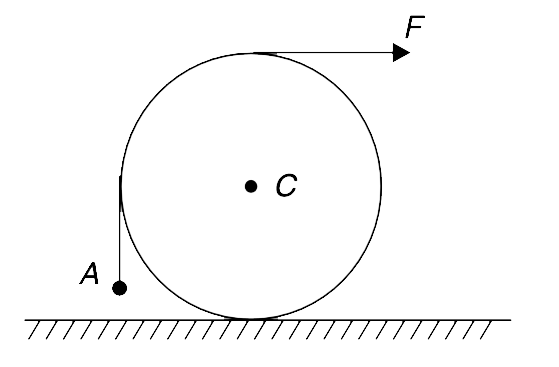 05:58View Solution
05:58View SolutionA hollow cylindrical pipe of mass M and radius R has a thin rod of mass m welded inside it, along its length. A light thread is tightly wound on the surface of the pipe. A mass `m_(0)` is attached to the end of the thread as shown in figure. The system stays in equilibrium when the cylinder is placed such that `alpha = 30^(@)` The pulley shown in figure is a disc of mass `(M)/(2)`
(a) Find the direction and magnitude of friction force acting on the cylinder.
(b) Express mass of the rod ‘m’ in terms of `m_(0)`
 04:32View Solution
04:32View SolutionA sphere of radius R is supported by a rope attached to the wall. The rope makes an angle `theta = 45^(@)` with respect to the wall. The point where the rope is attached to the wall is at a distance of `(3R)/(2)` from the point where the sphere touches the wall. Find the minimum coefficient of friction `(mu)` between the wall and the sphere for this equilibrium to be possible.
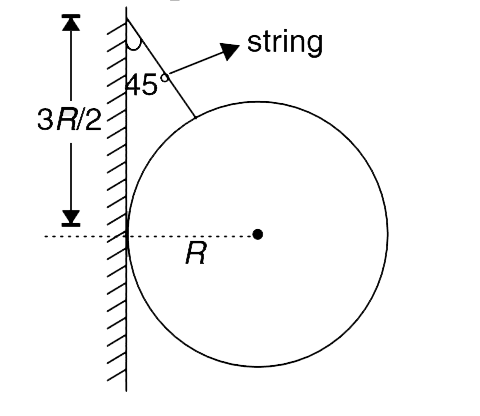 View Solution
View SolutionA uniform rod has mass M and length `4L`. It rests in equilibrium with one end on a rough horizontal surface at A. At point B, at a distance `3L` from A, it is supported by a fixed smooth roller. The rod just remains in equilibrium when `theta = 30^(@)`
(a) Find the normal force applied by the horizontal surface on the rod at point A.
(b) Find the coefficient of friction between the rod and the surface.
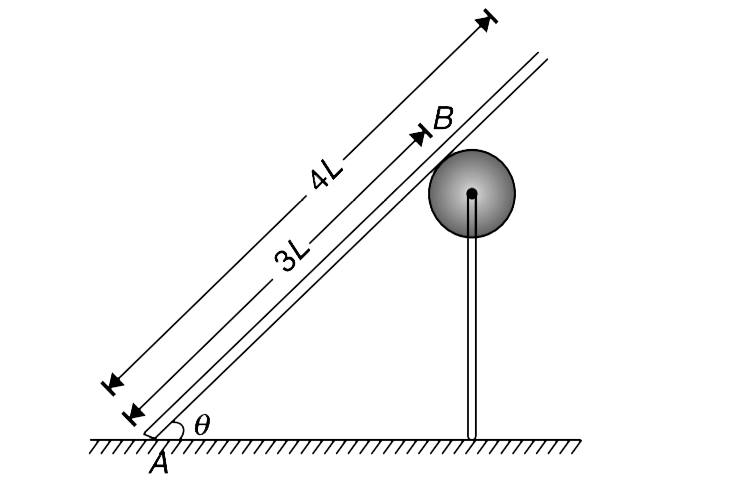 View Solution
View SolutionA wheel is mounted on frictionless central pivot and it can rotate freely in the vertical plane. There is a horizontal light rod fixed to the wheel below the pivot. There is a small sleeve of mass m which can slide along the rod without friction. The sleeve is connected to a light spring. The other end of the spring is fixed to the rim as shown. The sleeve is at the centre of the rod and the spring is relaxed. Now the wheel is held at rest and the sleeve is moved towards left so as to compress the sprig by some distance. The sleeve and the wheel are released simultaneously from this position.
(a) Is it possible that the wheel does not rotate as the sleeve perform SHM on the rod ?
(b) Find the value of spring constant `k` for situation described in (a) to be possible. The distance of rod from centre of the wheel is `d`.
 03:25View Solution
03:25View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed `omega`.
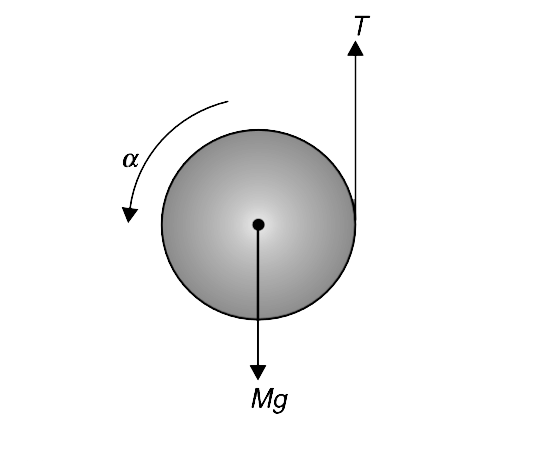 07:23View Solution
07:23View SolutionA mass less string is wrapped around a uniform disc of mass m and radius `r`. The string passes over a mass less pulley and is tied to a block of mass M at its other end (see figure). The system is released from rest. Assume that the string does not slip with respect to the disc.
(a) Find the acceleration of the block for the case `M = m`
(b) Find `(M)/(m)` for which the block can accelerate upwards.
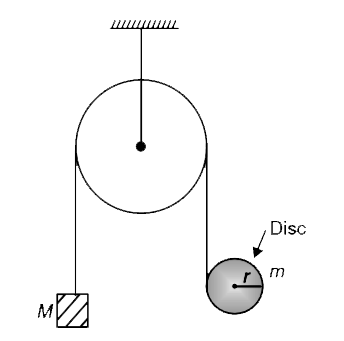 05:51View Solution
05:51View SolutionA solid uniform sphere of mass M and radius R can rotate about a fixed vertical axis. There is no frictional torque acting at the axis of rotation. A light string is wrapped around the equator of the sphere. The string has exactly 6 turns on the sphere. The string passes over a light pulley and carries a small mass m at its end (see figure). The string between the sphere and the pulley is always horizontal. The system is released from rest and the small mass falls down vertically. The string does not slip on the sphere till 5 turns get unwound. As soon as `5^(th)` turn gets unwound completely, the friction between the sphere and the string vanishes all of a sudden.
(a) Find the angular speed of the sphere as the string leaves it.
(b) Find the change in acceleration of the small mass `m` after 5 turns get unwound from the sphere.
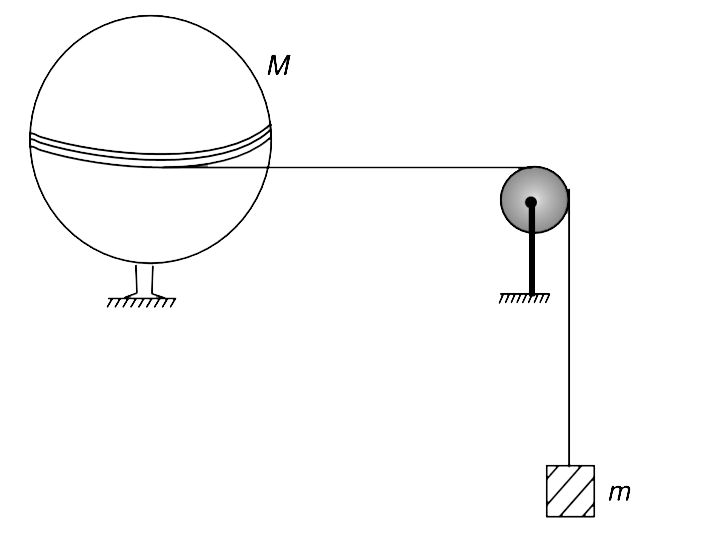 06:41View Solution
06:41View SolutionA disc of mass `m` and radius R lies flat on a smooth horizontal table. A mass less string runs halfway around it as shown in figure. One end of the string is attached to a small body of mass `m` and the other end is being pulled with a force F. The circumference of the disc is sufficiently rough so that the string does not slip over it. Find acceleration of the small body.
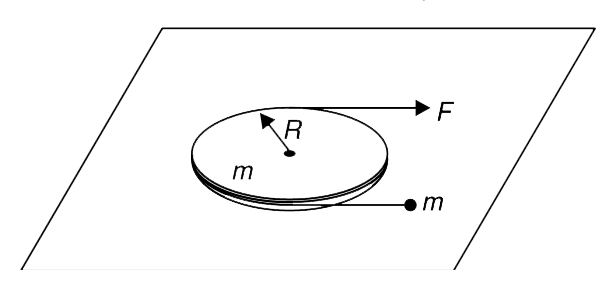 03:36View Solution
03:36View SolutionA uniform quarter circular thin rod of mass M and radius R is pivoted at a point B on the floor. It can rotate freely in the vertical plane about B. It is supported by a smooth vertical wall at its other free end A so that it remains at rest. Find the reaction force of wall on the rod.
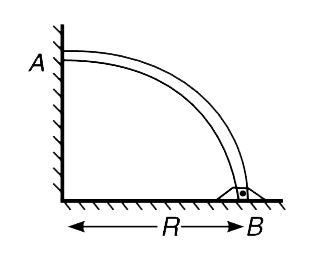 01:57View Solution
01:57View SolutionA ball is rolling without sliding down an incline. Is the force applied by the ball on the incline larger than or less than its (ball’s) own weight ?
02:14View SolutionA solid sphere of mass M and radius R is covered with a thin shell of mass M. There is no friction between the inner wall of the shell and the sphere. The ball is released from rest, and then it rolls without slipping down an incline that is inclined at an angle `theta` to the horizontal. Find the acceleration of the ball.
04:17View SolutionA homogeneous solid sphere of radius R is resting on a horizontal surface. It is set in motion by a horizontal impulse imparted to it at a height h above the centre. If `h` is greater than `h_(0)`, the velocity of the sphere increases in the direction of its motion after the start. If `h lt h_(0)` the velocity decreases after the start. Find `h_(0)`
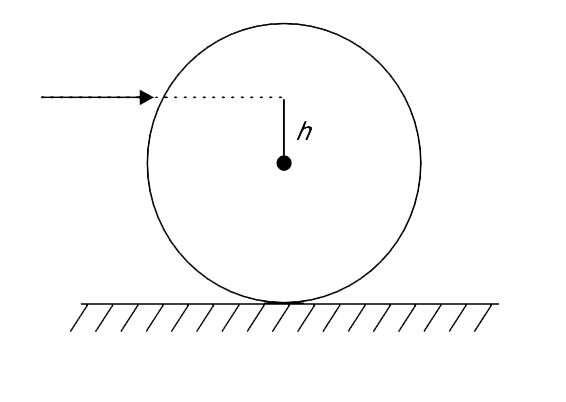 05:37View Solution
05:37View SolutionA boy pushes a cylinder of mass M with the help of a plank of mass `m` as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
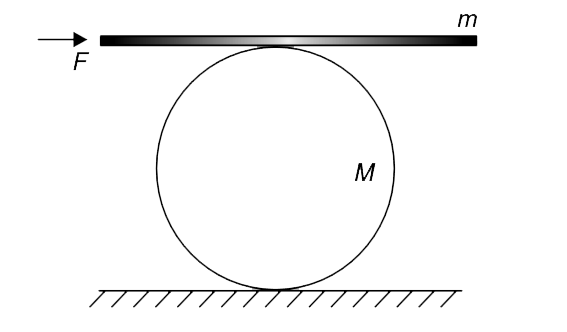 06:14View Solution
06:14View Solution(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A `(V_(A) = V_(0))` as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
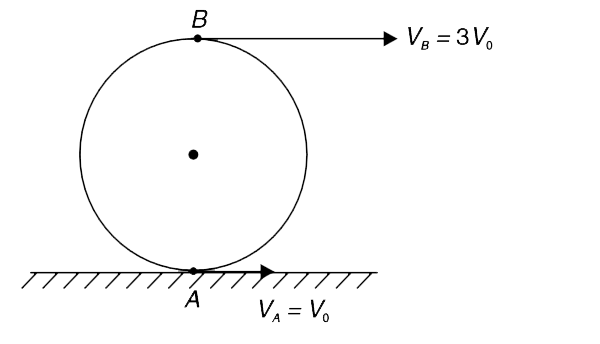
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity `V_(0)` towards right and its angular velocity being `omega_(0)` (in anticlockwise sense). Find the required relationship between `V_(0)` and `omega_(0)` so that -
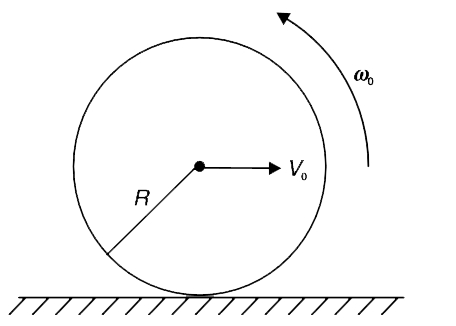
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.06:01View SolutionA thin pencil of mass M and length L is being moved in a plane so that its centre (i.e. centre of mass) goes in a circular path of radius R at a constant angular speed `omega`. However, the orientation of the pencil does not change in space. Its tip (A) always remains above the other end (B) in the figure shown
(a) Write the kinetic energy of the pencil.
(b) Find the magnitude of net force acting on the pencil.
 01:44View Solution
01:44View SolutionIn figure (a) there is a uniform cylinder of mass M and radius R. Length of the cylinder is `L = sqrt3R`. The cylinder is rolling without sliding on a horizontal surface with its centre moving at speed V. In figure (b) the same cylinder is moving on a horizontal surface with its centre moving at speed V and the cylinder rotating about a vertical axis passing through its centre. [Place your pencil on the table and give a sharp blow at its end. Look at the motion of the pencil. This is how the cylinder is moving]. The angular speed is `omega = (V)/(R)`. Write the kinetic energy of the cylinder in two cases. In which case, the kinetic energy would have been higher if length of the cylinder were doubled `(= 2 sqrt3 R)`.
(a) 04:02View Solution
04:02View SolutionThere is a fixed hollow cylinder having smooth inner surface. Radius of the cylinder is `R = 4m`. A uniform rod of `M = 4kg` and length `L = 4m` is released from vertical position inside the cylinder as shown in the figure. Convince yourself that the rod will perform pure rotation about the axis of the cylinder passing through O. Fid the angular speed of the rod when its becomes horizontal.
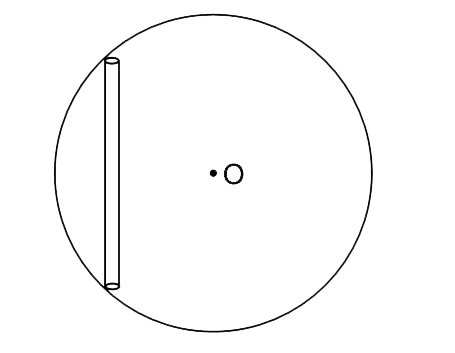 05:29View Solution
05:29View SolutionA disc shaped body has two tight windings of light threads - one on the inner rim of radius `R = 1m` and the other on outer rim of radius `2R` (see figure). It is kept on a horizontal surface and the ends of the two threads are pulled horizontally in opposite directions with force of equal magnitude `F = 20N`. Mass of the body and its moment of inertia about an axis through centre O and perpendicular to the plane of the figure are `M = 4kg` and `I = 8 kg - m^(2)` respectively. Find the kinetic energy of the body 2 seconds after the forces begin to act, if
(i) the surface is smooth,
(ii) the surface is rough enough to ensure rolling without sliding.
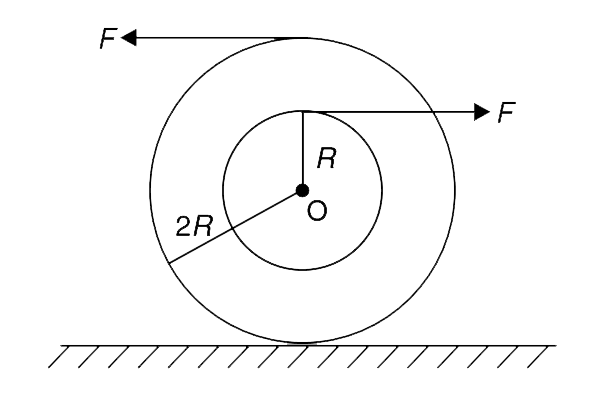 05:52View Solution
05:52View SolutionA uniform square plate has mass M and side length a. It is made to oscillate in vertical plane in two different ways shown in figure (A) and (B). In figure (A), the plate is hinged at its upper corners with the help of two mass less rigid rods each of length `a`. The rods can rotate freely about both ends.
(a)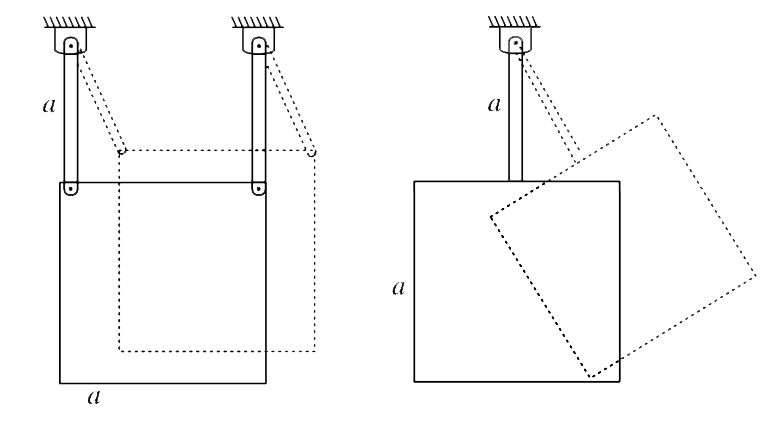
(b)
In figure (B) the plate is rigidly connected at the centre of its top edge to a mass less rod of length `a`. The rod can rotate about its upper end only. In both cases the plate is pushed from its equilibrium position so that centre of mass of the plate acquires a speed V. In which case will the centre of mass of the plate rise to a greater height. There is no friction.04:40View SolutionA thin carpet of mass `2m` is rolled over a hollow cylinder of mass `m`. The cylinder wall is thin and radius of the cylinder is R. The carpet rolled over it has outer radius 2R (see figure). This roll is placed on a rough horizontal surface and given gentle push so that the carpet begins to roll and unwind. Friction is large enough to prevent any slipping of the carpet on the floor. Also assume that the carpet does not slip on the surface of the cylinder. The entire carpet is laid out on the floor and the hollow cylinder rolls out with speed V. Find V.
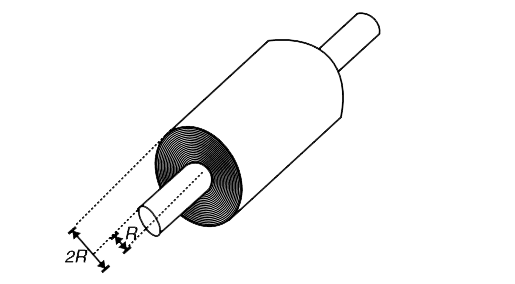 05:15View Solution
05:15View SolutionA uniform rod of mass M is moving in a plane and has a kinetic energy of `(4)/(3) MV^(2)` where V is speed of its centre of mass. Find the maximum and minimum possible speed of the end point of the rod.
03:02View SolutionThe propeller of a small airplane is mounted in the front. The propeller rotates clockwise if seen from behind by the pilot. The plane is flying horizontally and the pilot suddenly turns it to the right. Will the body of the plane have a tendency to get inclined to the horizontal? If yes, does the nose of the plane veer upward or downward? Why?
View SolutionA massive star is spinning about its diameter with an angular speed `omega_(0) = (pi)/(1000)` rad/day. After its fuel is exhausted, the star collapses under its own gravity to form a neutron star. Assume that the volume of the star decreases to `10^(-12)` times the original volume and its shape remains spherical. Assuming that density of the star is uniform, find the angular speed of the neutron star.
04:26View SolutionA square plate of side length `2m` has a groove made in the shape of two quarter circles joining at the centre of the plate. The plate is free to rotate about vertical axis passing through its centre. The moment of inertia of the plate about this axis is `4 kg - m^(2)`. A small block of mass 1 kg enters the groove at end A travelling with a velocity of `2//s` parallel to the side of the square plate. The block move along the frictionless groove of the horizontal plate and comes out at the other end B with speed V. Find V assuming that width of the groove is negligible.
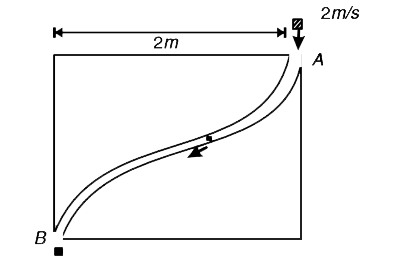 View Solution
View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance `(R)/(2)` from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
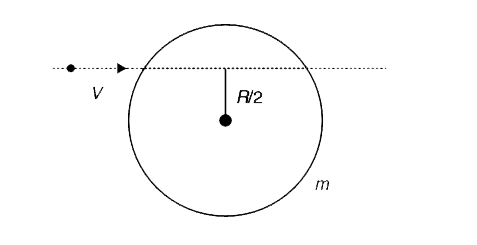 05:50View Solution
05:50View SolutionA disc of mass M and radius R is rotating with angular velocity `omega_(0)` about a vertical axis passing through its centre (O). A man of mass `(M)/(2)` and height `(R)/(2)` is standing on the periphery. The man gradually lies down on the disc such that his head is at a distance `(R)/(2)` from the centre and his feet touching the edge of the disc. For simplicity assume that the man can be modelled as a thin rod of length `(R)/(2)`. Calculate the angular speed `(omega)` of the platform after the man lies down.
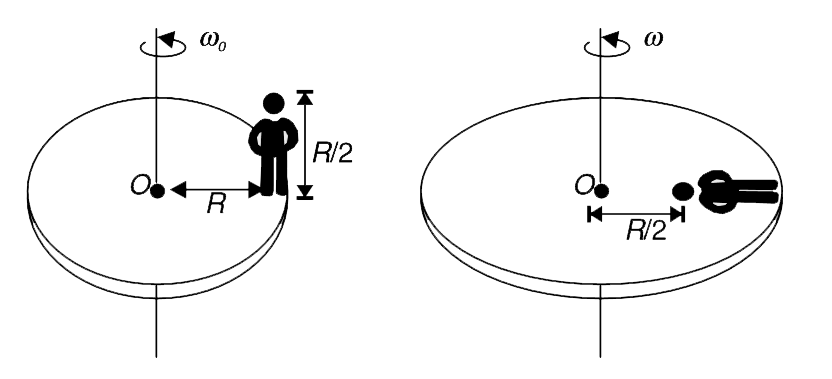 View Solution
View SolutionA uniform block of mass M and dimensions as shown in the figure is placed on a rough horizontal surface and given a velocity `V_(0)` to the right. A is a point on the surface to the left of the block.
(a) Write the angular momentum of the block about point A just after it begins to move
(b) Due to friction the block stops. What happened to its angular momentum about point A? Which torque is responsible for change in angular momentum of the block?
 View Solution
View SolutionABCFED is a uniform plate (shown in figure). ABC and DEF are circular arcs with common centre at O and having radii `a` and `2a` respectively. This plate is lying on a smooth horizontal table. A particle of mass half the mass of the plate strikes the plate at point A while travelling horizontally along the `x` direction with velocity `u`. The particle hits the plate and rebounds along negative `x` with velocity `(u)/(2)` . Find the velocity of point D of the plate immediately after the impact. [Take `(28)/(9 pi) cong 1` ]
 View Solution
View SolutionA uniform rod of mass `m` and length L is fixed to an axis, making an angle `theta` with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?
 05:45View Solution
05:45View SolutionA mass m in attached to a mass less string and swings in a horizontal circle, forming a conical pendulum, as shown in the figure. The other end of the string passes through a hole in the table and is dragged slowly so as to reduce the length `l`. The string is slowly drawn up so that the depth `h` shown in the figure becomes half. By what factor does the radius `(r)` of the circular path of the mass `m` change?
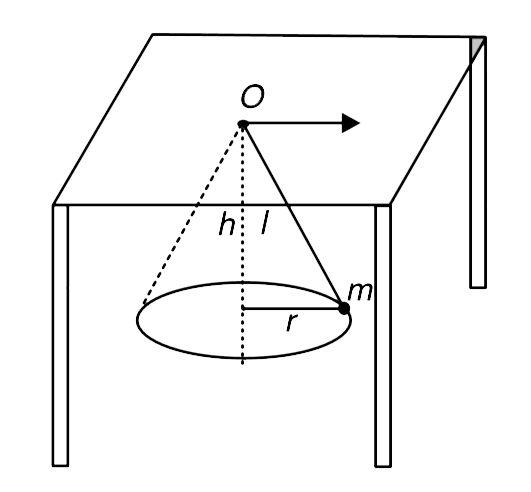 View Solution
View SolutionA flat rigid body is moving in `x – y` plane on a table. The plane of the body lies in the `x – y` plane. At an instant it was found that some of the velocity components of its three particles A, B and C were `V_(Ax) = 4 m//s, V_(Bx) = 3 m//s` and `V_(cy) = - 2 m//s`, respectively. At the instant the three particles A, B and C were located at (0,0) (3,4) , (4,3) (all in meter ) respectively in a co-ordinate system attached to the table.
(a) Find the velocity of A, B and C
(b) Find the angular velocity of the body.
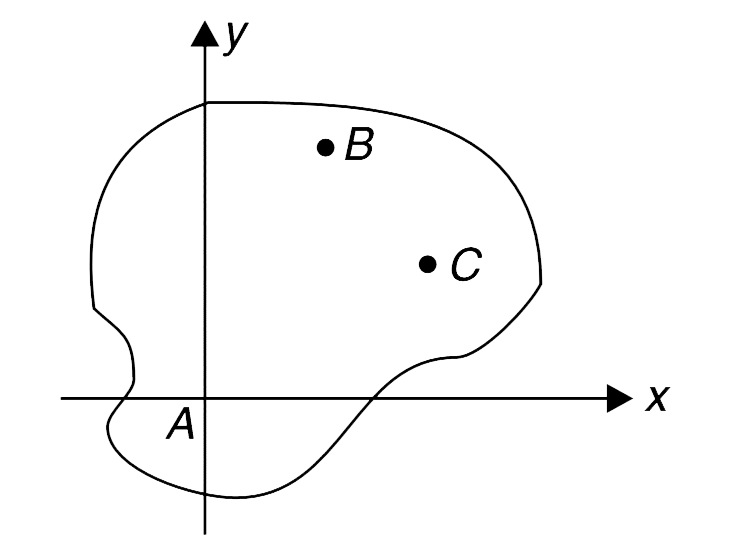 View Solution
View SolutionA wheel is rolling without sliding on a horizontal surface. Prove that velocities of all points on the circumference of the wheel are directed towards the top most point of the wheel.
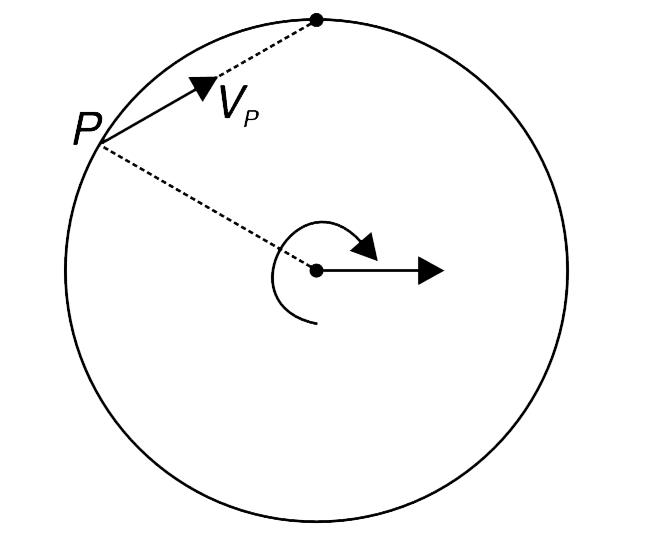 04:25View Solution
04:25View SolutionThere is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length `2R` leans against it as shown. At the instant shown, `theta = 30^(@)` and the right end of the rod is sliding with velocity `v`.
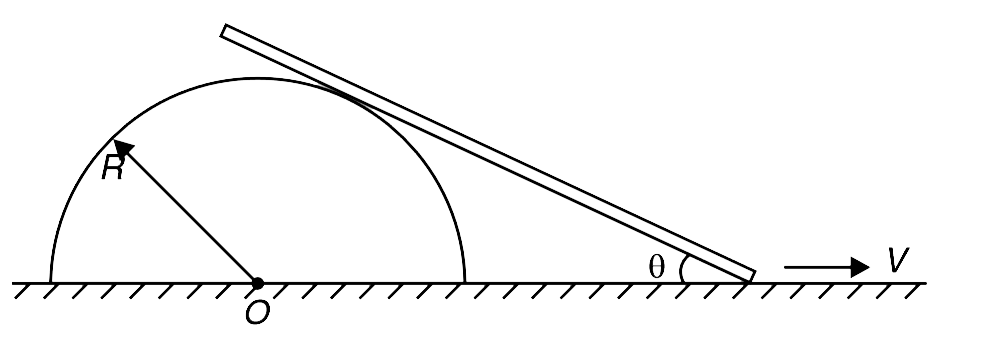
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.View SolutionA disc of radius R is rolling without sliding on a horizontal surface at a constant speed of `v`

(a) What is speed of points A and B on the vertical diameter of the disc ? Given `AB = (R)/(2)`
(b) After what time, for the first time, speed of point A becomes equal to present speed (i.e., the speed at the instant shown in the figure) of point B?07:34View SolutionA uniform disc of radius `R = 2 sqrt3 m` is moving on a horizontal surface without slipping. At some instant its angular velocity is `omega = 1` rad/s and angular acceleration is a `alpha = sqrt3 "rad"//s^(2)`.

(a) Find acceleration of the top point A.
(b) Find acceleration of contact point B.
(c) Find co - oridnates `(r , theta)` for a point P which has zero acceleration09:19View SolutionA convex surface has a uniform radius of curvature equal to 5R. A wheel of radius R is rolling without sliding on it with a constant speed `v`. Find the acceleration of the point (P) of the wheel which is in contact with the convex surface.
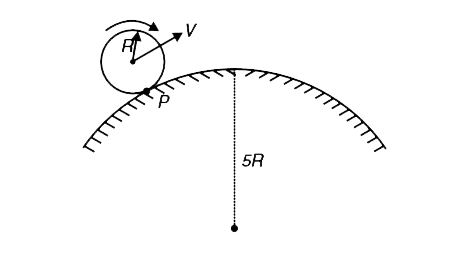 04:18View Solution
04:18View SolutionAB is a non uniform plank of length `L = 4R` with its centre of mass at C such that `AC = R`. It is placed on a step with its one end A supported by a cylinder of radius R as shown in figure. The centre of mass of the plank is just outside the edge of the step. The cylinder is slowly rolled on the lower step such that there is no slipping at any of its contacts. Calculate the distance through which the centre of the cylinder moves before the plank loses contact with the horizontal surface of the upper step.
 View Solution
View SolutionA wheel of radius R is rolling without sliding uniformly on a horizontal surface. Find the radius of curvature of the path of a point on its circumference when it is at highest point in its path.
03:53View SolutionA wall is inclined to a horizontal surface at an angle of `120^(@)` as shown. A rod AB of length `L = 0.75 m` is sliding with its two ends A and B on the horizontal surface and on the wall respectively. At the moment angle `theta = 20^(@)` (see figure), the velocity of end A is `v_(A) = 1.5` m/s towards right. Calculate the angular speed of the rod at this instant. [Take `cos 40^(@) = 0.766` ]
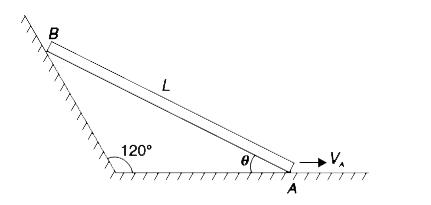 05:28View Solution
05:28View SolutionIn the figure the plank resting on two cylinders is horizontal. The plank is pulled to the right such that the centre of smaller cylinder moves with a constant velocity `v`. Friction is large enough to prevent slipping at all surfaces. Find-
(a) The velocity of the centre of larger cylinder.
(b) The ratio of accelerations of the points of contact of the two cylinders with the plank.
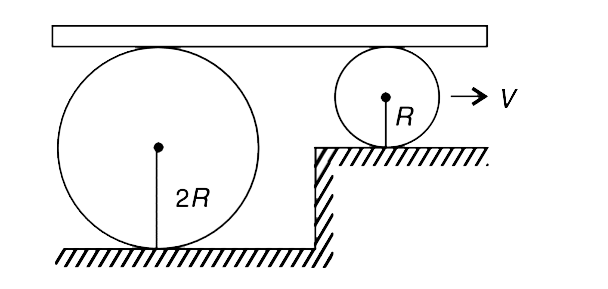 04:26View Solution
04:26View SolutionA wire of linear mass density `lambda (kg//m)` is bent into an arc of a circle of radius R subtending an angle `2 theta_(0)` at the centre. Calculate the moment o inertia of this circular arc about an axis passing through its midpoint (M) and perpendicular to its plane.
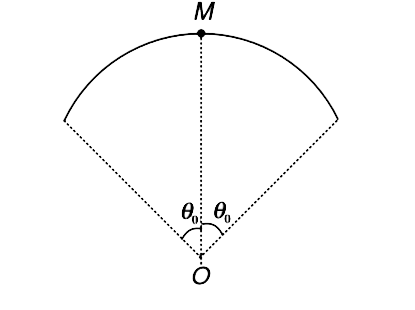 View Solution
View SolutionA metallic plate has been fabricated by welding two semicircular discs - `D_(1)` and `D_(2)` of radii R and `(R)/(2)` respectively (fig. a). O and O' are the centre of curvature of the two discs and each disc has a mass 6m. The plate is in `xy` plane. Now the plate is folded along the y axis so as to bring the part OAB in `yz` plane. (fig. b). The plate is now set free to be able to rotate freely about the z – axis. A particle of mass `m`, moving with a velocity `v` in the `xy` plane along the line `x = d` hits the plate and sticks to it `(d lt R)` . Just before collision speed of the particle was v.
(a)
(a) Find the moment of inertia of inertia of the plate about z axis.
(b) Find the angular speed of the plate after collision.View SolutionThere is a square plate of side length a. It is divided into nine identical squares each of side `(a)/(3)` and the central square is removed (see fig. (i)). Now each of the remaining eight squares of side length `(a)/(3)` are divided into nine identical squares and central square is removed from each of them (see fig. (ii)).
(a)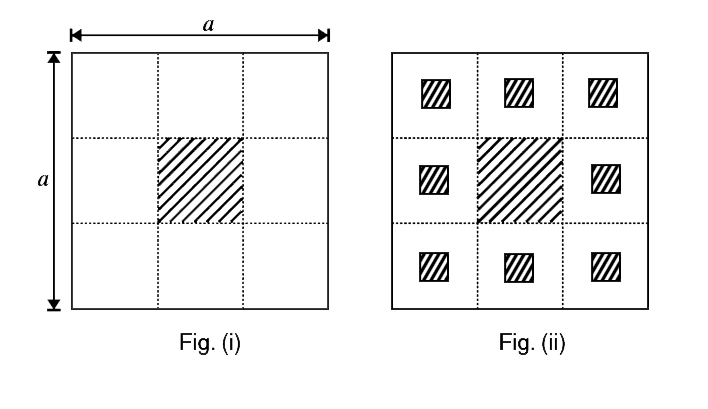
Mass of the plate with one big and eight small holes is M. Find its moment of inertia about an axis passing through its centre and perpendicular to its plane.10:51View SolutionABC is an isosceles triangle right angled at A. Mass of the triangular plate is M and its equal sides are of length `a`. Find the moment of inertia of this plate about an axis through A perpendicular to the plane of the plate. Use the expression of moment of inertia for a square plate that you might have studied.
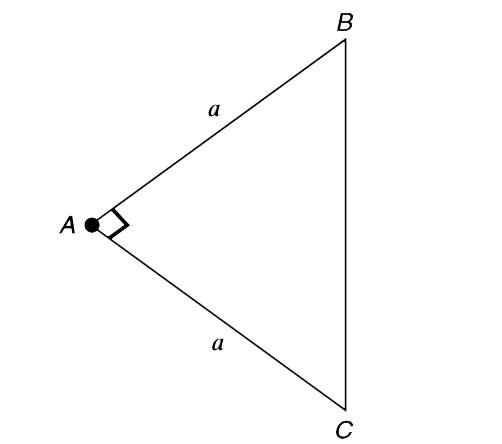 02:45View Solution
02:45View SolutionThe triangular plate described in the last question has angle `lt A = theta`. Now find its moment of inertia about an axis through A perpendicular to the plane of the plate.
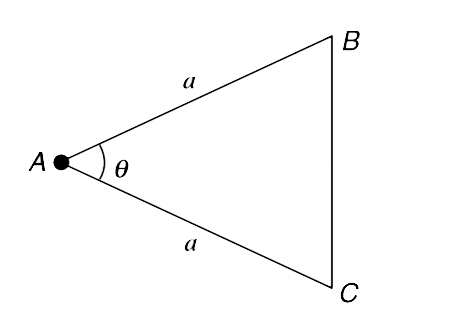 06:52View Solution
06:52View SolutionA thin uniform spherical shell of radius R is bored such that the axis of the boring rod passes through the centre of the sphere. The boring rod is a cylinder of radius `(R)/(2)`. Take the mass of the sphere before boring to be M.
(a) Find the mass of the leftover part
(b) Find the moment of inertia of the leftover part about the axis shown.
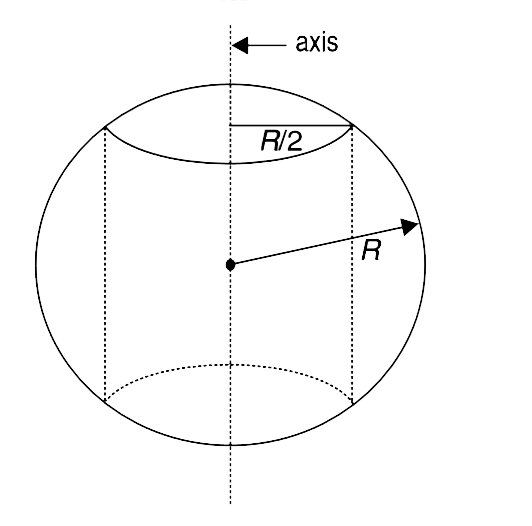 06:34View Solution
06:34View SolutionConsider an equilateral prism as shown in the figure. The mass of the prism is M and length of each side of its cross section is `a`. Find the moment of inertia of such a prism about the central axis shown.
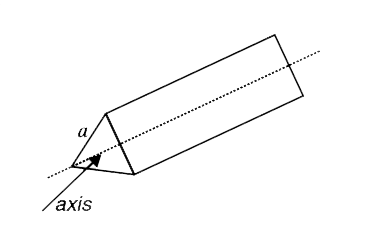 07:21View Solution
07:21View SolutionIn the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string.
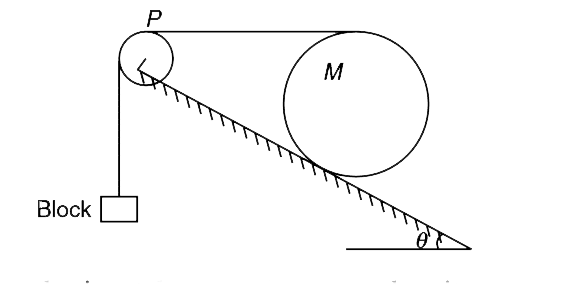 05:09View Solution
05:09View SolutionA horizontal stick of mass m has its right end attached to a pivot on a wall, while its left end rests on the top of a cylinder of mass `m` which in turn rests on an incline plane inclined at an angle `theta`. The stick remains horizontal. The coefficient of friction between the cylinder and both the plane and the stick is `mu`. Find the minimum value of `mu` as function of `theta` for which the system stays in equilibrium.
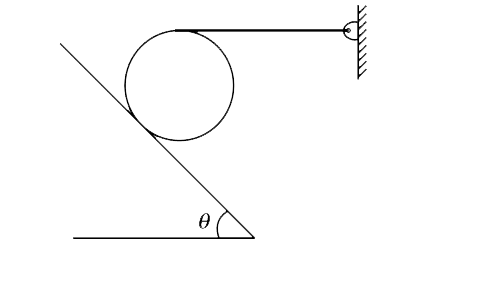 View Solution
View SolutionConsider the object shown in the figure. It consist of a solid hemisphere of mass M and radius R. There is a solid rod welded at its centre. The object is placed on a flat surface so that the rod is vertical. Mass of the rod per unit length is `(M)/(2R)`. What is the maximum length of the rod that can be welded so that the object can perform oscillations about the position shown in diagram?
Note : Centre of mass of a solid hemisphere is at a distance of `(3R)/(8)` from its base.
 View Solution
View SolutionTwo cylinders A and B have been placed in contact on an incline. They remain in equilibrium. The dimensions of the two cylinders are same. Which cylinder has larger mass?
 View Solution
View SolutionThe ladder shown in the figure is light and stands on a frictionless horizontal surface. Arms AB and BC are of equal length and M and N are their mid points. Length of MN is half that of AB. A man of mass M is standing at the midpoint of BM. Find the tension in the mass less rod MN. Consider the man to be a point object.
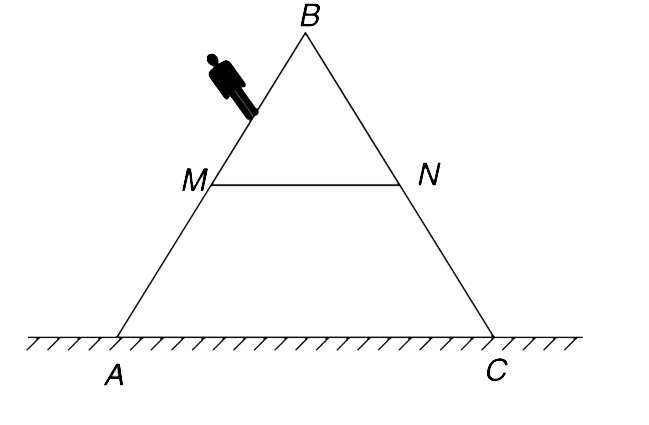 View Solution
View SolutionA uniform metal sheet of mass M has been folded to give it L shape and it is placed on a rough floor as shown in figure. Wind is blowing horizontally and hits the vertical face of the sheet as shown. The speed of air varies linearly from zero at floor level to `v_(0)` at height L from the floor. Density of air is `rho`. Find maximum value of `v_(0)` for which the sheet will not topple. Assume that air particles striking the sheet come to rest after collision, and that the friction is large enough to prevent the sheet from sliding
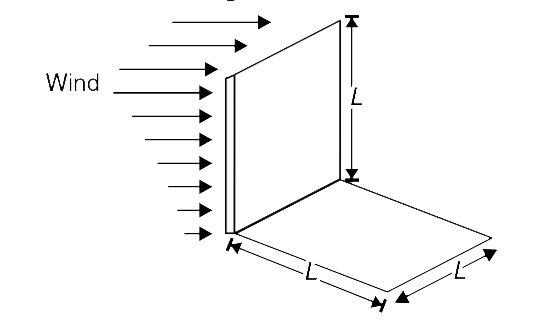 View Solution
View SolutionThree identical cylinders have mass M each and are placed as shown in the figure. The system is in equilibrium and there is no contact between B and C. Find the normal contact force between A and B.
 View Solution
View SolutionA spool is kept in equilibrium on an incline plane as shown in figure. The inner and outer radii of the spool are in ratio `(r)/(R) = (1)/(2)`. The force applied on the thread (wrapped on part of radius r) is horizontal. Find the angle that the force applied by the incline on the spool makes with the vertical.
[Take `tan^(-1) ((sqrt3)/(5)) cong 19^(@)` ]
 04:21View Solution
04:21View SolutionA uniform hemisphere placed on an incline is on verge of sliding. The coefficient of friction between the hemisphere and the incline is `mu = 0.3`.
Find the angle `phi` that the circular base of the hemisphere makes with the horizontal.
Given `sin (tan^(-1) 0.3) cong 0.29 " and "sin^(-1) (0.77) cong 50^(@)`
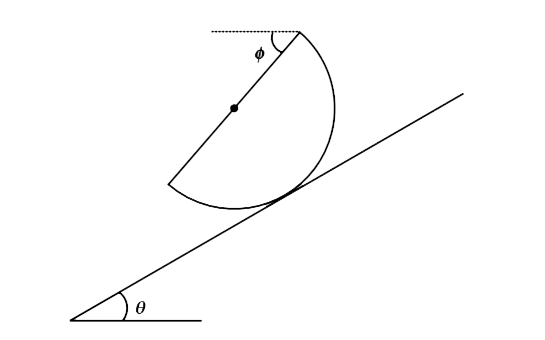 04:43View Solution
04:43View SolutionA L shaped, uniform rod has its two arms of length `l` and `2l`. It is placed on a horizontal table and a string is tied at the bend. The string is pulled horizontally so that the rod slides with constant speed. Find the angle `theta` that the longer side makes with the string. Assume that the rod exerts uniform pressure at all points on the table.
 View Solution
View SolutionA uniform meter stick AB of mass M is lying in state of rest on a rough horizontal plane. A small block of mass `m` is placed on it at its centre C. A variable force F is applied at the end B of the stick so as to rotate the stick slowly about A in vertical plane. The force F always remains perpendicular to the length of the stick. The stick is raised to `theta = 60^(@)` and it was observed that neither the end A slipped on the ground nor the block of mass `m` slipped on the stick.

(a) `F_(1)` is force applied by the stick on the block. Plot the variation of `F_(1)` with `theta (0 le theta le 60^(@))`.
(b) What must be the minimum coefficient of friction between the block and the stick.
(c) `f` is the friction force acting at end A of the stick. Plot variation of `f vs theta (0^(@) le theta le 60^(@))`.View SolutionA ladder of mass M and length L stays at rest against a smooth wall. The coefficient of friction between the ground and the ladder is `mu`
(a) Let `F_("wall")`, W and `F_(g)` be the force applied by wall, weight of the ladder and force applied by ground on the ladder. Argue to show that the line of action of these three forces must intersect.
(b) Using the result obtained in (a) show that line of action of Fg makes an angle `tan^(-1) (2 tan theta)` with the horizontal ground where `theta` is the angle made by the ladder with the ground.
(c) Find the smallest angle that the ladder can make with the ground and not slip.
(d) You climb up the ladder, your presence makes the ladder more likely to slip. Where are you at A or B? C is the centre of mass of the ladder.
 View Solution
View SolutionA uniform rod AB has mass M and length L. It is in equilibrium supported in vertical plane by three identical springs as shown in figure. The springs are connected at A, C and D such that `AC = CD = (L)/(3)`. Assume that the springs are very stiff and the angle a made by the rod with the horizontal in equilibrium position is very small. (All springs are nearly vertical). Calculate the tension in the three springs.
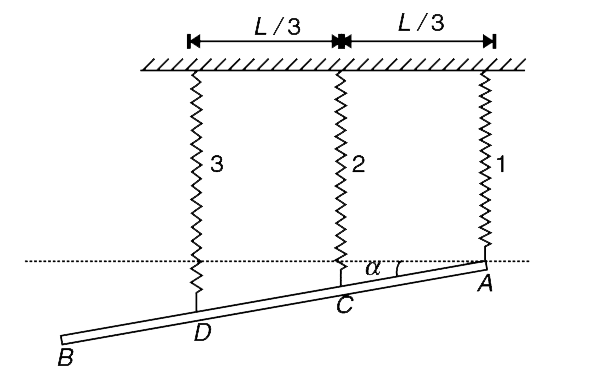 View Solution
View SolutionA uniform rod of length `b` can be balanced as shown in figure. The lower end of the rod is resting against a vertical wall. The coefficient of friction between the rod and the wall and that between the rod and the support at A is `mu`. Distance of support from the wall is `a`.
(a) Find the ratio `(a)/(b)` if the maximum value of `theta` is `theta_(1)`.
(b) Find the ratio `(a)/(b)` if the minimum value of `theta` is `theta_(2)`.
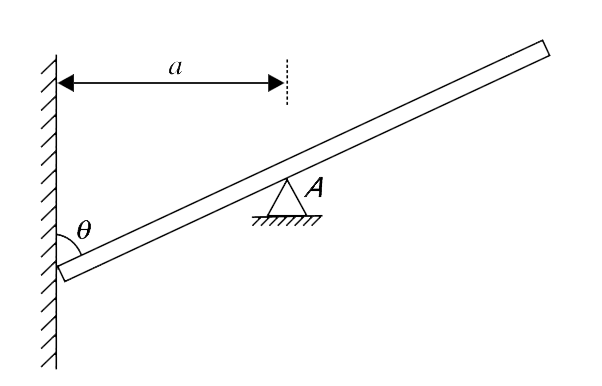 View Solution
View SolutionA uniform rectangular block is moving to the right on a rough horizontal floor (the block is retarding due to friction). The length of the block is L and its height is `h`. A small particle (A) of mass equal to that of the block is stuck at the upper left edge. Coefficient of friction between the block and the floor is `mu = (2)/(3)`. Find the value of h (in terms of L) if the normal reaction of the floor on the block effectively passes through the geometrical centre (C) of the block.
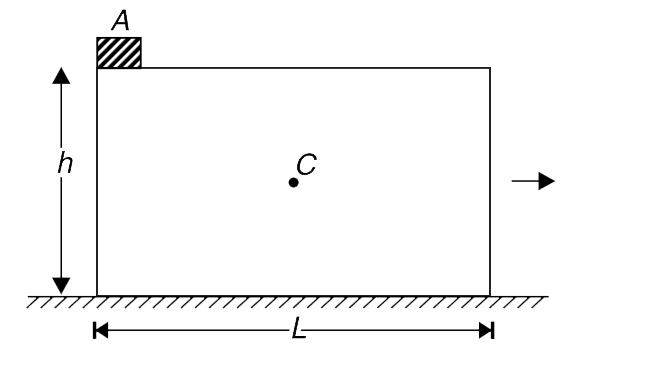 View Solution
View SolutionA uniform cubical block of mass M and side length L is lying on the edge of a rough table with `(1)/(4) th` of its edge overhanging. When a small block of mass m is placed on its top surface at the right edge (see fig.), the cube is on verge of toppling. The block of mass m is given a sharp horizontal impulse so that it acquires a velocity towards B. The small block moves on the top surface and falls on the other side. What is maximum coefficient of friction between the small block and the cube so that the cube does not rotate as the block moves over it. Assume that the friction between the cube and the table is large enough to prevent sliding of the cube on the table.
 View Solution
View SolutionA uniform rod of mass M and length L is hinged at its end to a wall so that it can rotate freely in a horizontal plane. When the rod is perpendicular to the wall a constant force F starts acting at the centre of the rod in a horizontal direction perpendicular to the rod. The force remains parallel to its original direction and acts at the centre of the rod as the rod rotates. (Neglect gravity).
(a) With what angular speed will the rod hit the wall ?
(b) At what angle `theta` (see figure) the hinge force will make a `45^(@)` angle with the rod ?
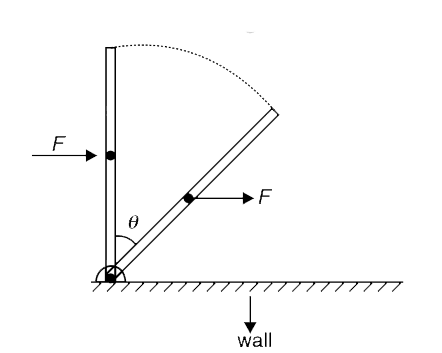 View Solution
View SolutionA rod of mass `M = 5kg` and length `L = 1.5 m` is held vertical on a table as shown. A gentle push is given to it and it starts falling. Friction is large enough to prevent end A from slipping on the table.
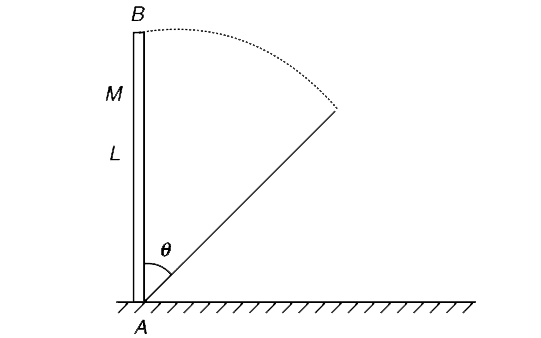
(a) Find the sum of linear momentum of all the particles of the rod when it rotates through an angle `theta = 37^(@)`
(b) Find the friction force and normal reaction force by the table on the rod, when `theta = 37^(@)`
(c) Find value of angle q when the friction force becomes zero.
`[tan 37^(@) = (3)/(4) " and " g = 10 m//s]`View Solution(a) In the system shown in figure 1, the uniform rod of length L and mass m is free to rotate in vertical plane about point O. The string an pulley are mass less. The block has mass equal to that of the rod. Find the acceleration of the block immediately after the system is released with rod in horizontal position.
(b) System shown in figure 2 is similar to that in figure 1 apart from the fact that rod is mass less and a block of mass m is attached to the centre of the rod with the help of a thread. Find the acceleration of both the blocks immediately after the system is released with rod in horizontal position.
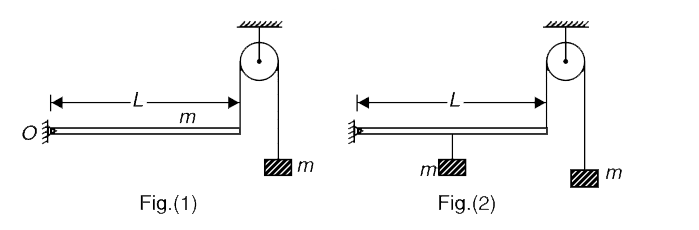 View Solution
View Solution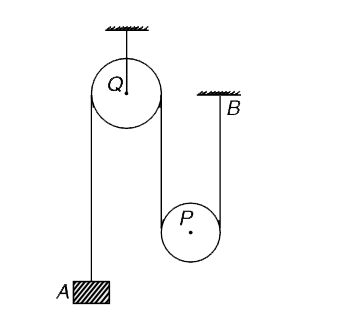
A light thread is wrapped tightly a few turns around a disc P of mass M. One end of the thread is fixed to the ceiling at B. The other end of the thread is passed over a mass less pulley (Q) and carries a block of mass M. All segment of the thread (apart from that on the pulley and disc) are vertical when the system is released. Find the acceleration of block A. On which object – the block A or the ceiling at B – does the thread exert more force ?View SolutionAn equilateral triangle is made from three mass less rods, each of length `l`. Two point masses m are attached to two vertices. The third vertex is hinged and triangle can swing freely in a vertical plane as shown. It is released the position shown with one of the rods vertical. Immediately after the system is released, find –
(a) tensions in all three rods (specify tension or compression),
(b) accelerations of the two masses
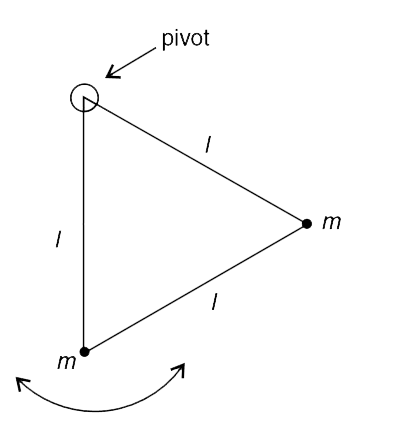 View Solution
View SolutionA uniform rod of mass `M` and length `L` is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
13:15View SolutionA disc is free to rotate about an axis passing through its centre and perpendicular to its plane. The moment of inertia of the disc about its rotation axis is I. A light ribbon is tightly wrapped over it in multiple layers. The end of the ribbon is pulled out at a constant speed of u. Let the radius of the ribboned disc be R at any time and thickness of the ribbon be `d (lt lt R)`. Find the force (F) required to pull the ribbon as a function of radius R.
 02:50View Solution
02:50View SolutionA uniform rod of mass M and length L is hinged at its lower end on a table. The rod can rotate freely in vertical plane and there is no friction at the hinge. A ball of mass M and radius `R = (L)/(3)` is placed in contact with the vertical rod and a horizontal force F is applied at the upper end of the rod.
(a) Find the acceleration of the ball immediately after the force starts acting.
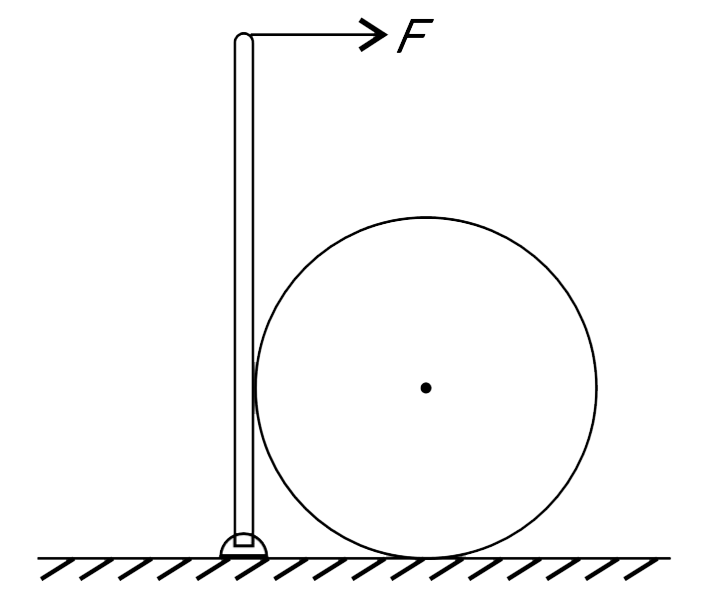
(b) Find the horizontal component of hinge force acting on the rod immediately after force F starts acting.07:56View Solution
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length `L = 2 sqrt3 R` is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if `theta = 60^(@)`. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.View SolutionA uniform semicircular wire is hinged at ‘A’ so that it can rotate freely in vertical plane about a horizontal axis through ‘A’. The semicircle is released from rest when its diameter AB is horizontal Find the hinge force at ‘A’ immediately after the wire is released.
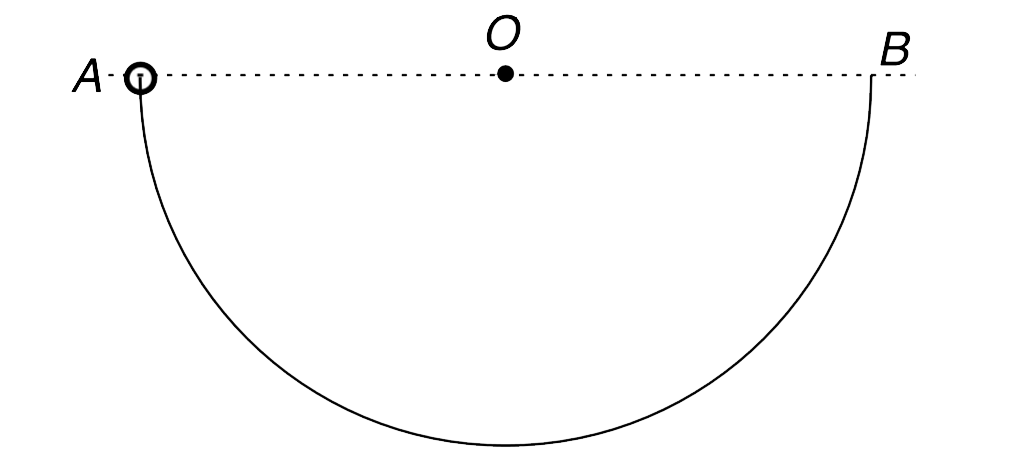 13:18View Solution
13:18View SolutionA uniform solid hemisphere A of mass M radius R is joined with a thin uniform hemispherical shell B of mass M and radius R (see fig.). The sphere thus formed is placed inside a fixed box as shown. The floor , as well as walls of the box are smooth. On slight disturbance, the sphere begins to rotate. Find its maximum angular speed `(omega)` and maximum angular acceleration `(alpha_(0))` during the subsequent motion. Do the walls of the box apply any force on the sphere while it rotates ?
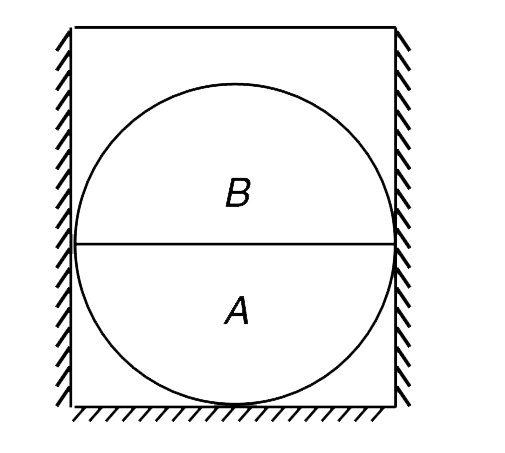 06:27View Solution
06:27View Solution
In the arrangement shown, the double pulley has a mass M and the two mass less threads have been tightly wound on the inner (radius `= r`) and outer circumference (radius `R = 2r`). The block shown has a mass 4 M. The moment of inertia of the double pulley system about a horizontal axis passing through its centre and perpendicular to the plane of the figure is `I = (Mr^(2))/(2)`.
(a) Find the acceleration of the center of the pulley after the system is released.
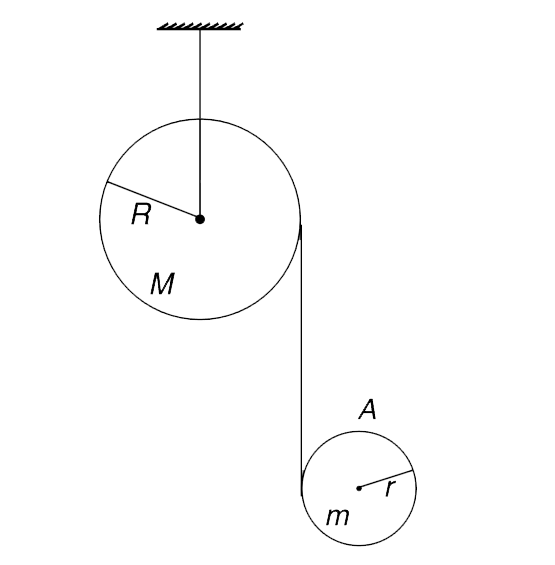
(b) Two seconds after the start of the motion the string holding the block breaks. How long after this the pulley will stop ascending?16:28View SolutionA thread is tightly wrapped on two pulleys as shown in figure. Both the pulleys are uniform disc with upper one having mass M and radius R being free to rotate about its central horizontal axis. The lower pulley has mass m and radius r and it is released from rest. It spins and falls down. At the instant of release a small mark (A) was at the top point of the lower pulley.
(a) After what minimum time `(t_(0))` the mark will again be at the top of the lower pulley?
(b) Find acceleration of the mark at time `t_(0)`.
(c) Is there any difference in magnitude of acceleration of the mark and that of a point located on the circumference at diametrically opposite end of the pulley.
 View Solution
View Solution
PHYSICS questions and complete solutions for chapter ROTATIONAL MOTION of ARIHANT PHYSICS (HINGLISH) of Class 11
