Complete Solutions to TRIANGLES of chapter CHAPTERWISE REVISION (STAGE 3) of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CHAPTERWISE REVISION (STAGE 3) |
| SELINA PUBLICATION | TRIANGLES |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
ABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
the triangles ADX and BAY are congruent.
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
` angle DXA = angle AYB `
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
DX is perpendicular to AY.
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that `angle PSQ and anglePTR` are right angles
Prove that the triangles PTR and PSQ are congruent.
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that `angle PSQ and anglePTR` are right angles
If OS and RT intersect at M, prove that the triangles PTM and PSM are congruent.
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PB = QC
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
If angle PQR is a rt. Angle find angle PRQ
View Solution` A B C\ a n d\ D B C` are two isosceles triangles on the same bas `B C` and vertices `A\ a n d\ D` are on the same side of `B C` . If `A D` is extended to intersect `B C` at `P ,` show that ` A B D\ ~= A C D` (ii) ` A B P\ ~= A C P`
View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
` Delta ABP ~= Delta ACP `
View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
AP bisects angle BAC and BDC.
View Solution` A B C\ a n d\ D B C` are two isosceles triangles on the same bas `B C` and vertices `A\ a n d\ D` are on the same side of `B C` . If `A D` is extended to intersect `B C` at `P ,` show that `A P` bisects `" "/_A` as well as `/_D` and `A P` is the perpendicular bisector of `B C`
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
` Delta APC ~= Delta BPD `
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
Angle DBC is a right angle.
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
` Delta DBC ~= Delta ACB `
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
` CP = ( 1)/(2)AB `
View SolutionIn the given figures , ABCD is a rectangle
Prove that : `Delta ABE ~= Delta CDF. `
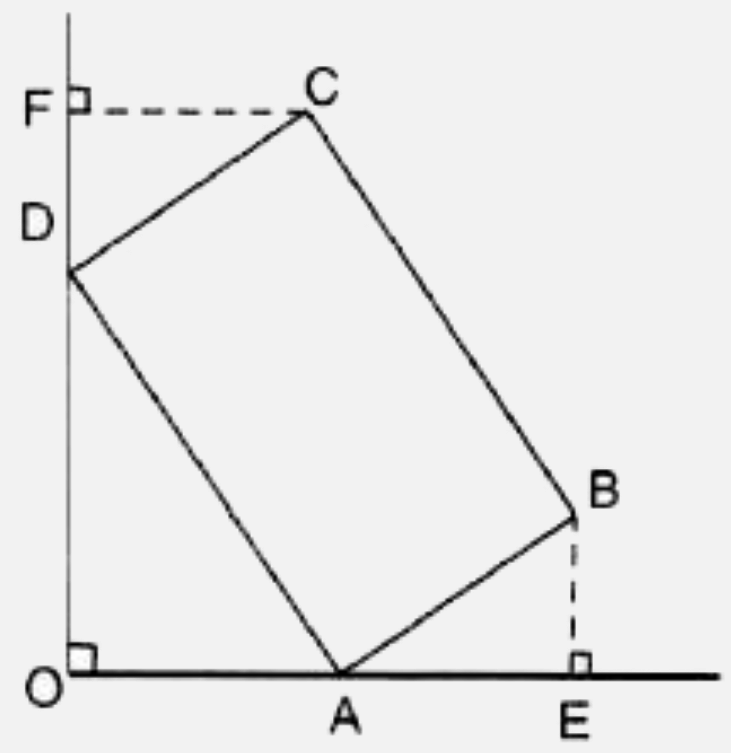
View SolutionIn quadrilateral PQRS , PS = QR and ` angle SPQ = angle RQP ` . Prove that :
` PR = QS `
View SolutionIn quadrilateral PQRS , PS = QR and ` angle SPQ = angle RQP ` . Prove that :
` angle QPR = angle PQS `
View Solution
TRIANGLES questions and complete solutions for chapter CHAPTERWISE REVISION (STAGE 3) of ICSE of Class 9
All Exercises from SELINA PUBLICATION Class 9 MATHS CHAPTERWISE REVISION (STAGE 3)
- AREA
- AREA AND PERIMETER OF PLANE FIGURES
- CIRCLE
- CO-ORDINATE GEOMETRY
- COMPOUND INTEREST
- CONSTRUCTIONS OF POLYGONS
- DISTANCE FORMULA
- FACTORS
- GRAPHICAL SOLUTION
- INDICES
- INEQUALITIES
- ISOSCELES TRIANGLES
- LOGARITHM
- MEAN AND MEDIAN
- MID- POINT THEOREM
- PYTHAGORAS THEOREM
- RATIONAL AND IRRATIONAL NUMBERS
- RECTILINEAR FIGURES
- SIMUTANEOUS EQUATIONS
- SOLIDS
- STATISTICS
- TRIANGLES
- TRIGONOMETRY