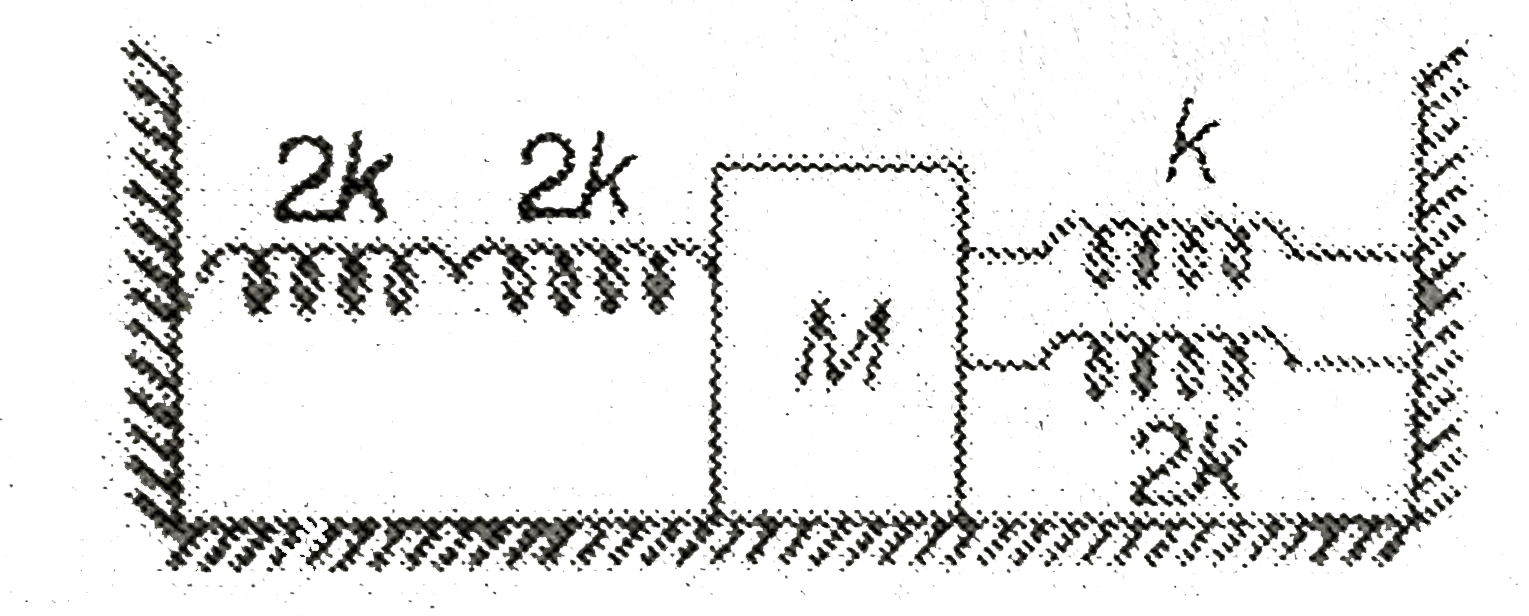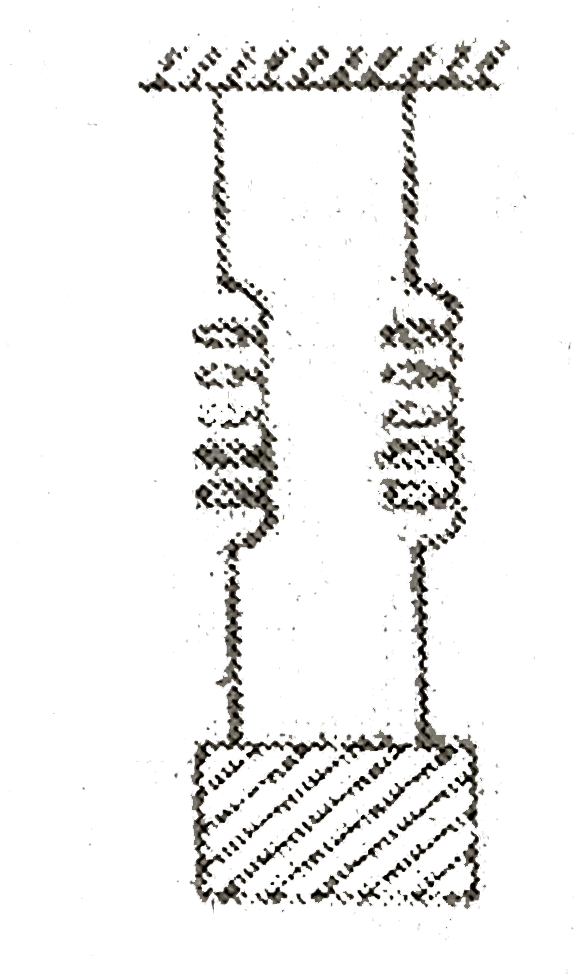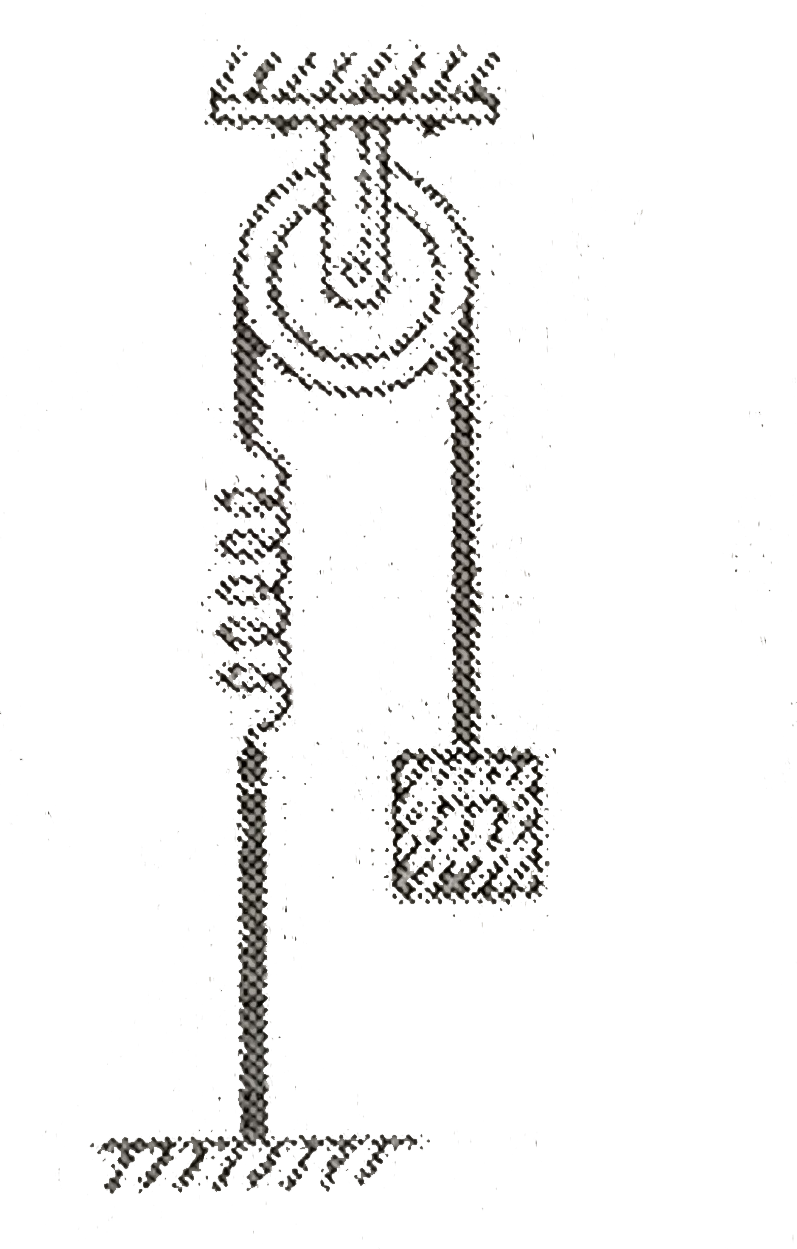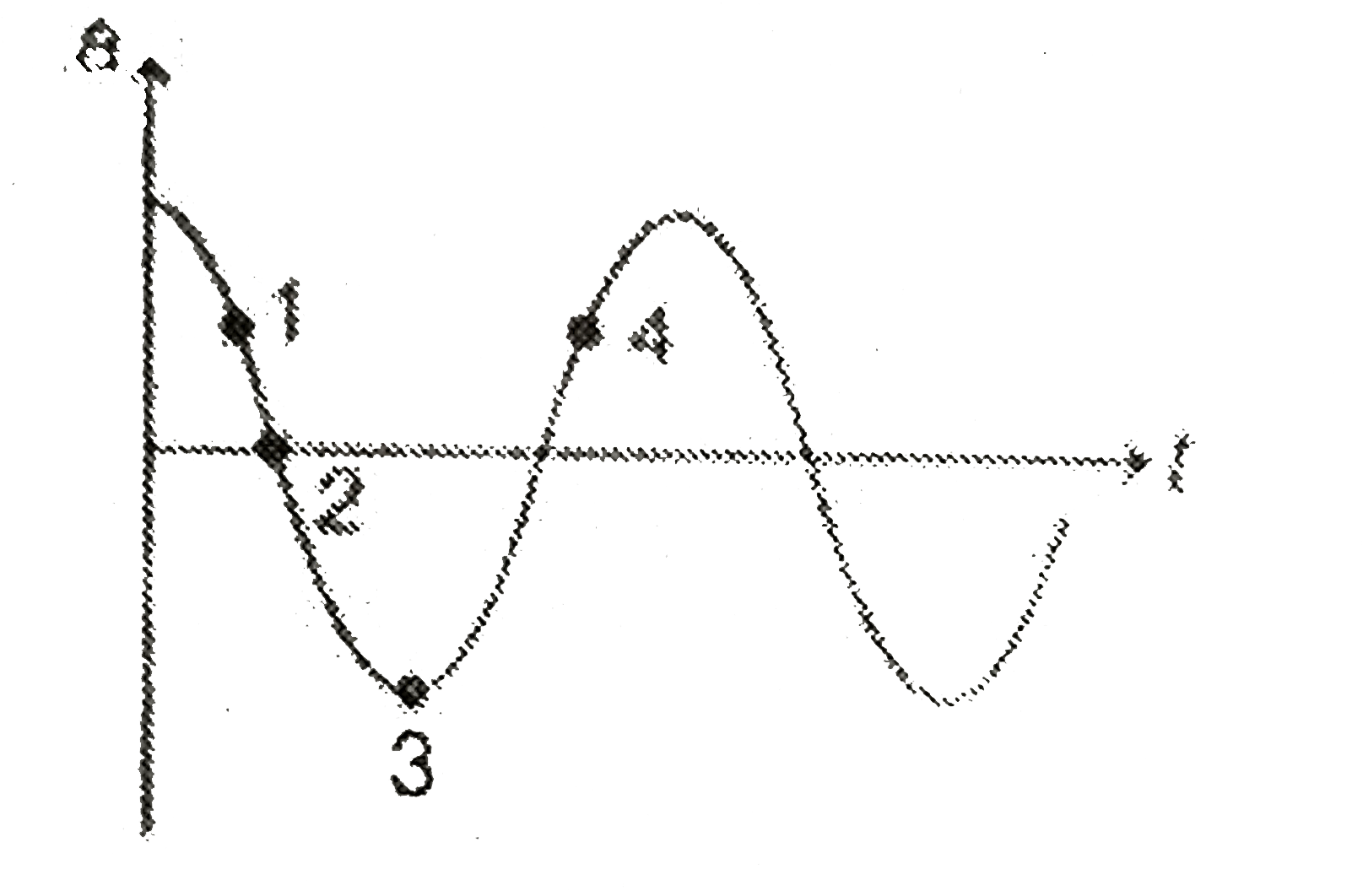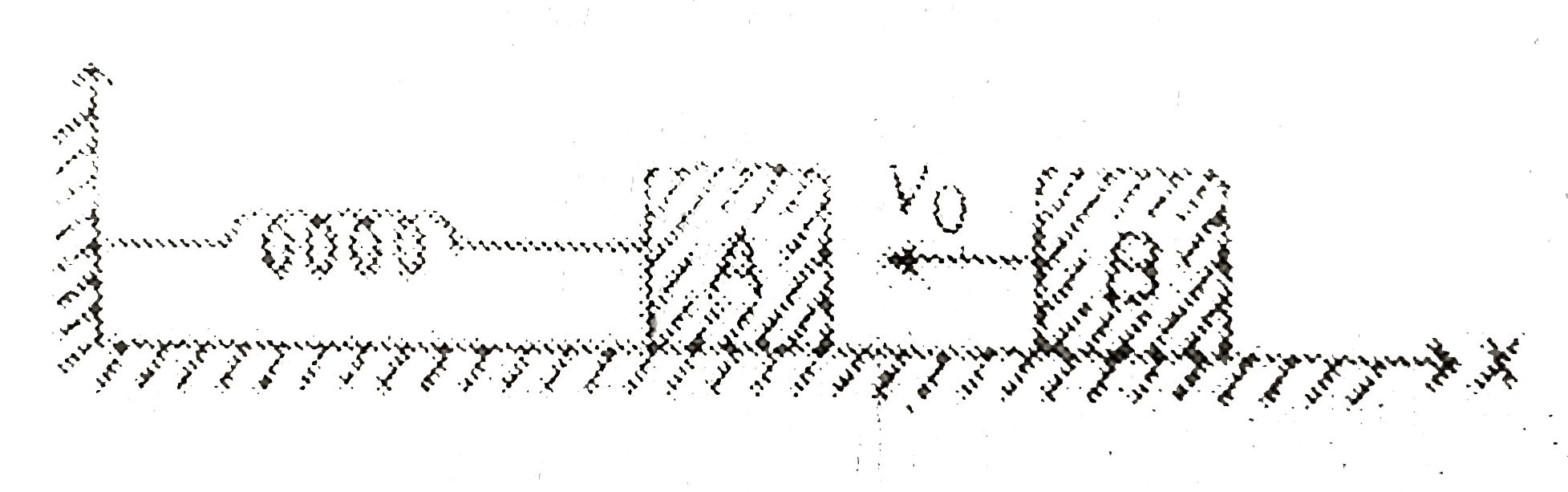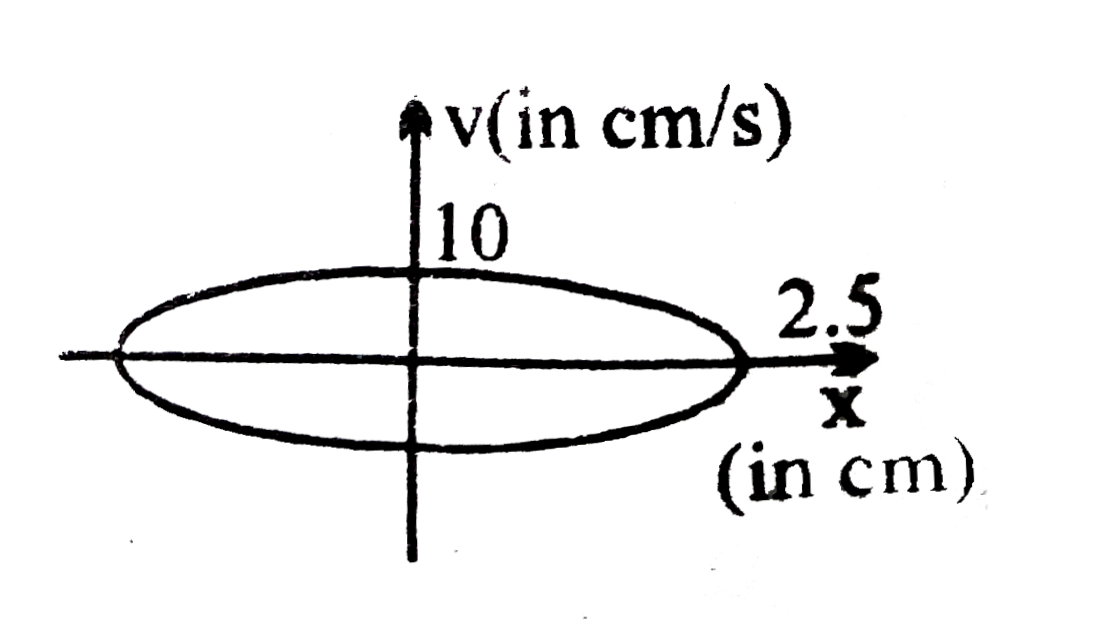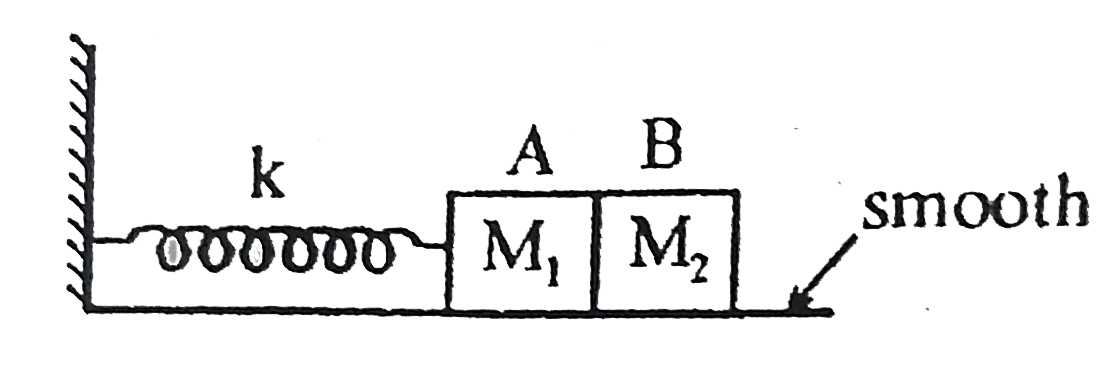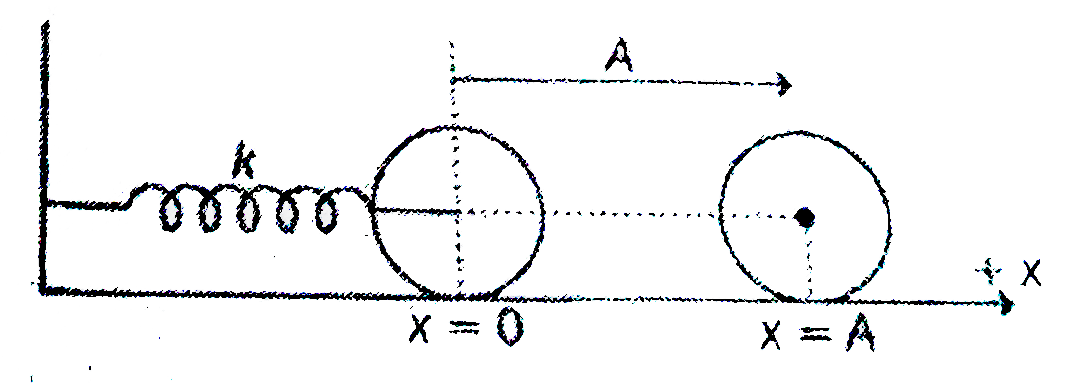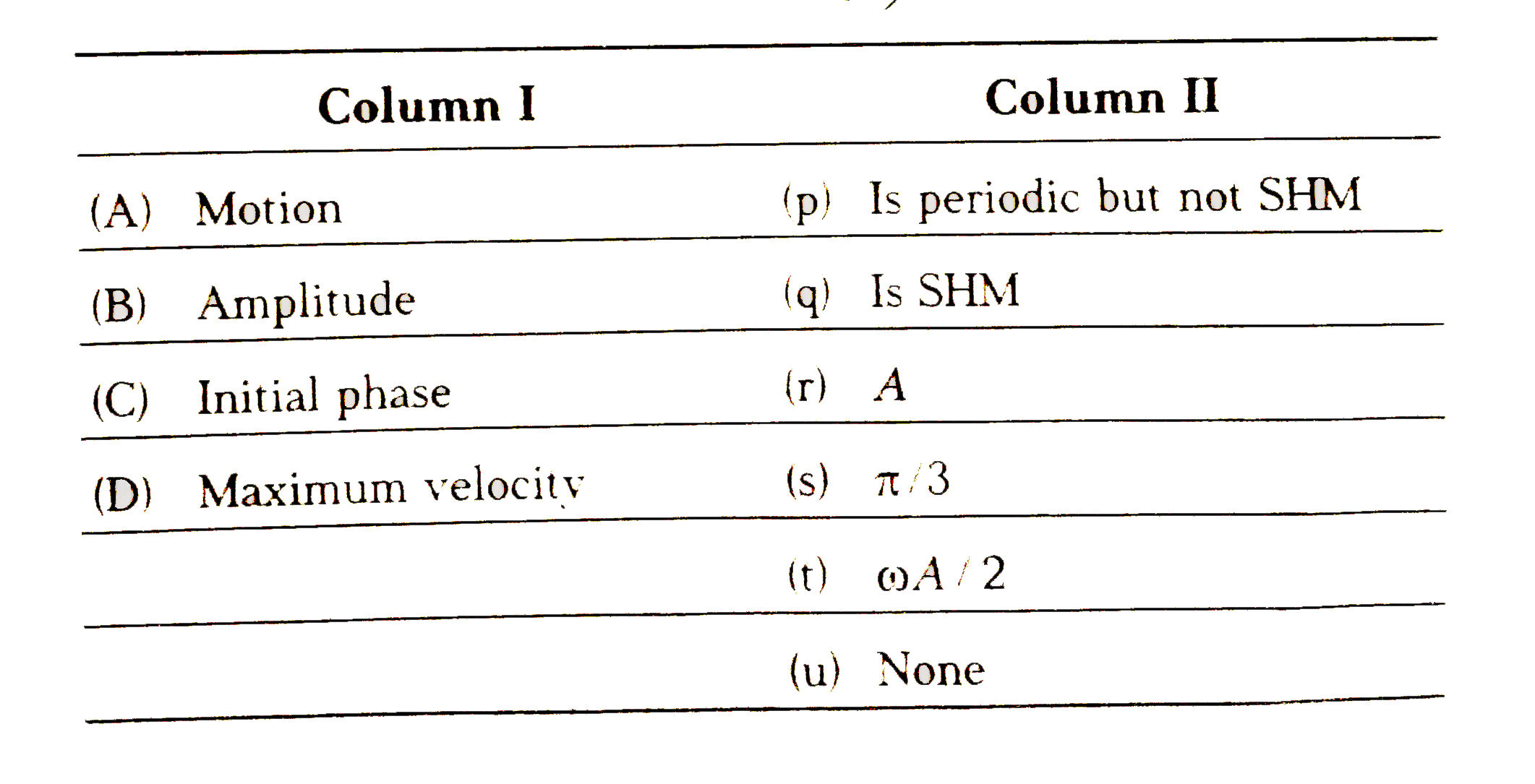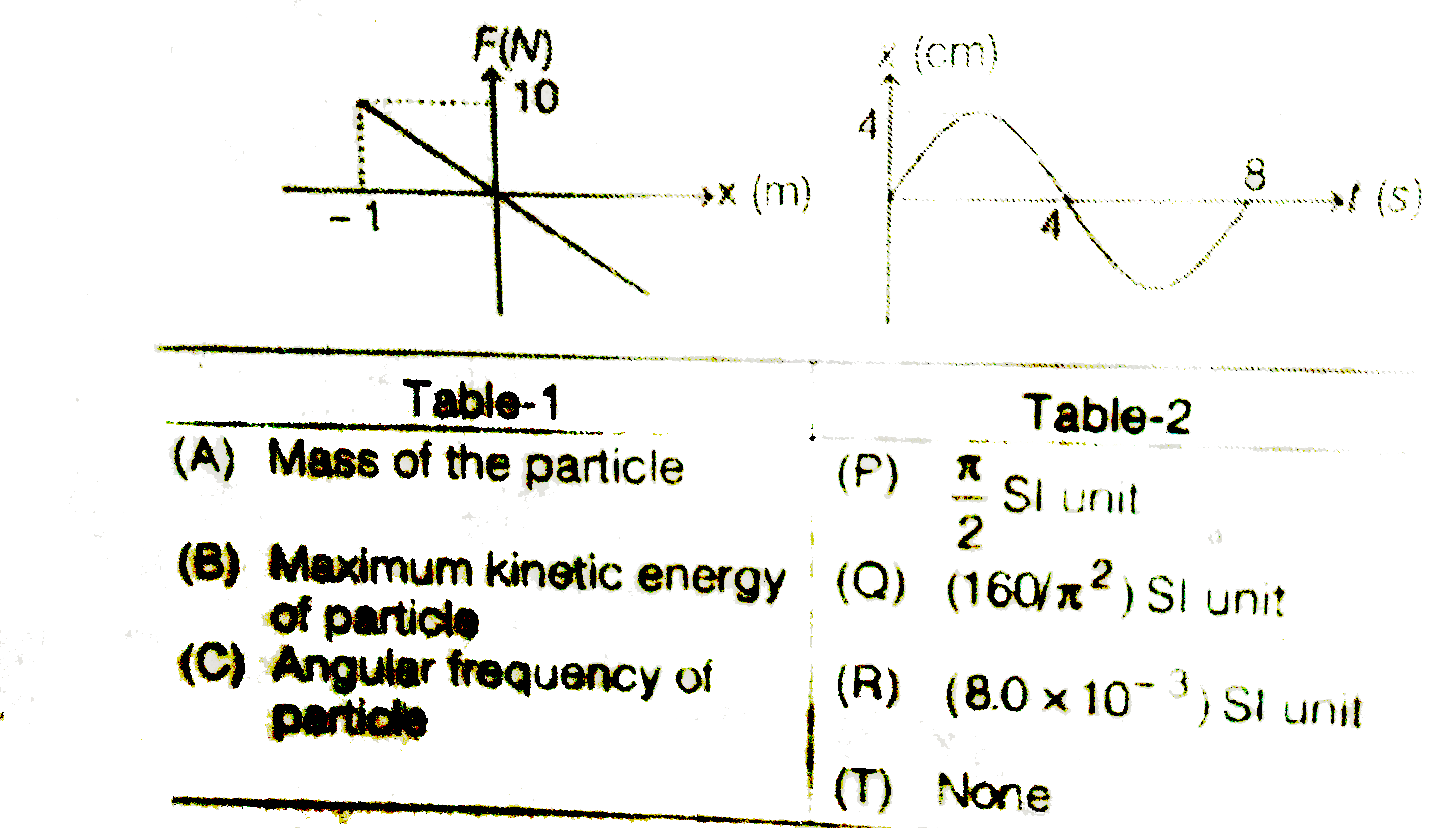Only one question is correct from DC PANDEY ENGLISH SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| DC PANDEY ENGLISH | Only one question is correct |
| Medium | English |
| Academic Year | 2023-2024 |
Question 9
Two particles undergo SHM along parallel lines with the same time period (T) and equal amplitudes. At particular instant, one particle is at its extreme position while the other is at its mean position. The move in the same direction. They will cross each other after a further time.View SolutionQuestion 21
A wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be
 View Solution
View SolutionQuestion 31
A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
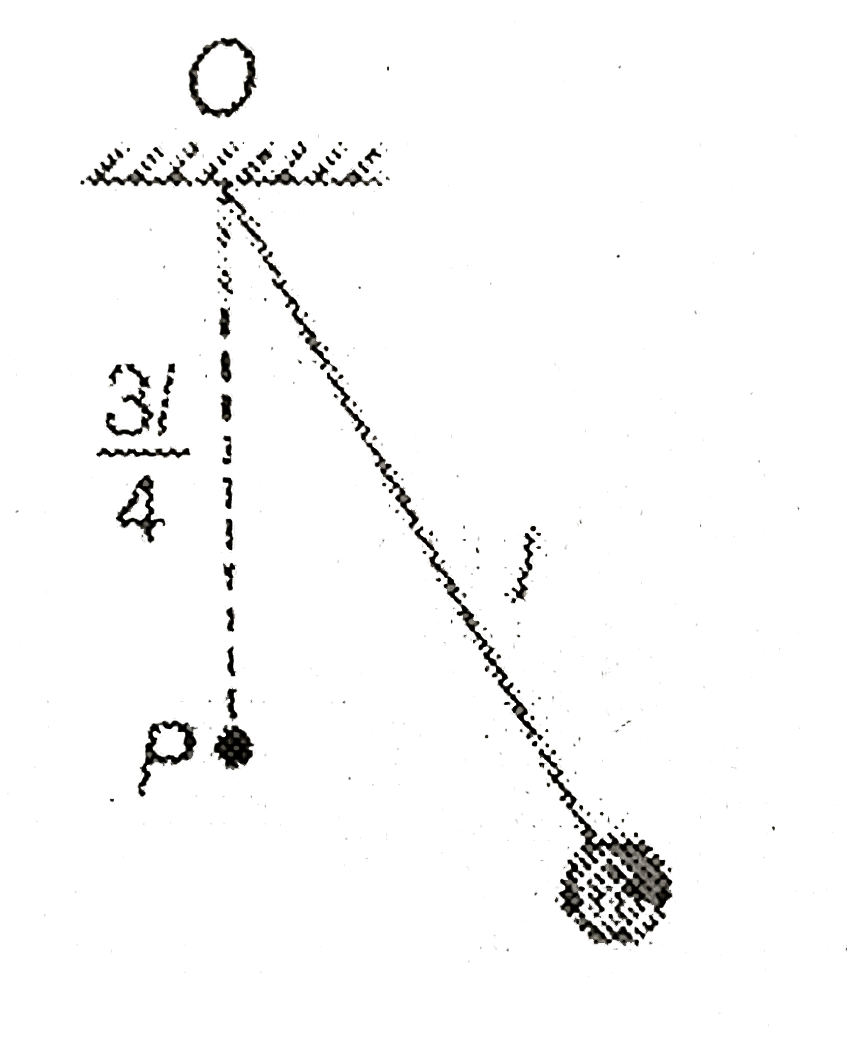 View Solution
View SolutionQuestion 42
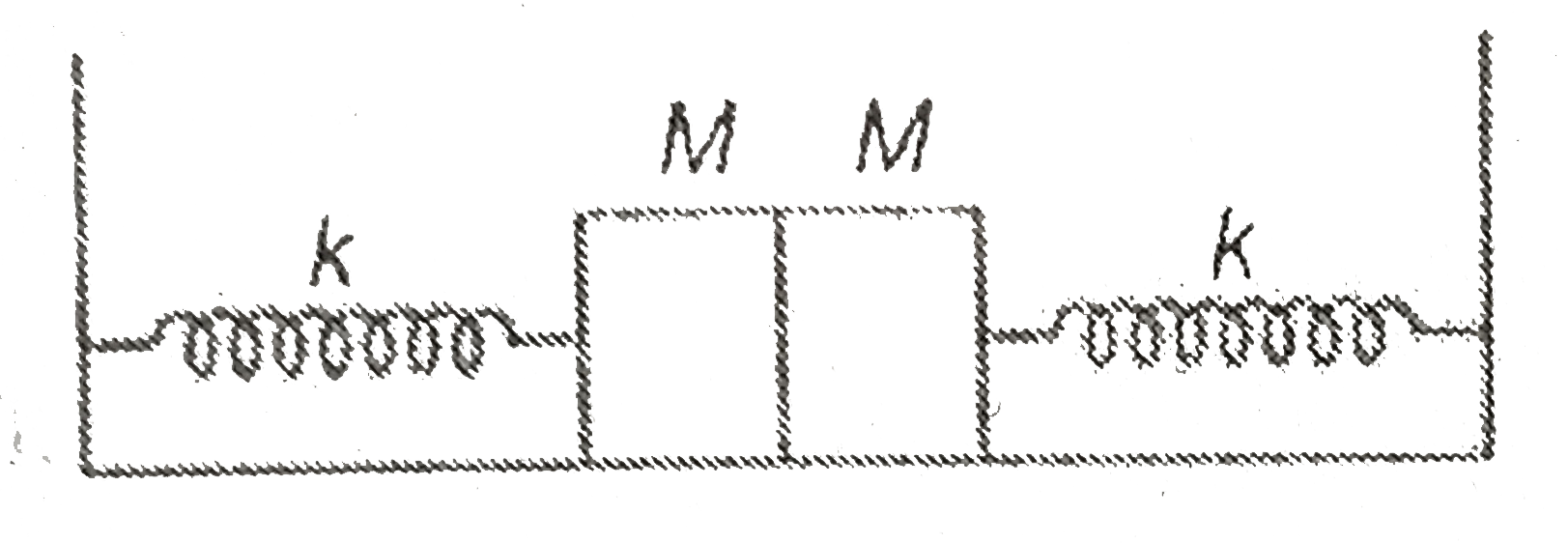
An assembly of identicl spring mass system is placed on a smooth horizontal surface as shown. Initially the springs are relaxed. The left mass is displaced to the left while the right mass is displaced to the right and released. The resulting collision is elastic. The time period of the oscillatins of the system is.
 View Solution
View SolutionQuestion 44
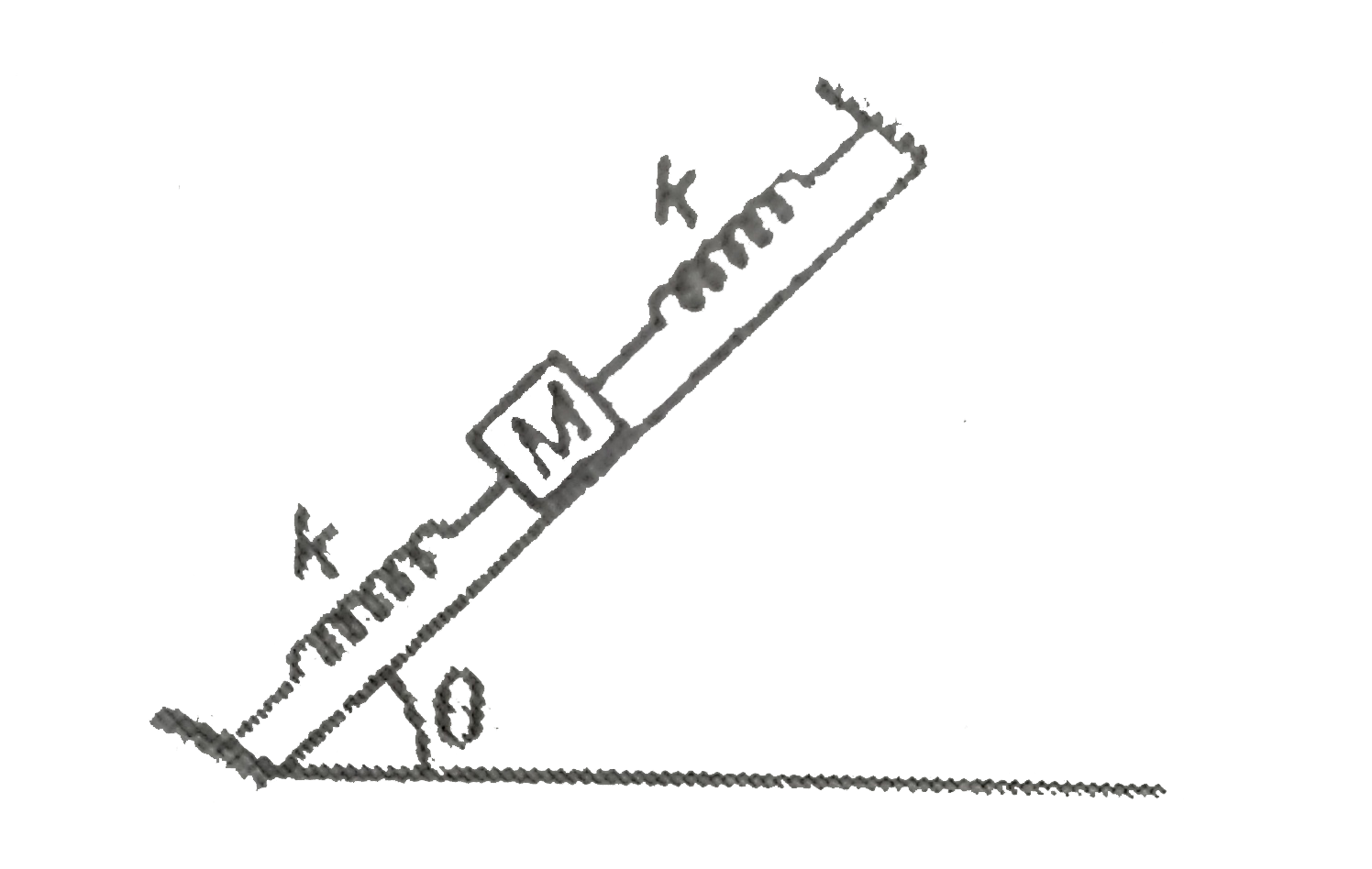
Two springs with negligible massess and force constant of k1=200Nm−1 and k2=160Nm−1 are attached to the block of mass m = 10kg as shown in the figure. Initially the block is at rest at the equilibrium position the block is at rest at the equilibrium position ir. Which both springs are neither stretched nor compressed. At time t = 0, sharp impulse of 50 N-s is given to the block in horizontal direction.
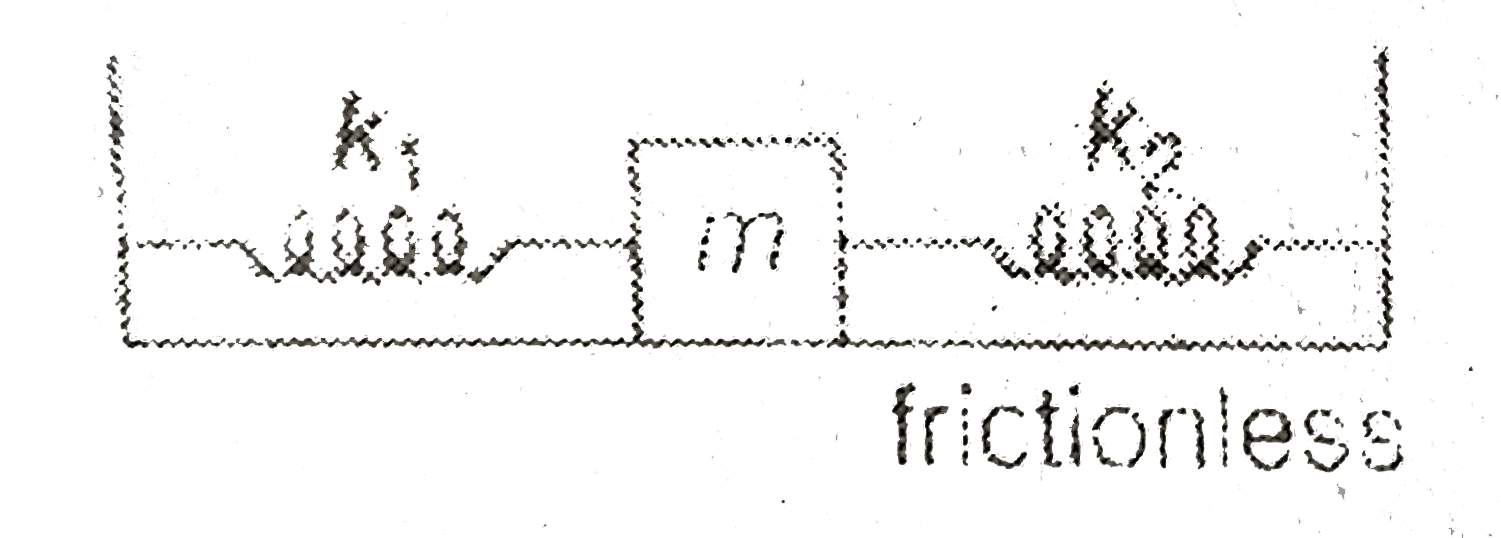 View Solution
View SolutionQuestion 54
In the figure, the block of mass m, attached to the spring of stiffness k is in contact with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely elastic then the time period of oscillation of the block will be
 View Solution
View SolutionQuestion 55
Vertical displacement of a plank with a body of mass m on it is varying according to the law y=sinωt+√3cosωt. The minimum value of ω for which the mass just breaks off the plank and the moment it occurs first time after t=0, are given by (y is positive towards vertically upwards).View SolutionQuestion 58
Two blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
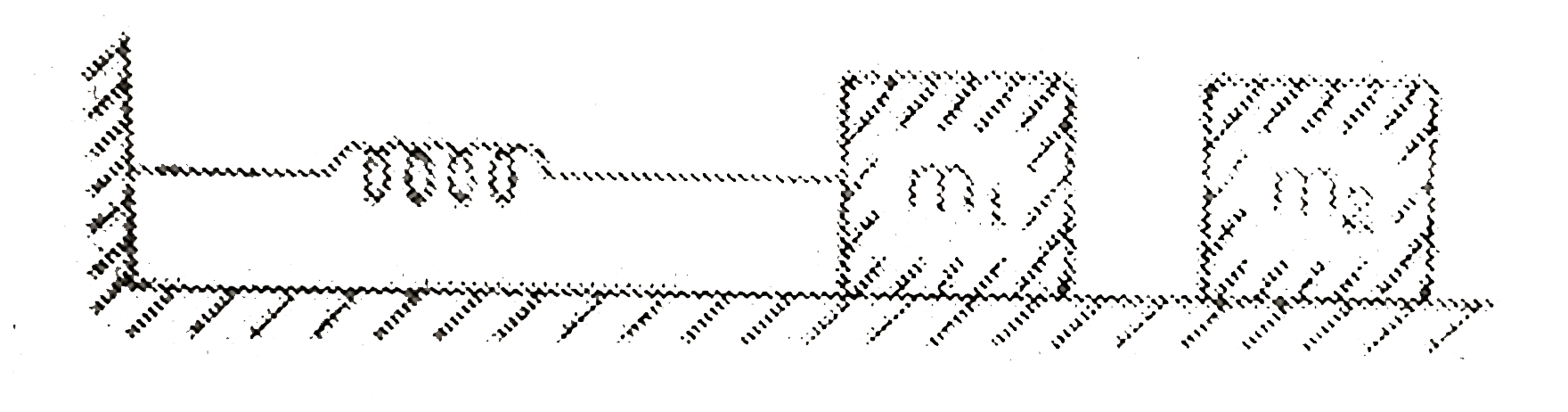 View Solution
View SolutionQuestion 62
Two particles are executing SHM in a straight line. Amplitude A and the time period T of both the particles are equal. At time t=0, one particle is at displacement x1=+A and the other x2=(−A2) and they are approaching towards each other. After what time they across each other? T4View SolutionQuestion 67
A ball of mass m when dropped from certain height as shown in diagram, strikes a wedge kept on smooth horizontal surface and move horizontally just after impact. If the ball strikes the ground at a distance d from its initial line of fall, thenthe amplitude of oscillation of wedge after being hit by the ball will be
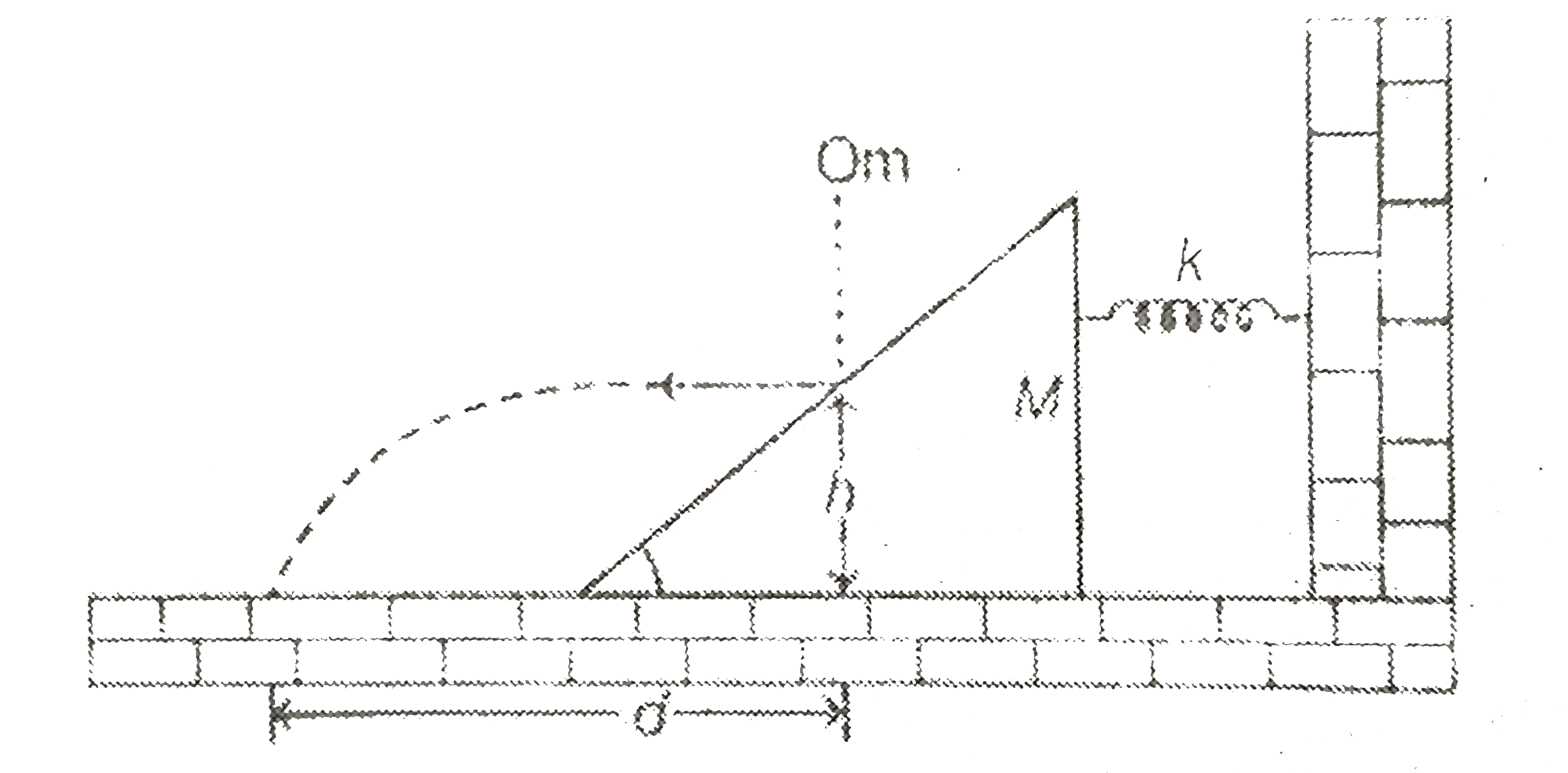 View Solution
View SolutionQuestion 69
The angular frequency of a spring block system is ω0. This system is suspended from the ceiling of an elevator moving downwards with a constant speed v0. The block is at rest relative to the elevator. Lift is suddenly stopped. Assuming the downward as a positive direction. Then View SolutionQuestion 77
A test tube of length l and area of cross-section A has some iron fillings of mass M. The test tube floats normally in a liquid of density ρ with length x dipped in the liquid. A disturbing force makes the tube oscillate in the liquid. The time period of oscillation is given by (neglect the mass of the test tube)View SolutionQuestion 80
In the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
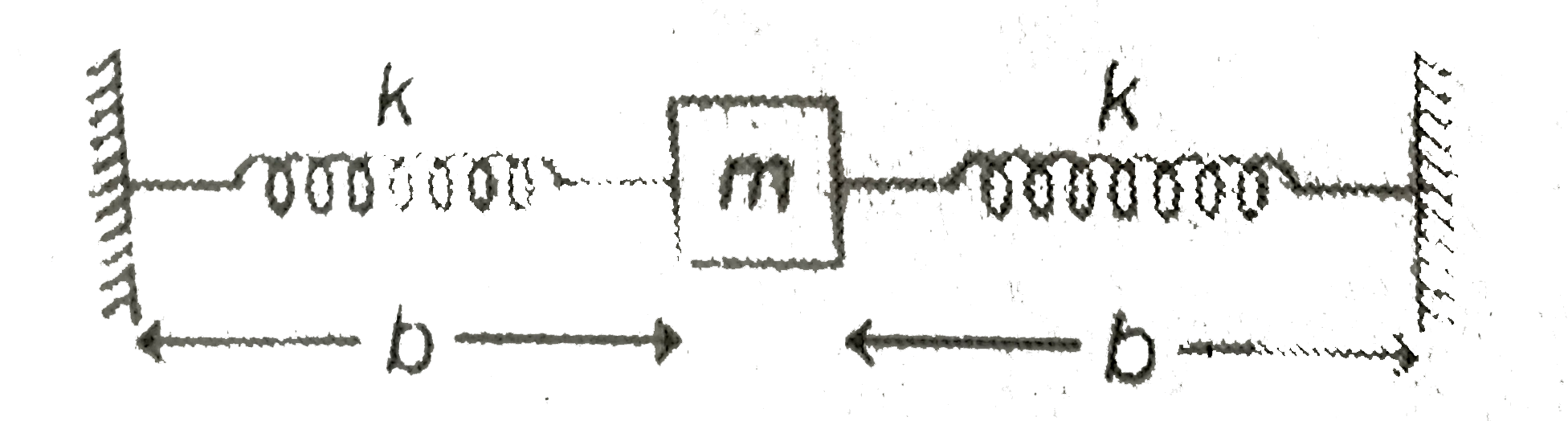 View Solution
View SolutionQuestion 81
A particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x2=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/s2)View SolutionQuestion 82
Two springs, each of spring constant k = 100N/m are attached to a block of mass 2kg as shown in figure. The block can slide smoothly along horizontal platform clamped to the opposite walls of a trolley of mass 5kg. The block is slightly displace dand then released. The period of oscillation is (in seconds). (all surfaces are smooth)
 View Solution
View SolutionQuestion 94
A block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck
 View Solution
View SolutionQuestion 96
Two particles undergo SHM along the same line with the same time period (T) and equal amplitude (A). At a particular instant one is at x=−A and the other is at x=0. If they start moving in the same direction then they will cross each other at

(i) t=4T3 (ii) t=3T8 (iii) x=A2 (iv) x=A√2 View SolutionQuestion 109
Two blocks of masses 3 kg and 6kg rest on horizontal smooth surface. The 3 kg block is attached to a spring with a force constant k=900Nm−1 which is compressed 2m from beyond the equilibrium position. The 6 kg mass is at rest at 1m from mean position. 3kg mass strikes the 6 kg mass and the two stick together.
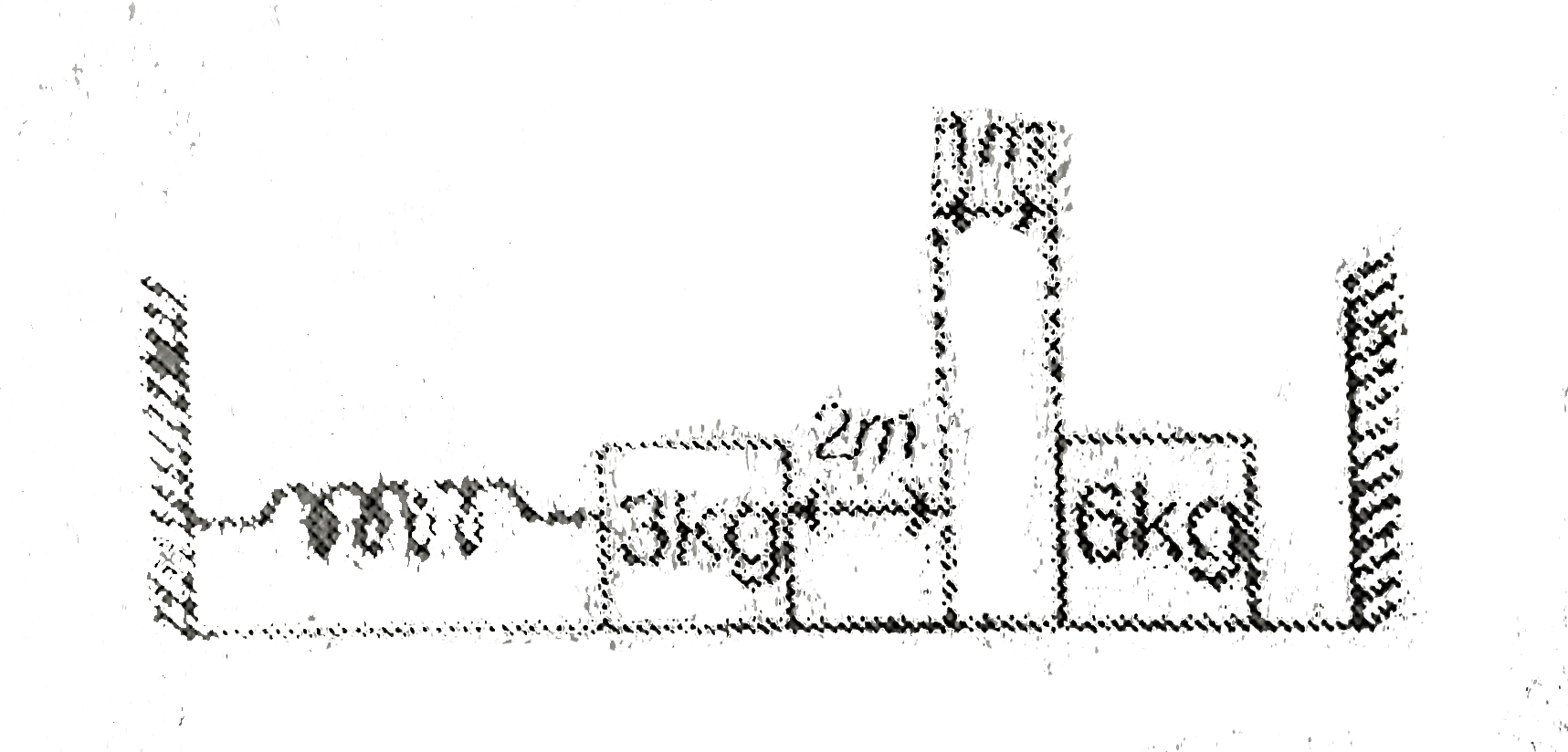 View Solution
View SolutionQuestion 110
Two springs with negligible massess and force constant of k1=200Nm−1 and k2=160Nm−1 are attached to the block of mass m = 10kg as shown in the figure. Initially the block is at rest at the equilibrium position the block is at rest at the equilibrium position nor compressed. At time t=0, sharp impulse of 50 N-s is given to the block.
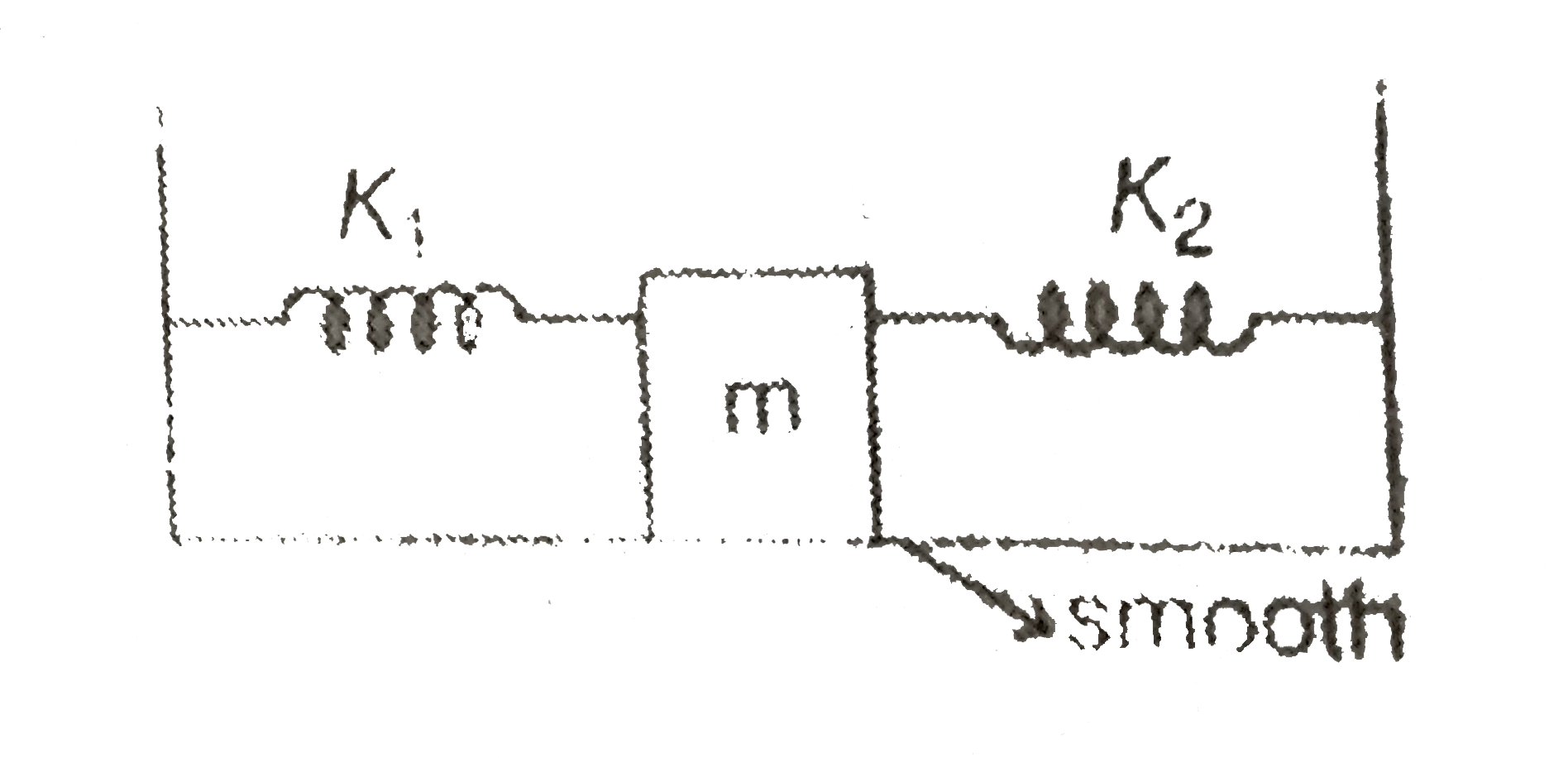 View Solution
View SolutionQuestion 113
Two smooth tunnels are dug from one side of earth's surface to the other side, one along a diameter are dropped from one end of each of the tunnels. Both particles oscillate simple harmonically along the tunnels. Let T1 and T2 be the time period of particles along the diameter and along the chord respectively. Then: View SolutionQuestion 116
In the figure shown, a block A of mass m is rigidy attached to a light spring of stiffness k and suspended from a fixed support. Another block B of same mass is just placed on it and blocks are in equilibrium. Suddenly the block B is removed. Choose the correct options (s) afterward.
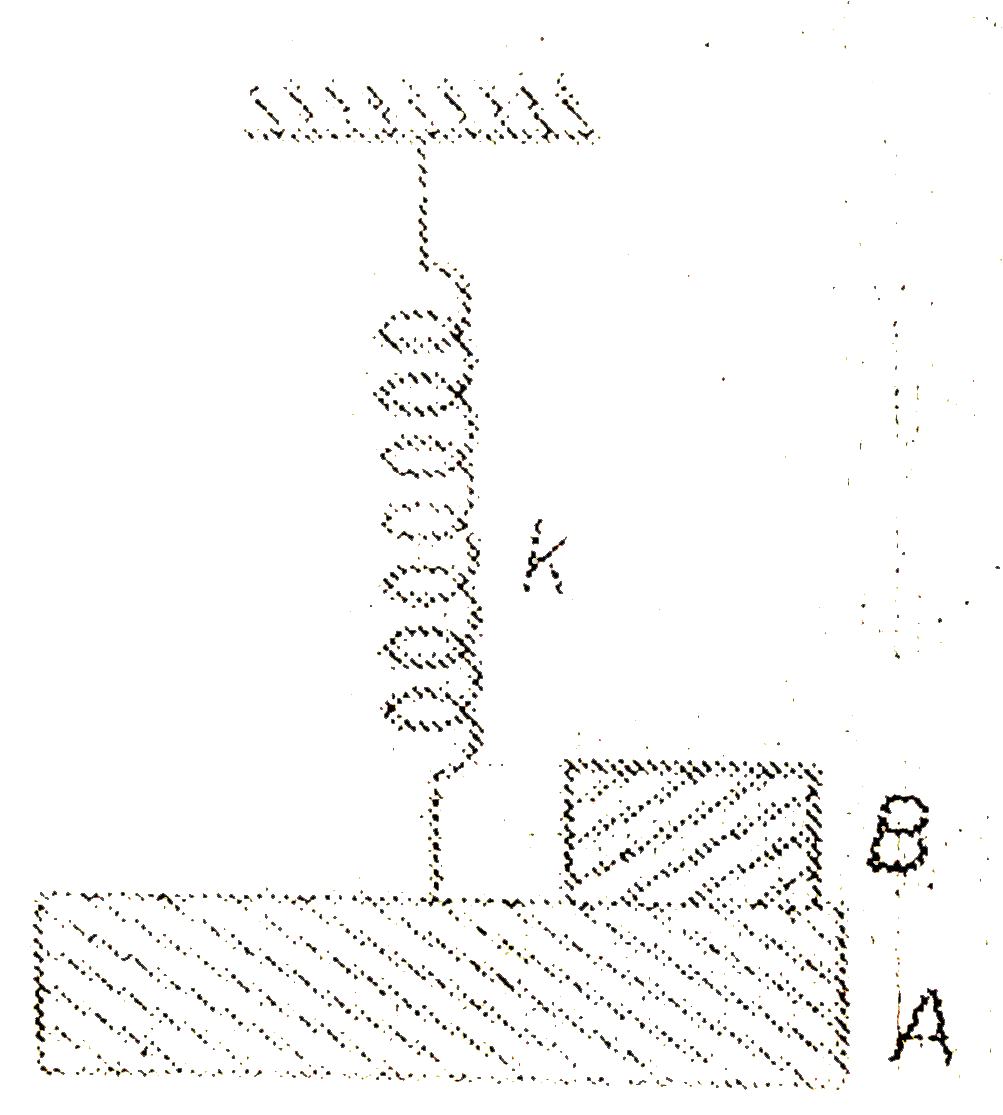 View Solution
View SolutionQuestion 117
Passage I) In simple harmonic motion force acting on a particle is given as F=−4x, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is −16ms2. Mass of the particle is 0.5 kg.
Potential energy of the particle at mean position is View SolutionQuestion 118
Passage I) In simple harmonic motion force acting on a particle is given as F=−4x, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is −16ms2. Mass of the particle is 0.5 kg.
Displacement time equation equation of the particle is View SolutionQuestion 119
Passage I) In simple harmonic motion force acting on a particle is given as F=−4x, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is −16ms2. Mass of the particle is 0.5 kg.
At x=+1m, potential energy and kinetic energy of the particle are View SolutionQuestion 120
Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
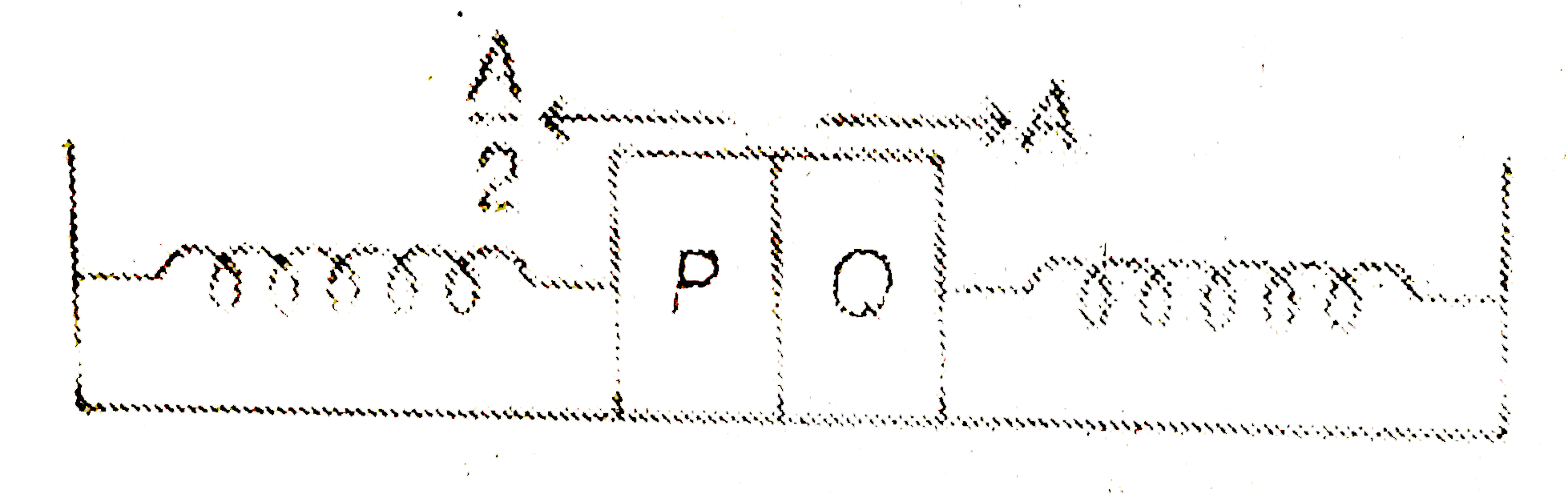
The time period of oscillation of combined mass is View SolutionQuestion 121
Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
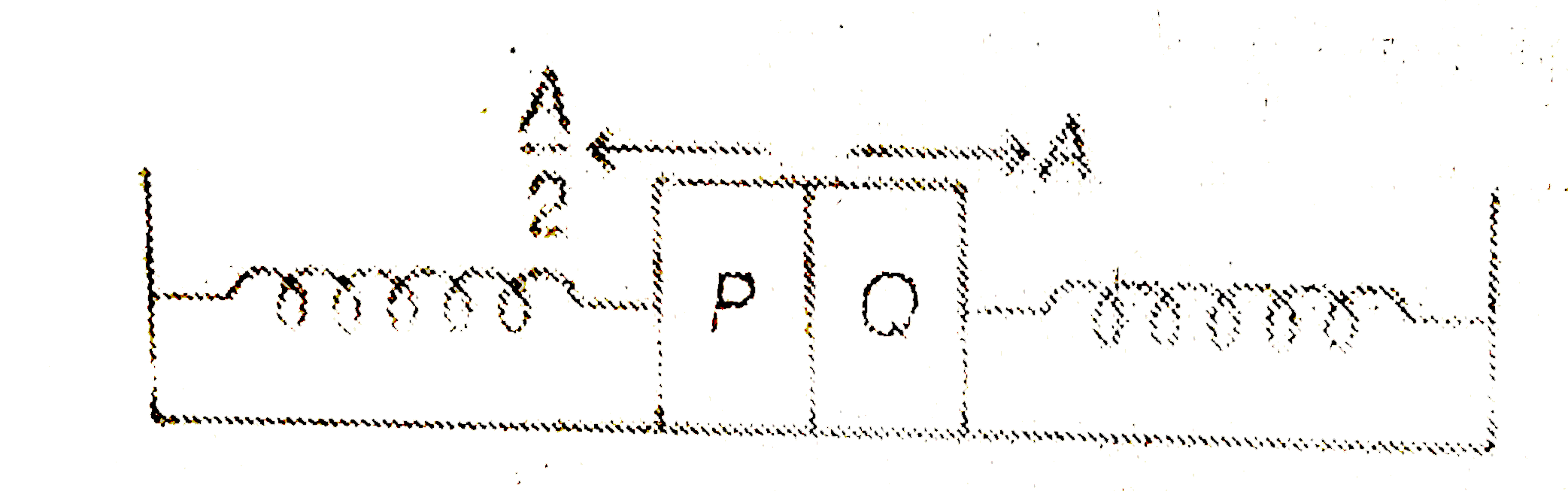
The amplitude of combined mass is View SolutionQuestion 122
Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
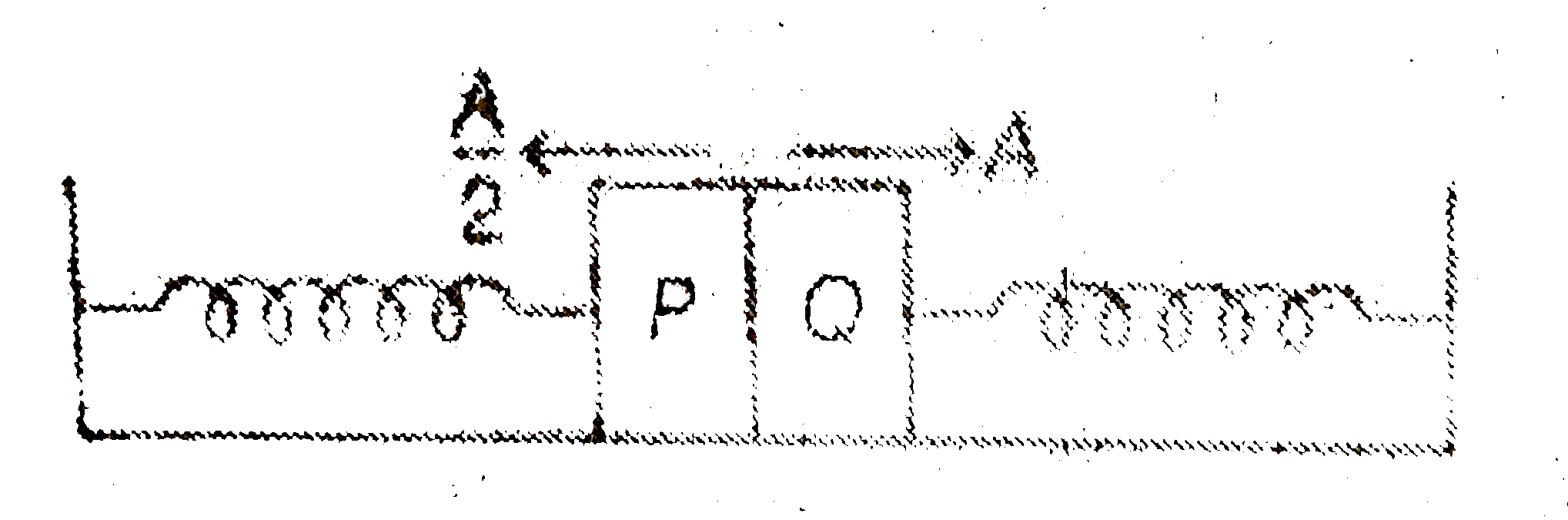
What is energy of osciallation of the combined mass? View SolutionQuestion 123
Passage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
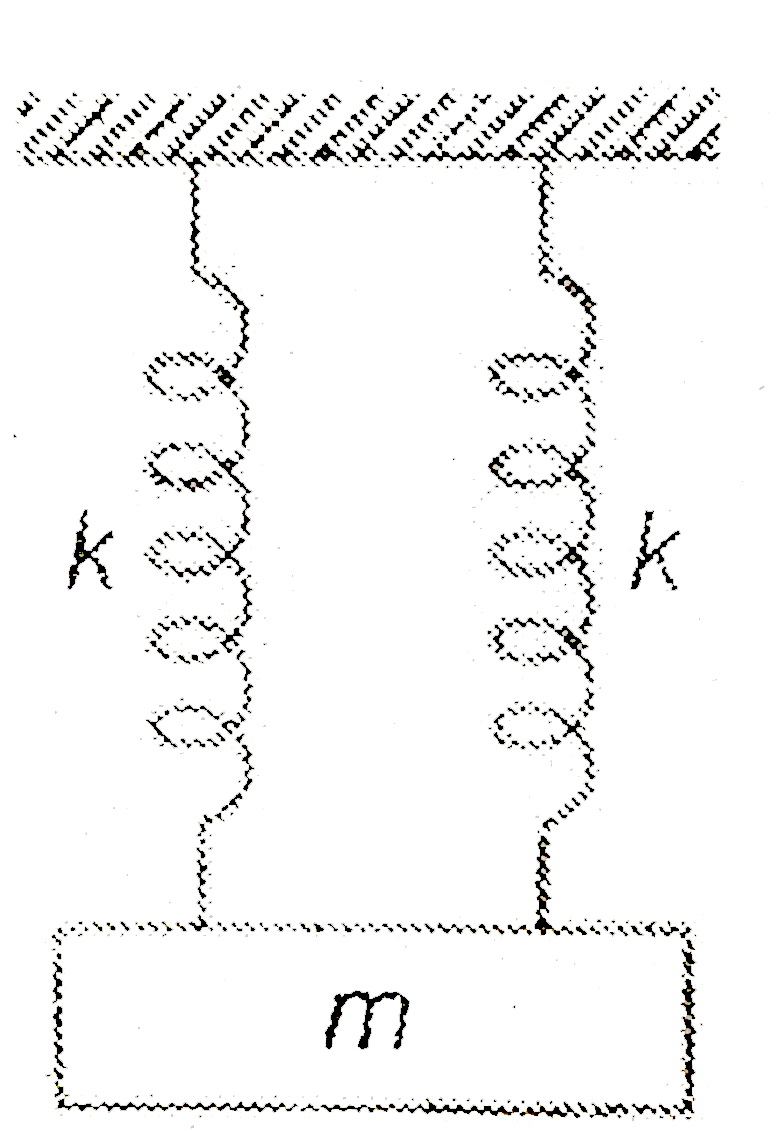
What is the new amplitude of osciallation of the block.View SolutionQuestion 124
Passage III A block of mass m =1/2 kg is attached with two springs each of force contant k=10N/m as shown. The block is oscillating vertically up and down with amplitude A=25cm. When the block is at its mean position one of the spring breaks without changing momentum of block.
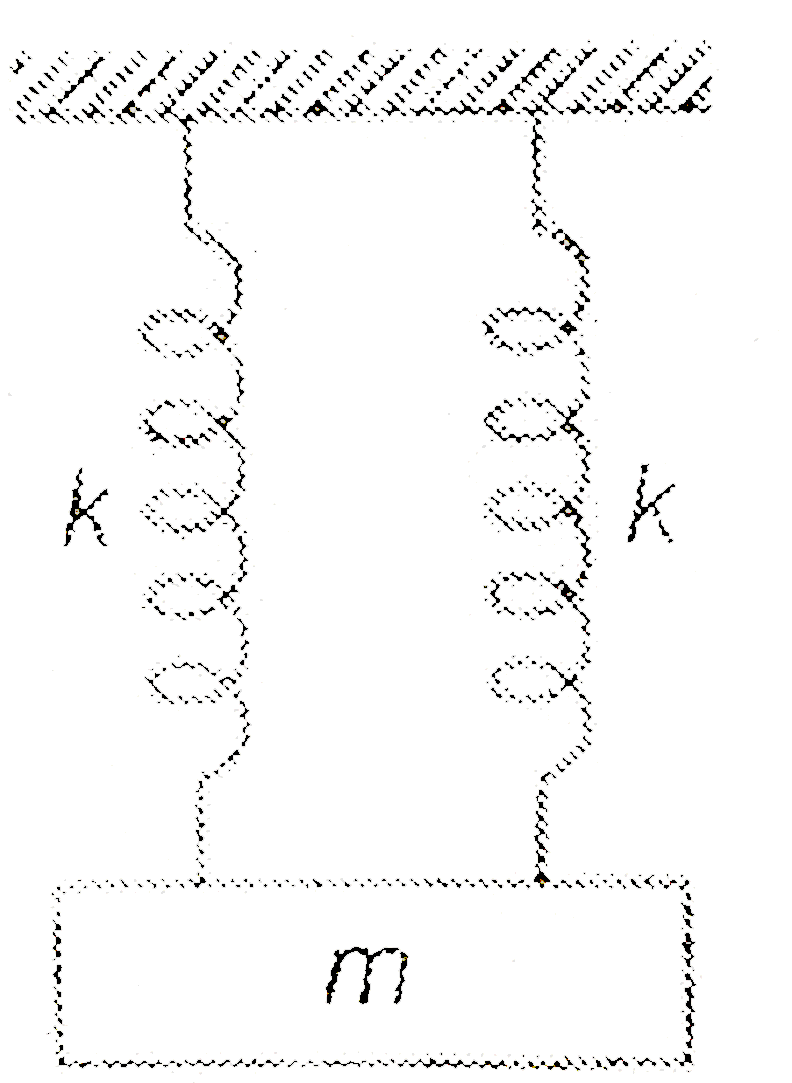
If instead of breaking one spring m/2 mass would have fallen from the block, then what will be the new amplitude? View SolutionQuestion 125
Passage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
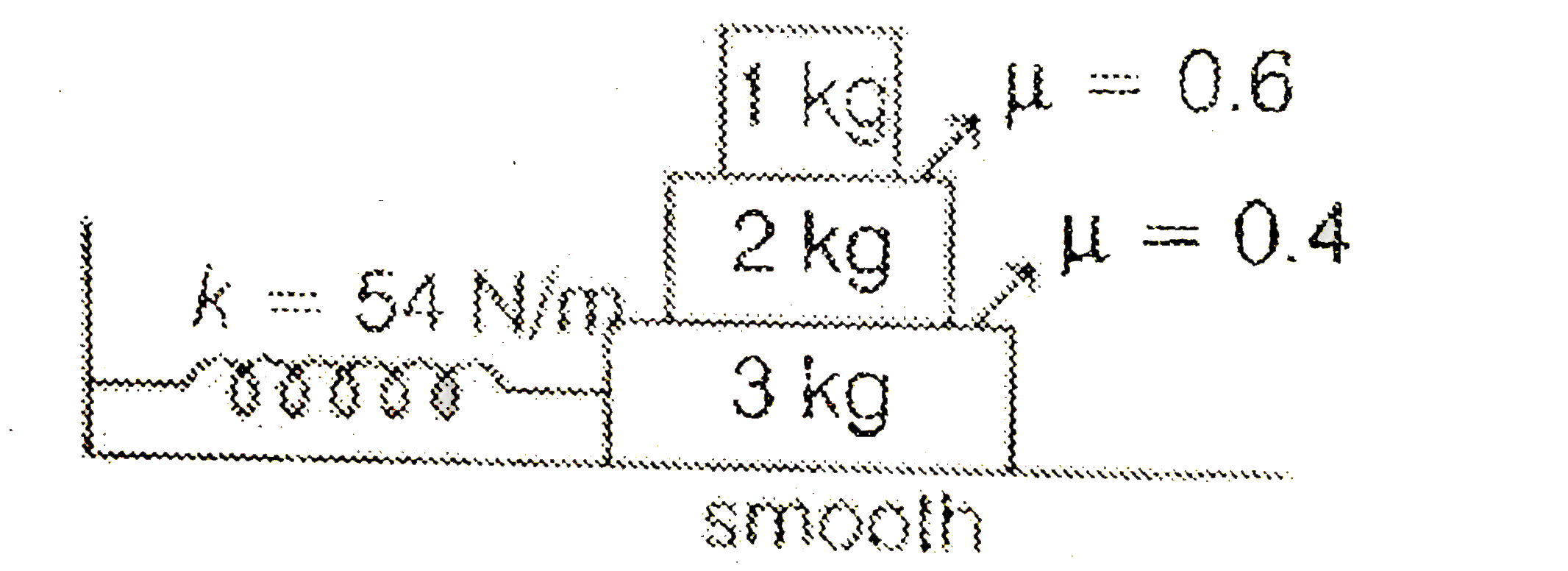
In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks?View SolutionQuestion 126
Angular frequnecy in SHM is given by ω=√km, Maximum acceleration in SHM is ω2A and maximum value of frication between two bodies in contact is μN, where ?N is the normal reaction between the bodies.
Now the value of k, the force constant is increased then the maximum amplitude calculated in above question will :-View SolutionQuestion 127
Passage V) In SHM displacement, velocity and acceleration all oscillate simple harmonically with same angular frequency ω. Phase difference between any two is π2 except that between displacement and acceleration which is π.
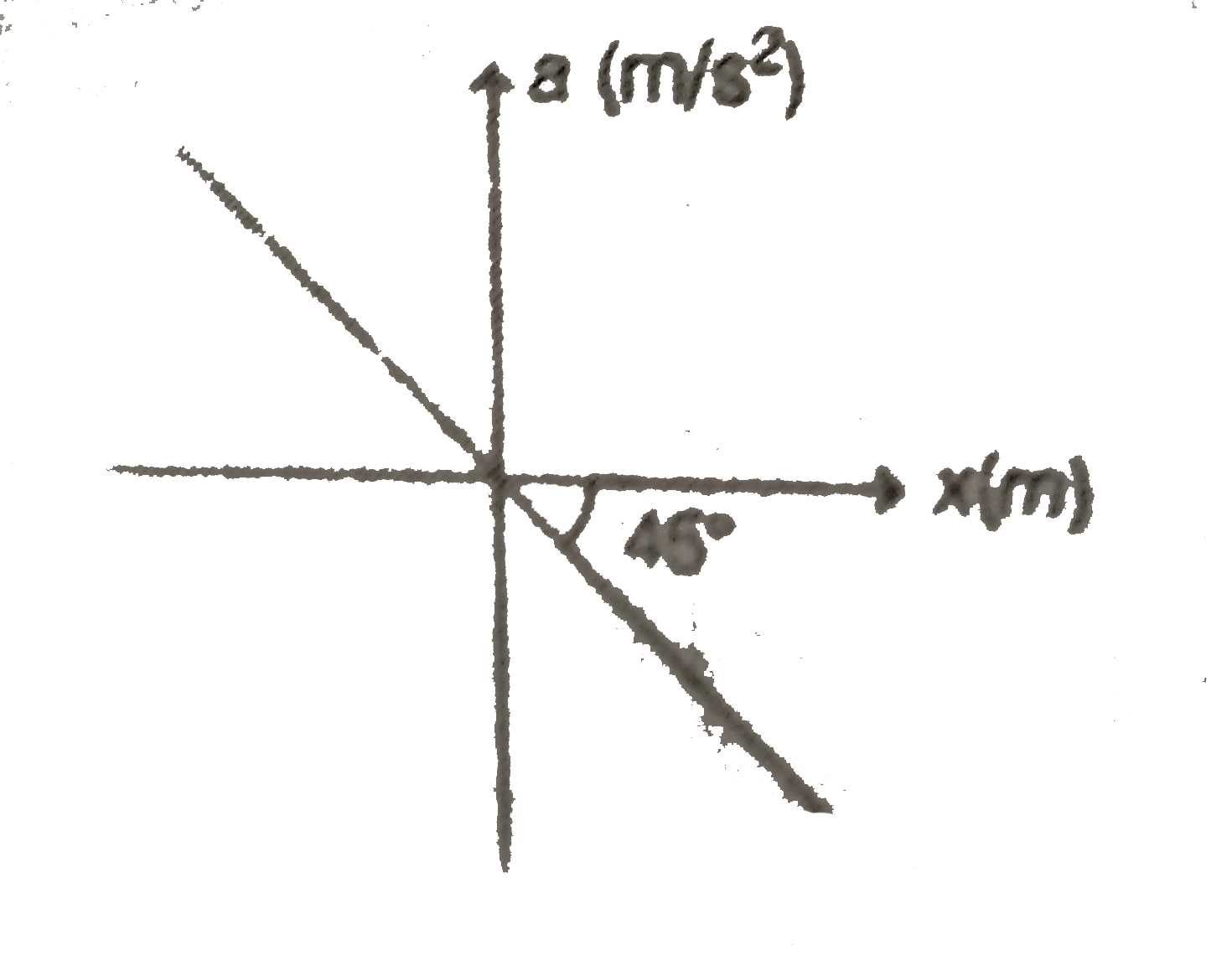
v-t graph of a particle is SHM is as shown in figure Choose the wrong option.
 View Solution
View SolutionQuestion 128
Passage V) In SHM displacement, velocity and acceleration all oscillate simple harmonically with same angular frequency ω. Phase difference between any two is π2 except that between displacement and acceleration which is π.
Displacement -time equation of a particle is given as x=Asin(ωt+π6)−Acos(ωt+π6), then: View SolutionQuestion 133
Passage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be as View SolutionQuestion 136
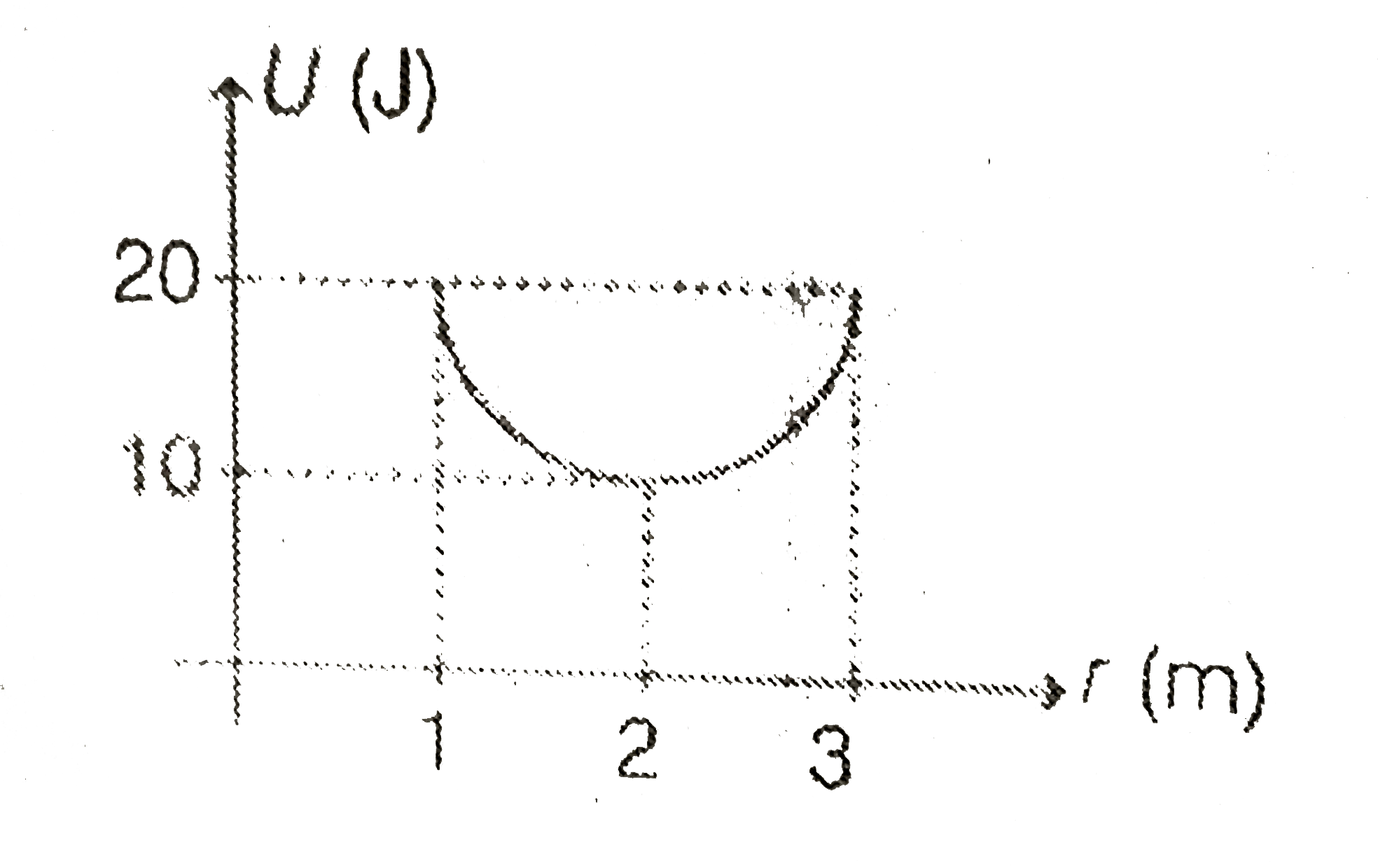
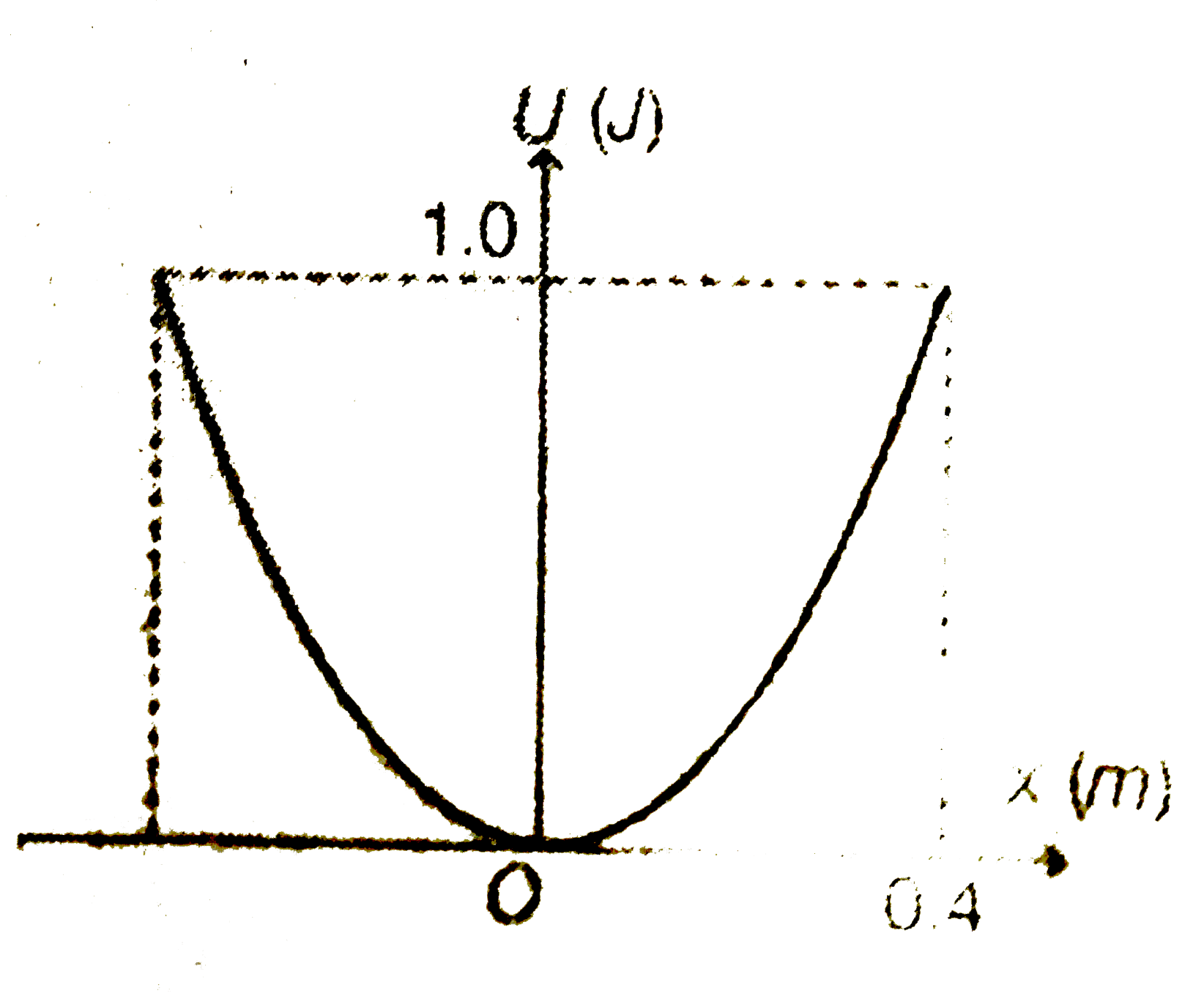
Passage IX) For SHM to take place force acting on the body should be proportional to -x or F = -kx. If A be the amplitude then energy of oscillation is 12kA2
Force acting on a block is F = ( − 4 x + 8 ) .
Here F is in Newton and x the position of block on x-axis in meter If energy of osciallation is 18 J, between what points the block will oscillate? View SolutionQuestion 137
Passage X) A 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400 N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5ms2 when the acceleration suddenly ceases at t=0 and the car moves upward with constant speed. (g=10m/s2)
What is the angular frequency of oscillation of the block after the acceleration ceases?View SolutionQuestion 138
Passage X) A 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400 N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5ms2 when the acceleration suddenly ceases at t=0 and the car moves upward with constant speed. (g=10m/s2)
The amplitude of the oscillations is View SolutionQuestion 139
A 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5m/s2 when the acceleration suddenly ceases at time t=0 and the car moves upward with constant speed (g=10m/s2 The amplitude of the oscillation isView SolutionQuestion 143
Passage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
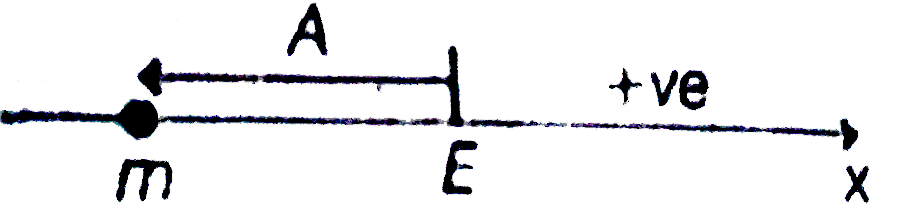 View Solution
View SolutionQuestion 144
Passage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
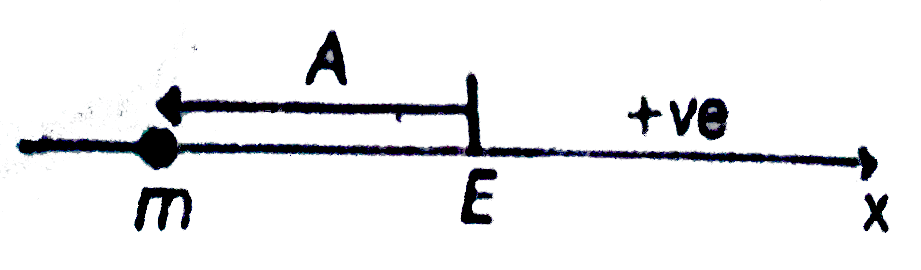 View Solution
View SolutionQuestion 145
Passage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Find minimum time it will take to reach from x=−A2 to 0
 View Solution
View SolutionQuestion 146
Passage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec−1 and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take (π2) = 10 and g = 10 m/s2. Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct]
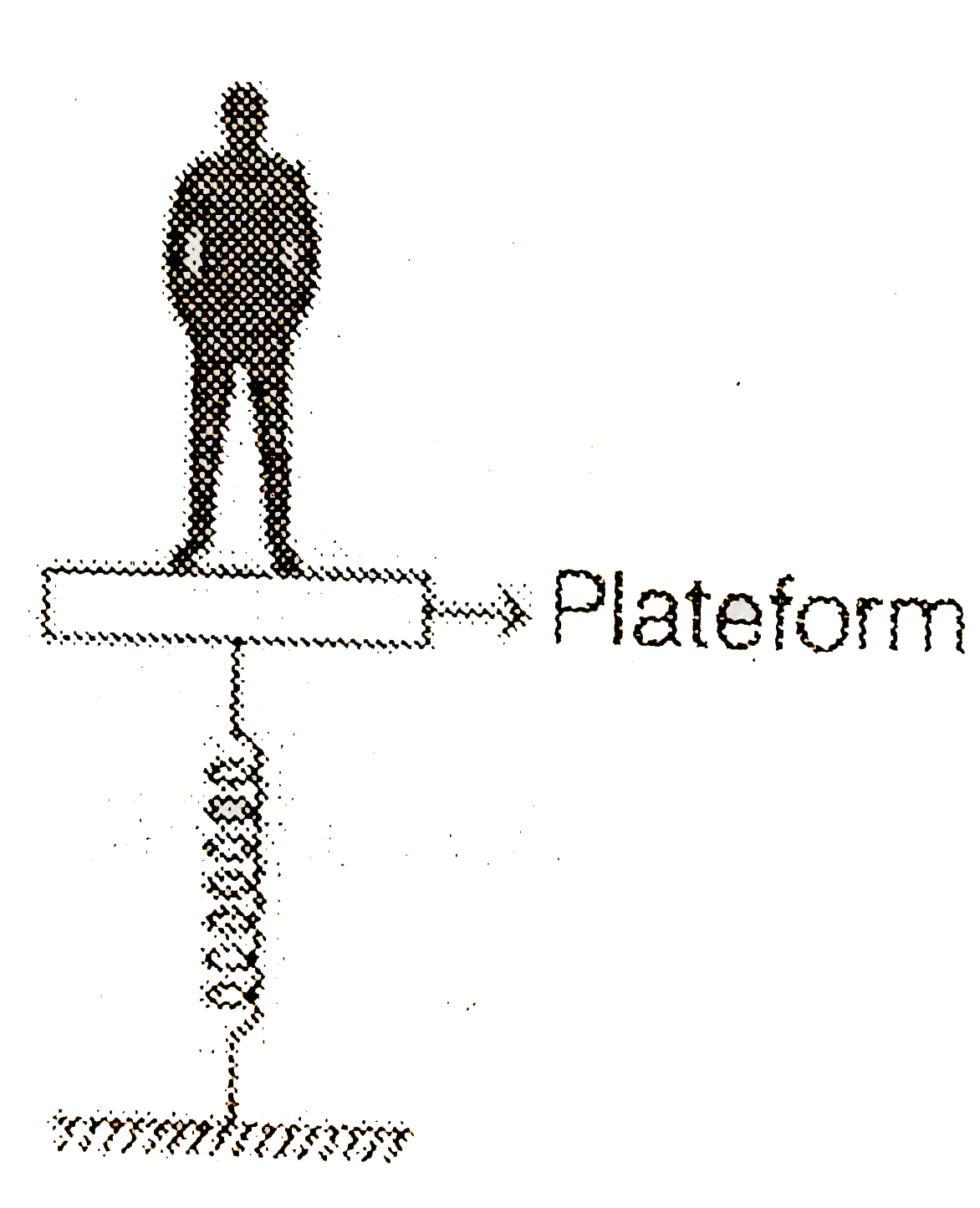
Which of the following will be correct for reading of weighting machine View SolutionQuestion 147
Passage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec−1 and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take (π2) = 10 and g = 10 m/s2. Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct]
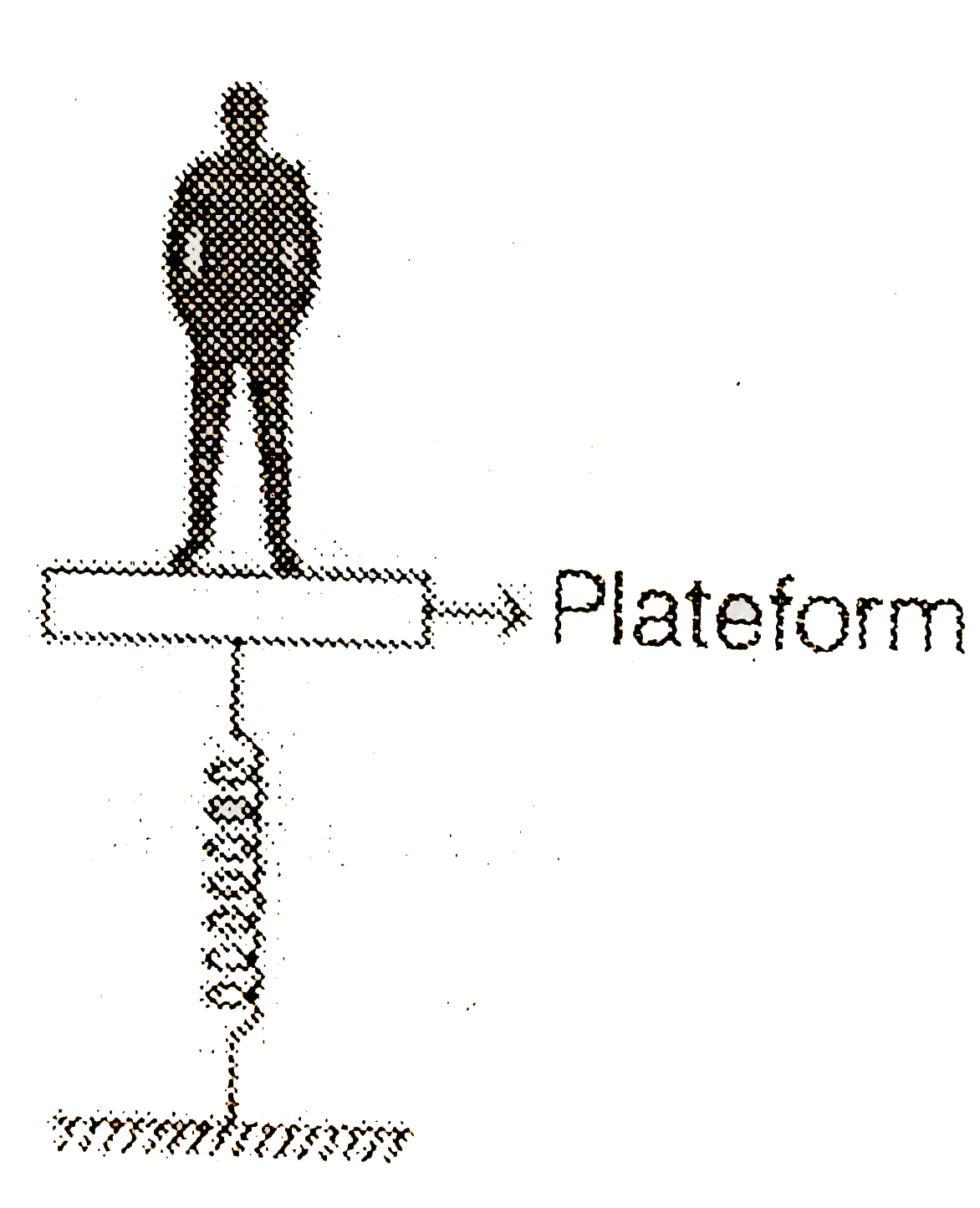
Which of the following will be correct for reading of weighting machine View SolutionQuestion 148
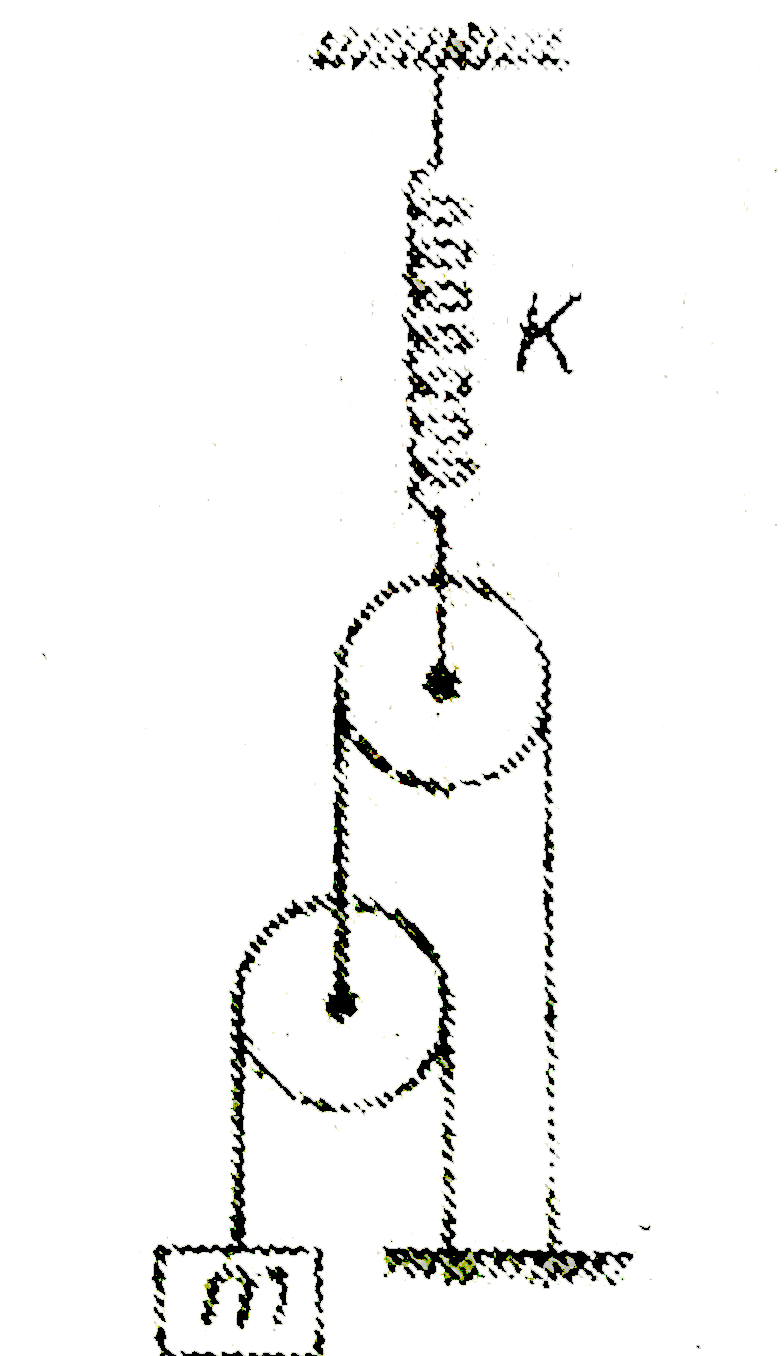
Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
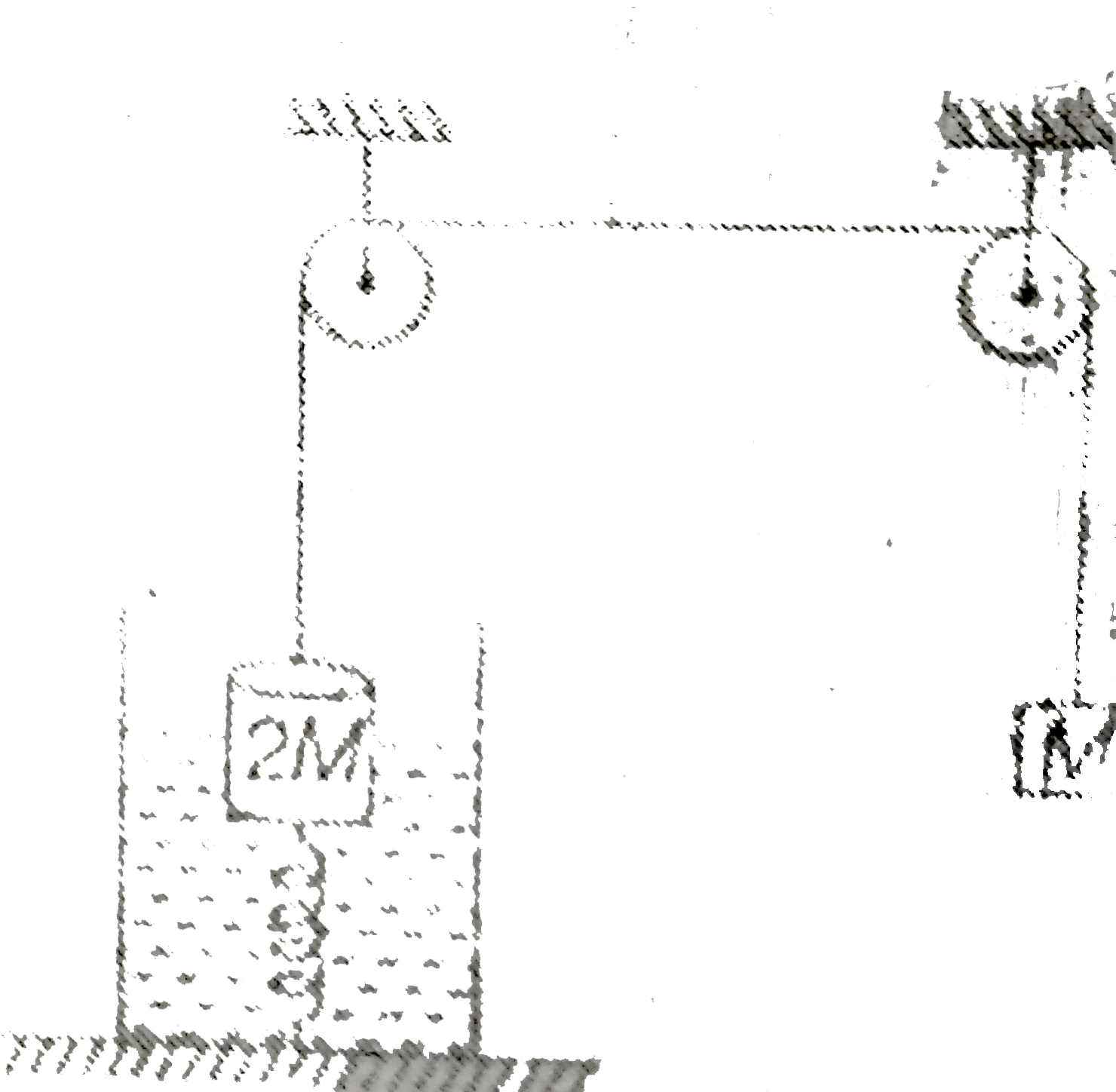 View Solution
View SolutionQuestion 149
Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]View SolutionQuestion 150
Passage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
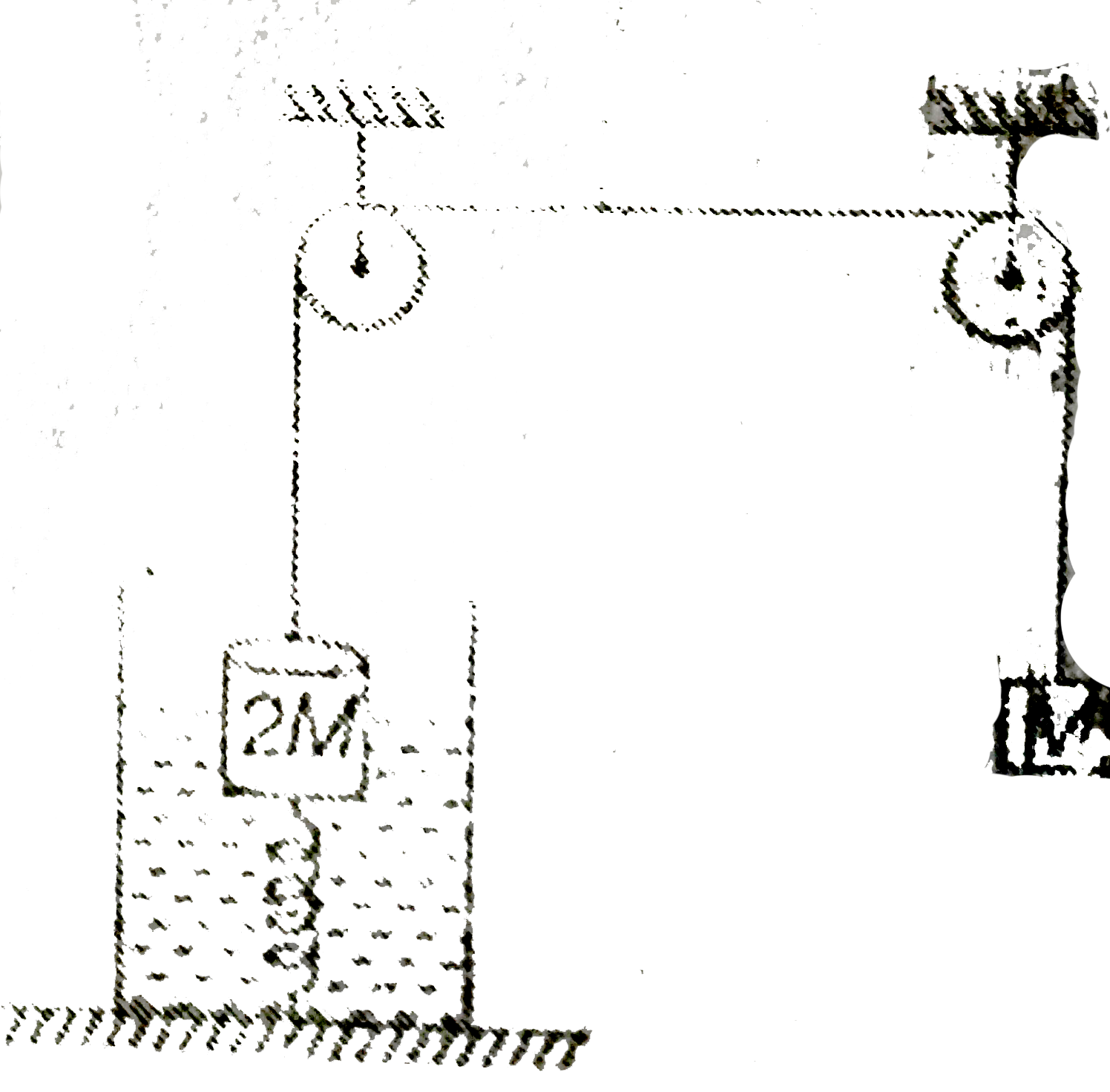
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion. View SolutionQuestion 163
A simple harmonic oscillator consists of a block attached to a spring with k=200N/m. The block slides on a frictionless horizontal surface, with equilibrium point x=0. A graph of the block velocity v as a function of time t is shown. Correct match the required information in the left column with the values given in table.
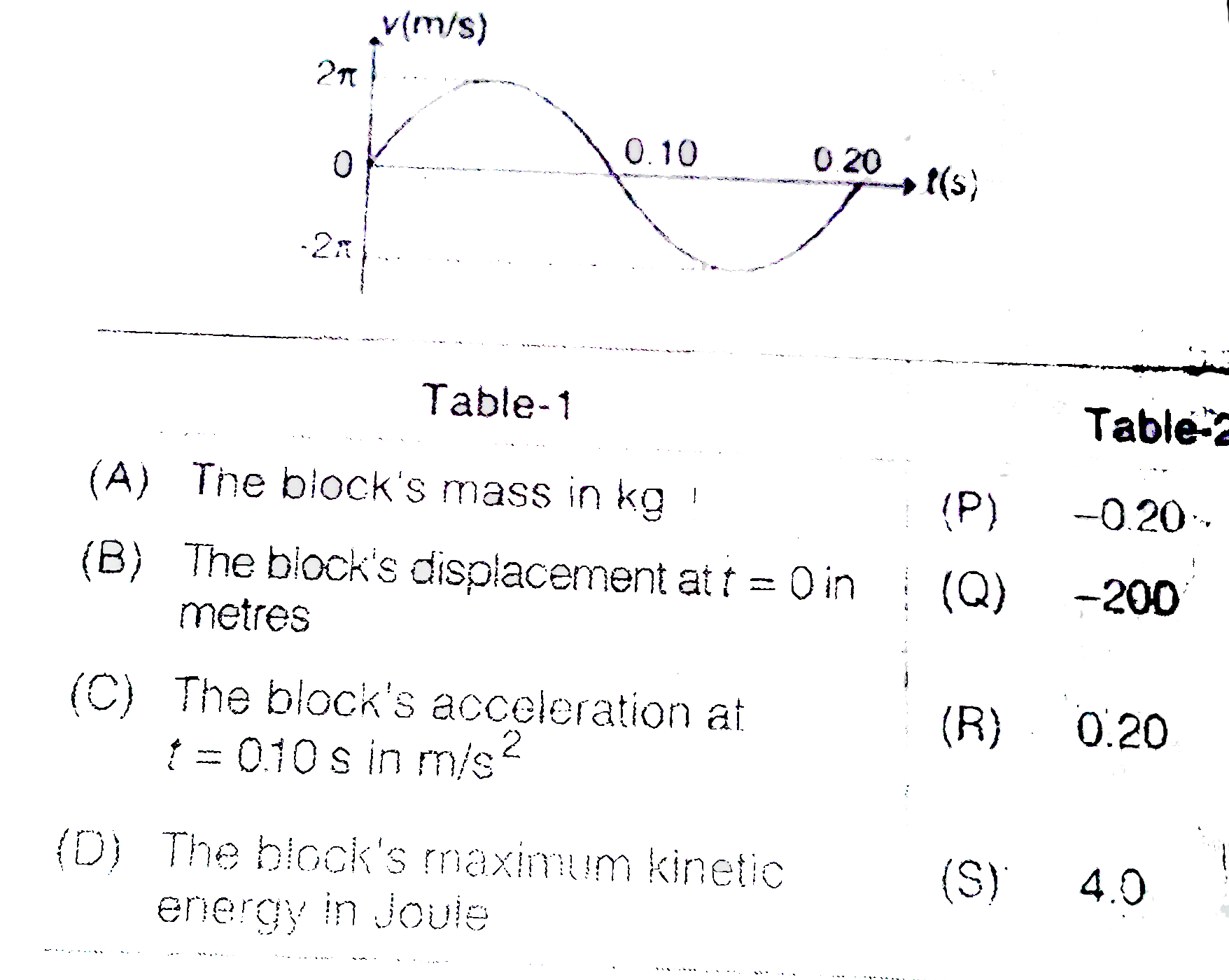 View Solution
View SolutionQuestion 166
A block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring. View SolutionQuestion 170
A cubical block of mass M vibrates horizontally with amplitude of 4.0 cm and a frequency of 2.0 Hz. A small block of mass is placed on the bigger block. In order that the smaller block does not side on the bigger block, the minimum value of the coefficient of static friction between the two blocks is (0.16x). Find the valule of x(Take π2=10 and g=10m/s2)View SolutionQuestion 171
A spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)View SolutionQuestion 175
Two springs of spring constant mgl each are attached to the end of a uniform rod of mass m and length l=53m which is hinged in vertical plane as shown in figure. As the rod is rotated slightly about the hinge, it undergoes SHM with angular frequency ω. Find ω in rad/s.) Take g=10ms2.
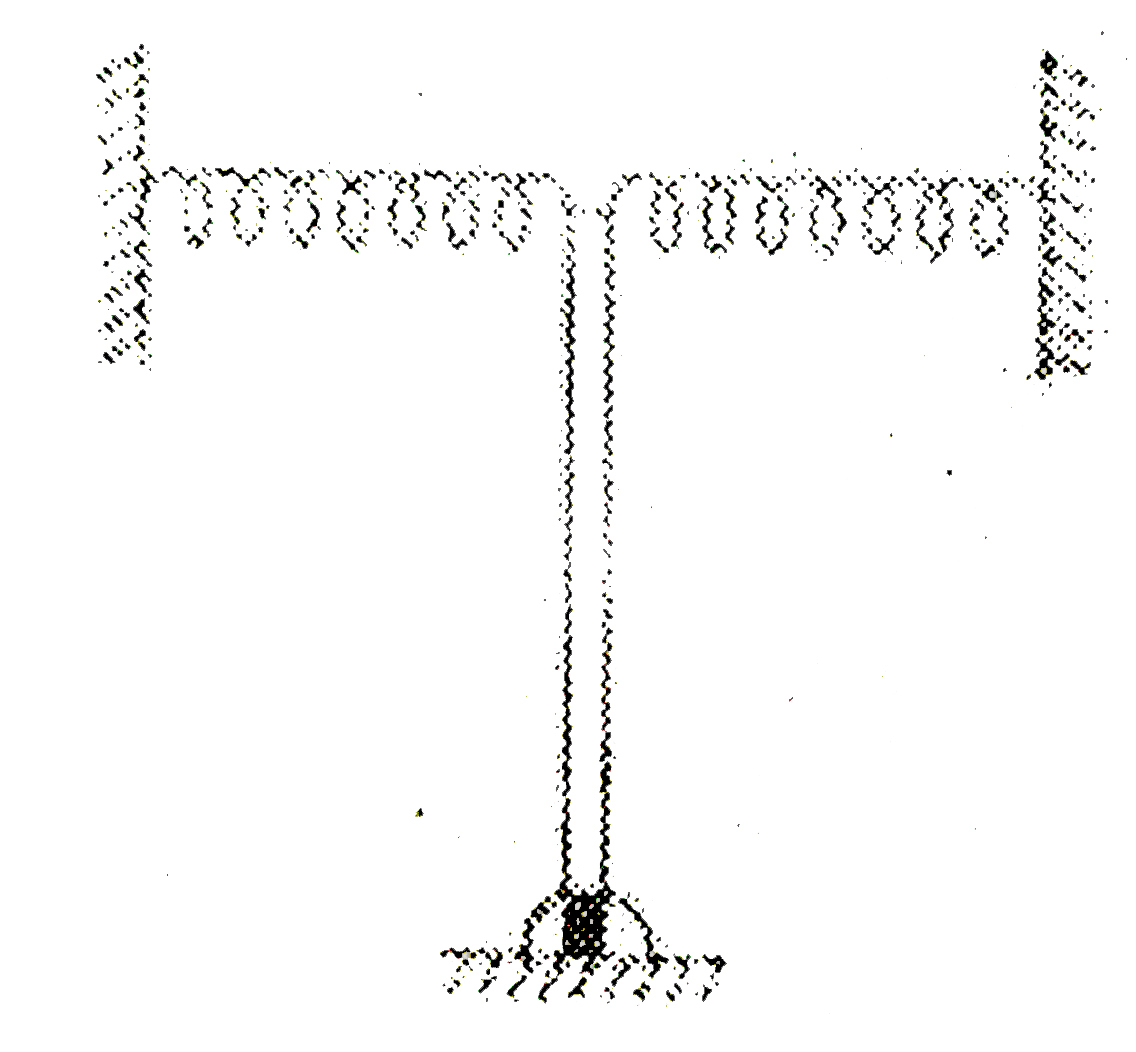 View Solution
View Solution
All Exercises from DC PANDEY ENGLISH Class 11 PHYSICS SIMPLE HARMONIC MOTION
- ASSERTION AND REASON
- CHAPTER EXERCISES
- CHECK POINT 11.1
- CHECK POINT 11.2
- CHECK POINT 11.3
- CHECK POINT 11.4
- COMPREHENSION TYPES
- EXERCISE 14.1
- EXERCISE 14.2
- EXERCISE 14.3
- EXERCISE 14.4
- INTEGER TYPE QUESTIONS
- INTRO. EXER.
- JEE ADVANCED
- LEVEL 1 ASSERTION AND REASON
- LEVEL 1 SINGLE CORRECT
- LEVEL 1 SUBJECTIVE
- LEVEL 2 COMPREHENSION
- LEVEL 2 MORE THAN ONE CORRECT
- LEVEL 2 SINGLE CORRECT
- LEVEL 2 SUBJECTIVE
- MATCH THE COLUMNS
- MATRIX MATCHING TYPE QUESTIONS
- MEDICAL ENTRACES GALLERY
- MORE THAN ONE OPTION IS CORRECT
- ONLY ONE QUESTION IS CORRECT
- EXAMPLE
- EXAMPLE TYPE 1
- EXAMPLE TYPE 10
- EXAMPLE TYPE 11
- EXAMPLE TYPE 12
- EXAMPLE TYPE 13
- EXAMPLE TYPE 2
- EXAMPLE TYPE 3
- EXAMPLE TYPE 4
- EXAMPLE TYPE 5
- EXAMPLE TYPE 6
- EXAMPLE TYPE 7
- EXAMPLE TYPE 8
- EXAMPLE TYPE 9
- EXAMPLES
- MISCELLANEOUS EXAMPLES