Level 1 Assertion And Reason from DC PANDEY ENGLISH SIMPLE HARMONIC MOTION for Class 11

Class 11	PHYSICS
Chapter	SIMPLE HARMONIC MOTION
DC PANDEY ENGLISH	Level 1 Assertion And Reason
Medium	English
Academic Year	2023-2024

Question 1
Assertion : In $x = A cos ω t$ , $x$ is the displacement measured from extreme position.
Reason : In the above equation $x = A$ at time $t = 0$ . View Solution
Question 2
Assertion : A particle is under SHM along the x - axis. Its mean position is $x = 2$ , amplitude is $A = 2$ and angular frequency $ω$ . At $t = 0$ , particle is at origin, then $x$ - co-ordinate versus time equation of the particle will be $x = - 2 cos ω t + 2$ .
Reason : At $t = 0$ , particle is at rest.View Solution
Question 3
Assertion : A spring block system is kept over a smooth surface as shown in figure. If a constant horizontal force $F$ is applied on the block it will start oscillating simple harmonically.
Reason : Time period of oscillation is less then $2 π \sqrt{\frac{m}{k}}$ .View Solution
Question 4
Assertion : Time taken by a particle in SHM to move from $x = A$ to $x = \frac{\sqrt{3 A}}{2}$ is same as the time taken by the particle to move from $x = \frac{\sqrt{3 A}}{2}$ to $x = \frac{A}{2}$ .
Reason : Corresponding angles rotated is the reference circle are same in the given time intervals. View Solution
Question 5
Assertion : Path of a particle in SHM is always a straight line.
Reason : All straight line motions are not simple harmonic.View Solution
Question 6
Assertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by $ω = \sqrt{\frac{k}{m}}$ .View Solution
Question 7
Assertion : All small oscillation are simple harmonic in nature.
Reason : Oscillation of spring block system are always simple harmonic whether amplitude is small or large.View Solution
Question 8
Assertion : In $x = A cos ω t$ , the dot product of acceleration and velocity is positive for time interval $0 < t < \frac{π}{2 ω}$ . Reason : Angle between them is $0^{\circ}$ .View Solution
Question 9
Assertion : For a given simple harmonic motion displacement (from the mean position) and acceleration have a constant ratio.
Reason : $T = 2 π \sqrt{∣ ∣ ∣ \frac{displacement}{acceleration} ∣ ∣ ∣}$ . View Solution
Question 10
Assertion : We can call circular motion also as simple harmonic motion.
Reason : Angular velocity in uniform circular motion and angular frequency in simple harmonic motion have the same meanings.View Solution
Question 11
A simple harmonic oscillation has an amplitude $A$ and time period $T$ . The time required to travel from $x = A$ to $x = \frac{A}{2}$ is View Solution
Question 12
The potential energy of a particle executing SHM varies sinusoidally with frequency $f$ . The frequency of oscillation of the particle will be View Solution
Question 13
For a particle undergoing simple harmonic motion, the velocity is plotted against displacement. The curve will be View Solution
Question 14
A simple pendulum is made of bob which is a hollow sphere full of sand suspended by means of a wire. If all the sand is drained out, the period of the pendulum will View Solution
Question 15
Two simple harmonic motions are given by $y_{1} = a sin [(\frac{π}{2}) t + ϕ]$ and $y_{2} = b sin [(\frac{2 π}{3}) t + ϕ]$ . The phase difference between these after $1 s$ is View Solution
Question 16
A particle starts performing simple harmonic motion. Its amplitude is $A$ . At one time its speed is half that of the maximum speed. At this moment the displacement is View Solution
Question 17
Which of the following is not simple harmonic function ?View Solution
Question 18
The displacement of a particle varies according to the relation $x = 4 (cos π t + sin π t)$ . The amplitude of the particle is.View Solution
Question 19
Two pendulums $X$ and $Y$ of time periods $4 s$ and $4.2 s$ are made to vibrate simultaneously. They are initially in same phase. After how many vibration of $X$ , they will be in the same phase again ?View Solution
Question 20
A mass $M$ is suspended from a massless spring. An additional mass $m$ stretches the spring further by a distance $x$ . The combined mass will oscillate with a period View Solution
Question 21
Two bodies $P$ and $Q$ of equal masses are suspended from two separate massless springs of force constants $k_{1}$ and $k_{2}$ respectively. If the two bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitude of $P$ to that of $Q$ is View Solution
Question 22
A disc of radius $R$ is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is View Solution
Question 23
Identify the correct variation of potential energy $U$ as a function of displacement $x$ from mean position (or $x^{2}$ ) of a harmonic oscillator ( $U$ at mean position $= 0$ )View Solution
Question 24
If the length of a simple pendulum is equal to the radius of the earth, its time period will be View Solution
Question 25
The displacement - time $(x - t)$ graph of a particle executing simple harmonic motion is shown in figure. The correct variation of net force F action on the particle as a function of time is
View Solution
Question 26
In the figure shown the time period and the amplitude respectively, when $m$ is left from rest when spring is relaxed are (the inclined plane is smooth)
View Solution
Question 27
The equation of motion of a particle of mass $1 g$ is $\frac{d^{2} x}{{d t}^{2}} + π^{2} x = 0$ , where $x$ is displacement (in m) from mean position. The frequency of oscillation is (in Hz)View Solution
Question 28
The spring as shown in figure is kept in a stretched position with extension $x$ when the system is relesed. Assuming the horizontal surface to be frictionless, the frequency of oscillation is
View Solution
Question 29
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this plenet. If is a second's pendulum on earth? View Solution
Question 30
The resultant amplitude due to superposition of three simple harmonic motions $x_{1} = 3 sin ω t$ ,
$x_{2} = 5 sin (ω t + 37^{\circ})$ and $x_{3} = - 15 cos ω t$ is View Solution
Question 31
Two SHMs $s_{1} = a sin ω t$ and $s_{2} = b sin ω t$ are superimposed on a particle. The $s_{1}$ and $s_{2}$ are along the direction which makes $37^{\circ}$ to each other View Solution
Question 32
The amplitude of a particle executing SHM about $O$ is $10 c m$ . Then View Solution
Question 33
A particle is attached to a vertical spring and is pulled down a distance $4 c m$ below its equilibrium and is released from rest. The initial upward acceleration is $0.5 m s^{- 2}$ . The angular frequency of oscillation is View Solution
Question 34
A block of mass $1 k g$ is kept on smooth floor of a truck. One end of a spring of force constant $100 N / m$ is attached to the block and other end is attached to the body of truck as shown in the figure. At $t = 0$ , truck begins to move with constant acceleration $2 m / s^{2}$ . The amplitude of oscillation of block relative to the floor of truck is
View Solution
Question 35
Find the period of oscillation of the system shown in figure.
View Solution
Question 36
A block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take $g = 10 m / s^{2}$ . Neglect friction
View Solution
Question 37
A body of weight $27 N$ hangs on a long spring of such stiffness that an extra force of $9 N$ stretches the spring by $0.05 m$ . If the body is pulled downward and released, what is the period ?View Solution
Question 38
A clock with an iron pendulum keeps correct time at $20^{\circ} C$ . How much time will it lose or gain in a day if the temperature changes to $40^{\circ} C$ . Thermal coefficient of liner expansion $α = 0.000012 p e r^{\circ} C$ . View Solution
Question 39
A $50 g$ mass hangs at the end of a massless spring. When $20 g$ more are added to the end of the spring, it stretches $7.0 c m$ more. (a) Find the spring constant. (b) If the $20 g$ are now removed, what will be the period of the motion ?View Solution
Question 40
An object suspended from a spring exhibits oscillations of period $T$ . Now ,the spring is cut in half and the two halves are used to support the same object, as shown in figure. The new period of oscillation is .
.View Solution
Question 41
The string, spring and the pulley shown in figure are light. Find the time period of the mass $m$ .
View Solution
Question 42
A simple pendulum with a solid metal bob has a period $T$ . What will be the period of the same pendulum if it is made to oscillate in a non - viscous liquid of density one - tenth of the of the metal of the bob ? View Solution
Question 43
A particle moves under the force $F (x) = (x^{2} - 6 x) N$ , where $x$ is in metres. For small displacements from the origin what is the force constant in the simple harmonic motion approximation ?View Solution
Question 44
The initial position and velocity of a body moving in SHM with period $T = 0.25 s$ are $x = 5.0 c m$ and $v = 218 c m / s$ . What are the amplitude and phase constant of the motion ? View Solution
Question 45
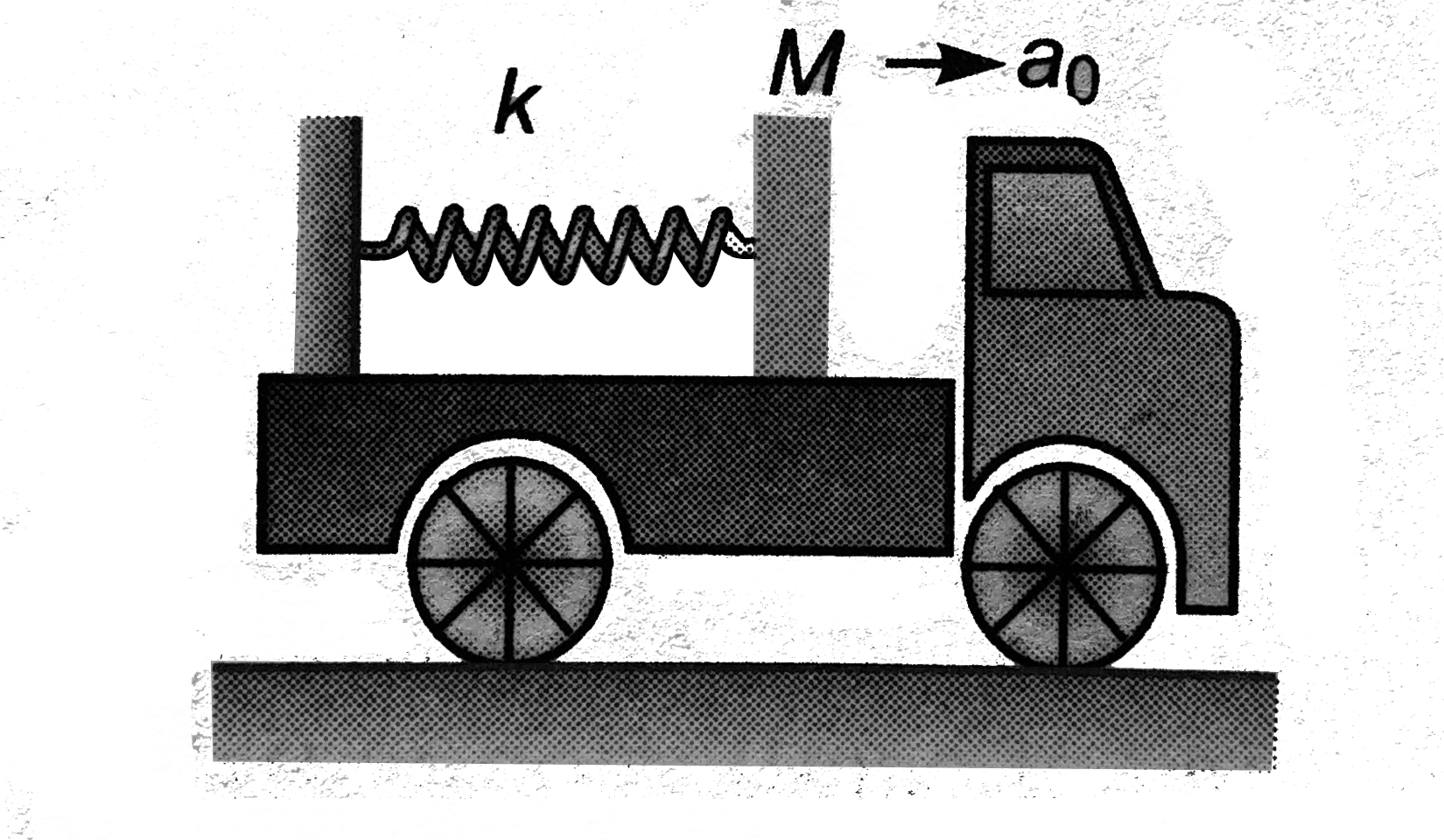A point particle if mass $0.1 k g$ is executing SHM of amplitude $0.1 m$ . When the particle passes through the mean position, its kinetic energy is $8 \times 10^{- 3} J$ . Write down the equation of motion of this particle when the initial phase of oscillation is $45^{\circ}$ .View Solution
Question 46
Potential energy of a particle in SHM along x - axis is gives by
$U = 10 + {(x - 2)}^{2}$
Here, $U$ is in joule and $x$ in metre. Total mechanical energy of the particle is $26 J$ . Mass of the particle is $2 k g$ . Find
(a) angular frequency of SHM,
(b) potential energy and kinetic energy at mean position and extreme position,
(c ) amplitude of oscillation,
(d) x - coordinates between which particle oscillates.View Solution
Question 47
A simple pendulum is taken at a place where its separation from the earth's surface is equal to the radius of the earth. Calculate the time period of small oscillation if the length of the string is $1.0 m$ . Take $g = π^{2} m / s^{2}$ at the surface of the earth.View Solution
Question 48
A solid cylinder of mass $M = 10 k g$ and cross - sectional area $A = 20 c m^{2}$ is suspended by a spring of force contant $k = 100 N / m$ and hangs partically immersed in water. Calculate the period of small oscillation of the cylinder.View Solution
Question 49
A simple pendulum of length $l$ and mass $m$ is suspended in a car that is moving with constant speed $v$ around a circle of radius $r$ . Find the period of oscillation and equilibrium position of the pendulum.View Solution
Question 50
A body of mass $0.10 k g$ is attached to vertical massless spring with force constant $4.0 \times 10^{3} N / m$ . The body is displaced $10.0 c m$ from its equilibrium position and released. How much time elapses as the body moves from a point $8.0 c m$ on one side of the equilibrium position to a point $6.0 c m$ on the same side of the equilibrium position ?View Solution
Question 51
A body of mass $200 g$ is in equibrium at $x = 0$ under the influence of a force $F (x) = (- 100 x + 10 x^{2}) N$ .
(a) If the body is displacement a small distance from equilibrium, what is the period of its oscillations ?
(b) If the amplitude is $4.0 c m$ , by how much do we eror in assuming that $F (x) = - k x$ at the end points of the motion.View Solution
Question 52
A ring of radius $r$ is suspended from a point on its circumference. Determine its angular frequency of small oscillations.
View Solution
Question 53
A spring mass system is hanging from the celling of an elevator in equilibrium. The elevator suddenly starts accelerating upwards with acceleration a. Find

(a) the frequency and
(b) the amplitude of the resulting SHM.View Solution
Question 54
A body makes angular simple harmonic motion of amplitude $π / 10 r a d$ and time period $0.05 s$ . If the body is at a displacement $θ = π / 10 r a d$ at $t = 0$ , write the equation giving angular displacement as a function of time.View Solution
Question 55
A particle executes simple harmonic motion of period $16 s$ . Two seconds later after it passes through the center of oscillation its velocity is found to be $2 m / s$ . Find the amplitude.View Solution
Question 56
A simple pendulum consists of a small sphere of mass $m$ suspended by a thread of length $l$ . the sphere carries a positive charge $q$ . The pendulum is placed in a uniform electric field of strength $E$ directed vertically upwards. With what period will the pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force? View Solution
Question 57
Find the period of oscillation of a pendulum of length $l$ if its point of suspension is
(a) moving vertically up with acceleration $a$
(b) moving vertically down with acceleration $a (< g)$
(c) failing freely under gravity
moving horizontal with acceleration $a$ .View Solution
Question 58
A block with mass $M$ attached to a horizontal spring with force constant $k$ is moving with simple harmonic motion having amplitude $A_{1}$ . At the instant when the block passes through its equilibrium position a lump of putty with mass $m$ is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.View Solution
Question 59
A bullet of mass $m$ strikes a block of mass $M$ . The bullet remains embedded in the block. Find the amplitude of the resulting SHM.
View Solution
Question 60
An annular ring of internal and outer radii $r$ and $R$ respectively oscillates in a vertical plane about a horizontal axis perpendicular to its plane and passing through a point on its outer edge. Calculate its time period and show that the length of an equivalent simple pendulum is $\frac{3 R}{2}$ as $r \to 0$ and $2 R$ as $r \to R$ .View Solution
Question 61
A body of mass $200 g$ oscillates about a horizontal axis at a distance of $20 c m$ from its centre of gravity . If the length of the equivalent simple pendulum is $35 c m$ , find its moment of inertia about the point of suspension. View Solution
Question 62
Show that the period of oscillation of simple pendulum at depth $h$ below earth's surface is inversely proportional to $\sqrt{R - h}$ , where $R$ is the radius of earth. Find out the time period of a second pendulum at a depth $R / 2$ from the earth's surface ? View Solution
Question 63
The period of a particle in SHM is $8 s$ . At $t = 0$ it is in its equilibrium position.
(a) Compare the distance travelled in the first $4 s$ and the second $4 s$ .
(b) Compare the distance travelled in the first $2 s$ and the second $2 s$ . View Solution
Question 64
(a) The motion of the particle in simple harmonic motion is given by $x = a sin ω t$ . If its speed is $u$ , when the displacement is $x_{1}$ and speed is $v$ , when the displacement is $x_{2}$ , show that the amplitude of the motion is
$A = {[\frac{v^{2} x_{1}^{2} - u^{2} x_{2}^{2}}{v^{2} - u^{2}}]}^{1 / 2}$
(b) A particle is moving with simple harmonic motion is a straight line. When the distance of the particle from the equilibrium position has the values $x_{1}$ and $x_{2}$ the corresponding values of velocity are $u_{1}$ and $u_{2}$ , show that the period is
$T = 2 π {[\frac{x_{2}^{2} - x_{1}^{2}}{u_{1}^{2} - u_{2}^{2}}]}^{1 / 2}$ View Solution
Question 65
Show that the combined spring energy and gravitational energy for a mass $m$ hanging from a light spring of force constant $k$ can be expressed as $U_{0} + \frac{1}{2} k y^{2}$ , where $y$ is the distance above or below the equilibrium position and $U_{0}$ is constant.View Solution
Question 66
The masses in figure slide on a frictionless table. $m_{1}$ but not $m_{2}$ , is fastened to the spring. If now $m_{1}$ and $m_{2}$ are pushed to the left , so that the spring is compressed a distance $d$ , what will be the amplitude of the oscillation of $m_{1}$ after the spring system is released ?
View Solution
Question 67
The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is $M$ . If the man exerts a constant force $F$ , find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.View Solution
Question 68
In figure, $k = 100 N / m, M = 1 k g$ and $F = 10 N$

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of $2 m / s$ to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?View Solution
Question 69
Pendulum $A$ is a physical pendulum made from a thin, rigid and uniform rod whose length is $d$ . One end of this rod is attached to the ceiling by a frictionless hinge, so that the rod is free to swing back and forth. Pendulum $B$ is a simple pendulum whose length is also $d$ . Obtain the ratio $\frac{T_{A}}{T_{B}}$ of their periods for small angle oscillations.View Solution
Question 70
A solid cylinder of mass $m$ is attached to a horizontal spring with force constant $k$ . The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period $T = 2 π \sqrt{\frac{3 m}{2 k}}$ , if displaced from mean position.
View Solution
Question 71
A cord is attached between a 0.50 kg block and a string with force constant $k = 20 N / m$ .The other end of the spring is attrached to the wall and the cord is placed over a pulley $(I = 0.60 M R^{2})$ of mass 5.0 kg and radius 0.50 m.(See the accompanying figure.) Assuming no slipping occurs what is the frequency of the oscillations when the body is set into motion ?
View Solution
Question 72
Two linear SHM of equal amplitudes $A$ and frequencies $ω$ and $2 ω$ are impressed on a particle along $x$ and $y - a x e s$ respectively. If the initial phase difference between them is $π / 2$ . Find the resultant path followed by the particle.View Solution
Question 73
A particle is subjected to two simple harmonic motions given by
$x_{1} = 2.0 sin (100 π t)$ and $x_{2} = 2.0 sin (120 π t + π / 3)$
where, $x$ is in $c m$ and $t$ in second. Find the displacement of the particle at
(a) $t = 0.0125$ ,
(b) $t = 0.025$ .View Solution
Question 74
A particle of mass $2 k g$ moves in simple harmonic motion and its potential energy $U$ varies with position $x$ as shown. The period of oscillation of the particle is
View Solution
Question 75
In the figure shown, a spring mass system is placed on a horizontal smooth surface in between two vertical rigid walls $W_{1}$ and $W_{2}$ . One end of spring is fixed with wall $W_{1}$ and other end is attached with mass $m$ which is free to move. Initially, spring is tension free and having natural length $l_{0}$ . Mass $m$ is compressed through a distance a and released. Taking the collision between wall $W_{2}$ and mass $m$ as elastic and $K$ as spring constant, the average force exerted by mass $m$ on wall $W_{2}$ in one oscillation of block is
View Solution
Question 76
Two simple harmonic motion are represrnted by the following equation $y_{1} = 40 sin ω t$ and $y_{2} = 10 (sin ω t + c cos ω t)$ . If their displacement amplitudes are equal, then the value of $c$ (in appropriate units) is View Solution
Question 77
A particle executes simple harmonic motion with frequqncy $2.5 H z$ and amplitude $2 m$ . The speed of the particle $0.3 s$ after crossing, the equilibrium position is View Solution
Question 78
A particle oscillates simple harmonic motion with a period of $16 s$ . Two second after crossing the equilibrium position its velocity becomes $1 m / s$ . The amplitude is View Solution
Question 79
A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of $4 m / s^{2}$ . Its period of oscillation is View Solution
Question 80
A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are $a$ and $v$ respectively, identify the graph which correctly represents the relation between $a$ and $v$ .View Solution
Question 81
In a vertical $U$ - tube a column of mercury oscillates simple harmonically. If the tube contains $1 k g$ of mercury and $1 c m$ of mercury column weighs $20 g$ , then the period of oscillation is View Solution
Question 82
A solid cube of side a and density $ρ_{0}$ floats on the surface of a liquid of density $ρ$ . If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of View Solution
Question 83
A uniform stick of length $l$ is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance $d$ from the centre of mass. The time period of small oscillation has a minimum value when $d / l$ is View Solution
Question 84
Three arrangements of spring - mass system are shown in figures (A), (B) and ( C). If $T_{1}$ , $T_{2}$ and $T_{3}$ represent the respective periods of oscillation, then correct relation is
View Solution
Question 85
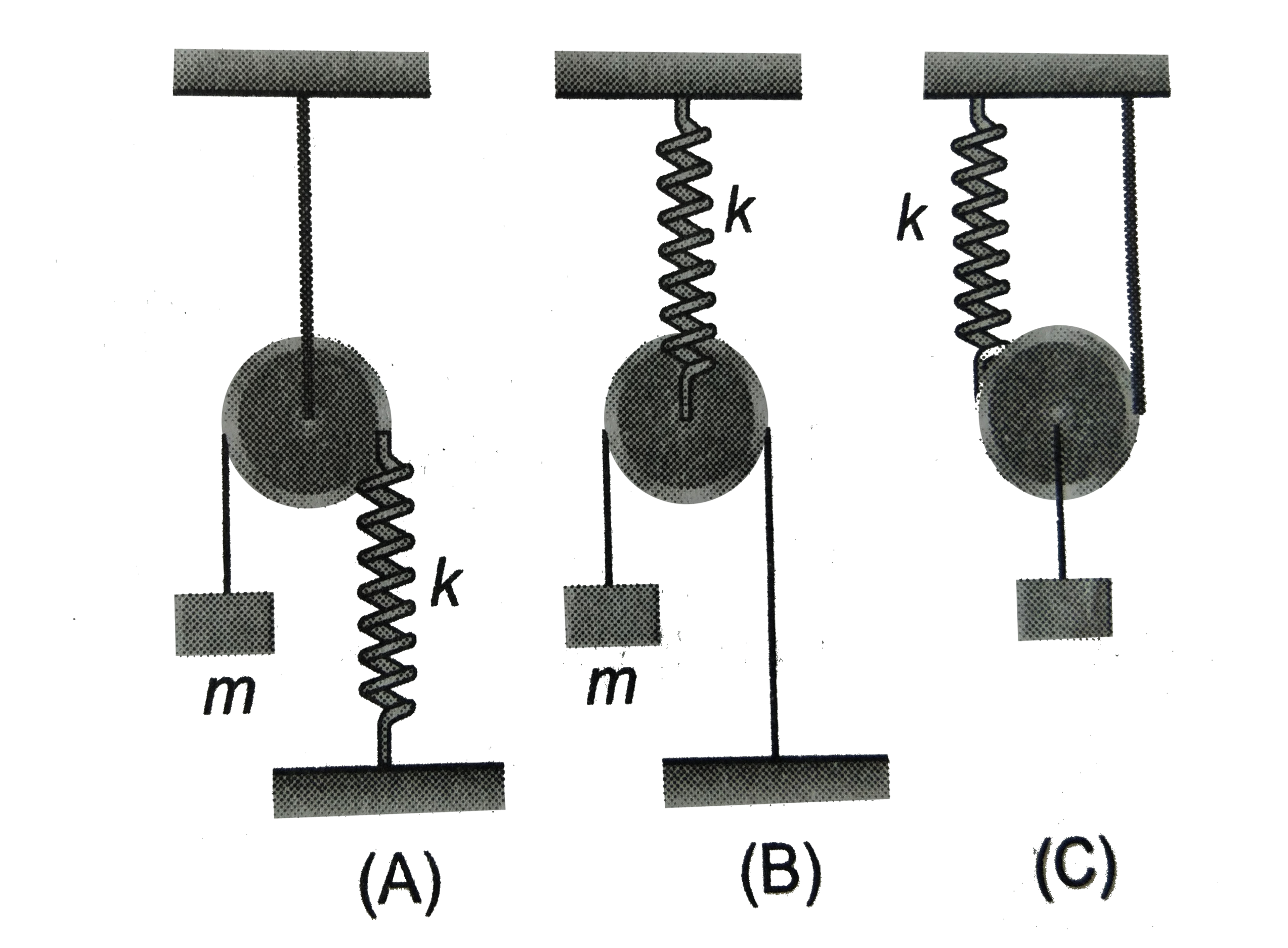
Three arrangements are shown in figure.

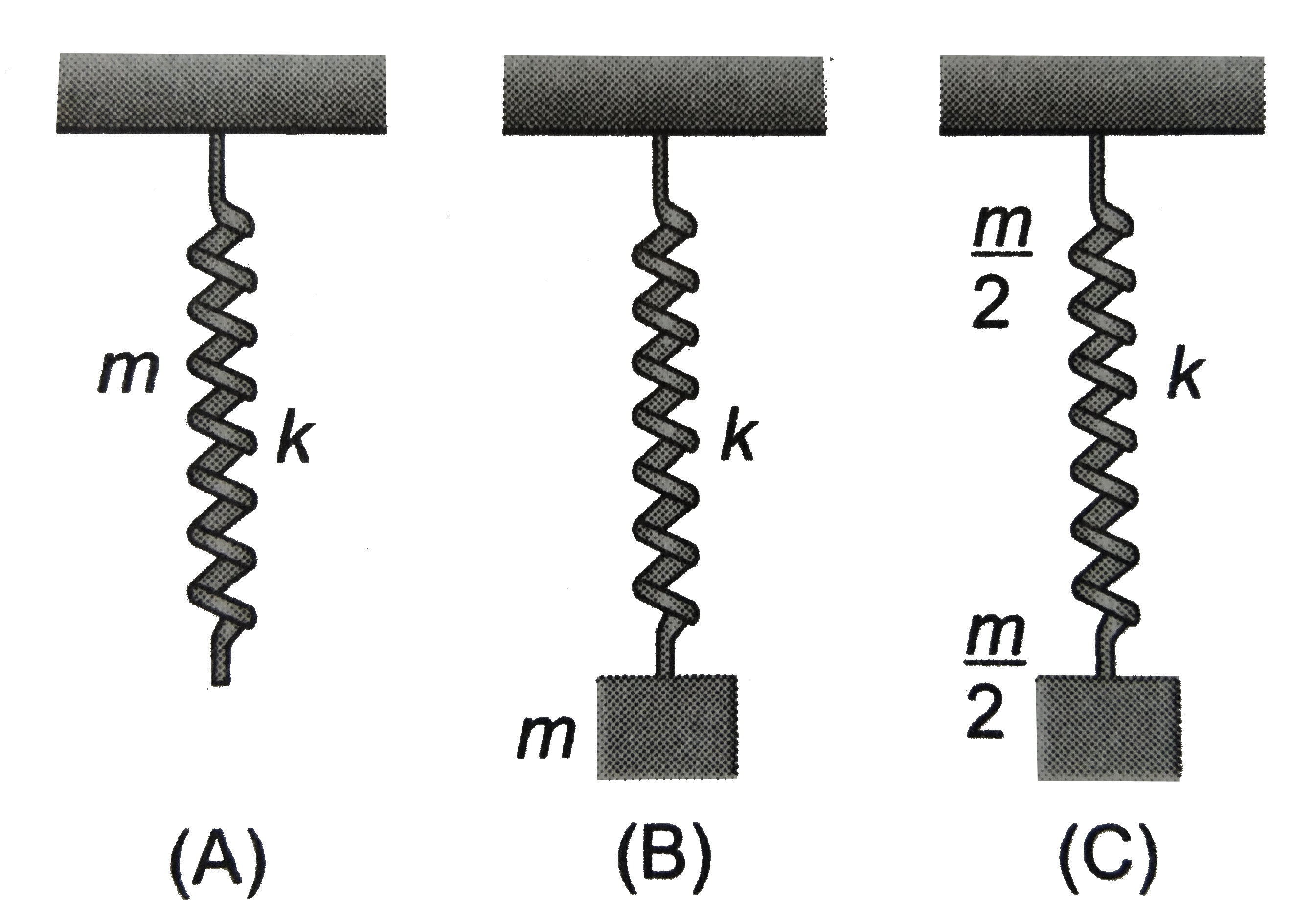
(a) A spring of mass $m$ and stiffness $k$
(b) A block of mass $m$ attached to massless spring of stiffness $k$
( c) A block of mass $\frac{m}{2}$ attached to a spring of mass $\frac{m}{2}$ and stiffness $k$
If $T_{1}$ , $T_{2}$ and $T_{3}$ represent the period of oscillation in the three cases respectively, then identify the correct relation. View Solution
Question 86
A block of mass $M$ is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted $(l_{0} / 2)$ from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be
View Solution
Question 87
A particle moving on x - axis has potential energy $U = 2 - 20 x + 5 x^{2}$ joule along x - axis. The particle is relesed at $x = - 3$ . The maximum value of $x$ will be ( $x$ is in metre)View Solution
Question 88
A block of mass $m$ , when attached to a uniform ideal apring with force constant $k$ and free length $L$ executes SHM. The spring is then cut in two pieces, one with free length n $L$ and other with free length $(1 - n) L$ . The block is also divided in the same fraction. The smaller part of the block attached to longer part of the spring executes SHM with frequency $f_{1}$ . The bigger part of the block attached to smaller part of the spring executes SHM with frequency $f_{2}$ . The ratio $f_{1} / f_{2}$ is View Solution
Question 89
A body performs simple harmonic oscillations along the straight line $A B C D E$ with $C$ as the midpoint of $A E$ . Its kinetic energies at $B$ and $D$ are each one fourth of its maximum value. If $A E = 2 R$ , the distance between $B$ and $D$ is
View Solution
Question 90
In the given figure, two elastic rods P and Q are rigidly joined to end supports. A small mass m is moving with velocity v between the rods. All collisions are assumed to be elastic and the surface is given to be smooth. The time period of small mass m will be (A=area of cross section, Y=Young's modulus, L=length of each rod)
View Solution
Question 91
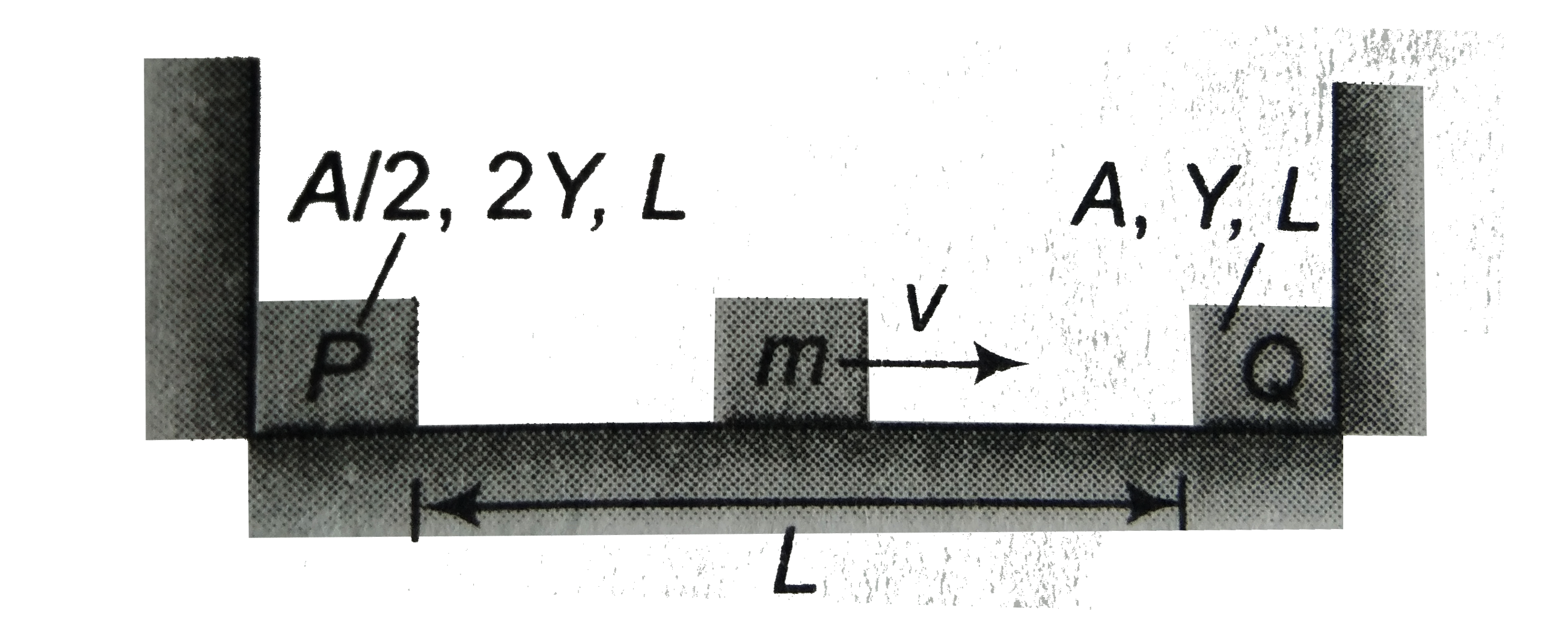A particle executes SHM of period $1.2 s$ and amplitude $8 c m$ . Find the time it takes to travel $3 c m$ from the positive extremity of its oscillation. $[{cos}^{- 1} (5 / 8) = 0.9 r a d]$ View Solution
Question 92
A wire frame in the shape of an equilateral triangle is hinged at one vertex so that it can swing freely in a vertical plane, with the plane of the $Δ$ always remaining vertical. The side of the frame is $1 / \sqrt{3} m$ . The time period in seconds of small oscillations of the frame will be-View Solution
Question 93
A particle moves along the x - axis according to $x = A [1 + sin ω t]$ . What distance does is travel in time interval from $t = 0$ to $t = 2.5 π / ω$ ?View Solution
Question 94
A small bob attached to a light inextensible thread of length $l$ has a periodic time $T$ when allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end $O$ of a vertical rigid rod of length $3 l / 4$ . If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be
View Solution
Question 95
A stone is swinging in a horizontal circle of diameter $0.8 m$ at $30 r e v / min$ . A distant light causes a shadow of the stone on a nearly wall. The amplitude and period of the SHM for the shadow of the stone are View Solution
Question 96
Part of SHM is graphed in the figure. Here, $y$ is displacement from mean position. The correct equation describing the SHM is
View Solution
Question 97
A particle performs SHM with a period $T$ and amplitude a. The mean velocity of particle over the time interval during which it travels $a / 2$ from the extreme position is View Solution
Question 98
A man of mass $60 k g$ is standing on a platform executing SHM in the vertical plane. The displacement from the mean position varies as $y = 0.5 sin (2 π f t)$ . The value of $f$ , for which the man will feel weightlessness at the highest point, is ( $y$ in metre)View Solution
Question 99
A particle performs SHM on a straight line with time period $T$ and amplitude $A$ . The average speed of the particle between two successive instants, when potential energy and kinetic energy become same is View Solution
Question 100
The time taken by a particle performing SHM to pass from point $A$ to $B$ where its velocities are same is $2 s$ . After another $2 s$ it returns to $B$ . The ratio of distance $O B$ to its a amplitude (where $O$ is the mean position) is View Solution
Question 101
A particle is executing SHM according to the equation $x = A cos ω t$ . Average speed of the particle during the interval $0 \leq t \leq \frac{π}{6 ω}$ is View Solution
Question 102
A simple pendulum with a bob of mass $m$ is suspended from the roof of a car moving with horizontal acceleration a View Solution
Question 103
A particle starts from a point $P$ at a distance of $A / 2$ from the mean position $O$ and travels towards left as shown in the figure. If the time period of SHM, executed about $O$ is $T$ and amplitude $A$ then the equation of the motion of particle is
View Solution
Question 104
A spring has natural length $40 c m$ and spring constant $500 N / m$ . A block of mass $1 k g$ is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length $45 c m$ .View Solution
Question 105
The displacement - time graph of a particle executing SHM is shown in figure. Which of the following statements is//are true ?
View Solution
Question 106
For a particle executing SHM, x = displacement from mean position, v = velocity and a = acceleration at any instant, then View Solution
Question 107
The acceleration of a particle is $a = - 100 x + 50$ . It is released from $x = 2$ . Here, $a$ and $x$ are in SI units View Solution
Question 108
Two particles are performing SHM in same phase. It means that View Solution
Question 109
A particle moves along y - axis according to the equation $y (in cm) = 3 sin 100 π t + 8 {sin}^{2} 50 π t - 6$ View Solution
Question 110
A $2 k g$ block hangs without vibrating at the bottom end of a spring with a force constant of $400 N / m$ . The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of $5 m / s^{2}$ when the acceleration suddenly ceases at time $t = 0$ and the car moves upward with constant speed $(g = 10 m / s^{2})$
What is the angular frequencyof the block after the acceleration ceases ?View Solution
Question 111
A $2 k g$ block hangs without vibrating at the bottom end of a spring with a force constant of $400 N / m$ . The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of $5 m / s^{2}$ when the acceleration suddenly ceases at time $t = 0$ and the car moves upward with constant speed $(g = 10 m / s^{2}$
The amplitude of the oscillation is View Solution
Question 112
A $1 k g$ block is executing simple harmonic motion of amplitude $0.1 m$ on a smooth horizontal surface under the restoring force of a spring of spring constant $100 N / m$ . A block of mass $3 k g$ is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together. Find the frequency and the amplitude of the motion.View Solution
Question 113
Two particles are in SHM along same line. Time period of each is $T$ and amplitude is $A$ . After how much time will they collide if at time $t = 0$ . (a) first particle is at $x_{1} = + \frac{A}{2}$ and moving towards positive x - axis and second particle is at $x_{2} = - \frac{A}{\sqrt{2}}$ and moving towards negative x - axis, (b) rest information are same as mentioned in part (a) except that particle first is also moving towards negative x - axis.View Solution
Question 114
A particle that hangs from a spring oscillates with an angular frequency of $2 r a d / s$ . The spring particle system is suspended from the celling of an elevator car and hangs motionless (relative to the elevator car) as the car descends at a constant speed of $1.5 m / s$ . The car then stops suddenly. (a) With what amplitude does the particle oscillate ? (b) What is the equation of motion for the particle ? (Choose upward as the position direction)View Solution
Question 115
A $2 k g$ mass is attached to a spring of force constant $600 N / m$ and rests on a smooth horizontal surface. A second mass of $1 k g$ slides along the surface toward the first at $6 m / s$ .
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position $x$ as a function of time $t$ for the mass attached to the spring, assuming that the collision occurs at time $t = 0$ . What is the impulse given to the 2kg mass in each case ?View Solution
Question 116
A block of mass $4 k g$ hangs from a spring of force constant $k = 400 N / m$ . The block is pulled down $15 c m$ below equilibrium and relesed. How long does it take block to go from $12 c m$ below equilibrium (on the way up) to $9 c m$ above equilibrium ?View Solution
Question 117
A plank with a body of mass $m$ placed on it starts moving straight up according to the law $y = a (1 - cos ω t)$ , where $y$ is the displacement from the initial position, $ω = 11 r a d / s$ . Find
(a) The time independence of the force that the body exerts on the plank.
(b) The minimum amplitude of oscillations of the plank at which the body starts falling behind the plank.View Solution
Question 118
A particle of mass $m$ free to move in the $x - y$ plane is subjected to a force whose components are $F_{x} = - k x$ and $F_{y} = - k y$ , where $k$ is a constant. The particle is released when $t = 0$ at the point $(2, 3)$ . Prove that the subsequent motion is simple harmonic along the straight line $2 y - 3 x = 0$ .View Solution
Question 119
Determine the natural frequency of vibration of the $100 N$ disk. Assume the disk does not slip on the inclined surface.
View Solution
Question 120
The disk has a weight of $100 N$ and rolls without slipping on the horizontal surface as it oscillates about its equilibrium position. If the disk is displaced, by rolling it counterclockwise $0.4 r a d$ , determine the equation which describes its oscillatory motion when it is released.
View Solution
Question 121
A solid uniform cylinder of mass $m$ performs small oscillations due to the action of two springs of stiffness $k$ each (figure). Find the period of these oscillation in the absence of sliding.
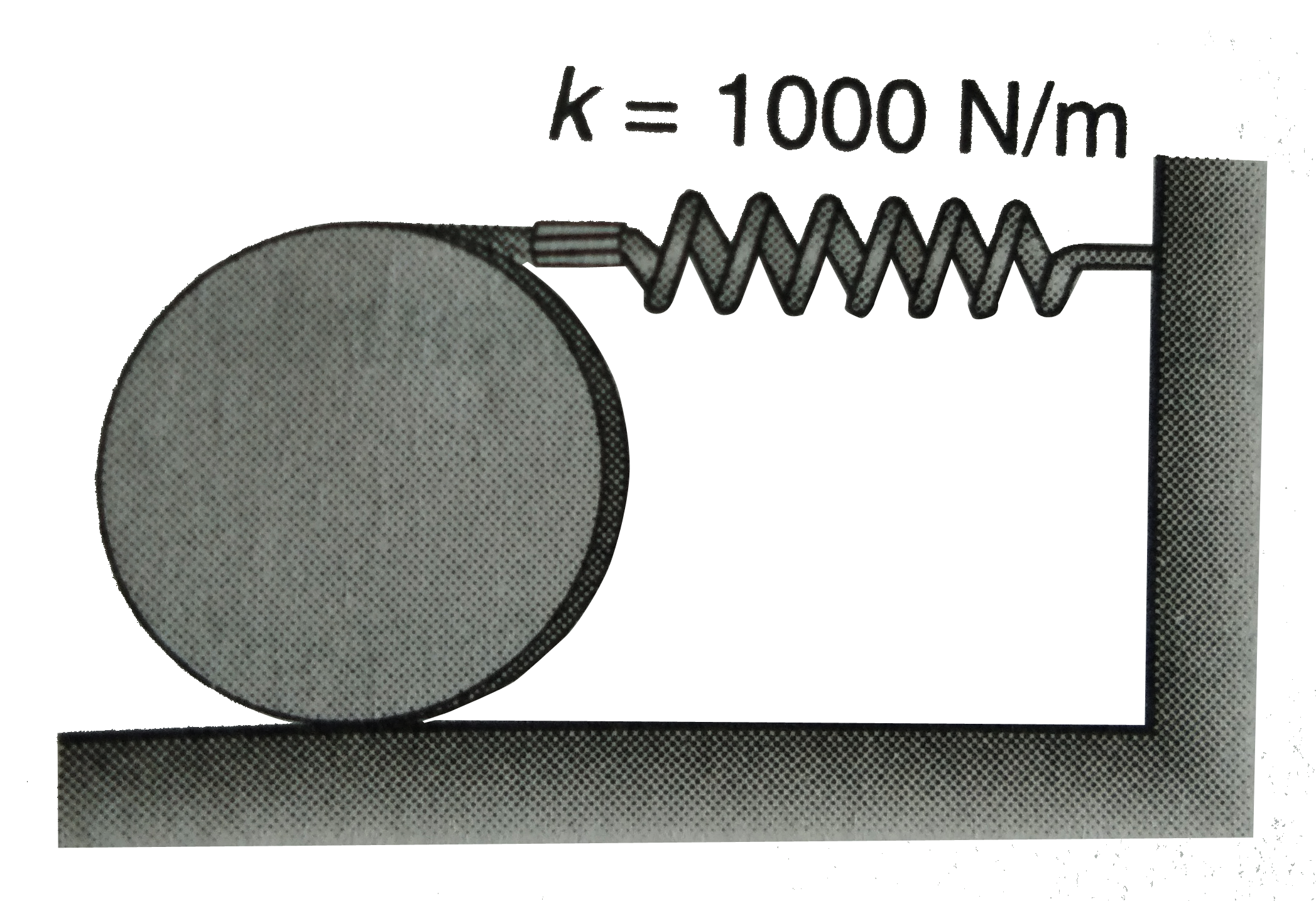$x$ View Solution
Question 122
A block of mass $m$ is attached to one end of a light inextensible string passing over a smooth light pulley $B$ and under another smooth light pulley $A$ as shown in the figure. The other end of the string is fixed to a ceiling. $A$ and $B$ are held by spring of spring constants $k_{1}$ and $k_{2}$ . Find angular frequency of small oscillations of small oscillations of the system.
View Solution
Question 123
In the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between $m_{2}$ and $m_{1}$ is $μ$ . There is no friction between $m_{1}$ and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock $m_{2}$ is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?View Solution
Question 124
Two block $A$ and $B$ of masses $m_{1} = 3 k g$ and $m_{2} = 6 k g$ respectively are connected with each other by a spring of force constant $k = 200 N / m$ as shown in figure. Blocks are pulled away from each other by $x_{0} = 3 c m$ and then released. When spring is in its natural length and block are moving towards each other, another block $C$ of mass $m = 3 k g$ moving with velocity $v_{0} = 0.4 m / s$ (towards right) collides with $A$ and gets stuck to it. Neglecting friction, calculate

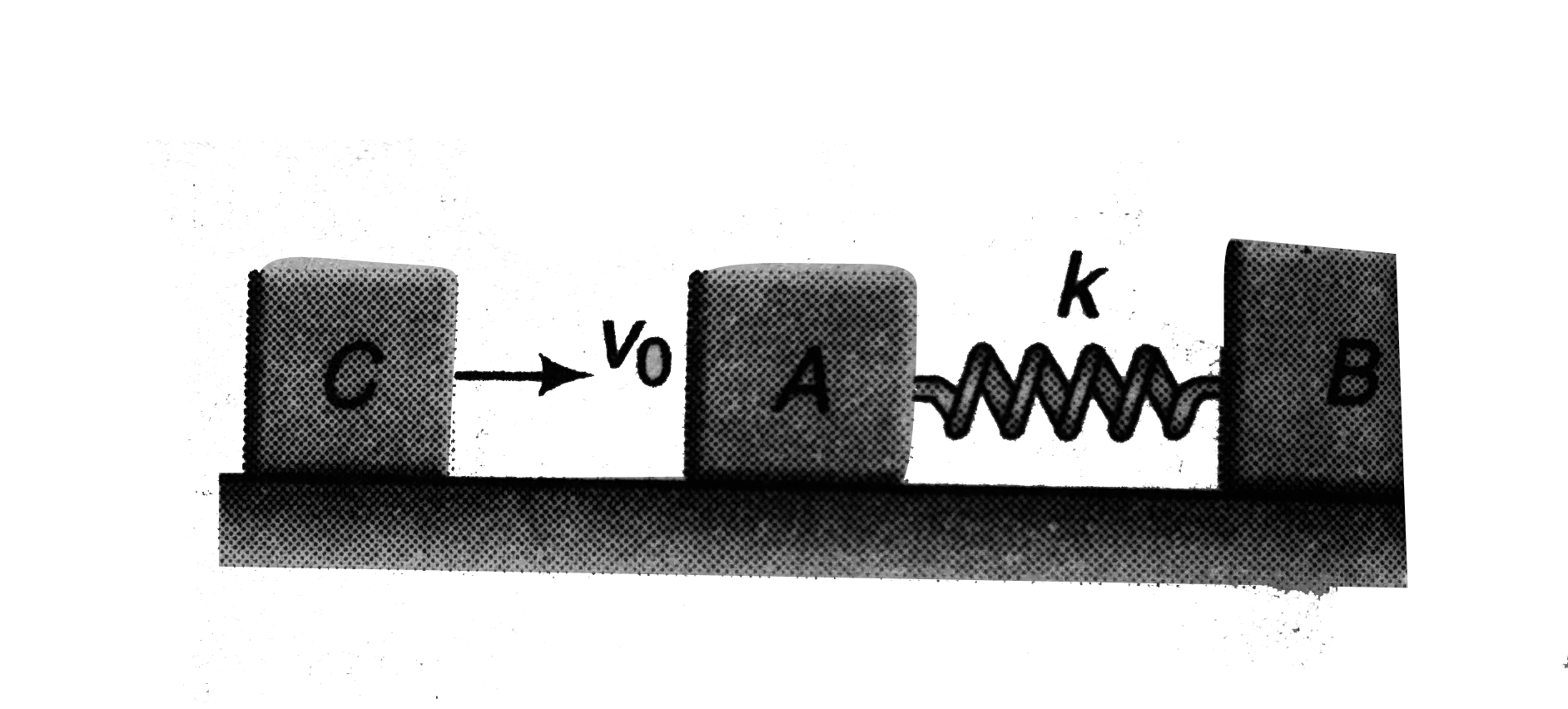
(a) velocity $v_{1}$ and $v_{2}$ of the blocks $A$ and $B$ respectively just before collision and their angular frequency .
(b) velocity of centre of mass of the system, after collision,
( c) amplitude of oscillation of combined body,
(d) loss of energy during collision.View Solution
Question 125
A rod of length $l$ and mass $m$ , pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant $k$ . Find the frequency of small oscillations about the equilibrium position.
View Solution
Question 126
In the arrangement shown in figure, pulleys are light and spring are ideal. $K_{1}$ , $k_{2}$ , $k_{3}$ and $k_{4}$ are force constant of the spring. Calculate period of small vertical oscillations of block of mass $m$ .
View Solution
Question 127
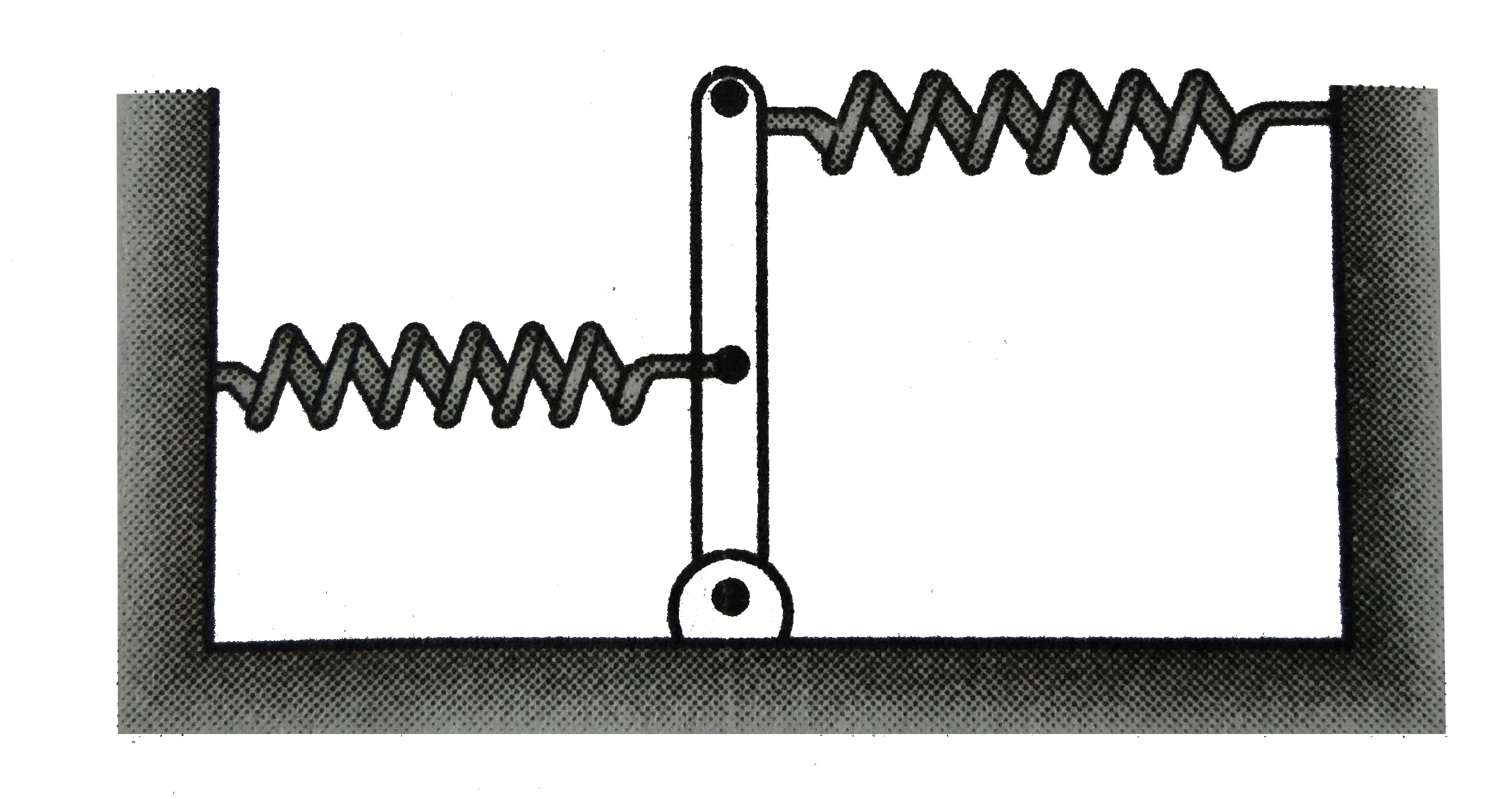
A light pulley is suspended at the lower end of a spring of constant $k_{1}$ , as shown in figure. An inextensible string passes over the pulley. At one end of string a mass $m$ is suspended, the other end of the string is attached to another spring of constant $k_{2}$ . The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass $m$ about equilibrium position.
View Solution
Question 128
Figure shows a solid uniform cylinder of radius $R$ and mass $M$ , which is free to rotate about a fixed horizontal axis $O$ and passes through centre of the cylinder. One end of an ideal spring of force constant $k$ is fixed and the other end is higed to the cylinder at $A$ . Distance $O A$ is equal to $\frac{R}{2}$ . An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass $M$ and having cross sectional area $A$ is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density $ρ$ .
If in equilibrium, spring is horizontal and line $O A$ is vertical, calculate frequency of small oscillations of the system.
View Solution
Question 129
Find the natural frequency of the system shown in figure. The pulleys are smooth and massless.
View Solution
Question 130
$a - x$ equation of a particle in SHM is $a + 4 x = 0$
Here, $a$ is in $c m / s^{2}$ and $x$ in cm.Find time period in second.View Solution
Question 131
At $x = \frac{A}{4}$ , what fraction of the mechanical energy is potential ? What fraction is kinetic ? Assume potential energy to be zero at mean position.View Solution
Question 132
A cart of mass $2.00 k g$ is attached to the end of a horizontal spring with force constant $k = 150 N / m$ . The cart is displaced $15.0 c m$ from its equilibrium position and released. What are
(a) the amplitude (b) the period ( c) the mechanical energy (e) the maximum velocity of the cart ? Neglect friction.View Solution
Question 133
A $0.5 k g$ body performs simple harmonic motion with a frequency of $2 H z$ and an amplitude of $8 m m$ . Find the maximum velocity of the body, its maximum acceleration and the maximum restoring force to which the body is subjected.View Solution
Question 134
Can we use the equation $v = u +$ at in SHM or not ?View Solution
Question 135
A $2.0 k g$ particle undergoes SHM according to $x = 1.5 cos (\frac{π t}{4} + \frac{π}{6})$ (in SI .units)
(a) What is the total mechanical energy of the particle ?
(b) What is the shortest time required for the particle to move from $x = 0.5 m$ to $x = - 0.75 m$ ?View Solution
Question 136
Given that the equation of motion of a mass is $x = 0.20 sin (3.0 t) m$ . Find the velocity and acceleration of the mass when the object is $5 c m$ from its equilibrium position. Repeat for $x = 0$ .View Solution
Question 137
A particle executes simple harmonic motion of amplitude $A$ along the x - axis. At $t = 0$ , the position of the particle is $x = \frac{A}{2}$ and it moves along the positive x - direction. Find the phase constant $δ$ , if of the equation is written as $x = A sin (ω t + δ)$ .View Solution
Question 138
An object of mass $0.8 k g$ is attached to one end of a spring and the system is set into simple harmonic motion. The displacement $x$ of the object as a fuction of time is shown in the figure. With the aid of the data, determine
(a) the amplitude $A$ of the motion,
(b) the angular frequency $ω$ ,
( c) the spring constant $K$ ,
(d) the speed of the object at $t = 1.0 s$ and
(e) the magnitude of the object's acceleration at $t = 1.0 s$ .
View Solution
Question 139
The equation of motion of a particle started at t=0 is given by $x = 5 sin (20 t + \frac{π}{3})$ , where x is in centimetre and t in second. When does the particle
a. first come rest
b. first have zero acceleration
c. first have maximum speed?View Solution
Question 140
Describe the motion corresponding to $x - t$ equation, $x = 10 - 4 cos ω t$ .View Solution
Question 141
$a - x$ equation of a body in SHM is $a + 16 x = 0$ . Here, $x$ is in $c m$ and a in $c m / s^{2}$ . Find time period of oscillations. View Solution
Question 142
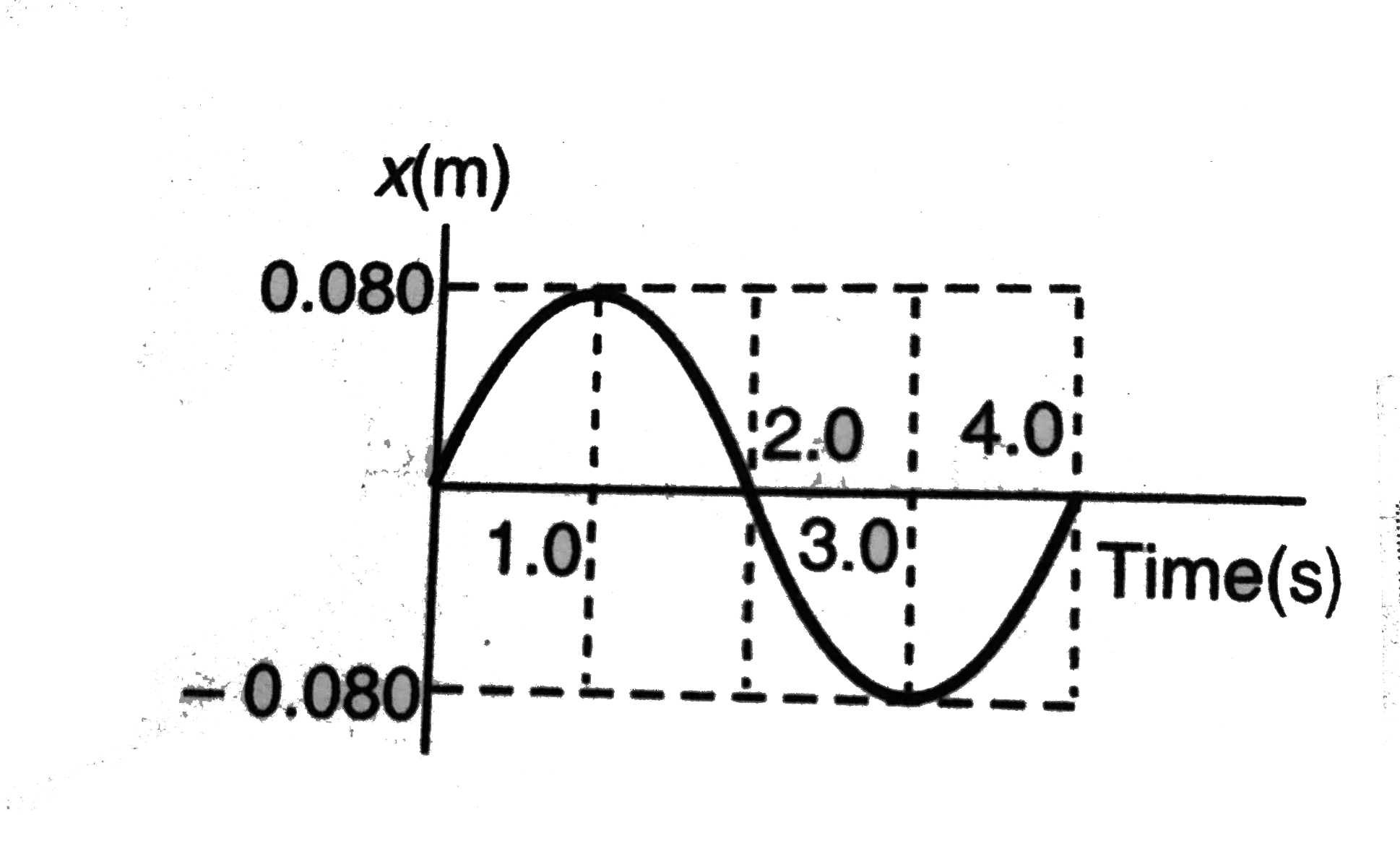$A$ mass $M$ , attached to a spring, oscillates with a period of $2 s$ . If the mass is increased by $4 k g$ , the time period increases by one second. Assuming that Hooke's law is obeyed, find the initial mass $M$ .View Solution
Question 143
Three masses of $500 g$ , $300 g$ and $100 g$ are suspended at the end of a spring as shown and are in equilibrium. When the $500 g$ mass is removed suddenly, the system oscillates with a period of $2 s$ . When the $300 g$ mass is also removed, it will oscillate with period $T$ . Find the value of $T$ .
View Solution
Question 144
A particle executes simple harmonic motion. Its instantaneous acceleration is given by $a = - p x$ , where $p$ is a positive constant and $x$ is the displacement from the mean position. Find angular frequency of oscillation.View Solution
Question 145
$A$ mass $M$ is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period $T$ . If the mass is increased by $m$ , the time period becomes $\frac{5 T}{3}$ . Find the ratio of $m / M$ .View Solution
Question 146
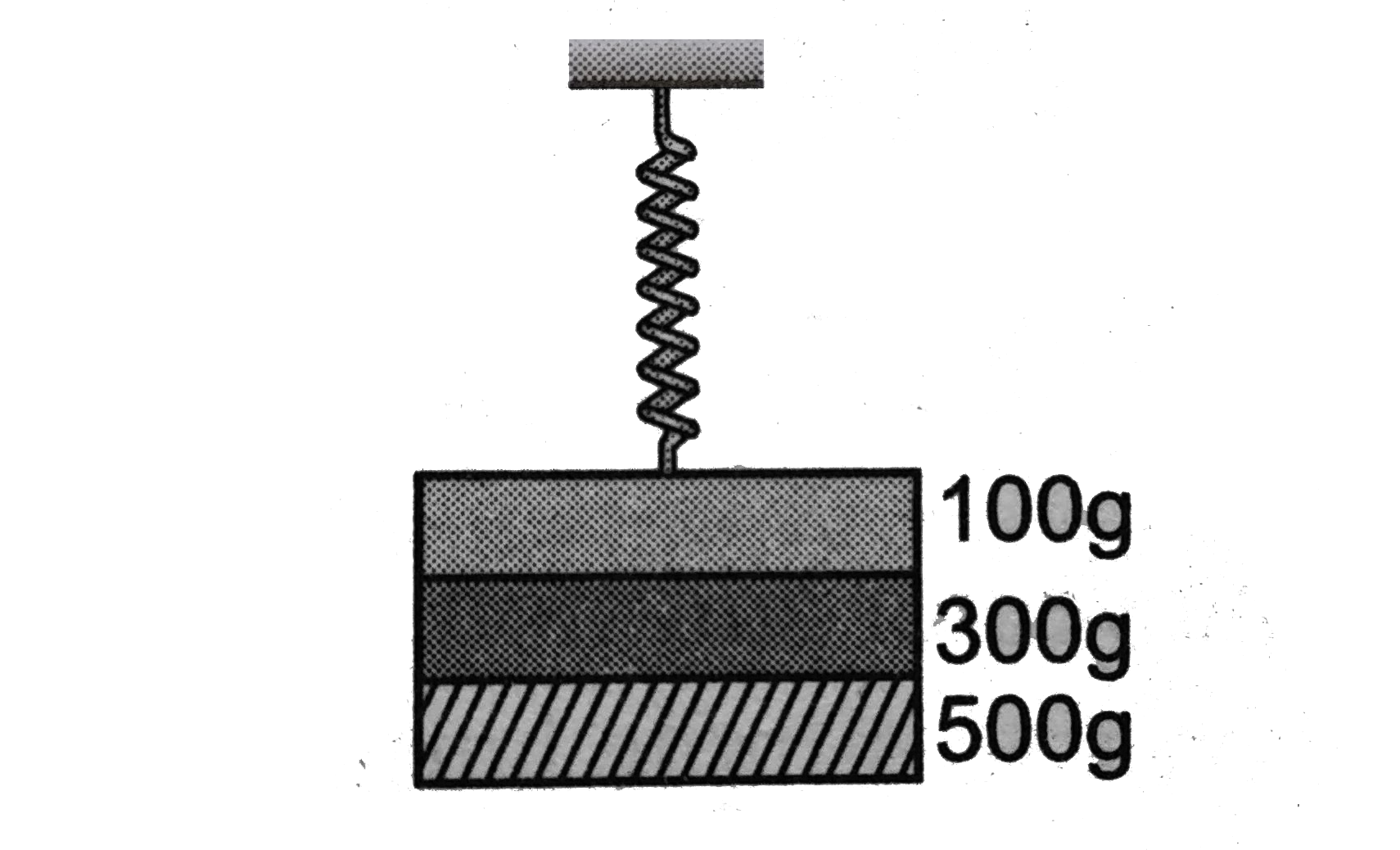The length of a simple pendulum is decreased by $21 %$ . Find the percentage change in its time period.View Solution
Question 147
A particle executes SHM on a straight line path. The amplitude of oscillation is $2 c m$ . When the displacement of the particle from the mean position is $1 c m$ , the numerical value of magnitude of acceleration is equal to the mumerical value of velocity. Find the frequency of SHM (in $H z$ ).View Solution
Question 148
A particle is subjected to two simple harmonic motions of the same frequency and direction. The amplitude of the first motion is $4.0 c m$ and that of the second is $3.0 c m$ . Find the resultant amplitude if the phase difference between the two motion is
(a) $0^{\circ}$
(b) $60^{\circ}$
( c) $90^{\circ}$
(d) $180^{\circ}$ View Solution
Question 149
A particle is subjected to two simple harmonic motions.
$x_{1} = 4.0 sin (100 π t)$ and $x_{2} = 3.0 sin (100 π t + \frac{π}{3})$
Find
(a) the displacement at $t = 0$
(b) the maximum speed of the particle and
(c ) the maximum acceleration of the particle.View Solution
Question 150
Three simple harmonic motion of equal amplitudes $A$ and equal time periods in the same direction combine. The phase of the second motion is $60^{\circ}$ ahead of the first and the phase of the third motion is $60^{\circ}$ ahead of the second. Find the amplitude of the resultant motion.View Solution
Question 151
A particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.View Solution

Home
Ask Doubt
Profile

Level 1 Assertion And Reason from DC PANDEY ENGLISH SIMPLE HARMONIC MOTION for Class 11

All Exercises from DC PANDEY ENGLISH Class 11 PHYSICS SIMPLE HARMONIC MOTION